尖子生辅导：向量与圆 最新 可下载 可修改 优质文档

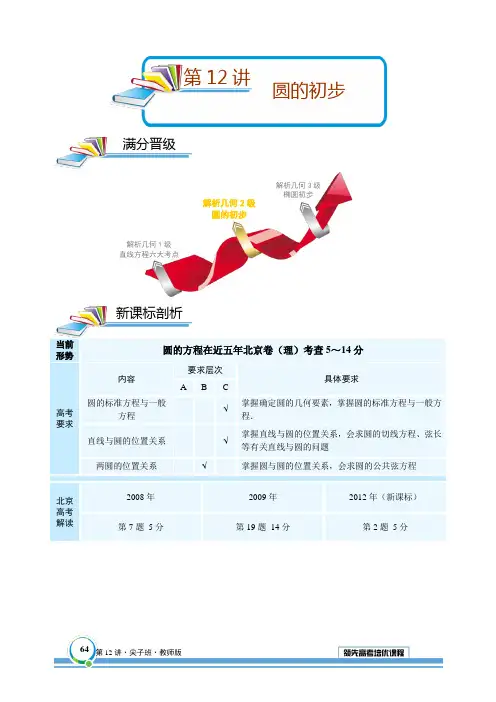
当前形势圆的方程在近五年北京卷（理）考查5～14分高考要求内容要求层次具体要求A B C圆的标准方程与一般方程√掌握确定圆的几何要素，掌握圆的标准方程与一般方程．直线与圆的位置关系√掌握直线与圆的位置关系，会求圆的切线方程、弦长等有关直线与圆的问题两圆的位置关系√掌握圆与圆的位置关系，会求圆的公共弦方程北京高考解读2008年2009年2012年（新课标）第7题5分第19题14分第2题5分新课标剖析满分晋级第12讲解析几何1级直线方程六大考点解析几何2级圆的初步解析几何3级椭圆初步圆的初步【教师备案】因为直线方程建议讲了4小时，所以本讲建议讲2小时考点1：圆的标准方程1. 圆的标准方程 ⑴以点()C a b ，为圆心，r 为半径的圆的方程：222()()x a y b r -+-= ⑵圆心在原点的圆的标准方程：222x y r +=【教师备案】⑴我们知道，平面内到一定点的距离等于定长的点的轨迹是圆，定点是圆心，定长是圆的半径．现在我们来求以()C a b ，为圆心，r 为半径的圆的方程．设()M x y ，是C e 上的任意一点．点M 在C e 上的条件是CM r =．也就是说，如果点M 在C e 上，则CM r =，反之，如果CM r =，则点M 在C e 上．由两点间的距离公式，所说条件可转化为方程表示：()()22x a y b r -+-=．两边平方，得()()222x a y b r -+-=①．显然，C e 上任意一点M 的坐标()x y ，适合方程①；如果平面上一点M 的坐标()x y ，适合方程①，可得CM r =，则点M 在C e 上．因此方程①是以点()C a b ，为圆心，r 为半径的圆的方程，叫做圆的标准知识切片知识点睛12.1圆的方程M COyxP (x, y )r Oy x方程．特别地，如果圆心在坐标原点，这时00a b ==，，圆的标准方程就是222x y r +=． ⑵圆的标准方程()()222x a y b r -+-=⇔圆心()a b ，，半径为r ，它体现了圆的几何性质，圆的标准方程直接给出了圆的圆心坐标和半径长，突出了确定一个圆的基本要素，因此， 有利于画出图形．⑶圆的标准方程中共有三个待定系数a b r ，，，只要确定出这三个量的值，圆的方程即被 确定．因此确定圆的方程需要三个独立的条件，其中圆心是圆的定位条件，半径是圆的 定形条件．⑷方程()()22x a y b t -+-=：①当0t >时，表示圆心为()C a b ，t ②当0t =时，表示一个点()C a b ，； ③当0t <时，不表示任何图形．2. 点与圆的位置关系圆的标准方程()()222x a y b r -+-=，圆心()A a b ，，半径r ， 若点()00M x y ，在圆上，则()()22200x a y b r -+-=； 若点()00M x y ，在圆外，则()()22200x a y b r -+->；若点()00M x y ，在圆内，则()()22200x a y b r -+-<；反之，也成立．【教师备案】判断点与圆的位置的方法是由两点间的距离公式，求出该点到圆心的距离，再与圆的半径比较大小即可．例：写出圆心为()23A -，，半径长等于5的圆的标准方程，并判断点()157M -，，()251M --是否在这个圆上，若不在这个圆上，是在圆内还是在圆外？【解析】 圆心为()23A -，，半径长等于5的圆的标准方程是()()222325x y -++=．把()157M -，的坐标代入上述方程中，有()()22527325-+-+=，即点1M 的坐标适合圆的方程，可知点1M 在这个圆上；把()251M -的坐标代入上述方程中，有()()225213134525--+-+=+，可知点2M 不在这个圆上，而在这个圆内．3. 确定圆的方法要求出圆的标准方程必须求出圆心和半径．确定圆的标准方程的主要方法是待定系数法，即列出a b r ，，的方程组，一般步骤为： ⑴根据题意，设所求的圆的标准方程()()222x a y b r -+-=；⑵根据已知条件，建立关于a b r ，，的方程组； ⑶解方程组，求出a b r ，，的值，并把它们代入所设的圆的方程中，就得到所求圆的方程． 条件 方程形式过原点 ()()()2222220x a y b a b a b -+-=++≠ 圆心在x 轴上 ()()2220x a y r r -+=≠圆心在y 轴上 ()()22220x y b r r +-=≠圆心在x 轴上且过原点()()2220x a y a a -+=≠圆心在y 轴上且过原点()()2220x y b b b +-=≠与x 轴相切 ()()()2220x a y b b b -+-=≠与y 轴相切 ()()()2220x a y b a a -+-=≠与两坐标轴都相切()()()2220x a y b a a b -+-==≠【例1】 圆的标准方程写出下列各圆的方程⑴经过点()63，，圆心为()22-，；⑵经过点()45A --，，()61B -，，且以线段AB 为直径．【解析】 ⑴所求圆的方程为()()222241x y -++=⑵所求圆的方程为()()221329x y -++=【备选】求以两直线1:5l x y -=，2:24l x y +=的交点为圆心，且与x 轴相切的圆的标准方程．【解析】 所求圆的标准方程为()()22324x y -++=．考点2：圆的一般方程1． 圆的一般方程220x y Dx Ey F ++++=，（2240D E F +->）说明：⑴2x 和2y 项的系数相等且都不为零；⑵没有xy 这样的二次项．⑶表示以,22D E ⎛⎫-- ⎪⎭为圆心，22142D E F +-为半径的圆．例：二元二次方程22232340x y x y +-++=是否表示圆．【解析】 ∵2x 和2y 的系数不相等，∴方程不表示圆．【教师备案】将圆的标准方程()()222x a y b r -+-=展开，得22222220x y ax by a b r +--++-=，由此可见，圆的方程具有如下形式：()220x y Dx Ey F ++++=*，其中D E F ，，为常数．那么，形如()*的方程是否都表示圆呢？将方程220x y Dx Ey F ++++=配方，得()222214224D E x y D E F ⎛⎫⎛⎫+++=+- ⎪ ⎪⎝⎭⎝⎭，与圆的标准方程比较，可知：经典精讲知识点睛①当2240D E F +->时，方程()*表示以22DE ⎛⎫-- ⎪⎝⎭，为圆心，22142D EF +-为半径的圆；②当2240D E F +-=时，方程()*只有一个解，表示一个点22DE ⎛⎫-- ⎪⎝⎭，；③当2240D E F +-<时，方程()*无实数解，它不表示任何图形．例：若220x y x y m +-+-=表示一个圆的方程，则m 的取值范围是（ ）A ．12m >-B ．12m -≥ C ．12m <- D ．2m >-【解析】 A2． 如何选用圆的方程圆的方程有标准方程和一般方程，求哪一种都需要三个独立条件，都要用到待定系数法，但要灵活选用圆的方程的形式，以便简化计算．一般来说．⑴如果由已知条件容易求得圆心坐标、半径或需利用圆心的坐标或半径来列方程的问题一般采用圆的标准方程，再用待定系数法求出a b r ，，；⑵如果已知条件和圆心或半径都无直接关系，一般采用圆的一般方程，再利用待定系数法求出常数D E F ，，．例：⑴求经过两点()14A -，、()32B ，且圆心在y 轴上的圆的方程；⑵求过三点(11)A -，，(14)B ，，(42)C -，的圆的方程，并求这个圆的半径和圆心坐标． 【解析】 ⑴ 圆的方程是()22110x y +-=．⑵所求圆的方程为227320x y x y +--+=． 半径522r =，圆心7322⎛⎫⎪⎝⎭，【教师备案】老师可以配合知识点睛中的例子先讲圆的一般方程以及一般方程表示圆的条件，然后让学生做例2以及相应班次的学案；最后再根据知识点睛中的例子讲如何选用圆的方程，然后再做例3和相应班次的学案．【例2】 方程220x y Dx Ey F ++++=表示圆的条件判断下列方程是否表示圆，若是，求出圆心和半径⑴ 22104x y x +-+=；⑵ ()22200x y ax a ++=≠；⑶ 22210x y ay ++-=；【追问】若表示圆，则当圆的面积最小时，a 的值为多少？ ⑷ 22220160x y x +++=．经典精讲⑸ 224250x y mx y m ++-+=【解析】 解法一：⑴22102x y ⎛⎫-+= ⎪⎝⎭表示一个点，坐标为102⎛⎫⎪⎝⎭，；⑵()()2220x a y a a ++=≠表示圆，圆心()0a -，，半径r a =； ⑶()2221x y a a ++=+表示圆，圆心()0a -，，半径21r a =+； 【追问】当0a =时，圆的面积取最小值． ⑷()22221010160x y ++=-<，不表示任何图形． ⑸1m >或14m <时表示圆，圆心为()21m -，，半径为2451m m -+． 当114m ≤≤时，方程不表示圆．【备选】若直线530x y -+=经过圆2222104m x y mx y +-++-=的圆心，则m 等于（ ）A ．16-B ．16C ．0或16D ．0或16-【解析】 A【例3】求圆的一般方程⑴已知ABC △三边所在直线方程:60AB x -=，:280BC x y --=，:20CA x y +=，求此三 角形外接圆的方程．⑵求过原点及()11A ，且在x 轴上截得的线段长为3的圆的方程． 【解析】 ⑴222143002x y x y +-++=． ⑵所求圆的方程为22350x y x y ++-=或2230x y x y +-+=．考点3：直线与圆的位置关系1．直线与圆的位置关系：①直线与圆相交，有两个公共点； ②直线与圆相切，有一个公共点；知识点睛12.2直线（圆）与圆的位置关系③直线与圆相离，没有公共点．2．直线与圆的位置关系的判定有两种方法：①代数法：判断直线0Ax By C ++=和圆220x y Dx Ey F ++++=的位置关系，可将2200Ax By C x y Dx Ey F ++=⎧⎨++++=⎩消去y （或x ），得20mx nx p ++=（或20my ny p ++=）． 当0∆>时，直线与圆相交，有两个公共点； 当0∆=时，直线与圆相切，有一个公共点； 当0∆<时，直线与圆相离，无公共点．②几何法：已知直线0Ax By C ++=和圆()()222x a y b r -+-=，可用圆心到直线的距离22Aa Bb Cd A B++=+与r 的大小关系判断直线与圆的位置关系．当d r <时，直线与圆相交，有两个公共点； 当d r =时，直线与圆相切，有一个公共点； 当d r >时，直线与圆相离，无公共点；<教师备案>一般的，判定直线与圆的位置关系都用几何法，代数法在圆锥曲线才会常用。

高考真题向量11L10已知a 与b 均为单位向量，其夹角为&,有下列四个命题11W13已知a 与b 为两个不共线的单位向量,k 为实数,若向量a+b 与向量ka-b 垂直,则 k= o1W2L13已知向量方3夹角为45°,且帀|=1, |2方一引=怖，贝ij|6|= _________________ 13WL13已知正方形ABCD 的边长为2, E 为CD 的中点，则応BD = ______________ 13WL13已知两个单位向最a , 〃的夹角为60°, c =ta^(l-t)b ,若b ・c = 0 ,贝胖= _________—,1 —.—.一 一.14L15.已知A,B,C 是圆0上的三点，若AO = -(AB + AC)f 则的夹角为 _______________________ 14WL3.设向量 £丿满足la^AhVlO, \a-b\ = 46 f 则 a- A =()A.1B. 2C. 3D. 514W6设D,E,F 分别为\ABC 的三边BC, CA, AB 的中点，则EB + FC =⑸〃设D 为AABC 所在平血内一点BC = 3CD,则()(A) AD = --AB^-AC3315L13.设向量A , b 不平行，向量Aa+b 与a + 2方平行，则实数人= 15W2已知点A (0, 1), B (3,2),向量疋二(-4, -3),则向最荒二(A) (-7, -4)(B) (7,4)(C) (-1,4)(D) (1, 4)15W4.向量a = (1,-1), * = (-1,2),贝IJ(2a+*)•« =A. —1B ・ 0C ・ 1D. 3P }:\a + b\>\<=^ % 0，¥P 2:0 + b|>1 oP 3 :”一> 1 <=> 其中的真命题是片：|o-b|>lu>&G —,龙(A)片£(B)P l9P 3(C) P 2,P 3A.7D B.丄乔2c. I BC2D ・BC(C) ~AD = -~AB + -AC3 3(S ))7D =-'AB --AC33精选习题：1、试化简：（1）CD + BC + AB(2) AB + DF + CD + BC + FA .-CD )-(AC -BD)2、如图所示，己知正六边形ABCDEF,O是它的中心，若BC = b,5.在厶ABC111AB =c, AC =b,若点Z)满足BD =2 DC ,则AD 等于(6.已知/XABC的三个顶点/、B、C及平而内一点尸满足PA + PB + PC=0 满足AB + AC =A AP,贝抄的值为（A. 2D. 6向量基础7、已知丨Q丨=丨b丨=1, I a + b I =1, 则丨a-b I等于（）A. 1B. V3C.D.2试用万，了将向量亦，丽，BD丽表示出來。

向量圆的综合应用
向量和圆在数学中是两个不同的概念，但它们可以结合在一起解决一些综合问题。

以下是一些向量和圆结合的例子：
1. 向量与圆的切线：给定一个圆和圆上的一点，以及一个过该点的切线，我们可以使用向量来表示切线的方向。

通过向量的运算，我们可以找到切线的长度和方向，进而解决与切线相关的问题。

2. 向量与圆的旋转：如果我们有一个向量和一个圆，我们可以将向量旋转一定的角度，使其与圆的某条直径对齐。

这可以用于解决与旋转相关的问题，例如在物理或工程中模拟旋转运动。

3. 向量与圆的面积：向量的点积和叉积可以用于计算与圆相关的面积。

例如，如果我们有一个向量场和一个包围该场的圆，我们可以使用向量的叉积来计算该圆的面积。

4. 向量与圆的几何变换：通过向量的线性变换，我们可以将一个圆变换到另一个位置或大小。

这可以用于图形处理、计算机图形学或机器人学等领域。

以上只是一些例子，实际上向量和圆的综合应用非常广泛，需要结合具体的问题进行分析和解决。

第1课时 空间中点、直线和平面的向量表示及空间中直线、平面的平行学习任务1．理解直线的方向向量与平面的法向量，会求一个平面的法向量．(重点)2．能用向量语言表述直线与直线、直线与平面、平面与平面的平行关系．3．娴熟驾驭用方向向量、法向量证明线线、线面、面面间的平行关系．(重点、难点) 核心素养1．通过空间中点、直线和平面的向量表示的学习，培育直观想象和逻辑推理素养．2．通过直线的方向向量和平面的法向量的学习，提升数学运算的核心素养．3．借助利用空间向量解决平行问题的学习，提升数学运算及逻辑推理素养．空间中点的位置向量如图，在空间中，我们取确定点O 作为基点，那么空间中随意一点P 就可以用向量OP →来表示．我们把向量OP →称为点P 的位置向量．做一做：在空间直角坐标系Oxyz 中，点A (1,2,3)的位置向量是 OA →＝(1,2,3) .[解析] 位置向量OA →＝(1,2,3). 空间中直线的向量表示式直线l 的方向向量为a ，且过点A .如图，取定空间中的随意一点O ，可以得到点P 在直线l 上的充要条件是存在实数t ，使OP →＝OA →＋t a ，①把AB →＝a 代入①式得OP →＝OA →＋t AB → ，②①式和②式都称为空间直线的向量表示式．思索1：依据空间直线的向量表达式OP →＝OA →＋tAB →，线段AB 的中点M 的向量表达式是什么？提示：OM →＝OA →＋12AB →＝12(OA →＋OB →)． 做一做：推断正误(正确的打“√”，错误的打“×”)(1)零向量不能作为直线的方向向量．( √ )(2)若向量v 是直线l 的方向向量，则λv (λ≠0)也是直线l 的方向向量．( √ )(3)直线l 的方向向量都平行，且方向相同．( × )空间中平面的向量表示式1.平面ABC 的向量表示式空间一点P 位于平面ABC 内的充要条件是存在实数x ，y ，使OP →＝OA →＋ xAB →＋yAC → .③我们把③式称为空间平面ABC 的向量表示式．2．平面的法向量如图，若直线l ⊥α，取直线l 的 方向向量a ，我们称a 为平面α的法向量；过点A 且以a 为法向量的平面完全确定，可以表示为集合{P |a ·AP →＝0}．思索2：假如n 为平面α的一个法向量，A ，B 为平面α内的两点，则n 与AB →有什么关系？提示：n ⊥AB →，即n ·AB →＝0.做一做：推断正误(正确的打“√”，错误的打“×”)(1)平面α的全部法向量都平行，且同向．( × )(2)若n 是平面α的一个法向量，则λn (λ∈R )也是平面α的一个法向量．( × )(3)向量i ＝(1,0,0)是坐标平面Oyz 的一个法向量．( √ )提示：(1)法向量也可能方向相反．(2)当λ＝0时，λn ＝0，不能作为平面的法向量．(3)x 轴垂直于坐标平面Oyz .空间中直线、平面平行的向量表达式提示：证明或判定直线和平面的位置关系有两类思路(1)转化为线线关系，然后利用两个向量的关系进行判定；(2)利用直线的方向向量和平面的法向量进行判定．做一做：1.若平面β外的一条直线l的方向向量是u＝(－1,2，－3)，平面β的法向量为n＝(4，－1，－2)，则l与β的位置关系是_l∥β__.[解析]由u·n＝(－1)×4＋2×(－1)＋(－3)×(－2)＝0知，l∥β.2．若两个不同平面α，β的法向量分别为u＝(1,2，－1)，v＝(－4，－8,4)，则平面α，β的位置是_α∥β__.[解析]由v＝－4u知u∥v，所以α∥β.。

位置关系第二课时圆与圆的位置关系高效测评北师大版必修2编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2016-2017学年高中数学第二章解析几何初步2.2.3 直线与圆、圆与圆的位置关系第二课时圆与圆的位置关系高效测评北师大版必修2）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2016-2017学年高中数学第二章解析几何初步2.2.3 直线与圆、圆与圆的位置关系第二课时圆与圆的位置关系高效测评北师大版必修2的全部内容。

与圆的位置关系第二课时圆与圆的位置关系高效测评北师大版必修2 (本栏目内容，在学生用书中以独立形式分册装订！)一、选择题（每小题5分，共20分）1．圆O1：x2＋y2＋2x＋4y＋3＝0与圆O2:x2＋y2－4x－2y－3＝0的位置关系是( ）A．内切B．外切C．相交D．相离解析：圆O1：(x＋1)2＋(y＋2)2＝2，圆O2：（x－2)2＋（y－1)2＝8，∴｜O1O2|＝错误!＝3错误!＝r1＋r2。

答案：B2．圆x2＋y2＝1与圆(x－1)2＋y2＝1的公共弦所在的直线方程为( ）A．x＝1 B．x＝错误!C．y＝x D．x＝错误!解析: (x－1）2＋y2－1－（x2＋y2－1）＝0得x＝错误!。

答案：B3．圆x2＋y2＝m2(m＞0)与x2＋y2＋6x－8y－11＝0内切,则m的值为( ）A．1 B．1或11C．11 D．6解析：圆x2＋y2＋6x－8y－11＝0可化为（x＋3）2＋(y－4)2＝36，∵两圆内切,∴圆心距d＝错误!＝5＝｜6－m｜，解得m＝1或m＝11.答案：B4．半径长为6的圆与x轴相切，且与圆x2＋(y－3）2＝1内切,则此圆的方程为（) A．（x－4）2＋（y－6）2＝6 B．（x±4）2＋(y－6）2＝6C．(x－4）2＋（y－6)2＝36 D．（x±4）2＋(y－6）2＝36解析：设圆心坐标为（a，b），∵半径长为6的圆与x轴相切，且与圆x2＋(y－3）2＝1内切,结合图形可得b＝6，又两圆内切，则两圆圆心的距离为半径之差，错误!＝5解得a＝±4,故所求圆的方程为（x±4）2＋(y－6)2＝36。

一．选择题（共16小题）1．圆心在直线y=x上，经过原点，且在x轴上截得弦长为2的圆的方程为（）A．（x﹣1）2+（y﹣1）2=2 B．（x﹣1）2+（y+1）2=2C．（x﹣1）2+（y﹣1）2=2或（x+1）2+（y+1）2=2 D．（x﹣1）2+（y+1）2=2或（x+1）2+（y﹣1）2=22．由点P向圆x2+y2=2引两条切线PA，PB，A，B是切点，则•的最小值是（）A．6﹣4B．3﹣2C．2﹣3 D．4﹣63．已知直线l：kx+y﹣2=0（k∈R）是圆C：x2+y2﹣6x+2y+9=0的对称轴，过点A（0，k）作圆C的一条切线，切点为B，则线段AB的长为（）A．2 B．2C．3 D．24．若直线ax﹣by+2=0（a＞0，b＞0）被圆x2+y2+2x﹣4y+1=0截得的弦长为4，则的最小值为（）A．B．C．+D．+25．在平面直角坐标系中，O为坐标原点，直线l：x﹣ky+1=0与圆C：x2+y2=4相交于A，B两点，=+．若点M在圆C上，则实数k=（）A．﹣2 B．﹣1 C．0 D．16．直线分割成的两段圆弧长之比为（）A．1：1 B．1：2 C．1：3 D．1：47．若直线2ax+by﹣2=0（a，b∈R+）平分圆x2+y2﹣2x﹣4y﹣6=0，则+的最小值是（）A．1 B．5 C．4D．3+28．已知向量为非零向量，，则夹角为（）A．B．C．D．9．已知，则=（）A．9 B．3 C．1 D．210．已知向量=（sinA，）与向量=（3，sinA+cosA）共线，其中A是△ABC的内角，则角A的大小为（）A．B．C．D．11．下列各对向量中，共线的是（）A．=（2，3），=（3，﹣2） B．=（2，3），=（4，﹣6） C．=（，﹣1），=（1，）D．=（1，），=（，2）12．已知向量，且∥，若x，y均为正数，则的最小值是（）A．24 B．8 C．D．13．设、是两个非零向量，则“（+）2=||2+||2”是“⊥”的（）A．充分不必要条件B．必要不充分条件C．充要条件 D．既不充分又不必要条件14．设非零向量、、满足，则向量与向量的夹角为（）A．150°B．120°C．60°D．30°15．已知向量=（1，cosθ），=（sinθ，﹣2），且⊥，则sin2θ+6cos2θ的值为（）A．B．2 C．2D．﹣216．定义两个平面向量的一种运算⊗=||•||sin＜，＞，则关于平面向量上述运算的以下结论中，①⊗=⊗，②λ（⊗）=（λ）⊗，③若=λ，则⊗=0，④若=λ，且λ＞0，则（+）⊗=（⊗）+（⊗）．恒成立的有（）A．4个B．3个C．2个D．1个二．填空题（共11小题）17．已知过点P（2，2）的直线与圆（x﹣1）2+y2=5相切，且与直线ax﹣y+1=0垂直，则a=．18．过原点向圆x2+y2﹣2x﹣4y+4=0引切线，则切线方程为．19．若直线l：ax+by+1=0始终平分圆M：x2+y2+4x+2y+1=0的周长，则（a﹣2）2+（b﹣2）2的最小值为．20．经过直线2x﹣y+3=0与圆x2+y2+2x﹣4y+1=0的两个交点，且面积最小的圆的方程是．21．如图所示，在△ABC中，D为BC边上的一点，且BD=2DC，若=m+n（m，n∈R），则=22．（2015•山东）过点P（1，）作圆x2+y2=1的两条切线，切点分别为A，B，则=．23．（2015•安徽）△ABC是边长为2的等边三角形，已知向量满足=2，=2+，则下列结论中正确的是．（写出所有正确结论得序号）①为单位向量；②为单位向量；③；④∥；⑤（4+）⊥．24．（2014•江西）已知单位向量与的夹角为α，且cosα=，若向量=3﹣2，则||=．25．（2014•江苏）如图，在平行四边形ABCD中，已知AB=8，AD=5，=3，•=2，则•的值是．26．（2013•山东）已知向量与的夹角为120°，且，．若，且，则实数λ=．27．（2010•天津）如图，在△ABC中，AD⊥AB，，，则=．2016年05月28日****************的高中数学组卷参考答案与试题解析一．选择题（共16小题）1．（2016•平度市一模）圆心在直线y=x上，经过原点，且在x轴上截得弦长为2的圆的方程为（）A．（x﹣1）2+（y﹣1）2=2 B．（x﹣1）2+（y+1）2=2C．（x﹣1）2+（y﹣1）2=2或（x+1）2+（y+1）2=2 D．（x﹣1）2+（y+1）2=2或（x+1）2+（y﹣1）2=2【分析】根据题意画出圆的方程，使圆A满足题意中的条件，分两种情况考虑，当点A在第一象限时，根据垂径定理即可得到OC的长度，根据直线y=x上点的横纵坐标相等，得到圆心A的坐标，根据勾股定理求出OA的长度即为圆A的半径，根据求出的圆心坐标和半径写出圆的标准方程；当点A′在第三象限时，同理可得圆心坐标和半径，根据圆心坐标和半径写出圆的标准方程即可．【解答】解：画出圆A满足题中的条件，有两个位置，当圆心A在第一象限时，过A作AC⊥x轴，又|OB|=2，根据垂径定理得到点C为弦OB的中点，则|OC|=1，由点A在直线y=x上，得到圆心A的坐标为（1，1），且半径|OA|=，则圆A的标准方程为：（x﹣1）2+（y﹣1）2=2；当圆心A′在第三象限时，过A′作A′C′⊥x轴，又|OB′|=2，根据垂径定理得到点C′为弦OB′的中点，则|OC′|=1，由点A′在直线y=x上，得到圆心A′的坐标为（﹣1，﹣1），且半径|OA′|=，则圆A′的标准方程为：（x+1）2+（y+1）2=2，综上，满足题意的圆的方程为：（x﹣1）2+（y﹣1）2=2或（x+1）2+（y+1）2=2．故选C2．（2016•广安模拟）由点P向圆x2+y2=2引两条切线PA，PB，A，B是切点，则•的最小值是（）A．6﹣4B．3﹣2C．2﹣3 D．4﹣6【分析】设圆心为O，OP=x，则PA2=x2﹣2，sin∠APO=，可得cos∠APB=1﹣，利用向量的数量积公式，结合基本不等式，即可求出•的最小值．【解答】解：设圆心为O，OP=x，则PA2=x2﹣2，sin∠APO=，∴cos∠APB=1﹣，∴•=（x2﹣2）（1﹣）=（x2+）﹣6≥4﹣6，∴•的最小值是4﹣6，故选：D．3．（2016•抚顺一模）已知直线l：kx+y﹣2=0（k∈R）是圆C：x2+y2﹣6x+2y+9=0的对称轴，过点A（0，k）作圆C的一条切线，切点为B，则线段AB的长为（）A．2 B．2C．3 D．2【分析】利用配方法求出圆的标准方程可得圆心和半径，由直线l：kx+y﹣2=0经过圆C的圆心（3，﹣1），求得k 的值，可得点A的坐标，再利用直线和圆相切的性质求得AB的值．【解答】解：由圆C：x2+y2﹣6x+2y+9=0得，（x﹣3）2+（y+1）2=1，表示以C（3，﹣11）为圆心、半径等于1的圆．由题意可得，直线l：kx+y﹣2=0经过圆C的圆心（3，﹣1），故有3k﹣1﹣2=0，得k=1，则点A（0，1），即|AC|=．则线段AB=．故选：D．4．（2016•石嘴山校级一模）若直线ax﹣by+2=0（a＞0，b＞0）被圆x2+y2+2x﹣4y+1=0截得的弦长为4，则的最小值为（）A．B．C．+D．+2【分析】圆即（x+1）2+（y﹣2）2=4，表示以M（﹣1，2）为圆心，以2为半径的圆，由题意可得圆心在直线ax ﹣by+2=0上，得到a+2b=2，故=+++1，利用基本不等式求得式子的最小值．【解答】解：圆x2+y2+2x﹣4y+1=0 即（x+1）2+（y﹣2）2=4，表示以M（﹣1，2）为圆心，以2为半径的圆，由题意可得圆心在直线ax﹣by+2=0（a＞0，b＞0）上，故﹣1a﹣2b+2=0，即a+2b=2，∴=+=+++1≥+2=，当且仅当时，等号成立，故选C．5．（2016•丹东一模）在平面直角坐标系中，O为坐标原点，直线l：x﹣ky+1=0与圆C：x2+y2=4相交于A，B两点，=+．若点M在圆C上，则实数k=（）A．﹣2 B．﹣1 C．0 D．1【分析】设AB的中点为D，有=+=2，即圆心到直线的距离等于半径的一半，由点到直线的距离公式列方程解出实数k的值．【解答】解：设AB的中点为D，有=+=2，∴||=2||=R=2，∴||=1．由点到直线的距离公式得1=，解得k=0，故选：C．6．（2016•河西区一模）直线分割成的两段圆弧长之比为（）A．1：1 B．1：2 C．1：3 D．1：4【分析】求出圆的圆心，半径r和圆心（1，0）到直线x﹣﹣2=0的距离，由此能求出直线圆相交的弦所对的圆心角，从而能够求出直线分割成的两段圆弧长之比．【解答】解：∵圆（x﹣1）2+y2=1的圆心（1，0），半径r=1，∴圆心（1，0）到直线x﹣﹣2=0的距离：d==，设直线圆相交的弦所对的圆心角为α，则cos==，∴=，解得，∴直线分割成的两段圆弧长之比为：=1：2．故选：B．7．（2016•江西模拟）若直线2ax+by﹣2=0（a，b∈R+）平分圆x2+y2﹣2x﹣4y﹣6=0，则+的最小值是（）A．1 B．5 C．4D．3+2【分析】求出圆心，根据直线平分圆，得到直线过圆心，得到a，b的关系，利用基本不等式即可得到结论．【解答】解：圆的标准方程为（x﹣1）2+（y﹣2）2=11，即圆心为（1，2），∵直线2ax+by﹣2=0（a，b∈R+）平分圆x2+y2﹣2x﹣4y﹣6=0，∴直线过圆心，即2a+2b﹣2=0，∴a+b=1，则+=（+）（a+b）=2+1+，当且仅当，即a=时取等号，故+的最小值是3+，故选：D．8．（2016•嘉峪关校级模拟）已知向量为非零向量，，则夹角为（）A．B．C．D．【分析】由条件即可得到，这样即可得到，且，从而可以求出，这样便可得出，的夹角．【解答】解：；∴，；∴；∴；∴；∴=；∴夹角为．故选：B．9．（2016•平度市模拟）已知，则=（）A．9 B．3 C．1 D．2【分析】由条件求得==1，且=1，由此求得=的值．【解答】解：∵已知，∴==1，﹣4 +4=1+4﹣4=1，解得=1．∴====3，故选B．10．（2016•惠州模拟）已知向量=（sinA，）与向量=（3，sinA+cosA）共线，其中A是△ABC的内角，则角A的大小为（）A．B．C．D．【分析】由，可得sinA（sinA+cosA）﹣=0，化为=1，由于A∈（0，π），即可得出．【解答】解：∵，∴sinA（sinA+cosA）﹣=0，∴2sin2A+2sinAcosA=3，化为1﹣cos2A+sin2A=3，∴=1，∵A∈（0，π），∴∈．∴=，解得A=．故选：C．11．（2016•福建模拟）下列各对向量中，共线的是（）A．=（2，3），=（3，﹣2） B．=（2，3），=（4，﹣6） C．=（，﹣1），=（1，）D．=（1，），=（，2）【分析】利用向量共线的充要条件即可判断出．【解答】解：由向量共线的充要条件可知：非零向量与共线，当且仅当存在唯一实数λ，使得．而只有D满足：∵，，∴．故选：D．12．（2016•茂名二模）已知向量，且∥，若x，y均为正数，则的最小值是（）A．24 B．8 C．D．【分析】根据向量共线定理列出方程，得出2x+3y=3，再求的最小值即可．【解答】解：∵∥，∴﹣2x﹣3（y﹣1）=0，化简得2x+3y=3，∴=（+）×（2x+3y）=（6+++6）≥（12+2）=8，当且仅当2x=3y=时，等号成立；∴的最小值是8．故选：B．13．（2016•银川校级一模）设、是两个非零向量，则“（+）2=||2+||2”是“⊥”的（）A．充分不必要条件B．必要不充分条件C．充要条件 D．既不充分又不必要条件【分析】设a、b是两个非零向量，“（a+b）2=|a|2+|b|2”⇒a•b=0，即a⊥b；a⊥b⇒a•b=0即（a+b）2=|a|2+|b|2⇒结论．【解答】解：设a、b是两个非零向量，“（a+b）2=|a|2+|b|2”⇒（a+b）2=|a|2+|b|2+2ab=|a|2+|b|2⇒a•b=0，即a⊥b；a⊥b⇒a•b=0即（a+b）2=|a|2+|b|2所以“（a+b）2=|a|2+|b|2”是“a⊥b”的充要条件．故选C．14．（2016•江西模拟）设非零向量、、满足，则向量与向量的夹角为（）A．150°B．120°C．60°D．30°【分析】由+=可得﹣=，两边平方，结合向量的数量积的性质和定义，即可得到所求夹角．【解答】解：设||=||=||=t，由+=可得﹣=，平方可得，（﹣）2=2，即有||2+||2﹣2•=||2，即为2•=||2=t2，即有2t2cos＜，＞=t2，即为cos＜，＞=，则向量与向量的夹角为60°．故选：C．15．（2016•河南模拟）已知向量=（1，cosθ），=（sinθ，﹣2），且⊥，则sin2θ+6cos2θ的值为（）A．B．2 C．2D．﹣2【分析】由题意可得tanθ=2，而sin2θ+6cos2θ=，分子分母同除以cos2θ，代入tanθ=2可得答案．【解答】解：由题意可得向量=（1，cosθ），=（sinθ，﹣2），且⊥，即tanθ=2，所以sin2θ+6cos2θ====2．故选：B．16．（2016•茂名一模）定义两个平面向量的一种运算⊗=||•||sin＜，＞，则关于平面向量上述运算的以下结论中，①⊗=⊗，②λ（⊗）=（λ）⊗，③若=λ，则⊗=0，④若=λ，且λ＞0，则（+）⊗=（⊗）+（⊗）．恒成立的有（）A．4个B．3个C．2个D．1个【分析】①由新定义可得⊗=|=⊗，即可判断出；②由新定义可得=λ，而=，当λ＜0时，λ（⊗）=（λ）⊗，不成立；③若=λ，可得，故⊗=0，即可判断出；④若=λ，且λ＞0，则，由新定义可得⊗=，而==．即可判断出．【解答】解：①∵⊗=|=⊗，故，故恒成立；②∵=λ，而=，当λ＜0时，λ（⊗）=（λ）⊗，不成立；③若=λ，则，得到⊗=0，故恒成立；④若=λ，且λ＞0，则+=（1+λ），∴+⊗=，而+=+=|1+λ|．故（+）⊗=（⊗）+（⊗）恒成立．综上可知：只有①③④恒成立．故选B．二．填空题（共11小题）17．（2016•太原校级二模）已知过点P（2，2）的直线与圆（x﹣1）2+y2=5相切，且与直线ax﹣y+1=0垂直，则a= 2．【分析】由题意判断点在圆上，求出P与圆心连线的斜率就是直线ax﹣y+1=0的斜率，然后求出a的值即可．【解答】解：因为点P（2，2）满足圆（x﹣1）2+y2=5的方程，所以P在圆上，又过点P（2，2）的直线与圆（x﹣1）2+y2=5相切，且与直线ax﹣y+1=0垂直，所以切点与圆心连线与直线ax﹣y+1=0平行，所以直线ax﹣y+1=0的斜率为：a==2．故答案为：2．18．（2016•大东区一模）过原点向圆x2+y2﹣2x﹣4y+4=0引切线，则切线方程为或x=0．【分析】求出圆的标准方程，求出圆心和半径，根据直线和圆相切的等价条件进行求解即可．【解答】解：圆的标准方程为（x﹣1）2+（y﹣2）2=1，则圆心为（1，2），半径R=1，若切线斜率k不存在，即x=0时，满足条件．若切线斜率k存在，则设切线方程为y=kx，即kx﹣y=0，圆心到直线的距离d==1，得|k﹣2|=，平方得k2﹣4k+4=1+k2，即k=，此时切线方程为，综上切线方程为：或x=0，故答案为：或x=0．19．（2016•梅州二模）若直线l：ax+by+1=0始终平分圆M：x2+y2+4x+2y+1=0的周长，则（a﹣2）2+（b﹣2）2的最小值为5．【分析】把圆的方程化为标准方程，找出圆心M的坐标和半径r，根据直线l始终平分圆M的周长，得到直线l过圆心M，故把M的坐标代入直线l，得到关于a与b的方程，所求的式子可看做（a，b）到（2，2）距离的平方，又点（2，2）到直线2a+b﹣1=0的距离最小值为点（2，2）到直线2a+b﹣1=0的距离，故用点到直线的距离公式求出（2，2）到直线2a+b﹣1=0的距离，平方后即可得到所求式子的最小值．【解答】解：把圆的方程化为标准方程得：（x+2）2+（y+1）2=4，∴圆心M坐标为（﹣2，﹣1），半径r=2，∵直线l始终平分圆M的周长，∴直线l过圆M的圆心M，把M（﹣2，﹣1）代入直线l：ax+by+1=0得：﹣2a﹣b+1=0，即2a+b﹣1=0，∵（2，2）到直线2a+b﹣1=0的距离d==，∴（a﹣2）2+（b﹣2）2的最小值为5．故答案为：520．（2016•静安区一模）经过直线2x﹣y+3=0与圆x2+y2+2x﹣4y+1=0的两个交点，且面积最小的圆的方程是5x2+5y2+6x﹣18y﹣1=0．【分析】题意可知，弦长为直径的圆的面积最小．求出半弦长，就是最小的圆的半径，求解即可．【解答】解：∵圆x2+y2+2x﹣4y+1=0的方程可化为（x+1）2+（y﹣2）2=4．∴圆心坐标为（﹣1，2），半径为r=2；∴圆心到直线2x﹣y+3=0的距离为d=．设直线2x﹣y+3=0和圆x2+y2+2x﹣4y+1=0的交点为A，B．则|AB|=2=2=．∴过点A，B的最小圆半径为．联立得5x2+6x﹣2=0，故，则圆心的横坐标为：，纵坐标为2×（﹣）+3=，∴最小圆的圆心为（，），∴最小圆的方程为（x+）2+（y﹣）2=．即5x2+5y2+6x﹣18y﹣1=0．故答案为：5x2+5y2+6x﹣18y﹣1=021．（2016•渭南一模）如图所示，在△ABC中，D为BC边上的一点，且BD=2DC，若=m+n（m，n∈R），则=﹣3【分析】根据向量减法的几何意义，以及向量的数乘运算便可由得到，这便可得到m=，从而可以求出．【解答】解：BD=2DC；∴；∴；∴；又；∴；∴．故答案为：﹣3．22．（2015•山东）过点P（1，）作圆x2+y2=1的两条切线，切点分别为A，B，则=．【分析】根据直线与圆相切的性质可求PA=PB，及∠∠APB，然后代入向量数量积的定义可求．【解答】解：连接OA，OB，PO则OA=OB=1，PO=，2，OA⊥PA，OB⊥PB，Rt△PAO中，OA=1，PO=2，PA=∴∠OPA=30°，∠BPA=2∠OPA=60°∴===故答案为：23．（2015•安徽）△ABC是边长为2的等边三角形，已知向量满足=2，=2+，则下列结论中正确的是①④⑤．（写出所有正确结论得序号）①为单位向量；②为单位向量；③；④∥；⑤（4+）⊥．【分析】利用向量的三角形法则以及向量数量积的公式对各结论分别分析选择．【解答】解：△ABC是边长为2的等边三角形，已知向量满足=2，=2+，则=，AB=2，所以||=1，即是单位向量；①正确；因为=2，所以，故||=2；故②错误；④正确；夹角为120°，故③错误；⑤（4+）•=4=4×1×2×cos120°+4=﹣4+4=0；故⑤正确．故答案为：①④⑤．24．（2014•江西）已知单位向量与的夹角为α，且cosα=，若向量=3﹣2，则||=3．【分析】由条件利用两个向量的数量积的定义求出的值，从而得到||的值．【解答】解：=9=9，∴||=3，故答案为：3．25．（2014•江苏）如图，在平行四边形ABCD中，已知AB=8，AD=5，=3，•=2，则•的值是22．【分析】由=3，可得=+，=﹣，进而由AB=8，AD=5，=3，•=2，构造方程，进而可得答案．【解答】解：∵=3，∴=+，=﹣，又∵AB=8，AD=5，∴•=（+）•（﹣）=||2﹣•﹣||2=25﹣•﹣12=2，故•=22，故答案为：22．26．（2013•山东）已知向量与的夹角为120°，且，．若，且，则实数λ=．【分析】利用，，表示向量，通过数量积为0，求出λ的值即可．【解答】解：由题意可知：，因为，所以，所以===﹣12λ+7=0解得λ=．故答案为：．27．（2010•天津）如图，在△ABC中，AD⊥AB，，，则=．【分析】本题主要考查平面向量的基本运算与解三角形的基础知识，属于难题．【解答】解：，∵，∴，∵，∴cos∠DAC=sin∠BAC，，在△ABC中，由正弦定理得变形得|AC|sin∠BAC=|BC|sinB，，=|BC|sinB==，故答案为．。

专题10圆
高中必备知识点1：直线与圆的位置关系
设有直线和圆心为且半径为的圆，怎样判断直线和圆的位置关系？
观察图3.3-1，不难发现直线与圆的位置关系为：当圆心到直线的距离时，直线和圆相离，如圆与直线；当圆心到直线的距离时，直线和圆相切，如圆与直线；当圆心到直线的距离时，直线和圆相交，如圆与直线.
在直线与圆相交时，设两个交点分别为A 、B.若直线经过圆心，则AB 为直径；若直线不经过圆心，如图3.3-2，连结圆心和弦的中点的线段垂直于这条弦.且在中，为圆的半径，为圆心到直线的距离
，为弦长的一半，根据勾股定理，有. l O r l O d r >O 1l d r =O 2l d r <O 3l O AB M OM AB Rt OMA V OA r OM d MA AB 222
()2AB
r d -=
当直线与圆相切时，如图3.3-3，为圆的切线，可得，，且在中，. 如图 3.3-4，为圆的切线，为圆的割线，我们可以证得，因而.
典型考题
【典型例题】
在同一平面直角坐标系中有5个点：A （1，1），B （﹣3，﹣1），C （﹣3，1），D （﹣2．﹣2）．,PA PB O PA PB .OA PA Rt POA 222
PO PA OA PT O PAB O PAT PTB 2PT PA PB。