等式基本性质及一元一次方程解法
- 格式:doc
- 大小:128.50 KB
- 文档页数:4

一元一次方程1.定义:方程与一元一次方程含有未知数的叫方程,方程必须具备两个条件:第一是等式,第二是含有未知数。
方程中只含有一个未知数,且未知数的次数都是1的整式方程叫做一元一次方程。
2.方程的解与解方程使等式左右两边相等的未知数的值叫方程的解;注意:“方程的解就能代入”!解方程就是求出使方程中左右两边均相等的未知数的值,是过程。
3.等式的性质(1):等式两边都加上(或减去)同一个数或同一个整式,所得结果仍是等式;(2):等式两边都乘以(或除以)同一个不为零的数,所得结果仍是等式.解方程的过程就是把方程逐步化为x=a(常数)的形式,等式的性质是重要的转化依据。
4.解方程(1)合并同类项与移项:合并时牢记:同类项的系数相加,字母连同指数不变,系数为负数时要注意符号。
(2)移项(移项要变号):移项就是把等式一边的某项变号后移到另一边。
一般把方程转化为含有未知数的在方程的左边,常数在方程的右边。
注意与加法交换律不一样。
移项是把某些项从方程的一边移到另一边,移动要变号,而加法交换律只是加数之间交换位置,改变的只是顺序不改变符号。
(3)去括号与去分母:去括号法则与整式去括号法则相同:括号外的因数是整数时,去括号后原括号内各项的符号与原来的符号相同。
括号外的因数是负数时,去括号内后,原括号内各项的符号与原来的符号相反。
去分数:先把分式化成整式再计算。
应注意各项都要乘以各分母的最小公倍数,不要漏乘分母的项,如果分子是一个多项式,去分母时要将分子作为一个整体加上括号。
当分母是小数时,要先利用分母的基本性质把小数转化成整数,然后再去分母。
(4)一元一次方程解法的一般步骤:化简方程----------分数基本性质去分母----------同乘(不漏乘)最简公分母去括号----------注意符号变化移项----------变号合并同类项--------合并后注意符号系数化为1---------未知数细数是几就除以几5.列方程(1)读题分析法:…………多用于“和,差,倍,分问题”仔细读题,找出表示相等关系的关键字,例如:“大,小,多,少,是,共,合,为,完成,增加,减少,配套-----”,利用这些关键字列出文字等式,并且据题意设出未知数,最后利用题目中的量与量的关系填入代数式,得到方程.(2)画图分析法: …………多用于“行程问题”利用图形分析数学问题是数形结合思想在数学中的体现,仔细读题,依照题意画出有关图形,使图形各部分具有特定的含义,通过图形找相等关系是解决问题的关键,从而取得列方程的依据,最后利用量与量之间的关系(可把未知数看做已知量),填入有关的代数式是获得方程的基础.6.列方程解决实际问题一般步骤:审设列解验答(1)配套问题等量关系:加工或者生产的总量相等或成比例。


一元一次方程的解法一元一次方程是一个数学常见的概念,对于初学者来说,如何解决一元一次方程可能会有些困难。
本文将介绍几种常见的解法,帮助读者轻松应对一元一次方程。
一、等式法等式法是最基本、最常用的解一元一次方程的方法。
它通过运用等式的性质将方程转化为等价方程,从而找到解。
例如,对于方程2x + 5 = 9,我们可以将它转化为等价方程2x = 9 - 5,进一步简化为2x = 4。
接下来,只需将x的系数2移至等号右边,得到x = 4 ÷ 2,最终得到x = 2。
因此,方程的解是x = 2。
二、因式分解法有些一元一次方程可以通过因式分解来解决。
通过找出方程中的公因式或将方程转化为乘积形式,可以得到方程的解。
举例来说,对于方程3(x + 2) = 12,我们可以将其进行因式分解,得到3x + 6 = 12。
接下来,只需将x的系数3移至等号右边,得到x =(12 - 6) ÷ 3,最终得到x = 2。
因此,方程的解是x = 2。
三、移项法移项法是解决一元一次方程的另一种常用方法。
通过将含有未知数的项移到等号的另一侧,可以得到方程的解。
例如,对于方程4x - 6 = 10,我们可以将-6移至等号的右边,得到4x = 10 + 6。
接下来,只需计算右边的和,得到4x = 16。
最后,将x的系数4移至等号右边,得到x = 16 ÷ 4,最终得到x = 4。
因此,方程的解是x = 4。
四、消元法消元法适用于有两个同系数未知数的一元一次方程组。
通过将方程组中的一个方程乘以适当的数值,使得其中一个未知数的系数相等,再将两个方程相减,可以消去一个未知数,从而求解另一个未知数。
举例来说,考虑方程组2x + 3y = 10和3x - 2y = 4。
我们可以通过将第一个方程的系数分别乘以2和3,第二个方程的系数分别乘以3和2,得到4x + 6y = 20和6x - 4y = 8。
接下来,将这两个方程相减,得到2x + 10y = 12。



一元一次方程的概念及解法4、等式的基本性质:(1)、等式的两边都加上(或减去)同一个数或同一个整式,所得结果仍是等式。
(2)、等式的两边都乘以(或除以)同一个数(除数不能是零),所得结果仍是等式。
5、解一元一次方程的基本步骤:【例题解析】那么a=bA . 2x 3yB . 7x 5 6x1C . 2、下列运用等式的性质对等式进行的变形中,正确的是【练习】:1、下列方程中是 元-次方程的是【知识点】: 1、一元一次方程的定义:只含有 未知数,并且未知数的次数都,这样的方程叫一元一次方程。
2、方程的解:使方程左右两边 的未知数的值叫方程的解。
3、解方程:求的过程叫做解方程。
(1):去分母;(2):去括号;(3):移项;(4):合并同类项;(5):系数化成 1。
例1、判断下列各式是不是一元 次方程,是的打“ V”,不是的打“X⑴ x+3y=4 2⑵ x -2x=6⑶-6x=0(4) 2m +n =0(5) 2x-y=8(6) 1 —+8=5yy例2、下列变形中, 正确的是A 、若 ac=bc ,那么 a=b 。
B 、a=b C 、b ,那么a=bD 、若 a 2 =b 2x 23、若x(n-2)+2n=0是关于x的方程一元一次方程,则n=—,此时方程的解是x= 。
其中变形正确的是((1) x + 2x +4x=140【练习】:1、下列叙述正确的是则a=b则a=b则a=b4、某数x 的43%比它的一半少 7,则列岀求x 的方程应是(A : 43%x 1B : 43%(x !) 7 C2 2 :43%X 7 43%x例3、给岀下面四个方程及其变形: ①4x 8 0变形为x 3x 变形为4x2 ③—x 3变形为2x515;4x2变形为x2; 3、解方程:(1)丄 y-3-5y= 1 ;、x X(2) =5;2 31(3 )0.6x- —x-3=032 4 例5、解方程:(利用去括号、移项等步骤解方程)(1) 2x 1 4 ;2(2)2( X — 2) - (4 X —1)=3(1—x )____________ ,根据是例6、解方程:(利用去分母、去括号、移项、合并同类项及系数化成1解方程)A .①③④B •①②④C.②③④D .①②③例4、解方程:(利用移项、合并同类项及系数化成1来解方程)(2) 3x + 20=4x-25①若a=b ,则 a+c=b+ c②若 a=b ,贝U a-c=b- c ③若a+c=b+ c ,则 a=b ④若,a-c=b- c ,⑤若a=b ,则 ac=bc ⑥若 ac=bc ,贝U a=b⑦若a=b ,则-ca b ⑧若—_,c c⑨若a=b ,则⑩若b ,则 a=b(11)若 a=b ,贝U a 2=b 2 (12)若 a 2=b 2,(13)若 a=b ,则 a 3=b 3(14)若 a 3=b 3,贝U a=b2、方程2y-6=y+7变形为 2y-y=7+6 ,这种变形叫解:去分母,得 _____________________________________ 依据 ________________去括号,得 ______________________________________ 依据 ____________________移项,得 ________________________________________ 依据 ____________________合并同类项,得 __________________________________ 依据 ___________________系数化为1,得x 6例7、数学小诊所:小马虎的解法对吗如果不对,应怎么改正解方程专=1-专 解:去分母 2 ( 2x-1)=1-4x-1 去括号4x-仁1-4x-1移项 4x+4x=1-1+1系数化为1x=8【练习】:解方程:归纳:解一元一次方程的步骤:依据合并8x=12x —1x+2 (1)=T +13x 1 4x 2 15(3) 4-3(2-x)=5x例7、已知关于x 的方程13x 2的解互为倒数,求m 的值.3 31、解方程2(x3)5(1x) 3(x1),去括号正确的是().(A) 2x 6 55x3x3(B) 2x 35x3x 3 (C) 2x 6 55x3x3(D) 2x 35x3x 13x 7 2、解方程3x 721x31的步骤中,去分母一项正确的是().(A)3(3x 7)22x6(B)3x 7(1x)1 (C)3(3x 7)2(1x)1(D)3(3x7)2(1x) 6 3x 1 2x 23、若的值比的值小1,则X的值为()23/ 1313_5/ 5(A)(B)- (C) (D)-—5513134、解方程4(x 1)x2(x1)步骤下:①去括号,得4x 4 x2x 1 ②移项,得4x x 2x 1 4③合并同类项,得3x 55④系数化为1,得x -检验知:x —不是原方程的根,说明解题的四个步骤有错,其中做错的一步是35、当x= _____ 时,2x 8的值等于一-的倒数.46、已知3x 6 (y 3) 0,则3x 2y 的值是 _____________7、当x = _____ 时,式子1(1 2x)与式子2(3x 1)的值相等8、解方程:9、已知 A=2x-5,B=3x+3,求A 比B 大7时的x 值.x 4x 210、如果方程8的解与方程4x (3a 1) 6x 2a 1的解相同,求式子321a 的值.a111、已知x 1是关于x 的方程1」(m3m(y 3) 2 m(2y 5).12,已知方程 4x 2m 3x 1与方程3x 2m 6x 1的解相同.3(A )①(B )② (C )③ (D )④1)、2x 3(2x 1) 16 (x 1)2x 3 4x 1.3)、142 51x [2 -(x 4)]2x 3、2x 110x 1 2x 1 ,)、 1 36 4x) 2x 的解,解关于y 的方程:(1)求m的值; (2)求代数式(m 3)2010 (2m 2)2011的值.。

3.1.2等式的性质学习目标:1.利用天平,通过观察、分析得出等式的两条性质。
2.会利用等式的两条性质解一元一次方程。
3.培养观察能力、思考能力、归纳能力和创新能力。
自学过程:1.复习回顾 ⑴.下列方程中属于一元一次方程的是( )A .x -y =3B .-x =1C .11x x+=D .2210x x -+=⑵.检验x =5是否为方程2122-=-x 的解。
2.探求新知⑴.2333152315m n n m x x x x y +=++=⨯+=⨯+=, , , 这样的式子叫 。
等式具有什么样的性质呢?我们不妨做一个实验,请同学们认真观察,然后用“>、<、=”填空: 5=5 5+6 5+6 ; -7=-7 -7-5 -7-5; a =b a +5 b+5a =b a -2 b-2 ; x =y x +m y +m a =b a +(m+n ) b+(m+n ) 你觉得等式的这个性质可以怎样描述:⑵.我们再看一个实验,请同学们认真观察后然后用“>、<、=”填空: 6=6 6×5 6×5;-3=-3 -3×(-2) -3×(-2); a =b 6a 6b 8=8 8÷2 8÷2;-10=-10 -10÷(-5) -10÷(-5); m 18n你觉得等式的这个性质可以怎样描述:讨论:1=m n m n = 运用了等式的哪一条性质?能否由m n = 得到1=mn?⑶.有了等式的性质,下面我们开始探究怎样用它解方程,你只需完成下面的两个问题你就可以轻松地用它解方程了。
① 方程的解在等式的结构上有什么特点?如x =5,解得左边是 ,右边是 。
② 2122-=-x 和它的解x =5在结构上有什么区别?左边多了一项: ,x 的系数是 而不是1,要想使2122-=-x 左边是x ,要经历两步,一是:去掉-12,二是使系数由2变成1,怎样由等式的性质完成这两步呢?2122-=-x解: 2x -12+12= -2+12 ( ) 2x =10 ( ) x =5 ( )⑷.我们得到的x =5是否正确?怎样检验我们的答案? 试一试:用等式的性质解方程。

一元一次方程知识点总结一、等式与方程1.等式:(1)定义:含有等号的式子叫做等式.(2)性质:①等式两边同时加上(或减去)同一个整式,等式的值不变.若a b=那么a c b c+=+②等式两边同时乘以一个数或除以同一个不为0的整式,等式的值不变.若a b=那么有ac bcc≠)÷=÷(0=或a c b c③对称性:若a b=,则b a=.④传递性:若a b=,b c=则a c=.(3)拓展:①等式两边取相反数,结果仍相等.如果a b=,那么a b-=-②等式两边不等于0时,两边取倒数,结果仍相等.如果0=≠,那么11a b=a b③等式的性质是解方程的基础,很多解方程的方法都要运用到等式的性质.如移项,运用了等式的性质①;去分母,运用了等式的性质②.④运用等式的性质,涉及除法运算时,要注意转换后除数不能为0,否则无意义.2.方程:(1)定义:含有未知数的等式叫做方程.(2)说明:①方程中一定有含一个或一个以上未知数,且方程是等式,两者缺一不可.②未知数:通常设x、y、z为未知数,也可以设别的字母,全部小写字母都可以.未知数称为元,有几个未知数就叫几元方程.一道题中设两个方程时,它们的未知数不能一样!③“次”:方程中次的概念和整式的“次”的概念相似.指的是含有未知数的项中,未知数次数最高的项对应的次数,也就是方程的次数.未知数次数最高是几就叫几次方程.④方程有整式方程和分式方程.整式方程:方程的两边都是关于未知数的整式的方程叫做整式方程.分式方程:分母中含有未知数的方程叫做分式方程.二、一元一次方程1.一元一次方程的概念:(1)定义:只含有一个未知数(元)且未知数的指数是1(次)的整式方程叫做一元一次方程.(2)一般形式:0+=(a,b为常数,x为未知数,且0a≠).ax b(3)注意:①该方程为整式方程.②该方程有且只含有一个未知数.③该方程中未知数的最高次数是1.④化简后未知数的系数不为0.如:212x x-=,它不是一元一次方程.⑤未知数在分母中时,它的次数不能看成是1次.如13x+=,它不是一x元一次方程.2.一元一次方程的解法:(1)方程的解:能使方程左右两边相等的未知数的值叫做方程的解,一般写作:“?x=”的形式.(2)解方程:求出方程的解的过程,也可以说是求方程中未知数的值的过程,叫解方程.(3)移项:①定义:从方程等号的一边移到等号另一边,这样的变形叫做移项.②说明:Ⅰ移项的标准:看是否跨过等号,跨过“=”号才称为移项;移项一定改变符号,不移项的不变.Ⅱ移项的依据:移项实际上就是对方程两边进行同时加减,根据是等式的性质①.Ⅲ移项的原则:移项时一般把含未知数的项向左移,常数项往右移,使左边对含未知数的项合并,右边对常数项合并,方便求解.(4)解一元一次方程的一般步骤及根据:①去分母——等式的性质②②去括号——分配律③移项——等式的性质①④合并——合并同类项法则⑤系数化为1——等式的性质②⑥检验——把方程的解分别代入方程的左右边看求得的值是否相等(在草纸上)(5)一般方法:①去分母,程两边同时乘各分母的最小公倍数.②去括号,一般先去小括号,再去中括号,最后去大括号.但顺序有时可依据情况而定使计算简便,本质就是根据乘法分配律.③移项,方程中含有未知数的项移到方程的另一边,其余各项移到方程的另一边移项时别忘记了要变号.(一般都是把未知数移到一起)④合并同类项,合并的是系数,将原方程化为ax b=(0a≠)的形式.⑤系数化1,两边都乘以未知数的系数的倒数.⑥检验,用代入法,在草稿纸上算.(6)注意:(对于一元一次方程的一般步骤要熟练掌握,更要观察所求方程的形式、特点,灵活变化解题步骤)①分母是小数时,根据分数的基本性质,把分母转化为整数,局部变形;②去分母时,方程两边各项都乘各分母的最小公倍数,Ⅰ此时不含分母的项切勿漏乘,即每一项都要乘Ⅱ分数线相当于括号,去分母后分子各项应加括号(整体思想);③去括号时,不要漏乘括号内的项,不要弄错符号;④移项时,切记要变号,不要丢项,有时先合并再移项,以免丢项;⑤系数化为1时,方程两边同乘以系数的倒数或同除以系数,不要弄错符号(打草稿认真计算);⑥不要生搬硬套解方程的步骤,具体问题具体分析,找到最佳解法;⑦分数、小数运算时不能嫌麻烦,不要跳步,一步步仔细算.(7)补充:分数的基本性质:与等式基本性质②不同.分数的分子分母两个整体同时乘以同一个不为0的数或除以同一个不为0的数,分数的值不变.3.一元一次方程的应用:(1)解决实际应用题的策略:①审题:就是多读题,读懂题,读的时候一定沉下心去,不能慌不要急躁,要细,一个字一个字的精读,要慢,边读边思考.找到已知条件,未知条件,找到数量关系和等量关系,可以用笔在题目中标注下来重要信息和数量关系,审题往往伴随下个步骤.②设出适当未知数,往往问什么设什么,有时也间接设未知数,然后用未知数通过关系表示出其他相关的量.③找出等量关系,用符号语言表示就是列出方程.(2)分析问题方法:①文字关系分析法,找关键字词句分析实际问题中的数量关系②表格分析法,借助表格分析分析实际问题中的数量关系③示意图分析法,通过画图帮助分析实际问题中的数量关系(3)设未知量方法:一个应用题,往往涉及到几个未知量,为了利用一元一次方程来解应用题,我们总是设其中一个未知量为x,并用这个未知数的代数式去表示其他的未知量,然后列出方程.①设未知量的原则就是设出的量要便于分析问题,与其它量关系多,好表示其它量,好表示等量关系;②有直接设未知量和间接设未知量,还有不常见的辅助设未知量.(4)找等量关系的方法:“等量关系”特指数量间的相等关系,是数量关系中的一种.数学题目中常含有多种等量关系,如果要求用方程解答时,就需找出题中的等量关系.①标关键词语,抓住关键句子确定等量关系.(比如多,少,倍,分,共)解题时只要找出这种关键语句,正确理解关键语句的含义,就能确定等量关系.②紧扣基本公式,利用基本关系确定等量关系就是根据常见的数量关系确定等量关系.(比如体积公式,单价×数量=总价,单产量×数量=总产量,速度×时间=路程,工效×时间=工作总量等.这些常见的基本数量关系,就是等量关系)③通过问题中不变的量,相等的量确定等量关系.就是用不同的方法表示同一个量,从而建立等量关系.④借助线段图确定等量关系。

初中数学等式的性质如何应用于解一元一次方程等式的性质是解决一元一次方程的重要工具。
在解题过程中,我们可以利用等式的性质来简化计算和转化等式,从而更加轻松地解决方程问题。
下面将介绍等式的性质在解一元一次方程中的应用。
一、等式的加法性质和减法性质一元一次方程的一般形式为ax + b = c,其中a,b,c 是已知数,x 是未知数。
我们可以利用等式的加法性质和减法性质来解决方程问题。
具体方法如下:1. 如果方程中有多项式,可以将其中的同类项合并,然后利用等式的加法性质和减法性质化简方程。
例如,对于方程2x + 3x + 4 = 7x + 2,我们可以将方程中的同类项合并:5x + 4 = 7x + 2,然后用等式的减法性质将5x 移到方程的一边,将常数项移到另一边:5x - 7x = 2 - 4,即-2x = -2。
最后,用等式的乘法性质将x 的系数消去,解得x = 1。
2. 如果方程中有分式,可以通过通分来化简方程。
例如,对于方程2/x + 1/(x+1) = 3/2,我们可以通过通分将方程化简为(4(x+1) + 2x) / (2x(x+1)) = 3/2,即6x + 6 = 3x^2 + 3x,然后移项得到3x^2 - 3x - 6 = 0。
最后,用一元二次方程的求解公式解得x = 2 或x = -1。
二、等式的乘法性质和除法性质一元一次方程的另一种解法是利用等式的乘法性质和除法性质。
具体方法如下:1. 如果方程中有一个未知数的系数为1,可以利用等式的乘法性质将系数移动到未知数的一边。
例如,对于方程x/3 + 2 = 5,我们可以通过等式的乘法性质将1/3 移到未知数x 的一边,得到x = 9。
2. 如果方程中有一个未知数的系数不为1,也可以利用等式的乘法性质来解决方程。
例如,对于方程2x/3 + 4 = 8,我们可以将方程两边都乘以3,得到2x + 12 = 24,然后移项得到2x = 12,最后解得x = 6。

自学资料方程式的由来十六世纪,随著各种数学符号的相继出现,特别是法国数学家韦达创立了较系统的表示未知量和已知量的符号以后,"含有未知数的等式" 这一专门概念出现了,当时拉丁语称它为"aequatio",英文为"equation".十七世纪前后,欧洲代数首次传进中国,当时译"equation"为"相等式.由於那时我国古代文化的势力还较强,西方近代科学文化未能及时在我国广泛传播和产生较的影响,因此"代数学"连同"相等式"等这些学科或概念都只是在极少数人中学习和研究.十九世纪中叶,近代西方数学再次传入我国.1859年,李善兰和英国传教士伟烈亚力,将英国数学家德.摩尔根的译出.李.伟两人很注重数学名词的正确翻译,他们借用或创设了近四百个数学的汉译名词,许多至今一直沿用.其中,"equation"的译名就是借用了我国古代的"方程"一词.这样,"方程"一词首次意为"含有未知数的等式.一、一元一次方程的定义【知识探索】1.只含有一个未知数(元),未知数的次数都是1,等号两边都是整式,这样的方程叫做一元一次方程(linear equation in one unknown)。
【错题精练】例1.如图所示,正方形的边长为a,试用字母a表示阴影部分的面积.【解答】根据阴影部分的面积等于扇形的面积减去半圆的面积可以求解.【答案】例2.已知方程2mx m﹣1+1=0是关于x的一元一次方程,求m的值及方程的解.第1页共20页自学七招之日计划护体神功:每日计划安排好,自学规划效率高非学科培训【答案】例3.已知方程2kx2+2kx+3k=4x2+x+1是关于x的一元一次方程,求k值,并求出这个方程的根.【答案】【举一反三】1.下列叙述中,正确的是()A. 方程是含有未知数的式子B. 方程是等式C. 只有含有字母x,y的等式才叫方程D. 带等号和字母的式子叫方程【答案】B2.已知方程(3m−4)x2−(5−3m)x−4m=−2m是关于x的一元一次方程,求m和x的值.第2页共20页自学七招之智慧树神拳:知识内容体系化,思维导图来助力非学科培训【答案】3.已知(a2﹣1)x2﹣(a+1)x+8=0是关于x的一元一次方程.求代数式199(a+x)(x﹣2a)+3a+4的值.【答案】解:∵(a2﹣1)x2﹣(a+1)x+8=0是关于x的一元一次方程,∴a2﹣1=0,a+1≠0.解得:a=1.将a=1代入得:199(a+x)(x﹣2a)+3a+4=199(1+x)(x﹣2)+3+4=199x2﹣199x﹣391.4.(|k|﹣1)x2+(k﹣1)x+3=0是关于x的一元一次方程,求k的值.【答案】二、方程的解【知识探索】1.如果未知数所取的某个值能使方程左右两边的值相等,那么这个未知数的值叫做方程的解(solution of equation).【错题精练】例1.若x=2是关于x的方程2x+3m﹣1=0的解,则m的值等于__________第3页共20页自学七招之提前完卷飞刀:考场控时莫紧张,跳跃答卷心不慌非学科培训【答案】-1例2.当x=__________ 时,代数式与x﹣3的值互为相反数.【答案】例3.若关于x的方程2k−3x=4与x−2=0的解相同,则k的值为()A. ﹣10;B. 10;C. ﹣5;D. 5.【答案】D【举一反三】1.已知关于x的方程3a﹣x=+3的解为2,则代数式a2﹣2a+1的值是__________ .【答案】12.若代数式x+2的值为1,则x等于()A. 1B. -1C. 3D. -3【答案】B3.当k为何值时,关于x的方程(k﹣5)x﹣7=x﹣1的解是﹣2?【答案】解:把x=﹣2代入方程得:﹣2(k﹣5)﹣7=﹣2﹣1,去括号得:﹣2k+10﹣7=﹣3,第4页共20页自学七招之智慧树神拳:知识内容体系化,思维导图来助力非学科培训移项合并得:﹣2k=﹣6,解得:k=3.三、等式的基本性质【知识探索】1.(1)等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等.如果,那么.(2)等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.如果,那么;如果(),那么.【错题精练】例1.下列方程中变形正确的是()①3x+6=0变形为x+2=0;②2x+8=5﹣3x变形为x=3;③=4去分母的3x+2x=24;④(x+2)﹣2(x﹣1)=0去括号得x+2﹣2x﹣2=0.A. ①③B. ①②③C. ①④D. ①③④【答案】A例2.下列变形符合等式基本性质的是()A. 如果2x-y=7,那么y=7-2xB. 如果ak=bk,那么a=bC. 如果-2x=5,那么x=5+2D. 如果a=1,那么a=-3【解答】A中,∵2x-y=7,∴y=2x-7,故A错误;B中,若k=0时,不符合等式性质,故B错误;C中,∵-2x=5,∴x=-2.5,变形方法是等式两边都除以-2,而不是都加上2,故C错误;D中,等式两边都乘-3,符合等式性质,故D正确;综上所述,选D.【答案】D第5页共20页自学七招之提前完卷飞刀:考场控时莫紧张,跳跃答卷心不慌非学科培训【举一反三】1.是否可以由方程10x+3=5x﹣7经过变形得到方程4x=﹣8?若能,请说明是怎样变形的,依据是什么?若不能,请说明理由.【解答】【答案】略2.将等式2a=2b的两边都减去a+b变形为a﹣b=b﹣a,两边再都除以a﹣b变形为1=﹣1,最后结果明显是错误的,请说明错在哪里?【解答】解:由2a=2b,可知a=b,∴a﹣b=0.两边再都除以a﹣b时,不满足等式的性质.故错在方程两边都除以a﹣b.【答案】解:由2a=2b,可知a=b,∴a﹣b=0.两边再都除以a﹣b时,不满足等式的性质.故错在方程两边都除以a﹣b.3.用等式的性质解下列方程:(1)x﹣7=2;(2)3=x+5.【解答】解:(1)等式的两边都加7,得x=9;(2)等式的两边都减5,得﹣2=x,即x=﹣2.【答案】略4.下列方程的变形,正确的是()第6页共20页自学七招之智慧树神拳:知识内容体系化,思维导图来助力非学科培训B. 由5x=4x+8,得5x﹣4x=8C.D. 由7x+6=5x,得7x﹣5x=6第7页共20页自学七招之提前完卷飞刀:考场控时莫紧张,跳跃答卷心不慌非学科培训第8页共20页自学七招之智慧树神拳:知识内容体系化,思维导图来助力非学科培训第9页 共20页 自学七招之提前完卷飞刀:考场控时莫紧张,跳跃答卷心不慌 非学科培训(3)12{x −13[x −14(x −23)]−32}=x +34.【解答】(1)解:移项合并得:2x =2,解得:x =1.(2)解:去分母得:20y +16+3y −3=24−5y +5,移项合并得:28y =16.解得:y =47.(3)解:去括号得:12x −16x +124(x −23)−34=x +34,去分母得:12x −4x +x −23−18=24x +18,即:36x −12x +3x −2−54=72x +54.移项合并得:−27x =66.解得:x =−229.【答案】(1)x =1;(2)y =47;(3)x =−229.例6.已知关于x 的方程a (2x ﹣1)=3x ﹣2无解,则a 的值是__________ .【解答】解:原式可化为:(2a ﹣3)x+2﹣a=0,∵方程无解,∴可得:2a ﹣3=0,2﹣a≠0,故a 的值为.故填.【答案】例7.已知是方程的解,则m=__________ .【解答】【答案】【举一反三】1.已知x=2是方程ax﹣1=x+3的一个解,那么a=__________ .【解答】解:把x=2代入方程ax﹣1=x+3,得:2a﹣1=2+3,解得:a=3.故填3.【答案】32.如果x=2是方程x+a=﹣1的根,那么a的值是__________ .【解答】解:把x=2代入x+a=﹣1中:得:×2+a=﹣1,解得:a=﹣2.故填:﹣2.【答案】-23.已知x=1是方程ax﹣6=5的一个解,则a=__________ .【解答】解:将x=1代入方程得:a﹣6=5,解得:a=11.故答案为:11.第10页共20页自学七招之智慧树神拳:知识内容体系化,思维导图来助力非学科培训例1.已知关于x的方程x−m2=x+2m与方程x+32=x−1的解相等,求m的值.【解答】解:第一个方程的解为x=−5m,第二个方程的解为x=5,∴−5m=5,即m=−1.【答案】-1.【举一反三】1.关于x的方程2x+5a=3的解与方程2x+2=0的解相同,则a的值是()A. 1; B. 4; C. 15; D. ﹣1.【答案】A2.已知方程6x﹣9=10x﹣45与方程3a﹣1=3(x+a)﹣2a的解相同.(1)求这个相同的解;(2)求a的值;(3)若[m]表示不大于m的最大整数,求[a﹣2]的值.【答案】解:(1)原方程6x﹣9=10x﹣45移项得6x﹣10x=﹣45+9,合并同类项得到﹣4x=﹣36,解得:x=9;(2)将x=9代入第二个方程得:3a﹣1=3(9+a)﹣2a,解得:a=14;(3)[a﹣2]=[×14﹣2]=[]=2.3.已知方程=与方程=+1的解相同,求m的值.【答案】六、特殊解问题【错题精练】例1.小王在解关于x的方程3a−2x=15时,误将−2x看作2x,得方程的解x=3.(1)求a的值;(2)求此方程正确的解;(3)若当y=a时,代数式my3+ny+1的值为5,求当y=−a时,代数式my3+ny+1的值.【解答】(1)解:把x=3代入3a−2x=15得3a+6=15,计算得出:a=3;(2)解:把a=3代入方程得:9−2x=15,计算得出:x=−3;(3)解:把y=a=3代入my3+ny+1得27m+3n+1=5,则27m+3n=4.当=−3时,my3+ny+1=−27m−3n+1=−(27m+3n)+1=−4+1=−3.【答案】(1)3;(2)-3;(3)-3.例2.已知方程|x+|3x+a||=2恰有4个不同的解,求参数a的取值范围.【答案】【举一反三】1.已知关于x的方程2|x|﹣k=kx﹣3的解为负数,则k的取值范围是__________【答案】七、含参问题【错题精练】例1.七年级一班的马虎同学在解关于x的方程3a−x=13时,误将−x看成+x,得方程的解x=−2,则原方程正确的解为()C. −12;D. 12.【答案】B例2.已知关于x 的方程与方程的解互为相反数,求m 的值.【答案】例3.若a ,b 为定值,关于x 的一元一次方程无论k 为何值时,它的解总是1,求a ,b 的值.【答案】【举一反三】1.若x=−2是关于x的方程2x+m=3的解,则关于x的方程3(1−2x)=m−1的解为();A. ﹣1;B. −12C. 1; D. 1.2【答案】B2.已知关于x的方程3x+a=x﹣7的根是正数,求实数a的取值范围.【答案】3.方程2﹣3(x+1)=0的解与关于x的方程的解互为倒数,求k的值.【答案】1.已知x=2是关于x的方程3−mx=x+m的解,m的值为.【答案】132.下列变形过程中,正确的是()A. 由2x=3,得x=23;B. 由x−13−1=1−x2,得2(x−1)−1=3(1−x);C. 由x−1=2,得x=2−1;D. 由−3(x+1)=2,得−3x−3=2.【答案】D3.根据等式的性质,下列变形正确的是()2x3【解答】(1)解:去括号,得2x+6=5x−15.移项,得2x−5x=6−15.合并同类项,得−3x=−21.系数化为1,得x=7.(2)解:去分母,得5(2x−1)=3(4−3x)−15x.去括号,得10x−5=12−9x−15x.移项,合并同类项,得34x=17.系数化为1,得x=1.2【答案】见解答.7.已知方程3(x﹣1)=4x﹣5与关于x的方程﹣=x﹣1有相同的解,求a的值.【答案】8.若关于x的方程||x﹣2|﹣1|=a有三个整数解,则a的值是()A. 0B. 1C. 2D. 3【答案】B9.适合关系式|3x﹣4|+|3x+2|=6的整数x的值有()个.A. 0B. 1C. 2D. 大于2的自然数【答案】C10.已知关于x的方程k(x+1)=k﹣2(x﹣2)中,求当k取什么整数值时,方程的解是整数【解答】解:去括号,得kx+k=k﹣2x+4,移项,得kx+2x=k﹣k+4,合并同类项,得(k+2)x=4.方程的解是整数,则k+2=±1或±2或±4.则k=﹣3或﹣1或﹣4或0或﹣6或2.【答案】k=﹣3或﹣1或﹣4或0或﹣6或2.● 代数式。
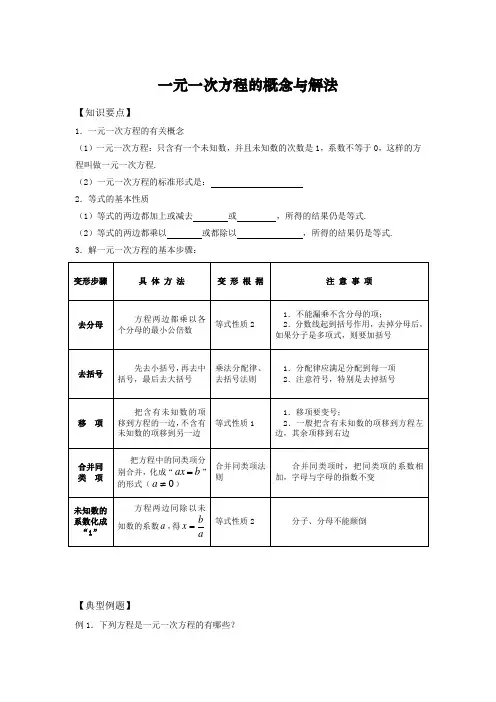
一元一次方程的概念与解法【知识要点】1.一元一次方程的有关概念(1)一元一次方程:只含有一个未知数,并且未知数的次数是1,系数不等于0,这样的方程叫做一元一次方程.(2)一元一次方程的标准形式是:2.等式的基本性质(1)等式的两边都加上或减去或,所得的结果仍是等式.(2)等式的两边都乘以或都除以,所得的结果仍是等式. 3.解一元一次方程的基本步骤:【典型例题】例1.下列方程是一元一次方程的有哪些?x+2y=9 x 2-3x=1 11=xx x 3121=-2x=1 3x –5 3+7=10 x 2+x=1例2. 用适当的数或整式填空,使得结果仍是等式,并说明是根据等式的哪条性质,通过怎样变形得到的.(1)如果________;-8x 3,853==+那么x(2)如果-1_x_________3,123=--=那么x x ;(3)如果;__________x ,521==那么x(4)如果________.3x ,32==那么yx例3.解下列简易方程1.5223-=+x x 2.4.7-3x=113.x x +-=-32.0 4.)3(4)12(3-=+x x例4.解方程 1.32243332=+--x x 2.1423(1)(64)5(3)25x x x --++=+3.21101211364x x x -++-=- 4.22314615+=+---x x x x 5.003.002.003.0255.09.03.0=+---+x x x 6.83161.20.20.55x x x +-+-=-例6.x 取何值时,代数式 63x + 与 832x- 的值相等.例7.已知方程104x x =-的解与方程522x m +=的解相同,求m 的值.例8. 已知1x =-是关于x 的方程 327350x x kx -++= 的解,求221195k k --的值.例9.当.38322倍的的值是为何值时,代数式x x x x ++-例10. 若对于任意的两个有理数m, n 都有m ※n=43nm +,解方程3x ※4=2.系统讲解一元一次方程的应用【知识梳理】一、知识结构二、知识要点归纳1.列方程解决实际问题的一般步骤(1)找——找准等量关系,找出能够表示题意的等量关系.(2)设——设未知数,弄清题意和找准等量系后,用字母表示题目中的一个未知数.(3)列——列出方程,用含未知数的代数式表示出题目中的各种数量,依据找准的等量关系,列出方程.(4) 解——解方程.解出所列的方程,求出未知数的值.(5) 答_作出应答,检验方程的解是否符合实际,作出回答且注明单位.水速度=船速-水速2.分析应用题中等量关系的一般方法(1)译式法:将题目中的关键性语言或数量及各数量间的关系译成代数式,然后根据代数式之间的内在联系找出等量关系.(2)线示法:用同一直线的线段表示应用题中的数量关系,然后根据线段的长度的内在联系,找出等量关系.(3)列表法:将已知条件和所求的未知量纳入表格,从而找出各种量之间的关系.(4)图示法:利用图表示题中的数量关系,它可以使量之间的关系更为直观,更方便找出其中的等量关系.三、考查解析一元一次方程应用问题,关键是考查同学们用一元一次方程的模型解决实际问题的能力,大多数属于当基本题或中档题,学习中应抓住其核心问题——建模,从等量关系入手,而不是只让学生套题型,套步骤去解应用题.【典型例题】劳动力分配问题例1.某车间有100个工人,每人平均每天可以加工螺栓18个或螺母24个,要使每天加工的螺栓与螺母配套(一个螺栓要配两个螺母)应如何分配加工螺栓、螺母的工人?分析:等量关系为螺栓数:螺母数=1︰2.设加工螺栓人数为x,则加工螺栓的总数为18x个,加工螺母总数为24(100-x)个.解:设加工螺栓的人数为x人,依题意有24xx⨯(=-2,18)100解得 40=x (人).∴加工螺母的人数为 100-x =100-40=60(人) 答:应分配40人去加工螺栓.点评:此题重点是培养学生寻找等量关系的意识和能力. 等体积问例2.一个圆柱形水桶,底面半径为11cm ,高25cm ,将满桶的水倒入底面长30cm ,宽20cm 的长方体容器,问此长方体容器的高度至少要多少才不溢出水(π取3.14,结果精确到0.1cm )? 分析:从相等关系入手,即圆柱形容器积=长方体器容积. 解:设长方体容器的高为x cm ,依题意,有 30×20x =25π×112,解方程,得 ≈=24121πx 15.9cm , 答:长方体容器的高至少需要15.9cm.点评:“等积变换”是中学数学的常用方法,要让学生理解和把握这方法,并能在实际问题中灵活应用. 盈亏问题例3.某服装个体户同时卖出两套服装,每件都以135元出售,按成本计算,其中一件盈利25%,另一件亏本25%.(1)在这次买卖中,这位个体户是赔是赚还是正好保本? (2)若将题中的135元改成为任何正数a 元,情况如何? 分析:关键把握等量关系: 进价(1+盈利率)=售价,进价(1-亏本率)=售价.解:(1)设第一件进价为x 元,则135%)251(=+x , 解得 108=x ,设第一件进价为y 元,则135%)251(=-y , 解得 180=y ,而 181352)180108(1352)(=⨯-+=⨯-+y x .所以赔18元.(2)仿前一小题方法可得: a x =+%)251(及a y =-%)251(, 解得 a x 54=, a y 34=,而 0152234542)(>=-⎪⎭⎫ ⎝⎛+=-+aa a a a y x , 所以此时仍然是亏本.点评:解决该题的关键是把握住此类问题中的几个等量关系,同时理解好一些常用“词”:如:打八折,进价,售价,盈利10%,亏本20%等.拓广:在例3中,将题中的135元改为任何正数a 元,同时又将题中的25%改为m%(0<m <100)情况如何?工程量问题例4.甲、乙两水管往水池中注水,甲管单独打开用20小时可注满一池水,乙管单独打开用40小时可注满一池水.现在甲管单独打开8小时后,乙管才开始工作,问两管一起打开后需多少小时可注满水池?分析:利用等量关系,甲管工作量+乙管工作量=1,来解题,为了理清工作量的关系,可列表如下:(设两管一起开后x 小时可注满全池)解:设两管一起打开后x 小时可注满全池,依题意,得140208=++xx . 解得 8=x (小时),答:两管一起打开后8小时可注满水池.点评:“列表法”在分析等量关系中,有其特点,但重点还应是在培养学生寻找等量关系的意识和能力上,提高“建模”能力.行程问题例5.由甲地到乙地前32的路是高速公路,后31的路是普通公路,高速公路和普通公路交界处是丙地.A 车在高速公路上的行驶速度是100千米/时,在普通公路的行驶速度是60千米/时.B 车在高速公路上的行驶速度是110千米/时,在普通公路上的行驶速度是70千米/时.A 、B 两车分别从甲、乙两地同时出发相向行驶,在距离丙地44千米处相遇,求甲、乙两地之间的距离是多少?分析:本题在相遇过程中A 、B 两车同时出发相向而行至相遇如图3-5-1所示,相等关系是A 车行驶时间=B 车行驶时间.距丙地44千米处,有两种可能,(1)相遇处在高速公路上距丙地44千米,(2)相遇处在普通公路上,解题时要考虑到这两种情况,再根据实际取舍.解:设甲、乙两地相距x 千米,A 车从甲地到丙地,需要15010032xx=(小时),B 车从乙地到丙地,需要2107031x x=(小时), ∵210150x x > ∴A 、B 两车只能在高速公路上距丙地44千米处相遇.列方程得,1104470311004432+=-xx 解得441=x .答:甲、乙两地之间的距离是441千米.点评:“线示法”分析等量关系比较方便.但要注意分类讨论各种情况,以免挂一漏万.利息问题例6.大宝、小宝共利用假期打工1000元,大宝把他的工钱按一年期教育储蓄存入银行,年利率为1.98%,免收利息税,小宝把他的工钱买了月利率为2.15%的债券,但要交纳20%的利息税,一年后两人得到的收益恰好相等,问两人的压岁钱各是多少?分析:抓住这一问题的等量关系.1.利息(免税的)=存入钱数×年利率,2.利息(不免税的)=存入钱数×年利率×(1-税率),3..大宝的收益=小宝的收益.解:设大宝的工钱为x元,则小宝的工钱为(1000-x)元,由题意,得.1⨯98%⨯⨯x.=x-(80%100012%).215解得510x(元),1000-x=490(元).=答:大宝的工钱是510元,小宝的工钱是490元.【自我测试】一、基础测试1.在高速公路上,一辆长4米,速度为110千米/时的轿车准备超越一辆长12米,速度为100千米/时的卡车,则轿车从开始追及超越卡车,需要花费的时间约是()A.1.6秒B.4.32秒C.5.76秒D.345.6秒2.有一旅客携带30公斤行李从某机场乘飞机返回绵阳,按民航规定,旅客最多可免费携带20公斤行李,超重部分每公斤按飞机票价格的1.5%购行李票,已知该旅客现已购行李票60元,则它的飞机票价为()A.300元B.400元C.600元D.800元3.一年期定期储蓄年利率为2.25%,所得利息要交纳20%的利息税,已知某储户有一笔一年期定期储蓄到期纳税后得利息450元,问该储户存入多少本金?4.某商品的进货单价为280元,按25%的利润率确定售价.后因市场发生变化,决定按原定价格的八五折出售,问这时每售出一件这种商品,商店获利多少?5.用内径18毫米的圆柱形试管盛满水后,向一个底面是边长为22毫米的正方形,高是15毫米的空长方体容器内倒水,倒满容器后试管内水面下降约多少毫米?6.一艘船在甲、乙两地之间航行,顺水要3小时,逆水要3.5小时,已知船在静水中航行速度是每小时26千米,求水流速度.7.两人在环形跑道上同向急走,一圈为400米,甲的速度为平均每分钟80米,乙的速度是甲的1.25倍,如果乙在甲的前面100米,多少分钟后两人相遇?8.某人原计划骑车以12km/h的速度由A地去B地.这样可在规定时间内到达B地.但他因事将原计划出发的时间推迟了20min,只好以15km/h的速度前进,结果比规定时间早4min到达B地,求A、B 两地的距离?二、综合能力测试题1.某商店先在广州以每件15元的价格购进一种商品10件,后来又到深圳以每件12.5元的价购进同样商品40件,如果商店销售这些商品时,要获利12%的利润,那么这种商品的销售价应该是_______.2.有一卷铁丝,第一次用去了它的一半少1m,第二次用去了剩下的一半多1m,结果还剩下10m,这卷铁丝原长多少?3.有大中小三个正方形水池,它们的内池分别为6m、3m、2m,把两堆碎石分别沉浸在中、小水池的水里,两个水池的水面分别升高了6cm和4cm,如果将这两堆碎石都沉浸在大水池的水里,大水池的水面升高了多少厘米?4.有一火车以每分钟600m的速度要过完第一、第二座铁桥,过第二座铁桥比过第一座铁桥多用5分钟,又知第二座铁桥的长度比第一座铁桥长度的2倍短50m,试求各铁桥的长?5.某公司向银行贷款40万元用来生产某种新产品,已知该贷的年利率为1.5%(不计复利),每人新产品的成本是2.3元,售价4元,应纳税是销售额的10%,如果每年生产该种产品20万个,并把所得利润用来归还贷款,问需要几年才能一次性还清?(利润=销售额-成本-应纳税款)6.某班共40名学生,其中33人数学成绩不低于80分,32人英语成绩不低于80分,且班上每人在这两科中至少有一科不低于80分.求两科成绩都不低地80分的人数.。
教你如何用等式的性质解一元一次方程。
一、等式的基本性质1.一等式两边加减相同的数/式,仍相等。
例如:若 $a=b$,则 $a+c=b+c$。
2.一等式两边乘除相同的数/式,仍相等。
例如:若 $a=b$,且 $c\neq0$,则$\dfrac{a}{c}=\dfrac{b}{c}$。
3.一等式两边交换位置,仍相等。
例如:若 $a=b$,则 $b=a$。
4.一等式两边同时乘法运算,仍相等。
例如:若 $a=b$,且 $c\neq0$,则 $ac=bc$。
5.一等式两求平方/开平方,两边仍相等。
例如:若 $a=b$,则 $a^2=b^2$,或 $a=\sqrt{b}$,则$a^2=b$。
二、利用等式的性质解一元一次方程在解一元一次方程中,通常采用“等式转化法”或“代入法”。
其中“等式转化法”又叫作“变形法”,即通过变形,使方程转化为形式相同的等式。
这里我们介绍如何利用等式的性质解一元一次方程。
1.同次数等式可以相减。
例如:解方程 $3x+2=5x-6$。
解法:将方程转化为同次数等式:$3x-5x=-6-2$。
由此得到:$-2x=-8$。
将等式两边都除以 $-2$,可得:$x=4$。
2.分式可以通分后相减。
例如:解方程 $\frac{1}{x}+\frac{3}{x-2}=2$。
解法:将分式通分转化为同分母分式:$\frac{x-2+3x}{x(x-2)}=2$。
由此得到:$\frac{4x-2}{x(x-2)}=2$。
将等式两边都乘以 $x(x-2)$,可得:$4x-2=2x^2-4x$。
化简后得到:$2x^2-8x+2=0$。
解得:$x=1-\sqrt{3}$ 或 $x=1+\sqrt{3}$。
3.方程两边可以求平方。
例如:解方程 $\sqrt{2x+5}=x-1$。
解法:将方程转换成同次数等式:$\sqrt{2x+5}=x-1$,即$2x+5=(x-1)^2$。
将方程化简:$x^2-4x+4-2x-5=0$。
各种方程(一元一次、二元一次、三元一次、一元一次、二元二次方程的解法)的解法一元一次、二元一次、三元一次、一元一次、二元二次方程的解法整理稿方程含有未知数的等式叫方程。
等式的基本性质1:等式两边同时加(或减)同一个数或同一个代数式,所得的结果仍是等式。
用字母表示为:若a=b,c为一个数或一个代数式。
则:(1)a+c=b+c(2)a-c=b-c等式的基本性质2:等式的两边同时乘或除以同一个不为0的数所得的结果仍是等式。
(3)若a=b,则b=a(等式的对称性)。
(4)若a=b,b=c则a=c(等式的传递性)。
【方程的一些概念】方程的解:使方程左右两边相等的未知数的值叫做方程的解。
解方程:求方程的解的过程叫做解方程。
解方程的依据:1.移项; 2.等式的基本性质; 3.合并同类项; 4. 加减乘除各部分间的关系。
解方程的步骤:1.能计算的先计算; 2.转化——计算——结果例如: 3x=5*63x=30x=30/3x=10移项:把方程中的某些项改变符号后,从方程的一边移到另一边,这种变形叫做移项,根据是等式的基本性质1。
方程有整式方程和分式方程。
整式方程:方程的两边都是关于未知数的整式的方程叫做整式方程。
分式方程:分母中含有未知数的方程叫做分式方程。
一元一次方程人教版5年级数学上册第四章会学到,冀教版7年级数学下册第七章会学到,苏教版5年级下第一章定义:只含有一个未知数,且未知数次数是一的整式方程叫一元一次方程。
通常形式是kx+b=0(k,b为常数,且k≠0)。
一般解法:⒈去分母方程两边同时乘各分母的最小公倍数。
⒉去括号一般先去小括号,再去中括号,最后去大括号。
但顺序有时可依据情况而定使计算简便。
可根据乘法分配律。
⒊移项把方程中含有未知数的项移到方程的另一边,其余各项移到方程的另一边移项时别忘记了要变号。
⒋合并同类项将原方程化为ax=b(a≠0)的形式。
⒌系数化一方程两边同时除以未知数的系数。
⒍得出方程的解。
3.1一元一次方程及其解法(1)
教材分析
本节课是小学与初中知识的衔接点,学生在小学已经初步接触过方程,了解了什么是方程,什么是方程的解,并学会了用等式性质解一些简单的方程。
本节课在描述一元一次方程的概念后,继续学习用等式基本性质解一元一次方程,从而引出用移项法则解一元一次方程,为学生进一步学习一元一次方程的解法和应用起到铺垫作用。
教学目标
(一)知识教学点
1.由实际问题得到的方程抽象出一元一次方程的概念。
2. 理解等式基本性质,并利用等式基本性质解一元一次方程,并学会检验。
3. 理解移项法则,会用移项法则解一元一次方程。
(二)能力训练点
1.通过对多种实际问题的分析,感受方程作为刻画现实世界的有效模型的意义.
2.由移项变形方法的教学,培养学生由算术解法过渡到代数解法的解方程的基本能力.(三)德育渗透点
增强学生用数学的意识,激发学生学数学的热情。
(四)美育渗透点
用移项法解方程明显比用等式性质方法解方程方便,体现了数学的方法美.
教学重点:利用移项法则解一元一次方程
教学难点:移项法则的理解和运用
教学方法:采用引导发现法发现法则,课堂训练体现学生的主体地位,引进竞争机制,调动课堂气氛。
教学准备:多媒体辅助
教学流程:
1.用猜谜引出学生身边的问题,从而引出一元一次方程的概念。
2.复习等式的基本性质。
3.利用等式基本性质解一元一次方程,同时给出检验的过程。
4.通过学生的观察、交流、归纳得到移项法则。
5.用移项法则解一元一次方程。
教学过程:
教学反思:。
高一数学寒假课程一元一次方程解法 (教师版) 1 / 12 初一数学暑假课程初一数学暑假班(教师版)知识点一解一元一次方程的一般步骤常用步骤具体做法依据注意事项去分母在方程两边都乘以各分母的最小公倍数等式基本性质2 防止漏乘(尤其整数项),注意添括号;去括号一般先去小括号,再去中括号,最后去大括号去括号法则、分配律注意变号,防止漏乘;移项把含有未知数的项都移到方程的一边,其他项都移到方程的另一边(记住移项要变号)等式基本性质1 移项要变号,不移不变号;合并同类项把方程化成ax=b(a≠0)的形式合并同类项法则计算要仔细,不要出差错;一元一次方程解法知识梳理高一数学寒假课程一元一次方程解法(教师版)2/ 12初一数学暑假课程高一数学寒假课程一元一次方程解法 (教师版) 3 / 12 初一数学暑假课程 系数化成1 在方程两边都除以未知数的系数a ,得到方程 的解x =等式基本性质2 计算要仔细,分子分母勿颠倒知识点二 理解方程ax=b 在不同条件下解的各种情况 ①0≠a 时,方程有唯一解ab x =; ②0,0==b a 时,方程有无穷解; ③0,0≠=b a 时,方程无解。
【例1】解方程(1)3(x ﹣1)+1=x ﹣3(2x ﹣1) (2).例题解析5 8;15【例2】解方程:(1)5x+3(2﹣x)=8(2)=1﹣(3)+=(4)[x﹣(x﹣1)]=(x﹣1)2.5;0.7;0.3;11 5【例3】数学迷小虎在解方程﹣1去分母时,方程右边的﹣1漏乘了3,因而求得方程的解为x=﹣2,请你帮小虎同学求出a的值,并且正确求出原方程的解.2a=-;4x=-【例4】方程2﹣3(x+1)=0的解与关于x的方程的解互为倒数,求k的值.-1【例5】已知,x=2是方程2﹣(m﹣x )=2x的解,求代数式m2﹣(6m+2)的值.-4高一数学寒假课程一元一次方程解法(教师版)4/ 12初一数学暑假课程【例6】小明在解方程=﹣1去分母时,方程右边的(﹣1)项没有乘3,因而求得的解是x=2,试求a的值,并求出方程正确的解.4【例7】已知关于x的方程2x﹣a=1与方程=﹣a的解的和为,求a的值.-3【例8】(1)已知式子与式子的值相等,求这个值是多少?(2)已知关于x的方程4x+2m=3x+1的解与方程3x+2m=6x+1的解相同,求m的值.4;0.5【例9】阅读理解:在解形如3|x﹣2|=|x﹣2|+4这一类含有绝对值的方程时,我们可以根据绝对值的意义分x<2和x≥2两种情况讨论:①当x<2时,原方程可化为﹣3(x﹣2)=﹣(x﹣2)+4,解得:x=0,符合x<2②当x≥2时,原方程可化为3(x﹣2)=(x﹣2)+4,解得:x=4,符合x≥2∴原方程的解为:x=0,x=4.解题回顾:本题中2为x﹣2的零点,它把数轴上的点所对应的数分成了x<2和x≥2两部分,所以分x<2和x≥2两种情况讨论.知识迁移:(1)运用整体思想先求|x ﹣3|的值,再去绝对值符号的方法解方程:|x﹣3|+8=3|x﹣3|;知识应用:初一数学暑假课程高一数学寒假课程一元一次方程解法(教师版)5/ 12(2)运用分类讨论先去绝对值符号的方法解类似的方程:|2﹣x|﹣3|x+1|=x﹣9.提示:本题中有两个零点,它们把数轴上的点所对应的数分成了几部分呢?7或-1;x≥-1,三部分【例10】阅读下面的解题过程:解方程:|5x|=2.解:(1)当5x≥0时,原方程可化为一元一次方程5x=2,解得x=;(2)当5x<0时,原方程可化为一元一次方程﹣5x=2,解得x=﹣.请同学们仿照上面例题的解法,解方程3|x﹣1|﹣2=10.5、-3【例11】如果方程的解与方程4x﹣(3a+1)=6x+2a﹣1的解相同,求式子的值.154【例12】方程和方程的解相同,求a的值.2512反思总结初一数学暑假课程高一数学寒假课程一元一次方程解法(教师版)6/ 12高一数学寒假课程一元一次方程解法 (教师版) 7 / 12 初一数学暑假课程理解方程ax=b 在不同条件下解的各种情况 ①0≠a 时,方程有唯一解ab x =; ②0,0==b a 时,方程有无穷解;③0,0≠=b a 时,方程无解。
等式的基本性质及一元一次方程的解法
一、 方程及一元一次方程的概念
1. 含有___________的等式叫做方程
2. 方程必须具备的两个基本的条件是:(1)必须是____________;(2)必须含有
_____________ 例1.下列各式中,是方程的是________________(只填序号)
①3x+5=7;②2+6=8;③6x+y ;④2x-9y=4;⑤x 2+2x-3=0;⑥z+3≠0;⑦
3
62
x =+ 3. 一元一次方程必须具备的三个基本的条件是:(1)只含______个未知数;(2)所含未
知数的次数都是______;(3)方程的两边都是____________; 例2.判断下列各式是否为一元一次方程:
①2
322x x -=-; ②37y x -=; ③1
32x x
-=+; ④325m m +=-
练一练1:
1.下列各式中是方程的是( ) A 2+3=5 B
174y - C 1
322
m m += D 4×1-3 2.下列方程中式一元一次方程的是( )
A 2
843x y -+= B 2
2
5(1)15x x -=-
C 1
345
y y --
=
D 2(32)22(22)x x x -=-- 二、等式的基本性质
1.等式的基本性质1:等式的两边________加上(或减去)
_____________________________________________,所得结果仍是等式。
即:如果a=b ,那么__________________
2.等式的基本性质2:等式的两边________乘以(或除以)
_____________________________________________,所得结果仍是等式。
即:如果a=b ,那么__________________,______________________ 3.如果a=b ,那么__________________(对称性)
4.如果a=b ,b=c ,那么_____________________(传递性)
例3.请用适当的数或整式填空,完成方程的变形,并说明是根据等式的哪一个基本变形以
及是怎样变形的?
(1)如果2x+1=9,那么2x=9-______( ) (2)如果3y=7.5,那么6y=_______( ) (3)如果-3a=3,那么a=_______( ) (4)如果11
22
x y -=-,那么x=_____( )
(5)如果-a=b ,则b=______( )
(6)如果∠1=45°,∠2=45°,那么________( ) 练一练2:
(1)将方程21)3(5)x x -=--(变形为2235x x -=-+的依据是_____________________ (2)将
101130.232
x y x y
-=-=变形为的依据是____________________ 三、方程的解的双重功能
1.检验一个数是不是方程的解
例4.以x =-3为解的方程的个数是( ) ①53x x +=;②
1(53)62x +=;③3(2)2(3)5x x x ---=;④115(1)(32)462
x x -=-- A 1 B 2 C 3 D 4
2.用于求值计算
例5.已知2x =是方程2(-3)+1=的一个解,则的解为x x +
m m ( )
A -1
B -2
C -3
D -4 练一练3:
关于x 的方程3(1)60x a +-=的解为x=-2,则a 的值为( ) A 2 B -2 C
12 D -12
四、三法巧解一元一次方程
1.化小数为整数 2.互为倒数式的巧用
例6.解方程:0.1254x = 例7.解方程:4513()1085435x ⎡⎤
--=-⎢⎥⎣⎦
3.整体代换法
例8.解方程:111141(1)23(1)3433x x x ⎡⎤
-+
--=-⎢⎥⎣⎦
五、解一元一次方程常见的错误
1.移项时出现的错误
例9.解方程:12252
x x +=-
2.去括号时出现的错误
(1)去括号时,括号内的项未变号 (2)去括号时,漏乘括号中的某项 例9.解方程:3(1)2(21)5x x ---= 例10.解方程:2(2)12x --=
3.去分母时出现的错误
(1)漏乘不含分母的项 (2)忽略了分数线的“括号”作用
例11.解方程:
223226x x +--= 例12.解方程:51312
423
x x x -+--=
(3)误以为“0”乘以一个数等于该数 例13.解方程:
2132023
x x
+--=
二、 系数化为1时出现的错误
(1)系数化为1时忘记变“倒数” (2)系数化为1时颠倒分子、分母 例14.
23
32
x =- 例15.2159x x -=-
家庭作业:
1. 若关于x 的一元一次方程
23132
x k x k
---=的解是x =-1,则k 的值是_____________ 2. 已知关于x 的方程1
32232
x m m x x x -+=+=-与方程的解相同,则m=___________
3. 已知x=1是方程(1)32m x x m -=+的解,求代数式2
421m m --的值 解下列方程: (1)52(1)21253x x ⎡⎤
--=+⎢⎥⎣⎦
(2)3272425335x x -++=-
(3)124816x x x x x =++++ (4)233 2.4 3.80.50.20.1
x x x
----=。