全圆方向观测法角度测量

全圆观测法（Full-circle observation method）和方向观测法（Directional observation method）是测量地理方向的两种方法，它们的区别在于测定方向的方式和精度。

1. 全圆观测法：全圆观测法是通过观测天体（如太阳、星星等）在天空中的位置来确定方向的方法。

在全圆观测法中，通过记录天体的仰角和方位角，结合天文学知识和仪器的辅助，计算出目标方向。

这种方法通常需要使用精密的天文仪器和精确的观测数据。

全圆观测法的优点是可以提供非常精确的方向测量结果，在导航和地理测量等领域中被广泛使用。

2. 方向观测法：方向观测法是通过测量地面上的方向标志（如测向标、导线等）来确定方向的方法。

在方向观测法中，通过使用测向仪或者经纬仪等测量仪器，对方向标志进行测量，以确定目标方向。

这种方法通常更适用于小范围的测量，例如在工程测量、土地测量和建筑测量等领域中常被使用。

方向观测法相对于全圆观测法而言，测量过程相对简便，但精度可能会稍低一些。

总结起来，全圆观测法是通过观测天体在天空中的位置来确定方向，提供较高精度的方向测量结果；而方向观测法是通过测量地面上的方向标志来确定方向，适用于小范围测量，
但精度相对较低。

选择使用哪种方法取决于具体的应用需求和测量精度要求。

在本例中：
12(L
R)
1(981928981930)98 1929
2
*
9
a
注意!
由于水平度盘是顺时针刻划注记的，所 以计算水平角时:
总是用右目标的读数减去左目标的读数。*
如果不够减，则应在右目标的读数上加上360˚， 再减去左目标的读数，决不可以倒过来减。
10
a
对一个角度观测多个测回时：
为了减弱度盘分划误差的影响，各测回在盘左 位置观测起始方向时，需要起始方向安置水平度盘 读数。
0 02 06
* B 37 44 15 217 44 05 +10 37 44 10 37 42 00 37 42 04
C 110 29 04 290 28 52 +12 110 28 58
。 D 150 14 51 330 14 43 +8 150 14 47 。 * A 0 02 18 180 02 08 +10 0 02 13
12
a
1．方向观测法的观测方法
设O为测站点，A、B、C、D为观测点。
B A
C D
O
（1）在测站点O安置经纬仪
在A、B、C、D观测目标处竖立观测标志。
13
a
B A
C D
OLeabharlann （2）盘左位置选择一个明显目标A作为起始方向，瞄准零方向A，将水 平度盘读数安置在稍大于0˚处，读取水平度盘读数； *
顺时针方向依次瞄准B、C、D各目标，分别读取水平
（1）计算两倍视准轴误差2c值 2c =盘左读数—（盘右读数±180˚）
以OA方向为例：
2 c 0 0 2 1 2 ( 1 0 2 8 0 0 1 0 ) 8 1 2 0

i=0.5m1m2*ρ/Pm 0m用皮尺丈量。 例：m1m2=5mm; 0m=30m Α= 21°05′18″
Pm=11.569
i=44.573 ″ (44.57)
• （5）竖盘指标差检验和校正
• 检验：左、右瞄准同一目标(横丝切顶)，指标水准管 居中，读数：L，R
x 1 R L 360
2C=L′-R′±180 R= R′+C 例： L′=10°02′36″
R′= 190°03′24″ 2C=-48 R= R′+C= 190°03′00″ L=L-C=R′= 10°03′00″
（4）横轴垂直于竖轴的检验 距墙20~30米左右安放仪器，以 盘左使仪器仰角约30度指向墙上 一个点P，拧紧水平制动螺旋， 将望远镜旋转到水平位置，标出 此 理 m合2时 盘 ，重的 右 测合十 得 说，字到明则丝另有表交一i明角叉个两影中点轴响心m垂，2点直。视m。若准1不。 m面1重同与和 竖直面的夹角，Pm是竖直面。
照准部180度，若气泡仍居中则表明两轴垂 直，否则若偏移量超过一格则需要进行校正。 （2）十字丝竖线垂直横轴检验
用十字丝交点精确瞄准一目标点，微动旋 转望远镜上下转动。若该点不偏离竖丝，表 示十字丝竖丝垂直于仪器横轴。否则应进行 校正
（3）视准轴垂直于横轴 检验
视准轴不垂直于横轴误差c, 对水平目标Xc=C,不考虑横 轴不水平误差，照准一大致 水平的目标，盘左盘右读数， 刚好相差180则视准轴垂直 于横轴，根据公式计算。
（1）丈量方法 基本方法同上，但每一尺段要两端读数，同时测
量拉力和温度。 （2）成果整理
经过检定的钢尺长度可用尺长方程式表示：
lt l0 l (t t0 )l0
lt—温度为t时的钢尺实际长度； lo—钢尺的名义长度； △l—尺长改正值，即温度在to时钢尺全长改正数； α—钢尺膨胀系数，一般取α=1.25×10-5 ; to—钢尺检定时的温度，一般取20°C； t—量距时的温度。

全圆方向法是适应于较低精度的角度观测方法，全 组合测角法适用高精度角度观测。
第3页/共14页
二、仪器视准轴误差和水平轴倾斜误差
㈠ 视准轴误差 仪器的视准轴不与水平轴正交所产生的误差称为 视准轴误差。 产生视准轴误差的主要原因有：
➢望远镜的十字丝分划板安置不正确； ➢望远镜调焦镜运行时晃动； ➢气温变化引起仪器部件的胀缩，特别是仪 器受热不均匀使视准轴位置变化。
第4页/共14页
如图所示，视准轴偏离了与水
平轴HH′正交的方向而产生视准轴
误差c，规定视准轴偏向垂直度盘
一侧时，c为正值；反之，c为负
值。测量学中已经证得，视准轴
误差c对水平方向观测值的影响
为 c
c c
cos
式中a为观测时照准目标的垂直 角。由式可知，c的大小除与c值 有关外，还随照准目标的垂直角a 的增大而增大，当a =0，则
c =0。
第5页/共14页
盘左时视准轴偏向垂直度盘一侧，正确的水平度盘读数L0 较有视 准轴误差影响c 时的实际读数L为小，故
L0 L c
以盘右观测时，视准轴则偏向盘左时的另一侧，这时正确的水平 度盘读数R0显然大于有视准轴误差影响 c的实际读数R，故
R0 R c
取盘左、盘右读数的中数，得 A 1 (L R) 2
2．用两个度盘位置取平均值的方法消除视准轴误差影响的前提条 件是什么?
3．垂直轴倾斜误差的垂直轴倾斜误差对方向观测值的影响与观测目标的垂 直角和方位有关？为了削弱垂直轴倾斜误差对方向观测的影响， 《规范》对观测操作有哪些规定?
5．影响方向观测精度的误差主要分哪三大类？各包括哪些主要内 容?
水平轴所形成的平面呈水平状态，下图中的 HN，1H即N 画有斜线的

角度测量
方向观测法（全圆测回法）适用于观测两个以上的方向
观测方法:
1.安置仪器：0点置经纬仪，A、B、C、D设置目标。

2.盘左：对零度，瞄A,再顺时针瞄B C D A,第二次瞄A称为归零，分别读数，记入手簿，上半测回
3.盘右：瞄A、逆时针瞄D C、B、A,分别读数记入手簿，下半测回。

4.上、下半测回，组成一测回：观测n测回时，起始方向读数变化为180° /n
5.计算⑴ 计算两倍照准差（2C） : 2C=t左-（盘右土180°）⑵ 计算各方向平均值：平均读数=［盘左+（盘右土180° ）］/2
6. 限差：⑴ 半测回归零差 ⑵ 上、下半测回同一方向的方向值之差 ⑶ 各测回的方向差 ⑷ 根据不同精度的仪器有不同的规定
水平角（全圆测回法）观测手薄
III
2000.11.21 者
;[2] 一测回起始方向与归零方向平均值： [90 01 09]=1/2(90 01 03+90 01 15)
[4 ][90 01 03]=1/2[90 01 00-270 01 06 士 180 ]
【下载本文档，可
以自由复制内容或自由编辑修改内容， 更多精彩文章，
期待你的好评和关注，我将一如既往为您服务】
⑶A 方向（归零）平均值，填写在括号内 ⑷ 计算归零后的方向值 ⑸ 计算各方向的测回平均值 ⑹计算各目标间角值 [1] 一测回起始方向与归零方向平均值: [3] [0 01 06]=1/2[0 01 00-180 01 12
[0 01 09]=1/2(0 01 06+0 01 12)
士 180;。

全站仪全圆法
全站仪全圆法是全站仪测量的一种方法，也称为逆向测量法。

它相对于其他测量方法
具有精度高、能够同时测量水平和垂直方向等优点，适用于建筑物、桥梁、道路等工程测
量中的定位和高程测量。

全站仪全圆法的测量步骤如下：
1. 全站仪架设：先选择一台全站仪，将其架设在测量点上。

在设置的过程中，应调
整好全站仪朝向和水平度。

2. 观测目标点：对于需要进行定位或高程测量的点，将其放置一个特殊的测量底座，使用采集棒观察该点并记录其坐标。

3. 测量朝向：使用全站仪的水平圆盘调整，使其水平圆盘指示正北方向，再将全站
仪旋转到指向目标点的方向，并用全站仪记录该方向的角度，称为初始方向。

4. 旋转全站仪：保持全站仪在稳定状态下旋转360度，将其记录下来。

这个步骤可以通过全站仪的抽象可视化图来进行辅助。

5. 计算目标点相对于初始方向的角度：通过前后两次测量全站仪朝向的角度，计算
目标点在初始方向下的角度。

例如，如果前一次测量全站仪朝向的角度为30度，后一次测量为200度，那么这个目标点的角度为（200-30）=170度。

6. 计算目标点的坐标：通过全站仪记录的数据，很容易可以计算得出目标点的坐标值。

通过以上的步骤，我们可以测量出目标点的坐标和方向角度，并且可以将其保存在文
档中，以便后续处理。

总结来看，全站仪全圆法是一种比较高精度的测量方法，具有兼测水平垂直的特点。

在实际应用中，需要注意测量全站仪的架设和调整，以及测量过程中的数据记录和处理。

当然，在具体应用中，还需要符合实际情况和相关标准，从而进行测量定位工作。

全圆测回法观测水平角的步骤嘿，朋友们！今天咱们来聊聊全圆测回法观测水平角这事儿，就像是一场超有趣的探秘之旅呢。

首先啊，你得像个准备出击的猎人一样，把仪器稳稳地架设在合适的地点。

那仪器啊，就像是我们的魔法武器，三脚架就像它坚实的三条腿小凳子，稳稳地托着它。

这一步可不能马虎，要是没架稳，就像盖房子没打好地基，后面全得乱套，那可就成了一场“摇摇欲坠的闹剧”啦。

接着呢，开始对中整平。

这就好比是给我们的魔法武器校准准星，要让它的视线像箭一样直直地射向目标。

这个过程就像是给调皮的小娃娃整理衣服，要这儿弄弄，那儿整整，直到它规规矩矩的。

然后啊，就正式开始观测啦。

先选定一个起始方向，这个起始方向就像是我们这场“角度狩猎”的起跑线。

把望远镜对准它的时候，感觉就像是用枪瞄准猎物，要聚精会神的。

观测第一个方向的时候，记录下这个角度值，这个数值就像是我们收获的第一个“猎物标记”。

然后呢，顺时针依次观测其他方向。

这就像沿着一个圆形的魔法阵逐个检查宝藏一样，每一个方向都是一个神秘的小宝藏等待我们去发现。

在观测的过程中，要特别注意照准的准确性。

就像是用筷子夹花生米，得又准又稳，稍微偏差一点，那得到的角度可能就像被施了魔法的数字，变得乱七八糟的。

每观测一个方向，都要仔细地记录下角度值。

这些数值在本子上排列起来，就像一串神秘的密码，只有我们按规则解读，才能知道这个“角度世界”的秘密。

当我们顺时针观测完一圈之后呢，还要再逆时针观测回来。

这就像是沿着魔法阵走了一圈又倒着走回来，看看有没有遗漏什么宝贝或者魔法陷阱。

在整个观测过程中，如果遇到什么问题，比如说视线被挡住啦，就像突然有个大怪兽横在你的面前，挡住了你的寻宝之路。

这时候可不能慌，要想办法调整，重新找到正确的方向。

最后呢，把所有的数据按照特定的公式进行计算和整理。

这一步就像是把我们收集到的宝藏碎片拼凑起来，形成一个完整的宝藏地图，让我们清晰地知道这个水平角到底是多少。

全圆测回法观测水平角虽然有点小复杂，但就像一场充满惊喜的冒险，只要我们认真对待，就能顺利完成这个“角度狩猎”任务啦。

D 240 15 57 60 15 49 +8 240 15 53 150 12 29
A 90 03 25 270 03 18 +7 90 03 22
*
*
4．计算方法
（1）半测回归零差: J2 ≤ 12 " ；J6 ≤ 18 " 。
（2）2C值（两倍照准误差）: 2C=盘左读数－（盘右读数±180°）。
3.通过前面的实践课，同学们会用测回 法观测、记录、计算水平角了没有？
展示学生成果
盘位 目标 水平度盘读数
水平角
半测回角
测回角
备 注
A 左
B
0゜01′24″ 60゜50′30″
60゜49′06″
0
60゜49′03″
C 180゜01′30″
右
60゜49′00″
D 240゜50′30″
展示学生成果
测站
目的：为了减少度盘分划误差的影响。
如n=2时，各测回起始方向值为180°/2=90°，即第一测回与第二 测回要错开90°，即第一测回为0°，第二测回为90°； 如n=3时，各测回起始方向值为180°/3=60°，即第一、第二、第 三测回要错开60°，即第一测回为0°，第二测回为60°，第三测 回为120°。
[小结]：
全圆测回法 （1）观测程序：先盘左，再盘右 （2）观测方法： （3）记录、计算
。 1.半测回归零差:J2 ≤ 12 " ；J6 ≤ 18 "
2.2C值（两倍照准误差）:2C=盘左读数－（盘右读数±180°）。 一测回内2C互差：J2≤18 " ；J6不作要求。
3.各方向盘左、盘右读数的平均值：
0
230 33 18 295 27 00

读数 bL＝ 52º33´40″， cL＝ 91º21´20″ dL＝ 138º42´30″， aL″ ＝ 0º02´00″ 以上过程称为上半测回。 （3） 倒转望远镜成盘右位置。观测A→D → C → B → : aR´ ＝ 180º02´12″，dR´ ＝318º42´50″ cR´ ＝ 271º21´30″，bR´ ＝ 232º33´40″ aR´ ＝ 180º02´10″ 称为下半测回。
计算归零后的方向值 把各方向值－0º02´06″＝归零方向值 计算各测回平均方向值 计算各方向之间水平角
（6）限差 DJ2 半测回归零差 2C变化范围 各测回同一方向差 12″ 18″ 12″ DJ6 18″ 44″ 24″
水平角观测~全园观测法
成功者决不放弃，放弃者绝不成功
第一ห้องสมุดไป่ตู้量队
张启才
全圆方向观测法
适用于观测多于三个方向之间的水平角 （1）经纬仪置于O点，盘左 （正镜），选择目标最清晰的 点为A，瞄A，对零度读数aL´ ＝ 0º 02´00″
（2） 再照准B、C、D点，重复再瞄A，称为上半测回归零。 目的：检查仪器是否发生变化。
A，读数
（4）若需观测n测回，起始方向读数改变180º /n （5）计算
计算同一方向的2C
2C＝盘左读数－（盘右读数± 180º） 计算各方向平均值 1 平均值＝ [盘左读数＋盘右读数± 180º）] 2 计算起始方向平均值，填写在小括号内
1 (002'05"002'06" ) 002'06" 2

竖直角观测（与全圆观测法测水平角）一、目的和要求1、掌握DJ6经纬仪的操作方法及水平度盘读数的配置方法。

2、掌握全圆方向观测法观测水平角的观测顺序、记录和计算方法。

3、掌握竖直角观测、记录及计算的方法。

4、掌握竖盘指标差的计算方法。

5、全圆方向法限差：半测回归零差不得超过±18″；各测回方向值之差不得超过±24″。

6、竖直角观测限差：同一目标各测回垂直角互差在±25″之内7：实验小组由5---6人组成二、任务在校内选取五个坐标点（1号教学楼北湖畔五根路灯杆），依据全圆方向观测法观测水平角，并做记录。

同时选取目标观测其竖直角。

三、仪器工具DJ6经纬仪1，记录本 1。

四、方法与操作步骤1、全圆方向观测法观测水平角1）、选定四个固定点的位置，并用花杆标定出来。

2）、选定一测站点的位置，并用木桩标定出来。

3）、在某测站点上安置仪器，对中整平后，按下述步骤观测：①盘左，瞄准左边目标A，并使水平度盘读数略大于零，读数并记录；顺时针转动照准部，依次瞄准B、C、D、A个目标，分别读取水平度盘读数并记录，检查归零差是否超限；②盘右，逆时针依次瞄准A、B、C、D、A个目标，读数并记录，检查归零差是否超限；③计算2C=盘左读数-（盘右读数±180°）各方向的平均读数=[盘左读数+（盘右读数±180°）]/2；将各方向的平均读数减去起始方向的平均读数，即得各方向的归零方向值。

第二测回观测时，起始方向的度盘读数安置于90°附近，同法观测。

各测回同一方向值的互差不超过±24″，取其平均值，作为该方向的结果。

2、竖直角观测1）、在某指定点上安置经纬仪。

2）、盘左位置照准目标，读取竖盘的读数L 读。

记录者将读数值L 读记入竖直角测量记录表中。

3)、根据确定的竖直角计算公式，在记录表中计算出盘左时的竖直角α左。

4)、再用盘右的位置照准目标，并读取其竖直度盘的读数R 读。

（2）盘左位置
选择一个明显目标A作为起始方向，瞄准零方向A，将 水平度盘读数安置在稍大于0˚处，读取水平度盘读数；
顺时针方向依次瞄准B、C、D各目标，分别读取水平 度盘读数。 为了校核，再次瞄准零方向 A，称为半测回归零，读 取水平度盘读数。
零方向A的两次读数之差的绝对值，称 为半测回归零差。 归零差不应超过相应的规定。 如果归零差超限，应重新观测。 以上称为上半测回。
光学经纬仪的构造
经纬仪按读数设备不同分为光学经 纬仪和电子经纬仪。
光 学 经 纬 仪按 测角精 度 ， 分 为 DJ07 、 DJ1、DJ2、DJ6和DJ15等不同级别。下标 数字07、1、2、6、15表示仪器的精度等 级，即“一测回方向观测中误差的秒 数”。 在工程中最常用的是DJ6和DJ2型光学 经纬仪。本节主要介绍DJ6型光学经纬仪。
竖直度盘 竖盘指标 竖盘指标水准管 竖盘指标水准管微动螺旋
当竖盘指标水准管气泡居中时，竖盘指标所处 的位置称为正确位置。 观测垂直角时，竖盘指标必须处于正确位置才 能读数。
光学经纬仪的竖直度盘得注记形式有两种：
顺时针方向注记
逆时针方向注记
竖直度盘构造的特点是：
当望远镜视线水平，竖盘指标水准管气 泡居中时，盘左位置的竖盘读数为90˚，盘右 位置的竖盘读数为270˚。
L bL aL 982048 001 30
98 1918
278 21 12 瞄准右目标B，读取水平度盘读数bR。 下半测回 180 01 42 瞄准左目标A，读取水平度盘读数aR。 盘右位置的水平角角值（也称下半测回角值）βR为：
（3）盘右位置
主要用途
二等平面控制 三、四等平面 图根控制测量 测量及精密工 控制测量及一 及一般工程测 量 般工程测量 程测量

，或者是过两条方向线的竖直面所夹的两面角。
如图3-1所示： 在过A点的铅垂线上，水平地安置一个有刻
度的圆盘(称为水平度盘)，度盘中心在o点，过
AB、AC竖直面与水平度盘交线为on、om，在水
平度盘上读数为n、m。则∠nom为所测得的水平
角。一般水平度盘是顺时针刻划，则：
∠nom=m-n=β
(3-1)
上半测回、下半测回、几个测回。 如要提高观测精度，须观测多个测 回。各测回仍按180°/n的角度间隔变换水 平度盘的起始位置。 半测回归零差，对于DJ6经纬仪，归 零差不应超过±18″，否则应重新观测。
工程测量学
3 角度测量
a.方向观测法步骤：
（1）安置仪器于C 点，首先 B 用盘左，水平度盘设置在0度
水平度盘套在竖轴中可以自由转动。
竖直度盘固定在横轴的一端与望远镜一起转动。
（2）水平度盘转动的控制装置：测水平角时水平度盘是不动的，这样照准
部转至不同的位置，可以在水平度盘上读数求得角值，但有时需要设定水平度盘 一定的读数时，就要转动水平度盘。
控制水平度盘转动的装置有位置变动手轮和复测装置两种。
工程测量学
水平度盘读数： 7工3 程 测04量 学24″
7 DJ6级光学经纬仪分微尺测微器光路图: b.读数方法:
134°53′.1
工程测量学
87°58′.1
3 角度测量
• (1)读取分微尺内度分划的度数； • (2)读取分微尺0分划至该度分划所在分微尺上的分数； • (3)计算以上二数之和为读数 窗的角度读数( ) 。 • 水平度盘角度是215°06.5′
图单平行玻璃测微器读数窗
平度盘。读数时，转动测微手轮，使度盘分划线精确地平分双指标，按双指标线

技巧：气泡移动方向与左手大拇指移动方向一致。
用光学对点器对中时，对 中和整平会相互影响，应 反复调整，直至两者都满 足。
二、经纬仪的基本基本操作及注意事项
3.瞄准 松开水平制动扳手和垂直制动扳手，将望远镜 转向明亮的背景，转动目镜对光螺旋，使十字 丝清晰；旋转仪器，通过粗瞄器对准目标，拧 紧水平制动扳手；转动物镜对光螺旋，使目标 成像清晰，并消除视差；转动望远镜，瞄准标 杆的底部，拧紧垂直制动扳手。旋转水平微动 和垂直微动螺旋，用十字丝单竖丝精确瞄准标 杆底部的中央。如果看不到标杆的底部，可用 双竖丝夹住直立的标杆。 4.读数 读数前应熟悉仪器的读数装置和读数方法，分 清水平度盘和竖直度盘。用分微尺测微器读数 时，估读至0.1'(6")。
一、水平角测量 (一)测回法
水平角(测回法)观测手簿
测站 目标 A 左 竖直度 水平度盘读数 半测回角值 一测回角值 各测回平均值 º ' " º ' " º ' " º ' " 盘位置 0º 01'10" 147º 11'20" 备注
B
O A 右 B A
147º 12'30"
147º 11'13" 180º 01'50" 147º 11'05" 327º 12'55" 147º 11'11" 90º 02'35"
基座锁紧 望远镜围绕横轴可垂直翻转。 轮(固定螺旋)
一、TDJ6E型光学经纬仪的基本构造
粗瞄器 (三)读数装置 包括水平度盘及控制装置、竖直度盘、 光路系统、读数显微镜和测微器。 1.水平度盘及控制装置 水平度盘是由光学玻璃制成的圆盘， 垂直制动 扳手 边缘按顺时针刻有0~360º 分划。 压下转盘手轮的压杆，将转盘手轮推 望远镜 进，转动手轮，可改变水平度盘读数。 物镜 2.竖直度盘及控制装置 垂直微动 螺旋 竖度盘用于观测竖直角，盘体垂直固 定在横轴一端，与望远镜同步转动。 照准部 观测竖直角时，整平仪器，将补偿器 水准管 锁紧轮转到ON，即可进行观测。观测 水平微动 完毕，要转到OFF，防止损坏补偿器。 螺旋

竖直读盘 反光镜 测微轮
换像手轮
水平读盘 反光镜
（二） 经纬仪的操作
1、光学对中
要求：3mm （1）大致水平大致对中 眼睛看着对中器，拖动三脚架两个脚,使仪器 大致对中,并保持“架头”大致水平。 （2）伸缩脚架粗平 根据气泡位置，伸缩三脚架两个脚，使圆水 准气泡居中。
B
2、整平(leveling) 要求：1格
C
H L C V
H L
L’
L’
V
一、经纬仪轴线应满足的条件
1、VV⊥LL ——照准部水准
C
管轴的检校。
2、HH⊥十字丝竖丝——十字 H
H C V L
丝竖丝的检校
3、HH⊥CC ——视准轴的检
L
校
V
L’
L’
4．HH⊥VV
——横轴
C
的检校
5．竖盘指标差应为零 — —指标差的检校 6．光学垂线与VV重合 — —光学对中器的检校 7. LL∥VV——圆水 准器的检验与校正(次 要)
水平角(horizontal
竖直角(vertical
angle)测量
angle)测量
（一）水平角(horizontal angle) 定义
水平度盘(horizontal circle)
地面一点至两目标方
向线在水平面上投影 的夹角，称为水平角。 范围：顺时针00~3600
O
a
A b
B
β＝b－a
a o b
270 0
180
x
90
2、计算公式
1 （1）指标差: x ( L R 360) 2 1 或 x ( 右 左） 2
对于顺时针注记的：
正确的竖直角α=(90°+x) -L=α左+x

第3章 角 度 测 量内容提示：本章主要介绍了角度测量的原理和方法、经纬仪技术操作、检验与校正、角度测量误差的影响与消除方法，并介绍了电子经纬仪。

其重点内容为经纬仪技术操作和主要条件的检验校正、水平角和竖直角观测与计算方法。

其难点为方向观测法观测水平角和竖直角的计算、角度测量误差的消除方法。

3.1 角度测量原理角度是确定地面点位的三要素之一。

角度测量是测量工作的基本内容，它包括水平角测量和竖直角测量。

角度测量仪器为经纬仪。

3.1.1 水平角测量原理地面上一点到两个目标点连接的两条空间方向线垂直投影在水平面上所形成的夹角，或过空间两条相交方向线的竖直面所夹的两面角，称为水平角，通常用β表示。

如图3.1所示，A、O、B为地面上三点，过OA、OB直线的竖直面V1、V2，在水平面H上的交线O'A'、O'B'，所夹的角∠A'O'B'就是OA和OB之间的水平角。

图3.1 角度测量原理为了测量水平角，设想在过O点的铅垂线上，水平地安置一个刻度盘(简称为水平度盘)，使刻度盘刻划中心(称为度盘中心)o与O在同一铅垂线上。

竖直面V1、V2与水平度盘有交线oA"、oB"，通过oA"、oB"在水平度盘读数为a、b(称为方向观测值，简称方向值)，一般水平度盘是顺时针刻划和注记，则所测得的水平角为β(3-1)=b−a由上式可知，水平角值为两方向值之差。

水平角取值范围为0 ～360 ，且无负值。

第3章 角度测量·49··49·3.1.2 竖直角测量原理 在同一竖直面内，地面某点至目标的方向线与水平线的夹角，称为竖直角或倾斜角。

用α表示。

若目标方向线在水平线之上，该竖直角称为仰角，取值为"＋"；若目标方向线在水平线之下，该竖直角称为俯角，取值为"－"。

如图3.l 所示，A α为正值，B α为负值。

二、方向观测法方向观测法，也称为全圆观测法，通常用于一个测站上照准目标多于三个的观测。

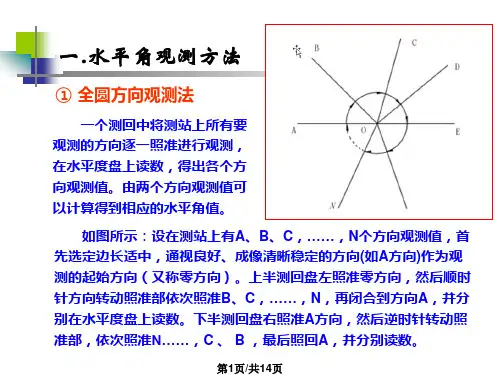
如图3-10所示，设O为测站点，A、O、C、D为目标点，在此情况下通常采用方向观测法。

1．方向观测法的观测方法(1)安经纬仪于站点O上，对中、整平后使仪器处于水平。

①照准起始方向(又称零方向)A，将水平度盘配置为所需读数，精确照准后读取水平度盘的读数(如00°12'42")。

②松开水平制动螺旋，按顺时针旋转照准部，照准目标b，读取水平度盘的读数(如60°18'42")；③同样依次观测目标C、D，并读取照准各目标时的水平度盘读数(如116°40'18"、185°17'30")；④继续顺时针转动望远镜，最后再观测零方向A，并读取水平度盘的读数(如00°02'30")，此照准A称之为归零。

此次零方向的水平度盘读数与第一次照准零方向的水平度盘读数之差称为归零差，若归零差满足要求(DJ6限定为18")，即完成了上半测回的观测。

(2)纵转望远镜使仪器处于盘右状态，再按逆时针方向依次照准目标A、D、C、B、A，称为下半测回。

同上半测回一样，照准各目标时，分别读取水平度盘的读数并记入记录手簿。

下半测回也存在归零差，若归零差满足要求，下半测回也告结束。

上、下半测回合称一个测回。

2 方向观测法的角值计算方向观测法的计算步骤：(1)计算两倍照准误差2c值：2c值=盘左读数—(盘右读数±180°)盘左读数大于180°时取“+”号，盘左读数小于180°时取“-”号。

(2)计算各目标的方向值的平均读数照准某一目标时，水平度盘的读数，称为该目标的方向值。

方向值平均读数=[盘左读数+(盘右读数±180°)]／2 (式中加减号取法同前)。