七 主梁截面承载力与应力验算
- 格式:doc
- 大小:242.92 KB
- 文档页数:18

梁正截面承载力计算公式梁正截面承载力计算公式是结构工程中非常重要的一部分,它关系到梁在受力情况下的安全性和稳定性。
咱们先来说说梁正截面承载力是个啥。
想象一下,一根大梁横跨在两个支撑点上,上面承受着各种重量和压力。
这时候,梁的正截面,也就是从正面看被切开的那个面,能够承受多大的力而不发生破坏,这就是梁正截面承载力要研究的问题。
梁正截面承载力的计算公式可不是随便来的,那是经过无数科学家和工程师们反复试验、研究和推导出来的。
比如说,在一次建筑工地上,我就看到工人们在为一根大梁的设计犯愁。
他们拿着图纸,对照着各种规范和公式,眉头紧锁。
我凑过去一看,原来是在计算这根梁的正截面承载力是否满足要求。
这计算公式里包含了好多因素呢,像混凝土的强度、钢筋的强度和数量、梁的截面尺寸等等。
就拿混凝土强度来说吧,不同强度等级的混凝土,能提供的承载能力可大不一样。
比如说,C30 的混凝土和 C50 的混凝土,强度上就有明显的差别。
在计算梁正截面承载力的时候,就得把这些差别考虑进去。
要是用错了混凝土的强度等级,那可就麻烦啦!再说说钢筋。
钢筋在梁中就像是骨架一样,起着增强承载能力的作用。
钢筋的数量、直径、布置方式都会影响梁的正截面承载力。
有一次,我看到一个工程案例,就是因为钢筋布置不合理,导致梁在使用过程中出现了裂缝,差点酿成大祸。
梁的截面尺寸也很关键。
截面越大,通常能承受的力也就越大。
但也不是说截面越大就越好,还得考虑建筑空间的限制和成本的问题。
在实际应用中,计算梁正截面承载力可不能马虎。
一个小小的错误,可能就会导致严重的后果。
所以工程师们在计算的时候,那是要反复核对,确保万无一失。
比如说,在一个大型商场的建设中,设计师们为了确定主梁的正截面承载力,进行了大量的计算和模拟。
他们不仅要考虑商场内部的货架、人员等荷载,还要考虑可能的地震、风等自然灾害的影响。
每一个数据,每一个参数,都要经过精心的选择和计算。
总之,梁正截面承载力计算公式是建筑结构设计中的重要工具,它就像是一把尺子,帮助我们衡量梁的承载能力是否足够,是否能够安全可靠地为我们服务。

混凝土梁受剪承载力验算方法研究一、前言混凝土梁是建筑结构中常见的构件,在设计和施工中需要考虑其受剪承载力。
本文将探讨混凝土梁受剪承载力验算方法,包括验算方法原理、验算步骤和实例应用。
二、验算方法原理混凝土梁受剪承载力的验算方法基于混凝土的本构关系、梁截面的几何形状和受力状态、混凝土与钢筋之间的黏结性等因素。
常用的验算方法包括弯剪理论、杆件效应理论、塑性铰理论等。
其中,弯剪理论是最常用的一种方法。
其基本假设是梁截面在受力时形成一个塑性铰,使得梁截面分为一个受弯区和一个受剪区。
在此基础上,可以得到混凝土梁受剪承载力的计算公式。
三、验算步骤混凝土梁受剪承载力的验算步骤如下:1. 确定受力状态和截面形状首先需要确定混凝土梁的受力状态和截面形状,包括梁的跨度、荷载和间距等参数。
同时需要确定梁截面的几何形状,如矩形截面、T形截面、L形截面等。
2. 计算混凝土的抗剪强度根据混凝土的强度等级和配合比等参数,可以计算出混凝土的抗剪强度。
常用的计算公式包括:fcu = 0.28fck^(2/3)fctm = 0.7fctk^(2/3)fcd = fcu/γc其中,fcu为混凝土的极限抗压强度,fck为混凝土的标准立方体抗压强度,fctm为混凝土的平均拉应力,fctk为混凝土的标准立方体拉应力,fcd为混凝土的设计抗压强度,γc为混凝土的安全系数。
3. 计算钢筋的抗剪强度钢筋的抗剪强度一般可以按照其强度等级和截面积计算得出。
常用的计算公式包括:Asv = ρsv Afsv = fyv/γsVsw = Asv fsv其中,Asv为钢筋的截面积,ρsv为钢筋的配筋率,A为梁截面的面积,fyv为钢筋的屈服强度,γs为钢筋的安全系数,Vsw为钢筋的抗剪力。
4. 计算混凝土和钢筋的干涉区域混凝土和钢筋之间的黏结性是影响混凝土梁抗剪承载力的重要因素。
需要计算混凝土和钢筋的干涉区域,以确定钢筋的有效长度和抗剪力的传递路径。
5. 计算混凝土梁的抗剪承载力根据弯剪理论,可以得到混凝土梁的抗剪承载力计算公式:Vrd = Vc + Vs其中,Vrd为混凝土梁的设计抗剪承载力,Vc为混凝土的抗剪承载力,Vs为钢筋的抗剪承载力。

土木工程中的桥梁承载力评估与检测土木工程是一门涵盖广泛领域的学科,其中桥梁工程是非常重要的一部分。
桥梁作为连接两地的纽带,其承载力评估与检测显得尤为重要。
本文将探讨土木工程中的桥梁承载力评估与检测的相关知识。
一、桥梁的承载力评估桥梁的承载力评估是指对桥梁的结构负荷能力进行评估,以确定其是否满足设计要求和使用要求。
评估的过程通常包括承载力计算、结构安全评估和结构健康监测等。
1. 承载力计算承载力计算是桥梁结构设计的基础,它通过对桥梁各部分材料的力学性质和力学行为进行研究,计算出桥梁结构的内力和应力分布,以及结构的强度和稳定性。
承载力计算基于材料力学和结构力学的理论原则,结合工程实践经验,可以准确预测桥梁的承载能力。
2. 结构安全评估结构安全评估是指对桥梁结构的强度、稳定性和使用安全性进行评估,以确定其在设计使用寿命内是否具备足够的安全储备。
评估的内容包括结构的破坏形式、临界荷载和抗震性能等方面。
通过结构安全评估,可以发现桥梁结构存在的弱点和隐患,提出相应的加固和修复方案,确保桥梁的安全可靠运行。
3. 结构健康监测结构健康监测是指对桥梁结构进行定期或实时的监测与检测,以获取结构受力状态和健康状况的信息。
通过使用传感器和数据采集系统,可以获得桥梁的应变、振动和变位等数据,进而对其结构的承载能力和安全状况进行评估。
结构健康监测能够及时发现桥梁结构的异常变化和损伤,为后续的维修和加固工作提供科学依据。
二、桥梁承载力检测技术桥梁承载力检测是指通过现场实验和检测手段,对桥梁结构的承载能力进行量化评估和验证。
下面介绍几种常用的桥梁承载力检测技术。
1. 静载试验静载试验是一种常用的桥梁承载力检测方法,通过在桥梁上加压、加荷等方式,测量桥梁的位移、应变和反力等参数,以评估桥梁结构的承载能力。
静载试验具有操作简单、数据准确等优点,可以在实际使用条件下对桥梁的承载能力进行评估。
2. 动力试验动力试验是一种利用震动激励和响应信号来评估桥梁动力特性和承载能力的方法。
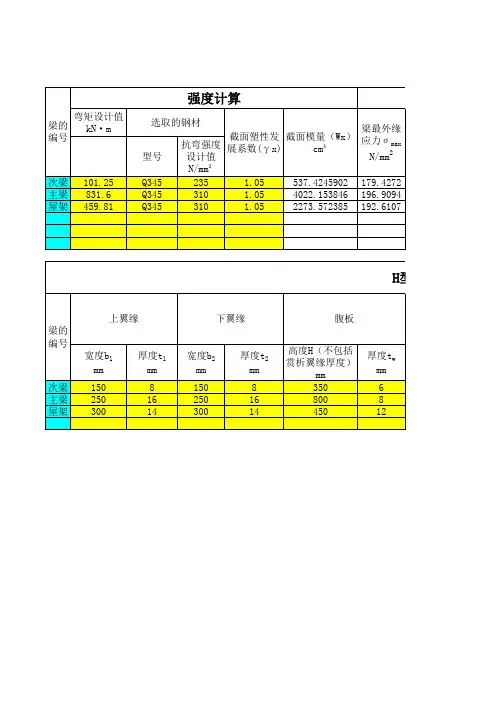
![3[1].6 主梁截面验算](https://uimg.taocdn.com/331d75d2240c844769eaee7f.webp)
3.6 主梁截面验算3.6.1 截面强度验算在承载能力极限状态下,预应力混凝土梁沿着正截面和斜截面都有可能 破坏,下面验算这两用人才类截面的强度。
1) 正截面强度验算① 按“公预规”第3.2.2条规定,对于T 形截面受压区翼缘计算宽度b f ′应取用下列三者中的最小值:cm l b f 3.971329143==≤' cm b f 220≤'cm h b b b f h f 314812*********=⨯+⨯+='++≤' 故取b f ′﹦220cm 。
图17示出了正截面强度计算图示。
h f =1216b h =81b f =220b 2=2181h 0=183.1h =200f cd —混凝土轴心抗压设计强度,根据“公预规”取32.4MPa 。
由于221760822014844.321260745.5cm cm A ha =⨯≤=⨯⨯=∴受压区高度x 在翼缘板内,故cm x 75.62201484==为了防止构件出现脆性破坏,应对受压区高度x 有所限制,“公预规”规定:0h x jh ξ≤(7―2)式中 ζjh —预应力混凝土受弯构件受压区高度界限系数,查表取0.40。
经验算满足要求。
③ 验算正截面强度由“公预规”第5.1.7条,正截面强度按下式计算:()()⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛'-'-⨯-'⋅'⋅+⎪⎭⎫ ⎝⎛'-⋅'⋅-'⋅+⎪⎭⎫ ⎝⎛-⋅⋅≤323210200f b f cd b b f cd cd cj h h h b b h f h h h b b f x h x b f r M 式中 c γ—混凝土安全系数,取用1.25。
则上式右边﹦9301.819kNm由表12(见22页)可知,控制截面跨中截面设计的计算弯矩为:≤⋅=m kN M j 58.6057右边主梁跨中正截面满足强度要求,其余截面同理也满足。

10.主梁截面承载力与应力验算预应力混凝土梁从预加力开始到是受荷破坏,需经受预加应力、使用荷载作用,裂缝出现和破坏等四个受力阶段,为保证主梁受力可靠并予以控制。
应对控制截面进行各个阶段的验算。
在以下内容中,先进行持久状态承载能力极限状态承载力验算,再分别验算持久状态抗裂验算和应力验算,最后进行短暂状态构件的截面应力验算。
对于抗裂验算,《公预规》根据公路简支标准设计的经验,对于全预应力梁在使用阶段短期效应组合作用下,只要截面不出现拉应力就可满足。
10。
1持久状况承载能力极限状态承载力验算在承载能力极限状态下,预应力混凝土梁沿正截面和斜截面都有可能破坏,下面验算这两类截面的承载力。
10。
1.1正截面承载力验算 (1)确定混凝土受压区高度根据《公预规》5。
2。
3条规定,对于带承托翼缘板的T 形截面; 当''Pd P cd f f f A f b h ≤成立时,中性轴带翼缘板内,否则在腹板内。
左边=Pd P f A =1260×50。
4×0。
1=6350.4(kN) 右边=''cd f f f b h =22。
4×220×15×0。
1=7392(kN)''Pd P cd f f f A f b h ≤成立,即中性轴在翼板内。
设中性轴到截面上缘距离为x ,则: x=0'126050.412.89()0.4(200012.85)74.86()22.4220pd p b cd ff A cm h cm f b ξ⨯==<=⨯-=⨯式中:ξb ——预应力受压区高度界限系数,按《公预规》表5。
2。
1采用,对于C50混凝土和钢绞线,ξb =0。
40; h 0——梁的有效高,0p h h a =-, 说明该截面破坏时属于塑性破坏状态。
(2)验算正截面承载力:由《公预规》5。
2.5条,正截面承载力按下式计算:'000()2cd f xM f b x h γ≤-式中:γ0-—桥梁结构的重要性系数,按《公预规》5。

混凝土梁极限承载力计算方法一、背景介绍混凝土结构中的梁是一种常见的结构构件,其承载能力的计算是设计师必须要考虑的问题。
混凝土梁的承载能力与其几何形状、材料特性以及受力方式等因素有关。
因此,本文将详细介绍混凝土梁极限承载力计算方法。
二、混凝土梁的基本性质混凝土梁的基本性质包括以下几个方面:1.几何形状:混凝土梁的截面形状通常为矩形、T形、I形等,其宽度、高度和截面系数等参数对梁的承载能力有着重要的影响。
2.材料特性:混凝土的强度和钢筋的强度是影响梁承载能力的重要因素。
混凝土的强度可以通过混凝土强度等级来确定,而钢筋的强度则取决于钢筋的种类和规格。
3.受力方式:混凝土梁通常受到弯曲和剪力作用,因此其承载能力的计算需要考虑这两种受力方式的影响。
三、混凝土梁弯曲承载力计算方法混凝土梁的弯曲承载力计算方法包括以下步骤:1.计算混凝土梁的截面惯性矩和截面模量,其中截面惯性矩可以通过以下公式计算:I = (bh^3)/12式中,b为梁的宽度,h为梁的高度。
而截面模量可以通过以下公式计算:W = (bh^2)/62.计算混凝土梁的受弯区高度,即截面中受弯区域距离梁底部的高度。
对于受弯区域位于矩形梁的中心线上的情况,受弯区高度为h/2;对于受弯区域位于T形梁或I形梁的情况,受弯区高度需要根据具体情况进行计算。
3.计算混凝土梁的极限弯矩,即可以引起梁破坏的最大弯矩。
极限弯矩可以通过以下公式计算:M = fcbWx式中,fcb为混凝土抗压强度设计值,W为截面模量,x为受弯区高度。
4.确定混凝土梁的极限承载力,即可以引起梁破坏的最大荷载。
极限承载力可以通过以下公式计算:P = M / e式中,M为极限弯矩,e为混凝土梁的跨度。
四、混凝土梁剪力承载力计算方法混凝土梁的剪力承载力计算方法包括以下步骤:1.计算混凝土梁的截面面积和周长,其中截面面积可以通过以下公式计算:A = bh而周长可以通过以下公式计算:P = b + 2h2.计算混凝土梁的剪跨比,即跨度和截面深度的比值。

截面应力验算4.6.1使用荷载作用阶段计算 (1)混凝土法向应力验算此阶段为有预加力和全部恒载作用的阶段,通常是跨中截面上缘可能出现最大压应力和下缘最大拉应力(或最小应力)。
计算公式如下: s pg js g js y j y s W M M W M W M A N 021+++-=σspg jsg jsy jy s W M M W M W M A N 021---+=σ式中:N y 、M y —由有效预加力产生的预加内力; W js 、W jx —分别为对上、下缘的净截面抵抗矩; W 0s 、W 0x —分别为对上、下缘的换算截面抵抗矩; W g1、W g2—分别由第一期、第二期恒载产生的弯矩; M p —由活载产生的弯矩,有组合Ⅰ和Ⅲ的两种情况;混凝土法向应力验算:按规定,载使用荷载使用下,混凝土法向压应力极限值如下: 荷载组合Ⅰ: 0.5R a b =14MPa (见表10) 荷载组合Ⅲ: 0.6R a b =16.8MPa在使用荷载(组合Ⅰ)作用下,全预应力梁截面受拉边缘由预加力引起的预压应力必须大于或等于由使用荷载引起的拉应力,即σh ≥0通过各截面上下缘混凝土法向应力计算,其结果表明受拉区(组合Ⅰ)都未出现拉应力,最大压应力为11.336MPa ,故符合上述各项规定。
(2)混凝土主应力验算此项验算包括混凝土主拉应力和主压应力,对前者验算主要为了保证主梁斜截面具有与正截面同等的抗裂安全度,而验算后者是保证混凝土在沿主压应力方向破坏时也具有足够的安全度。
计算混凝土主应力时应选择跨径中最不利位置截面,对该截面的重心处和宽度急剧改变处进行验算,所以选择1号梁的变化点截面,对其上梗胁、净轴、换轴和下梗胁等四处分别进行主应力验算: a.剪应力计算计算公式: τ=τg1+τp+g2-τy式中:τ—由使用荷载和弯起的预应力钢束在主应力计算点上产生的混凝土剪应力;τg1—第一期恒载引起的剪应力,其中载截面净轴(j-j ) 上τg1=bI S Q j jj g -1;在换轴(o-o )上τg1=bI S Q j oo g -1;τp+g2—活载及第二期恒载共同引起的剪应力,其中在净轴(j-j )上j j bpg g p S I Q Q -++=022τ;在o-o 上的o o bpg g p S I Q Q -++=022τ;Q p —活载剪力,有(汽-20+人群)和挂-100两种情况; τy —预加力引起的剪应力,由钢束锚固时产生的和σs Ⅱ损失产生的剪应力组合而成;各项剪应力计算和组合情况见表22所示。

主梁应力验算注意事项1.材料性能:在进行主梁应力验算时,首先需要确保使用的材料符合相关规范和要求。
包括混凝土的强度等级、钢材的规格和强度等,这些参数直接关系到主梁的受力性能。
2.受力情况:在进行应力验算时,需要明确主梁在工作过程中所受到的荷载情况,包括永久荷载、活载和风载等。
同时,还需要考虑可能产生的不利影响因素,如温度变化、腐蚀等。
3.下垫面的支撑情况:主梁的应力验算需要考虑其下垫面的支撑情况。
比如,主梁是否直接承受地基承载或地下水压力。
如果是,则需要根据地基的承载能力进行计算;如果不是,则需要考虑设置地基或者其他支撑结构。
4.断面尺寸的合理性:主梁的应力验算需要根据结构形式和荷载情况,确定主梁的断面尺寸。
这个断面尺寸应该是经过合理设计和考虑的,既能满足强度和刚度的要求,又能尽可能减小结构重量和材料消耗。
5.弯矩、剪力和轴力的计算:在进行主梁应力验算时,需要计算主梁的弯矩、剪力和轴力等参数。
这些参数反映了主梁受力的紧张程度和安全性能。
6.构件连接的可靠性:主梁应力验算还需要考虑构件之间的连接方式和连接的可靠性。
如主梁与柱子之间的连接、梁与墙体之间的连接等。
这些连接部位应该经过合理设计和验算,确保其能够满足应力传递和稳定性的要求。
7.验算的合理性和准确性:在进行主梁应力验算时,需要确保验算的方法和步骤的合理性和准确性。
这需要根据实际情况选择合适的验算方法和工具,并且进行严密的计算和分析。
8.监测和维护:主梁应力验算只是一种静态的方法,不能完全反映实际的工作状态。
因此,在主梁的使用过程中,还需要进行定期的监测和维护工作,及时发现和处理可能存在的问题,确保主梁的安全性能。
总之,主梁应力验算是建筑工程中不可或缺的一环,需要注意上述事项,确保主梁在工作过程中的稳定性和安全性能。
同时,还需要根据实际情况进行灵活的应用和调整,以满足不同工程的具体需求。

底层梁左端截面设计=========================================================== 1 已知条件及计算要求:(1)已知条件:矩形梁b=300mm,h=600mm。
砼强度等级 C25,fc=11.90N/mm2,纵筋级别 HRB335,fy=300N/mm2,箍筋级别 HPB235,fy=210N/mm2。
弯矩设计值 M=272.85kN.m,剪力设计值 V=101.10kN,扭矩设计值 T=0.00kN.m。
(2)计算要求:1.正截面受弯承载力计算2.斜截面受剪承载力计算3.受扭承载力计算4.裂缝宽度计算。
----------------------------------------------------------- 2 截面验算:(1)截面验算:V=101.10kN < 0.250βc fcbh=504.26kN 截面满足截面配筋按纯剪计算。
----------------------------------------------------------- 3 正截面受弯承载力计算:(1)按单筋计算:as下=35mm,相对受压区高度ξ=x/h=0.278 < ξb=0.550(2)上部纵筋:按构造配筋As=360mm2,配筋率ρ=0.20%(3)下部纵筋:As=ξa1fcbh/fy=1870mm2ρmin=0.20% < ρ=1.04% < ρmax=2.18%----------------------------------------------------------- 4 斜截面受剪承载力计算:(1)受剪箍筋计算:Asv/s=-334.33mm2/m ρsv =-0.11% < ρsvmin=0.15% 按构造配筋Av/s=435mm2/m----------------------------------------------------------- 5 配置钢筋:(1)上部纵筋:计算As=360mm2,实配2D12+1D14(380mm2ρ=0.21%),配筋满足(2)腰筋:计算构造As=b*hw*0.2%=339mm2,实配4D12(452mm2ρ=0.25%),配筋满足(3)下部纵筋:计算As=1870mm2,实配5D22(1901mm2ρ=1.06%),配筋满足(4)箍筋:计算Av/s=435mm2/m,实配d8@300三肢(503mm2/m ρsv=0.17%),配筋满足-----------------------------------------------------------6 裂缝计算:(1)计算参数:Mk=42.86kN.m,最大裂缝宽度限值0.400mm。

一、概述主梁承载力极限状态检算是建筑结构设计中非常重要的一环,其结果直接关系到结构的安全性和稳定性。
在进行主梁承载力极限状态检算时,需要综合考虑材料性能、结构形式、载荷情况等诸多因素,以确保结构在极限状态下仍能保持良好的工作性能。
二、承载力计算的基本原理1. 材料力学参数的确定在主梁承载力极限状态检算中,首先需要明确主要构件所采用的材料的力学参数,例如混凝土的抗压强度、钢材的屈服强度等。
这些参数是承载力计算的基础,直接影响到结构的受力性能。
2. 结构形式与受力分析结构的形式和受力分析对于承载力计算同样至关重要。
不同的结构形式在受力作用下的受力状况各异,需要进行相应的分析和计算。
在梁的计算中,需要考虑梁的跨度、截面形状、荷载情况等因素。
3. 极限状态下的安全系数在承载力计算中,安全系数是一个至关重要的参数。
极限状态设计要求结构在设计荷载下依然能保持安全,因此需要合理确定安全系数,并在承载力计算中予以考虑。
三、承载力计算的方法和步骤1. 弯矩承载力计算在主梁承载力极限状态检算中,弯矩承载力是一个关键的指标。
弯矩承载力的计算方法包括荷载效应方法、结构特性方法等,需要根据具体的结构情况进行选择。
2. 剪切承载力计算除了弯矩承载力外,剪切承载力也是主梁承载力极限状态检算中的重要内容。
剪切承载力的计算方法有综合剪切承载力设计方法、构造剪切承载力设计方法等,需要根据实际情况进行选择。
3. 受拉承载力计算受拉承载力计算同样不容忽视。
在计算受拉承载力时,需要考虑构件受拉极限状态下的变形和破坏情况,保证结构在受拉作用下依然能保持稳定。
四、案例分析以某主梁为例,进行承载力极限状态检算。
首先确定主要构件所采用的材料参数,结合结构形式和受力分析,计算主梁的弯矩承载力、剪切承载力和受拉承载力,最终得出主梁在极限状态下的承载能力。
五、结论及建议通过本文的分析可以得出,主梁承载力极限状态检算是建筑结构设计中不可或缺的一部分。
在进行承载力计算时,需要充分考虑材料力学参数、结构形式和受力分析等多方面因素,并合理确定安全系数,保证结构在承载力极限状态下仍具有良好的工作性能。
桥梁结构检测及其承载力评定分析桥梁是连接两岸或两地的重要交通工具,其承载力能力直接决定着交通的畅通和安全性,因此桥梁的结构检测及其承载力评定分析十分必要。
本文将从桥梁结构检测方法、承载力评定分析流程、桥梁改造及修缮几个方面进行详细介绍。
一、桥梁结构检测方法桥梁结构检测方法主要有目视观察法、人工检测法和无损检测法三种。
1.目视观察法目视观察法是最为简单的一种桥梁结构检测方法,通过肉眼观察桥梁结构表面的裂缝、变形、腐蚀等问题,并记录下来。
但是该方法对于内部隐患的检测效果较差,需要综合其他方法进行检测。
2.人工检测法人工检测法是通过人工攀爬、敲击等方式,对桥梁结构进行细致的检测。
该方法的检测范围更广,包括桥梁内部结构的检测,有利于发现更多的缺陷和隐患。
但是该方法不仅较为耗时,而且人为因素较大,结果的准确性也有所欠缺。
3.无损检测法无损检测法主要是通过一系列的无损检测仪器,对桥梁结构进行电磁波、超声波、磁粉等多种方法的综合检测。
该方法能够有效地发现桥梁结构内部的缺陷、裂纹等问题,能够高效、准确地确定桥梁的结构安全性。
二、承载力评定分析流程对于已经检测出来存在问题的桥梁,需要进行承载力评定分析,判断其是否可以继续使用,或者进行相应的改造和修缮。
承载力评定分析的流程包括以下几个步骤:1.分析桥梁的载荷历史数据,了解桥梁所承担的最大荷载以及荷载分布情况。
2.对桥梁的结构参数进行分析,确定各项参数对于桥梁承载能力的影响程度,包括桥墩、梁段、承台等组成部分的建筑、材料、连接部位等参数。
3.评估桥梁的承载能力,主要是通过对比荷载历史数据和桥梁结构参数确定的最大荷载值,判断当前桥梁是否强度不足。
4.评估桥梁的结构疲劳性能,主要是对桥梁的载荷及运行历史数据以及结构材料性能进行分析,评估桥梁在重复运行过程中是否会出现结构疲劳破坏。
5.综合以上几个步骤,确定桥梁结构的实际承载能力和剩余使用寿命,给出相应的维修改造建议。
三、桥梁改造及修缮对于承载能力不足或者存在缺陷的桥梁,需要进行相应的改造和修缮。
钢结构设计中的承载力计算与验证钢结构是一种重要的建筑结构形式,其特点包括高强度、轻质化以及抗震性能优越。
在钢结构设计中,承载力计算和验证是至关重要的步骤。
本文将介绍钢结构设计中的承载力计算与验证的关键内容,并探讨其在实践中的应用。
1. 强度设计在钢结构设计中,强度是一个基本参数。
承载力的计算和验证是通过对结构的强度进行评估。
其中,扭矩、弯曲和剪切是常见的强度考虑因素。
钢结构的承载力计算和验证需要根据相应的国家或行业标准进行。
在计算过程中,结构的几何形状、材料性能和荷载条件都需要被准确地考虑。
此外,设计者还需要确保钢结构在其使用寿命内具有足够的安全储备,以防止意外事故的发生。
2. 框架结构的计算钢结构中常见的一种形式是框架结构。
在框架结构的承载力计算与验证中,设计师需要考虑各个节点的强度和稳定性。
一方面,节点处的连接必须具备足够的强度,以保证整体结构的稳定性。
另一方面,节点需要具备良好的可预测性和可维修性。
因此,设计者需要选择合适的连接形式,并合理设计节点的几何形状,以满足设计要求。
3. 随机荷载的考虑承载力计算和验证中,随机荷载的考虑是一个重要的方面。
在实际使用中,钢结构可能会承受不同类型和大小的荷载,如静载、动载和温度变化引起的变形。
为了保证结构的安全性和可靠性,设计师需要对这些荷载进行合理的估计和分析。
通过结构的强度计算和验证,可以确定结构是否满足所需的承载能力要求,并对结构进行必要的调整和改进。
4. 特殊情况下的计算与验证除了常规的承载力计算和验证,特殊情况下的设计需求也需要被考虑。
在某些特殊的工程项目中,钢结构可能会遇到更为严峻的环境和荷载条件,如高海拔地区、强风区或强地震区。
在这些情况下,设计者需要针对特殊要求进行更加细致的计算和验证,并采取相应的加固措施,以确保结构的安全性和可靠性。
5. 监测与修复钢结构的承载力计算与验证不应仅停留在设计阶段,而应该是一个持续的过程。
一旦结构建成投入使用,定期的监测和检测就变得至关重要。
支撑构件的截面承载力验算支撑的截面承载力应根据各个施工阶段中最不利的荷载组合作用效应进行验算。
1.腰梁截面验算腰梁的平面截面承载刀一般情况下按受弯构件验算。
当支撑与腰梁斜交时,还应验算偏心受压时的截面强度,此时构件的受压计算长度取内力分析时的计算跨度。
对于按连续梁计算的钢筋混凝土腰梁,支座负弯矩可以考虑塑性变形内力重分布,乘以调幅系数0.8~0.9,但此时梁的联动中正E弯矩应相应增加。
2.水平.支撑截面验算水平支撑的截面承载力通常应按偏心受压构件验算。
在竖向平面立柱计算长度取相邻立柱的中心距∶在水平面内的受压计算长度交叉取与计算支撑担交的相邻横向水平支撑的中心距;对干钢支撑,当纵横向支撑不在同一标高上相交时,其平面内的受玉计算长度取与之相交的相邻横向的提振中心距水平1.5~2.0倍。
支撑截面上的偏心弯矩除由竖向荷载所产生之外。
还疗需要考虑轴向力对构件初始偏心距所引起的附加弯矩。
构件的初始偏心距可取支撑铁制计算长度的2%。
~3%,对于混凝土支撑不宜略高于20mr,钢支撑不宜小于40mm。
现浇混凝土支撑在竖向平面内的内所支座风压可以乘以0.8~0.9的调幅系数折减,但跨中弯矩应相应增加。
3.立柱截面验算立柱截面承载力应按偏心受压构件验算。
其受压计算长度取竖向相邻水平支撑中心距,最下一层支撑以下的立柱受压计算长度取该层支撑中心线至开挖面以下5倍立柱直径(或边长)处之间的距离。
除了截面承载力验算外,开挖面以下的立柱尚应按单桩承载力的计算方法验算立柱的竖向和水平承载力。
4,竖向斜撑体系截面验算竖向斜撑体系应验算以下项目∶(1)预留土坡的边坡稳定验算,稳定安全系数尽量少小于1.5。
(2)斜撑截面承载力,可近似按轴心受压构件验算,受压计算长度(当不设立柱时)取支撑全长。
(3)腰梁截面承载力验算同水平支撑体系中心腰梁验算。
(4)斜撑基础验算,按天然地基上浅基础的设计方法验算其竖向承载力。
(5)基础压杆可近似按轴心受压构件验算截面承载力。
10.主梁截面承载力与应力验算预应力混凝土梁从预加力开始到是受荷破坏,需经受预加应力、使用荷载作用,裂缝出现和破坏等四个受力阶段,为保证主梁受力可靠并予以控制。
应对控制截面进行各个阶段的验算。
在以下内容中,先进行持久状态承载能力极限状态承载力验算,再分别验算持久状态抗裂验算和应力验算,最后进行短暂状态构件的截面应力验算。
对于抗裂验算,《公预规》根据公路简支标准设计的经验,对于全预应力梁在使用阶段短期效应组合作用下,只要截面不出现拉应力就可满足。
持久状况承载能力极限状态承载力验算在承载能力极限状态下,预应力混凝土梁沿正截面和斜截面都有可能破坏,下面验算这两类截面的承载力。
正截面承载力验算(1)确定混凝土受压区高度根据《公预规》条规定,对于带承托翼缘板的T 形截面; 当''Pd P cd f f f A f b h ≤成立时,中性轴带翼缘板内,否则在腹板内。
左边=Pd P f A =1260××=(kN)右边=''cd f f f b h =×220×15×=7392(kN)''Pd P cd f f f A f b h ≤成立,即中性轴在翼板内。
设中性轴到截面上缘距离为x ,则: x=0'126050.412.89()0.4(200012.85)74.86()22.4220pd p b cd ff A cm h cm f b ξ⨯==<=⨯-=⨯式中:ξb ——预应力受压区高度界限系数,按《公预规》表采用,对于C50混凝土和钢绞线,ξb =;h 0——梁的有效高,0p h h a =-, 说明该截面破坏时属于塑性破坏状态。
(2)验算正截面承载力:由《公预规》条,正截面承载力按下式计算:'000()2cd f x M f b x h γ≤-式中:γ0——桥梁结构的重要性系数,按《公预规》条采用,本设计取。
主梁承载力验算一、极限工作状态下主梁承载力计算在极限工作状态时,可能出现全部荷载施加在汽车吊某端支腿座落的主梁上的情况。
即汽车吊自重+工作荷载共计320KN全部施加在落于主梁的两支支腿上,每支支腿向梁施加160KN集中荷载。
1、恒荷载计算:楼板厚120mm;主梁尺寸400×600,净跨L=7.4m。
说明:本工程实际为井字梁结构,实际其荷载图与下图有异。
但为了计算简便,本方案将井字梁区考虑为整板,按下图进行荷载分布计算,其结果大于实际情况,有利于整体计算结果的安全性。
在实际情况中可能有某些情况在本方案中没有预计,故在荷载组合时特将恒荷载×1.4的系数,或荷载×1.2的系数,以确保整个计算结果的保守。
楼板荷载在主梁上分布图板q’=0.12×8×25=24KN/mq1= 5q/8=15KN/m梁q2=0.4×0.6×25=6KN/m梁板均布荷载q=q1+q2=21KN/mMmax1=-M A1=M B1=qL2/12=95.83KN·mM C1=qL2/24=47.92KN·m插图2、活荷载(吊车、起重量)计算:考虑最不利情况,所有荷载集中于两支座上,每支座最大荷载值为160KN。
a1=1m,b1=6.4m;a2=6.4m,b2=1m。
插土Mmax2=-M A2=M B2= (a1×b12+a22×b2)× F/L2=138.38KN·m3、荷载组合结果:主梁上最大弯距为梁支座处:Mmax=1.2Mmax1+1.4Mmax2=308.728KN·m4、主梁正截面抗弯截面验算:该梁为400×600;220+625-6/2;525上部筋:一排220+425 As1 =2592mm2二排425 As2 =982mm2下部筋:525 As’=2454mm2先仅按第一排算:fc=14.3N/mm2,fy=fy’=360 N/mm2αs =25+25/2=37.5mmh0=600-37.5=562.5mm因为fyAs- fy'As'8.685fc bx mm==<2αs,所以M=fyAs(h0-αs)=489.9 KN·m>Mmax=308.728KN·m由于只计算第一排钢筋就已经满足承载力要求,故不再进行其他排钢筋的计算。
10.主梁截面承载力与应力验算预应力混凝土梁从预加力开始到是受荷破坏,需经受预加应力、使用荷载作用,裂缝出现和破坏等四个受力阶段,为保证主梁受力可靠并予以控制。
应对控制截面进行各个阶段的验算。
在以下内容中,先进行持久状态承载能力极限状态承载力验算,再分别验算持久状态抗裂验算和应力验算,最后进行短暂状态构件的截面应力验算。
对于抗裂验算,《公预规》根据公路简支标准设计的经验,对于全预应力梁在使用阶段短期效应组合作用下,只要截面不出现拉应力就可满足。
10.1持久状况承载能力极限状态承载力验算在承载能力极限状态下,预应力混凝土梁沿正截面和斜截面都有可能破坏,下面验算这两类截面的承载力。
10.1.1正截面承载力验算 (1)确定混凝土受压区高度根据《公预规》5.2.3条规定,对于带承托翼缘板的T 形截面; 当''Pd P cd f f f A f b h ≤成立时,中性轴带翼缘板内,否则在腹板内。
左边=Pd P f A =1260×50.4×0.1=6350.4(kN) 右边=''cd f f f b h =22.4×220×15×0.1=7392(kN)''Pd P cd f f f A f b h ≤成立,即中性轴在翼板内。
设中性轴到截面上缘距离为x ,则: x=0'126050.412.89()0.4(200012.85)74.86()22.4220pd p b cd ff A cm h cm f b ξ⨯==<=⨯-=⨯式中:ξb ——预应力受压区高度界限系数,按《公预规》表5.2.1采用,对于C50混凝土和钢绞线,ξb =0.40; h 0——梁的有效高,0p h h a =-, 说明该截面破坏时属于塑性破坏状态。
(2)验算正截面承载力:由《公预规》5.2.5条,正截面承载力按下式计算:'000()2cd f x M f b x h γ≤-式中:γ0——桥梁结构的重要性系数,按《公预规》5.1.5条采用,本设计取1.0。
右边=30.128522.410 2.20.1289(20.1285)11478.732kN m ⨯⨯⨯⨯--=⋅ 08658.42(d M kN m >ϒ=⋅跨中)所以,主梁跨中正截面承载能力满足要求。
(3)验算最小配筋率由《公预规》9.1.12条,预应力混凝土受弯构件最小配筋率应满足下列条件:udcrM 1.0M ≥式中: M ud ——受弯构件正截面抗弯承载力设计植,由以上计算可知M ud =9734.58(kN ·m );Mcr ——受弯构件正截面开裂弯矩值,按下式计算:0()cr PC tk M f W σγ=+02oS W γ=PCp P nnxN M A W σ=+式中:S 0——全截面换算截面重心轴以上(或以下)部分截面对重心轴的面积矩,;W 0——换算截面抗裂边缘的弹性抵抗矩;σpc ——扣除预应力损失预应力筋在构件抗裂边缘产生的混凝土预压应力。
MPa W M A N nx pn ppc 27.21300079594819911.7458727.1081=+=+=σ022297327 1.533387732o S W γ⨯===m N W f M tk pc cr ⋅=⨯⨯⨯+=+=-k 20.982210387732)65.2533.127.21()(30γσudcrM 1.0M <,尚需配置普通钢筋来满足最小配筋率的要求。
①计算受压区高度x)2(00x h x b f M f cd d -'≤γ )28715.12.2(2.2104.2232.119043xx --⨯⨯=求解得0.134()0.7486()b o x m h m ξ=<⨯=②计算普通钢筋s A4222.4 2.20.134126050.4109.04()280cd pd ps sd f bx f A A m f --⨯⨯-⨯⨯===即在梁底部配置6根直径16mm 的HRB335钢筋,s A =12.062cm .以满足最小配筋率的要求。
10.1.2 斜截面承载力验算(1) 斜截面抗剪承载力验算:根据《公预规》5.2.6条,计算受弯构件斜截面抗剪承载力时,其计算位置应按下列规定采用:① 距离支座1/2 h 截面处; ② 受拉区弯起钢筋弯起点处截面;③ 锚于受拉区的纵向钢筋开始不受力处的截面; ④ 箍筋数量或间距改变处的截面; ⑤ 构件腹板宽度变化处的截面。
1) 复核主梁尺寸T 形截面梁当进行斜截面抗剪承载力计算时,其截面尺寸应符合《公预规》5.2.9条规定,即000.5110d V γ-≤⨯式中:d V ——经内力组合后支点截面的最大剪力(kN ),1号梁的d V 为1021.23kN ;b ——支点截面腹板厚度(mm ),即b=550mm ; h 0——支点截面的有效高度(mm),即h 0=h -a p =2000-786.6=11213.4(cm)f cu,k ——混凝土强度等级(MPa ) 上边右式=00.51105501213.42406.701021.23d kN V kN γ-⨯⨯=>=所以本设计主梁的T 形截面尺寸符合要求。
2)截面抗剪承载力验算:验算是否需进行斜截面抗剪承载力计算根据《公预规》5.2.10条规定,若符合下列公式要求时,则不需进行斜截面抗剪承载力计算。
γ0V d ≤0.50×10-3α2td f bh 0式中:td f —混凝土抗拉强度设计值(MPa )α2—预应力提高系数,对预应力混凝土受压构件,取1.25。
上式右边=0.50×10-3×1.25×1.83×550×1328.5=835.709kN <γ0V d =968.32(kN) 因此该设计需进行斜截面抗剪承载力计算. ①选定斜截面顶端位置距支座h/2处截面的横坐标为x=33900/2-200/2=15950mm,正截面有效高度0h =1328.5mm 。
现取 c ’≈ 0h =1328.5mm ,则得到选定的斜截面顶端位置,其横坐标为x=15950-1328.5=14621.5mm 则,,/2d,,/22214.622()157.97(1021.23157.97)902.66533.9d A d l o d l x V V V V L ⨯=+-==+-⨯=KN ②箍筋计算:根据《公预规》9.4.1条,腹板内箍筋直径不小于10mm ,且应采用带肋钢筋,间距不应大于250mm ,本设计选用φ10@200的双肢箍筋,则箍筋的总面积为:A sv =2×78.5=157(mm 2)箍筋间距S V =200mm,箍筋抗拉强度设计值f sv =280MPa,箍筋配筋率ρsv 为:1570.19%200405sv sv v A S b ρ===⨯ 式中:b ——斜截面受压端正截面处T 形截面腹板宽度,此处b=405mm 。
满足《公预规》9.3.13条“箍筋配筋率ρsv ,HRB335钢筋不应小于0.12%”的要求。
同时,根据《公预规》9.4.1条,在距支点一倍梁高范围内,箍筋间距缩小至100mm 。
③抗剪承载力计算根据《公预规》5.2.7条规定,主梁斜截面抗剪承载力应按下式计算:γ0V d ≤V cs +V pb式中:V d ——斜截面受压端正截面内最大剪力组合设计值,为142.67kN;V cs ——斜截面内混凝土与箍筋共同的抗剪承载力 (kN) ,按下式计算:V cs = α1α2α30.45×10-3bh 0sv sv K cu f f P ρ,)6.02(+α1——异号弯矩影响系数,简支梁取1.0;α2——预应力提高系数,对预应力混凝土受弯构件,取1.25; α3——受压翼缘的影响系数,取1.1;b ——斜截面受压端正截面处,T 形截面腹板宽度,此处b=466mm; h 0——斜截面受压端正截面处梁的有效高度, h 0=1574cm ;P ——斜截面内纵向受拉钢筋的陪筋率,P=100ρ,ρ=(A p +A pb )/(bh 0),当P >2.5时,取P=2.5;k cu f ,——混凝土强度等级;sv ρ——斜截面内箍筋配筋率,sv ρ=A sv /(S v b);sv f ——箍筋抗拉设计强度;A sv ——斜截面内配置在同一截面的箍筋各肢总截面面积(mm 2); S v ——斜截面内箍筋间距(mm );pb V ——与斜截面相交的预应力弯起钢束的抗剪承载力(kN),按下式计算:30.7510sin pb pd pb p V f A θ-=⨯∑pb A ——斜截面内在同一弯起平面的预应力弯起钢筋的截面面积(mm 2);pd f ——预应力弯起钢束的抗拉设计强度(MPa ),该设计的—pd f =1260MPa; p θ——预应力弯起钢筋在斜截面受压端正截面处的切线与水平线的夹角,见表如下50.40.0079140.51574p pbA A bh ρ+===⨯1000.791P ρ==0.0019sv sv vAbS ρ==31.0 1.25 1.10.45104661501cs V -=⨯⨯⨯⨯⨯⨯1203.44kN =2sin 840[2(0.03267610.926845)0.1995264+0.2131218]557.23mm pb p A θ=⨯⨯++=∑V pb = 0.75×10-3×1260×557.23=526.58kNV cs +V pb =1203.44+526.58=1730.02kN >γ0V d = 902.665kN说明主梁距支座1/2 h 处斜截面抗剪承载力满足要求,同时也说明上述箍筋的配置是合理的(2)斜截面抗弯承载力验算由《公预规》5.2.12条进行斜截面抗弯强度计算,由于钢束都在梁端锚固,钢束根数沿梁跨几乎没有变化,并且钢束在梁中无截断,锚固长度均满足要求,可不必进行该项承载力验算,通过构造加以保证。
7.2持久状况正常使用极限状态抗裂验算长期以来,桥梁预应力构件的抗裂验算,都是以构件混凝土的拉应力是否超过规定的限值来表示,分为正截面抗裂和斜截面抗裂验算。
10.2.1正截面抗裂验算根据《公预规》6.3.1条,对预制的全预应力混凝土构件,在作用长期菏载效应组合下,应符合下列要求:085.0 -pc st ≤σσ式中:st σ——在作用短期效应组合下构件抗裂验算边缘混凝土的法向拉应力,按下式计算:ox p nxg st W M W M +=1σnxp np pc W M A N +=σ下表示出了正截面抗裂验算的计算过程和结果,可见其结果符合规范要求。