武汉理工大学数学建模与仿真论文
- 格式:doc
- 大小:54.12 KB
- 文档页数:8

2017年全国大学生数学建模竞赛优秀论文数学是知识的工具,亦是其它知识工具的泉源。
所有研究顺序和度量的科学均和数学有关,数学建模是培养学生运用数学工具解决实际问题的最好表现。
下文是店铺为大家搜集整理的关于2017年全国大学生数学建模竞赛优秀论文的内容,欢迎大家阅读参考!2017年全国大学生数学建模竞赛优秀论文篇1浅析数学建模课程改革及其教学方法论文关键词:数学课程;数学建模;课程设置;课程改革论文摘要:数学建模教学和竞赛的开展,是培养学生创新能力的重要途径。
对数学建模竞赛中出现的问题进行分析,找出问题产生的根源与必修课和专业课设置不合理有关,应对高校数学课程的设置、教学方式等进行改革,并提出具体改革建议。
1. 前言数学建模,从宏观上讲是人们借助数学改造自然、征服自然的过程,从微观上讲是把数学作为一种工具并应用它解决实际问题的教学活动方式。
数学建模教育本身是一种素质教育,数学建模的教学与竞赛是实施素质教育的有效途径,它既增强了学生的数学应用意识,又提高了学生运用数学知识和计算机技术分析和解决问题的能力。
因而加强数学建模教育,培养学生的数学应用意识与能力已成为我国高校数学建模课程改革的重要目标之一。
虽然目前我国许多高校在数学建模方面取得了一些成绩,但大学生们在竞赛中也暴露出了许多问题,引发出对传统的课程设置和教学方法的思考。
2. 数学建模的现状和所存在问题与原因分析2.1 建模竞赛的现状根据竞赛时间(九月中下旬),我国大部分高校每年一般在七月中旬便开始组织学生的报名培训工作。
培训内容分为两个部分:首先集中讲解一些基础知识,主要包括常微分方程、概率与数理统计、运筹学、数学实验、建模基础等课程;然后进行建模的模拟训练,以往届国内外普通组和大专组的部分竞赛题为选题,让学生自愿结组,在规定时间内完成,并自愿为同学讲解各自的解题思路和方法。
参赛学生首先要参加培训,他们一般是先关注校园网上的通知,再到各院系自愿报名而组成,经培训后选拔出参赛队员。

目录1.课程设计任务书…………………………………P22.设计一……………………………………………P33.设计二……………………………………………P154.参考文献…………………………………………P185.课程设计就成绩评定表…………………………P19生产系统建模与仿真课程设计任务书设计1:经过8道工序加工相同的8个零件,每道工序只有一台加工设备,每道工序时间分别为12 min, 5 min, 15 min, 7 min, 9 min, 11 min, 22 min, 5 min,请分别用顺序移动方式、平行移动方式、平行顺序移动方式对生产过程进行仿真,输出三种方式的总加工时间、总设备等待时间、总设备闲置时间,以及Flexsim仿真结果,并绘制工序图,将不同移动方式进行比较与分析。
设计2:现要加工n个相同零件,n=(10或20)+学号个位数,共8道工序,工序如下:请设计一种你认为好的方案,说明设计方法、过程、理由、结果,并输出该方案的总加工时间、总设备等待时间、总设备闲置时间,工序图、以及方案分析报告。
以上两项设计要求:提交设计说明书。
提示:设计说明书不少于12面1.设计一1.1顺序移动方式进行加工按照顺序移动进行方式加工,最大的优点是没有等待时间,零件是批量的进行加工。
即在每道工序全部加工完成之后,再进行下一道工序的加工,一旦加工设备启用,没有多余的空闲时间,这样会造成设备的闲置时间过长,整个加工的周期也随之变长。
1.1.1工序图:1.1.2时间计算:设总的加工时间为T O、总设备等待时间为T1、总设备闲置时间T2,T O=每道工序的加工时间之和=12*8+5*8+15*8+7*8+9*8+11*8+22*8+5*8=688(min)≈11.46(h)t1为第二道工序的设备闲置时间; t2为第三道工序的设备闲置时间;t3为第四道工序的设备闲置时间; t4为第五道工序的设备闲置时间;t5为第六道工序的设备闲置时间; t6为第七道工序的设备闲置时间;t7为第八道工序的设备闲置时间;T1=t1+t2+t3+t4+t5+t6+t7=12*8+(12*8+5*8)+(12*8+5*8+15*8)+(12*8+5*8+15*8+7*8)+(12*8+5*8+15*8+7*8+9*8)+(12 *8+5*8+15*8+7*8+9*8+11*8)+(12*8+5*8+15*8+7*8+9*8+11*8+22*8)=2304(min)≈38.4(h)T2=0(min) 既设备的等待时间为01.1.3 Flexsim仿真结果:(图表)以上这个表就反映了制作Flexsim仿真时所需的相关的数据,Processor3到Processor17,是所选用加工零件设备的编号,因为还包括相关的缓冲设备,既Queue,每个Processor的后面都会有一个Queue作为每道工序加工加完了的零件的存储,同时它也是进行下一道工序的零件的来源。

大学数学建模论文范文3000字第1篇一、小学数学建模_数学建模_已经越来越被广大教师所接受和采用,所谓的_数学建模_思想就是通过创建数学模型的方式来解决问题,我们把该过程简称为_数学建模_,其实质是对数学思维的运用,方法和知识解决在实际过程中遇到的数学问题,这一模式已经成为数学教育的重要模式和基本内容。
叶其孝曾发表《数学建模教学活动与大学数学教育改革》,该书指出,数学建模的本质就是将数学中抽象的内容进行简化而成为实际问题,然后通过参数和变量之间的规律来解决数学问题,并将解得的结果进行证明和解释,因此使问题得到深化,循环解决问题的过程。
二、小学数学建模的定位1.定位于儿童的生活经验儿童是小学数学的主要教学对象,因此数学问题中研究的内容复杂程度要适中,要与儿童的生活和发展情况相结合。
_数学建模_要以儿童为出发点,在数学课堂上要多引用发生在日常生活中的案例,使儿童在数学教材上遇到的问题与现实生活中的问题相结合,从而激发学生学习的积极性,使学生通过自身的经验,积极地感受数学模型的作用。
同时,小学数学建模要遵循循序渐进的原则,既要适合学生的年龄特征,赋予适当的.挑战性;又要照顾儿童发展的差异性,尊重儿童的个性,促进每一个学生在原有的基础上得到发展。
2.定位于儿童的思维方式小学生的特点是年龄小,思维简单。
因此小学的数学建模必须与小学生的实际情况相结合,循序渐进的进行,使其与小学生的认知能力相适应。
实际情况表明,教师要想使学生能够积极主动的思考问题,提高他们将数学思维运用到实际生活中的能力,就必须把握好儿童在数学建模过程中的情感、认知和思维起点。
我们以《常见的数量关系》中关于速度、时间和路程的教学为例,有的老师启发学生与二年级所学的乘除法相结合,使乘除法这一知识点与时间、速度和路程建立了关联,从而使_数量关系_与数学原型_一乘两除_结合起来,并且使学生利用抽象与类比的思维方法完成了_数量关系_的_意义建模_,从而创建了完善的认知体系。

数学建模竞赛优秀大学生论文医学论文》1数学建模的过程1.1模型准备首先要了解实际背景,寻找内在规律,形成一个比较清晰的轮廓,提出问题。
1.2模型假设在明确目的、掌握资料的基础上,抓住问题的本质,舍弃次要因素,对实际问题做出合理的简化假设。
1.3模型建立在所作的假设条件下,用适当的数学方法去刻画变量之间的关系,得出一个数学结构,即数学模型。
原则上,在能够达到预期效果的基础上,选择的数学方法应越简单越好。
1.4模型求解建模后要对模型进行分析、求解,求解会涉及图解、定理证明及解方程等不同数学方法,有时还需用计算机求数值解。
1.5模型分析、检验、应用模型的结果应当能解释已存的现象,处理方法应该是最优的决策和控制方案,所以,对模型的解需要进行分析检验。
把求得的数学结果返回到实际问题中去,检验其合理性。
如果理论结果符合实际情况,那么就可以用它来指导实践,否则需再重新提出假设、建模、求解,直到模型结果与实际相符,才能进行实际应用。
总之,数学建模是一项富有创造性的工作,不可能用一些条条框框的规则规定的十分死板,只要是能够做到全面兼顾、能抓住问题的本质、最终检验结果合理,都是一个好的数学模型。
2数学建模在生物医学中的应用2.1DNA序列分类模型DNA分子是遗传信息存储的基本单位,许多生命科学中的重大问题都依赖于对这种特殊分子的深入了解。
因此,关于DNA分子结构与功能的问题,成为二十一世纪最重大的课题之一。
DNA序列分类问题是研究DNA分子结构的基础,它常用的方法是聚类分析法。
聚类分析是使用数据建模简化数据的一种方法,它将数据分成不同的类或者簇,同一个簇中的数据有很大的同质性,而不同的簇中的数据有很大的相异性。
在对DNA序列进行分类时,需首先引入样品变量,比如说单个碱基的丰度、两碱基丰度之比等;然后计算出每条DNA序列的样品变量值,存入到向量中;最后根据相似度度量原理,计算出所有序列两两之间的Lance与Williams距离,依据距离的远近进行分类。
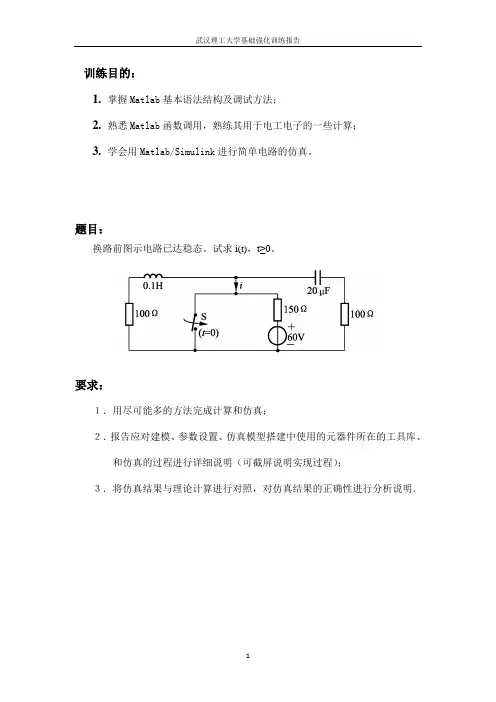
训练目的:1.掌握Matlab基本语法结构及调试方法;2.熟悉Matlab函数调用,熟练其用于电工电子的一些计算;3.学会用Matlab/Simulink进行简单电路的仿真。
题目:换路前图示电路已达稳态。
试求i(t),t≥0。
要求:1.用尽可能多的方法完成计算和仿真;2.报告应对建模、参数设置、仿真模型搭建中使用的元器件所在的工具库、和仿真的过程进行详细说明(可截屏说明实现过程);3.将仿真结果与理论计算进行对照,对仿真结果的正确性进行分析说明.目录摘要 2 1.电路模型求解 3 1.1 初始值的求解 3 1.2 利用微分方程求解 31.3 利用拉普拉斯求解 42. 利用MATLAB计算和仿真 5 2.1 用微分方程设计程序 5 2.2 用微分方程建立仿真模型 62.3 用拉普拉斯变换设计程序 93.仿真结果与理论值的比较 104.总结与体会 115.参考文献 11摘要本次基础强化训练的问题是求一电路的零输入响应,并且通过matlab的编程计算或matlab的simulink工具箱进行仿真.我先通过基础电路当中所学的电路知识,通过两种方法进行求解:一种方法是通过微分方程求解,另一种方法是通过拉普拉斯变换及其逆变换,得到相应的零输入响应.求解电路完之后,我再利用matlab编程和matlab中的simulink工具箱进行仿真,仿真中也采用三种方法进行仿真:一种是利用微分方程设计程序计算,一种是利用微分方程进行simulink 仿真,另一种是利用拉普拉斯变换设计程序计算,得到仿真图形,与实际理论值进行比较。
关键字:simulink工具箱;微分方程;拉普拉斯变换基础强化训练论文1.电路模型求解:试求下图电路的零输入响应i(t),t≥0。
1.1初始值的求解图 1-1由图1-1,用KVL 定律,易求得 (0)(0)24c c u u V+-== 11(0)(0)0.24i i A+-==-1.2利用微分方程求解图1-2 KVL 电压与电流定律图形由KVL 电压定律,得到如下表达式:1110di L R di dt += .....................( 1 )20c c du R C u dt += ...................... ( 2 )又由于22c u R i = 代入2式得2220di R Ci dt += ...................... ( 3 )初始值:1(0)0.24i A+=- ...................... ( 4 )22(0)24(0)0.24100c u i A R ++=== .................... ( 5 )代入数值到1式和3式得到:111000di i dt =- ...................... ( 6 )22500di i dt =- ..................... ( 7 )分析电路易知:12i i i =+ .................... ( 8 )做到这一步之后,我已经基本解决了该问题,剩下的是通过高等数学的微分方程知识来求解该微分方程:从而解得微分方程得到:5001000()0.240.24t ti t e e --=- (t≥0)1.2 利用拉普拉斯变换来求解该模型:在电路中我们学习过利用拉普拉斯来求解电路响应,首先要将电路转化为拉普拉斯变换的形式,再通过相应的电路定律来求解电路.我通过电路转化,得到如下的拉普拉斯电路形式:图1-3 拉普拉斯变换电路图形同理,我利用KVL 电压定律有得到下面的拉普拉斯方程:111()(0)()0s L I s L i R Is --+= ..........................( 9 )222(0)1()()0u I s R I s sC s -++= ...........................( 10 )12()()()I s I s I s =- .........................( 11 )解得 ,66()25250002512500I s s s -=+++ ...........................( 12 )得到所需求响应的拉普拉斯形式之后,再利用拉普拉斯逆变换来求得响应的时间域响应形式,得到下面的表达式:5001000()0.240.24t ti t e e --=- (t≥0)2.电路仿真:2.1利用微分方程设计程序搭建微分方程: 111000di i dt =-22500dii dt =-12i i i =+M 程序为: i1=dsolve('Di1=-1000*i1','i1(0)=-0.24');i2=dsolve('Di2=-500*i2','i2(0)=0.24'); i0=char(i1+i2);ezplot(i0,[0,0.01])得到仿真图像为:图2-12.2利用微分方程搭建电路仿真模型有:搭建微分方程:111000 dii dt=-22500diidt=-12i i i=+图2-2 微分方程模型图Gain的参数设置为:图2-3Gain1的参数设置为:图2-4 Gain1参数设置图Step1和Step2的参数设置均为:图2-5 step参数设置图通过上面的参数设置之后,我得到了关于时间t与i(t)的图像,下面就是仿真图像:图2-6 i(t)仿真图形2.3利用拉普拉斯变换设计程序:拉普拉斯变换得到的最后结果为:2120()1500500000I s s s =++M 程序为: syms s; b=[120];a=[1,1500,500000];is=poly2sym(b,s)/poly2sym(a,s); it=ilaplace(is); ezplot(it,[0,0.01])得到图像为:图2-73.仿真结果与理论值的比较:通过1中的理论计算和2中的仿真运用,我们可以看到仿真结果与理论计算比较吻合,能够很好的反应出理论值,因此我可以认为仿真结果是正确的.不过,仿真的缺点是不能到达时间为无穷远处,只能仿真出在有限时间内的图形.同时为了能够更好的得到仿真结果与理论值的比较,我根据所求得的理论表达式得到理论图形如图2-1和图2-7。

武汉理工大学数学建模与仿真个性化课程论文说明●此次论文为命题论文,从两个个题目中选择一道,题目见后第2页。
注意论文为一个人一题,不是三个人一题!●论文(答卷)用白色A4纸打印,上下左右各留出2.5厘米的页边距。
●论文必须有封面,格式见后第二页;论文题目和摘要写在论文第二页上,从第三页(若无英文摘要)开始是论文正文。
●论文从正文开始编写页码,页码必须位于每页页脚中部,用阿拉伯数字从“1”开始连续编号,注意,论文一律要求从左侧面装订。
●论文题目用三号黑体字、一级标题用四号黑体字,并居中。
论文中其它汉字一律采用小四号宋体字,行距用1倍行距。
●引用别人的成果或其他公开的资料(包括网上查到的资料) 必须按照规定的参考文献的表述方式在正文引用处和参考文献中均明确列出。
正文引用处用方括号标示参考文献的编号,如[1][3]等;引用书籍还必须指出页码。
参考文献按正文中的引用次序列出,其中书籍的表述方式为:[编号] 作者,书名,出版地:出版社,出版年。
参考文献中期刊杂志论文的表述方式为:[编号] 作者,论文名,杂志名,卷期号:起止页码,出版年。
参考文献中网上资源的表述方式为:[编号] 作者,资源标题,网址,访问时间(年月日)。
●论文中使用到的程序源代码放在附录中给出。
●论文提交时间:4月18日-4月22日,每天均为早上2点至下午5点。
提前和逾期作零分处理。
●论文提交地点:南湖新校区数学与统计楼319室孔老师处。
●论文作弊一律记0分。
●本规范的最终解释权属于武汉理工大学数学建模教练组。
武汉理工大学数学建模教练组2016年3月论文封面格式,打印论文时此行删除武汉理工大学2016年数学建模与仿真课程论文题目:╳╳╳╳╳╳╳╳╳╳╳╳╳╳╳╳╳姓名:╳╳╳╳学院:╳╳╳╳专业:╳╳╳╳学号:╳╳╳╳选课老师:╳╳╳╳2016年╳月╳日武汉理工大学2016年数学建模与仿真课程论文题目A题:同工同酬,该公司做到了吗?B题:个人笔记本电脑购买方案。



承诺书我们仔细阅读了第十五届数学建模校内热身赛参赛规则我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛章程和参赛规则的,如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛章程和参赛规则,以保证竞赛的公正、公平性。
如有违反竞赛章程和参赛规则的行为,我们将受到严肃处理。
我们授权武汉理工大学校数学建模协会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等)。
我们参赛选择的题号是(从A/B/中选择一项填写):我们的参赛报名号为:参赛队员: 1.2.3.(论文纸质版与电子版中的以上信息必须一致,只是电子版中无需签名。
以上内容请仔细核对,提交后将不再允许做任何修改。
如填写错误,论文可能被取消评奖资格。
)日期:年月日编号专用页评阅编号:全校统一编号:全校评阅编号对于高校课表安排问题的研究与分析摘要排课问题是一个有约束的、多目标的组合优化问题,并且己经被证明是一个完全NP问题。
一套高质量的课表,在时间、教室资源、课程安排等很多方面都应该做到科学的安排,并且应该具有人性化的考虑。
课表问题的难点在于如何保证课表在时间的分配上符合一切共性和个性要求,质量过关,没有违法规则的地方,在此基础上,所有的课程都能够安排合适的时间和教室,使排课方案在各个目标上尽量达到全局最优。
本文采用遗传算法建立模型,对排课问题的多个目标进行量化分析。
遗传算法(Genetic Algorithm,GA)是一种借鉴生物界自然选择和进化机制发展起来的高度并行、随机、自适应的随机搜索算法[1]。
由于其具有健壮性,特别适合于处理传统搜索算法解决不好的复杂的和非线形问题。
我们在满足课程安排不发生冲突的基础上,充分考虑各个各课程对教学条件,例如依据教室容量来确定合班或分班上课等等,以此来设计适应度函数,进行冲突检测和各个遗传算子的操作设计。

百度文库- 让每个人平等地提升自我I 武汉理工大学毕业设计(论文)千瓦级水力发电机的建模与仿真学院(系):自动化学院专业班级:电气学生姓名:XXXXXXXX指导教师:XXXXXXXX百度文库- 让每个人平等地提升自我I摘要本文首先通过介绍当今世界能源短缺的现状,引出了要研究的千瓦级水力发电。
千瓦级水力发电属于微型水力发电的范畴,因此本文又介绍了水力发展现状和微型水力发电的技术进展与市场调研。
在千瓦级水力发电机的建模前,我还根据水轮发电机的分类对其中的各部分进行了选型,并分析了水轮发电机组各部分,引水系统,水轮机,发电机励磁系统等的数学模型。
然后运用MATLAB软件对水轮发电机的各部分分别建模后再依据互相之间的关系建立整个系统的模型,最后在动态的条件下对水轮发电机的运行状态进行仿真分析。
论文主要研究了水轮发电机的工作原理和水轮发电机的建模仿真。
研究结果表明,在动态的情况下,所设计的水轮发电机组的运行状态基本能够保持稳定,满足用电的基本要求。
本文的特色通过反馈同步发电机的运行状态来控制水轮发电机,最后让发电机运行状态基本保持稳定。
关键词:千瓦级水力发电;水轮发电机;数学模型;MATLAB建模仿真百度文库- 让每个人平等地提升自我IIAbstractFirstly, by introducing the world's energy shortage situation,this article leads tothe need to study kilowatt hydroelectric power. Kilowatt hydroelectric power belongs to the category of micro- hydro, so this article describes the technical progress and status of hydro and micro- hydro development and market research.Before modeling kilowatt hydroelectric, I also according to the classification of the various parts of hydro which conducted the selection and analysis of the various parts of hydroelectric generating set, such as water systems, turbine, generator excitation systems, etc. mathematical model.Then use MATLAB software for modeling each part separately and then build hydro entire system based on the model of the relationship between each other , and finally under dynamic conditions ,I simulation analysis the running state of my is mainly on the working principle and the modeling and simulation of hydro turbine results show that: In the dynamic case,the design of the operational status of hydro-generating unit can maintain the basic stability of electricity and meet the basic requirements.Features of this article: synchronous generator through feedback to control the hydro, and let the generator run status remained stable.Key Words:kilowatt hydroelectric power ; hydro ; mathematical model ; MATLAB modeling and simulation百度文库- 让每个人平等地提升自我III 目录第1章绪论 (1)选题的目的与意义 (1)国内外水力发电现状 (1)国内外水力发电发展现状 (1)小水电发展现状 (2)微水电开发利用技术进展 (4)千瓦级水力发电——微水电 (4)水力发电原理 (4)微水电简介 (4)微型水力发电的市场调研 (6)根据水流信息的发电容量的计算方法 (6)第2章千瓦级水力发电机组的选型 (9)微型水力发电机组的选型 (9)水轮机的类型及选择 (9)发电机的类型及选择 (10)第3章千瓦级水力发电机组的数学模型 (12)引水系统的数学模型 (12)水轮机调节系统数学模型 (13)水轮机的数学模型 (13)调节器的数学模型 (14)发电机系统数学模型 (15)负载数学模型 (16)第4章千瓦级水力发电机组的建模与仿真 (18)软件简介 (18)仿真模型建立 (19)水轮机系统建模 (19)发电机及励磁控制系统建模 (20)千瓦级水力发电机组系统模型 (21)仿真分析 (22)正常运行时发电机运行状态 (22)突甩负载和突加负载时发电机运行状态 (23)第5章结论 (25)参考文献 (26)附录 (27)致谢 (28)百度文库- 让每个人平等地提升自我1 第1章绪论选题的目的与意义水能是目前世界上可大规模开发的可再生能源之一。

第十四届华中杯数学建模A题优秀论文数学建模论文范文一:建模在高等数学教学中的作用及其具体运用一、高等数学教学的现状(一) 教学观念陈旧化就当前高等数学的教育教学而言,高数老师对学生的计算能力、思考能力以及逻辑思维能力过于重视,一切以课本为基础开展教学活动。
作为一门充满活力并让人感到新奇的学科,由于教育观念和思想的落后,课堂教学之中没有穿插应用实例,在工作的时候学生不知道怎样把问题解决,工作效率无法进一步提升,不仅如此,陈旧的教学理念和思想让学生渐渐的失去学习的兴趣和动力。
(二) 教学方法传统化教学方法的优秀与否在学生学习的过程中发挥着重要的作用,也直接影响着学生的学习成绩。
一般高数老师在授课的时候都是以课本的顺次进行,也就意味着老师“由定义到定理”、“由习题到练习”,这种默守陈规的教学方式无法为学生营造活跃的学习氛围,让学生独自学习、思考的能力进一步下降。
这就要求教师致力于和谐课堂氛围营造以及使用新颖的教育教学方法,让学生在课堂中主动参与学习。
二、建模在高等数学教学中的促进作用对学生的想象力、观察力、发现、分析并解决问题的能力进行培养的过程中,数学建模发挥着重要的作用。
最近几年,国内出现很多以数学建模为主体的赛事活动以及教研活动,其在学生学习兴趣的提升、激发学生主动学习的积极性上扮演着重要的角色,发挥着突出的作用,在高等数学教学中引入数学建模还能培养学生不畏困难的品质,培养踏实的工作精神,在协调学生学习的知识、实际应用能力等上有突出的作用。
虽然国内高等院校大都开设了数学建模选修课或者培训班,但是由于课程的要求和学生的认知水平差异较大,所以课程无法普及为大众化的教育。
如今,高等院校都在积极的寻找一种载体,对学生的整体素质进行培养,提升学生的创新精神以及创造力,让学生满足社会对复合型人才的需求,而最好的载体则是高等数学。
高等数学做为工科类学生的一门基础课,由于其必修课的性质,把数学建模导入高等数学课堂中具备最广的影响力。
学生学号实验课成绩学生实验报告书实验课程名称成型模拟分析基础开课学院材料学院指导教师姓名学生姓名学生专业班级2011-- 2012学年第一学期实验教学管理基本规范实验是培养学生动手能力、分析解决问题能力的重要环节;实验报告是反映实验教学水平与质量的重要依据。
为加强实验过程管理,改革实验成绩考核方法,改善实验教学效果,提高学生质量,特制定实验教学管理基本规范。
1、本规范适用于理工科类专业实验课程,文、经、管、计算机类实验课程可根据具体情况参照执行或暂不执行。
2、每门实验课程一般会包括许多实验项目,除非常简单的验证演示性实验项目可以不写实验报告外,其他实验项目均应按本格式完成实验报告。
3、实验报告应由实验预习、实验过程、结果分析三大部分组成。
每部分均在实验成绩中占一定比例。
各部分成绩的观测点、考核目标、所占比例可参考附表执行。
各专业也可以根据具体情况,调整考核内容和评分标准。
4、学生必须在完成实验预习内容的前提下进行实验。
教师要在实验过程中抽查学生预习情况,在学生离开实验室前,检查学生实验操作和记录情况,并在实验报告第二部分教师签字栏签名,以确保实验记录的真实性。
5、教师应及时评阅学生的实验报告并给出各实验项目成绩,完整保存实验报告。
在完成所有实验项目后,教师应按学生姓名将批改好的各实验项目实验报告装订成册,构成该实验课程总报告,按班级交课程承担单位(实验中心或实验室)保管存档。
6、实验课程成绩按其类型采取百分制或优、良、中、及格和不及格五级评定。
附表:实验考核参考内容及标准观测点考核目标成绩组成实验预习1.预习报告2.提问3.对于设计型实验,着重考查设计方案的科学性、可行性和创新性对实验目的和基本原理的认识程度,对实验方案的设计能力20%实验过程1.是否按时参加实验2.对实验过程的熟悉程度3.对基本操作的规范程度4.对突发事件的应急处理能力5.实验原始记录的完整程度6.同学之间的团结协作精神着重考查学生的实验态度、基本操作技能;严谨的治学态度、团结协作精神30%结果分析1.所分析结果是否用原始记录数据2.计算结果是否正确3.实验结果分析是否合理4.对于综合实验,各项内容之间是否有分析、比较与判断等考查学生对实验数据处理和现象分析的能力;对专业知识的综合应用能力;事实求实的精神50%实验课程名称材料成型数值模拟实验项目名称利用DEFORM3D模拟镦粗锻造成型实验成绩实验者专业班级组别同组者实验日期2011年11月6日第一部分:实验预习报告(包括实验目的、意义,实验基本原理与方法,主要仪器设备及耗材,实验方案与技术路线等)一、实验目的1)了解认识DEFORM-3D软件的窗口界面。
二级倒立摆的建模与MATLAB仿真摘要:本文根据牛顿力学原理,使用机理建模法对二级倒立摆系统进行了建模与仿真研究。
利用最优化控制理论,研究了线性二次型最优控制器对倒立摆系统进行了有效控制。
基于MATLAB程序的设计、仿真的运行,结果表明,二级倒立摆的数学建模法是切实可行的,而且十分可靠,同时利用LQR 控制器实现了对系统的控制,可以达到系统所需要的稳定性,鲁棒性。
关键词:二次型最优控制;二级倒立摆;MATLAB1 引言倒立摆系统是一个常用的、简单的、典型的可进行控制理论研究的实验平台,很多难以用常规实验研究的控制理论问题,都可以通过倒立摆系统来进行研究从而使这些抽象的控制理论问题,通过该系统可以直观的鲜明的显示出来。
所以倒立摆系统一直是控制领域的热点,并且在这些年来在不断的发展进步对控制理论的研究起到了重要作用。
倒立摆系统是一个典型的不稳定系统,具有多变量、强耦合、非线性等特点。
同时也是仿人类行走机器人和火箭发射飞行的过程调整和直升机飞行等实际运用控制对象的最简模型。
本文建立在牛顿力学定律的基础上,研究对象设置为二级倒立摆,对其进行数学建模,再使用二次型最优控制器(linear quadratic regulator,LQR)可以得到一个最优状态反馈的矩阵K,然后在通过对Q和R两个加权矩阵的严谨选取从而实现对二级倒立摆系统良好的自动控制。
2 二级倒立摆模型建立一个典型的二级倒立摆系统主要由机械部分和电气装置两部分组成。
机械装置的结构主要由小车、摆杆1、摆杆2及连接轴等组成,电气装置的主要结构是功率放大器、电动机、驱动电路、保护电路等。
其系统的结构如图1所示。
实验假设如下:(1)小车、摆杆1、摆杆2的材料性质都是刚体的。
(2)小车的驱动力和放大器的输出直接的,无滞后的作用于小车上。
(3)忽略实验中过程中出现的不可避免的各种摩擦力如库伦摩擦力等。
图1 二级倒立摆控制系统的结构二级倒立摆的参数设定如表1。
课程设计任务书学生姓名:张亚男专业班级:通信1104班指导教师:张小梅工作单位:信息工程学院题目: PSK和DPSK信号的仿真分析初始条件:在MATLAB仿真软件系统中设计并实现PSK和DPSK信号系统的仿真,并进行调试和仿真波形分析。
要求完成的主要任务: (包括课程设计工作量及技术要求,以及说明书撰写等具体要求)1、课程设计工作量:5天。
2、技术要求:调制信号:300Hz正弦信号,经过μ律PCM编码;载波频率:100kHz;要求:画出调制信号、已调信号、解调信号的波形、频谱以及误码率与输入信噪比的关系曲线3、查阅至少5篇参考文献。
按《武汉理工大学课程设计工作规范》要求撰写设计报告书。
全文用A4纸打印,图纸应符合绘图规范。
时间安排:1、2013年5 月16 日,布置课设具体实施计划与课程设计报告格式的要求说明。
2、2013年6 月27 日至2013年6 月29 日,方案选择和电路设计。
3、2013年6 月30 日至2013年7 月3 日,电路调试和设计说明书撰写。
4、2013年7 月5 日,上交课程设计成果及报告,同时进行答辩。
指导教师签名:年月日系主任(或责任教师)签名:年月日目录摘要....................................................... 错误!未定义书签。
Abstract.................................................... 错误!未定义书签。
1 方案设计................................................. 错误!未定义书签。
1.1 调制部分方案选择..................................... 错误!未定义书签。
1.2 解调部分方案选择..................................... 错误!未定义书签。
武汉理工大学2014年数学建模课程论文题目:金属板切割问题姓名:学院:专业:学号:选课老师:黄小为2014年6月23日金属板切割问题:在一个金属板加工车间内将要从尺寸为48分米×96分米的大块矩形金属板上切割下小块的金属板。
此车间接到订单要求为:生产8块大小为36分米×50分米的矩形金属板,13块大小为24分米×36分米的矩形金属板,以及15块大小为18分米×30分米的矩形金属板。
这些金属板都需要从现有的大块金属板上切割下。
为生产出满足订单要求的金属板,最少可以使用多少块大块金属板?摘要本文介绍了金属板切割问题的数学模型的建立方法。
要求对车间生产切割金属板的方式进行数学规划,以达到经济效益最大化。
可以采用穷举法和实际意义相结合的方法,找出题目的隐含条件,通过各种搭配找到合理的切割金属板的模式。
在找到各种模式后,通过建立非线性规划的数学模型,以模式为基点,将本题中的订单转化为切割金属板的各种约束条件。
最后通过LINGO软件中的数学规划模型求解功能求解出目标函数值,并且通过验证证明,该模型求解出的最少原料使用量与具体切割方式是完全满足题目要求的。
关键词:切割方式;非线性规划;LINGO1.问题要求本题主要是讨论金属板的最优切割方式,并拟定最合理的方案使工厂经济效益实现最大化。
由已知条件知道工厂需要将一块完整的大矩形金属板切割成多块不同的小矩形金属板,并且已经给出了所需产品的尺寸和数量。
从经济方面来看,金属板材料是最大的成本因素,因此,建立出的模型必须要遵循着节约材料的原则,然后结合实际情况,制定最合理的切割计划。
2.模型假设(1)假设车间是以减少原料投入为主要节省方式。
实际上,金属加工生产中的余废料价值远远小于完整的原料价值,因此这样假设确立了模型是以最小原料使用量为目标。
(2)金属切割时不发生原料总面积减少。
在生产实践当中,由于切割工艺问题, 在切割板材是会使切割线位置出现原料耗损(如融化,形变等)。
武汉市环境污染问题的因子分析摘要:九十年代以来,武汉市经济建设取得长足发展,人民生活水平不断提高。
十二五期间,随着高铁网络的逐步建设,武汉市交通枢纽的地位愈发显著;复兴大武汉战略提出后,武汉市经济快速发展,城市建设日新月异。
但在经济快速发展的同时,也带来了一些社会问题,其中环境污染问题日益严重,愈发影响人民生活水平的进一步提高,阻碍了武汉市经济社会的良性循环发展。
本文应用数理统计中所学的因子分析的知识,对武汉地区的环境污染问题的分析与评价。
所得到的分析结果可以为武汉市的环境治理与整治提供一定的参考价值和理论基础。
关键词:环境污染、因子分析、数理统计、SPSS 。
一 问题提出与分析环境问题中,各个指标错综复杂,这不利于我们分析问题。
如何从数据中抓住主要规律,从而分析样本或总体的主要性质呢?这就需要运用到因子分析的统计学方法了。
因子分析是一种把原来多个指标化为少数几个互不相关的综合指标的一种统计方法,可以达到简化数据、揭示变量之间的关系和进行统计解释的目的,为进一步分析总体的性质和数据的统计特性提供一些重要信息。
本文就武汉市2008年—2013年的废水排放总量、工业废水排放量、废气排放总量、二氧化硫排放量、工业中二氧化硫排放量、烟尘排放量、工业烟尘排放量、工业固体废物产生量等8个环境污染指标之间的关系进行了一定的分析,为武汉市的环境治理提供一定的理论依据。
二 数学模型、原理及算法2.1因子分析的一般模型因子分析的一般模是:112233...,(1,2,3...)i i i i im m X a f a f a f a f i i k ε=+++++=,在这个模型中:(1)12,,...k X X X 为原始变量经过标准化处理后的标准化变量。
标准化处理可以消除量纲的影响,而且标准化变换不影响变量的相关系数。
这里的X i 都具有均值为0,方差为1的特征。
(2)12,...m f f f 叫做公因子,它们是在各个变量表达式中都出现的因子。
武汉理工大学2014年数学建模课程论文题目:金属板的切割问题
姓名:李冬波
学院:自动化学院
专业:自动化
学号:012121136329
选课老师:何朗
2014年6月22日
摘要
金属板的切割问题要求对金属板的切割方式进行构思,希望通过数学可以达到效率较高、成本较低的可能性。
应该先通过穷举的方法找到所有可能性,在所有可能性中保留最优的可能性。
所谓最优即效率较高、成本较低的可能。
在确立了6种切割模式的基础上,再建立非线性规划的数学模型,以模式为基点,将题中订单需求转化为求解金属原料此目标函数的约束条件。
在通过LINGO软件的数学规划模型求解功能求解出目标函数值,并通过检验证明,该模型求解出的最少原料使用量与具体切割模式是完全满足题目要求的。
关键词:切割模式、非线性规划、 LINGO
目录
一、问题重述 ------------------------------4
二、问题假设 ------------------------------4
三、模型建立----------------------------------------------5
符号说明------------------------------------------------5
建立模型------------------------------------------------5
四、模型求解----------------------------------------------6
五、求解结果---------------------------------------------7
六、结果检验分析---------------------------------------7 七丶结论-----------------------------------------------8 八、参考文献---------------------------------------------8
板材切割的最优化问题
一、问题重述
本题主要是讨论在切割大面积金属时,通过建立数学模型的方法使切割时的成本最低、效率最高。
本题中只考虑切割切割金属的面积。
题目中已经给出了已知大面积金属板的实际面积大小,并给消费者们需要切割的小块金属的面积与需要的个数。
由于利润和控制成本是生产商最重要的东西,所以在实际切割的时候,一定要考虑效率和成本。
尽量最大的进行成本节约。
我们采用数学建模的方式来解决这一实际问题。
通过这样的方式处理问题可以做到高效、直观和准确。
二、模型假设
(1)假设车间是以减少原料投入为主要节省方式。
实际上,金属加工生产中的余废料价值远远小于完整的原料价值,因此这样假设确立了模型是以最小原料使用量为目标。
(2)金属切割时不发生原料总面积减少。
在生产实践当中,由于切割工艺问题,在切割板材是会使切割线位置出现原料耗损(如融化,形变等)。
在模型中假设这种耗损不存在。
(3)不考虑切割方式增加所带来的成本成本增加。
作为简单的直线切割问题,生产模式的增加对设备要求、人力要求很少,因此对成本的增加微乎其微可以忽略,即不限制切割模式的数量。
(4)假设所有原材料的大小规格完全一致,这样假设避免一些不确定因素对模型求解时的不利影响,简化模型。
三、模型建立
符号说明:
Z 原料使用量
Xi(i=1,2,3,4,5,6) 第i种方案所用的原料数
A 36*50(dm)的产品
B 24*36(dm)的产品
C 18*30(dm)的产品
问题分析:
根据题目可知,将原料48*96的金属板切割成A、B、C三种样式的产品。
由于题中所设计的数据量较少,因此只需建立一个简单的非线性规划模型,求解目标函数Z的最优解即可。
在求解Z的最优值的时候,根据订单所需的各项指标,采用原料使用量最小原则,已达到工厂经济效益的最大化。
建立模型
1.利用穷举法得到一个所有情况的表格:
2.非线性规划:
确立目标函数:
Z=X1+X2+X3+X4+X5+X6
由于采用原料使用量最少原则,因此只需将各种模式下使用原材料的数量加和得到目标函数Z,并求解其最小值。
再确立目标函数的各项约束条件:
x1+x2+x3>=8;
图表中所给模式当中,有模式1、2、3可以切割A型产品,且其条件如上,其余依次可得:
2*x1+x2+5*x4+4*x5>=13;
x2+3*x3+x5+8*x6>=15;
四、模型求解
编写lingo软件程序,利用其中的数学规划功能求解该问题。
MIN=x1+x2+x3+x4+x5+x6;
x1+x2+x3>=8;
2*x1+x2+5*x4+4*x5>=13;
x2+3*x3+x5+8*x6>=15;
@gin(x1);@gin(x2);@gin(x3);
@gin(x4);@gin(x5);@gin(x6);
五、求解结果
Global optimal solution found.
Objective value: 10.00000
Objective bound: 10.00000
Infeasibilities: 0.000000
Extended solver steps: 0
Total solver iterations: 7
Variable Value Reduced Cost
X1 7.000000 1.000000
X2 0.000000 1.000000
X3 1.000000 1.000000
X4 0.000000 1.000000
X5 0.000000 1.000000
X6 2.000000 1.000000
由计算结果知,最少用金属块数量为10,其分配方案为7块采用x1切割方式,1块用x3切割方式,2块用x6切割方式。
虽然有些许多余金属块,但此方案还是符合条件下的最佳分配方式。
六、结果检验分析
由运算结果可知,将10块金属板材分别用模式1、3、6进行切割,最终可得:8块大小为36分米×50分米的矩形金属板,13块大小为24分米×36分米的矩形金属板,以及15块大小为18分米×30分米的矩形金属板。
虽然部分产品型号超过了订单需求,而使超过需求的部分成为废料,但如此规划切割模式,仍然能使所用大金属板的数量达到最小。
在实际生产当中,成型的板材废料比切割过程中出现的边角废料的可利用率更高。
因此,该模型求解结果依然具
有较强的现实意义。
七、模型的优缺点
模型的优点即,在建立过程中,充分考虑了在解决此问题当中的实际意义,确立了以所用原料最少的目标函数,使模型的大体方向正确,利于解决实际问题。
模型的缺点为,对于一个二维的非线性规划问题,如果一点涉及的规划条件复杂化,很难采用穷举法将所有可能的情况全部举例说明,而且可能遗漏部分需要讨论的情况。
因此,对待更加复杂的非线性规划问题,应该采用模型约束条件来限制目标函数。
参考文献
[1] 百度文库 Lingo 教程
/fei_woo/blog/static/4010677520077268522253/。