空间曲面的一般方程
- 格式:docx
- 大小:37.18 KB
- 文档页数:3

曲面方程一般表达式
曲面方程是描述三维空间中曲面的数学公式。
一般来说,曲面方程可以用一般表达式来表示。
一般表达式是指一个包含三个变量x、y、z的二次方程,其形式为:
Ax² + By² + Cz² + Dxy + Exz + Fyz + Gx + Hy + Iz + J = 0
其中A、B、C、D、E、F、G、H、I、J是常数,且A、B、C不全为0。
这个方程描述了一个三维空间中的曲面,它的形状和大小取决于方程中的系数。
例如,当A、B、C都为正数时,曲面是一个椭球体;当A、B、C中有一个为0时,曲面是一个抛物面或一个圆锥面;当A、B、C中有两个为0时,曲面是一个平面或一个圆柱面。
曲面方程的一般表达式可以用来解决许多实际问题。
例如,在物理学中,曲面方程可以用来描述电场、磁场、重力场等物理现象;在工程学中,曲面方程可以用来设计汽车、飞机、船舶等产品的外形;在计算机图形学中,曲面方程可以用来生成三维模型,实现真实感渲染等。
曲面方程的求解是一个复杂的数学问题。
一般来说,可以通过数值计算或解析方法来求解。
数值计算是指通过计算机程序来求解方程的数值解,这种方法适用于一般表达式比较简单的情况。
解析方法
是指通过数学推导来求解方程的解析解,这种方法适用于一般表达式比较复杂的情况。
曲面方程的一般表达式是描述三维空间中曲面的重要工具,它在许多领域都有广泛的应用。

常用曲线和曲面的方程及其性质曲线和曲面在三维空间中是常见的数学对象。
它们的方程可以通过几何性质描述它们的性质。
本文将介绍一些常用的曲线和曲面方程及其性质。
一、曲线方程1. 直线方程直线是一种最基本的曲线,它的方程可以写成一般式和斜截式两种形式。
一般式:$Ax+By+C=0$;斜截式:$y=kx+b$,其中$k$是直线的斜率,$b$是截距。
直线的斜率表示的是直线倾斜的程度,斜率越大表示直线越陡峭。
斜率等于零表示直线水平,而无限大则表示直线垂直于$x$轴。
2. 圆的方程圆是一种具有球面对称性质的曲线,它的方程可以写成两种形式:标准式和一般式。
标准式:$(x-a)^2+(y-b)^2=r^2$,其中$(a,b)$为圆心坐标,$r$为半径长度。
一般式:$x^2+y^2+Ax+By+C=0$,其中$A,B,C$是常数。
圆的标准式方程可以通过圆心和半径来描述圆的几何性质;而一般式方程则可以通过求圆的中心和半径来转化为标准式方程。
3. 椭圆的方程椭圆是一种内离于两个焦点的平面曲线,它的方程可以写成一般式和标准式两种形式。
标准式:$\frac{(x-a)^2}{a^2}+\frac{(y-b)^2}{b^2}=1$,其中$(a,b)$为椭圆中心坐标,$a$是横轴半径,$b$是纵轴半径。
一般式:$Ax^2+By^2+Cx+Dy+E=0$,其中$A,B,C,D,E$是常数。
椭圆的标准式方程中的$a$和$b$决定了椭圆的形状和大小。
当$a=b$时,椭圆变成了圆。
4. 抛物线的方程抛物线是一种开口朝上或朝下的U形曲线,它的方程可以写成两种形式:标准式和一般式。
标准式:$y=ax^2$,其中$a$是抛物线的参数。
一般式:$Ax^2+By+C=0$,其中$A,B,C$是常数。
抛物线的标准式方程中的参数$a$可以决定抛物线的开口方向,当$a>0$时开口向上,$a<0$时则开口向下。
5. 双曲线的方程双曲线是一种形状类似于抛物线的曲线,但它却有两个分支。


空间曲面方程总结一、引言空间曲面方程是数学中的一种重要概念,它描述了三维空间中的曲面形状。
在工程、物理学、计算机图形学等领域都有广泛应用。
本文将从定义、分类、求解方法等方面对空间曲面方程进行总结。
二、定义空间曲面是指在三维空间中的一个二维曲面,可以用数学公式来表示。
通常情况下,我们使用参数方程或者一般式方程来表示空间曲面。
三、分类1. 隐式方程:隐式方程是指将一个空间曲面看做一个点集合,而不是函数关系式。
其表达方式为F(x,y,z)=0,其中F(x,y,z)为多项式函数。
2. 参数方程:参数方程是指将一个空间曲面表示为两个或三个参数的函数形式。
例如x=f(u,v), y=g(u,v), z=h(u,v)。
3. 一般式方程:一般式方程是指将一个空间曲面表示为x^2+y^2+z^2+ax+by+cz+d=0的形式。
四、求解方法1. 隐式求导法:该方法适用于隐式方程和一般式方程。
通过对隐函数进行求导,可以得到切向量和法向量。
2. 参数求导法:该方法适用于参数方程。
通过对参数进行求导,可以得到切向量和法向量。
3. 矩阵法:该方法适用于参数方程和一般式方程。
通过构造矩阵,可以得到切向量和法向量。
五、应用1. 工程领域:空间曲面方程可以用来描述物体的形状,例如汽车、飞机等。
2. 物理学领域:空间曲面方程可以用来描述电场、磁场等物理现象。
3. 计算机图形学领域:空间曲面方程可以用来生成三维图形。
六、总结空间曲面方程是数学中的重要概念,它描述了三维空间中的曲面形状。
根据表达方式的不同,空间曲面方程可分为隐式方程、参数方程和一般式方程。
求解方法主要有隐式求导法、参数求导法和矩阵法。
在工程、物理学、计算机图形学等领域都有广泛应用。



曲面与曲面相切判别式曲面是几何学中的一个重要概念,指的是具有弯曲形状的平面之外的物体。
在三维空间中,我们可以通过判断两个曲面是否相切来研究它们的关系和性质。
为了判断曲面之间是否相切,我们需要依据一定的判别式来进行分析和计算。
1. 曲面与曲面相切的定义曲面与曲面相切指的是两个曲面在某一点上具有相同法线方向。
这意味着两个曲面在这一点上的切平面相同,即两个曲面的切空间重合。
2. 曲面方程的一般形式一般地,表示曲面的方程可以用以下形式表示:F(x, y, z) = 0其中,F(x, y, z)是一个关于变量x, y, z的函数。
该函数决定了曲面在空间中的形状和性质。
3. 曲面方程的法向量曲面的法向量是垂直于曲面上每一点的向量,通常用n表示。
法向量的方向决定了曲面的朝向,也是我们判断曲面相切的关键依据。
4. 曲面的梯度曲面方程的梯度用∇F(x, y, z)表示,表示F(x, y, z)在点(x, y, z)处的梯度。
梯度是一个向量,其方向与曲面在该点的法向量相同。
5. 判别式的计算为了判断两个曲面是否相切,我们需要计算它们在某一点上的判别式。
判别式可以通过计算两个曲面的法向量之间的内积来实现。
具体地,判别式可以表示为:∇F1(x, y, z) ·∇F2(x, y, z) = 0其中,F1(x, y, z)和F2(x, y, z)分别是两个曲面的方程。
如果判别式为零,则说明两个曲面在该点上相切;如果判别式不为零,则说明两个曲面在该点上不相切。
6. 曲面相切的判断根据判别式的计算结果,我们可以得出曲面与曲面相切的判断。
如果在曲面方程中存在参数,我们可以将其代入判别式中进行计算。
如果判别式对所有参数值均成立,则说明两个曲面在所有点上相切;如果判别式对某些参数值不成立,则说明两个曲面在某些点上不相切。
7. 实例分析为了更好地理解曲面与曲面相切的判别式,我们来分析一个具体的实例。
假设有两个曲面的方程分别为:F1(x, y, z) = x^2 + y^2 + z^2 - 4 = 0F2(x, y, z) = x^2 + y^2 + z - 2 = 0首先,我们需要计算两个曲面方程的梯度。

空间曲线与空间曲面的学习总结王德才201121102340电子商务1133班一、曲面方程1 曲面方程的概念及一般方程如果曲面S与三元方程F(x, y, z)=0 (1)有下述关系:(1)曲面S上任一点的坐标都满足方程(1);(2)不在曲面S上的点的坐标都不满足方程(1),那末,方程(1)就叫做曲面S的方程,而曲面S就叫做方程(1)的图形。
2. 平面方程的几种形式(1)一般形式:Ax+By+Cy+D=0,其中{A,B,C}是平面法向,。
(2)点法式方程:(3)截距式方程:(4)三点式方程:已知平面过空间三点,,,则平面方程为3.几种特殊的曲面方程(1)球面方程:空间中与一定点的距离为定值的动点的轨迹。
定点称为球心,定距离称为半径。
球面也可以看成是由半圆绕着它的直径旋转一周所形成的曲面。
,0≤θ≤2π,0≤φ≤π(2)旋转曲面方程定义:曲线C绕定直线旋转一周所形成的曲面称为旋转曲面。
其中C——母线轴,与垂直的任一平面与旋转曲面交成一圆——维圆,过的任一平面与旋转曲面交成一圆——经线(子午线)注:旋转曲面的母线不唯一,它的任一经线均是其母线。
设平面曲线z轴旋转,则旋转曲线方程为角坐标系中,只含两个变量的二次方程一般总表示一个二次柱面或者两个平面。
若一动直线沿已知曲线C移动,且始终与某一定直线平行,则这样形成的曲面称为柱面。
曲线C称为准线。
动直线L称为母线。
F(x,y)=0 表示母线平行于z轴的柱面。
F(y,z)=0 表示母线平行于x轴的柱面。
F(x,z)=0 表示母线平行于y轴的柱面。
母线平行与坐标轴的柱面方程为不完全的三元方程,如F(y, z)=0就表示母线平行与x轴,准线为.二空间曲线的方程1、普通方程(1)定义:设L为空间曲线,空间中建立了坐标系之后,若L上任一点M(x,y,z)的坐标都满足方程组,而且凡坐标满足方程组的点都在曲线L上,L的普通方程,又称一般方程,记作(图2.8)注: 1°在空间坐标系下,任一曲线的方程定是两方程联立而成的方程组; 2°用方程组去表达曲线,其几何意义是将曲线看成了二曲面的交线(如图2.8);3°空间曲线的方程不唯一(但它们同解),如均表示z轴(2)用曲线的射影柱面的方程来表达曲线以曲线L为准线,母线平行于坐标轴的柱面称为L的射影柱面,若记L的三射影柱面的方程为 (x,y)=0,则便是L的用射影柱面表达的方程若已知曲线只需从L的方程中,分别消去x,y,z便三射影柱面的方程(y,z)=0, (z,x)=0,例:设有曲线试求L的射影柱面,并用射影柱面方程表达曲线.解:从L的方程中分别消去x,y,z得到z²-4y=4z,x²+z²=4z,x²+4z=0它们即为L的射影柱面,而便均是L的用射影柱面表达的方程注:利用方程(2)即可作出L的草图2、参数方程:(1)定义:设L为一空间曲线,r=r(t),t∈A为一元矢函数,在空间坐标系下,∈L,∈A,(t),∈A,必有P∈L,使r(t),则称r=r(t),t∈A为曲线L的矢量式参数方程,记作L=r=r(t),t∈A,t ——参数若点r(t)={x(t),y(t),z(t)}∈A为L的坐标式参数方程注:空间曲线的参数方程中,仅有一个参数,而曲面的参数方程中,有两个参数,所以习惯上,称曲线是单参数的,而曲面是双参数的。

空间中曲线与曲面方程在三维空间中,曲线和曲面是几何学中重要的概念,在数学和物理学等领域有广泛的应用。
曲线是指在空间中表示为一系列点的集合,而曲面是在空间中表示为一系列点的集合的一个二维面。
本文将就空间中曲线与曲面方程进行探讨。
一、空间曲线的方程在三维空间中,曲线可以用参数方程或者一般方程来表示。
参数方程是指将曲线的坐标用参数表示,例如(x(t), y(t), z(t))。
每个参数t对应曲线上的一个点。
一般方程则是通过给出曲线上的点满足的关系式来表示,例如F(x, y, z) = 0。
参数方程的优势在于可以轻松描述曲线的形状,通常直接从曲线的定义出发,选择合适的参数方程。
而一般方程则更适合用于描述曲线的性质和特征。
二、空间曲面的方程空间中的曲面可以用参数方程、一般方程或者隐函数方程来表示。
参数方程类似于曲线的参数方程,将曲面上的点用参数表示,例如(x(u, v), y(u, v), z(u, v))。
每个参数对应曲面上的一个点。
一般方程则通过给出曲面上的点满足的关系式来表示,例如F(x, y, z) = 0。
隐函数方程则将曲面的方程化简为一个关于x、y、z的方程,例如F(x, y, z) = 0。
选择曲面的方程格式取决于具体的问题和需求。
参数方程可以直观地描述曲面的形状,适用于绘制和计算曲面上的点。
一般方程和隐函数方程更适合用于分析曲面的性质和特征。
三、曲线和曲面的方程求解对于空间中的曲线和曲面方程,求解其解析式是数学中一个重要的问题。
有时可以通过直接求解得到解析式,有时需要借助计算机和数值方法进行求解。
对于一些简单的曲线和曲面方程,可以通过代数运算得到解析式。
例如对于一条直线,可以通过给出直线上两点的坐标,然后通过两点间的直线方程求解出直线的解析式。
对于一些复杂的曲线和曲面方程,可以通过数值方法进行求解,如迭代法、线性插值等,以获得近似解。
四、曲线和曲面方程的应用曲线和曲面方程在数学和物理学中有广泛的应用。

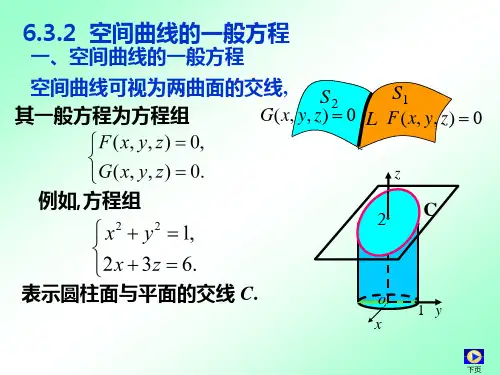
1第四节空间曲线及其方程⎩⎨⎧==0),,(0),,(z y x G z y x F 曲线上的点都满足方程,不在曲线上的点不能同时满足两个方程.xozy1S 2S C空间曲线C 可看作空间两曲面的交线.特点:一、空间曲线的一般方程2方程组表示怎样的曲线?⎩⎨⎧=++=+6332122z y x y x 解122=+y x 表示圆柱面,6332=++z y x 表示平面,⎩⎨⎧=++=+6332122z y x y x 交线为椭圆.例13方程组表示怎样的曲线?⎪⎩⎪⎨⎧=+---=4)2(222222a y a x y x a z 解222yx a z --=上半球面,4)2(222a y a x =+-母线平行于z 轴的圆柱面,交线如图.例2Oxyz准线为xOy 面上的圆, 圆心在点.2),0,2(a a 半径为4⎩⎨⎧==0),,(0),,(z y x G z y x F 消去变量z 后得:0),(=y x H 曲线关于的投影柱面xoy 设空间曲线的一般方程:以此空间曲线为准线,垂直于所投影的坐标面.投影柱面的特征:二、空间曲线在坐标面上的投影如图:投影曲线的研究过程.投影柱面空间曲线投影曲线56类似地:可定义空间曲线在其他坐标面上的投影⎩⎨⎧==00),(x z y R ⎩⎨⎧==00),(y z x T 面上的投影曲线,yoz 面上的投影曲线,xoz ⎩⎨⎧==00),(z y x H 空间曲线在面上的投影曲线xoy7求曲线在坐标面上的投影.⎪⎩⎪⎨⎧==++211222z z y x (1)消去变量z 后得,4322=+y x 在面上的投影为xoy ,04322⎪⎩⎪⎨⎧==+z y x 解例38求曲线在坐标面上的投影.⎪⎩⎪⎨⎧==++211222z z y x 解例3所以在面上的投影为线段.xoz ;23||,021≤⎪⎩⎪⎨⎧==x y z (3)同理在面上的投影也为线段.yoz .23||,021≤⎪⎩⎪⎨⎧==y x z (2) 因为曲线在平面上,21=z9求曲线⎪⎩⎪⎨⎧+=--=)(342222y x z yx z 在xOy 面上的投影.消去z 得:122=+y x ,所求投影为圆周⎩⎨⎧==+0122z y x . 注:所围立体在xy 面上的投影为:122≤+y x .即上半球面与圆锥面的交线.解例4。
曲面与空间曲线的总结椭圆柱面;12222=+yx 122=-y x曲面与空间曲线一.曲面及其方程:1.曲面方程的一般概念: 定义:若曲面上的点的坐标(x,y,z)都满足方程F(x,y,z)=0,而满足此方程的点都在曲面上,则称此方程为 该曲面的方程,而曲面称为此方程的‘图形’。
例1:求与A(2,3,1)和B(4,5,6)等距离的点的运动规迹。
解: 设M(x,y,z)为动点的坐标,动点应满足的条件是 |AM|=|BM|由距离公式得此即所求点的规迹方程,为一平面方程。
2.坐标面及与坐标面平行的平面方程: ①坐标平面xOy 的方程:z=0②过点(a,b,c)且与xOy 面平行的平面方程:z=c③坐标面yOz 、坐标面zOx 以及过(a,b,c)点且分别与之平行的平面方程:x=0; y=0; x=a; y=b 3. 球面方程:①球面的标准方程:以M0(x0,y0,z0)为球心,R 为半径 的球面方程为(x-x0)2+(y-y0)2+(z-z0)2=R2 ②球面的一般方程:x2+y2+z2+Ax+By+Cz+D=0球面方程的特点:平方项系数相同;没有交叉项。
例2:求x2+y2+z2+2x-2y-2=0表示的曲面 解:整理得: (x+1)2+(y-1)2+z2=22故此为一个球心在(-1,1,0),半径为2的球。
4.母线平行于坐标轴的柱面方程:一般我们将动直线l 沿定曲线c 平行移动所形成的轨迹 称为柱面。
其中直线l 称为柱面的母线,定曲线c 称为柱面 的准线。
本章中我们只研究母线平行于坐标轴的柱面方程。
此时有以下结论:若柱面的母线平行于z 轴,准线c 是xOy 面上的一条曲线,其方程为F(x,y)=0,则该柱面的方程为F(x,y)=0; 同理,G(x,z)=0,H(y,z)=0在空间中分别表示母线平行于y 轴和x 轴的柱面。
分析:母线平行于坐标轴的柱面的特点为:平行于某轴,则在其方程中无此坐标项。
空间曲面的一般方程
是描述三维空间中曲面形态的数学方程。
它通常以向量函数或参数式给出,具体形态和性质因曲面类型而异。
本文将介绍及其相关概念和应用。
一、向量函数
向量函数是一种描述空间内对象运动或变化的数学工具。
对于空间曲面,其常常使用向量函数进行描述。
向量函数可用参数 t 来表示曲面上的位置,它的形式为:
r(t) = xi + yj + zk
其中,i、j、k 为三维空间的基准向量,x,y,z 是曲面上任意一点的坐标。
这个向量函数描述了一个以 (x, y, z) 为顶点的曲面,这个顶点即为曲面在参数 t 对应的位置。
向量函数还可以直接给出曲面的法向量和切向量。
二、参数式
参数式是另一种描述空间曲面的数学工具,也通过参数来描述曲面的位置和形态。
参数式为:
x = f(u,v)
y = g(u,v)
z = h(u,v)
其中,x、y、z 表示曲面上任意一点的坐标,u,v 为参数。
这种参数式常常通过二维平面上的图像来描述曲面的形态。
例如,球面的参数式为:
x = r sinθ cosφ
y = r sinθ sinφ
z = r cosθ
其中,r、θ、φ分别表示球坐标系下的半径、极角和方位角。
这个参数式描述了所有球面上任意一点的坐标,因此可以用来精确地描述球面的形态和性质。
三、曲面类型
根据曲面的形态和性质,我们可以将空间曲面分为若干类别。
比较常见的曲面包括平面、圆柱面、球面、圆锥面等。
这些曲面
都有其特定的方程和性质,学习者需要了解这些特性,才能更好
地理解和应用曲面方程。
四、应用
常常被用于求解空间中物体的运动轨迹、计算曲面上的切向量
和法向量、以及进行曲面的积分等计算。
例如,利用球面参数式,可以计算出某球体上的面积或体积等物理量;利用向量函数,可
以求出某点在某一时刻的速度和加速度等物理量。
而对于计算机
图形学来说,曲面方程则是绘制 3D 图像的基本工具。
总之,是描述三维空间中曲面形态的重要数学工具,它不仅包
含了向量函数和参数式,还涉及曲面类型和应用等方面。
学习者
需深入了解这些概念及其相互关系,才能更好地应用于学术研究
和实际应用中。