《微观经济学》第五讲需求
- 格式:pptx
- 大小:668.90 KB
- 文档页数:23



微观经济学第五讲效用论第五讲效用论(一)第一节效用论概述效用的概念基数效用和序数效用基数效用论和边际分析法效用的概念指商品满足人的欲望的能力;或者指消费者在消费商品时所感受到的满足程度。
注意,商品是否有效用,须具备两个条件:(1)消费者是否有消费的欲望;(2)商品是否有满足欲望的能力。
主观心理评价相应问题,下面说法正确吗?同样的一个苹果,不管是今天,明天,还是后天,对小明来说,其效用都是一样的。
同样一件棉衣,不管是在寒冷的北方,还是在炎热的南方,对小明来说,其效用都是一样的。
同样一个香蕉,对任何一个人来说,其效用都是一样的。
一元钱对穷人和富人来说其效用是一样的。
同一商品会因人、因时、因地之不同而有不同的效用。
基数效用19世纪20世纪初期,西方经济学家普遍使用基数效用的概念。
是指用基数来表示效用的大小,如1,2,3…。
基数效用论者认为,效用如同长度、重量等概念一样,可以具体衡量并加总求和,具体的效用量之间的比较是有意义的。
表示效用大小的计量单位被称作效用单位。
例如:小王今天听课的效用是9>8效用单位,打球的效用是5效用单位,则总效用为13效用单位序数效用20世纪30年代,序数效用的概念为大多数西方经济学家所使用。
是指用序数来表示效用的大小如第一,第二,第三…。
序数效用论者认为,效用是一个有点类似于香、臭、美、丑一样的概念,效用的大小是无法具体衡量的,效用之间的比较只能通过顺序或等级来表示。
例如:小王认为今天宁愿去逛街,而不愿来上课。
基数效用论和边际效用分析边际效用递减规律-228730 6 1 2 30 5 2 4 28 4 3 6 24 3 4 8 18 2 5 10 10价格边际效用总效用商品数消费者在一定的时间内从一定数量的商品的消费中所得到的效用量的总和消费者在一定的时间内增加一单位商品的消费所得到的效用量的增量边际效用递减规律:在一定时间内,在其他商品的消费数量保持不变的条件下,随着消费者对某种商品消费量的增加,消费者从该商品连续增加的每一消费单位中所得到的效用增量即边际效用是递减的。

第五讲局部均衡和一般均衡第讲局部均衡和般均衡局部均衡与福利分析⏹⏹从局部均衡到一般均衡⏹纯交换经济⏹含有生产的一般均衡模型竞争性市场的局部均衡分析⏹在前面的章节中我们始终假设,我们所考察的商品的市场是竞争性市场⏹在用局部均衡理论分析某种商品的竞争性市场时,可以使用供给需求模型假设其他商品的价格都固定不变❑❑根据市场条件决定供给和需求曲线❑给定供给和需求曲线,求出均衡的价格和数量❑市场条件变化导致市场均衡变化(比较静态分析)竞争性市场假设的适用条件某个商品的市场是竞争性的最重要的个条⏹某个商品的市场是竞争性的,最重要的一个条件是所有消费者和生产者都是价格接受者⏹但这一假设在什么条件下能够成立?直观上当只有很少几个消费者和生产者时⏹直观上,当只有很少几个消费者和生产者时,竞争性假设肯定不能成立,只有当消费者人数和生产者数量都趋于无穷大时才有可能成立❑下面我们借助一个市场博弈来说明这一点局部均衡的一个市场博弈模型局部均衡的个市场博弈模型分别用S )⏹S 和B 表示某个商品的卖家(生产者) 和买家(消费者) 集合,人数分别是n s 和n b 其中的收入⏹卖家i 的利润是,其中t i 是i 的收入,q i 是i 生产的商品数量⏹买家j 的效用是,其中q j 是j 购买的商品数量,t 是的支付额j j ⏹假设商品是无限可分的交易数量可以是任意非负⏹商品是无限可分的,交易数量可以是任意非负实数局部均衡的竞争性均衡⏹我们关心这个市场博弈的交易结果,通常的竞争性假设要求所有人都按照某个市场价格交易定义:市场博弈的一个结果⏹定义:市场博弈的个结果被称为竞争性价格p下的一个竞争性均衡,如果有:❑每个卖家的利润都达到最大❑每个买家的效用都达到最大❑交易是可行的竞争性均衡的存在性⏹竞争性均衡是否一定存在?不一定,因为我们对效用函数和成本函数没有做足够的限制❑例:当时,要求有解⏹边际成本递增假设:对任意i,c i是递增的凸函数,且在有限产量之外为无穷大函数且在有限产量之外为无穷大⏹边际效用递减假设:对任意j,u j是递增的凹函数,且饱和数量之外为不变量函数且饱和数量之外为不变量定市场博弈在假设存在竞争性均衡⏹定理:市场博弈在上述假设下存在竞争性均衡❑竞争性均衡是如何达到的?下面我们用合作博弈理论对此进行简单的分析Cooperative games 合作博弈p g ⏹一个效用可转移(transferable utility, TU) 的合作博弈可以表示为G = (N , v )❑N = {1, 2, …, n } N {,,,}是参与人集合,的任意一个子集S 称为一个联盟(characteristic function):❑v 是特征函数(characteristic function): 对任意联盟S ,v (S ) 是一个实数,表示联盟S 所有成员能够得到并分配的最大总支付,称为联盟S 的价值(value)()❑假设v 满足超可加性(superadditivity):对任意两个不相交的联盟S 和T :v S ∪T ) ≥ v S ) + v T ()()()❑为简便起见,通常还假设所有联盟的价值都非负,且空集的价值等于零合作博弈的解solution可行支付向量⏹:⏹全体可行支付向量的集合记为E,但其中哪些是对博弈可能的结果的合理预测呢?合作博弈的一个解是的一个子集,包括了所⏹合作博弈的个解是E的个子集,包括了所有“合理的”支付向量23时可以较方便的用图像来描述合⏹当n = 2, 3时,可以较方便的用图像来描述合作博弈的解核core核是合作博弈的最重要的解之一⏹核是合作博弈的最重要的解之⏹给定,如果存在联盟S,,我们称可以被联盟S所阻止(block)(bl k)⏹核是所有不能被任何联盟所阻止的可行支付向量的集合❑一旦按照核中的某个支付向量进行分配,没有任何联盟能够一致同意改变这个结果❑核包含了在彻底自由的竞争下所有稳定的结果核:一些讨论核讨论核是合作博弈中最直观最常用的个解概念⏹核是合作博弈中最直观最常用的一个解概念⏹但核也有一些缺点:有可能是空集❑❑经常不唯一❑即使存在唯一的核,有时也可能非常不合理⏹幸运的是,当我们使用合作博弈来考察一般均衡时,核没有上述缺点例:三人多数博弈例人多数博弈⏹设,且等式组有解⏹这个博弈的核非空等价于下面(不)等式组有解:即(图像如何表示?)例手套博弈例:手套博弈有个人每人拥有一个右手手套,+1⏹n个人每人拥有个右手手套,n+1 人每人拥有一个左手手套。






第五讲、效用最大化UMP主要内容:(pp1-32) 1、 Introduction:()max .xn u x s tx B X +∈⊆⊆consumption set, feasible set, preference and utility, and behavioral assumption2、 contents:消费者的偏好与预算集,消费者均衡的特征,由效用函数推导需求函数,间接效用函数及其性质。
第一节、budget constraint and feasible set一、定义definitions 1、 商品 goods ,economic goods 和free goods度量:离散还是连续,infinitely divisible, i x +∈ 同质还是差异产品,different goods, 2、商品空间goods spaceconsumption bundle or plan ()12,,...nn x x x +=∈x nonnegative orthant3、消费集consumption set or choice setset of all alternative consumption plans which is conceivable and feasible given the technological and institutional situation.(without consideration of economic realities)消费集内的元素是alternatives 技术和制度上的可能性 assumptions:X ≠∅,使问题有意义出于分析上的方便和需要:X is closed, X is convexpay more attention to feasible set 4、竞争性预算集预算约束刻画消费者所处的经济环境:稀缺性和可替代性 竞争性预算集(1)假设:市场完备性和竞争性(2){},ny +B =∈≤x x px(3)预算约束线1122p x p x y += (4)预算约束线的斜率及其经济学含义11220p dx p dx +=,trade-off2112dx pdx p =-:斜率取决于商品的相对价格 12p p 的含义是增加一个单位的第一种商品必须放弃掉12pp 个单位的第二种商品,也往往被称为机会成本。
微观经济学需求的概念嘿,朋友!咱今天来聊聊微观经济学里那个神秘又有趣的“需求”概念。
你想啊,咱们日常生活中,是不是经常会有各种各样想要的东西?比如,你馋那美味的冰淇淋,渴望新出的酷炫手机,或者心心念念一款时尚的包包。
这其实就是需求的一种表现。
那到底啥是微观经济学里说的需求呢?简单来说,需求就是在一定的时期内,在各种可能的价格水平下,消费者愿意并且能够购买的商品或服务的数量。
咱举个例子,就说水果吧。
夏天来了,西瓜大受欢迎。
假如西瓜一斤两块钱的时候,你可能会买一个;可要是一斤涨到十块钱,你可能就只买半个,甚至不买了。
这价格的变化,就影响了你的购买意愿和购买能力,也就影响了对西瓜的需求。
需求这东西可不是一成不变的哟!它就像个调皮的孩子,会随着好多因素到处跑。
比如说你的收入,你工资涨了,是不是就更舍得去买那些以前觉得贵的东西啦?这需求不就增加了嘛。
再比如你的喜好,突然迷上了健身,那对健身器材的需求可不就蹭蹭往上涨。
还有啊,替代品和互补品也会对需求产生影响。
就像咖啡和茶,要是咖啡价格飙升,很多人可能就转去喝茶了,茶的需求不就增加了嘛。
而汽车和汽油就是互补品,汽车买得多,汽油的需求自然也跟着多。
那需求和欲望又有啥不一样呢?欲望可以无边无际,比如你想要天上的星星,可这能实现吗?不能啊!但需求是你不仅想要,还得有能力买得到。
需求的变化还能影响市场呢。
如果大家对某种商品的需求突然大增,商家肯定乐开了花,赶紧加大生产,价格说不定也跟着涨。
反过来,需求大幅减少,商家就得发愁啦,可能得降价促销。
所以说,弄明白需求这个概念,对咱们理解市场的变化,做出明智的消费决策,那可是相当重要啊!你想想,要是不了解需求,盲目消费,钱袋子可就守不住啦!总之,微观经济学中的需求概念,就像我们生活中的指南针,能帮助我们在消费的海洋里不迷路,做出更聪明的选择,让我们的生活更加精彩!。
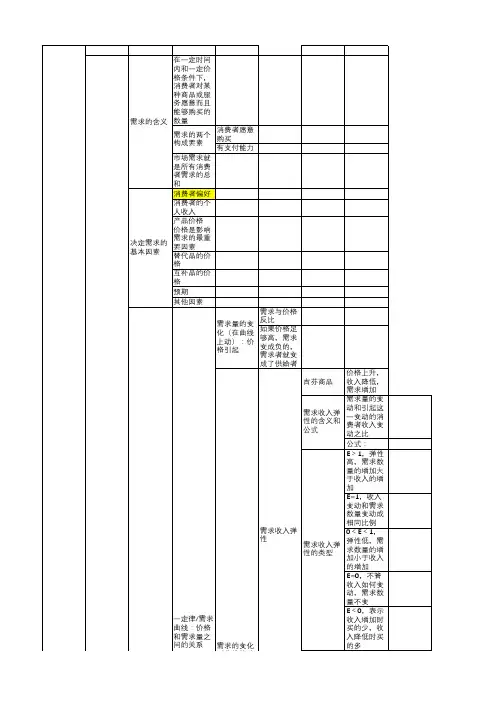
需求1.需求的概念2.需求的影响因素3.需求函数4.需求表5.需求曲线6.需求法则•一种商品的需求是指消费者在一定时期内在各种可能的价格水平愿意而且能够购买的该商品的数量。
•分析:根据定义,需求是指既有购买欲望又有购买能力的有效需求。
缺少这两个条件中任何一个都不能算作需求,而只是潜在需求。
2.•商品的自身价格(P)一般说来,一种商品的价格越高,该商品的需求量就会越小。
相反,价格越低,需求量就会越大。
•消费者的收入(I)对于多数正常物品来说,当消费者的收入水平提高时,就会增加对商品的需求。
相反,当消费者的收入水平下降时,就会减少对商品的需求。
•相关商品的价格(互补品价格Px,替代品价格Py)互补品,是指互相补充共同满足同一欲望或需要的两种商品。
当一种商品的价格提高,其互补品的需求就会减少。
相反,价格降低,其互补品的需求就会增加。
替代品,是指可以互相代替来共同满足同一欲望或需要的两种商品。
当一种商品的价格提高,其替代品的需求就会增加。
相反,价格降低,其替代品的需求就会减少。
2.•消费者的偏好(F)当消费者对某种商品的偏好程度增强时,该商品的需求就会增加。
相反,偏好程度减弱,需求就会减少。
•消费者对商品的价格预期(Pe)当消费者预期某种商品的价格在下一期会上升时,就会增加对该商品的现期需求。
当消费者预期某商品的价格在下一期会下降时,就会减少对该商品的现期需求。
f P ()Q d (,,,,,f P I P P F P x y e Q d •需求函数是表示一种商品的需求量和影响该商品需求数量的各种因素之间的相互关系。
•为简化分析,假定其他条件保持不变,把一种商品的需求量仅看成是该商品的价格的函数。
即:•表示一种商品的需求量和该商品价格之间存在着一一对应关系。
……)==4.•商品的需求量和商品价格之间的函数关系可以分别用商品的需求表和需求曲线来表示。
•商品的需求表是表示某种商品的各种价格和与各种价格相对应的该商品的需求量之间关系的数字序列表。