最新人教版高中数学必修4第一章《任意角的三角函数》课后训练

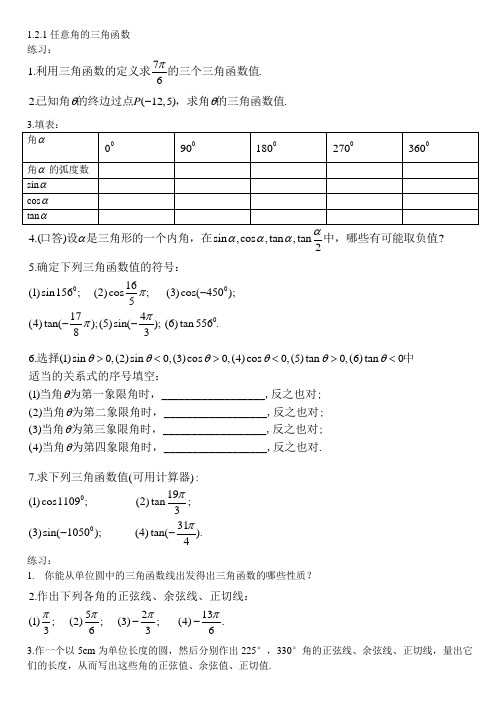
1.2.1任意角的三角函数 练习：71..6π利用三角函数的定义求的三个三角函数值 2.(12,5).P θθ-已知角的终边过点，求角的三角函数值4.()sin ,cos ,tan ,tan?2αααα口答设是三角形的一个内角，在中，哪些有可能取负值0005.16(1)sin156;(2)cos;(3)cos(450);5174(4)tan();(5)sin();(6)tan 556.83πππ---确定下列三角函数值的符号：6.(1)sin 0,(2)sin 0,(3)cos 0,(4)cos 0,(5)tan 0,(6)tan 0(1)(2)(3)(4)θθθθθθθθθθ><><><选择中适当的关系式的序号填空：当角为第一象限角时，__________________,反之也对;当角为第二象限角时，__________________,反之也对;当角为第三象限角时，__________________,反之也对;当角为第四象限角时，__________________,反之也对.007.():19(1)cos1109;(2)tan;331(3)sin(1050);(4)tan().4ππ--求下列三角函数值可用计算器 练习：1. 你能从单位圆中的三角函数线出发得出三角函数的哪些性质？2.5213(1);(2);(3);(4).3636ππππ--作出下列各角的正弦线、余弦线、正切线：3.作一个以5cm 为单位长度的圆，然后分别作出225°，330°角的正弦线、余弦线、正切线，量出它们的长度，从而写出这些角的正弦值、余弦值、正切值.4.你认为三角函数线对认识三角函数概念有哪些作用? 1.2.2同角三角函数的基本关系 练习：41.cos ,sin ,tan .5αααα=-已知且为第三象限角，求的值2.tan sin ,cos .ϕϕϕ=已知求的值3.sin =0.35cos ,tan (.θθθ已知，求的值计算结果保留两个有效数字） 224.2cos 1(1)cos tan ;(2).12sin αθθα--化简： 442242225.:(1)sin cos sin cos ;(2)sin sin cos cos 1.αααααααα-=-++=求证 1.3三角函数的诱导公式 练习：01.13(1)cos________;(2)sin(1)___________;9(3)sin()_______;(4)cos(706')_________.5πππ=+=-=-=将下列三角函数转化为锐角三角函数，并填在题中横线上：002.7(1)cos(420);(2)sin();679(3)sin(1300);(4)cos().6ππ----利用公式求下列三角函数值：0033.(1)sin(180)cos()sin(180);(2)sin ()cos(2)tan().ααααπααπ+----+--化简：005.:3(1)tan ________;(2)tan10021'____________;531(3)tan ________;(4)tan 32432'____________.36ππ====将下列三角函数转化为锐角三角函数，并填在题中的横线上0006.:6531(1)cos;(2)sin();(3)cos(118213');6426(4)sin(67039');(5)tan();(6)tan 58021'.3πππ---用诱导公式求下列三角函数值（可用计算器） 027.cos()2(1)sin(2)cos(2);5sin()2tan(360)(2)cos ().sin()πααππαπαααα---++---化简：1.4三角函数的图像与性质1.4.1正弦函数、余弦函数的图像 练习：1.sin ,[0,2],3cos ,[,]22..y x x y x x πππ=∈=∈-用多种方法在同一直角坐标系中，画出函数的图像通过观察两条曲线，说出它们的异同32.sin()cos 2y x y x π=-=想一想函数和的图像，并在同一直角坐标系中，画出它们的草图. 1.4.2正弦函数、余弦函数的性质 练习：00001.sin(30120)sin30sin ,y x x R +==∈等式是否成立？如果这个等式成立，能否说120是正弦函数的一个周期？为什么？2.:3(1)sin ,;4(2)cos 4,;1(3)cos ,;21(4)sin(),.34y x x R y x x R y x x R y x x R π=∈=∈=∈=+∈求下列函数的周期2. 你认为我们应当如何利用函数的周期性来认识周期函数的其他性质？练习:1.(1)sin 0;(2)sin 0;(3)cos 0;(4)cos 0.x x x x ><><观察正弦曲线和余弦曲线，写出满足下列条件的区间：22.12cos 3;(2)sin 0.5.x x ==下列各等式能否成立？为什么？（）3..(1)2sin ,;(2)2cos ,.3xy x x R y x R =∈=-∈求使下列函数取得最大值、最小值的自变量的集合，并写出最大值、最小值各是多少 4.4sin ,[,]22220,02222y x x ππππππππππππππππππ=∈--选择题：下列关于函数的单调性的叙述，正确的是().(A)在[-,0]上是增函数，在[0,]上是减函数(B)在[-,]上是增函数，在[-,-]及[,]上是减函数(C)在[,]上是增函数，在[]上是减函数(D)在[,]及[-,-]上是增函数，在[-,]上是减函数。

暑假数学课外辅导(必修4)第一章 三角函数一、基本内容串讲本章主干知识：三角函数的定义、图象、性质及应用，函数()ϕω+=x A y sin 的图象，三角函数模型在解决具有周期变化规律问题中的应用。

1．任意角和弧度制从运动的角度，在旋转方向及旋转圈数上引进负角及大于3600的角。

在直角坐标系中，当角的终边确定时，其大小不一定（通常使角的顶点与原点重合，角的始边与x 轴非负半轴重合）。

为了把握这些角之间的联系，引进终边相同的角的概念，凡是与终边α相同的角，都可以表示成α+k ·3600 （k ∈Z ）的形式，特例，终边在x 轴上的角的集合为{α|α=k ·1800，k ∈Z}，终边在y 轴上的角的集合为{α|α=900+k ·18000，k ∈Z}，终边在坐标轴上的角的集合为{α|α=k ·900，k ∈Z}。

另外，角的终边落在第几象限，就说这个角是第几象限的角。

弧度制是角的度量的重要表示法，能正确地进行弧度与角度的换算，熟记特殊角的弧度制。

在弧度制下，扇形弧长公式=|α|R ，扇形面积公式||R 21R 21S 2α== ，其中α为弧所对圆心角的弧度数。

2．任意角的三角函数利用直角坐标系，可以把直角三角形中的三角函数推广到任意角的三角函数。

设P(x ，y)是角α终边上任一点（与原点不重合），记22y x |OP |r +==，则r y s i n =α，r x cos =α，xy tan =α。

3．同角三角函数的基本关系式（1）平方关系：22sincos 1αα+= （2）商数关系：sin tan cos ααα= 4．三角函数的诱导公式利用三角函数定义，可以得到诱导公式：即πα2k+与α之间函数值的关系（k ∈Z ），其规律是“奇变偶不变，符号看象限”。

5．三角函数的图象与性质6．函数()ϕω+=x A y sin 的图象作函数y A x =+sin()ωϕ的图象主要有以下两种方法： （1）用“五点法”作图用“五点法”作y A x =+sin()ωϕ的简图，主要是通过变量代换，设ϕω+=x z ，由z 取0，2π，π，23π，2π来求出相应的x ，通过列表，计算得出五点坐标，描点后得出图象。

§1.2.1.任意角的三角函数班级 姓名 学号 得分一.选择题1.函数y =|sin |sin x x +cos |cos |x x +|tan |tan x x的值域是 ( ) (A){-1，1} (B){-1，1，3} (C) {-1，3} (D){1，3}2.已知角θ的终边上有一点P （-4a ,3a )（a ≠0）,则2sin θ+cos θ的值是 ( ) (A) 25 (B) -25 (C) 25或 -25 (D) 不确定3.设A 是第三象限角，且|sin2A |= -sin 2A ,则2A 是 ( ) (A) 第一象限角 (B) 第二象限角 (C) 第三象限角 (D) 第四象限角4. sin2cos3tan4的值 ( )(A)大于0 (B)小于0 (C)等于0 (D)不确定5.在△ABC 中,若cos A cos B cos C <0，则△ABC 是 ( )(A)锐角三角形 (B)直角三角形 (C)钝角三角形 (D)锐角或钝角三角形 *6.已知|cos θ|=cos θ, |tan θ|= -tan θ,则2的终边在 ( ) (A)第二、四象限 (B)第一、三象限(C)第一、三象限或x 轴上 (D)第二、四象限或x 轴上二.填空题7.若sin θ·cos θ＞0, 则θ是第 象限的角;8.求值：sin(-236π)+cos 137π·tan4π -cos 133π= ; 9.角θ(0<θ<2π)的正弦线与余弦线的长度相等且符号相同，则θ的值为 ;*10.设M =sin θ+cos θ, -1<M <1,则角θ是第 象限角.三.解答题11.求函数y =lg(2cos x12.求：13sin 330tan()319cos()cos6906ππ︒⋅--⋅︒的值.13.已知：P (-2，y )是角θ终边上一点，且sin θ= -55,求cos θ的值.*14.如果角α∈(0,2π),利用三角函数线,求证:sin α<α<tan α.参考答案§1.2.1 任意角的三角函数一、CCDBCD二、7.一、三； 8. 0 ； 9.4π或54π； 10.二、四 三、11.[2kπ, 2kπ,+2)3π( k ∈Z)12.13.∵sin θ= -55，∴角θ终边与单位圆的交点（cos θ，sin θ）=（,-55） 又∵P (-2, y )是角θ终边上一点, ∴cos θ<0,∴cos θ= -525. 14.略.。

第一章三角函数1.1 任意角和弧度制1.1.1 任意角课后篇巩固探究1.200°角是( )A.第一象限角B.第二象限角C.第三象限角D.第四象限角180°<200°<270°,第三象限角α的取值范围为k·360°+180°<α<k·360°+270°,k∈Z,所以200°角是第三象限角.2.在-360°≤α<0°范围内与60°角终边相同的角为( )A.-300°B.-300°,60°C.60°D.420°60°角终边相同的角α可表示为α=60°+k·360°,当k=-1时,α=-300°,故在-360°≤α<0°范围内与60°角终边相同的角为-300°.3.若角θ是第四象限角,则90°+θ是( )A.第一象限角B.第二象限角C.第三象限角D.第四象限角,将θ的终边按逆时针方向旋转90°得90°+θ的终边,则90°+θ是第一象限角.4.角α=45°+k×180°(k∈Z)的终边落在( )A.第一或第三象限B.第一或第二象限C.第二或第四象限D.第三或第四象限k是偶数时,角α是第一象限角,当k是奇数时,角α是第三象限角.5.如图,终边在阴影部分(含边界)的角的集合是( )A.{α|-45°≤α≤120°}B.{α|120°≤α≤315°}C.{α|-45°+k·360°≤α≤120°+k·360°,k∈Z}D.{α|120°+k·360°≤α≤315°+k·360°,k∈Z},终边落在阴影部分(含边界)的角的集合是{α|-45°+k·360°≤α≤120°+k·360°,k∈Z}.故选C.±45°,k∈Z},P=,P之间的关系为( ) 6.已知集合M={x|x=k·180°2A.M=PB.M⊆PC.M⊇PD.M∩P=⌀±45°=k·90°±45°=(2k±1)·45°,k∈Z, M,x=k·180°2对于集合P,x=k·180°±90°=k·45°±90°=(k±2)·45°,k∈Z.∴4M⊆P.7.已知角α,β的终边关于直线x+y=0对称,且α=-60°,则β=.-90°到0°的范围内,-60°角的终边关于直线y=-x对称的射线的对应角为-45°+15°=-30°,所以β=-30°+k·360°,k∈Z.30°+k·360°,k∈Z8.若角α与角288°终边相同,则在0°~360°内终边与角α4终边相同的角是.,得α=288°+k·360°(k∈Z),α4=72°+k·90°(k∈Z).又α4在0°~360°内,所以k=0,1,2,3,相应地有α4=72°,162°,252°,342°.9.终边落在图中阴影部分所示的区域内(包括边界)的角的集合为.由图易知在0°~360°范围内,终边落在阴影区域内(包括边界)的角为45°≤α≤90°与225°≤α≤270°,故终边落在阴影部分所示的区域内(包括边界)的角的集合为{α|k·360°+45°≤α≤k·360°+90°,k ∈Z}∪{α|k·360°+225°≤α≤k·360°+270°,k∈Z}={α|k·180°+45°≤α≤k·180°+90°,k∈Z}.Z}10.已知α=-1 910°.(1)把α写成β+k·360°(k∈Z,0°≤β<360°)的形式,并指出它是第几象限角;(2)求θ,使θ与α的终边相同,且-720°≤θ<0°.设α=β+k·360°(k∈Z),则β=-1910°-k·360°(k∈Z).令-1910°-k·360°≥0,解得k≤-1910360=-51136.k的最大整数解为k=-6,求出相应的β=250°,于是α=250°-6×360°,它是第三象限角.(2)令θ=250°+n·360°(n∈Z),取n=-1,-2就得到符合-720°≤θ<0°的角. 250°-360°=-110°,250°-720°=-470°.故θ=-110°或θ=-470°.11.已知角α的终边在图中阴影部分所表示的范围内(不包括边界),写出角α的集合.0°~360°范围内,终边落在阴影部分内的角为30°<α<150°与210°<α<330°,故所有满足题意的角α的集合为{α|k·360°+30°<α<k·360°+150°,k∈Z}∪{α|k·360°+210°<α<k·360°+330°,k∈Z}={α|n·180°+30°<α<n·180°+150°,n∈Z}.12.已知α,β都是锐角,且α+β的终边与-280°角的终边相同,α-β的终边与670°角的终边相同,求角α,β的大小.-280°+k·360°,k∈Z.∵α,β都是锐角,∴0°<α+β<180°.取k=1,得α+β=80°.①α-β=670°+k·360°,k∈Z.∵α,β都是锐角,∴-90°<α-β<90°.取k=-2,得α-β=-50°.②由①②,得α=15°,β=65°.。

第一章 三角函数1.2 任意角的三角函数1.2.1 任意角的三角函数A 级 基础巩固一、选择题1．已知角α终边经过P ⎝ ⎛⎭⎪⎫32，12，则cos α等于( )A.12B.32C.33 D ．±122．如果MP 和OM 分别是角α＝7π8的正弦线和余弦线，那么下列结论正确的是( )A ．MP ＜OM ＜0B ．OM ＞0＞MPC ．OM ＜MP ＜0D ．MP ＞0＞OM3．若α＝2π3，则α的终边与单位圆的交点P 的坐标是( )A.⎝ ⎛⎭⎪⎫12，32B.⎝ ⎛⎭⎪⎫－12，32C.⎝⎛⎭⎪⎫－32，12D.⎝ ⎛⎭⎪⎫12，－324．若三角形的两内角α，β满足sin αcos β＜0，则此三角形必为( )A ．锐角三角形B ．钝角三角形C ．直角三角形D ．以上三种情况都可能5．函数y ＝11＋sin x的定义域为( )A.⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x ≠3π2＋2k π，k ∈ZB.⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x ≠π2＋2k π，k ∈ZC.{}x |x ≠2k π，k ∈ZD.⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x ≠－3π2＋2k π，k ∈Z二、填空题6．(2016·四川卷)sin 750°＝________． 7．sin 1 485°的值为________．8．已知θ∈⎝ ⎛⎭⎪⎫π3，π2，在单位圆中角θ的正弦线、余弦线、正切线分别是MP ，OM ，AT ，则它们从大到小的顺序为____________．三、解答题9．求下列各式的值：(1)sin(－1 320°)cos(1 110°)＋cos(－1 020°)sin 750°； (2)cos ⎝ ⎛⎭⎪⎫－233π＋tan 17π4.10．已知P (－2，y )是角α终边上一点，且sin α＝－55，求cosα与tan α的值．B 级 能力提升1．若α是第三象限角，则|sin α|sin α－cos α|cos α|＝( )A ．0B ．1C ．2D ．－22．已知角α的终边过点(－3cos θ，4cos θ)，其中θ∈⎝ ⎛⎭⎪⎫π2，π，则cos α＝________．3．利用三角函数线，写出满足|cos α|＞|sin α|的角α的集合．参考答案第一章 三角函数1.2 任意角的三角函数1.2.1 任意角的三角函数A 级 基础巩固一、选择题1．已知角α终边经过P ⎝ ⎛⎭⎪⎫32，12，则cos α等于( )A.12B.32C.33 D ．±12解析：由三角函数定义可知，角α的终边与单位圆交点的横坐标为角α的余弦值，故cos α＝32. 答案：B2．如果MP 和OM 分别是角α＝7π8的正弦线和余弦线，那么下列结论正确的是( )A ．MP ＜OM ＜0B ．OM ＞0＞MPC ．OM ＜MP ＜0D ．MP ＞0＞OM解析：因为78π是第二象限角，所以sin 78π＞0，cos 78π＜0，所以MP ＞0，OM ＜0， 所以MP ＞0＞OM . 答案：D3．若α＝2π3，则α的终边与单位圆的交点P 的坐标是( )A.⎝ ⎛⎭⎪⎫12，32B.⎝ ⎛⎭⎪⎫－12，32C.⎝⎛⎭⎪⎫－32，12D.⎝ ⎛⎭⎪⎫12，－32解析：设P (x ，y )，因为角α＝2π3在第二象限，所以x ＝－12，y ＝1－⎝ ⎛⎭⎪⎫－122＝32，所以P ⎝ ⎛⎭⎪⎫－12，32.答案：B4．若三角形的两内角α，β满足sin αcos β＜0，则此三角形必为( )A ．锐角三角形B ．钝角三角形C ．直角三角形D ．以上三种情况都可能解析：因为sin αcos β＜0，α，β∈(0，π)，所以sin α＞0，cos β＜0，所以β为钝角．答案：B 5．函数y ＝11＋sin x的定义域为( )A.⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x ≠3π2＋2k π，k ∈ZB.⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x ≠π2＋2k π，k ∈ZC.{}x |x ≠2k π，k ∈ZD.⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x ≠－3π2＋2k π，k ∈Z解析：因为1＋sin x ≠0，所以sin x ≠－1. 又sin 3π2＝－1，所以x ≠3π2＋2k π，k ∈Z. 答案：A 二、填空题6．(2016·四川卷)sin 750°＝________． 解析：sin 750°＝sin(30°＋2×360°)＝sin 30°＝12.答案：127．sin 1 485°的值为________．解析：sin 1 485°＝sin(4×360°＋45°)＝sin 45°＝22.答案：228．已知θ∈⎝ ⎛⎭⎪⎫π3，π2，在单位圆中角θ的正弦线、余弦线、正切线分别是MP ，OM ，AT ，则它们从大到小的顺序为____________．解析：作图如下，因为θ∈⎝ ⎛⎭⎪⎫π3，π2，所以θ >π4，根据三角函数线的定义可知AT >MP >OM .答案：AT >MP >OM 三、解答题9．求下列各式的值：(1)sin(－1 320°)cos(1 110°)＋cos(－1 020°)sin 750°； (2)cos ⎝ ⎛⎭⎪⎫－233π＋tan 17π4.解：(1)原式＝sin(－4×360°＋120°)cos(3×360°＋30°)＋cos(－3×360°＋60°)sin(2×360°＋30°)＝sin 120°cos 30°＋cos 60°sin 30°＝32×32＋12×12＝1. (2)原式＝cos ⎣⎢⎡⎦⎥⎤π3＋（－4）×2π＋tan ⎝ ⎛⎭⎪⎫π4＋2×2π＝cosπ3＋tan π4＝12＋1＝32. 10．已知P (－2，y )是角α终边上一点，且sin α＝－55，求cos α与tan α的值．解：因为点P 到原点的距离为r ＝4＋y 2，所以sin α＝y4＋y 2＝－55，所以y 2＋4＝5y 2，所以y 2＝1.又易知y <0，所以y ＝－1，所以r ＝5，所以cos α＝－25＝－255，tan α＝－1－2＝12.B 级 能力提升1．若α是第三象限角，则|sin α|sin α－cos α|cos α|＝( )A ．0B ．1C ．2D ．－2解析：因为α是第三象限角，所以sin α<0，cos α<0， 所以|sin α|sin α－cos α|cos α|＝－1－(－1)＝0.答案：A2．已知角α的终边过点(－3cos θ，4cos θ)，其中θ∈⎝ ⎛⎭⎪⎫π2，π，则cos α＝________．解析：因为θ∈⎝ ⎛⎭⎪⎫π2，π，所以cos θ<0，所以点(－3cos θ，4cos θ)到原点的距离r ＝5|cos θ|＝－5cos θ， 所以cos α＝－3cos θ－5cos θ＝35.答案：353．利用三角函数线，写出满足|cos α|＞|sin α|的角α的集合． 解：如图，作出单位圆．所以角α满足的集合为⎩⎨⎧⎭⎬⎫a ⎪⎪⎪k π－π4＜α＜k π＋π4，k ∈Z .。

（数学4必修）第一章 三角函数（）一、选择题1． 设α角属于第二象限，且2cos 2cos αα-=，则2α角属于（ ） A ． 第一象限 B ． 第二象限 C ． 第三象限 D ． 第四象限2． 给出下列各函数值：①)1000sin(0-；②)2200cos(0-；③)10tan(-；④917tan cos 107sin πππ． 其中符号为负的有（ ） A ． ① B ． ② C ． ③ D ． ④3． 02120sin 等于（ ）A ． 23±B ． 23C ． 23-D ． 21 4． 已知4sin 5α=，并且α是第二象限的角，那么tan α的值等于（ ） A ． 43- B ． 34- C ． 43 D ． 34 5． 若α是第四象限的角，则πα-是（ ） A ． 第一象限的角 B ． 第二象限的角 C ． 第三象限的角 D ． 第四象限的角6． 4tan 3cos 2sin 的值（ ）A ． 小于0B ． 大于0C ． 等于0D ． 不存在二、填空题1． 设θ分别是第二、三、四象限角，则点)cos ,(sin θθP 分别在第___、___、___象限．2． 设MP 和OM 分别是角1817π的正弦线和余弦线，则给出的以下不等式： ①0<<OM MP ；②0OM MP <<； ③0<<MP OM ；④OM MP <<0， 其中正确的是_____________________________．3． 若角α与角β的终边关于y 轴对称，则α与β的关系是___________．4． 设扇形的周长为8cm ，面积为24cm ，则扇形的圆心角的弧度数是 ．5． 与02002-终边相同的最小正角是_______________． 三、解答题1． 已知1tan tan αα，是关于x 的方程2230x kx k -+-=的两个实根，且παπ273<<，求ααsin cos +的值．2． 已知2tan =x ，求xx x x sin cos sin cos -+的值．3． 化简：)sin()360cos()810tan()450tan(1)900tan()540sin(00000x x x x x x --⋅--⋅--4． 已知)1,2(,cos sin ≠≤=+m m m x x 且， 求（1）x x 33cos sin +；（2）x x 44cos sin +的值．数学4（必修）第一章 三角函数（上）参考答案一、选择题1． C 22,(),,(),2422k k k Z k k k Z ππαππαππππ+<<+∈+<<+∈当2,()k n n Z =∈时，2α在第一象限；当21,()k n n Z =+∈时，2α在第三象限； 而cos coscos 0222ααα=-⇒≤，2α∴在第三象限； 2． C 00sin(1000)sin 800-=>；000cos(2200)cos(40)cos 400-=-=>tan(10)tan(310)0π-=-<；77sincos sin 7171010,sin 0,tan 01717109tan tan 99πππππππ-=>< 3． B0sin1202== 4． A 43sin 4sin ,cos ,tan 55cos 3ααααα==-==- 5． Cπααπ-=-+，若α是第四象限的角，则α-是第一象限的角，再逆时针旋转0180 6．A 32,sin 20;3,cos30;4,tan 40;sin 2cos3tan 40222ππππππ<<><<<<<>< 二、填空题1． 四、三、二 当θ是第二象限角时，sin 0,cos 0θθ><；当θ是第三象限角时，sin 0,cos 0θθ<<；当θ是第四象限角时，sin 0,cos 0θθ<>；2． ② 1717sin 0,cos 01818MP OM ππ=>=< 3． 2k αβππ+=+ α与βπ+关于x 轴对称4． 2 21(82)4,440,2,4,22l S r r r r r l rα=-=-+===== 5． 0158 0000020022160158,(21603606)-=-+=⨯三、解答题1. 解：21tan 31,2tan k k αα⋅=-=∴=±，而παπ273<<，则1tan 2,tan k αα+==得tan 1α=，则sin cos 2αα==-，cos sin αα∴+= 2． 解：cos sin 1tan 123cos sin 1tan 12x x x x x x +++===---- 3． 解：原式=000sin(180)1cos tan()tan(90)tan(90)sin()x x x x x x -⋅⋅---- sin 1tan tan ()sin tan tan x x x x x x=⋅⋅-=- 4． 解：由sin cos ,x x m +=得212sin cos ,x x m +=即21sin cos ,2m x x -= （1）233313sin cos (sin cos )(1sin cos )(1)22m m m x x x x x x m --+=+-=-=（2）24244222121sin cos 12sin cos 12()22m m m x x x x --+++=-=-=。

课后集训基础达标1.已知下列三角函数，其中函数值为负的有（ ）①sin(-680°) ②cos(-730°) ③tan320° ④sin(-130°)·cos850°A.1个B.2个C.3个D.4个解析：由诱导公式转化到0°—360°之间，判断其所在象限，或者利用三角函数线求解. 答案：A2.角θ的终边有一点P （a,a ）(a≠0),则sinθ的值是（ ） A.22 B.-22 C.±22 D.1 答案：C3.函数y=x x cos sin -+的定义域是( )A.［kπ+2π,(2k+1)π］（k ∈Z ） B.［2kπ+2π,(2k+1)π］（k ∈Z ） C.［kπ+2π,(k+1)π］（k ∈Z ） D.［2kπ,(2k+1)π］（k ∈Z ） 解析：由题意可得⎩⎨⎧≤≥,0cos ,0sin x x 设角x 终边与单位圆交点为P （x,y ），则由三角函数定义⎩⎨⎧≤≥,0,0x y 从而选B.也可利用特值或三角函数线求解.答案：B4.已知α为第二象限角，其终边上一点为P （x,5）,且cosα=42x,则sinα的值为（ ） A.410 B.46 C.42 D.-410 解析：r=52+x .∵cosα=x 42, ∴,4252x x x=+ 解得：x=±3.∵α是第二象限角，∴x=-3.∴sinα=85=410.故选A.答案：A 5.y=xx x x x x tan |tan |cos |cos |sin |sin |++属于（ ） A.{1，-1} B.{-1，1，3} C.{-1，3} D.{1，3}解析：当x 是第一象限角，则y=1+1+1=3;当x 是第二象限角，则y=1-1-1=-1;当x 是第三象限角，则y=-1-1+1=-1;当x 是第四象限角，则y=-1+1-1=-1.∴y ∈{-1,3}.故选C.答案：C6.若-43π＜α＜-2π,从单位圆中的三角函数线观察sinα、cosα、tanα的大小是_____________. 解析：由三角函数线可得.答案：sinα＜cosα＜tanα综合运用7.已知θ为第三象限角，且|cos 2θ|=-cos 2θ,则角2θ属于（ ） A.第一象限 B.第二象限 C.第三象限 D.第四象限解析：∵θ 是第三象限角,∴2kπ+π＜θ＜2kπ+π23,k ∈Z ,则kπ+2π＜2θ＜kπ+π43,k ∈Z .当k 为偶数，2θ是第二象限角.当k 是奇数时，2θ是第四象限角. ∵|cos2θ|=-cos 2θ, ∴2θ一定是第二象限角.故选B. 答案：B8.若0＜α＜π,则10sin α、lgsinα、sin 10α三个数之间的大小关系是（ ）A.sin 10α＜10sin α＜lgsinαB.lgsinα＜sin 10α＜10sin αC.10sin α＜lgsinα＜sin 10αD.lgsinα＜10sin α＜sin 10α解析：∵0＜α＜π,∴0＜sinα≤1.∴lgsinα＜0,10sin α＞1,0＜sin 10α＜1.∴lgsinα＜sin 10α＜10sin α.故选B.答案：B9.已知点P （sinα-cosα,tanα）在第一象限，α在［0，2π］内，α的取值范围是______________. 解析：由题意得：⎩⎨⎧>>-,0tan ,0cos sin ααα即)2()1(.0tan ,cos sin ⎩⎨⎧>>ααα 由①得：4π＜α＜45π. 由②得0＜α＜2π或π＜α＜π23. ∴4π＜α＜2π或π＜α＜π45. 答案：4π＜α＜2π或π＜α＜π45 拓展探究10.（1）若α为锐角，证明：sinα+cosα＞1.证明：∵α为锐角,∴0＜sinα＜1,0＜cosα＜1.∵函数y=a x (0＜a ＜1)在R 上是减函数，∴sin 2α＜sinα,cos 2α＜cosα.∴sin 2α+cos 2α＜sinα+cosα,∴sinα+cosα＞1.(2)若α为锐角.求证：sin 3α+cos 3α＜1.证明：∵α是锐角，∴0＜sinα＜1,0＜cosα＜1.∵函数y=a x (0＜a ＜1)在R 上是减函数,∴sin 3α＜sin 2α,cos 3α＜cos 2α∴sin 3α+cos 3α＜sin 2α+cos 2α=1,∴sin 3α+cos 3α＜1.备选习题11.已知α的终边经过点（3a-9,a+2）,且cosα≤0,sinα＞0,则a 的取值范围是_____________. 解析：∵cosα≤0,sinα＞0,∴⎩⎨⎧>+≤-,02,093a a ∴-2＜a≤3.答案：-2＜a≤312.确定下列式子的符号. (1)8sin 5cos )3tan(-;(2)lg(cos6-sin6). 解：（1）∵-π＜-3＜-2π, ∴tan(-3)＞0. ∵23π＜5＜2π,∴cos5＞0. ∵π25＜8＜3π,∴sin8＞0.故8sin 5cos )3tan(-＞0. (2)∵23π＜6＜2π,∴cos6＞0,sin6＜0. ∴cos6-sin6＞0.由单位圆中的三角函数线可知，cos6-sin6＞1.∴lg(cos6-sin6)＞0.13.求值.sin(-1 740°)·cos1 470°+cos(-660°)sin750°+2sin 21 125°.解：sin(-1 740°)·cos1 470°+cos(-660°)sin750°+2sin 21 125°=sin(-5×360°+60°)·cos(4×360°+30°)+cos(-2×360°+60°)·sin(2×360°+30°)+2sin 2(3×360°+45°) =sin60°·cos30°+cos60°·sin30°+2sin 245° =2)22(221212323⨯+⨯+⨯=2. 14.求y=lgsin2x+29x -的定义域.解：由题意得⎩⎨⎧≥->.09,02sin 2x x 由sin2x ＞0,得2kπ＜2x ＜2kπ+π,(k ∈Z ),即kπ＜x ＜kπ+2π,(k ∈Z )① 由9-x 2≥0,得-3≤x≤3②由①②得-3≤x ＜-2π或0＜x ＜2π. 故函数的定义域为{x|-3≤x ＜-2π或0＜x ＜2π}. 15.设f(x)=⎪⎪⎩⎪⎪⎨⎧≥+-<).21(1)1(),21(sin x x f x x π 求f(41)+f(67)的值. 解析：∵41＜21,∴f(41)=sin 4π=22. 又67＞21, ∴f(67)=f(67-1)+1=f(61)+1.而61＜21,∴f(67)=f(61)+1 =sin 6π+1=23, 则f(41)+f(67) =22+22323+=. 答案：223+ 16.（经典回放）已知sinα＞sinβ,那么下列命题成立的是（ ）A.若α、β是第一象限角，则cosα＞cosβB.若α、β是第二象限角，则tanα＞tanβC.若α、β是第三象限角，则cosα＞cosβD.若α、β是第四象限角，则tanα＞tanβ 解析：运用单位圆中的三角函数线，采用排除法，容易判断.如下图.∴选D.答案：D。

高中数学学习材料金戈铁骑整理制作1.2.1 任意角的三角函数(一)班级:__________姓名:__________设计人:__________日期:__________课后练习基础过关1．角α的终边经过点(3m −9,m +2)，且cosα≤0,sinα>0，那么m 的取值范围为 A. (−2,3)B. [−2,3)C. (−2,3]D. [−2,3]2．已知角θ的终边过点P (−4k ，3k )(k ＜0)，则2sin θ+cos θ的值是 A. 25B. −25C. 25或−25D.随着k 的取值不同其值不同3．在△ABC 中,若sin A cos B tan C <0,则△ABC 是A.锐角三角形 B .直角三角形C .钝角三角形D .锐角三角形或钝角三角形4．已知角α的终边经过点P (3a -9，a +2)，且cos α≤0,sin α>0，则a 的取值范围是________. 5．设α是第二象限角，且|cos α2|=−cos α2，则角α2是第_______象限角.6．判断下列各式的符号. (1)sin3·cos4·tan5. (2)sin(cosθ)cos(sinθ)(θ为第二象限角)7．已知tan α,1tanα是关于x 的方程3x 2-3kx +3k 2-13=0的两实根，且3π<α<7π2，求cos(3π+α)+sin(π+α)的值.8．已知角α的终边上有一点P(−√3,m)，且sinα=√2m4，求cos α，tan α的值.能力提升1．化简：tanx+tanx⋅sinx tanx+sinx ⋅(1+cosx)sinx(1+sinx)cosx .2．求函数y=|cosx|cosx+tanx |tanx|的值域.1.2.1 任意角的三角函数(一)详细答案【基础过关】 1．C【解析】本题考查三角函数的定义.根据定义cosα=x r≤0,sinα=y r>0,于是可得{3m −9≤0m +2>0解得−2<m ≤3. 【备注】不要忽视cosα=0即α终边在x 轴上的情形.2．B【解析】∵角θ的终边过点P(−4k ，3k )(k ＜0)，∴r =√(−4k)2+(3k)2=5|k|=−5k ， ∴sinθ=3k−5k =−35，cosθ=−4k−5k =45， ∴2sinθ+cosθ=2×(−35)+45=−25.故选B.3．C【解析】因为三角形内角的取值范围为(0,π),故sin A>0,故由sin A cos B tan C <0可得cos B tan C <0,所以B ,C 中必有一个为钝角,即△ABC 为钝角三角形.【备注】该题易出现的问题是忽视三角形内角的取值范围,从而无法准确判断sin A 的符号,导致判断失误. 4．(2,3]- 5．三【解析】因为角α是第二象限角，所以22()2k k k Z ππαππ+<<+∈， 所以()422k k k Z παπππ+<<+∈，当k 为偶数时，2α是第一象限角；当k 为奇数时，2α是第三象限角，又因为coscos22αα=-，即cos02α<，所以2α是第三象限角. 6．（1）因为32ππ<<，342ππ<<，3522ππ<<，所以sin 30,cos 40,tan 50><<，所以sin 3cos 4tan 50⋅⋅>.（2）因为θ为第二象限角，所以0sin 12πθ<<<，1cos 02πθ-<-<<， 所以sin(cos )0θ<，cos(sin )0θ>，所以sin(cos )0cos(sin )θθ<. 7．312+ 8．由题意知x =−√3，y ＝m ，所以r 2=(−√3)2+m 2，所以r =√3+m 2，从而sinα=√2m 4=m r=m √3+m2，解得m ＝0或sinα=√2m 4=m r=m √3+m 2.当m ＝0时，r =√3，r =√3，cosα=x r=−1，tanα=yx =0；当m =√5时，r =2√2，x =−√3，cosα=x r=−√64，tanα=yx =−√153； 当m =−√5时，r =2√2，x =−√3，cosα=x r=−√64，tanα=yx =√153. 【能力提升】 1．原式=sinx+sin 2xsinx+sinxcosx ·(1+cosx)sinx(1+sinx)cosx=sinx(1+sinx)sinx(1+cosx)⋅sinx(1+cosx)cosx(1+sinx)=sinx cosx=tanx.【解析】本题考查三角函数式的化简.化简三角函数式时,要灵活运用同角三角函数基本关系式,即正用,逆用和变形应用等技巧,注意常数1的变形.2．由题意得cos x≠0,且tan x≠0,∴角x 的终边不在x 轴上,也不在y 轴上. 当x 是第一象限角时,|cos x|=cos x,|tan x|=tan x,∴y=|cosx|cosx+tanx |tanx|=2; 当x 是第二象限角时,|cos x|=-cos x ,|tan x|=-tan x,∴y=|cosx|cosx +tanx |tanx|=-2;当x 是第三象限角时,|cos x|=-cos x ,|tan x|=tan x, ∴y=|cosx|cosx +tanx |tanx|=0;当x 是第四象限角时,|cos x|=cos x ,|tan x|=-tan x,∴y=|cosx|cosx+tanx|tanx|=0.故函数y 的值域为{-2,0,2}.。

第1课时 三角函数的定义练习1．cos 1110°的值为( )A ．12B C ．12- D ．2．已知P (2，－3)是角θ终边上一点，则tan(2π＋θ)等于( ) A ．32 B ．23 C ．32- D ．23-( )A ．cos 201.2°B ．－cos 201.2°C ．sin 201.2°D ．tan 201.2°4．已知角α的终边经过点P (m ，－3)，且cos α＝45-，则m 等于( ) A ．114- B ．114 C ．－4D ．4 5．如果点P (sin θ＋cos θ，sin θcos θ)位于第二象限，那么角θ所在的象限是( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限6．已知角θ的终边经过点122⎛⎫- ⎪ ⎪⎝⎭，那么tan θ的值是__________． 7．已知角α的终边经过点P (x ，－6)，且tan α＝35-，则x 的值为__________． 8．已知α的终边经过点(3a －9，a ＋2)，且sin α＞0，cos α＜0，则a 的取值范围是__________．9．利用定义求7sin 3π，7cos 3π，7tan 3π. 10．已知角α的终边经过点P (－3cos θ，4cos θ)，其中θ∈2,22k k ππππ⎛⎫++ ⎪⎝⎭(k ∈Z )，求角α的各个三角函数值．参考答案1. 答案：B2. 答案：C3．答案：B4. 答案：C5. 答案：C6. 答案：3-7. 答案：108. 答案：(－2,3)9. 分析：根据三角函数的定义，作出角7π3的终边与单位圆的交点，并求出交点坐标，再求解．解：在直角坐标系中，作出角73π，如图所示，易知角73π的终边与单位圆的交点坐标为1,22P ⎛ ⎝⎭，所以7sin 32π=71cos 32π=，7tan 3π=10分析：本题中的点P 的坐标是用θ的三角函数表示的，在求点P 到原点的距离时，应特别注意角θ的范围对r 值的影响．解：∵θ∈2,22k k ππππ⎛⎫++ ⎪⎝⎭(k ∈Z )， ∴cos θ＜0.∴点P 在第四象限．∵x ＝－3cos θ，y ＝4cos θ，∴r =＝|5cos θ|＝－5cos θ.∴sin α＝45-，cos α＝35，tan α＝43-.。

高中数学第1章三角函数1.1.1任意角课后课时精练新人教A 版必修4A 级：基础巩固练一、选择题1．下列说法正确的个数是( )①终边在x 轴非负半轴上的角是零角；②钝角一定大于第一象限的角；③第二象限的角一定大于第一象限的角；④第四象限角一定是负角．A ．0B ．1C ．2D ．3答案 A解析 ①错，终边在x 轴非负半轴上的角为k ·360°，k ∈Z ，显然不只是零角；②错，390°是第一象限的角，大于任一钝角α(90°<α<180°)；③错，第二象限角中的－210°小于第一象限角中的30°；④错，285°角为第四象限角，但不是负角．故选A.2．已知角α，β的终边相同，则角(α－β)的终边在( )A ．x 轴的非负半轴上B ．y 轴的非负半轴上C ．x 轴的非正半轴上D ．y 轴的非正半轴上答案 A解析 ∵角α，β的终边相同，∴α＝k ·360°＋β，k ∈Z .∴α－β＝k ·360°，k ∈Z ，∴α－β的终边在x 轴的非负半轴上，故选A.3．射线OA 绕端点O 逆时针旋转120°到达OB 位置，由OB 位置顺时针旋转270°到达OC 位置，则∠AOC ＝( )A ．150° B．－150° C．390° D．－390°答案 B解析 各角和的旋转量等于各角旋转量的和．∴120°＋(－270°)＝－150°.故选B.4．若角α和角β的终边关于x 轴对称，则角α可以用角β表示为( )A ．k ·360°＋β(k ∈Z )B ．k ·360°－β(k ∈Z )C ．k ·180°＋β(k ∈Z )D ．k ·180°－β(k ∈Z )答案 B解析 因为角α和角β的终边关于x 轴对称，所以α＋β＝k ·360°(k ∈Z )，所以α＝k ·360°－β(k ∈Z )．故选B.5．若角α为第二象限角，则α3的终边一定不在( ) A ．第一象限 B ．第二象限C ．第三象限D ．第四象限答案 C解析 因为角α为第二象限角，所以k ·360°＋90°<α<k ·360°＋180°，k ∈Z ，所以k ·120°＋30°<α3<k ·120°＋60°，k ∈Z .对k 进行讨论，当k ＝3n ，k ＝3n ＋1，k ＝3n ＋2(n ∈Z )时，α3的取值范围分别为(n ·360°＋30°，n ·360°＋60°)，(n ·360°＋150°，n ·360°＋180°)，(n ·360°＋270°，n ·360°＋300°)，n ∈Z ，所以α3的终边落在第一或二或四象限，故选C.二、填空题6．从13：00到14：00，时针转过的角为________，分针转过的角为________．答案 －30° －360°解析 经过一小时，时针顺时针旋转30°，分针顺时针旋转360°，结合负角的定义可知时针转过的角为－30°，分针转过的角为－360°.7．若α，β两角的终边互为反向延长线，且α＝－120°，则β＝________.答案 k ·360°＋60°，k ∈Z解析 先求出β的一个角，β＝α＋180°＝60°.再由终边相同角的概念知：β＝k ·360°＋60°，k ∈Z .8．若集合M ＝{x |x ＝k ·90°＋45°，k ∈Z }，N ＝{x |x ＝k ·45°＋90°，k ∈Z }，则M ________N ．(填“”“”)答案解析 M ＝{x |x ＝k ·90°＋45°，k ∈Z }＝{x |x ＝45°·(2k ＋1)，k ∈Z }，N ＝{x |x ＝k ·45°＋90°，k ∈Z }＝{x |x ＝45°·(k ＋2)，k ∈Z }，∵k ∈Z ，∴k ＋2∈Z ，且2k ＋1为奇数，∴M N .三、解答题9．已知角x 的终边落在图示阴影部分区域，写出角x 组成的集合．解 (1){x |k ·360°－135°≤x ≤k ·360°＋135°，k ∈Z }．(2){x |k ·360°＋30°≤x ≤k ·360°＋60°，k ∈Z }∪{x |k ·360°＋210°≤x ≤k ·360°＋240°，k ∈Z }＝{x |2k ·180°＋30°≤x ≤2k ·180°＋60°或(2k ＋1)·180°＋30°≤x ≤(2k ＋1)·180°＋60°，k ∈Z }＝{x |n ·180°＋30°≤x ≤n ·180°＋60°，n ∈Z }．10．已知α，β都是锐角，且α＋β的终边与－280°角的终边相同，α－β的终边与670°角的终边相同，求角α，β的大小．解 由题意可知，α＋β＝－280°＋k ·360°，k ∈Z .∵α，β都是锐角，∴0°<α＋β<180°.取k ＝1，得α＋β＝80°.①∵α－β＝670°＋k ·360°，k ∈Z ，α，β都是锐角，∴－90°<α－β<90°.取k ＝－2，得α－β＝－50°.②由①②，得α＝15°，β＝65°.B 级：能力提升练1．在角的集合{α|α＝k ·90°＋45°，k ∈Z }中，(1)有几种终边不同的角？(2)写出区间(－180°，180°)内的角；(3)写出第二象限的角的一般表示法．解 (1)在α＝k ·90°＋45°中，令k ＝0,1,2,3知，α＝45°，135°，225°，315°.∴在给定的角的集合中，终边不同的角共有4种．(2)由－180°<k ·90°＋45°<180°，得－52<k <32. 又k ∈Z ，故k ＝－2，－1,0,1.∴在区间(－180°，180°)内的角有－135°，－45°，45°，135°.(3)其中第二象限的角可表示为k ·360°＋135°，k ∈Z .2．已知角β的终边在直线3x －y ＝0上．(1)写出角β的集合S ；(2)写出S 中适合不等式－360°<β<720°的元素．解 (1)如图，直线3x －y ＝0过原点，倾斜角为60°，在0°～360°范围内，终边落在射线OA 上的角是60°，终边落在射线OB 上的角是240°，所以以射线OA ，OB 为终边的角的集合为：S 1＝{β|β＝60°＋k ·360°，k ∈Z }，S 2＝{β|β＝240°＋k ·360°，k ∈Z }，所以，角β的集合S ＝S 1∪S 2＝{β|β＝60°＋k ·360°，k ∈Z }∪{β|β＝60°＋180°＋k ·360°，k ∈Z }＝{β|β＝60°＋2k ·180°，k ∈Z }∪{β|β＝60°＋(2k ＋1)·180°，k ∈Z }＝{β|β＝60°＋n ·180°，n ∈Z }．(2)由于－360°<β<720°，即－360°<60°＋n ·180°<720°，n ∈Z .解得－73<n <113，n ∈Z ，所以n ＝－2，－1，0,1,2,3.所以S 中适合不等式－360°<β<720°的元素为：60°－2×180°＝－300°；60°－1×180°＝－120°；60°＋0×180°＝60°；60°＋1×180°＝240°；60°＋2×180°＝420°；60°＋3×180°＝600°.。