2013中考数学压轴题

2013年中考数学冲刺必备压轴题汇编安徽10.在一张直角三角形纸片的两直角边上各取一点，分别沿斜边中点与这两点的连线剪去两个三角形，剩下的部分是如图所示的直角梯形，其中三边长分别为2、4、3，则原直角三角形纸片的斜边长是（ ）A .10B .54C . 10或54D .10或172解析：考虑两种情况．要分清从斜边中点向哪个边沿着垂线段过去裁剪的.解答：解：如下图，54)44()22(22=++⨯，1054)44()32(22=++⨯14.如图，P 是矩形ABCD 内的任意一点，连接PA 、PB 、PC 、PD ，得到△PAB 、△PBC 、△PCD 、△PDA ，设它们的面积分别是S 1、S 2、S 3、S 4，给出如下结论： ①S 1+S 2=S 3+S 4 ② S 2+S 4= S 1+ S 3 ③若S 3=2 S 1，则S 4=2 S 2 ④若S 1= S 2，则P 点在矩形的对角线上其中正确的结论的序号是_____________解析：过点P 分别向AD 、BC 作垂线段，两个三角形的面积之和42S S +等于矩形面积的一半，同理，过点P 分别向AB 、CD 作垂线段，两个三角形的面积之和31S S +等于矩形面积的一半. 31S S +=42S S +,又因为21S S =，则32S S +=ABCD S S S 2141=+,所以④一定成立 安徽22.如图1，在△ABC 中，D 、E 、F 分别为三边的中点，G 点在边AB 上，△BDG 与四边形ACDG 的周长相等，设BC =a 、AC =b 、AB =c .（1）求线段BG 的长；（2）求证：DG 平分∠EDF ;（3）连接CG ，如图2，若△BDG 与△DFG 相似，求证：BG ⊥CG . 解（1）∵D 、C 、F 分别是△ABC 三边中点 ∴DE ∥21AB ,DF ∥21AC ， 又∵△BDG 与四边形ACDG 周长相等 即BD +DG +BG =AC +CD +DG +AG∴BG =AC +AG ∵BG =AB －AG ∴BG =2AC AB +=2cb +（2）证明：BG =2c b +，FG =BG －BF =2c b +－22bc = ∴FG =DF ,∴∠FDG =∠FGD 又∵DE ∥AB∴∠EDG =∠FGD ∠FDG =∠EDG ∴DG 平分∠EDF （3）在△DFG 中，∠FDG =∠FGD , △DFG 是等腰三角形,∵△BDG 与△DFG 相似,∴△BDG 是等腰三角形,∴∠B =∠BGD ,∴BD =DG , 则CD = BD =DG ,∴B 、CG 、三点共圆, ∴∠BGC =90°,∴BG ⊥CG23.如图，排球运动员站在点O 处练习发球，将球从O 点正上方2m 的A 处发出，把球看成点，其运行的高度y （m ）与运行的水平距离x (m )满足关系式y =a (x －6)2+h .已知球网与O 点的水平距离为9m ，高度为2.43m ，球场的边界距O 点的水平距离为18m 。

1、如图12，已知直线12y x =与双曲线(0)k y k x =>交于A B ，两点，且点A 的横坐标为4． （1）求k 的值；（2）若双曲线(0)ky k x =>上一点C 的纵坐标为8，求A O C △的面积；（3）过原点O 的另一条直线l 交双曲线(0)ky k x =>于P Q ，两点（P 点在第一象限），若由点A B P Q ，，，为顶点组成的四边形面积为24，求点P 的坐标．解：(1)∵点A 横坐标为4 , ∴当 x = 4时，y = 2 .∴ 点A 的坐标为（ 4，2 ）.∵ 点A 是直线 与双曲线 （k>0）的交点 , ∴ k = 4 ×2 = 8 .(2) 解法一：如图12-1，∵ 点C 在双曲线上，y = 8时，x = 1∴ 点C 的坐标为 ( 1, 8 ) .过点A 、C 分别做x 轴、y 轴的垂线，垂足为M 、N ，得矩形DMON .S 矩形ONDM = 32 ， S △ONC = 4 ， S △CDA = 9， S △OAM = 4 .S △AOC = S 矩形ONDM - S △ONC - S △CDA - S △OAM = 32 - 4 - 9 - 4 = 15 .解法二：如图12-2，过点 C 、A 分别做x 轴的垂线，垂足为E 、F ，∵ 点C 在双曲线8y x =上，当y = 8时，x = 1 .∴ 点C 的坐标为 ( 1, 8 ).图12O x A y B x y 21x y 8=∵ 点C 、A 都在双曲线8y x =上 ,∴ S △COE = S △AOF = 4 。

∴ S △COE + S 梯形CEFA = S △COA + S △AOF .∴ S △COA = S 梯形CEFA .∵ S 梯形CEFA = 12×（2+8）×3 = 15 ,∴ S △COA = 15 .（3）∵ 反比例函数图象是关于原点O 的中心对称图形 ,∴ OP=OQ ，OA=OB .∴ 四边形APBQ 是平行四边形 .∴ S △POA = S 平行四边形APBQ = ×24 = 6 .设点P 的横坐标为m （m > 0且4m ≠）,得P ( m , ) .过点P 、A 分别做x 轴的垂线，垂足为E 、F ，∵ 点P 、A 在双曲线上，∴S △POE = S △AOF = 4 .若0＜m ＜4，如图12-3，∵ S △POE + S 梯形PEFA = S △POA + S △AOF ,∴ S 梯形PEFA = S △POA = 6 .∴ 18(2)(4)62m m +⋅-=.4141m8解得m = 2，m = - 8(舍去) .∴ P （2，4）.若 m ＞ 4，如图12-4，∵ S △AOF + S 梯形AFEP = S △AOP + S △POE ,∴ S 梯形PEFA = S △POA = 6 .∴18(2)(4)62m m +⋅-=，解得m = 8，m = - 2 (舍去) .∴ P （8，1）.∴ 点P 的坐标是P （2，4）或P （8，1）.2、如图，抛物线212y x mx n =++交x 轴于A 、B 两点，交y 轴于点C ，点P 是它的顶点，点A的横坐标是-3，点B 的横坐标是1．(1)求m 、n 的值；(2）求直线PC 的解析式；(3）请探究以点A 为圆心、直径为5的圆与直线 PC 的位置关系，并说明理由．(参考数：2 1.41≈，3 1.73≈，5 2.24≈) 解： (1)由已知条件可知： 抛物线212y x mx n =++经过A (-3，0)、B (1，0)两点． ∴ 903,210.2m n m n ⎧=-+⎪⎪⎨⎪=++⎪⎩ ……………………………………2分解得 31,2m n ==-． ………………………3分 (2) ∵21322yx x =+-， ∴ P (-1，-2)，C 3(0,)2-． …………………4分设直线PC 的解析式是y kx b =+，则2,3.2k b b -=-+⎧⎪⎨=-⎪⎩ 解得13,22k b ==-． ∴ 直线PC 的解析式是1322yx =-． …………………………6分 说明：只要求对1322k b ==-，，不写最后一步，不扣分．(3) 如图，过点A 作AE ⊥PC ，垂足为E ．设直线PC 与x 轴交于点D ，则点D 的坐标为(3，0)． ………………………7分 在Rt△O CD 中，∵ O C =32，3O D =， ∴ 2233()3522C D =+=． …………8分∵ O A =3，3O D =，∴AD =6． (9)分 ∵ ∠C O D =∠AED =90o ，∠CD O 公用，∴ △C O D ∽△AED ． ……………10分 ∴ OCC D AEAD =， 即335226AE =． ∴ 655AE =． …………………11分 ∵ 65 2.688 2.55> ，∴ 以点A 为圆心、直径为5的圆与直线PC 相离． …………12分。

25. 设,a b 是任意两个不相等的实数，我们规定：满足不等式a x b ≤≤的实数x 的所有取值的全体叫做闭区间，表示为[],a b . 对于一个函数，如果它的自变量x 与函数值y 满足：当m x n ≤≤时，有m y n ≤≤，我们就称此函数是闭区间[],m n 上的“闭函数”.
(1)请你判断：反比例函数2013y x
=是闭区间[]1,2013上的“闭函数”吗？并说明理由. (2)若一次函数(0)y kx b k =+≠是闭区间[],m n 上的“闭函数”，试求此函数的解析式.
(3) 若二次函数2147555
y x x =-- 是闭区间[],a b 上的“闭函数”，试求实数,a b 的值.
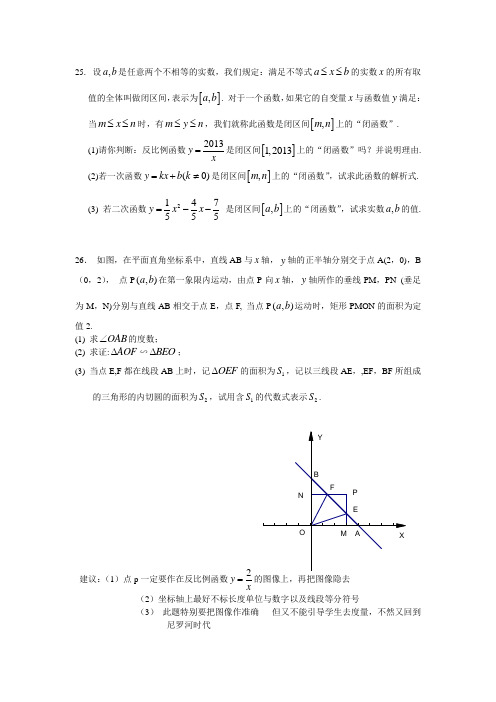
26． 如图，在平面直角坐标系中，直线AB 与x 轴，y 轴的正半轴分别交于点A(2，0)，B （0，2）， 点P (,)a b 在第一象限内运动，由点P 向x 轴，y 轴所作的垂线PM ，PN (垂足为M ，N)分别与直线AB 相交于点E ，点F, 当点P (,)a b 运动时，矩形PMON 的面积为定值2.
(1) 求OAB ∠的度数；
(2) 求证:AOF ∆∽BEO ∆；
(3) 当点E,F 都在线段AB 上时，记OEF ∆的面积为1S ，记以三线段AE ，,EF ，BF 所组成
的三角形的内切圆的面积为2S ，试用含1S 的代数式表示2S .
建议：（1）点p 一定要作在反比例函数2y x
=的图像上，再把图像隐去 （2）坐标轴上最好不标长度单位与数字以及线段等分符号
（3） 此题特别要把图像作准确 但又不能引导学生去度量，不然又回到
尼罗河时代。

2013年各地数学中考附加题（2013.宜宾）1.如图，AB是⊙O的直径，∠B=∠CAD．（1）求证：AC是⊙O的切线；（2）若点E是⌒BD错误！未指定书签。

的中点，连接AE交BC于点F，当BD=5，CD=4时，求AF的值．（2013.宜宾）2.如图，抛物线y1=x2-1交x轴的正半轴于点A，交y轴于点B，将此抛物线向右平移4个单位得抛物线y2，两条抛物线相交于点C．（1）请直接写出抛物线y2的解析式；（2）若点P是x轴上一动点，且满足∠CPA=∠OBA，求出所有满足条件的P点坐标；（3）在第四象限内抛物线y2上，是否存在点Q，使得△QOC中OC边上的高h有最大值？若存在，请求出点Q 的坐标及h的最大值；若不存在，请说明理由（2013.宁波）3.若一个四边形的一条对角线把四边形分成两个等腰三角形，我们把这条对角线叫这个四边形的和谐线，这个四边形叫做和谐四边形．如菱形就是和谐四边形．（1）如图1，在梯形ABCD中，AD∥BC，∠BAD=120°，∠C=75°，BD平分∠ABC．求证：BD是梯形ABCD的和谐线；（2）如图2，在12×16的网格图上（每个小正方形的边长为1）有一个扇形BAC，点A．B．C均在格点上，请在答题卷给出的两个网格图上各找一个点D，使得以A、B、C、D为顶点的四边形的两条对角线都是和谐线，并画出相应的和谐四边形；（3）四边形ABCD中，AB=AD=BC，∠BAD=90°，AC是四边形ABCD的和谐线，求∠BCD的度数．（2013.宁波）4. 如图，在平面直角坐标系中，O为坐标原点，点A的坐标为（0，4），点B的坐标为（4，0），点C的坐标为（-4，0），点P在射线AB上运动，连结CP与y轴交于点D，连结BD．过P，D，B三点作⊙Q与y轴的另一个交点为E，延长DQ交⊙Q于点F，连结EF，BF．（1）求直线AB的函数解析式；（2）当点P在线段AB（不包括A，B两点）上时．①求证：∠BDE=∠ADP；②设DE=x，DF=y．请求出y关于x的函数解析式；（3）请你探究：点P在运动过程中，是否存在以B，D，F为顶点的直角三角形，满足两条直角边之比为2：1？如果存在，求出此时点P的坐标：如果不存在，请说明理由．（2013.徐州）5.如图，在Rt△ABC中，∠C=90°，翻折∠C，使点C落在斜边AB上某一点D处，折痕为EF （点E、F分别在边AC、BC上）（1）若△CEF与△ABC相似．①当AC=BC=2时，AD的长为____；②当AC=3，BC=4时，AD的长为___；（2）当点D是AB的中点时，△CEF与△ABC相似吗？请说明理由．(2013.徐州）6.如图，二次函数y=12 x 2+bx-32的图象与x 轴交于点A （-3，0）和点B ，以AB 为边在x 轴上方作正方形ABCD ，点P 是x 轴上一动点，连接DP ，过点P 作DP 的垂线与y 轴交于点E ．（1）请直接写出点D 的坐标：______;（2）当点P 在线段AO （点P 不与A 、O 重合）上运动至何处时，线段OE 的长有最大值，求出这个最大值；（3）是否存在这样的点P ，使△PED 是等腰三角形？若存在，请求出点P 的坐标及此时△PED 与正方形ABCD 重叠部分的面积；若不存在，请说明理由．(2013.滨州）7.根据要求，解答下列问题：（1）已知直线l 1的函数表达式为y=x ，请直接写出过原点且与l 1垂直的直线l 2的函数表达式；（2）如图，过原点的直线l 3向上的方向与x 轴的正方向所成的角为30°． ①求直线l 3的函数表达式；②把直线l 3绕原点O 按逆时针方向旋转90°得到的直线l 4，求直线l 4的函数表达式．（3）分别观察（1）（2）中的两个函数表达式，请猜想：当两直线垂直时，它们的函数表达式中自变量的系数之间有何关系？请根据猜想结论直接写出过原点且与直线y=-15x 垂直的直线l 5的函数表达式．(2013.湖州）8.一节数学课后，老师布置了一道课后练习题：如图，已知在Rt△ABC 中，AB=BC ，∠ABC=90°，BO⊥AC，于点O ，点PD 分别在AO 和BC 上，PB=PD ，DE⊥AC 于点E ，求证：△BPO≌△PDE．（1）理清思路，完成解答（2）本题证明的思路可用下列框图表示：根据上述思路，请你完整地书写本题的证明过程．（2）特殊位置，证明结论若PB 平分∠ABO，其余条件不变．求证：AP=CD ．（3）知识迁移，探索新知若点P 是一个动点，点P 运动到OC 的中点P′时，满足题中条件的点D 也随之在直线BC 上运动到点D′，请直接写出CD′与AP′的数量关系．（不必写解答过程）（2013.湖州）9.如图①，O 为坐标原点，点B 在x 轴的正半轴上，四边形OACB 是平行四边形，sin∠AOB=45反比例函数y=k x（k ＞0）在第一象限内的图象经过点A ，与BC 交于点F ． （1）若OA=10，求反比例函数解析式；（2）若点F 为BC 的中点，且△AOF 的面积S=12，求OA 的长和点C 的坐标；（3）在（2）中的条件下，过点F 作EF∥OB，交OA 于点E （如图②），点P 为直线EF 上的一个动点，连接PA ，PO ．是否存在这样的点P ，使以P 、O 、A 为顶点的三角形是直角三角形？若存在，请直接写出所有点P 的坐标；若不存在，请说明理由．(2013.湛江）10.如图，在平面直角坐标系中，顶点为（3，4）的抛物线交y 轴于A 点，交x 轴于B 、C 两点（点B 在点C 的左侧），已知A 点坐标为（0，-5）．（1）求此抛物线的解析式；（2）过点B 作线段AB 的垂线交抛物线于点D ，如果以点C 为圆心的圆与直线BD 相切，请判断抛物线的对称轴l 与⊙C 有什么位置关系，并给出证明；（3）在抛物线上是否存在一点P ，使△ACP 是以AC 为直角边的直角三角形？若存在，求出点P 的坐标；若不存在，请说明理由．（2013.杭州）11.（1）先求解下列两题： ①如图①，点B ，D 在射线AM 上，点C ，E 在射线AN 上，且AB=BC=CD=DE ，已知∠EDM=84°，求∠A 的度数； ②如图②，在直角坐标系中，点A 在y 轴正半轴上，AC∥x 轴，点B ，C 的横坐标都是3，且BC=2，点D 在AC 上，且横坐标为1，若反比例函数y=k x(x ＞0)的图象经过点B ，D ，求k 的值．（2）解题后，你发现以上两小题有什么共同点？请简单地写出．（2013.杭州）12.如图，已知正方形ABCD 的边长为4，对称中心为点P ，点F 为BC 边上一个动点，点E 在AB 边上，且满足条件∠EPF=45°，图中两块阴影部分图形关于直线AC 成轴对称，设它们的面积和为S 1．（1）求证：∠APE=∠CFP；（2）设四边形CMPF 的面积为S 2，CF=x ，y= S 1S 2错误！未指定书签。

2013年中考压轴题精选”“XX专题训练一．解答题（共7小题）1．（2010•绵阳）如图，抛物线y=ax2+bx+4与x轴的两个交点分别为A（﹣4，0）、B（2，0），与y轴交于点C，顶点为D．E（1，2）为线段BC的中点，BC的垂直平分线与x轴、y轴分别交于F、G．（1）求抛物线的函数解析式，并写出顶点D的坐标；（2）在直线EF上求一点H，使△CDH的周长最小，并求出最小周长；（3）若点K在x轴上方的抛物线上运动，当K运动到什么位置时，△EFK的面积最大？并求出最大面积．2．已知抛物线y=ax2+bx+c的图象如图所示，根据图象解答下列问题：（1）抛物线与x轴的另一个交点坐标；_________；（2）方程ax2+bx+c=0的两个根是_________；（3）不等式ax2+bx+c＜0的解是_________；（4）y随x的增大而减小的自变量x的取值范围是_________；（5）求出抛物线的解析式及顶点坐标．3．（2012•遵义）如图，已知抛物线y=ax2+bx+c（a≠0）的图象经过原点O，交x轴于点A，其顶点B的坐标为（3，﹣）．（1）求抛物线的函数解析式及点A的坐标；（2）在抛物线上求点P，使S△POA=2S△AOB；（3）在抛物线上是否存在点Q，使△AQO与△AOB相似？如果存在，请求出Q点的坐标；如果不存在，请说明理由．4．如图，在平面直角坐标系中，矩形OABC的顶点A（3，0），C（0，1）．将矩形OABC绕原点逆时针旋转90°，得到矩形OA′B′C′．设直线BB′与x轴交于点M、与y轴交于点N，抛物线y=ax2+bx+c的图象经过点C′、M、N．解答下列问题：（1）求出该抛物线所表示的函数解析式；（2）将△MON沿直线BB′翻折，点O落在点P处，请你判断点P是否在该抛物线上，并请说明理由；（3）将该抛物线进行一次平移（沿上下或左右方向），使它恰好经过原点O，求出所有符合要求新抛物线的解析式．5．（2009•柳州）如图，已知抛物线y=ax2﹣2ax﹣b（a＞0）与x轴的一个交点为B（﹣1，0），与y轴的负半轴交于点C，顶点为D．（1）直接写出抛物线的对称轴，及抛物线与x轴的另一个交点A的坐标；（2）以AD为直径的圆经过点C．①求抛物线的解析式；②点E在抛物线的对称轴上，点F在抛物线上，且以B，A，F，E四点为顶点的四边形为平行四边形，求点F的坐标．6．如图，在直角坐标平面内，O为原点，抛物线y=ax2+bx经过点A（6，0），且顶点B（m，6）在直线y=2x上．（1）求m的值和抛物线y=ax2+bx的解析式；（2）如在线段OB上有一点C，满足OC=2CB，在x轴上一点D（10，0），连接DC，且直线DC与y轴交于点E．①求直线DC的解析式；②如点M是直线DC上的一个动点，在x轴上方的平面内有另一点N，且以O、E、M、N为顶点的四边形是菱形，请求出点N的坐标．（直接写出结果，不需要过程．）7．（2008•宜宾）已知：如图，抛物线y=﹣x2+bx+c与x轴、y轴分别相交于点A（﹣1，0）、B（0，3）两点，其顶点为D．（1）求该抛物线的解析式；（2）若该抛物线与x轴的另一个交点为E．求四边形ABDE的面积；（3）△AOB与△BDE是否相似？如果相似，请予以证明；如果不相似，请说明理由．（注：抛物线y=ax2+bx+c（a≠0）的顶点坐标为）如图所示，在平面直角坐标系中，抛物线y=ax2+bx+c经过A（﹣1，0）、B（0，﹣5）、C（5，0）．（1）求此抛物线的表达式；（2）若平行于x轴的直线与此抛物线交于E、F两点，以线段EF为直径的圆与x轴相切，求该圆的半径；（3）在点B、点C之间的抛物线上有点D，使△BDC的面积最大，求此时点D的坐标及△BDC的面积．，解得因为抛物线的对称轴为直线解得：解得所以圆的半径为答：该圆的半径是．）代入得：解得：时，，，﹣，，﹣的面积是．。

2013中考压轴试题代数几何综合1、（2013年潍坊市压轴题）如图，抛物线c bx ax y ++=2关于直线1=x 对称，与坐标轴交于C B A 、、三点，且4=AB ,点⎪⎭⎫ ⎝⎛232，D 在抛物线上，直线是一次函数()02≠-=k kx y 的图象，点O 是坐标原点.（）求抛物线的解析式；（）若直线平分四边形OBDC 的面积，求k 的值.（）把抛物线向左平移1个单位，再向下平移2个单位，所得抛物线与直线交于N M 、两点，问在y 轴正半轴上是否存在一定点P ，使得不论k 取何值，直线PM 与PN 总是关于y 轴对称？若存在，求出P 点坐标；若不存在，请说明理由.答案：（1）因为抛物线关于直线x=1对称，AB=4，所以A(-1，0),B(3，0),由点D(2，1.5)在抛物线上，所以⎩⎨⎧=++=+-5.1240c b a c b a ，所以3a+3b=1.5,即a+b=0.5,又12=-a b ，即b=-2a,代入上式解得a =-0.5,b =1,从而c=1.5,所以23212++-=x x y . （）由（1）知23212++-=x x y ，令x=0,得c(0,1.5),所以CD//AB,令kx -2=1.5,得l 与CD 的交点F(23,27k )，令kx -2=0，得l 与x 轴的交点E(0,2k)，根据S 四边形OEFC =S 四边形EBDF 得：OE+CF=DF+BE,即：,511),272()23(272=-+-=+k k k k k 解得 （3）由（1）知,2)1(21232122+--=++-=x x x y所以把抛物线向左平移1个单位，再向下平移2个单位，所得抛物线的解析式为221x y -=假设在y 轴上存在一点P(0，t)，t ＞0，使直线PM 与PN 关于y 轴对称，过点M 、N 分别向y 轴作垂线MM 1、NN 1，垂足分别为M 1、N 1，因为∠MPO=∠NPO,所以Rt △MPM 1∽Rt △NPN 1, 所以1111PN PM NN MM =,………………(1) 不妨设M(x M ,y M )在点N(x N ,y N )的左侧，因为P 点在y 轴正半轴上， 则（1）式变为NMN M y t y t x x --=-,又y M =k x M -2, y N =k x N -2,把2交（（（D （点A(-1,0)、点B 是二次函数y=ax 2-2 的图象与x 轴的交点，a-2=0,a=2. 二次函数的解析式为y=2x 2-2；②点B 与点A(-1,0)关于直线x=0对称，点B 的坐标为（1，0）； （2）∠BOC=∠PDB=90º，点P 在直线x=m 上，设点P 的坐标为（m,p ）, OB=1， OC=2， DB= m-1 , DP=|p| ，①当△BOC ∽△PDB 时，OB OC = DP DB ,12= |p|m-1 ,p= m-12 或p = 1- m2,点P 的坐标为（m ，m-12 ）或（m ，1- m2 ）；②当△BOC ∽△BDP 时，OB OC = DB DP ，12= m-1|p|，p=2m-2或p=2-2m, 点P 的坐标为（m ，2m-2）或（m ，2-2m ）；综上所述点P 的坐标为（m ，m-12 ）、（m ，1- m2 ）、（m ，2m-2）或（m ，2-2m ）；（3）不存在满足条件的点Q 。

8.已知：如图14，抛物线2334y x =-+与x 轴交于点A ，点B ，与直线34y x b =-+相交于点B ，点C ，直线34y x b =-+与y 轴交于点E ． （1）写出直线BC 的解析式．（2）求ABC △的面积．（3）若点M 在线段AB 上以每秒1个单位长度的速度从A 向B 运动（不与A B ，重合），同时，点N 在射线BC 上以每秒2个单位长度的速度从B 向C 运动．设运动时间为t 秒，请写出MNB △的面积S 与t 的函数关系式，并求出点M 运动多少时间时，MNB △的面积最大，最大面积是多少？（解析）解：（1）在2334y x =-+中，令0y = 23304x ∴-+=12x ∴=，22x =- (20)A ∴-，，(20)B ， ··················································· 1分又 点B 在34y x b =-+上 302b ∴=-+32b = BC ∴的解析式为3342y x =-+ ····················································································· 2分 （2）由23343342y x y x ⎧=-+⎪⎪⎨⎪=-+⎪⎩，得11194x y =-⎧⎪⎨=⎪⎩ 2220x y =⎧⎨=⎩ ························································· 4分 914C ⎛⎫∴- ⎪⎝⎭，，(20)B ， 4AB ∴=，94CD = ······································································································· 5分 1994242ABC S ∴=⨯⨯=△ ································································································· 6分 （3）过点N 作NP MB ⊥于点PEO MB ⊥NP EO ∴∥BNP BEO ∴△∽△ ········································································································ 7分BN NP BE EO∴= ···················································································································· 8分 由直线3342y x =-+可得：302E ⎛⎫ ⎪⎝⎭， ∴在BEO △中，2BO =，32EO =，则52BE = 25322t NP ∴=，65NP t ∴= ······························································································· 9分 16(4)25S t t ∴=- 2312(04)55S t t t =-+<< ··························································································· 10分 2312(2)55S t =--+ ····································································································· 11分 此抛物线开口向下，∴当2t =时，125S =最大 ∴当点M 运动2秒时，MNB △的面积达到最大，最大为125． ······························ 12分 16.如图，已知与x 轴交于点(10)A ，和(50)B ，的抛物线1l 的顶点为(34)C ，，抛物线2l 与1l 关于x 轴对称，顶点为C '．（1）求抛物线2l 的函数关系式；（2）已知原点O ，定点(04)D ，，2l 上的点P 与1l 上的点P '始终关于x 轴对称，则当点P 运动到何处时，以点D O P P '，，，为顶点的四边形是平行四边形？（3）在2l 上是否存在点M ，使ABM △是以AB 为斜边且一个角为30 的直角三角形？若存，求出点M 的坐标；若不存在，说明理由．解：（1）由题意知点C '的坐标为(34)-，． 设2l 的函数关系式为2(3)4y a x =--． 又 点(10)A ，在抛物线2(3)4y a x =--上， 2(13)40a ∴--=，解得1a =．∴抛物线2l 的函数关系式为2(3)4y x =--（或265y x x =-+）．（2）P 与P '始终关于x 轴对称，PP '∴与y 轴平行．设点P 的横坐标为m ，则其纵坐标为265m m -+， 4OD = ，22654m m ∴-+=，即2652m m -+=±．当2652m m -+=时，解得36m =±．当2652m m -+=-时，解得32m =±． ∴当点P 运动到(362)-，或(362)+，或(322)--，或(322)+-，时，P P OD '∥，以点D O P P '，，，为顶点的四边形是平行四边形．（3）满足条件的点M 不存在．理由如下：若存在满足条件的点M 在2l 上，则 90AMB ∠= ，30BAM ∠= （或30ABM ∠= ），114222BM AB ∴==⨯=． 过点M 作ME AB ⊥于点E ，可得30BME BAM ∠=∠= ．112122EB BM ∴==⨯=，3EM =，4OE =． ∴点M 的坐标为(43)-，．但是，当4x =时，246451624533y =-⨯+=-+=-≠-． ∴不存在这样的点M 构成满足条件的直角三角形．。

2013年中考数学压轴题精选1. 如图，在平面直角坐标系中，直线112y x =+与抛物线y ＝ax 2＋bx －3交于A 、B 两点，点A 在x 轴上，点B 的纵坐标为3．点P 是直线AB 下方的抛物线上的一动点（不与点A 、B 重合），过点P 作x 轴的垂线交直线AB 于点C ，作PD ⊥AB 于点D ．（1）求a 、b 及sin ∠ACP 的值；（2）设点P 的横坐标为m ．①用含m 的代数式表示线段PD 的长，并求出线段PD 长的最大值；②连结PB ，线段PC 把△PDB 分成两个三角形，是否存在适合的m 的值，使这两个三角形的面积比为 9∶10？若存在，直接写出m 的值；若不存在，请说明理由．2. 如图1，已知抛物线212y x bx c =++（b 、c 是常数，且c ＜0）与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴的负半轴交于点C ，点A 的坐标为(－1,0)．（1）b ＝______，点B 的横坐标为_______（上述结果均用含c 的代数式表示）；（2）连结BC ，过点A 作直线AE //BC ，与抛物线交于点E ．点D 是x 轴上一点，坐标为(2,0)，当C 、D 、E 三点在同一直线上时，求抛物线的解析式；（3）在（2）的条件下，点P 是x 轴下方的抛物线上的一动点，连结PB 、PC ．设△PBC 的面积为S ． ①求S 的取值范围；②若△PBC 的面积S 为正整数，则这样的△PBC 共有_____个．3.如图1，在Rt△ABC中，∠C＝90°，AC＝6，BC＝8，动点P从点A开始沿边AC向点C以每秒1个单位长度的速度运动，动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动，过点P作PD//BC，交AB于点D，联结PQ．点P、Q分别从点A、C同时出发，当其中一点到达端点时，另一点也随之停止运动，设运动的时间为t秒（t≥0）．（1）直接用含t的代数式分别表示：QB＝_______，PD＝_______；（2）是否存在t的值，使四边形PDBQ为菱形？若存在，求出t的值；若不存在，说明理由，并探究如何改变点Q的速度（匀速运动），使四边形PDBQ在某一时刻为菱形，求点Q的速度；（3）如图2，在整个运动过程中，求出线段PQ的中点M所经过的路径长．图1 图24.如图1，在△ABC中，∠C＝90°，A C＝3，BC＝4，CD是斜边AB上的高，点E在斜边AB上，过点E 作直线与△ABC的直角边相交于点F，设AE＝x，△AEF的面积为y．（1）求线段AD的长；（2）若EF⊥AB，当点E在斜边AB上移动时，①求y与x的函数关系式（写出自变量x的取值范围）；②当x取何值时，y有最大值？并求出最大值．（3）若点F在直角边AC上（点F与A、C不重合），点E在斜边AB上移动，试问，是否存在直线EF将△ABC的周长和面积同时平分？若存在直线EF，求出x的值；若不存在直线EF，请说明理由．图1 备用图C 5. 如图，在等腰梯形ABCD 中，AB ∥DC ，cm BC AD 5==,AB =12 cm,CD =6cm , 点P 从A 开始沿AB 边向B 以每秒3cm 的速度移动，点Q 从C 开始沿CD 边向D 以每秒1cm 的速度移动，如果点P 、Q 分别从A 、C 同时出发，当其中一点到达终点时运动停止。

2012中考数学压轴题及答案1.（2011年四川省宜宾市）已知:如图,抛物线y=-x 2+bx+c 与x 轴、y 轴分别相交于点A （-1，0）、B （0，3）两点，其顶点为D.（1） 求该抛物线的解析式；（2） 若该抛物线与x 轴的另一个交点为E. 求四边形ABDE 的面积；（3） △AOB 与△BDE 是否相似？如果相似，请予以证明；如果不相似，请说明理由.（注：抛物线y=ax 2+bx+c(a ≠0)的顶点坐标为⎪⎪⎭⎫ ⎝⎛--a b ac a b 44,22）2. （11浙江衢州）已知直角梯形纸片OABC 在平面直角坐标系中的位置如图所示，四个顶点的坐标分别为O(0，0)，A(10，0)，B(8，32)，C(0，32)，点T 在线段OA 上(不与线段端点重合)，将纸片折叠，使点A 落在射线AB 上(记为点A ′)，折痕经过点T ，折痕TP 与射线AB 交于点P ，设点T 的横坐标为t ，折叠后纸片重叠部分(图中的阴影部分)的面积为S ；(1)求∠OAB 的度数，并求当点A ′在线段AB 上时，S 关于t 的函数关系式；(2)当纸片重叠部分的图形是四边形时，求t 的取值范围；(3)S 存在最大值吗？若存在，求出这个最大值，并求此时t 的值；若不存在，请说明理由.3. （11浙江温州）如图，在Rt ABC △中，90A ∠=，6AB =，8AC =，D E ，分别是边AB AC ，的中点，点P 从点D 出发沿DE 方向运动，过点P 作PQ BC ⊥于Q ，过点Q 作QR BA ∥交AC 于R ，当点Q 与点C 重合时，点P 停止运动．设BQ x =，QR y =．（1）求点D 到BC 的距离DH 的长；（2）求y 关于x 的函数关系式（不要求写出自变量的取值范围）；（3）是否存在点P ，使P Q R △为等腰三角形？若存在，请求出所有满足要求的x 的值；若不存在，请说明理由．4.（11山东省日照市）在△ABC 中，∠A ＝90°，AB ＝4，AC ＝3，M 是AB 上的动点（不与A ，B 重合），过M 点作MN ∥BC 交AC 于点N ．以MN 为直径作⊙O ，并在⊙O 内作内接矩形AMPN ．令AM ＝x ．（1）用含x 的代数式表示△ＭNP 的面积S ；（2）当x 为何值时，⊙O 与直线BC 相切？（3）在动点M 的运动过程中，记△ＭNP 与梯形BCNM 重合的面积为y ，试求y 关于x 的函数表达式，并求x 为何值时，y 的值最大，最大值是多少？5、（2007浙江金华）如图1，已知双曲线y=xk (k>0)与直线y=k ′x 交于A ，B 两点，点A 在第一象限.试解答下列问题：(1)若点A 的坐标为(4，2).则点B 的坐标为 ；若点A 的横坐标为m ，则点B 的坐标可表示为 ；（2）如图2，过原点O 作另一条直线l ，交双曲线y=xk (k>0)于P ，Q 两点，点P 在第一象限.①说明四边形APBQ 一定是平行四边形；②设点A.P 的横坐标分别为m ，n ，四边形APBQ 可能是矩形吗?可能是正方形吗?若可能，直接写出mn 应满足的条件；若不可能，请说明理由.8. (2011浙江义乌)如图1所示，直角梯形OABC 的顶点A 、C 分别在y 轴正半轴与x 轴负半轴上.过点B 、C 作直线l ．将直线l 平移，平移后的直线l 与x 轴交于点D ，与y 轴交于点E ．（1）将直线l 向右平移，设平移距离CD 为t (t ≥0)，直角梯形OABC 被直线l 扫过的面积（图中阴影部份）为s ，s 关于t 的函数图象如图2所示， OM 为线段，MN 为抛物线的一部分，NQ 为射线，N 点横坐标为4．①求梯形上底AB 的长及直角梯形OABC 的面积；②当42<<t 时，求S 关于t 的函数解析式；（2）在第（1）题的条件下，当直线l 向左或向右平移时（包括l 与直线BC 重合），在直线．．AB ．．上是否存在点P ，使PDE ∆为等腰直角三角形?若存在，请直接写出所有满足条件的点P 的坐标;若不存在，请说明理由．9.(2011山东烟台)如图，菱形ABCD 的边长为2，BD=2，E 、F 分别是边AD ，CD 上的两个动点，且满足AE+CF=2.（1）求证：△BDE ≌△BCF ；（2）判断△BEF 的形状，并说明理由；（3）设△BEF 的面积为S ，求S 的取值范围.10.(2011山东烟台)如图，抛物线21:23L y x x =--+交x 轴于A 、B 两点，交y 轴于M 点.抛物线1L 向右平移2个单位后得到抛物线2L ，2L 交x 轴于C 、D 两点.（1）求抛物线2L 对应的函数表达式；（2）抛物线1L 或2L 在x 轴上方的部分是否存在点N ，使以A ，C ，M ，N 为顶点的四边形是平行四边形.若存在，求出点N 的坐标；若不存在，请说明理由；（3）若点P 是抛物线1L 上的一个动点（P 不与点A 、B 重合），那么点P 关于原点的对称点Q 是否在抛物线2L 上，请说明理由.13.（2011山东威海）如图，在梯形ABCD 中，AB ∥CD ，AB ＝7，CD ＝1，AD ＝BC ＝5．点M ，N 分别在边AD ，BC 上运动，并保持MN ∥AB ，ME ⊥AB ，NF ⊥AB ，垂足分别为E ，F ．（1）求梯形ABCD 的面积；（2）求四边形MEFN 面积的最大值．（3）试判断四边形MEFN 能否为正方形，若能，求出正方形MEFN 的面积；若不能，请说明理由．16.(2011年浙江省绍兴市)将一矩形纸片OABC 放在平面直角坐标系中，(00)O ，，(60)A ，，(03)C ，．动点Q 从点O 出发以每秒1个单位长的速度沿OC 向终点C 运动，运动23秒时，动点P 从点A 出发以相等的速度沿AO 向终点O 运动．当其中一点到达终点时，另一点也停止运动．设点P 的运动时间为t （秒）． （1）用含t 的代数式表示OP OQ ，；（2）当1t 时，如图1，将OPQ △沿PQ 翻折，点O 恰好落在CB 边上的点D 处，求点D 的坐标；（4） 连结AC ，将OPQ △沿PQ 翻折，得到EPQ △，如图2．问：PQ 与AC 能否平行？PE 与AC能否垂直？若能，求出相应的t 值；若不能，说明理由．17.(2011年辽宁省十二市)如图16，在平面直角坐标系中，直线33y x =--与x 轴交于点A ，与y 轴交于点C ，抛物线223(0)3y ax x c a =-+≠经过A B C ，，三点． （1）求过A B C ，，三点抛物线的解析式并求出顶点F 的坐标；（2）在抛物线上是否存在点P ，使ABP △为直角三角形，若存在，直接写出P 点坐标；若不存在，请说明理由；（3）试探究在直线AC 上是否存在一点M ，使得MBF △的周长最小，若存在，求出M 点的坐标；若不存在，请说明理由．18.(2011年沈阳市)如图所示，在平面直角坐标系中，矩形ABOC 的边BO 在x 轴的负半轴上，边OC 在y 轴的正半轴上，且1AB =，3OB =，矩形ABOC 绕点O 按顺时针方向旋转60后得到矩形EFOD ．点A 的对应点为点E ，点B 的对应点为点F ，点C 的对应点为点D ，抛物线2y ax bx c =++过点A E D ，，．（1）判断点E 是否在y 轴上，并说明理由；（2）求抛物线的函数表达式；（3）在x 轴的上方是否存在点P ，点Q ，使以点O B P Q ，，，为顶点的平行四边形的面积是矩形ABOC 面积的2倍，且点P 在抛物线上，若存在，请求出点P ，点Q 的坐标；若不存在，请说明理由．19.(2011年四川省巴中市) 已知：如图14，抛物线2334y x =-+与x 轴交于点A ，点B ，与直线34y x b =-+相交于点B ，点C ，直线34y x b =-+与y 轴交于点E ． （1）写出直线BC 的解析式．（2）求ABC △的面积．（3）若点M 在线段AB 上以每秒1个单位长度的速度从A 向B 运动（不与A B ，重合），同时，点N 在射线BC 上以每秒2个单位长度的速度从B 向C 运动．设运动时间为t 秒，请写出MNB △的面积S 与t 的函数关系式，并求出点M 运动多少时间时，MNB △的面积最大，最大面积是多少？20.(2011年成都市)如图，在平面直角坐标系xOy 中，△OAB 的顶点Ａ的坐标为（10，0），顶点B 在第一象限内，且AB =35，sin ∠OAB=55. （1）若点C 是点B 关于x 轴的对称点，求经过O 、C 、A 三点的抛物线的函数表达式；（2）在(1)中，抛物线上是否存在一点P ，使以P 、O 、C 、A 为顶点的四边形为梯形？若存在，求出点P 的坐标；若不存在，请说明理由；（3）若将点O 、点A 分别变换为点Q （ -2k ,0）、点R （5k ，0）（k>1的常数），设过Q 、R 两点，且以QR 的垂直平分线为对称轴的抛物线与y 轴的交点为N ，其顶点为M ，记△QNM 的面积为QMN S ∆，△QNR 的面积Q NR S ∆，求QMN S ∆∶Q NR S ∆的值.22.(2011年四川省宜宾市)已知:如图,抛物线y=-x 2+bx+c 与x 轴、y 轴分别相交于点A （-1，0）、B （0，3）两点，其顶点为D.(1)求该抛物线的解析式；(2)若该抛物线与x 轴的另一个交点为E. 求四边形ABDE 的面积；(3)△AOB 与△BDE 是否相似？如果相似，请予以证明；如果不相似，请说明理由.（注：抛物线y=ax 2+bx+c(a ≠0)的顶点坐标为⎪⎪⎭⎫ ⎝⎛--a b ac a b 44,22）．24.(2011年大庆市)如图①，四边形AEFG 和ABCD 都是正方形，它们的边长分别为a b ，（2b a ≥），且点F 在AD 上（以下问题的结果均可用a b ，的代数式表示）．（1）求DBF S △；（2）把正方形AEFG 绕点A 按逆时针方向旋转45°得图②，求图②中的DBF S △；（3）把正方形AEFG 绕点A 旋转一周，在旋转的过程中，DBF S △是否存在最大值、最小值？如果存在，直接写出最大值、最小值；如果不存在，请说明理由．25. （2011年上海市）已知24AB AD ==，，90DAB ∠=，AD BC ∥（如图13）．E 是射线BC 上的动点（点E 与点B 不重合），M 是线段DE 的中点．（1）设BE x ，ABM △的面积为y ，求y 关于x 的函数解析式，并写出函数的定义域；（2）如果以线段AB 为直径的圆与以线段DE 为直径的圆外切，求线段BE 的长；（3）联结BD ，交线段AM 于点N ，如果以A N D ，，为顶点的三角形与BME △相似，求线段BE 的长．27. （2011年山东省青岛市）已知：如图①，在Rt △ACB 中，∠C ＝90°，AC ＝4cm ，BC ＝3cm ，点P 由B 出发沿BA 方向向点A 匀速运动，速度为1cm/s ；点Q 由A 出发沿AC 方向向点C 匀速运动，速度为2cm/s ；连接PQ ．若设运动的时间为t （s ）（0＜t ＜2），解答下列问题：（1）当t 为何值时，PQ ∥BC ？（2）设△AQP 的面积为y （2cm ），求y 与t 之间的函数关系式；（3）是否存在某一时刻t ，使线段PQ 恰好把Rt △ACB 的周长和面积同时平分？若存在，求出此时t 的值；若不存在，说明理由；（4）如图②，连接PC ，并把△PQC 沿QC 翻折，得到四边形PQP ′C ，那么是否存在某一时刻t ，使四边形PQP ′C 为菱形？若存在，求出此时菱形的边长；若不存在，说明理由．28.（2011年江苏省南通市）已知双曲线kyx=与直线14y x=相交于A、B两点.第一象限上的点M（m，n）（在A点左侧）是双曲线kyx=上的动点.过点B作BD∥y轴于点D.过N（0，－n）作NC∥x轴交双曲线kyx=于点E，交BD于点C.（1）若点D坐标是（－8，0），求A、B两点坐标及k的值.（2）若B是CD的中点，四边形OBCE的面积为4，求直线CM的解析式.（3）设直线AM、BM分别与y轴相交于P、Q两点，且MA＝pMP，MB＝qMQ，求p－q的值.29.（2011年江苏省无锡市）一种电讯信号转发装置的发射直径为31km．现要求：在一边长为30km的正方形城区选择若干个安装点，每个点安装一个这种转发装置，使这些装置转发的信号能完全覆盖这个城市．问：（1）能否找到这样的4个安装点，使得这些点安装了这种转发装置后能达到预设的要求？（2）至少需要选择多少个安装点，才能使这些点安装了这种转发装置后达到预设的要求？答题要求：请你在解答时，画出必要的示意图，并用必要的计算、推理和文字来说明你的理由．（下面给出了几个边长为30km的正方形城区示意图，供解题时选用）压轴题答案1.解：（ 1）由已知得：310c b c =⎧⎨--+=⎩解得c=3,b =2∴抛物线的线的解析式为223y x x =-++(2)由顶点坐标公式得顶点坐标为（1，4）所以对称轴为x=1,A,E 关于x=1对称，所以E(3,0)设对称轴与x 轴的交点为F所以四边形ABDE 的面积=ABO DFE BOFD S S S ∆∆++梯形 =111()222AO BO BO DF OF EF DF ⋅++⋅+⋅ =11113(34)124222⨯⨯++⨯+⨯⨯ =9 （3）相似如图，BD=2222112BG DG +=+= BE=22223332BO OE +=+= DE=22222425DF EF +=+=所以2220BD BE +=, 220DE =即： 222BD BE DE +=,所以BDE ∆是直角三角形 所以90AOB DBE ∠=∠=︒,且22AO BO BD BE ==, 所以AOB DBE ∆∆.2. (1) ∵A ，B 两点的坐标分别是A(10，0)和B(8，32)，∴381032OAB tan =-=∠， ∴︒=∠60OAB当点A ´在线段AB 上时，∵︒=∠60OAB ，TA=TA ´，∴△A ´TA 是等边三角形，且A T TP '⊥，∴)t 10(2360sin )t 10(T P -=︒-=，)t 10(21AT 21AP P A -==='，○2当6t 2<≤时，由图○1，重叠部分的面积EB A TP A S S S '∆'∆-=∵△A ´EB 的高是︒'60sin B A ， ∴23)4t 10(21)t 10(83S 22⨯----= 34)2t (83)28t 4t (8322+--=++-=当t=2时，S 的值最大是34；○3当2t 0<<，即当点A ´和点P 都在线段AB 的延长线是(如图○2，其中E 是TA ´与CB 的交点，F 是TP 与CB 的交点)，∵ETF FTP EFT ∠=∠=∠，四边形ETAB 是等腰形，∴EF=ET=AB=4， ∴3432421OC EF 21S =⨯⨯=⋅= 综上所述，S 的最大值是34，此时t 的值是2t 0≤<.3. 解：（1）Rt A ∠=∠，6AB =，8AC =，10BC ∴=．点D 为AB 中点，132BD AB ∴==． 90DHB A ∠=∠=，B B ∠=∠．BHD BAC ∴△∽△，DH BD AC BC ∴=，3128105BD DH AC BC ∴==⨯=． （2）QR AB ∥，90QRC A ∴∠=∠=． C C ∠=∠，RQC ABC ∴△∽△，RQ QC AB BC ∴=，10610y x -∴=， 即y 关于x 的函数关系式为：365y x =-+． （3）存在，分三种情况：①当PQ PR =时，过点P 作PM QR ⊥于M ，则QM RM =．1290∠+∠=，290C ∠+∠=，1C ∴∠=∠．84cos 1cos 105C ∴∠===，45QM QP ∴=， 1364251255x ⎛⎫-+ ⎪⎝⎭∴=，185x ∴=． ②当PQ RQ =时，312655x -+=， 6x ∴=．③当PR QR =时，则R 为PQ 中垂线上的点，于是点R 为EC 的中点，11224CR CE AC ∴===． tan QR BA C CR CA ==， 366528x -+∴=，152x ∴=． 综上所述，当x 为185或6或152时，PQR △为等腰三角形．4.解：（1）∵MN ∥BC ，∴∠AMN =∠B ，∠ANM ＝∠C ．∴ △AMN ∽ △ABC ．∴ AM AN AB AC =，即43x AN =． ∴ AN ＝43x ． ……………2分 ∴ S =2133248MNP AMN S S x x x ∆∆==⋅⋅=．（0＜x ＜4） ……………3分 （2）如图2，设直线BC 与⊙O 相切于点D ，连结AO ，OD ，则AO =OD =21MN ．在Rt △ABC 中，BC ＝22AB AC +=5．由（1）知 △AMN ∽ △ABC ．∴ AM MN AB BC =，即45x MN =． ∴ 54MN x =， ∴ 58OD x =． …………………5分 过M 点作MQ ⊥BC 于Q ，则58MQ OD x ==． 在Rt △BMQ 与Rt △BCA 中，∠B 是公共角，∴ △BMQ ∽△BCA ．∴ BM QM BC AC=． ∴ 55258324x BM x ⨯==，25424AB BM MA x x =+=+=．∴ x ＝4996． ∴ 当x ＝4996时，⊙O 与直线B C 相切．…………………………………7分故以下分两种情况讨论：① 当0＜x ≤2时，2Δ83x S y PMN ==． ∴ 当x ＝2时，2332.82y =⨯=最大 ……………………………………8分② 当2＜x ＜4时，设PM ，PN 分别交BC 于E ，F ．∵ 四边形AMPN 是矩形，∴ PN ∥AM ，PN ＝AM ＝x ．又∵ MN ∥BC ，∴ 四边形MBFN 是平行四边形．∴ FN ＝BM ＝4－x ．∴ ()424PF x x x =--=-．又△PEF ∽ △ACB ．∴ 2PEF ABC S PF AB S ∆∆⎛⎫= ⎪⎝⎭． ∴ ()2322PEF S x ∆=-． ……………………………………………… 9分 MNP PEF y S S ∆∆=-＝()222339266828x x x x --=-+-．……………………10分 当2＜x ＜4时，29668y x x =-+-298283x ⎛⎫=--+ ⎪⎝⎭． ∴ 当83x =时，满足2＜x ＜4，2y =最大． ……………………11分 综上所述，当83x =时，y 值最大，最大值是2． …………………………12分 5. 解：（1）（-4，-2）；（-m,-k m） (2) ①由于双曲线是关于原点成中心对称的，所以OP=OQ,OA=OB,所以四边形APBQ一定是平行四边形②可能是矩形，mn=k 即可不可能是正方形，因为Op 不能与OA 垂直.解：（1）作BE ⊥OA ，∴ΔAOB 是等边三角形∴BE=OB ·sin60o =23，∴B(23,2)∵A(0,4),设AB 的解析式为4y kx =+,所以2342k +=,解得33k =-,的以直线AB 的解析式为 343y x =-+（2）由旋转知，AP=AD, ∠PAD=60o, ∴ΔAPD 是等边三角形，PD=PA=2219AO OP +=6. 解：（1）作BE ⊥OA ，∴ΔAOB 是等边三角形∴BE=OB ·sin60o =23，∴B(23,2)∵A(0,4),设AB 的解析式为4y kx =+,所以2342k +=,解得33k =-, 以直线AB 的解析式为343y x =-+ （2）由旋转知，AP=AD, ∠PAD=60o ,∴ΔAPD 是等边三角形，PD=PA=2219AO OP +=（1）①2AB = ……………………………………………………………………………2分842OA ==，4OC =，S 梯形OABC =12 ……………………………………………2分 ②当42<<t 时，直角梯形OABC 被直线l 扫过的面积=直角梯形OABC 面积－直角三角开DOE 面积2112(4)2(4)842S t t t t =--⨯-=-+-…………………………………………4分（2） 存在 ……………………………………………………………………………………1分123458(12,4),(4,4),(,4),(4,4),(8,4)3P P P P P --- …（每个点对各得1分）……5分 对于第（2）题我们提供如下详细解答（评分无此要求）.下面提供参考解法二： ① 以点D 为直角顶点，作1PP x ⊥轴同理在③二图中分别可得P点的生标为P（－4，4）（与①情形二重合舍去）、P（4，4），E点在A点下方不可能.综上可得P点的生标共5个解，分别为P（－12，4）、P（－4，4）、P（－83，4）、P（8，4）、P（4，4）．下面提供参考解法二：以直角进行分类进行讨论（分三类）： 第一类如上解法⑴中所示图22P DE y x b ∠=+为直角：设直线：，D 此时（-b,o)，E(O,2b) 的中点坐标为b (-,b)2，直线DE 的中垂线方程：1()22by b x -=-+，令4y =得3(8,4)2b P -．由已知可得2PE DE =即222232(8)(42)42b b b b ⨯-+-=+化简得2332640b b -+=解得 121883b b P P ==∴=3b，将之代入（-8，4）（4，4)、22(4,4)P -；第二类如上解法②中所示图22E DE y x b ∠=+为直角：设直线：，D 此时（-b,o)，E(O,2b) ，直线PE 的方程：122y x b =-+，令4y =得(48,4)P b -．由已知可得PE DE =即2222(48)(42)4b b b b -+-=+化简得22(28)b b =-解之得 ，123443b b P P ==∴=，将之代入（4b-8，4）（8，4)、48(,4)3P - 第三类如上解法③中所示图22D DE y x b ∠=+为直角：设直线：，D 此时（-b,o)，E(O,2b) ，直线PD 的方程：1()2y x b =-+，令4y =得(8,4)P b --．由已知可得PD DE =即2222844b b +=+解得12544b b P P ==-∴=，将之代入（-b-8，4）（-12，4)、 6(4,4)P -（6(4,4)P -与2P 重合舍去）．综上可得P 点的生标共5个解，分别为P （－12，4）、P （－4，4）、P （－83，4）、 P （8，4）、P （4，4）．事实上，我们可以得到更一般的结论：如果得出AB a OC b ==、、OA h =、设b ak h-=，则P 点的情形如下∴ 6494738)2(7342+⎪⎭⎫ ⎝⎛--=-=⋅=x x x EF ME S MEFN矩形． ……………………8分当x ＝47时，ME ＝37＜4，∴四边形MEFN 面积的最大值为649．……………9分（3）能． ……………………………………………………………………10分 由（2）可知，设AE ＝x ，则EF ＝7－2x ，ME ＝x 34． 若四边形MEFN 为正方形，则ME ＝EF ． 即=34x 7－2x ．解，得 1021=x ． ……………………………………………11分 ∴ EF ＝21147272105x -=-⨯=＜4． ∴ 四边形MEFN 能为正方形，其面积为251965142=⎪⎭⎫ ⎝⎛=MEFNS 正方形． ∴ 6494738)2(7342+⎪⎭⎫ ⎝⎛--=-=⋅=x x x EF ME S MEFN矩形． ……………………8分当x ＝47时，ME ＝37＜4，∴四边形MEFN 面积的最大值为649．……………9分（3）能． ……………………………………………………………………10分 由（2）可知，设AE ＝x ，则EF ＝7－2x ，ME ＝x 34． 若四边形MEFN 为正方形，则ME ＝EF ． 即=34x 7－2x ．解，得 1021=x ． ……………………………………………11分 ∴ EF ＝21147272105x -=-⨯=＜4． ∴ 四边形MEFN 能为正方形，其面积为251965142=⎪⎭⎫ ⎝⎛=MEFN S 正方形．（2）当1t =时，过D 点作1DD OA ⊥，交OA 于1D ，如图1， 则53DQ QO ==，43QC =，1CD ∴=，(13)D ∴，．（3）①PQ 能与AC 平行．若PQ AC ∥，如图2，则OP OAOQ OC=， 即66233t t -=+，149t ∴=，而703t ≤≤， 149t ∴=． ②PE 不能与AC 垂直．若PE AC ⊥，延长QE 交OA 于F ，如图3，则23335t QF OQ QFAC OC +==．253QF t ⎛⎫∴=+ ⎪⎝⎭．EF QF QE QF OQ ∴=-=-22533t t ⎛⎫⎛⎫=+-+ ⎪ ⎪⎝⎭⎝⎭2(51)(51)3t =-+-．又Rt Rt EPF OCA △∽△，PE OCEF OA∴=， 6326(51)3t t -∴=⎛⎫-+ ⎪⎝⎭，3.45t ∴≈，而703t ≤≤，t ∴不存在．17. 解：（1）直线33y x =--与x 轴交于点A ，与y 轴交于点C ．(10)A ∴-，，(03)C -， ··························································································· 1分 点A C ，都在抛物线上，23033a c c ⎧=++⎪∴⎨⎪-=⎩ 333a c ⎧=⎪∴⎨⎪=-⎩∴抛物线的解析式为2323333y x x =-- ·························································· 3分 ∴顶点4313F ⎛⎫- ⎪ ⎪⎝⎭， ································································································ 4分 （2）存在 ················································································································ 5分 1(03)P -， ·············································································································· 7分2(23)P -， ·············································································································· 9分 （3）存在 ·············································································································· 10分 理由： 解法一：延长BC 到点B '，使BC B C '=，连接B F '交直线AC 于点M ，则点M 就是所求的点．····················································································· 11分在Rt BB H '△中，1232B H BB ''==， 36BH B H '==，3OH ∴=，(323)B '∴--， ·················································· 12分 设直线B F '的解析式为y kx b =+233433k b k b ⎧-=-+⎪∴⎨-=+⎪⎩ 解得36332k b ⎧=⎪⎪⎨⎪=-⎪⎩33362y x ∴=- ································································································· 13分 3333362y x y x ⎧=--⎪∴⎨=-⎪⎩ 解得371037x y ⎧=⎪⎪⎨⎪=-⎪⎩，310377M ⎛⎫∴- ⎪ ⎪⎝⎭，∴在直线AC 上存在点M ，使得MBF △的周长最小，此时310377M ⎛⎫- ⎪ ⎪⎝⎭，． ····· 14分03533k b b =+⎧⎪⎨=-⎪⎩ 解得539533k b ⎧=⎪⎪⎨⎪=-⎪⎩ 553393y ∴=- ································································································· 13分 55339333y x y x ⎧=-⎪∴⎨⎪=--⎩ 解得371037x y ⎧=⎪⎪⎨⎪=-⎪⎩310377M ⎛⎫∴- ⎪ ⎪⎝⎭， ∴在直线AC 上存在点M ，使得MBF △的周长最小，此时310377M ⎛⎫- ⎪ ⎪⎝⎭，． 1 18. 解：（1）点E 在y 轴上 ···················································································· 1分 理由如下：连接AO ，如图所示，在Rt ABO △中，1AB =，3BO =，2AO ∴=1sin 2AOB ∴∠=，30AOB ∴∠= 由题意可知：60AOE ∠=306090BOE AOB AOE ∴∠=∠+∠=+=点B 在x 轴上，∴点E 在y 轴上． ······································································· 3分（2）过点D 作DM x ⊥轴于点M1OD =，30DOM ∠=∴在Rt DOM △中，12DM =，32OM = 点D 在第一象限， ∴点D 的坐标为3122⎛⎫ ⎪ ⎪⎝⎭， ························································································ 5分 由（1）知2EO AO ==，点E 在y 轴的正半轴上∴点E 的坐标为(02)，∴点A 的坐标为(31)-， ·························································································· 6分 抛物线2y ax bx c =++经过点E ，2c ∴= 由题意，将(31)A -，，3122D ⎛⎫ ⎪ ⎪⎝⎭，代入22y ax bx =++中得33213312422a b a b ⎧-+=⎪⎨++=⎪⎩ 解得89539a b ⎧=-⎪⎪⎨⎪=-⎪⎩∴所求抛物线表达式为：2853299y x x =--+ ······················································ 9分 （3）存在符合条件的点P ，点Q ． ······································································ 10分 理由如下：矩形ABOC 的面积3AB BO ==∴以O B P Q ，，，为顶点的平行四边形面积为23．由题意可知OB 为此平行四边形一边， 又3OB =OB ∴边上的高为2 ································································································ 11分依题意设点P 的坐标为(2)m ， 点P 在抛物线2853299y x x =--+上 28532299m m ∴--+= 解得，10m =，2538m =-1(02)P ∴，，25328P ⎛⎫- ⎪ ⎪⎝⎭，以O B P Q ，，，为顶点的四边形是平行四边形，PQ OB ∴∥，3PQ OB ==，∴当点1P 的坐标为(02)，时， 点Q 的坐标分别为1(32)Q -，，2(32)Q ，；当点2P 的坐标为5328⎛⎫- ⎪ ⎪⎝⎭，时，点Q 的坐标分别为313328Q ⎛⎫-⎪ ⎪⎝⎭，，43328Q ⎛⎫ ⎪ ⎪⎝⎭，． ·············································· 14分 （以上答案仅供参考，如有其它做法，可参照给分）19.解：（1）在2334y x =-+中，令0y = 23304x ∴-+=12x ∴=，22x =-(20)A ∴-，，(20)B ， ··················································· 1分 又点B 在34y x b =-+上 302b ∴=-+ 32b = BC ∴的解析式为3342y x =-+ ················································································ 2分 （2）由23343342y x y x ⎧=-+⎪⎪⎨⎪=-+⎪⎩，得11194x y =-⎧⎪⎨=⎪⎩ 2220x y =⎧⎨=⎩ ······················································· 4分 914C ⎛⎫∴- ⎪⎝⎭，，(20)B ， 4AB ∴=，94CD = ································································································ 5分 1994242ABC S ∴=⨯⨯=△ ··························································································· 6分 （3）过点N 作NP MB ⊥于点PEO MB ⊥NP EO ∴∥BNP BEO ∴△∽△ ································································································· 7分 BN NP BE EO∴= ··········································································································· 8分 由直线3342y x =-+可得：302E ⎛⎫ ⎪⎝⎭，∴在BEO △中，2BO =，32EO =，则52BE = 25322t NP ∴=，65NP t ∴= ························································································· 9分 16(4)25S t t ∴=- 2312(04)55S t t t =-+<< ······················································································ 10分 2312(2)55S t =--+ ······························································································· 11分 此抛物线开口向下，∴当2t =时，125S =最大 ∴当点M 运动2秒时，MNB △的面积达到最大，最大为125． 20. 解：（1）如图，过点B 作BD ⊥OA 于点D.在Rt △ABD 中，∵∣AB ∣=35,sin ∠OAB=55, ∴∣BD ∣=∣AB ∣·sin ∠OAB =35×55=3. 又由勾股定理，得22A D AB B D =- 22(35)36=-=∴∣OD ∣=∣OA ∣-∣AD ∣=10-6=4.∵点B 在第一象限，∴点B 的坐标为（4，3）. ……3分。

【2013 •北京• 24题】在厶ABC 中，AB=AC ，/ BAC a (0°VaV 60°,将线段 BC 绕点B 逆时针旋转60°得到 线段BD 。

(1) 如图1,直接写出/ ABD 的大小(用含 a 的式子表示)；(2) 如图2,Z BCE=150，/ ABE=60，判断△ ABE 的形状并加以证明;(3) 在(2)的条件下，连接 DE ,若/ DEC=45，求a 的值。

解:(1)AB=AC •/ BC=BD/ ABC= / ACB• △ ABD ◎△ EBC(AAS ) / BAC+ / ABC+ / ACB=180，/ BAC= a • AB=EB1/ ABC=90 ——a•△ ABE 是等腰三角形2•••/ ABE=60/ ABC= / ABD+ / DBC ，且/ DBC=604• △ ABE 是等边三角形1/ ABD=30 ——a(3)vZ BCE=150，/ BCD=60连接AD 、 CD 、ED 。

DEC=45•/ BC=BD ，/ DBC=60DCE 是等腰直角三角形是等边三角形•CE=CD •BD=CD •/ BC=CD•/ AB=AC,AD=AD•BC=CE•••由⑵知，/ CBE=301BEC= a2/ ACD= / ABD=30• 30° -2/ DBC=60• / DBE+ / ABD= / DBE+ / CBE • / CBE= / ABD=30 - - a2•••/ BCE=150• / BEC=180 - / BCE- / CBE= 1 a2• / BEC= / BAD= 1 a2【2013 •北京• 25题】对于平面直角坐标系 xOy 中的点P 和O C ,给出如下定义：若O C 上存在两个点 A 、B ,11使得/ APB=60，则称P 为O C 的关联点。

已知点 DE ( 0, -2),F (2 J3 , 0)22(1 )当0 O 的半径为1时，① 在点D 、E 、F 中，O O 的关联点是 ________________② 过点F 作直线I 交y 轴正半轴于点 G ,使/ GFO=30，若直线I 上的点P (m , n )是O O 的关联点，求 m 的取值范围； (2)若线段EF 上的所有点都是某个圆的关联点，求这个圆的半径r 的取值范围。