opengl 图形的变换与裁剪

《计算机图形学实验》报告任课教师：钱文华2016年春季学期实验:梁友栋裁剪实验时间：2016年11月17日实验地点：信息学院2204实验目的：掌握梁友栋裁剪程序代码：#include <stdio.h>#include <glut.h>#include <stdlib.h>#include <math.h>class wcPt2D{public:GLfloat x,y;void setCoords(GLfloat xCoord,GLfloat yCoord){x=xCoord;y=yCoord;}GLfloat getx() const{return x;}GLfloat gety() const{return y;}};inline GLint round(const GLfloat a){return GLint(a+0.5);}void setPixel(int x,int y){glBegin(GL_POINTS);glVertex2i(x,y);glEnd();}void init(){glClearColor(1.0,1.0,1.0,0.0);glMatrixMode (GL_PROJECTION);gluOrtho2D(-200.0,200.0,-200.0,200.0);}void lineBres(GLfloat x0,GLfloat y0,GLfloat xEnd,GLfloat yEnd){ int dx = fabs(xEnd - x0),dy = fabs(yEnd - y0);int p = 2*dy - dx;int twoDy = 2*dy,twoDyMinusDx = 2*(dy - dx);int x,y;if(x0>xEnd){x = xEnd;y = yEnd;xEnd = x0;}else{x = x0;y = y0;}setPixel(x,y);while(x<xEnd){x++;if(p<0)p+=twoDy;else{y++;p+=twoDyMinusDx;}setPixel(x,y);}}GLint clipTest(GLfloat p,GLfloat q,GLfloat *u1,GLfloat *u2){ GLfloat r;GLint returnValue = true;if(p<0.0){r = q/p;if(r>*u2)returnValue = false;elseif(r>*u1)*u1 = r;}elseif(p>0.0){r = q/p;if(r<*u1)returnValue = false;else if(r<*u2)*u2 = r;}elseif(q<0.0)returnValue = false;return(returnValue);}void lineClipLiangBarsk(wcPt2D winMin,wcPt2D winMax,wcPt2D p1,wcPt2D p2){GLfloat u1 = 0.0,u2 = 1.0,dx = p2.getx()-p1.getx(),dy;GLfloat x1 = p1.getx(),y1 = p1.gety();GLfloat x2 = p2.getx(),y2 = p2.gety();if(clipTest(-dx,p1.getx()-winMin.getx(),&u1,&u2))if(clipTest(dx,winMax.getx()-p1.getx(),&u1,&u2)){dy = p2.gety()-p1.gety();if(clipTest(-dy,p1.gety()-winMin.gety(),&u1,&u2)){if(clipTest(dy,winMax.gety()-p1.gety(),&u1,&u2)){if(u2<1.0){p2.setCoords(p1.getx()+u2*dx,p1.gety()+u2*dy);}if(u1>0.0){p1.setCoords(p1.getx()+u1*dx,p1.gety()+u1*dy);}glColor3f(0.0,0.0,0.0);lineBres(x1,y1,p1.getx(),p1.gety());lineBres(p2.getx(),p2.gety(),x2,y2);glColor3f(1.0,0.0,0.0);lineBres(p1.getx(),p1.gety(),p2.getx(),p2.gety());}}else{glColor3f(0.0,0.0,0.0);lineBres(x1,y1,x2,y2);}}}void displayliangyoudongcaijian(){glClear(GL_COLOR_BUFFER_BIT);glLineWidth(5.0);glColor3f(0.0,0.0,0.0);glBegin(GL_LINE_LOOP);glVertex2i(100,100);glVertex2i(100,-100);glVertex2i(-100,-100);glVertex2i(-100,100);glEnd();glPointSize(4);wcPt2D test1[4] = {{-100.0,-100.0},{100.0,100.0},{-150.0,-200.0},{200.0,120.0}};wcPt2D test2[4] = {{-100.0,-100.0},{100.0,100.0},{-150.0,-120.0},{0.0,0.0}};wcPt2D test3[4] = {{-100.0,-100.0},{100.0,100.0},{-50.0,50.0},{150.0,150.0}};wcPt2D test4[4] = {{-100.0,-100.0},{100.0,100.0},{-50.0,0.0},{60.0,50.0}};wcPt2D test5[4] = {{-100.0,-100.0},{100.0,100.0},{-170.0,-200.0},{200.0,-120.0}};lineClipLiangBarsk(test1[0],test1[1],test1[2],test1[3]);lineClipLiangBarsk(test2[0],test2[1],test2[2],test2[3]);lineClipLiangBarsk(test3[0],test3[1],test3[2],test3[3]);lineClipLiangBarsk(test4[0],test4[1],test4[2],test4[3]);lineClipLiangBarsk(test5[0],test5[1],test5[2],test5[3]);glFlush();}void main(int argc, char* argv[]){glutInit(&argc,argv);glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);glutInitWindowPosition(50,100);glutInitWindowSize(400,300);glutCreateWindow("梁友栋裁剪算法");init();glutDisplayFunc(displayliangyoudongcaijian);glutMainLoop();}实验结果：。

gltranslatef函数
glTranslatef函数是一种OpenGL图形系统提供的基本函数，它的作用是改变图形的位置。

它接受三个参数，分别是X轴、Y轴和Z 轴的转换值。

它可以实现3D图形的平移操作，也可以用于2D图形的平移操作。

glTranslatef函数的一般语法如下：
glTranslatef (x, y, z);
其中，参数x,y,z是位移的量，表示在X,Y,Z轴上平移的距离。

glTranslatef函数可以用来实现对图形对象统一的平移操作，这样可以减少程序的开发和调试工作量，更加便捷。

同时，也可以用来在3D世界中实现物体的移动。

例如，要将一个物体平移到另一个位置，可以使用glTranslatef函数来实现，传递参数x,y,z表示物体在X，Y，Z轴上的位移。

在OpenGL中，图形的变换操作（包括缩放、旋转、平移等）都是以矩阵形式进行操作的。

在调用glTranslatef函数时，系统会使用一个4x4的矩阵来改变图形的位置，矩阵的第4列的四个元素就是glTranslatef传入的参数x,y,z。

glTranslatef函数是OpenGL中非常重要的一个函数，它可以实现最基本的平移操作：x，y，z轴上的位移。

同时，它也可以用于实现3D世界中物体移动的操作，因此，glTranslatef函数在OpenGL
图形系统中十分重要，也是非常常用的函数。

- 1 -。

计算机图形学实验报告
在计算机图形学课程中，实验是不可或缺的一部分。

通过实验，我们可以更好地理解课程中所学的知识，并且在实践中掌握这些
知识。

在本次实验中，我学习了如何使用OpenGL绘制三维图形，并了解了一些基本的图形变换和视图变换。

首先，我们需要通过OpenGL的基本命令来绘制基本图形，例
如线段、矩形、圆等。

这些基本的绘制命令需要首先设置OpenGL 的状态，例如绘制颜色、线段宽度等，才能正确地绘制出所需的
图形。

然后，在实验中我们学习了图形的变换。

变换是指通过一定的
规则将图形的形状、位置、大小等进行改变。

我们可以通过平移、旋转、缩放等变换来改变图形。

变换需要按照一定的顺序进行，
例如先进行旋转再进行平移等。

在OpenGL中，我们可以通过设
置变换矩阵来完成图形的变换。

变换矩阵包含了平移、旋转、缩
放等信息，通过矩阵乘法可以完成图形的复合变换。

最后，视图变换是指将三维场景中的图形投影到二维平面上，
成为我们所见到的图形。

在实验中，我们学习了透视投影和正交
投影两种方式。

透视投影是指将场景中的图形按照视点不同而产
生不同的远近缩放，使得图形呈现出三维感。

而正交投影则是简单地将场景中的图形按照平行投影的方式呈现在屏幕上。

在OpenGL中，我们可以通过设置视图矩阵和投影矩阵来完成视图变换。

通过本次实验，我对于计算机图形学有了更深入的了解，并掌握了一些基本的图形绘制和变换知识。

在今后的学习中，我将继续学习更高级的图形绘制技术，并应用于实际的项目中。

深入分析OpenGL实现原理与优化方法OpenGL是一种广泛应用于计算机图形学领域的开源API。

它提供了一套用于绘制三维图像的工具包，既可以在桌面应用中使用，也可以在移动应用和Web应用中使用。

OpenGL使用C语言编写，并允许程序员自定义实现方法，以满足不同需求。

OpenGL的工作原理OpenGL的工作基于两个基本概念：渲染管道和状态机。

渲染管道指的是将输入的图形数据转换成最终显示在屏幕上的像素的处理过程。

渲染管道包括：顶点处理、几何处理、光栅化和片元处理。

状态机将OpenGL的状态分为多个状态，能够按照需要切换不同的状态，从而控制OpenGL的一些行为，如深度测试、剔除等。

OpenGL的工作流程为：先将图形数据通过顶点处理器进行处理，再经过几何处理器处理为顶点可能需要的形式，并进行坐标映射和变换处理等。

接下来，OpenGL对形状进行光栅化，将每个点转换为一个像素点，并对特定区域进行操作。

最后，将特定的像素点按照一定的顺序绘制出来，形成最终的图像。

OpenGL的性能优化方法OpenGL的性能直接影响着三维场景的流畅体验。

在实际应用中，处理逻辑复杂的三维场景时，需要使用一些优化方法来提高OpenGL的性能。

1. 缩小绘制范围绘制的范围越小，执行的次数就越少，能够显著提高OpenGL 的性能。

因此，需要保证只绘制可见的图像区域，同时尽可能少绘制不可见区域。

2. 减少光照计算光照处理需要很大的计算量，影响OpenGL性能。

可以通过一些技巧，如减少光源的数量，简化物体材质等方式减少光照计算量。

3. 减少纹理数量和大小OpenGL需要消耗大量的内存来维护纹理，特别是在绘制大型场景时，如果每个物体都使用高质量的纹理，会占用大量内存和处理时间。

因此，可以通过降低纹理质量或减少纹理数量来优化OpenGL的性能。

4. 合并绘制在绘制物体时，可以合并相邻的物体，以减少绘制次数，提高OpenGL的性能。

5. 使用缓存在OpenGL中，使用缓存可以减少CPU与GPU之间的数据传输时间，提高性能。

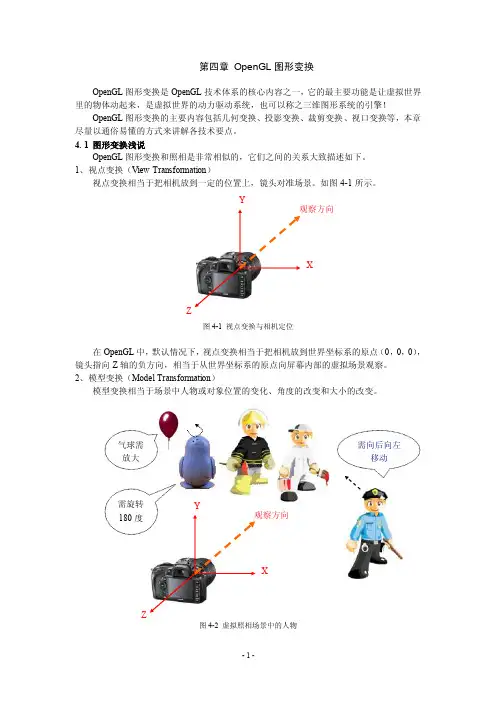
第四章 OpenGL 图形变换OpenGL 图形变换是OpenGL 技术体系的核心内容之一，它的最主要功能是让虚拟世界里的物体动起来，是虚拟世界的动力驱动系统，也可以称之三维图形系统的引擎！OpenGL 图形变换的主要内容包括几何变换、投影变换、裁剪变换、视口变换等，本章尽量以通俗易懂的方式来讲解各技术要点。

4. 1 图形变换浅说OpenGL 图形变换和照相是非常相似的，它们之间的关系大致描述如下。

1、视点变换（View Transformation ） 视点变换相当于把相机放到一定的位置上，镜头对准场景。

如图4-1所示。

图4-1 视点变换与相机定位在OpenGL中，默认情况下，视点变换相当于把相机放到世界坐标系的原点（0，0，0），镜头指向Z轴的负方向，相当于从世界坐标系的原点向屏幕内部的虚拟场景观察。

2、模型变换（Model Transformation）模型变换相当于场景中人物或对象位置的变化、角度的改变和大小的改变。

图4-2 虚拟照相场景中的人物YXZ观察方向X照相时场景中的人物或对象需要作调整，以便他们位于场景中合适的位置上。

有此时候人物不在视野范围内时，还要走动一下，进入镜头场景内，方向不对时，还要转动一下，眼睛转向镜头。

比如图4-2所示，照相时，警察不在镜头场景内，他需要向后向移动。

中间的企鹅背对镜头，他需要转过向来面向镜头。

企鹅向左边的气球中吹气，气球变大。

调整后的场景如图4-3所示。

图4-3 虚拟照相场景中的调整后人物或对象上述调整过程中的人员移动 和企鹅的转身动作 和气球充气变大 都属于模型变换。

3、投影变换（Projection Transformation ） 投影变换相当于调整相机镜头焦距，放大或缩小景物（如图4-4所示）。

图4-4 投影变换与相机焦距调整OpenGL 中投影变换的本质功能是定义一个视景体，使视景体外的多余部分被裁剪掉，再把景物变换到一个规则投影体（高、宽、深均为2个单位的立方体）。

计算机图形学的裁剪算法
计算机图形学的裁剪算法是图形学的一种重要算法，它的基本思想是将一个完整的几何图形（如线段、多边形、圆圈等）按照指定的裁剪窗口（矩形）进行裁剪，只保留在窗口内的部分，而把窗口外的部分抛弃掉。

由于裁剪算法的应用非常广泛，像图形显示系统、图形设备接口（GDI）和图形处理器（GPU）等都广泛使用裁剪算法。

计算机图形学的裁剪算法可以分为两种：2D裁剪算法和
3D裁剪算法。

2D裁剪算法是基于二维空间的，它将一个几何
图形投影到一个平面上，然后按照指定的窗口裁剪；而3D裁
剪算法是基于三维空间的，它将一个几何图形投影到一个三维空间，然后按照指定的窗口裁剪。

2D裁剪算法的基本步骤如下：首先，将要裁剪的几何图
形投影到平面上；其次，计算出投影后的几何图形以及裁剪窗口之间的交点；最后，将裁剪窗口内的部分保留，而把窗口外的部分抛弃掉。

3D裁剪算法的基本步骤如下：首先，将要裁剪的几何图
形投影到三维空间；其次，计算出投影后的几何图形以及裁剪窗口之间的交点；最后，将裁剪窗口内的部分保留，而把窗口外的部分抛弃掉。

计算机图形学的裁剪算法在图形处理中有着重要的作用，它不仅能够有效减少图形处理时间，而且还可以节约存储空间。

此外，它还可以有效提高图形处理效率，提高图形显示效果。

但是，它也存在着一定的局限性，比如，当几何图形的运动变得复杂时，它就会变得费时费力，这就对性能产生了一定的影响。

总之，计算机图形学的裁剪算法是图形学的重要算法，它的应用非常广泛，在图形处理中有着重要的作用。

虽然它也存在着一定的局限性，但是它仍然是一种有效的图形处理算法。

高级图形图像第一次实验报告一、实验描述以及关键步骤1.opengl编程环境组建(基于VC6.0)1)下载opengl开发库文件夹；2)复制glut32.dll和glut.dll到…\windows\system32；3)复制glut.h到...\Microsoft Visual Studio\VC98\Include\GL；4)复制glut32.lib和glut.lib到…\Microsoft Visual Studio\VC98\Lib；5)新建工程后，进入Project菜单，选Settings项，弹出 Settings 对话框，选Link项，在 Libraries 栏目中加入OpenGL库：opengl32.lib glu32.lib glaux.lib。

2.基本图形绘制首先运行一个Windows环境下的一个基本OpenGL程序，直接打开60version文件夹内的工程，它将显示一个空的OpenGL窗口,可以在定制窗口大小和全屏模式下切换（按F1）,按ESC退出，该程序为以后的应用程序提供了实验平台，并预留了绘图接口。

根据教材P67-70，了解绘制函数，根据附件2提供的源码baseshape.cpp，将该文件内的场景绘制函数Drawsence()替代空窗口程序中的同名函数，修改图形绘制命令和参数，显示出点、线、矩形、三角形等，可设置不同线宽。

3.图形的二维变换根据附件3提供源码，将该文件内的场景绘制函数Drawsence()替代空窗口程序中的同名函数，通过调用glTranslate*, glRotate*,glscale*等二维变换函数实现平移、旋转、缩放等变换，通过参数操作和矩阵操作两种方式执行。

glTranslatef：在opengl中，函数glTranslatef的作用就是移动坐标原点。

glRotatef：glRotatef( angle, x, y, z )函数的作用是将当前坐标系以a( x, y, z )向量为旋转轴旋转angle角度，满足右手法则，即沿着右手握拳时四个手指指向的方向旋转。

OpenGL图形变换OpenGL图形软件包是为三维应用设计的，其中包含了大量的有关三维变换的操作，二维变换则可以看作是三维变换的特例。

OpenGL中常用的变换包括模型视图变换、投影变换和视见区变换。

一、矩阵堆栈在计算机图形学中，所有的变换都是通过矩阵乘法来实现的，即将三维形体顶点构成的齐次坐标矩阵乘以三维变换矩阵就得到了变换后的形体顶点的齐次坐标矩阵，这样只要求出形体的三维变换矩阵，就可以得到变换后的形体。

在OpenGL中，对象的坐标变换也是通过矩阵来实现的。

OpenGL中包含了两个重要的矩阵：模型视图矩阵和投影矩阵，其中模型视图矩阵用于物体的模型视图变换，投影矩阵用于投影变换。

一般来说，在进行矩阵操作之前，需要指定当前操作的矩阵对象，这可以使用函数：glMatrixMode（GLenum mode）；定义。

其中当mode取GL_MODELVIEW时，表示对模型视图矩阵进行操作；当mode取GL_PROJECTION时表示对投影矩阵进行操作，并且一旦设置了当前操作矩阵，它就将保持为当前的矩阵对象，直到再次调用函数glMatrixMode修改它为止。

默认情况下，系统处理的当前矩阵是模型视图矩阵。

OpenGL为模型视图矩阵和投影矩阵各维护着一个“矩阵堆栈”，其中堆栈的栈顶矩阵就是当前的模型视图矩阵或投影矩阵。

在调用变换函数的时候，系统自动计算变换函数对应的变换矩阵与当前操作的矩阵堆栈栈顶矩阵的乘积，并置为栈顶矩阵，绘制图形时使用栈顶矩阵作为图形的变换矩阵。

矩阵堆栈主要用来保存和恢复矩阵的状态。

OpenGL中利用函数：void glPushMatrix（void）；void glPopMatrix（void）；实现矩阵堆栈的操作。

其中函数glPushMatrix将当前矩阵堆栈的栈顶矩阵复制一个，并将其压入当前矩阵堆栈，以保存当前变换矩阵。

函数glPopMatrix用于将当前矩阵堆栈的栈顶矩阵弹出，这样，堆栈中的下一个矩阵变为栈顶矩阵（当前变换矩阵），用来恢复当前变换矩阵原先的状态。

逆变换和模拟变换几何处理管线擅长使用视图和投影矩阵以及用于裁剪的视口把顶点的世界（物体）坐标变换为窗口（屏幕）坐标。

但是，在有些情况下，需要反转这个过程。

一种常见的情形就是应用程序的用户利用鼠标选择了三维空间中的一个位置。

鼠标只返回一个二维值，也就是鼠标光标的屏幕位置。

因此，应用程序必须反转变换过程，确定这个屏幕位置源于三维空间的什么地方。

OpenGL工具函数库中gluUnProject()和gluUnProject4()函数用于执行这种逆变换操作。

只要提供一个经过变换的顶点的三维窗口坐标以及所有对它产生影响的变换，gluUnProject()就可以返回这个顶点的源物体坐标。

如果深度范围不是默认的[0, 1]，应该使用gluUnProject4()函数。

int gluUnProject(GLdouble winx, GLdouble winy, GLdouble winz,const GLdouble modelMatrix[16],const GLdouble projMatrix[16],const GLint viewport[4],GLdouble *objx, GLdouble *objy, GLdouble *objz);这个函数使用由模型视图矩阵（modelMatrix）、投影矩阵（projMatrix）和视口（viewpo rt）定义的变换，把指定的窗口坐标（winx, winy, winz）映射到物体坐标。

它产生的物体坐标是在o bjx、objy和objz中返回的。

这个函数返回GL_TRUE（表示成功）或GL_FALSE（表示失败，例如矩阵不可逆）。

这个函数并不会使用视口对坐标进行裁剪，也不会消除那些位于glDepthRange()范围之外的深度值。

对变换过程进行逆操作存在一些固有的难度。

二维屏幕上的一个位置可以来自于三维空间中一条直线上的任意一点。

为了消除这种歧义，gluUnProject()要求提供一个窗口深度坐标（win z），它是根据glDepthRange()函数指定的。

OpenGL ES总结（二）OpenGL坐标变换之平移及旋转世界坐标系：在OpenGL中，世界坐标系是以屏幕中心为原点(0, 0, 0)，且是始终不变的。

你面对屏幕，你的右边是x正轴，上面是y正轴，屏幕指向你的为z正轴。

长度单位这样来定：窗口范围按此单位恰好是(-1,-1)到(1,1)，即屏幕左下角坐标为（-1，-1），右上角坐标为（1,1）。

当前绘图坐标系：是绘制物体时的坐标系。

程序刚初始化时，世界坐标系和当前绘图坐标系是重合的。

当用glTranslatef()，glScalef(), glRotatef()等对当前绘图坐标系进行平移、伸缩、旋转变换之后，世界坐标系和当前绘图坐标系不再重合。

注意，这里的平移旋转是将当前绘图坐标系看做一个整体在世界坐标系中进行旋转平移。

然后，改变以后，再用glVertex3f()等绘图函数绘图时，都是在当前绘图坐标系进行绘图，所有的函数参数也都是相对当前绘图坐标系来讲的。

其中四种坐标经常要在程序中用到：世界坐标，物体坐标，设备坐标和眼坐标。

1、世界坐标是OpenGL中用来描述场景的坐标，Z+轴垂直屏幕向外，X+从左到右，Y+轴从下到上，是右手笛卡尔坐标系统。

我们用这个坐标系来描述物体及光源的位置。

将物体放到场景中也就是将物体平移到特定位置、旋转一定角度，这些操作就是坐标变换。

OpenGL中提供了glTranslate*/glRotate*/glScale*三条坐标变换命令，利用OpenGL的矩阵运算命令，则可以实现任意复杂的坐标变换。

OpenGL中有一个坐标变换矩阵栈(ModelView)，栈顶就是当前坐标变换矩阵，进入OpenGL 管道的每个坐标(齐次坐标)都会先乘上这个矩阵，结果才是对应点在场景中的世界坐标。

OpenGL中的坐标变换都是通过矩阵运算完成的，与图形学课本的描述完全一致。

要注意的是变换中的矩阵乘法是左乘，而矩阵乘法与算术乘法不同，不符合交换律(万一不明白去看矩阵代数书好了)。

OpenGL中旋转平移缩放等变换的顺序对模型的影响
l 前提：
0x01. 假设绘制顶点的语句为Draw Array，变换的语句（旋转、平移、缩放）为M，⽽
M0;
M1;
M2;
Draw Array;
则称对Array先进⾏M2再进⾏M1、M0
0x02. 本⽂基于SharpGL版本的OpenGL(C#版本)
l 预备知识：
0x01. gl.Rotate是按照右⼿系来计算的，即设旋转轴为⼤拇指⽅向，则从指跟到指尖的⽅希为正⽅向。

0x02. gl.Scale 会改变法向量的值，从⽽会对颜⾊有影响。

通过gl.Enable(OpenGL.GL_NORMALIZE)或者
gl.Disable(OpenGL.GL_LIGHTING)可消除其影响。

l 实验
0x01. 先gl.Rotate(0,0,90)，再gl.Translate(100,0,0)：可见旋转不影响坐标系的⽅向，旋转后平移的⽅向和原坐标系⽅向相同
0x02. 先gl.Scale(0.5, 0.5, 0.5),再gl.Translate(100, 0, 0)：可见放缩不会影响平移的长度，其长度和原坐标系长度保持⼀致
0x03. 先gl.Scale(0.5, -0.5, 0.5)，再gl.Rotate(0, 0, -90)：可见放缩放值为负值，形成轴对称的情形下，旋转的⽅向还是原坐标系中旋转的⽅向
0x04. 先gl.Translate(100, 0, 0)，再gl.Scale(0.5, -0.5, 0.5)，再gl.Rotate(0, 0, -90)：旋转和缩放都是在原坐标系下进⾏的
l 总结
⽆论进⾏说明转换操作，都不会改变原坐标系，⽽后续的转换操作也都是基于原坐标系进⾏的。

实验3OpenGL几何变换1.实验目的理解并掌握O penGL二维平移、旋转、缩放变换的方法。

2.实验内容(1)阅读实验原理,运行示范实验代码,掌握0penGL程序平移、旋转、缩放变换的方法。

(2)根据示范代码,完成实验作业。

3.实验原理(1)OpenGL下的几何变换在OpenGL的核心库中,每一种几何变换都有一个独立的函数,所有变换都在三维空间中定义。

平移矩阵构造函数为glTranslate<f,d>(t x,ty,tz),作用是把当前矩阵和一一个表示移动物体的矩阵相乘。

t x、 ty、 tz指定这个移动物体的矩阵,它们可以是任意的实数值,后缀为f (单精度浮点fl oat)或d(双精度浮点double),对于二维应用来说, tz=0.0。

旋转矩阵构造函数为glRotate<f,d>(theta, vx, vy, vz),作用是把当前矩阵和一个表示旋转物体的矩阵相乘。

theta, vx, vy, vz指定这个旋转物体的矩阵,物体将围绕(0,0,0)到(x,y,z) 的直线以逆时针旋转, 参数theta表示旋转的角度.向量 v=(v x,vy,vz)的分量可以是任意的实数值,该向量用于定义通过坐标原点的旋转轴的方向,后缀为 f(单精度浮点f l oat)或d (双精度浮点double),对于二维旋转来说, vx=0.0, vy=0.0, vz=1.0。

缩放矩阵构造函数为glScale<f,d>(sx, sy, sz),作用是把当前矩阵和一个表示缩放物体的矩阵相乘。

sx, sy, sz指定这个缩放物体的矩阵,分别表示在x, y, z方向上的缩放比例, 它们可以是任意的实数值,当缩放参数为负值时,该函数为反射矩阵,缩放相对于原点进行,后缀为 f(单精度浮点fl oat)或d(双精度浮点double)。

注意这里都是说“把当前矩阵和一个表示移动<旋转, 缩放>物体的矩阵相乘”, 而不是直接说“这个函数就是旋转”或者“这个函数就是移动”,这是有原因的, 马上就会讲到。

OpenGL的空间变换（下）：空间变换通过本⽂的上篇，我们了解到矩阵的基础概念。

并且掌握了矩阵在空间⼏何中的应⽤。

接下来，我们将结合矩阵来了解 OpenGL 的空间变换。

在使⽤ OpenGL 的应⽤程序中，当我们指定了模型的顶点后，顶点依次会变换到不同的 OpenGL 空间中：世界空间模型空间（也称为对象空间）视图空间（也称为视点空间、摄像机空间）裁剪空间标准设备坐标空间窗⼝空间在经过这⼀系列的空间变换之后，顶点才会被显⽰在屏幕上。

世界空间（World Space）世界空间相对于其他坐标空间来说是固定不变的。

所以，它也被⽤作空间变换的参考系。

我们把它的坐标系称为世界坐标系。

在没有特别说明的情况下，我们⽤来描述⼀个⼏何对象（点、向量或坐标）的数值数据，都是基于世界坐标系来设定的。

世界坐标系⽤矩阵来表⽰就是⼀个单位矩阵。

模型空间（Model Space）模型空间，也称为对象空间。

如果把世界空间⽐作现实世界的话，那么模型就好⽐⼀座房⼦或者房⼦⾥的⼀个⼈等等。

假设以⼈的重⼼为原点，正⾯向前的⽅向为 z-轴，头顶的⽅向为 y-轴，左侧⽅向为 x-轴来构建⼀个坐标系。

我们可以⽤这个坐标系来描述这个⼈⾃⾝的模型空间。

这个坐标系也称为模型坐标系（或对象坐标系）。

模型坐标系并不是绝对的，如果以⼈的⿐尖为原点，头顶的⽅向改为 z-轴，正⾯向前的⽅向为 y-轴，右侧⽅向为 z-轴来构建其模型坐标系。

这个模型坐标系同样可以⽤来描述这个⼈⾃⾝的模型空间。

只不过⽤不同坐标系来描述时，描述出来的数据不⼀定相同。

⼀般来说，我们都是基于世界坐标系来描述模型坐标系的。

在这种情况下，世界坐标系可以看作是模型坐标系的⽗坐标系：其中，⿊⾊的坐标系为世界坐标系；灰⾊的坐标系为模型坐标系。

模型变换（模型-世界变换）默认情况下模型坐标系的原点位于世界坐标系的原点，并且坐标轴的⽅向与世界坐标系的坐标轴⼀致。

我们可以通过⼀系列的缩放、旋转和*移，将模型以任意⾓度摆在任意位置上。

glViewport()和glOrtho()的理解-OpenGL在OpenGL中有两个比较重要的投影变换函数，glViewport和glOrtho.ortho实际上是orthographic projection正交投影的缩写。

glViewport是视口变换它是设置视口，它设置的视口的左下角，以及宽度和高度。

glOrtho是窗口变换，设置的是世界窗口俗称窗口。

二维绘图来说世界窗口由gluOrth2D(GLdouble left, GLdouble right, GLdouble bottom, GLdouble top)设定。

三维绘图的世界窗口由glOrtho(left, right, bottom, top, near, far)设定。

glOrtho是创建一个正交平行的视景体。

一般用于物体不会因为离屏幕的远近而产生大小的变换的情况。

比如，常用的工程中的制图等。

需要比较精确的显示。

而作为它的对立情况, glFrustum则产生一个透视投影。

这是一种模拟真是生活中，人们视野观测物体的真实情况。

例如：观察两条平行的火车到，在过了很远之后，这两条铁轨是会相交于一处的。

还有，离眼睛近的物体看起来大一些，远的物体看起来小一些。

glOrtho(left, right, bottom, top, near, far)， left表示视景体左面的坐标，right表示右面的坐标，bottom表示下面的，top表示上面的。

这个函数简单理解起来，就是一个物体摆在那里，你怎么去截取他。

这里，我们先抛开glViewport函数不看。

先单独理解glOrtho的功能。

假设有一个球体，半径为1，圆心在(0, 0, 0)，那么，我们设定glOrtho(-1.5, 1.5, -1.5, 1.5, -10, 10);就表示用一个宽高都是3的框框把这个球体整个都装了进来。

如果设定glOrtho(0.0, 1.5, -1.5, 1.5, -10, 10);就表示用一个宽是1.5，高是3的框框把整个球体的右面装进来;如果设定glOrtho(0.0, 1.5, 0.0, 1.5, -10, 10)；就表示用一个宽和高都是1.5的框框把球体的右上角装了进来。