当前位置：文档之家 › 二次函数的图像和性质PPT课件

二次函数的图像和性质PPT课件

  • 格式：ppt
  • 大小：1.00 MB
  • 文档页数：17

下载文档原格式

  / 17

合集下载

二次函数的图像和性质(共82张PPT)

二次函数的图像和性质(共82张PPT)

y＝ax2
向上
y轴 (0，0)
向下
y轴 (0，0)
4、二次函数y＝2x2＋1的图象与二次函数y＝
2x2的图象开口方向、对称轴和顶点坐标是否相
同?它们有什么关系？我们应该采取什么方法
来研究这个问题？
画出函数y＝2x2和函数y＝ 2x2+1的图象， 并加以比较
x … –1.5 –1 –0.5 0 0.5 1 1.5 …
y 1 x2 ··· 2
8
4.5
2 0.5 0 0.5 2 4.5
8
···
x
·· －2 －1.5 －1 －0.5 0 0.5 1 1.5 2 ···
y 2x2 · 8 4.5 2 0.5 0 0.5 2 4.5 8
·· ·
y y x2 8
y 2x2
···
6
y 1 x2
4
2
2
－4
－2 O
24
在对称轴左侧,y都随x的增大而增大,
在对称轴右侧,y都随 x的增大而减小 .
联系: y=a(x-h)²+k(a≠0) 的图象可以看成y=ax²的图象先沿x轴整体左(右)平移| |个单位(当 >0时,向右平移;当 <0时,向左平移),
再沿对称轴整体上(下)平移|
|个单位 (当
>0时向上平移;当 <0时,向下平移)得到的.
y 1 x2
y1
1 3
x2
2
3
y2
1 3
x2
2
的图像
在同一直角坐标系中
画出函数 y 1 x2 5 y
y1
1 3
x2
2
3
y2
的图像

二次函数图像与性质ppt课件

二次函数图像与性质ppt课件

D．f(1)＞25
答案：A
三基能力强化
2．若函数f(x)＝ax2＋bx＋c满足 f(4)＝f(1)，那么( )
A．f(2)＞f(3) B．f(3)＞f(2) C．f(3)＝f(2) D．f(3)与f(2)的大小关系不确定 答案：C
三基能力强化
3．已知函数y＝x2－2x＋3在闭区
间[0，m]上有最大值3，最小值2，则
课堂互动讲练
【思路点拨】 (1)待定系数法．(2) 二次函数的单调性．
【解】 (1)依题意，方程f(x)＝ax2 ＋bx＝x有等根，
则有Δ＝(b－1)2＝0，∴b＝1. 2分 又f(－x＋5)＝f(x－3)， 故f(x)的图象关于直线x＝1对称， ∴－2ba＝1，解得 a＝－12，
∴f(x)＝－21x2＋x. 5 分
基础知识梳理
2．二次函数的图象及其性质
基础知识梳理
基础知识梳理
基础知识梳理
二次函数可以为奇函数吗？ 【思考·提示】 不会为奇 函数．
三基能力强化
1．已知函数f(x)＝4x2－mx＋5在
区间[－2，＋∞)上是增函数，则f(1)的
范围是( )
A．f(1)≥25
B．f(1)＝25
C．f(1)≤2＋2＝(x＋a)2＋2 －a2的对称轴为x＝－a，
∵f(x)在[－5,5]上是单调函数， ∴－a≤－5，或－a≥5， 解得a≤－5，或a≥5. 10分
规律方法总结
1．二次函数f(x)＝ax2＋bx＋c(a ＞0)在区间[m，n]上的最值．
当－2ba＜m 时，函数在区间[m， n]上单调递增，最小值为 f(m)，最大 值为 f(n)；
基础知识梳理
1．二次函数的解析式有三种常用表 达形式

《二次函数的图像和性质》PPT课件 人教版九年级数学

《二次函数的图像和性质》PPT课件 人教版九年级数学
2
y=20x2+40x+20③
d=
学生以小组形式讨论，并由每组代表总结.
探究新知
【分析】认真观察以上出现的三个函数解析式，
分别说出哪些是常数、自变量和函数．
函数解析式
y=6x2
自变量
函数
x
y
n
d
x
y
这些函数自变量的最高次项都是二次的！
这些函数有什
么共同点？
探究新知
二次函数的定义
一般地，形如y=ax²+bx+c(a,b,c是常数,a≠ 0)的
总结二次
函数概念
二次函数y=ax²+bx+c
（a，b，c为常数，a≠0）
确定二次函数解
析式及自变量的
取值范围
二次函数的判别:
①含未知数的代数式为整式；
②未知数最高次数为2；
③二次项系数不为0.
人教版 数学 九年级 上册
22.1 二次函数的图象和性质
22.1.2
二次函数y=ax2的
图象和性质
导入新知
探究新知
方法点拨
运用定义法判断一个函数是否为二次函数的
步骤：
（1）将函数解析式右边整理为含自变量的代
数式，左边是函数（因变量）的形式；
（2）判断右边含自变量的代数式是否是整式；
（3）判断自变量的最高次数是否是2；
（4）判断二次项系数是否不等于0.
巩固练习
下列函数中,哪些是二次函数？
(1) y=3(x-1)²+1（是）
（1） 你们喜欢打篮球吗？
（2）你们知道投篮时，篮球运动的路线是什么
曲线？怎样计算篮球达到最高点时的高度？
素养目标

《二次函数的图像和性质》PPT(第1课时)

《二次函数的图像和性质》PPT(第1课时)
第三十章 二次函数
二次函数的图像和性质
第1课时
导入新课
讲授新课
当堂练习
-.
课堂小结
学习目标
1.正确理解抛物线的有关概念.（重点） 2.会用描点法画出二次函数y=ax²的图像，概括出图像 的特点.（难点） 3.掌握形如y=ax²的二次函数图像的性质，并会应用. （难点）
导入新课
情境引入
讲授新课
一 二次函数y=ax2的图像
问题2：观察图形，y随x的变化如何变化？
y x2
y ax2
(-1,-1) (-2,-4)
(1,-1) (2,-4)
知识要点
对于抛物线 y = ax 2 （a＜0）
当x＞0时，y随x取值的增大而减小； 当x<0时，y随x取值的增大而增大.
例2 在同一直角坐标系中，画出函数 y 1 x2, y 2x2 的图像．
关系是什么？
y y=ax2
二次项系数互为相反数，
开口相反，大小相同，
它们关于x轴对称.
O
x y=-ax2
二 二次函数y=ax2的性质 问题1：观察图形，y随x的变化如何变化？
(-2,4)
(2,4)
(-1,1)
(1,1)
y x2
y ax2
知识要点
对于抛物线 y = ax 2 （a＞0） 当x＞0时，y随x取值的增大而增大； 当x<0时，y随x取值的增大而减小.
< (1)若点(－2，y1)与(3，y2)在此二次函数的图像上，则y1_____y2；
(填“>”“＝”或“<”)；
(2)如图，此二次函数的图像经过点(0，0)，长方形ABCD的顶
点A、B在x轴上，C、D恰好在二次函数的图像上，B点的横坐标

二次函数的图像和性质(共48张PPT)

二次函数的图像和性质(共48张PPT)
C、对于直线 y=ax+b 来说，由图象可以判断，a＞0，b＞0；而对于抛物线 y=ax2﹣bx 来说，图象开口向上，对称轴 x= ＞0，应在 y 轴的右侧，故符合 题意； D、对于直线 y=ax+b 来说，由图象可以判断，a＞0，b＞0；而对于抛物线 y=ax2﹣bx 来说，图象开口向下，a＜0，故不合题意，图形错误； 故选：C．
即当 x＜－2ba时， 当 x＜－2ba时，y 随 x y 随 x 的增大而减
的增大而增大；在对 小；在对称轴的右
称轴的右侧，即当 x 侧，即当 x＞－2ba ＞－2ba时，y 随 x 的 时，y 随 x 的增大
增大而减小，简记为 而增大，简记为
“左增右减” “左减右增”
15
最值
抛物线有最 抛物线有最
1、二次函数的图像和性质
函数
二次函数 y＝ax2＋bx＋c
(a，b，c 为常数，a≠0)
a<0
a>0
图象
13
开口 对称轴、顶点
抛物线开口向 抛物线开口向
上，并向上无限 下，并向下无限
延伸
延伸
对称轴是x＝－
b 2a
，顶点坐标是
－2ba，4ac4－a b2
14
增减性
在对称轴的左侧， 在对称轴的左侧，即
低点，当 高点，当
x＝－2ba时， x＝－2ba时，
y 有最小值， y 有最大值，
y ＝ 最小值
y ＝ 最大值
4ac－b2 4a
4ac－b2 4a
16
2、二次函数y＝ax2＋bx＋c的图象特征
与系数a，b，c的关系
项目 字母
字母的符号
图象的特征
a＞0 a
a＜0

二次函数 的图象和性质--PPT课件

二次函数 的图象和性质--PPT课件

点（h，k）坐标 Nhomakorabea对
称
x=h
轴
最 值
最小值为k
最大值为k
新知应用-----基础知识
新知应用-----拓展提高
这节课你学到了什么
图像及性质 合作、分享 类比、化归
知识 方法 思想
作业布置
• 课后习题 • 练习册
送给大家
函数是纲 纲举目张 数形结合 相得益彰
形如y=a（x-h）2+k二次函数图像性质探索
文件名
抛物 线
开口 方向
顶点 坐标
对称 轴
y=ax2(a>0) y=ax2(a<0)
向上
向下
（0，0） y轴
最值 最小值为0 最大值为0
温馨提示：鼠标拖动点A
文件名
抛物 线
开口 方向
顶点 坐标
对称 轴
y=ax2+k y=ax2+k （a>0) （a<0)
向上
向下
（0，K）
y轴
最值 最小值为k 最大值为k
文件名
抛物 线
开口 方向
顶点 坐标
对称 轴
最值
y=a（x-h）2 y=a（x-h）2
（a>0)
（a<0)
向上
向下
（h，0）
x=h
最小值为0
最大值为0
文件名
抛
物 y=a（x-h）2+k
线
（a>0)
y=a（x-h）2+k （a<0)
开
口
向上
方
向
向下
顶

二次函数的图像和性质PPT课件(共21张PPT)

二次函数的图像和性质PPT课件(共21张PPT)

相同点
相同点：开口都向下，顶点是
原点而且是抛物线的最高点，
对称轴是 y 轴.
不同点
不同点：|a|越大，抛物线的
开口越小．
x
O
y
－4 －2
2
4
－2
－4
－6
y 1 x2 2
－8
y x2
y 2x2
尝试应用
1、函数y=2x2的图象的开向口上 ,对称轴y轴 ,顶点是(0,0;)
2、函数y=－3x2的图象的开口向下 ,对称轴y轴 ,顶点是(0,0;) 3、已知抛物线y＝ax2经过点A(-2，-8).
不在此抛物线上。
小结
1. 二次函数的图像都是什么图形？
2. 抛物线y=ax2的图像性质: (1) 抛物线y=ax2的对称轴是y轴,顶点是原点.
(2)当a>0时,抛物线的开口向上,顶点是抛物 线的最低点;
当a<0时,抛物线的开口向下,顶点是抛物 线的最高点;
（3）抛物线的增减性
（4）|a|越大,抛物线的开口越小;
得到y=-x2的图像.
y 1
-5 -4 -3 -2 -1-1 o 1 2 3 4 5 x
-2
-3 -4
-5
-6
y=－x2
-7
-8 -9
-10
二次函数的图像
从图像可以看出,二次函数y=x2和y=－x2的图像都是一条
曲线,它的形状类似于投篮球或投掷ห้องสมุดไป่ตู้球时球在空中所经过
的路线.
这样的曲线叫做抛物线.
y=x2的图像叫做抛物线y=x2.
解：分别填表，再画出它们的图象，如图 当a<0时,抛物线的开口向下,顶点是抛物线的最高点;
在同一直角坐标系中画出函数y=-x2、y=-2x2、y=- x2的图象，有什么共同点和不同点? -8=a(-2)2,解出a= -2,所求函数解析式为y= -2x2.

1.2二次函数的图象与性质(第1课时)课件(共13张ppt)

1.2二次函数的图象与性质(第1课时)课件(共13张ppt)
图象的开口向 上 ； 图象是轴对称图形，对称轴是_y轴____x_=_0 对称轴与图象的交点是 O(0，0) ；
图象在对称轴左边的部分，函数值随
自变量取值的增大而 减小 ，
简称为“左降”；
图象在对称轴右边的部分，函数值随自变量取
值的增大而 增大 ， 简称为“右升”； 当x= 0 时，函数值最 小 .
谢谢观赏
You made my day!
我们，还在路上……
当x= 0 时，函数值最 小 .
类似地，当a＞0时，y=ax2的图象也具 有上述性质.
于是我们在画y=ax2(a＞0)的图象时，可以先画出图象在y轴 右边的部分，然后利用对称性，画出图象在y轴左边的部分.
在画右边部分时，只要“列表、描点、连线”三个步骤 就可以了(因为我们知道了图象的性质).
例1 画二次函数y=x2的图象. 列表： x 0 0.5 1 1.5 2 3
，简称为“右升”.
观察
我们已经正确地画出了y =
现在可以从图象看出
y
=
1 2
x
2
的12 x其2 的他图一象些，性因质此(除，
了上面已经知道的关于y轴对称和“右升”外)：
对称轴与图象的交点是 O(0，0) ；图象的开口向 上 ；
图象在对称轴左边的部分，函数值随自变量取值的
增大而 减小 ， 简称为“左降”；
解：（1）把A（2，8）代人y=ax2 ∴ a=2 ∴ y=2x2
（2） 当x=1时，y=2 ≠ 4 ∴ B(1，4)不在y=2x2的图像上。
（3） 当y=18时，即2x2=18，x=3或x=-3 ∴ 纵坐标是18的点是：（3,18）和（-3,18）
对于y=ax2（当a＞0时）的图象也具有上述性质.

二次函数的图像和性质PPT课件

二次函数的图像和性质PPT课件
顶点形式
二次函数的顶点形式是f(x) = a(x - h)^2 + k，其中(h, k)为顶点坐标。
二次函数图像的性质
对称轴
二次函数的对称轴是x = -最大值。
开口方向
二次函数开口向上当且仅当a > 0，开口向下当且仅当a < 0。
二次函数的变换
导数
二次函数的导数是一条直线，表示了函数的变化率。
凹性质
二次函数的凹性质取决于a的值，a > 0时函数向上凹，a < 0时函数向下凹。
凸性质
二次函数的凸性质取决于a的值，a > 0时函数向上凸，a < 0时函数向下凸。
二次函数的非负和非正性质
1 非负性质
2 非正性质
当a > 0时，二次函数的图像位于x轴以上。
建筑
物理
二次函数的图像和性质可应用 于建筑设计，优化结构和形状。
P物理实验中，二次函数可以 用于描述运动曲线和力学模型。
总结和展望
通过本课程，我们深入了解了二次函数的图像和性质，掌握了解析和图像求 解的方法，并应用于实际领域。希望你喜欢这次学习！继续思考和探索，创 造性地应用二次函数。
1
平移
平移变换可通过改变顶点来实现，横向平移表示为f(x ± h)，纵向平移表示为f(x) ± k。
2
缩放
缩放变换可通过改变a的值来实现，a > 1时函数变窄，0 < a < 1时函数变宽。
3
反转
反转变换可通过改变a的符号来实现，a > 0时函数朝上，a < 0时函数朝下。
二次函数的导数和凹凸性质
二次函数的图像和性质
欢迎来到二次函数的图像和性质课程！通过本课程，您将学习二次函数的定 义和表达形式，并探索其图像的性质和变换。让我们开始吧！

《二次函数》ppt课件

《二次函数》ppt课件

判别式意义
当 $Delta > 0$ 时，方程有两个不相等 的实根，抛物线与 $x$ 轴有两个交点。
02
二次函数与一元二次方程 关系
一元二次方程求解方法
01
02
03
公式法
对于一般形式的一元二次 方程，可以使用求根公式 进行求解。
配方法
通过配方将一元二次方程 转化为完全平方形式，从 而求解。
因式分解法
首先，通过配方将二次函数转 化为顶点式f(x) = a(x - h)^2 + k，其中(h, k)为顶点坐标。然后， 根据二次函数的性质，对称轴 为x = h，顶点坐标为(h, k)。最 后，代入具体的a、b、c值求解。
已知二次函数f(x) = x^2 - 2x， 求在区间[-1, 3]上的最值。
首先，将二次函数配方为f(x) = (x - 1)^2 - 1，确定对称轴为x = 1。然后，根据二次函数的单 调性，在区间[-1, 1]上单调递减， 在[1, 3]上单调递增。因此，在x = 1处取得最小值f(1) = -1，在 x = 3处取得最大值f(3) = 3。
04
根的判别式Δ=b²-4ac可 以用于判断二次函数与x 轴交点的个数。
当Δ>0时，二次函数与x 轴有两个不同的交点。
当Δ=0时，二次函数与x 轴有一个重根，即一个 交点。
当Δ<0时，二次函数与x 轴无交点。
03
二次函数图像变换与性质 分析
平移变换对图像影响
平移方向
二次函数图像在平面直角坐标系中可 沿x轴或y轴方向进行平移。
04
二次函数在实际问题中应 用举例
利润最大化问题建模与求解
1 2 3
问题描述
某公司生产一种产品，其成本和销售价格与产量 之间存在一定的关系。公司希望通过调整产量来 实现利润最大化。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

-5 -4 -3 -2 -1 o 1 2 3 4 5 x -1 -2 -3 -4 -5 -6 2 y= － x -7 -8 -9 -10
从图像可以看出,二次函数y=x2和y=－x2的图像都 是一条曲线,它的形状类似于投篮球或投掷铅球时球在 y y 空中所经过的路线 . o x 这样的曲线叫做抛物线.
当x=0时,函数 y的值最小，
最小值0.
抛物线 y= -x2在x轴下方(除顶点外)，顶点
是它的最高点，开口向下，并且向下无限伸展，
当x=0时，函数y的值最大，最大值是0.
y
y x
2
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
探究
例3.在同一直角坐标系中画出函数y=-x2、y=-2x2、 y=- x2的图象，有什么共同点和不同点?
（2）对称轴：y轴，顶点坐标：（0,0），开口向下.
-8=a(-2)2,解出a= -2,所求函数解析式为y= -2x2.
（3）因为 4 2(1) 2 ，所以点B（-1 ，-4）
不在此抛物线上。
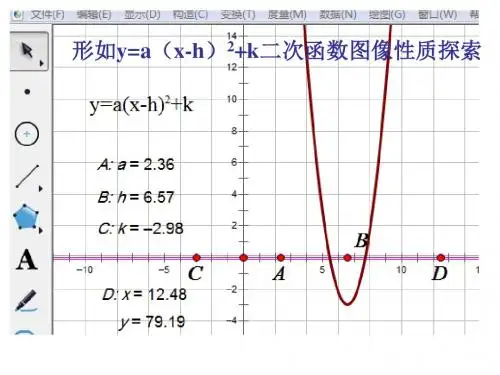
1. 二次函数的图像都是什么图形？ 2. 抛物线y=ax2的图像性质: (1) 抛物线y=ax2的对称轴是y轴,顶点是原点. (2)当a>0时,抛物线的开口向上,顶点是 抛物线的最低点; 当a<0时,抛物线的开口向下,顶点是 抛物线的最高点;
二次函数的图像和性质
衡水市景县连镇王克义
创设情境，导入新课
问题：
你们喜欢篮球吗？：投篮时，篮球运动的路 线是什么曲线？怎样计算篮球达到最高点 时的高度？
今天让我们来研究一下二次函数的图像 和性质吧
二次函数:
一般地,形如 y=ax2+bx+c(a、b、c为常数,a≠0)的函 数,叫做二次函数.其中,x是自变量,a,b,c分别是函数表 达式的二次项系数、一次项系数和常数项.
相同点
相同点：开口都向下，顶 点是原点而且是抛物线的 最高点，对称轴是 y 轴.
－4 －2 －2 －4 2 4
不同点
不同点：|a|越大，抛物 线的开口越小．
y x2
－6
－8
1 y x2 2
y 2 x 2
向上 ,对称轴 y轴 1、函数y=2x2的图象的开口
(0,0) ,顶点是
;
(0,0) ; 向下 ,对称轴 y轴 ,顶点是 2、函数y=－3x2的图象的开口 3、已知抛物线y＝ax2经过点A(-2，-8).
(1) 求此抛物线的函数解析式
2,得 解（ 1 ）把（ -2 ， -8 ）代入 y=ax （3）判断点（-1，-4）是否在此抛物线上；
（2）写出这个二次函数图象的对称轴，顶点坐标及开口方向；
y=x2的图像叫做抛物线y=x2. y=－x2的图像叫做抛物线y=－x2.
y=x2 x 实际上,二次函数的图像 它们的开口向上或者向下. 都是抛物线. 一般地,二次函数y=ax2+bx+c 的图像叫做抛物线y=ax2+bx+c. 还可以看出,二次函数y=x2和y=－x2的图像 都是轴对称图形,y轴是它们的对称轴. 抛物线与对称轴的交点(0,0)叫做抛物线的顶点. 抛物线y=x2的顶点(0,0)是它的最低点. 抛物线y=－x2的顶点(0,0)是它的最高点. o
-5 -4 -3 -2 -1 o 1 2 3 4 5
x
请画函数y=－x2的图像 解:(1) 列表 x … -3 -2 -1 0 1 2 3 … (2) 描点 y=-x2 … -9 -4 -1 0 -1 -4 -9 … (3) 连线
1
y
根据表中x,y的数值在 坐标平面中描点(x,y), 再用平滑曲线顺次连接 各点,就得到y=-x2的图 像.
o y
a>0
（3）抛物线的增减性
x
（4）|a|越大,抛物线的开口越小;
a<0
结束寄语
下课了!
• 生活是数学的源泉.
•
探索是数学的生命线.
yx
2
8 6 4 2
y 2 x2
1 2 y x 2
2
－4
－2
4
画函数y=x2的图像 解: (1) 列表 x … -3 -2 -1 (2) 描点y=x2 … 9 4 1 (3) 连线
0 0
10 9 8 7 6 5 4 3 2 1 y
1 1
2 4
3 … 9 …
y=x2
根据表中x,y的数值在 坐标平面中描点(x,y), 再用平滑曲线顺次连 接各点,就得到y=x2的 图像.
对称轴、顶点、最低点、最高点
yx
2
这条抛物线关于 y轴对称，y轴就
是它的对称轴.
对称轴与抛物 线的交点叫做
抛物线的顶点.
yx
2
抛物线 y=x2在x轴上方
(除顶点外)，顶点是它的最
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
低点，开口向上，并且向上 无限伸展;
下列哪些函数是二次函数？哪些是一次函数？
(1) y=3x-l (3) y=x² +6
直线 （1）一次函数的图象是一条_____ ，
(2) 通常怎样画一个函数的图象？
(2) y=2x² (4) y=-3x² -2x+4
列表、描点、连线
(3) 二次函数的图象是什么形 状呢？
从最简单的二 次函数开始！
22.1.2二次函数y=ax2的图象和性质