10数轴(表示不等式的解)

不等式解集数轴的画法
不等式解集数轴又称“x轴”，它是一种具有理论和实用价值的图形绘制方法，用于说明某一问题的解决方案。

这种方法可以用来描绘一系列的等式或不等式的解集，从而更清楚地阐明该问题的解决过程。

下面我们将详细介绍不等式解集数轴的画法。

首先，我们必须对待求解的不等式给出正确的读法，也就是将不等式给出相应的文字描述。

根据不等式的结构，可以将不等式分为两类：小于等于（≤)式和大于等于（≥)式。

当不等式中存在等号时，可以将其分类为小于或等于（≤）式或大于或等于（≥）式。

接下来，要绘制不等式解集数轴，需要按照以下步骤：
第一步，在x轴上定义一个自变量，用来代表每一个不等式中的x坐标；
第二步，在x轴上画出不等式中每个x坐标所对应的解集值；
第三步，在x轴上画出不等式中x坐标所对应的解集范围，即大于或等于（≥）式或小于或等于（≤）式；
第四步，根据不等式中x坐标所对应的解集范围画出不等式的解集，从而得到最终解的图形表示。

不等式解集数轴是一种有效的问题求解方法，它可以帮助我们更好地理解问题的解决过程，提高解决问题的效率。

此外，不等式解集数轴还有助于我们检验问题的正确性，从而避免出现错误的结果。

总之，不等式解集数轴的绘制是一项研究活动，它对数学知识的学习具有重要意义。

它不仅可以帮助我们更好地理解不等式的求解过
程，还可以有效地帮助我们进行问题的检验和验证。

因此，学习不等式解集数轴的绘制对数学科学的学习者来说，是在科学研究方面十分有益的。

不等式的有关概念1、不等式定义:用符号“<”、“≤”、“>”、“≥”、“≠”连接而成的数学式子,叫做不等式。

这5个用来连接的符号统称不等号。

只含有一个未知数，且含未知数的式子都是整式，未知数的次数是1，系数不为0.这样的不等式，叫做一元一次不等式。

2、列不等式:步骤如下(1)根据所给条件中的关系确定不等式两边的代数式;(2)选择与题意符合的不等号将表示不等关系的两个式子连接起来。

3、用数轴表示不等式(1)a<x: 表示小于a 的全体实数,在数轴上表示a 左边的所有点,不包括a 在内。

(2)a≥x: 表示大于或等于a 的全体实数,在数轴上表示a 右边的所有点,包括a 在内。

(3)b<x<a: 表示大于b 而小于a 的全体实数。

4、不等式的基本性质(1)基本性质1:若a<b,b<c,则a<c。

(不等式的传递性)(2)基本性质2:不等式的两边都加上(或减去)同一个数,所得到的不等式仍成立。

①若a>b>c,则a+c>b+c,a-c>b-c ;②若a<b<c,则a+c<b+c ,a-c<b-c。

(3)基本性质3:①不等式的两边都乘(或都除以)同一个正数,所得的不等式仍成立; 若a>b ,且0>c ,则ac>bc.②不等式的两边都乘(或都除以)同一个负数,必须把不等号的方向改变,所得的不等式成立。

若a>b ,且0<c ,则ac<bc .要点诠释：(1)不等式基本性质1的学习与等式的性质的学习类似，可对比等式的性质掌握.（2)“不等号的方向不变”，指的是如果原来是“＞”，那么变化后仍是“＞”；如果原来是“≤”，那么变化后仍是“≤”；“不等号的方向改变”指的是如果原来是“＞”，那么变化后将成为“<”；如果原来是“≤”，那么变化后将成为“≥”.5、一元一次不等式的解法：与一元一次方程的解法类似，其根据是不等式的基本性质，解一元一次不等式的一般步骤为：【(1)去分母；(2)去括号；(3)移项；(4)合并同类项；(5)系数化为1.】(1)求分解,分别解不等式组中的每一个不等式,并求出它们的解;(2)画公解,将每一个不等式的解集画在同一数轴上,并找出它们的公共部分;(3)写组解,将(2)步中所确定的公共部分用不等式表示出来,就是原不等式组的解集。

不等式数轴表示方法Understanding how to represent inequalities on a number line is crucial for mastering algebra. Inequalities are relationships between two values that are not equal to each other. They are represented using symbols such as < (less than), > (greater than), ≤ (less than or equal to), and ≥ (greater than or equal to). When representing inequalities on a number line, it is important to understand the direction in which the values are moving and how they relate to each other.了解如何在数轴上表示不等式对于掌握代数知识至关重要。

不等式是两个不相等数值之间的关系。

它们使用诸如<（小于）,>（大于）,≤（小于或等于）和≥（大于或等于）等符号表示。

在数轴上表示不等式时，重要的是理解数值的移动方向以及它们之间的关系。

When representing an inequality on a number line, we use open or closed circles to indicate whether the endpoint is included in the solution set. An open circle indicates that the endpoint is not included in the solution set, while a closed circle indicates that the endpoint is included in the solution set. Arrows are used to show thedirection in which the values are moving along the number line. For example, if we have the inequality x > 3, we would use an open circle on 3 to indicate that it is not included in the solution set, and an arrow pointing to the right to show that the values greater than 3 are included in the solution set.在数轴上表示不等式时，我们使用开或闭圆圈来指示端点是否包括在解集中。

数轴的几何意义和代数意义数轴是数学中常用的工具，它在几何意义和代数意义上都有重要的应用。

本文将分别从几何意义和代数意义两个方面探讨数轴的含义和用途。

一、数轴的几何意义数轴是一条直线，上面的点与实数一一对应。

我们可以将数轴理解为一个均匀刻度的直尺，其中0点位于中心位置。

数轴的两侧是正半轴和负半轴，分别表示正数和负数。

通过数轴，我们可以直观地理解数与位置之间的关系，从而更好地理解数的大小和相对关系。

在几何意义上，数轴可以用来表示点、线段和区间。

例如，我们可以将数轴的某个点与一个实数一一对应，表示该点的位置。

两个不同的点可以通过线段连接起来，线段的长度即为两个实数之间的差值。

而一个区间则可以表示数轴上的一段连续的实数集合。

数轴的几何意义在几何图形的运动、形状和相似性等问题中有广泛应用。

例如，在平面几何中，我们可以通过数轴来表示线段的长度，从而比较不同线段的大小。

在解决几何问题时，我们可以利用数轴的刻度和坐标系来确定几何图形的位置和长度。

二、数轴的代数意义数轴在代数意义上是一个有序的实数集合。

我们可以通过数轴上的点与实数之间的对应关系，在代数运算中进行数值计算和推理。

在代数意义上，数轴可以用来表示数值的相对大小和关系。

通过数轴，我们可以比较不同实数的大小，并进行加减乘除等运算。

例如，当我们要计算两个实数的和时，可以通过数轴上的刻度和坐标系来确定两个实数的位置，然后将它们相加得到结果。

数轴还可以用来表示不等式和方程的解集。

例如，当我们解决一个线性不等式时，可以将不等式表示在数轴上，然后确定不等式的解集。

同样地，当我们解决一个一元一次方程时，可以将方程的解表示在数轴上，从而更好地理解方程的解集。

数轴的代数意义在代数学习和实际问题求解中有重要作用。

通过数轴，我们可以直观地理解实数的大小和相对关系，从而更好地理解和运用数学知识。

数轴在几何意义和代数意义上都有重要的应用。

在几何意义上，数轴可以用来表示点、线段和区间，帮助我们理解几何图形的位置和长度。

不等式的解集 典型例题例题1 分别试写出一个不等式，使它的解集满足下列条件：（1）1=x 是不等式的一个解；（2）它的正整数解为1，2，3，4．例题2 11=x 是不是不等式1623-<+-x 的解？3=x 是不是不等式1623-<+-x 的解？你能知道不等式1623-<+-x 的解集吗？例题3 当x 取下列数值时，哪些是不等式36x +<的解？哪些不是？-4，-2.5，0，1，3.5，4，4.5，7例题4 试判断－2，1，2，211-，10，0，3是否是不等式532>+x 的解？再找出这个不等式的另外两个小于2的解．例题5 求不等式63<+x 的正整数解．例题6 方程93=x 的解有 个，不等式39x <的解有 个，其中非负整数有几 个.例题7 对于不等式21<+x ，小东认为所有非正数（负数与零的统称）都是这个不等式的解，马上写下“该不等式的解集是0≤x ”，你认为对吗？为什么？例题8 将下列不等式的解集在数轴上表示出来．（1）3>x ；（2）31≥+x ；（3）5≤x 的非负整数解．例题9 将数轴上x 的范围用不等式表示．（1）（2）（3）例题10 将下列不等式的解集在数轴上表示出来：（1）2>x ； （2）2<x ； （3）2≥x ；（4）2≤x ； （5）3-≥x ； （6）a x ≤（0>a ）例题11 已知－4是不等式9>ax 的解集中的一个值，试求a 的取值范围．参考答案例题1 分析 只要写出一个满足条件的不等式即可，事实上，满足这个条件的式子有无数个．解答 （1）13>x ． （2）5.62<+x ．例题2 解答 ∵当11=x 时，1631211323-<-=+⨯-=+-x ，∴11=x 是1623-<+-x 的解．∵当3=x 时，723323-=+⨯-=+-x 不小于－16，∴3=x 不是1623-<+-x 的解．在1623-<+-x 的两边都减去2，得183-<-x ，再在两边都除以－3，得6>x 是不等式1623-<+-x 的解集．例题3 分析 利用定义，只要把每个值代入不等式加以验算，就可得出结论.解答 当4-=x 时,1343-=+-=+x ,而16-<,所以4-是不等式36x +<的解.当4=x 时，7343=+=+x ，而7≮6（“≮”读作“不小于”），所以4不是不等式36x +<的解.类似地，我们可得：4-，5.2-，0，1都是不等式36x +<的解；5.3，4，5.4，7都不是不等式36x +<的解.例题4 分析 分别将题中所给的各数代入不等式的左边，求出对应值，然后比较左边的值是否大于5，．根据上述情况，确定不小于2的解．解答 （1）当2-=x 时，不等式的左边<-=+-⨯=13)2(2右边，所以2-=x 不是不等式的解；（2）当1=x 时，不等式的左边＝2×1＋3＝5＝右边，故1=x 不是不等式的解；（3）当2=x 时，不等式的左边>=+⨯=7322右边，故2=x 是不等式的解；（4）当211-=x 时，不等式的左边<=+⎪⎭⎫ ⎝⎛-⨯=03232右边，故211-=x 不是不等式的解；（5）当10=x 时，不等式的左边>=+⨯=233102右边，故10=x 是不等式的解；（6）当0=x 时，不等式的左边<=+⨯=3302右边，故0=x 不是不等式的解：（7）当3=x 时，不等式的左边>=+⨯=9332右边，故3=x 是不等式的解． 由上述可知，当1=x 时不等式的左边与右边相等，且负数和0都不是不等式的解，可推得不等式的解的值应大于1．故不等式小于2的解应在1与2之间，如311,211等，都是不等式小于2的解． 例题5 解答 由不等式的基本性质1，得36-<x ，即3<x 是不等式63<+x 的解集，因此不等式63<+x 的正整数解为1，2，共两个．说明 本例是求不等式的特殊解（正整数解），可先利用不等式的基本性质求出不等式的所有解（即不等式的解集），然后从所有解中筛选出特殊解．例题 6 解答 方程93=x 是一个一元一次方程，它只有一个解3=x ；而不等式39x <有无数多个解，表示为3x <，只要比3小的数都是它的解；比3小的非负整数有0，1，2三个.例题7 分析 显然，所有非正数都能使该不等式成立，但所有非正数不是这个不等式解的全部．我们发现，还有0.1，0.2，0.3，…，0.11，0.12，0.3，…都是这个不等式的解．因此，小东写出的解集0≤x 是错误的．解答 不对．因为还有满足10<<x 的数是这个不等式的解，所以说这个不等式的解集应为1<x ．例题8 分析 将不等式的解集在数轴上表示时，应注意：①不等号的方向；②不含某一数时用空心点表示，含某一数时用实心点表示．本例中的（3）表示时是一些间断点，不连续．解答 （1）（2）（3） 例题9 分析 （1）中，包括212-这一点，解集在212-的正方向． （2）中，不包括1这一点，解集在1的负方向；（3）包括－2，不包括212，解集在－2和212之间． 解答 （1）212-≥x ；（2）1<x ；（3）2122<≤-x ． 说明 解这类题时，先看实心点还是空心点，再看该点表示的数，最后看方向．例题10 解答 （1）如图1 （2）如图2图1 图2（3）如图3 （4）如图4图3 图4（5）如图5 （6）如图6图5 图6说明 在数轴上表示不等式的解集时，要特别注意画线的方向和起点：大于向右画，小于向在画；不等号中含有等号起点画实心圆点，不含有等号起点画圆圈．例题11 解答 由94>-a 得49-<a 说明 －4是不等式的解集中的一个值，可代入，训练逆向思维能力．知识拓展:借助于不等式的解集解题不等式的解集是研究不等式问题的一个重要内容，它在实际解题中有着广泛的应用，现举几例说明.一、确定字母的范围例1 已知关于x 的不等式2x a -≤1的正整数解是1，2，3，4，5，6，7，8，试求a 的取值范围.分析 若能用含a 的不等式表示出不等式的解集，再由已知的正整数解，即可确定解集中最大解的取值范围，从而建立关于a 的不等式即可求解. 解 解关于x 的不等式2x a -≤1，得x ≤2+a . 因为关于x 的不等式2x a -≤1的正整数解是1，2，3，4，5，6，7，8， 所以有不等式8≤2+a ＜9，解得6≤a ＜7.说明 求解本题时逆用了不等式的解集的概念.二、确定另一个相关不等式的解集例2 若关于不x 等式mx ＞n 的解集为x ＜43.试解关于x 的不等式：(2m －n )x +m －5n ＞0.分析 因为一次不等式的解集只有一个，即不等式的解集是唯一的，所以此类题可先由解集存在的唯一性，列方程求系数间的关系，再代入另一个不等式求解集.解 因为mx ＞n 的解集为x ＜43，所以可知m ＜0，当m ＜0时，则x ＜m n ， 所以m n ＝43，所以n ＝43m . 所以不等式(2m －n )x +m －5n ＞0即可转化为54mx ＞114m . 说明 本题实际上运用了不等式的解集存在的唯一性求解.三、求代数式的值例3 若不等式组24,25x a x a b +>⎧⎨--<⎩的解是0＜x ＜2，试求a +b 的值. 分析 视a 与b 为常数，确定不等式组24,25x a x a b +>⎧⎨--<⎩的解集，进而利用已知条件构造方程组即可求出a 与b 的值，从而使问题获解.解 视a 与b 为常数，解不等式组24,25,x a x a b +>⎧⎨--<⎩得42,5.2x a a b x >-⎧⎪⎨++<⎪⎩ 因为不等式组24,25x a x a b +>⎧⎨--<⎩的解是0＜x ＜2，所以有420,5 2.2a ab -=⎧⎪⎨++=⎪⎩解得2,3.a b =⎧⎨=-⎩ 所以当a ＝2，b ＝－3时，a +b ＝－1.说明 解此类题的关键的要熟悉逆向应用不等式或不等式组的解集，从而根据解集存在的唯一性，列出方程或方程组求解.下面几道题目供同学们自己练习：1，已知关于(1－a )x ＞2的不等式的解集为x ＜a-12，则a 的范围是＿＿＿. 2，若不等式组⎩⎨⎧->+<121m x m x 无解，试确定m 的取值范围. 3，若关于不x 等式mx ＞n 的解集为x ＜53，试解关于x 的不等式(2m －n )x ＞m +5n .4，若不等式组21,23x a x b -<⎧⎨->⎩的解集为－1＜x ＜1，求(a +1)(b －1)的值.参考答案：1，由不等式的性质可知：当(1－a )x ＞2的解集为x ＜a-12时，只有在1－a ＜0的前提下，才能成立，故a ＞1.2，因不等式组无解，所以两个解集x ＜m +1与x ＞2m －1无公共部分,，可以借助数轴可观察到：点m +1在点2m －1的左边或两点重合，所以m +1≤2m －1，所以得m ≥2. 3，由mx ＞n 的解集为x ＜53，可知m ＜0，当m ＜0时，则x ＜m n ，所以mn ＝53，所以n ＝53m ，不等式(2m －n )x ＞m +5n 可化为75mx ＞2m ，又m ＜0，所以解得x ＜710. 4，原不等式组可化为1,232.a x xb +⎧<⎪⎨⎪>+⎩又知解集为－1＜x ＜1，所以12a +＝1，3+2b ＝－1，所以a ＝1，b ＝－2，所以(a +1)(b －1)＝－6.。

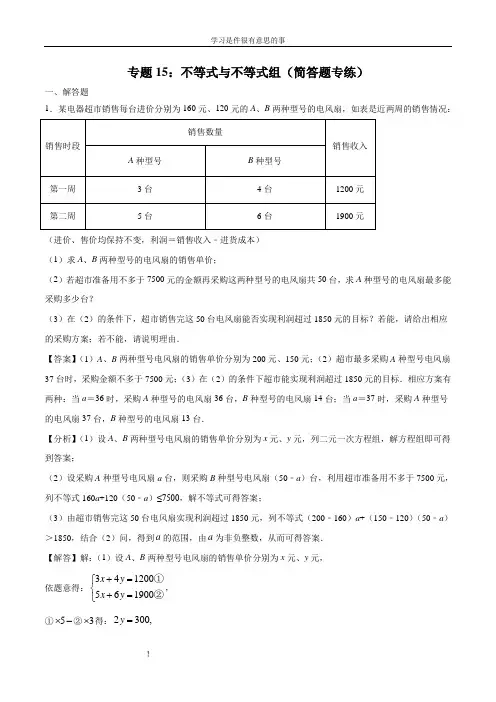
专题15：不等式与不等式组（简答题专练）一、解答题1．某电器超市销售每台进价分别为160元、120元的A 、B 两种型号的电风扇，如表是近两周的销售情况：（进价、售价均保持不变，利润＝销售收入﹣进货成本） （1）求A 、B 两种型号的电风扇的销售单价；（2）若超市准备用不多于7500元的金额再采购这两种型号的电风扇共50台，求A 种型号的电风扇最多能采购多少台？（3）在（2）的条件下，超市销售完这50台电风扇能否实现利润超过1850元的目标？若能，请给出相应的采购方案；若不能，请说明理由．【答案】（1）A 、B 两种型号电风扇的销售单价分别为200元、150元；（2）超市最多采购A 种型号电风扇37台时，采购金额不多于7500元；（3）在（2）的条件下超市能实现利润超过1850元的目标．相应方案有两种：当a ＝36时，采购A 种型号的电风扇36台，B 种型号的电风扇14台；当a ＝37时，采购A 种型号的电风扇37台，B 种型号的电风扇13台．【分析】（1）设A 、B 两种型号电风扇的销售单价分别为x 元、y 元，列二元一次方程组，解方程组即可得到答案；（2）设采购A 种型号电风扇a 台，则采购B 种型号电风扇（50﹣a ）台，利用超市准备用不多于7500元，列不等式160a +120（50﹣a ）≤7500，解不等式可得答案；（3）由超市销售完这50台电风扇实现利润超过1850元，列不等式（200﹣160）a +（150﹣120）（50﹣a ）＞1850，结合（2）问，得到a 的范围，由a 为非负整数，从而可得答案． 【解答】解：（1）设A 、B 两种型号电风扇的销售单价分别为x 元、y 元， 依题意得：341200561900x y x y +=⎧⎨+=⎩①②，①5⨯-②3⨯得：2300,y =150,y ∴=把150y =代入①得：200,x =解得：200150x y =⎧⎨=⎩，答：A 、B 两种型号电风扇的销售单价分别为200元、150元．（2）设采购A 种型号电风扇a 台，则采购B 种型号电风扇（50﹣a ）台． 依题意得：160a +120（50﹣a ）≤7500，401500,a ∴≤解得：a ≤1372． 因为：a 为非负整数，所以：a 的最大整数值是37.答：超市最多采购A 种型号电风扇37台时，采购金额不多于7500元． （3）根据题意得：（200﹣160）a +（150﹣120）（50﹣a ）＞1850， 10a ∴＞350， 解得：a ＞35， ∵a ≤1372， 35∴＜a 1372≤,a 为非负整数，36a =或37.a =∴在（2）的条件下超市能实现利润超过1850元的目标．相应方案有两种： 当a ＝36时，采购A 种型号的电风扇36台，B 种型号的电风扇14台； 当a ＝37时，采购A 种型号的电风扇37台，B 种型号的电风扇13台．【点评】本题考查的是二元一次方程组的应用，一元一次不等式，一元一次不等式组的应用的方案问题，掌握以上知识是解题的关键．2．解不等式组1(1)1212x x ⎧-≤⎪⎨⎪-⎩＜并写出该不等式组的所有整数解.【答案】解集是－1<x≤3;整数解是0，1，2，3【分析】分别解出每个不等式的解集，确定不等式组的解集,然后在解集中确定所有整数解即可. 【解答】解不等式1(1)12x -≤得：x≤3 解不等式12x -＜得：x ＞-1 所以不等式组的解集是－1<x≤3.大于－1而小于或等于3的所有整数有0，1，2，3， ∴该不等式组的所有整数解为0，1，2，3.【点评】本题考查了解不等式组，解决本题的关键是先计算出每个不等式的解集，然后确定不等式组的解集.3．（1）解不等式413x x -> （2）解不等式组()()315121531123x x x x ⎧-+-⎪⎨-+-⎪⎩【答案】(1)1x >; (2)13x ≥. 【分析】（1）移项、合并同类项即可；（2）分别求出两个不等式的解集，再根据同大取大即可确定不等式组的解集. 【解答】解：（1）移项得：431x x ->合并同类项得：1x >（2）()()315121531123x x x x ⎧-+-⎪⎨-+-⎪⎩①②解不等式①得3x ≥-， 解不等式②得13x ≥, 不等式组的解集为: 13x ≥【点评】本题考查了解一元一次不等式（组），熟练掌握解不等式的基本步骤是解决此题的关键.在利用不等式的性质同乘或除时，不等式的两边都乘以（或除以）同一个负数时，不等号的方向改变.在确定不等式组的解集时需注意：同大取大；同小取小；大小小大中间找；大大小小找不到． 4．若关于x 的方程2x 3m 2m 4x 4-=-+的解不小于7183m--，求m 的最小值. 【答案】14-【分析】首先求解关于x的方程2x−3m＝2m−4x＋4，即可求得x的值，根据方程的解的解不小于7183m--，即可得到关于m的不等式，即可求得m的范围，从而求解．【解答】由54 232446546mx m m x x m x+ -=-+=+=，得，即.根据题意，得5471683m m+-≥-，解得14m,≥-所以m的最小值为1 4 -.【点评】本题考查了解简单不等式的能力，解答这类题学生往往在解题时不注意移项要改变符号这一点而出错．解不等式要依据不等式的基本性质，在不等式的两边同时加上或减去同一个数或整式不等号的方向不变；在不等式的两边同时乘以或除以同一个正数不等号的方向不变；在不等式的两边同时乘以或除以同一个负数不等号的方向改变．5．我们用[a]表示不大于a的最大整数,例如:[2.5]＝2,[3]＝3,[－2.5]＝－3;用＜a＞表示大于a的最小整数,例如:＜2.5＞=3,＜4.5＞=5,＜－1.5＞=－1.解决下列问题.（1）[－4.5]＝_____ ;＜3.5＞=________;（2）若[x]＝2,则x的取值范围是________;若＜y＞=－1，则y的取值范围是_______ .（3）若[]21 3x x=-，则x为_________.（4）已知x、y满足方程组[][]32336x yx y⎧+=⎪⎨-=-⎪⎩＜＞＜＞，求x、y的取值范围.【答案】（1）-5; 4，（2）2≤x＜3；-2≤y＜-1,；（3）x=-3（4）x，y的取值分别为-1≤x＜0,2≤y＜3. 【分析】（1）根据新定义与不等式的性质即可求解；（2）根据[a]表示不大于a的最大整数与＜a＞表示大于a的最小整数与不等式的性质求解；（3）根据[]21 3x x=-得到关于x的方程即可求解；（4）先求出[x]、＜y＞的值，再根据新定义即可求解. 【解答】（1）依题意得[－4.5]＝-5;＜3.5＞=4，（2）∵[x]＝2,则x的取值范围是2≤x＜3；∵＜y＞=－1，则y的取值范围是-2≤y＜-1,；（3）∵[x]≤x,[]21 3x x=-化为213x x=-，解得x=-3，符合题意，故x=-3（4）∵[][]323326x y x y ⎧+=⎪⎨-=-⎪⎩＜＞＜＞，解得[]13x y ⎧=-⎨=⎩＜＞ ∴x ，y 的取值分别为-1≤x ＜0,2≤y ＜3.【点评】此题主要考查不等式的应用，解题的关键是熟知不等式的性质. 6．求不等式()()2130x x -+>的解集。

用数轴表示不等式的解集数轴是数学中比较基础的，而且也是很重要的概念之一。

数轴可以用来表示实数集合，其中包括整数、小数、负数以及无理数等。

数轴的基本原理是把实数的大小与放置在它上面的点的相对位置联系在一起。

当我们需要解决一个不等式时，我们可以使用数轴来表示它的解集，这种方法是非常有效和直观的。

什么是不等式？在数学中，不等式是一个包含一个不等式符号（例如"<"，">"，"≤"，"≥"）以及两个表示数量的数的数学表达式。

不等式可以表示出两个数之间的关系，例如其中一个数大于另一个数，或者其中一个数小于另一个数。

例如，下面的不等式表示x大于等于2：x ≥ 2用数轴表示不等式的解集使用数轴可视化不等式，有助于我们更好地理解和找到解决方案。

基本原理是把不等式所表示的含义转换成点在数轴上的位置。

例如，假设我们需要解决以下不等式：x > 2我们可以使用一个数轴来表示这个不等式的解集。

首先，我们把0放在数轴的中心点，然后把2放在右边。

接下来，我们画一条垂直于数轴的线，把它放在2的右侧，因为不等式的符号是">"。

此时我们发现，所有"x"值的位置都必须在2的右侧才能满足不等式。

因此，数轴上的解集就是一个包含无穷多个点的线段，它的左端点是2，右端未定。

解集用数学表达式表示为：{x | x > 2}{x|2 < x < ∞}或者(2, ∞)我们可以看出，这个不等式的解集包括所有大于2的实数，包括小数、整数以及无理数等。

另外一个例子，如果我们需要解决以下不等式：x ≤ -3我们可以使用类似的方法来绘制解集。

首先，我们把0放在数轴的中心点，然后把-3放在左边。

接下来，我们画一条垂直于数轴的线，把它放在-3的左侧，因为不等式的符号是"≤"。

我们可以看出，所有"x"值的位置都必须在-3的左侧才能满足不等式。

索罗学院
在数轴上表示不等式的解
疑惑：不等式的解在数轴上的表示方法
解析：不等式的解集指的是一个范围，题目经常要求我们在数轴上表示不等式的解集，在数轴上表示时需要注意：如果带有等号，也就是取到了端点，此时在端点处需标上实心圆，反之不带等号则在端点处标记空心圆。

几种常见情况如下：1、不等式解集表示单方向时，在数轴上的表示方法(1)x>3 (2)x≤-1 2、不等式解集表示一个公共区域或多个区域时，在数轴上表示方法 (1)-1≤x<3 (2)x>2 且x≤-2
结论：当不等式的解集取到端点时，需要在端点处标记实心圆，反之没有取到端点，则标记空心圆。

本文由索罗学院整理索罗学院是一个免费的中小学生学习网，上面有大量免费学习视频，欢迎大家前往观看！。

第8讲用数轴表示不等式的解集及一元一次不等式组知识精要一、不等式的解集1、不等式解的全体叫做不等式的解集。

（注：一般情况下一元一次方程的解只有一个，一元一次不等式的解可以有无数个。

）2、不等式的解集可以再数轴上直观的表示出来。

如：在数轴上表示大于3的数的点应该数3所对应点的左边还是右边？(右边)因此我们可以在数轴上把x＞3直观地表示出来.画图时要注意方向(向右)和端点(不包括数3,在对应点画空心圆圈).如图所示:同样，如果某个不等式的解集为x≤-2,那么它表示x取那些数？此时在作x≤-2的数轴表示时，要包括-2的对应点,因而在该点处应画实心圆点.如图所示:引导学生总结出在数轴上表示不等式解集的要点：小于向左画，大于向右画；无等号画空心圆圈，有等号画实心圆点。

2、一元一次不等式组1、有几个含有同一个未知数的一次不等式组成的不等式组，叫做一元一次不等式组。

2、不等式组中所有不等式的解集的公共部分叫做这个不等式组的解集。

3、求不等式组的解集的过程叫做解不等式组。

4、解一元一次不等式组的一般步骤是:（1）求出不等式组中各个不等式的解集；（2）在数轴上表示各个不等式的解集；（3）确定各个不等式解集的公共部分，就得到这个不等式组的解集。

【典型例题】例1. 解不等式3(1)5182x x x +-+>-【思路点拨】不等式中含有分母，应先根据不等式的基本性质2去掉分母，再作其他变形．去分母时，不要忘记给分子加括号．【答案与解析】解：去分母，得8x+3(x+1)＞8-4(x -5)， 去括号，得8x+3x+3＞8-4x+20， 移项，得8x+3x+4x ＞8+20-3，合并同类项，得15x ＞25，系数化为1．得．53x >∴不等式的解集为．53x >【总结升华】解一元一次不等式与解一元一次方程的步骤异同见下表：ax ＝bax ＞bax ＜b解：当a ≠0时，；b x a=当a ＝0，b ≠0时，无解；当a ＝0，b ＝0时，x为任意有理数．解：当a ＞0时，；b x a>当a ＜0时，；b x a<当a ＝0，b ≥0时，无解；当a ＝0，b ＜0时，x 为任意有理数．解：当a ＞0时，；b x a<当a ＜０时，；b xa>当a ＝0，b ≤0时，无解；当a ＝0，b ＞0时，x 为任意有理数．【变式】(湖南益阳)解不等式，并把解集在数轴上表示出来．5113x x -->解：去分母得5x -1-3x ＞3，移项、合并同类项，得2x ＞4， 系数化为1，得x ＞2，解集在数轴上的表示如图所示．例2.某市居民用电的电价实行阶梯收费，收费标准如下表：一户居民每月用电量x （单位：度）电费价格（单位：元/度）0＜x≤200a 200＜x≤400b x ＞4000.92（1）已知李叔家四月份用电286度，缴纳电费178.76元；五月份用电316度，缴纳电费198.56元，请你根据以上数据，求出表格中a ，b 的值．（2）六月份是用电高峰期，李叔计划六月份电费支出不超过300元，那么李叔家六月份最多可用电多少度？【思路点拨】（1）根据题意即可得到方程组，然后解此方程组即可求得答案；（2）根据题意列不等式，解不等式．【答案与解析】解：（1）根据题意得：，解得：．（2）设李叔家六月份最多可用电x 度，根据题意得：200×0.61+200×0.66+0.92（x﹣400）≤300，解得：x≤450．答：李叔家六月份最多可用电450度．【总结升华】考查了一元一次方程组与一元一次不等式的应用．注意根据题意得到等量关系是关键．例3. 解不等式组： ，并求出正整数解。

不等式的概念、性质及解法考试要求：例题精讲：板块一、不等式的概念和性质☞不等式的概念1.不等式：用不等号表示不相等关系的式子，叫做不等式，例如：252,314,10,10,0,35a x a x a a -<-+>-++≤+>≥≠等都是不等式．2.常见的不等号有５种：“≠”、“＞”、“＜”、“≥”、“≤”．注意：不等式３≥２成立；而不等式３≥３也成立，因为３＝３成立，所以不等式３≥３成立．3.不等号“>”和“<”称为互为相反方向的符号，所谓不等号的方向改变，就是指原来的不等号的方向改变成与其相反的方向，如：“>”改变方向后，就变成了“<”。

【例1】 用不等式表示数量的不等关系．（1） a 是正数 （2）a 是非负数 （3）a 的相反数不大于1 （4） x 与y 的差是负数 （5）m 的4倍不小于8 （6）q 的相反数与q 的一半的差不是正数 （7）x 的3倍不大于x 的13（8） a 不比0大【解析】略．【答案】⑴0a >；⑵0a ≥；⑶1a -≤；⑷0x y -<；⑸48m ≥；⑹102q q --≤；⑺133x x ≤；⑻0a ≤．【巩固】用不等式表示：⑴ x 的15与6的差大于2； ⑵ y 的23与4的和小于x ；⑶ a 的3倍与b 的12的差是非负数； ⑷ x 与5的和的30%不大于2-．【解析】略．【答案】⑴ 1625x ->；⑵ 243y x +<；⑶ 1302a b -≥；⑷ 30%(5)2x +≤-．【巩固】用不等式表示：⑴a 是非负数； ⑵y 的3倍小于2； ⑶x 与1的和大于0；⑷x 与4的和大于1 【解析】注意表示不等关系的关键词语，如“非负数”、“不大于”、“不小于”、“大于或等于”、“小于或等于”【答案】⑴0a ≥；⑵32y <；⑶10x +≤；⑷41x +>☞不等式的性质 不等式基本性质：基本性质１：不等式两边都加上(或减去)同一个数(或式子)，不等号方向不变．如果a b >，那么a c b c ±>± 如果a b <，那么32(1)x a x +≥-基本性质２：不等式两边都乘以(或除以)同一个正数，不等号的方向不变．如果a b >，并且0c >，那么ac bc >(或a bc c >)如果a b <，并且0c >，那么ac bc <(或a bc c<)基本性质３：不等式两边都乘以(或除以)同一个负数，不等号的方向改变．如果a b >，并且0c <，那么ac bc <(或a bc c<)如果a b <，并且0c <，那么ac bc >(或ax b >)不等式的互逆性：如果a b >，那么b a <；如果b a <，那么a b >． 不等式的传递性：如果a b >，b c >，那么a c >．易错点：①不等式两边都乘(或除以)同一个负数，不等号的方向改变．②在计算的时候符号方向容易忘记改变．【例2】 ⑴ 如果a b >，则2a a b >+，是根据 ；⑵ 如果a b >，则33a b >，是根据 ； ⑶ 如果a b >，则a b -<-，是根据 ； ⑷ 如果1a >，则2a a >，是根据 ； ⑸ 如果1a <-，则2a a >-，是根据 ．【解析】略．【答案】⑴ 不等式两边都加上同一个数，不等号方向不变；⑵ 不等式两边都乘以同一个正数，不等号的方向不变； ⑶ 不等式两边都乘以同一个负数，不等号的方向改变； ⑷ 不等式两边都乘以同一个正数，不等号的方向不变； ⑸ 不等式两边都乘以同一个负数，不等号的方向改变．【巩固】利用不等式的基本性质，用“＜”或“＞”号填空．⑴ 若a b <，则2a _______2b ； ⑵ 若a b >，则4a -______4b -；⑶ 若362x ->，则x ______4-；⑷ 若a b >，0c >，则ac ______bc ；⑸ 若0x <，0y >，0z <，则()x y z -_______0．【解析】略．【答案】⑴ ＜；⑵ ＜；⑶ ＜；⑷ ＞；⑸ ＞．【巩固】若a b <，用“>”或“<”填空⑴2_____2a b ++； ⑵2_____2a b -- ⑶11______33a b ； ⑷____a b -- 【解析】略【答案】⑴“<”、⑵“<”、⑶“<”、⑷“>”【巩固】若a b <，则下列各式中不正确的是（ ）A.88a b -<+B.1188a b < C. 1212a b -<- D.22a b -<- 【解析】略 【答案】C【例3】 已知a b >，要使bm am -<-成立，则m 必须满足( )A ．0m >B ．0m =C ．0m <D ．m 为任意数【解析】0m -<，0m >．选择A ． 【答案】A【巩固】如果关于x 的不等式(1)1a x a +>+的解集为1x <，那么a 的取值范围是（ ）A.0a >B.0a <C.1a >-D.1a <-【解析】略 【答案】D【巩固】若0a b <<，则下列不等成立的是( )A ． 11a b< B ． 2ab b < C ． 2a ab > D ． ||||a b <【解析】略． 【答案】C【巩固】如果a b >，可知下面哪个不等式一定成立( )A ． a b ->-B ． 11a b< C ． 2a b b +> D ． 2a ab >【解析】略． 【答案】C【巩固】如果2x >，那么下列四个式子中：①22x x > ②2xy y > ③2x x > ④112x <正确的式子的个数共有 ( )A ．4个B ．3个C ．2个D ．1个【解析】①、③、④正确，所以选择B 【答案】B【巩固】根据a b >，则下面哪个不等式不一定成立( )A ． 22a c b c +>+B ． 22a c b c ->-C ． 22ac bc >D ． 2211a bc c >++ 【解析】选择C ，正确应为22ac bc ≥． 【答案】C☞不等式的解集 1.不等式的解：使不等式成立的每一个未知数的值叫做不等式的解．例如：4-，2-，0，1，2都是不等式2x ≤的解，当然它的解还有许多． 2.不等式的解集：能使不等式成立的所有未知数的集合，叫做不等式的解集．不等式的解集是一个范围，在这个范围内的每一个值都是不等式的解． 不等式的解集可以用数轴来表示．不等式的解与不等式的解集是两个不同的概念，不等式的解是指使这个不等式成立的未知数的某个值，而不等式的解集，是指使这个不等式成立的未知数的所有的值；不等式的所有解组成了解集，解集包括了每一个解． 在数轴上表示不等式的解集(示意图)：【例4】 下列说法中错误的是（ ）A.不等式28x -<的解集是4x >-；B.40-是不等式28x <-的一个解C.不等式6x <的正整数解有无数多个D.不等式6x <正整数解有无限个【解析】略 【答案】C【例5】 在数轴上表示下列不等式的解集：⑴1x <； ⑵2x ≥-； ⑶2x <-或1x ≥； ⑷21x -≤<【解析】略【答案】如图【巩固】在12-、1-、2-、0、3-、12、32-中，能使不等式32x +<成立的有（ ）A.4个B.3个C.2个D.1个【解析】略 【答案】B【巩固】下列不等式：①76->-；②a a >-；③1a a +>；④0a >；⑤210a +>，其中一定成立的有（ ）A.1个B.2个C.3个D.4个【解析】③、⑤ 【答案】B板块二、一元一次不等式的解法1.一元一次不等式：经过去分母、去括号、移项、合并同类项等变形后，能化为ax b <或ax b >的形式，其中x 是未知数，,a b 是已知数，并且0a ≠，这样的不等式叫一元一次不等式． ax b <或ax b >(0a ≠)叫做一元一次不等式的标准形式． 2.解一元一次不等式：去分母→去括号→移项→合并同类项(化成ax b <或ax b >形式)→系数化一(化成bx a>或bx a <的形式)【例6】 求不等式3(1)5182x x x +-+>-的解集． 【解析】对本例，首先应去分母，化成标准形式求解．去分母，得()()831845x x x ++>-- 去括号，得8338420x x x ++>-+ 移项， 得8348203x x x ++>+-合并同类项，得1525x >系数化为1，得53x >【答案】53x >【巩固】解不等式：5192311236x x x +--+≤【解析】略④③②①01231201231230123123213210【答案】9837 x≥【巩固】解不等式2110155364x xx++--≥，并把它的解集在数轴上表示出来．【解析】略【答案】2x≤．在数轴上表示解集如图所示．【巩固】解不等式2(1)34(1)5x x x+->++【解析】采用整体思想，2(1)3(1)24(1)x x x+-+->+，易得75x<-．【答案】75 x<-【巩固】当x为何值时，代数式2113x+-的值不小于354x+的值？【解析】解决此类问题首先应理解“不小于”的意思，进而再列出不等式，按照解一元一次不等式方法求解．依题意，得2135134 x x++-≥∴()() 42112335x x+-+≥8159124x x-+-≥717x-≥∴177x-≤所以，当177x-≤时，代数式2113x+-的值不小于354x+的值．【答案】177 x-≤【例7】求不等式4512x-＜1的正整数解．【解析】对于求不等式的正整数解，应先不考虑这一限制条件，按解一元一次不等式的方法求解后，再研究限制条件，便可达到目的．去分母，得4512x-<移项，合并，得417x<系数化为1，得174 x<∵求原不等式正整数解．∴1234x=，，，为原不等式正整解．【答案】1234x=，，，【巩固】不等式132x x +>的负整数解是_______． 【解析】略【答案】5-，4-，3-，2-，1-【巩固】不等式111326y y y +---≥的正整数解为__________． 【解析】解得3y ≤，故正整数解为1，2，3． 【答案】1，2，3．【巩固】求不等式12123x x +-≥的非负整数解． 【解析】首先解这个不等式，然后在不等式的解集中找出符合题意的解．12123x x +-≥，()()31221x x +-≥，33x x +≥4-2，5x --≥，5x ≤． 所以满足这个不等式的非负整数解为x =0，1，2，3，4，5．【答案】x =0，1，2，3，4，5．板块三、一元一次不等式组的解法1.一元一次不等式和它的解法 一般地，几个一元一次不等式的解集的公共部分，叫做由它们所组成的一元一次不等式组的解集2.解一元一次不等式组的一般步骤：①求出这个不等式组中各个不等式的解集：②利用数轴求出这些不等式的解集的公共部分，即可求出这个不等式组的解集注意：①利用数轴表示不等式的解集时，要注意表示数的点的位置上是空心圆圈，还是实心圆点；②若不等式组中各个不等式的解集没有公共部分，则这个不等式组无解3.由两个一元一次不等式组成的不等式组的解集的情况有如下四种：【例8】 解不等式组31422x x x ->-⎧⎨<+⎩，并把它的解集表示在数轴上．【解析】31422x x x ->-⎧⎨<+⎩12x x >-⎧⇒⎨<⎩12x ⇒-<<.∴原不等式组的解集是12x -<<. 在数轴上表示为：【答案】12x -<<【巩固】求不等式组2(2)43251x x x x -≤-⎧⎨--⎩＜ ①②的整数解．【解析】由①得 12x ≥-； 由②得 2x <．∴ 此不等式组的解集为122x -≤<．∴ 此不等式组的整数解为0，1．【答案】0，1【例9】 解不等式：32122x--<≤； 【解析】略【答案】解，由题意得，32123222x x -⎧-<⎪⎪⎨-⎪≤⎪⎩，解得5212x x ⎧<⎪⎪⎨⎪≥-⎪⎩，∴1522x -≤<【巩固】解不等式：2312142x x -≤≤+【解析】原不等式相当于：23241212x x -⎧≤⎪⎪⎨⎪≤+⎪⎩，解得1122x ≤≤．【答案】1122x ≤≤0123123【例10】 解不等式组：11141010372x x x x x ⎧-+>+⎪⎪--⎨⎪+>+⎪⎩；【解析】原方程组的解为5108x x x >=⎧/⎨>⎩且，综合得8x >且10x =/；【答案】8x >且10x =/【巩固】解不等式组：323(1)12123x x x x x +≥--⎧⎪-+⎨->-⎪⎩【解析】略 【答案】0x ≥【例11】 解不等式组：2(20)203(34)2521623x x x x x -+≥-+⎧⎪-+⎨<⎪⎩【解析】略． 【答案】2x ≤【巩固】解不等式组：734342555(4)2(4)3x x x x x -+⎧-≥-⎪⎪⎨⎪+-≤-⎪⎩【解析】略 【答案】无解.【例12】 解不等式组()121123621[41]43x x x x x x x --+⎧->-⎪⎪⎨⎪---⎪⎩①≥②。

在数轴上表示不等式的解集一、选择题（本题共计 10 小题，每题 3 分，共计30分，）1. 如图所示的不等式的解集是（）A.a>1B.a<1C.a≥1D.a≤12. 关于x的不等式x−a≥−2的解集如图所示，则a的值等于( )A.0B.1C.−1D.−23. 不等式组{x<2x≥12的解集在数轴上应表示为（）A. B. C. D.4. 下列不等式组的解集，在数轴上表示为如图所示的是()A.x>−1B.−1<x≤2C.−1≤x<2D.x≤25. 不等式8−4x≥0的解集在数轴上表示为（）A. B.C. D.6. 不等式组{x −1>0，−3x +6≥0的解集在数轴上表示为( ) A. B.C.D.7. 不等式组{3x −1>2，8−4x ≤0的解集在数轴上表示为( ) A.B.C.D.8. 如图，在数轴上表示的是下列哪个不等式( )A.x >−2B.x <−2C.x ≥−2D.x ≤−29. 不等式组{x −2≤0−x +1>0的解集为（ ） A.x <1B.x ≤2C.1<x ≤2D.无解10. 把不等式x ≥−2的解集在数轴上表示正确的是（ ） A. B.C. D.二、填空题（本题共计 10 小题，每题 3 分，共计30分，）11. 如图，张小雨把不等式3x>2x−3的解集表示在数轴上，则阴影部分盖住的数字是________．12. 已知两个不等式的解集在数轴上的表示如图所示，则这两个不等式组成的不等式组的解集是________．13. 写出如图所表示的某不等式组的解集________．14. 已知一个关于x的一元一次不等式组的解集在数轴上表示如图所示，则此不等式组的解集为________．15. 下图表示的不等式组的解集为________．16. 如图所示，数轴上所表示的不等式的解集分别是________．17. 关于x的不等式3x−2a≥−1的解集如图所示，则a=________．18. 关于x的不等式x−2a≤−3的解集如图所示，则a的值是________．19. 关于x 的不等式x −a ≥−2的解集如图所示，那么a =________．20. 在数轴上表示不等式组{x >3x >−1的解集如图，则不等式组{x <−1x ≤3的解集为________． 三、 解答题 （本题共计 10 小题 ，每题 10 分 ，共计100分 ， ）21. 解不等式（组）：（1），并把它的解集在数轴上表示出来．（2）22. 解不等式组并把它的解集在数轴上表示出来．23. 将不等式x >−2的解集表示在如图的数轴上．24. 解不等式组{x −1<1，x −5≥4x +1，并把解集在数轴上表示出来.25. 在数轴上表示下列不等式的解集．（1）x >2.5（2）x <−2.5（3）x ≥3．26. 解不等式组{3x +3≤2x +7①5(x −1)>3x −1②，并把它的解集在数轴上表示出来．27. （1）解不等式，并把解集在数轴上表示出来． 27.（2）解不等式组28. 解下列不等式(组)，并在数轴上表示解集．（1）（2）29. 解不等式组，请结合题意填空，完成本题的解答：（1）解不等式①，得（2）解不等式②，得（3）把不等式①和②的解集在数轴上表示出来(Ⅳ)原不等式的解集为 ．30. 写出下列各数轴所表示的不等式的解集：（1）（2）参考答案与试题解析在数轴上表示不等式的解集一、选择题（本题共计 10 小题，每题 3 分，共计30分）1.【答案】A【考点】在数轴上表示不等式的解集【解析】本题考查的是在数轴上表示不等式的解集，熟知实心圆点与空心圆点的区别是解答此题的关键．【解答】解：：数轴上1处是空心原点，且折线向右，∴不等式的解集是a>1．故选A．2.【答案】A【考点】在数轴上表示不等式的解集【解析】此题暂无解析【解答】解：x−a≥−2，x≥a−2.a−2=−2，得a=0.故选A.3.【答案】B【考点】在数轴上表示不等式的解集【解析】根据不等式画出数轴，实心圆点包括该点，空心圆圈不包括该点，大于向右小于向左．两个不等式的公共部分就是不等式组的解集．【解答】≤x<2，在数轴上可表示为：解：不等式组的解集是12故选：B．4.【答案】B【考点】在数轴上表示不等式的解集【解析】此题暂无解析【解答】解：由数轴可看出，从−1出发向右画出的线且−1处是空心圆，表示x>−1；从2出发向左画出的线且2处是实心圆，表示x≤2，所以表示的解集为−1<x≤2．故选B.5.【答案】B【考点】在数轴上表示不等式的解集【解析】此题暂无解析【解答】解：不等式8−4x≥0得，x≤2，所以不等式的解集在数轴上表示为选项B．故选B．6.【答案】C【考点】在数轴上表示不等式的解集【解析】先在数轴上表示不等式组的解集，再选出即可．【解答】解：由{x−1>0，−3x+6≥0，解得1<x≤2，在数轴上可表示为：故选C．7.【答案】A【考点】在数轴上表示不等式的解集【解析】先求出各个不等式的解集，再求出这些解集的公共部分即可．【解答】解：{3x−1>2①，8−4x≤0②，由①得，x>1，由②得，x≥2，故此不等式组的解集为x≥2，在数轴上表示为：故选A.8.【答案】C【考点】在数轴上表示不等式的解集【解析】根据数轴上不等式解集的表示方法得出此不等式组的解集，再对各选项进行逐一判断即可得到|x≥−2故选C．本题考查的是在数轴上表示一元一次不等式组的解集，根据题意得出数轴上不等式组的解集是解答此题的关键，注意实点和虚点的区别．【解答】此题暂无解答9.【答案】A【考点】在数轴上表示不等式的解集【解析】此题暂无解析【解答】解：{x−2≤0①−x+1>0②由①，得：x≤2，由②，得：x<1，则不等式组的解集为：x<1，故选A．10.【答案】B【考点】在数轴上表示不等式的解集【解析】将已知解集表示在数轴上即可．【解答】解：不等式x≥−2的解集在数轴上表示为：．故选B．二、填空题（本题共计 10 小题，每题 3 分，共计30分）11.【答案】−3【考点】在数轴上表示不等式的解集【解析】先求出不等式的解，即可求出答案．【解答】由3x>2x−3，解得：x>−3…阴影部分盖住的数字是：−3．故答案是：−3．12.【答案】x>4【考点】在数轴上表示不等式的解集【解析】根据在数轴表示不等式组解集的方法得出不等式组的解集即可．【解答】解：由图可知，两不等式解集的公共部分是x>4．故答案为：x>4．13.【答案】x>2【考点】在数轴上表示不等式的解集【解析】两个不等式的公共部分就是不等式组的解集，据此即可确定．【解答】解：不等式组的解集是：x>2．故答案是：x>2．14.【答案】−2≤x<3【考点】在数轴上表示不等式的解集【解析】数轴的某一段上面，表示解集的线的条数，与不等式的个数一样，那么这段就是不等式组的解集．实心圆点包括该点，空心圆圈不包括该点，大于向右小于向左．两个不等式的公共部分就是不等式组的解集．解：由图示可看出，从−2出发向右画出的线且−2处是实心圆，表示x≥−2；从3出发向左画出的线且3处是空心圆，表示x<3，不等式组的解集是指它们的公共部分．所以这个不等式组为−2≤x<3．15.【答案】−4≤x<1【考点】在数轴上表示不等式的解集【解析】数轴的某一段上面表示解集的线的条数，与不等式的个数一样，那么这段就是不等式组的解集．实心圆点包括该点，空心圆圈不包括该点，大于向右小于向左．【解答】解：由图示可看出，从−4出发向右画出的线且−4处是实心圆，表示x≥−4；从1出发向左画出的线且1处是空心圆，表示x<1，不等式组的解集是指它们的公共部分．所以这个不等式组的解集是−4≤x<116.【答案】x≥−2，x≥−1，x<1【考点】在数轴上表示不等式的解集【解析】根据利用数轴表示不等式的解集的方法，向右表示大于，向左表示小于，有等号用实心圆点，没有等号用空心圆圈表示，写出不等式的解集即可．【解答】解：观察图形可知，所表示的不等式的解集分别是，x≥−2，x≥−1，x<1．故答案为：x≥−2，x≥−1，x<1．17.【答案】−1【考点】在数轴上表示不等式的解集【解析】先把a当作已知条件表示出不等式的解集，再根据数轴上不等式的解集即可得出a的值．【解答】解：解不等式3x−2a≥−1得，x≥2a−1，3∵由数轴上不等式的解集可知x≥−1，∴2a−1=−1，3解得a=−1．故答案为：−1．18.1【考点】在数轴上表示不等式的解集【解析】先把a当作已知条件表示出x的取值范围，再与数轴上不等式的解集相比较即可得出结论．【解答】解：解不等式x−2a≤−3得，x≤−3+2a．∵数轴上不等式的解集为x≤−1，∴−3+2a=−1，解得a=1．故答案为：1．19.【答案】1【考点】在数轴上表示不等式的解集【解析】不等式x−a≥−2的解集是x≥a−2，数轴表示的解集是x≥−1．则a−2=−1，a=1．【解答】解：∵不等式x−a≥−2的解集为：x≥a−2，又不等式x−a≥−2的在数轴上的解集为x≥−1，∴a−2=−1，故a=1．20.【答案】x<−1【考点】在数轴上表示不等式的解集【解析】根据不等式的解集在数轴上表示方法画出图示求解即可．【解答】解：在数轴上表示如下：不等式组的解集是x<−1．故答案为：x<−1．三、解答题（本题共计 10 小题，每题 10 分，共计100分）21.【答案】（1）【答5(11>3，在数轴上表示见解析；（2）2≤x<4【考点】在数轴上表示不等式的解集（1）去括号、移项、合并同类项、系数化成1即可；（2）先求出每个不等式的解集，再求出不等式组的解集即可．【解答】（1）2x −11≤4(x −5)+32x −11<4x −20+32x −4x <−20+3+1−2x <−6x >3在数轴上表示为：−2−1012345(2{3x −(x −2)≥6①x +1>4x −13…解不等式①得：x ≥2解不等式②得：x <4…不等式组的解集是2≤x <422.【答案】加加1−2≤x ≤3【考点】在数轴上表示不等式的解集【解析】分别解两个一元一次不等式，再取解得公共部分，即为一元一次不等式组的解集，将其解集在数轴上表示出来【解答】 原式：{3(x −1)<5x +1①x−12≥2x −42 由①可得，3x −3<5x +1移项得−2x <4，解得x >−2由②可得，x +1≥4x −8移项得3x ≤9，解得x ≤3故原不等式组的解集为−2<x ≤3，在数轴上表示如图所示：23.【答案】解：不等式x >−2的解集表示在数轴上，如图所示：【考点】在数轴上表示不等式的解集【解析】根据不等式的解集在数轴上表示方法画出图示即可求得．【解答】解：不等式x>−2的解集表示在数轴上，如图所示：24.【答案】解：x−1<1，解得x<2；x−5≥4x+1，解得x≤−2.则不等式组的解集为：x≤−2.作图如下：【考点】在数轴上表示不等式的解集【解析】此题暂无解析【解答】解：x−1<1，解得x<2；x−5≥4x+1，解得x≤−2.则不等式组的解集为：x≤−2.作图如下：25.【答案】解：（1）；（2）；（3）【考点】在数轴上表示不等式的解集【解析】将各自的解集表示在数轴上即可．【解答】解：（1）；（2）；（3）26.【答案】解：不等式组的解集为2<x≤4．解集在数轴上表示略．【考点】在数轴上表示不等式的解集【解析】此题暂无解析【解答】解：不等式组的解集为2<x≤4．解集在数轴上表示略．27.【答案】（1）x\gt\dfrac{1}{4}}$ ，数轴表示见解析；(2))−1≤x<3【考点】在数轴上表示不等式的解集【解析】（1）根据一元一次不等式的解法，去分母，去括号，移项，合并同类项，系数化为1即可得解；（2）先求出两个不等式的解集，再求其公共解．【解答】（1）去分母得，6−(2x−1)<2(5x+2)去括号得，7−2x<10x+4移项得，−2x−10x<4−7合并同类项得，−12x<−3系数化为1得，x>14解集在数轴上表示如下：01 4①（2）{2x+5≤3(x+2) x−12≤x3(2)解不等式①得x≥−1解不等式②得，x<3所以，不等式组的解集为−1≤x<328.【答案】（1）x≤4，数轴表示见解析；（2）x≥−1；数轴表示见解析【考点】在数轴上表示不等式的解集【解析】（1）先去分母、去括号，再移项，合并同类项，把x的系数化为1即可；（2）分别求出各不等式的解集，再求出其公共解集，并在数轴上表示出来即可．【解答】（1）3x−25≥2x+13−13(3x−2)≥5(2x+1)−159x−6≥10x+5−15−x≥−4x≤4在数轴表示不等式的解集：（2）解⑩得：x≥−1解①得：x>−2不等式组的解集为：x≥−1在数轴上表示为：29.【答案】（1）x≥−1(2)x<2（2）图形见解析（3）−1≤x<2【考点】在数轴上表示不等式的解集【解析】（1）试题分析：根据不等式的解法，分别求解两个不等式，然后把它们表示在同一数轴上，最后写出解集即可．①【解答】（1）解不等式①，得x≥−1（2）解不等式②，得x<2（3）把不等式①和②的解集在数轴上表示出来−3−21012345(Ⅳ)原不等式的解集为−1≤x<230.【答案】解：（1）∵−2处是实心原点且折线向右，∴不等式的解集为：x≥−2；（2）∵4处是空心原点且折线向左，∴x<4．【考点】在数轴上表示不等式的解集【解析】（1）根据−2处是实心原点且折线向右即可得出结论；（2）根据4处是空心原点且折线向左即可得出结论．【解答】解：（1）∵−2处是实心原点且折线向右，∴不等式的解集为：x≥−2；（2）∵4处是空心原点且折线向左，∴x<4．。

课题利用数轴解决一元一次不等式组的解集问题课型复习1课时授课教师邵赛赛授课班级八（3）班岔路中学教学目标1、掌握利用数轴解决含字母的一元一次不等式的解集问题2、直观感受数形结合思想在这些问题中的应用3、直观感受分类讨论思想在这些问题中的应用重点利用数轴解决含参数的一元一次不等式组的解集问题难点根据条件在数轴上表示出图像、临界点是否取到是本节课教学的难点学具习题小测教学流程环节指正引入【师】让学生一起回忆如何解下列这两个一元一次不等式组：4x-3x-1≥2 4x-3x-1≤2-x≥-1 -x≤-1 【生】一起回答，回忆解不等式组的步骤及如何在数轴上表示解集【师】让学生自己尝试解另一个一元一次不等式组【设计意图】回顾旧知，同时让学生感知到在数轴上表示出两个不等式的解，如果有公共部分，那么这个不等式组有解，反之则无解例题探究一、教师带领学生探究含字母的一元一次不等式组求字母的取值范围【师】1.抛出一个变式：4x-3x-1≤2-x≤-a让学生们思考：如果这个不等式组有解，求出a 的取值范围。

2.引导学生思考：这个不等式组有解，意味着什么？【生】可以得到这两个不等式组的解有公共部分【师】那么你能在数轴上表示出这两个不等式的解吗？【生】学生通过解不等式可以发现，我们可以表示出第一个不等式，但是第二个不等式无法确定【师】进一步引导：那么我们可以确定第二个不等式的什么？【生】开口方向【师】那么你能通过这个开口方向结合第一个不等式的解得到在什么情况下这个不等式组会有公共部分吗？例题教学【生】学生自己尝试，画出了大致图像【师】进一步让学生观察数轴：这个时候你能发现a的位置有什么特点吗？【生】学生很容易可以感知到a＜3【师】提问：这个就是a的最终范围了吗？【生】学生比较容易会考虑到还有临界点的情况，因此可以确定出a最终的范围是a≤3【师】教师梳理解决这个问题的步骤并板书：1.求出不等式的解2.在数轴上表示出能确定的解3.根据题目要求确定大致图像4.确定字母的大致范围5.思考临界点是否可以取到6.确定字母的最终范围【设计意图】让学生从这道题目中能够感知如何来处理这类问题自主探究二、学生自主探究解决问题【师】提问：如果这个不等式组无解，能确定a的取值范围吗？【生】自己尝试使用刚才的步骤，并画出大致图像，最后再解决临界点问题决定最终的取值范围【师】进一步思考：如果这个不等式组恰有3个整数解，你能求出范围吗？【生】学生自己在习题小测中尝试【师】请学生自己上台操作，可以在这时候提出问题【设计意图】活学活用，让学生对这一步骤有更好的认识与应用例题练习一、基础练习【例题1】关于x的一元一次不等式组：x≥b 的解是x＞3,那么b的取值范围3x+2＜4x-1是多少？【例题2】关于x的一元一次不等式组：3x-1＜4（x-1）x＜m 的解是x＜3,那么m的取值范围是_________【设计意图】刚才探究的问题是＞与＜的关系，这个时候可以让学生来探究＞与＞以及＜与＜的关系，达到举一反三的效果【例题3】关于x的一元一次不等式组：x≥3m-1 无解，你能求出m的取值范围.x＜3【变式】关于x的一元一次不等式组：x≥3m-1X≤3 无解，你能求出m的取值范围吗？【设计意图】让学生感受到临界点能否取到的问题【例题4】对于任意实数m，n，定义一种运算：m※n=mn-m-n+3，例如：3※5=3×5-3-5+3=10请根据定义解决问题：若a＜2 ※x<7，且解集中有两个整数解，则a的取值范围是___________【例题5】关于x的一元一次不等式组：x-2m＜0x+m＞2 有解，那么m的取值范围是_________小【师】通过今天的学习，你们收获到了什么？结布置完成习题小测中的剩余题目作业谢谢各位老师批评指正！。

1。

如图,数轴上所表示关于的不等式组的解集是（）A。

B.C.D。

2.已知不等式组的两个不等式的解集在数轴上如图表示,那么这个不等式组的解集为（）A。

B。

C。

D.3。

一个不等式组的解集在数轴上的表示如图，则这个不等式组的解集是( ）A.B。

C。

D。

4.不等式组的解集在数轴上表示为如图，则原不等式组的解集为（ )A. B. C.D。

5。

如图，在数轴上表示某不等式组中的两个不等式的解集,则该不等式组的解集为（）A。

B。

C. D.6.如图，在数轴上表示某不等式组中的两个不等式的解集，则该不等式组的解集为（）A.B。

C。

D.7.如图，在数轴上表示某不等式组中的两个不等式的解集,则该不等式组的解集为( )A. B. C. D.8.把一个不等式组的解集表示在数轴上,如图所示,那么这个不等式组的解集是（）A.B。

9.把一个不等式组的解集表示在数轴上，如图所示，则该不等式组的解集为( ）A. B.D.C.10.不等式组的解集在数轴上可以表示为( ）A. B.C。

D.11.不等式组的解集在数轴上可以表示为（）A.B。

C.D。

12.不等式组的解集在数轴上可表示为（）A.B。

C。

D。

13。

不等式组的解集在数轴上可表示为（ )A. B.C.D。

14.不等式组的解集在数轴上的正确表示是( )A.B。

C.D.15。

如果一个不等式组的解集在数轴上的表示如图所示，则该不等式组的解集是（）A.B 。

C. D.16.已知点在第四象限，则的取值范围在数轴上表示正确的是( )A。

B。

C。

D.17。

已知点在第一象限，则的取值范围在数轴上表示正确的是（）A。

B。

C. D.18.如果点在第四象限,那么的取值范围在数轴上表示正确的是( ）A。

B。

C。

D.(完整版)在数轴上表示不等式的解集19。

如果点在平面直角坐标系的第四象限内,那么的取值范围在数轴上可表示为（）A. B.C.D。

20.如图所示，在数轴上表示某不等式中的两个不等式的解集，则该不等式组的解集为________．21。