1 En (n ) 2 (n 0,1,2,)
12.6-7 薛定谔方程小结 (Summary and revision) 1、薛定谔得出的波动方程
定义: 能量算符,动量算符和坐标算符 ˆ ˆ x i ˆx E i p x t x 2 哈密顿算符 ˆ H 2 U 2m 定态薛定谔方程(一维) 2 2 Ψ Ψ 条件:U=U(x,y,z) U ( x )Ψ i 2 2 m x t 不随时间变化。
3 i Y sin e 1 1 8 Y 3 cos 1 0 4
§ 12.8.2 氢原子 (Hydrogen atom)
一、氢原子的薛定谔方程
薛定谔方程提出后,首先被用于求解氢原子,取 得了巨大成功。在氢原子中,电子在原子核的库仑 场中运动,势能函数为: e2
即 m l 0,1,2,
由波函数的归一化条件
2
0
( ) d A
2
2
2
0
d 2 A 1
2
得 A 1 / 2 ,则角动量在z轴上的投影 ˆ l 的归一化本征波函数为:
m l ( ) 1 iml e , 2 m l 0,1, 2,...
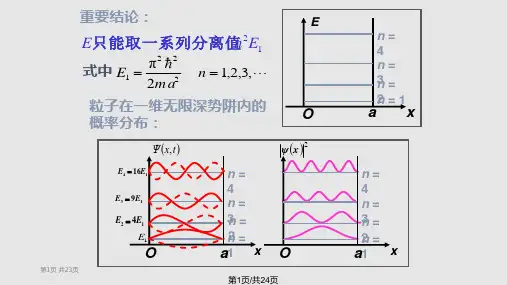
5 E 2 h 2
1 E 0 h 2 x
3 E1 h 2
零点能:谐振子的最低 能量不等于零,即它永 n=3 远不能静止不动。这与 经典力学截然不同, 是波 n=2 粒二向性的表现,可用 不确定关系加以说明。 n=1 3. 谐振子运动中可能 进入势能大于其总能 量的区域。
U ( x)
第二激发态(n=3) 帕邢系(m=3,红外光) 第一激发态(n=2)
巴耳末系(m=2, 可见光,400nm—700nm)