数学家范德蒙生平
- 格式:pdf
- 大小:99.28 KB
- 文档页数:4

范德蒙德行列式经典例题
范德蒙德行列式是超过三个未知数的线性方程组的一种简捷的求解方法,因为英国数学家范德蒙德(Thomas Fermont)发现此方法而得名,也称费马的行列式法,简写为F-L方法。
范德蒙德行列式是一种表格-数学形式,通过寻找满足增广矩阵=0的解,求出线性方程组的解。
这种实用技术在数学上有其自身的独特性,例如解非齐次线性方程组,解大型线性方程组等等。
它的优点是简单,易于使用,不需要数学推理的能力,通过轻松的计算,就可以找到答案。
范德蒙德行列式的典型应用就是对三元线性方程组求解。
这里有一个经典例题来介绍:令x+y+z=3, x-y-z=1, 2x+z=5,求解x,y,z的值:
根据范德蒙德行列式求解此例题,可以将方程组用增广矩阵表示出来:
|1 1 1 | |x | |3 |
|-1 -1 -1 | * |y | = |1 |
|2 0 1 | |z | |5 |
解增广矩阵,我们可以将它进行初等变换:
|1 1 1 | |1 0 -2 | |x | |3 |
|-1 -1 -1 | * |0 1 3 | * |y | = |1 |
|2 0 1 | |0 0 -1 | |z | |5 |
最后,我们得到:
x=4, y=-1,z=2
经过以上的例题,我们对这种求解三元线性方程组的方式有了详尽的了解。
范德蒙德行列式可以有效地、快速地求解含有三个未知数的线性方程组,最重要的是,不需要数学推理能力,只需要简单的计算就可以得到所有答案。

四阶范德蒙行列式计算四阶范德蒙行列式是一种特殊的行列式形式,它在数学中具有重要的应用。
范德蒙行列式是由比利时数学家亨利·范·德蒙于19世纪提出的,它是一种特殊的行列式形式,具有一些独特的性质和特点。
范德蒙行列式的计算公式如下:$$\begin{vmatrix}1 & a_1 & a_1^2 & a_1^3 \\1 & a_2 & a_2^2 & a_2^3 \\1 & a_3 & a_3^2 & a_3^3 \\1 & a_4 & a_4^2 & a_4^3 \\\end{vmatrix}$$其中$a_1, a_2, a_3, a_4$是给定的实数或复数。
通过使用范德蒙行列式的计算公式,我们可以计算出该行列式的值。
范德蒙行列式在数学中具有广泛的应用,尤其在线性代数和数值分析领域。
它可以用来解决方程组、计算多项式插值、线性回归等问题。
范德蒙行列式还可以用来求解最小二乘问题,即找到一条曲线或平面,使其与一组数据点的拟合误差最小。
范德蒙行列式的计算过程相对简单,只需要按照公式将给定的数值代入到行列式中,并按照行列式的性质进行计算即可。
例如,对于一个四阶范德蒙行列式,我们首先需要将给定的四个数值代入到行列式中,然后按照行列式的定义进行计算。
最后,我们可以得到该范德蒙行列式的值。
范德蒙行列式的计算结果通常是一个数值,它代表了给定的一组数值的某种特定关系。
通过计算范德蒙行列式,我们可以获得一些有关这组数值的重要信息。
例如,范德蒙行列式的值可以用来判断给定的数值是否线性相关,或者用来计算数值之间的相关系数。
除了计算范德蒙行列式的值外,还可以通过范德蒙行列式来解决一些实际问题。
例如,在数值分析中,我们经常需要根据一组数据点拟合一个多项式函数。
通过计算范德蒙行列式,我们可以找到最佳的多项式拟合函数,并根据范德蒙行列式的值来评估拟合的质量。

排列组合的数学历史小故事虽然数数始于结绳计数的远古时代,由于那时人的智力的发展尚处于低级阶段,谈不上有什么技巧。
随着人们对于数的了解和研究,在形成与数密切相关的数学分支的过程中,如数论、代数、函数论以至泛函的形成与发展,逐步地从数的多样性发现数数的多样性,产生了各种数数的技巧。
同时,人们对数有了深入的了解和研究,在形成与形密切相关的各种数学分支的过程中,如几何学、拓扑学以至范畴论的形成与发展,逐步地从形的多样性也发现了数形的多样性,产生了各种数形的技巧。
近代的集合论、数理逻辑等反映了潜在的数与形之间的结合。
而现代的代数拓扑和代数几何等则将数与形密切地联系在一起了。
这些,对于以数的技巧为中心课题的近代组合学的形成与发展都产生了而且还将会继续产生深刻的影响。
由此观之,组合学与其他数学分支有着必然的密切联系。
它的一些研究内容与方法来自各个分支也应用于各个分支。
当然,组合学与其他数学分支一样也有其独特的研究问题与方法,它源于人们对于客观世界中存在的数与形及其关系的发现和认识。
例如,中国古代的《易经》中用十个天干和十二个地支以六十为周期来记载月和年,以及在洛书河图中关于幻方的记载,是人们至今所了解的最早发现的组合问题甚或是架构语境学。
于11和12世纪间,贾宪就发现了二项式系数,杨辉将它整理记载在他的《续古抉奇法》一书中。
这就是中国通常称的杨辉三角。
事实上,于12世纪印度的婆什迦罗第二也发现了这种组合数。
13世纪波斯的哲学家曾讲授过此类三角。
而在西方,布莱士·帕斯卡发现这个三角形是在17世纪中期。
这个三角形在其他数学分支的应用也是屡见不鲜的。
同时,帕斯卡和费马均发现了许多与概率论有关的经典组合学的结果。
因此,西方人认为组合学开始于17世纪。
组合学一词是德国数学家莱布尼茨在数学的意义下首次应用。
也许,在那时他已经预感到了其将来的蓬勃发展。
然而只有到了18世纪欧拉所处时代,组合学才可以说开始了作为一门科学的发展,因为那时,他解决了柯尼斯堡七桥问题,发现了多面体(首先是凸多面体,即平面图的情形)的顶点数、边数和面数之间的简单关系,被人们称为欧拉公式。

范德蒙行列式.范德蒙行列式是线性代数中的一个重要概念,也是数学中的一个经典问题。
它在矩阵论、代数学、数论等领域中都有广泛的应用,被誉为"代数学中最基本的行列式"。
范德蒙行列式最初由比利时数学家范德蒙提出,它定义如下:对于序列$x_1,x_2,...,x_n$和序列$y_1,y_2,...,y_n$,我们定义范德蒙行列式为:$$ \begin{vmatrix} 1&x_1&x_1^2&...&x_1^{n-1}\\ 1&x_2&x_2^2&...&x_2^{n-1}\\\vdots&\vdots&\vdots&\ddots&\vdots\\1&x_n&x_n^2&...&x_n^{n-1} \end{vmatrix}=\prod_{1\leq i<j\leq n}(x_j-x_i) $$范德蒙行列式的值等于以$x_1,x_2,...,x_n$为根的$n$阶多项式在$y_1,y_2,...,y_n$处的插值多项式在$x_i = y_i$时的函数值。
当$x_1,x_2,...,x_n$两两不同的时候,范德蒙行列式的值为$\prod_{1\leq i<j\leq n}(x_j-x_i)$。
因此,范德蒙行列式常常被称为"互不相同的因子"。
范德蒙行列式具有一些重要的性质。
例如,当$x_1,x_2,...,x_n$其中有两个相同时,范德蒙行列式的值为0。
这是因为此时第$i$和$j$列完全相同,行列式的值完全由这两列的线性相关性决定,因此为0。
此外,范德蒙行列式还具有如下的递推公式:$$ D_n(x_1,x_2,...,x_n) = D_{n-1}(x_1,x_2,...,x_{n-1})\prod_{i=1}^{n-1}(x_n-x_i) $$其中$D_n(x_1,x_2,...,x_n)$表示$x_1,x_2,...,x_n$序列的$n$阶范德蒙行列式。

范德蒙德方程组的解范德蒙德方程组是一类常见的线性方程组,由荷兰数学家范德蒙德于18世纪初提出。
该方程组在数学、工程、物理等领域中都有着重要的应用,因此求解范德蒙德方程组一直是一个很有意义的问题。
范德蒙德方程组可以表示为:x1 + x2 + ... + xn = c1a1x1 + a2x2 + ... + anxn = c2...an-1x1 + an-2x2 + ... + a1xn = cn其中,a1、a2、...、an和c1、c2、...、cn为已知常数。
要求解范德蒙德方程组,首先需要了解矩阵的概念。
将范德蒙德方程组的系数和常数构成n阶方阵,称为系数矩阵A。
将未知量构成的列向量(即x1,x2,...,xn)称为未知量向量x,将常数构成的列向量(即c1,c2,...,cn)称为常数向量b,则范德蒙德方程组可以表示为Ax=b。
接下来,可以用高斯消元法求解范德蒙德方程组。
具体地,将方程组的系数矩阵A和常数向量b联合起来,形成增广矩阵,然后通过一系列初等行变换,将增广矩阵化为行最简阶梯矩阵。
对于化为行最简阶梯矩阵的增广矩阵,如果它的最后一行不全为零,则方程组无解;如果它的最后一行全为零且前面的每一行最左边的非零元素都在主对角线上,则方程组有唯一解;如果它的最后一行全为零但存在某一行最左边的非零元素不在主对角线上,则方程组有无数解。
需要注意的是,如果范德蒙德方程组的系数矩阵A是奇异矩阵(即行列式为零),则方程组无解或有无数解。
除了高斯消元法外,还可以使用矩阵的逆来求解范德蒙德方程组。
具体地,将方程组表示为Ax=b,将A的逆记为A-1,则x=A-1b。
在实际应用中,范德蒙德方程组的解法很多,需要根据具体情况选用最适合的方法。
同时,也需要注意实际应用中的误差问题,以免给结果带来误差。
总之,范德蒙德方程组的解法是求解线性方程组的重要部分,它在数学和应用领域中都有广泛的应用。
通过认真学习和理解范德蒙德方程组的求解方法,我们可以更好地应对实际问题,提高解决问题的能力。


范德蒙行列式的证明及其应用work Information Technology Company.2020YEAR范德蒙德行列式的证明及其应用摘要:介绍了n阶范德蒙行列式的定义,用递推法和拉普拉斯定理两种方法证明了范德蒙行列式,辅以实例研究了它在高等代数中的一些应用.向量空间理论用来解决线性问题;在线性变换理论、多项式理论和微积分理论中,主要用它构造线性方程组,进而应用克拉默法则或相关定理判断根的情况;在行列式计算中,主要运用范德蒙行列式的结论简化n阶行列式的计算过程.探究范德蒙行列式的历史及相关应用,为更进一步钻研其相关性质与应用奠定了良好的基础.关键词:范德蒙德行列式;向量空间;线性变换;应用1引言行列式本身有着长远的历史发展过程.它的理论最早可追溯到十七世纪末,在十九世纪末,其理论体系已基本形成.1683年,定义行列式概念的是日本数学家关孝和.同一年,德国数学家莱布尼茨首先开始使用指标数的系数集合来表示有三个未知数的三个一次方程组的系数.他这种解决方程组的思维方式为行列式理论的深入研究工作打下了坚实地基础.1771年,范德蒙创造性的在深入研究行列式理论的基础上,尝试解线性方程组.他这种勇于创新、敢于探索的精神为大家所认可,被公认为行列式的奠基人.他以现在被大家所熟悉的拉格朗日著作中的相关知识为理论基础,进行了反复的钻研,为后来研究群的概念奠定了良好的基础.第一个阐述行列式的数学家便是范德蒙.他运用自己的聪明才智、活跃的思维、批判的科研态度给出了现代代数书中二阶子式及余子式的定义,经过推理,演绎这一系列严谨的过程,完善了行列式的概念,并给出了行列式的数学符号记录.1772年,皮埃尔-西蒙.拉普拉斯在范德蒙著作和自身灵感的启示下,思维方法发生了变化,得出了子类型的概念.自此起,人们对行列式展开了单独的研究.人们为了深入了解行列式理论的本质特征,在19世纪展开了更深层次的研究.柯西积极吸收前人的劳动成果的同时,首次给出了行列式的系统理论.包括双重组标记法、行列式的乘法定理等.1832年至1833年,问卡尔.雅可给出了一个特殊的行列式的计算结果.基于此,1839年,卡塔兰发现了Jacobian行列式.范德蒙行列式整齐、完美的结构形式让我们体验到数学之美.简单探索它的应用,感悟数学的魅力.如果我们能够深入探索范德蒙行列式并灵活运用它,未来将更广泛的应用在数学各个领域.2范德蒙行列式的定义及证明2.1定义行列式1121121111---n nn n na a a a a a(1)称为n 阶的范德蒙(Vandermonde )行列式.由范德蒙行列式的定义,我们可以得出结论:对任意的(2)n n ≥阶范德蒙行列式等于n a a a ,,21这n 个数的所有可能的差)1(n i j a a j i ≤<≤-的乘积. 2.2范德蒙德行列式的证明 2.2.1用递推法证明12112211120011111221111a a a a a a a a a a D n n n n n n n n r a r r a r r a r n n n n n -----------−−−−−−→−---)()()()()()(12132312221133122123121a a a a a a a a a a a a a a a a a a a a a a a a n n n n n n n n c ---------−−−→−---展开按上式112312)())((----=n n D a a a a a a仿上做法,有2224231)())((-----=n n n D a a a a a a D 再递推下去,直到11=D .故)()()())()(())((112242311312j i ni j n n n n n a a a a a a a a a a a a a a a a D -=-------=∏≤<≤-2.2.2用Laplace 定理证明已知在n 级行列式nnnjn in iji n j a a a a a a a a a D111111= 中,除第i 行(或第j 列)的元素ij a 以外,行列式中其余元素全是零,则由Laplace 定理得:此行列式等于ij a 与它的代数余子式ij A 的乘积ij ij A a D =,在113121122322213211111----=n nn n n nnn a a a a a a a a a a a a D中,从最后一行开始,每一行减去它相邻前一行的1a 倍,得)()()(0)()()(0011111213231222113312211312a a a a a a a a a a a a a a a a a a a a a a a a D n n n n n n n n n ---------=---根据上述定理)()()()()()(1213231222113312211312a a a a a a a a a a a a a a a a a a a a a a a a D n n n n n n n n n ---------=---把每列的公因子提出来,得223223211312111)())((------=n nn n nn n a a a a a a a a a a a a D等式右边的第二个因子是1-n 阶行列式,用1-n D 表示,则上式中111312)())((----=n n n D a a a a a a D同样地,可以得到2224231)())((-----=n n n D a a a a a a D此处2-n D 是一个2-n 阶范德蒙行列式,一直继续下去,得)()())(())((122311312-------=n n n n n a a a a a a a a a a a a D)(1j i ni j a a -=∏≤<≤3范德蒙德行列式的应用3.1在向量空间理论中的应用在解析几何中,直观上我们经常认为一维、二维、三维向量空间是有意义的.当3>n 时,就没有直接的现实意义,但在高等代数这门课程中,n 维向量空间却是很常见的.当涉及线性相关问题时,通常我们通过构造同构映射的方法,将其转化为范德蒙行列式的问题,进而利用该行列式是否为零判断线性相关性.例 1.设V 是数域F 上的n 维向量空间,任给正整数n m ≥,则在V 中存m 个向量,其中任取n 个向量都线性无关]7[.证明:因为n F F ≅,所以只须在n F 中考虑.取)3,,3,3,1(121-=n a))3(,,3,1(2122-=n a))3(,,3,1(1m n m m a -= 令.1,)3()3(31)3()3(31)3()3(312112*********1m k k k D n k n k k k n k k k n k n nnnk≤≤≤≤≤=---121212)3()3(31)3()3(31)3()3(31222111---=n k k k n k k k n k k k n n n nD 是范德蒙行列式 且0≠n D ,所以n k k k a a a ,,,21 线性无关.3.2在线性变换中的应用线性变换是代数学中的一个重要概念,它的抽象性使我们在掌握这个概念时比较困难.此时,我们可以应用线性变换的定义及性质,考虑构造新函数,运用方程思想解决此类问题.例 2.设数域F 上的n 维向量V 的线性变换σ有个互异的特征值n λλλ,,,21 ,则与σ可交换的V 的线性变换是12,,,,-n e σσσ 的线性组合,这里e 为恒等变换.证明:由题意,由于σ是n 维向量V 上的线性变换,由线性变换的定义得n i i i i ,,2,1,)( ==αλασ,假设{}F k k V i ∈=|αλ是δ的不变子空间.根据不变子空间的特点,δ是与σ可交换的线性变换.令112210--++++=n n x x x e x σσσδ 且n i k i i i ,,2,1,)( ==αασ,则有以下方程组⎪⎪⎩⎪⎪⎨⎧+++=+++=+++=------111012121021111101n n n n nn n n n x x x k x x x k x x x k λλλλλλ (2) 由于线性方程组的系数矩阵的行列式)(j 1j i ni D λλ-∏=≤<≤,所以方程组(2)有唯一解,即就是12,,,,-n e σσσ 这n 个向量线性无关,题目得证. 3.3多项式理论中的应用在多项式理论中,许多题目涉及求根问题.一般情况下,我们可以用综合除法解决这类问题,但是在不知道多项式函数最高次项系数和常数项系数的条件下,我们可根据题意列出线性方程组.通过计算该线性方程组对应的系数矩阵的行列式是否为零判断根的情况,进而得出结论.例 3.设n n x c x c c x f +++= 110)(.若()f x 至少有1+n 个不同的根,则0)(=x f .证明:取121,,,+n x x x 为()f x 的1+n 个不同的根.则有由齐次线性方程组⎪⎪⎩⎪⎪⎨⎧=++++=++++=++++++000121211022222101212110n n n n n nn n n x c x c x c c x c x c x c c x c x c x c c (3) 其中n c c c ,,,10 看作未知量.且0)(1≠-∏=≤<≤j i ni j x x D .由于该方程组的等式右端的数均为零,由变形后的定理得:此方程组的解全为零.从而010====n c c c .即)(x f 是零多项式. 3.4微积分中的应用例4.设)(y f 在],[b a 上连续,在),(b a 内存在2阶导数]2[.证明:在b x a <<上有)(21)()()()(''c a b a f b f a x a f x f f=-----.这里),(b a c ∈证明:在],[b a 上构造函数)(1)(1)(1)(1)(2222b f b bx f x x a f a a y f y y y F =是范德蒙行列式,而函数)(y F 满足中值定理条件: 因)()()(y F x F a F ==.由中值定理,在),(b a 内存在b x x x a <<<<21,使0)()(2''1''==x F x F .故存在),(21x x c ∈,使0)(''=c F .即就是0)(1)(1)(1)(200)(222''''==b f b b x f x x a f a ac f c F .按行列式定义展开,即得所证. 3.5行列式计算中的应用涉及行列式计算问题时,经常运用行列式的性质解决问题,但其复杂多变的形式给行列式的计算增加了难度.对于具体的行列式,我们可以根据它的性质和定义解决.但对于那些结构特殊的、抽象的行列式,可通过观察、归纳总结,我们可以用特殊的方法迅速解决问题. (1)用提取公因式计算行列式例5.计算nn n n n n n D 222333222111= 解:由观察得到:该行列式中每行元素都分别是同一个数的不同方幂,并且其方幂次数从左至右依次增加,但它的次数是由1递加至n ,由行列式的相关性质,得1212121333122211111321---⨯⨯⨯⨯=n n n n n n n n D仔细观察,我们在右边的行列式中,从第2行开始,每行的1都写成该行中这个自然数的零次幂的形式,则它为n 阶范德蒙行列式,故)]1([)2()24)(23)(1()13)(12(!--------=n n n n n D n!1!2)!2()!1(! --=n n n (2)对换行列式中每一行(或每一列)的次序例6.计算1111)()()1()1(1111n b b b n b n b b b b b D n n n n n nn ------=---+ 分析:遇到这类问题,我们经常考虑运用行列式的六条性质来解决.为此,我们可以调换该行列式的次序,将它化为标准形式.解:把1+n 行依次与上面的每一行交换至第1行,第n 行依次与上面的每一行交换至第2行,以此类推,由自然数排列的逆序原则,共经过2)1(12)2()1(+=+++-+-+n n n n n 次交换 得到1+n 阶范德蒙行nn nn n n n n n n b b b n b b b nb b b D)()1()()1(1111)1(1112)1(1-------=---++)]1([)]1(2)[()2)(1()1(2)1(--------------=+n b n b b b b n b b b b b n n !1k nk =∏=(3)用拆行(列)计算行列式n 阶行列式中的i 行(列)由两个互异元素构成,且任意相邻两行(列)都含有共同元素,那么我们可以利用行列式的初等变换原则,通过消去一些分行中某一元素的方法,巧妙运用范德蒙行列式结论.例7.计算4阶行列式3424332332223121244233222211432111111111a a a a a a a a a a a a a a a a a a a a D ++++++++++++=分析:观察此行列式,我们可以看出:该行列式满足拆项行(列)计算行列式的特点,因此我们可以用该方法来解决这个问题.解:消去此行列式第二行每一项中的数字1,得:342433233222312124423322221143211111a a a a a a a a a a a a a a a a a a a a ++++++++ (4) 消去行列式 (4)第三行中加号前的元素,得:34243323322231212423222143211111a a a a a a a a a a a a a a a a ++++ (5) 再从行列式(5)中消去第4行中与第三行一样的元素得:343332312423222143211111aaaaa a a aa a a a因为该行列式为4阶范德蒙行列式,故)(11114134333231242322214321j i i j a a a a a a a a a a a a a a -∏==≤<≤ (4)用加边法计算行列式行列式的各行(或列)有明显范德蒙行列式定义的特点,但共同元素的方幂并不是按连续的自然数的顺序依次增加,此时我们可以考虑用加边法.例8.计算4级行列式444422221111d c b a dcbad c b a D =分析:D 不是范德蒙德行列式,但具有该行列式的特点,可考虑构造5级的范德蒙德行列式,再利用范德蒙德行列式的结果,间接求出D 的值. 解:构造5阶范德蒙行列式按第五列展开得45534523525155x A x A x A x A A D ++++= 其中3x 的系数为D D A -=-=+5445)1(又利用范德蒙行列式的结果得))()()(())()()()()((5d x c x c d b x b d b c a x a d a c a b D ----⨯------= ])([))()()()()((34 ++++-⨯------=x d c b a x c d b d b c a d a c a b其中3x 的系数为))()()()()()((d c b a c d b d b c a d a c a b D +++------=故))()()()()()((d c b a c d b d b c a d a c a b D +++------=4结束语范德蒙德行列式还可以应用于数学其他科目上.例如:在数学分析中,我们可以用它来构造高阶无穷小量,在线性代数中,我们可以用它来解决向量组线性相关性的证明问题.范德蒙行列式广泛的作用更加激发了我们深入探索它的欲望.我们希望在掌握相关的基础课程和基本理论之上,研究范德蒙行列式,用科学技术指导实践,更好的服务社会,促进经济发展.参考文献:[1]范臣君.范德蒙行列式在构造高阶无穷小的应用[J].吉林师范大学学报,2015.2(1) [2]万勇,李兵.线性代数[M].上海:复旦大学出版社,2006. [3]何江妮.范德蒙德行列式的证明及其应用[J].科教文化.[4]Kenneth C .Louden .Compiler Construction Principles and Practice[M].北京:机械工业出版社,2002.4444433333222225a 11111x d c b a x dc b a xd c b a x d c b D =[5]徐杰.范德蒙行列式的应用[J].科技信息,2009(17).[6]SERGE Lang.Linear Algebra(2nd ed)[M].NeW York:Columbia University,1988.[7]刘彦信.高等代数(第三版)[M].西北工业大学出版社,2004.[8]北京大学数学系几何与代数教研室代数小组.高等代数(第三版)[M].北京:高等教育出版社,2003.[9]北京大学数学系几何与代数教研室代数小组.高等代数(第三版)[M].北京:高等教育出版社,2003.Proof of Fandemengde Determinant and its ApplicationAbstract:This paper introduces the definition of n-order Vandermonde determinant. We proved Vandermonde determinant by recurisive method and Laplasse theorem , and explored its application in the higher algebra by some examples.Vector space theory is used to solve linear problem; It was used to structure linear equcations in linear transformation theory, polynomial theory and calculus theory , and judge the situation of root by Cramers rule or related theorem; In the calculation process of determinant calculation,It is maily used to simplify the n-order determinant. It laid a good foundation for further studying its properties and application by exploring the history of Vandermonde determinant and related applications.Keywords: fandemeng determinant; vectort space; linear trasformation; application- 10 -。

代数学发展历程在宽广的数学领域范围内,代数学只是其中的一个分支,一个部分.“代数学”这个名称,在我国是1859年正式开始使用的.那么什么是代数?代数学又是如何发展的呢?1847年,英国人伟烈亚力来到上海,他用中文写了一本《数学启蒙》,在序中说:“有代数、微分诸书在,余将续梓之.”这是第一次使用代数这个词来作为数学分科的名称.李善兰是我国清代数学家.1859年和伟烈亚力合译英国棣么甘(Augustus De Morgan)的“Elements of Algebra”正式定名为《代数学》.这是我国第一本代数学书,代数的名称就是这样来的.代数是对字母、字母表达式进行运算或变换的学问.在初等数学中字母代表数,在近代数学中字母可以代表更广泛的对象,如向量、张量、矩阵、变换等.代数的发展大致分为三个时期.第一个时期从九世纪的花拉子米始,到十六世纪止.这个时期人们把代数看成为对字母进行运算,关于字母公式的变换以及关于代数方程式的学问.这些就是目前中学代数的内容.第二个时期从十六世纪开始到十九世纪,这时意大利数学家解出了三次方程和四次方程.由此人们开始研究更高次的代数方程.代数的中心问题逐渐变为代数方程式的理论了.十九世纪谢尔的两卷本的代数问世,在这部书中代数被定义为方程式论.这在当时是个创举.在第二个时期内,行列式与矩阵的理论,二次型与变换的理论,特别是不变量的理论等代数工具也发展起来了.在这个时期内群论及不变量的理论的发展对几何学的发展起了重大影响.第三个时期从上世纪末到本世纪.这时在力学,物理以及数学本身越来越频繁地研究到一些对象,对这些对象也要考虑加法、减法,有时要考虑乘法和除法.这些对象中有矩阵、张量、旋量、超复数等.这样人们就不得不考虑某种更一般的集合,在这种集合中有某种运算,并满足一定的运算法则.这就是说,我们不得不考虑某种代数系统.这样一来,代数的目的是研究各种代数系统.这就是公理化,或抽象化的代数.说它是抽象的,是因为所考虑的代数系统是用字母表示的.说它是公理化的,是因为它只遵从作为它的基础的那些公理.有趣的是这样的代数系统无论就数学本身而言,或就它的应用而言都具有巨大意义.以下我是通过初等代数,高等代数以及抽象代数三个阶段的发展来研究代数学领域的发展的.1.初等代数初等代数是研究数字和文字的代数运算理论和方法,更确切的说,是研究实数和复数,以及以它们为系数的多项式的代数运算理论和方法的数学分支学科.初等代数是更古老的算术的推广和发展.在古代,当算术里积累了大量的,关于各种数量问题的解法后,为了寻求有系统的、更普遍的方法,以解决各种数量关系的问题,就产生了以解方程的原理为中心问题的初等代数.代数是由算术演变来的,这是毫无疑问的.代数和算术的主要区别,就在于前者引入未知量,根据问题的条件列出方程,然后解方程求出未知量的值.至于什么年代产生的代数学这门学科,就很不容易说清楚了.比如,如果你认为“代数学”是指解这类用符号表示的方程的技巧,那么,这种“代数学”是在十六世纪才发展起来的.如果我们对代数符号不是要求象现在这样简练,那么代数学可以上溯到更早的年代.大约在公元前2000年,巴比伦算术已经演化成为一种高度发展的用文字叙述的代数学.从载有数字表的文件中,可以获得巴比伦人的数系和数字运算方面的许多知识.他们既能用相当于代入一般公式的方法,又能用配方法来解二次方程,还讨论了某些三次方程和双二次(四次)方程.已经发现一块书板,它给出的数表不仅包括从1到30的整数的平方和立方,还包括了这个范围的整数组合.公元前2500年左右,埃及的草片文书(Ahmes)中有求一个未知量问题的解法,这个问题大体上相当于今日的一元一次方程.不过用的方法纯粹是算术的,并且在埃及人心目中这并不成其为一门独特的学科——解方程.公元200—1200年时期,印度人也在代数上获得一些进展.他们用缩写文字和一些记号来描述运算.印度人认识到二次方程有两个根,而且包括负根和无理根.在不定方程方面印度人超过了Diaphanous,印度人要求出所有整数解,而Diaphanous则只得出一个有理的解.印度人也研究了不定二次方程.他们解出了(其中不是平方数)这种类型的方程,并可看出这种类型对处理很重要.西方人将公元前三世纪古希腊数学家Diaphanous看作是代数学的鼻祖.而在中国,用文字来表达的代数问题出现得就更早了.“代数”作为一个数学专有名词,代表一门数学分支在我国正式使用,最早是在1859年.那年,清代数学家李善兰和英国人韦列亚力共同翻译了英国人棣么甘所写的一本书,译本的名称就叫做《代数学》.当然,代数的内容和方法,我国古代早就产生了,比如成书于公元一世纪初的《九章算术》中就有方程问题.在《九章》方程章中,经刘徽注给方程予以最早的定义:“程,课程也.群物总杂,各列有数,总言其实.令每行为率,二物者再程,三物者三程,皆如物数程之,并列为行,帮谓之方程”.这里的“群物总杂,各列有数,总言其实”是说每一行(相当于今称的方程式)的系数、未知数和常数项(此叫“实”)的组成方法.令每行为率(就是列出几个等式),二物者再乘(两个未知数,列两个等式或程式),三物三乘(三个未知数列三个等式或程式),如物数程之(就是有几个未知数,就列出几个等式或程式),用算筹并列成一方形,所以叫做方程.在方程的定义里,“程”就是“课”,而“课”的本义是试验,考核.正是在试验与考核的意义上,“程”与“课”是相通的.由“课”将数学应用题转化为盈亏类问题,而由“程”把问题布列为“方程”.这种问题模式化的思想和方法是一脉相承的.当然,在这里方程的定义是狭隘的,仅指线性方程组,但《九章》实际上还涉及到二次方程,而且已能用“带从开方术”(“从”读“纵”)求出方程的正根.共步骤相当于“配方法”.《九章》关于多元一次方程组的解法,是将其“所出率”用算筹摆成一个方阵,然后应用“遍乘,通约,齐同”三种基本演算,达到“消元”为目的.《九章》称解方程组的过程为“直除”,即现代的消元法.《九章》方程解法有方程术和正负术,刘徽注又添了新方程术,反映了我国古代方程理论发展的不同阶段.这些解法经刘徽注释,把它们作为比率理论的应用和发展,从而获得了统一的理论基础.初等代数的中心内容是解方程,因而长期以来都把代数学理解成方程的科学,数学家们也把主要精力集中在方程的研究上.它的研究方法是高度计算性的.要讨论方程,首先遇到的一个问题是如何把实际中的数量关系组成代数式,然后根据等量关系列出方程.所以初等代数的一个重要内容就是代数式.由于事物中的数量关系的不同,大体上初等代数形成了整式,分式和根式这三大类代数式.代数式是数的化身,因而在代数中它们都可以进行四则运算,服从基本运算定律,而且还可以进行乘方和开方两种新的运算.通常把这六种运算叫做代数运算,以区别于只包含四种运算的算术运算.在初等代数的产生和发展的过程中,通过解方程的研究也促进了数的概念的进一步发展,将算术中讨论的整数和分数的概念扩充到有理数的范围,使数包括正负整数、正负分数和零.这是初等代数的又一重要内容,就是数的概念的扩充.有了有理数,初等代数能解决的问题就大大地扩充了.但是,有些方程在有理数范围内仍然没有解.于是,数的概念再一次扩充到了实数,进而又进一步扩充到了复数.那么到了复数范围内是不是仍然有方程没有解,还必须把复数再进行扩展呢?数学家们说:不用了.这就是代数里的一个著名的定理——代数基本定理.这个定理简单地说就是n个方程有n个根.1742年12月15日,瑞士数学家欧拉曾在一封信中明确地做了陈述.后来另一个数学家德国的高斯在1799年给出了严格的证明.把上面分析过了的内容综合起来,组成初等代数的基本内容就是:三种数——有理数、无理数、复数.三种式——整式、分式、根式.中心内容是方程——整式方程、分式方程、根式方程和方程组.初等代数的内容大体上相当于现代中学设置的代数课程的内容,但又不完全相同.比如严格地说,数的概念,排列和组合应归入算术的内容;函数是分析数学的内容;不等式的解法有点像解方程的方法,但不等式作为一种估算数值的方法,本质上是属于分析数学的范围;坐标法是研究解析几何的…….这些都只是历史上形成的一种编排方法.初等代数是算术的继续和推广,初等代数研究的对象是代数式的运算和方程的求解.代数运算的特点是只进行有限次的运算.全部初等代数总起来有十条规则.这是学习初等代数需要理解并掌握的要点.这十条规则是:五条基本运算律:加法交换律、加法结合律、乘法交换律、乘法结合律、乘法对加法的分配律;两条等式基本性质:等式两边同时加上一个数,等式不变;等式两边同时乘以一个非零的数,等式不变;三条指数律:同底数幂相乘,底数不变指数相加;幂的乘方等于底数不变指数相乘;积的乘方等于乘方的积.初等代数学进一步向两个方面发展,一方面是研究未知数更多的一次方程组;另一方面是研究未知数次数更高的高次方程.这时候,代数学已由初等代数向着高等代数的方向发展了.2.高等代数初等代数从最简单的一元一次方程开始,一方面进而讨论二元及三元的一次方程组,另一方面研究二次以上及可以转化为二次的方程组.沿着这两个方向继续发展,代数在讨论任意多个未知数的一次方程组(也叫线性方程组)的同时还研究次数更高的一元方程组.发展到这个阶段,就叫做高等代数.高等代数是代数学发展到高级阶段的总称,它包括许多分支.现在大学里开设的高等代数一般包括两部分:线性代数、多项式代数.高等代数在初等代数的基础上研究对象进一步扩充,引进了许多新的概念以及与通常很不相同的量,比如最基本的有集合、向量和向量空间等.这些量具有和数相类似的运算特点,不过研究的方法和运算的方法都更加繁复.集合是具有某种属性的事物的全体;向量是除了具有数值还同时具有方向的量;向量空间也叫线性空间,是由许多向量组成的并且符合某些规则的集合.向量空间中的运算对象已经不只是数,而是向量了,其运算性质也有了很大的不同.古典代数学(即初等代数学)的中心课题是解方程问题.就方程本身而言,它是向两个方向发展的.一个方向是一元高次方程,另一个方向是多元一次方程组与多元高次联立方程组.前者发展成为后来的方程论(或多项式论)的研究,方程论的扩展便是高等代数学.到了十九世纪,还诱发了近世代数的出现.后者的发展形成了线性代数学,它的中心内容是行列式与线性方程组,矩阵及线性空间和线性变换的理论等.多项式是一类最常见,最简单的函数,它的应用非常广泛.多项式理论是以代数方程的根的计算和分布作为中心问题的,也叫做方程论.研究多项式理论,主要在于探讨代数方程的性质,从而寻找简易的解方程的方法.多项式代数所研究的内容,包括整除性理论,因式分解理论等.这些大体上和中学代数里的内容类似.多项式的整除性质对于解代数方程是很有用的.解代数方程无非就是求对应多项式的零点,零点不存在的时候,所对应的代数方程就没有解.我们知道一次方程叫线性方程,讨论线性方程的代数就叫做线性代数.线性代数学的兴起与发展是随着十七、十八世纪生产和科学技术的发展与要求而发展的.在线性代数中最重要的内容是行列式和矩阵.早在十七世纪和十八世纪初,行列式在解方程中就得到了发展.在线性方程组中,由于碰到方程的个数与未知量个数相等,所以就提出行列式这个词.行列式的概念最早是由十七世纪日本数学家关孝和提出来的,他在1683年写了一部叫做《解伏题之法》的著作,标题的意思是“解行列式问题的方法”,书中对行列式的概念和它的展开已经有了清楚的叙述.此外,1750年瑞士克莱姆(C ramer,1704--1752)的“克莱姆法则”也出现,但没有把行列式作为一个单独理论加以研究和阐述.欧洲第一个提出行列式概念的是德国的数学家莱布尼茨.1772年法国数学家范德蒙(Vandermonde,1735--1796)首先把行列式作为专门理论独立于线性方程组之外进行研究.故人们称他是行列式理论的奠基者.德国数学家雅可比于1841年发表了《论行列式的形式与性质》一文标志着行列式的系统理论的建立.行列式有一定的计算规则,利用行列式可以把一个线性方程组的解表示成公式,因此行列式是解线性方程组的工具.行列式可以把一个线性方程组的解表示成公式,也就是说行列式代表着一个数.因为行列式要求行数等于列数,排成的表总是正方形的,通过对它的研究又发现了矩阵的理论.矩阵概念和行列式一样是从解线性方程组中产生的.矩阵概念最早也出现在我国的《九章算术》方程章里.该书所说的“方程”实际是“矩阵”,所说的“方程术”的中心内容是对“方程”(即矩阵)施行“遍乘”与“直除”两种运算.在欧洲,由于有行列式的成果作为基础,1850年前后,矩阵的理论发展是非常迅速的.“矩阵”这个词是西勒维斯特(J.J.Sylvester,1814--1897)在1850年首先提出并使用的.他在碰到线性方程组的方程的个数与未知量个数不等,无法运用行列式概念时提出这个词的.1855年凯莱也引出了矩阵概念.他在文章中介绍他发现这一概念的思想时说:“我决不是通过四元数而获得矩阵概念的,它或是直接从行列式的概念而来,或是作为一个表达方程组的方便的方法而来的.”矩阵也是由数排成行和列的数表,行数和列数可以相等也可以不等.矩阵和行列式是两个完全不同的概念,行列式代表着一个数,而矩阵仅仅是一些数的有顺序的摆法.利用矩阵这个工具可以把线性方程组中的系数组成向量空间中的向量,这样对于一个多元线性方程组的解的情况,以及不同解之间的关系等等一系列理论上的问题,就都可以彻底地解决.矩阵的应用是多方面的,不仅在数学领域里,而且在力学、物理、科技等方面都有十分广泛的应用.1879年,德国数学家弗罗尼乌斯(Frobenius)引入矩阵秩的概念,英国数学家史密斯(H.J.S Smith,1826--1883)引入增广矩阵的概念,证明了n 个未知数m个方程的方程组相容的充分必要条件是其增广矩阵与非增广矩阵的秩相等.在行列式的理论和矩阵理论与应用发展的同时,线性空间以及与之相联系的线性变换的理论也蓬蓬勃勃地发展起来.由于采用向量的概念,可以使得解析几何特别地简单和清楚.向量可以相加,也可以相乘,并且满足如下运算规律:1.2.存在着“零元素”0,使得对任意x,3.对于任意元素x,存在着一个逆元素-x,使得4.5.6.7.8.这里x、y、z是线性空间里的元素,而1、、、是数.如果向量由它的坐标(即它在坐标轴上的射影)给出,那么在向量上进行的加法运算和数乘运算就相应着由它的坐标所组成的行(或列)上同名的运算.这样一来,由三个数组成的行或列就宜于几何上地解释作三维空间中的向量,同时在“行”(或“列”)上进行的运算就解释作为空间中向量上所进行的相应的运算,使得由三个数所组成行(或列)的代数在形式上与三维空间中的向量代数没有差别.线性方程组的系数、线性方程组的解是一个多元有序数组,在多元有序数组集合中引进加法、数乘运算,可以简化线性方程组的讨论,这使它们自然地将三维向量空间推广到n元有序数组集合的n维向量空间.不仅n维向量的集合具备上面所说的这些特性,就是同一类型的矩阵集合以及物理向量:力、速度、加速度等等也具备这些性质.完全是另外性质的数学对象,如一个变元的多项式全体、已知区间[a,b]上的连续函数的全体,线性齐次微分方程解的全体等等,也都具备这些性质.这些例子引导人们进一步推广向量空间的概念,这种空间的元素可以是任意数学对象或物理对象,这就引进了一般的线性空间的概念.同样它们满足加法和数乘一定的运算规律.在很多数学研究中需要改换变数,即从一组变数,…… ,过渡到与它们有函数关系的另一组变数,,…….例如,如果变数是平面上或空间中点的坐标,那么从一个坐标系过渡到另一个坐标系就引起坐标的一个交换,它将原来的坐标用新的坐标表出.此外,在研究一个物体从一个位置或状态变为另一个位置或状态时,如果它的位置或状态由变数的值所给出,变数的变换也会产生.线性变换是线性空间到自身的变换.线性空间中每一个线性变换都对应着一个方阵,变换本身可以用矩阵语言写成形状,这里x是原向量的坐标组成的列,y是变换后的向量的坐标组成的列,是变换的系数矩阵.欧氏空间中,将保持向量长度不变的线性变换称为正交变换.正交变换是将三维空间中坐标原点不动的旋转或旋转与对通过原点的某一平面的反射的联合对n维空间的推广.正交变换是非退化变换的重要特殊情形.线性空间与线性变换是线性代数的几何架构,数组向量和矩阵实际上是它们的代数形式,其间的转换枢纽是基底,就好象是平面和立体几何里的坐标系.然而线性代数里的向量空间却往往从抽象定义开始,这只是相当大的一般性.3.抽象代数在十八世纪后半叶,数学内部悄悄积累的矛盾已经开始酝酿新的变革.当时数学家们面临一系列数学发展进程中自身提出的、长期悬而未决的问题,其中在代数方面最突出的是:高于四次的代数方程的根式求解问题.在十九世纪初,这个问题已变得越发尖锐而不可回避.它们引起了数学家们集中的关注和热烈的探讨,并导致了代数学发展的新突破.在前面曾经说过,中世纪的阿拉伯数学家把代数学看成是解方程的学问.直到十九世纪初,代数学研究仍未超出这个范围.不过这时数学家们的注意力集中在了五次和高于五次的代数方程上.考虑一般的五次式更高次的方程能否像二、三、四次方程一样来求解,也就是说对于形如:(其中)的代数方程,它的解能否通过只对方程的系数作加、减、乘、除和求正整数次方根等运算的公式得到呢?遗憾的是这个问题虽然耗费了许多数学家的时间和精力,但一直持续了长达三个多世纪都没有解决.最终,阿贝尔(1802--1829)解决了五次和高于五次的一般方程的求解问题,证明了五次或五次以上方程不可能有代数解.即这些方程的根不能用方程的系数通过加、减、乘、除、乘方、开方这些代数运算表示出来.他还考虑了一些特殊的能用根式求解的方程,其中的一类被称为“阿贝尔方程”.在这一工作中,他实际上引进了“域”这一重要的近世代数概念,虽然他没有这样来称呼.但他没能解决判定已知方程是否可用根式来求解的问题.这个问题最终由另一个年轻的天才数学家法国的伽罗瓦彻底解决.在十九世纪,代数学的研究对象已突破了数(包括用符号表示的数)的范畴,这种突破是由伽罗瓦群的概念开始的.伽罗瓦20岁的时候,因为积极参加法国资产阶级革命运动曾两次被捕入狱,1832年4月,他出狱不久便在一次私人决斗中死去,年仅21岁.伽罗瓦在临死前预料自己难以摆脱死亡的命运,所以曾连夜给朋友写信,仓促地把自己生平的数学研究心得扼要写出,并附以论文手稿.他在给朋友舍瓦利叶的信中说:“我在分析方面做了一些新发现.有些是关于方程论的;有些是关于整函数的……公开请求雅可比或高斯,不是对这些定理的正确性而是对这些定理的重要性发表意见.我希望将来有人发现消除所有这些混乱对它们是有益的.”伽罗瓦死后,按照他的遗愿,舍瓦利叶把他的信发表在《百科评论》中.他的论文手稿过了14年,才由刘维尔(1809--1882)编辑出版了他的部分文章,并向数学界推荐.随着时间的推移,伽罗瓦的研究成果的重要意义愈来愈为人们所认识.伽罗瓦虽然十分年轻,但是他在数学史上做出的贡献,不仅是解决了几个世纪以来一直没有解决的高次方程的代数解的问题,更重要的是他在解决这个问题中提出了“群”的概念.在伽罗瓦之后,群的概念本身进一步发展,除了有限的、离散的群,又出现了无限群、连续群等,并由此发展了一整套关于群和域的理论,开辟了代数学的一个崭新的天地,直接影响了代数学研究方法的变革.从此,代数学不再以方程理论为中心内容,而转向对代数结构性质的研究,促进了代数学的进一步发展.在数学大师们的经典著作中,伽罗瓦的论文是最薄的,但他的数学思想却是光彩夺目的.代数对象的扩张,在十九世纪还沿着其他途径进行,先后产生了许多其他代数系统,例如四元数与超复数、域、理想等.十九世纪数学家还引进了环(戴德金,1871.克罗内克也研究过环并称之为“order”,希尔伯特首先使用了“ring”即环这个名称)和格(戴德金,1897)等.。

高等代数拓展内容之十四数学家关孝和、克莱姆、范德蒙、雅可比、凯莱简介关孝和(约1642—1708年):关孝和,字子豹,日本数学家。
1642年生于江户小石川(一说1637年生于上野国藤冈),1708年10月24日卒于江户。
出身于武士家庭,据载曾随数学名家高原吉种学过数学,人称数学神童。
后长期在江户任贵族家府家臣,掌管财赋,直到1706年退职。
他是日本古典数学(和算)的奠基人,也是关氏学派(或称关流)的创始人,在日本被尊称为算圣。
生前仅有一部《发微算法》(1674年)出版,逝世后又由学生荒木村英(1640—1718年)整理出版了一部遗稿《括要算法》(1712年)。
另有多种学派内部秘传的抄本著作,如《三部抄》(《解见题之法》、《解隐题之法》(1685年)、《解伏题之法》(1683年))、《七部书》(《开方翻变》、《病题明致》、《题术辩议》等)。
关孝和的主要成就有:改进了朱世杰《算学启蒙》(1299年)中的天元术算法,开创了和算独有的笔算代数;建立了行列式概念及其初步理论;完善了中国传入的数字方程的近似解法;发现方程正负根存在的条件;对勾股定理、椭圆面积公式、阿基米德螺线、圆周率的研究;开创“圆理”(径、弧、矢间关系的无穷级数表达式)研究;幻方理论;连分数理论等等。
他还写过数种天文历法方面的著作,如《授时历经立成》四卷、《授时历经立成立法》(1681年)、《授时发明》、《四余算法》(1697年)、《星曜算法》等。
其思想由弟子建部贤弘(1664—1739年)、松永良弼(1692—1744年)等人继承和应用,对日本数学的发展产生重要影响。
他的许多发现独立于西方而存在,有些在理论上更广泛,时间上也早些。
克莱姆(Cramer, Gabriel, 1704-1752)克莱姆,瑞士数学家。
1704年7月31日生于日内瓦。
1752年1月4日卒於法国塞兹河畔巴尼奥勒。
早年在日内瓦读书,1724 年起在日内瓦加尔文学院任教,1734年成为几何学教授,1750年任哲学教授。

范德蒙德行列式的应用探讨李珊珊摘要:范德蒙德行列式作为一种重要的、著名的行列式性质独特、形式优美,利用范德蒙德行列式能大大降低我们解题时的难度,起到事半功倍的效果. 本文将介绍范德蒙德行列式的概念及其性质,并且给出范德蒙德行列式在行列式计算,向量空间理论,线性变换理论,多项式理论和微积分问题五个方面较全面的具体应用,并对方法和技巧做出概括和总结.关键词:范德蒙德行列式;向量空间;线性变换;多项式;微积分中图分类号:O13Discussion on The Application of VandermondeDeterminantLi Shan-shanAbstract:The determinant is an important tool in Mathematics. It is the basis of the follow-up to the content system, such as linear equations, matrix, vector spaces and linear transformations. And it has a wide range of applications. As an important and famous determinant, Vandermonde determinant has not only unique structure, but also exquisite form. Using V andermonde determinant can greatly reduce our computation on solving problems. That is also the essence of using V andermonde determinant. This article will introduce the concept of V andermonde determinant and its calculation method and properties. What's more, this article will summarize V andermonde determinant in determinant computation, vector space, linear transformation theory, theory of polynomial and solving the problems of calculus in specific applications. And the article in the methods and techniques of Vandermonde determinant will make a summary.Keywords: V andermonde determinant; vector space; linear transformation; polynomial; Calculus1. 引言行列式在高等代数中是一个重要的数学工具,活跃在数学的各个分支. 行列式最早出现在16世纪关于求解线性方程组的问题中. 它的研究是伴随着线性代数的发展而发展起来的. 18世纪,法国著名的数学家范德蒙德(A.T.V andermonde ,1735-1796)将行列式的理论脱离线性方程组,而放到理论高度作为专门的理论进行研究,并在此基础上确立了行列式的一些性质,使行列式逐步成为一门独立的数学研究课题. 范德蒙德行列式是范德蒙德在1772年提出的一种著名的行列式,具有重要的理论研究价值和广泛的应用价值. 利用范德蒙德行列式和它的一些性质,我们可以使计算变得更为简单、直接,从而大大的提高对高等代数和数学分析中问题的计算速度. 自上世纪50年代以来,数学工作者对范德蒙德行列式的计算方法和在一些应用方面进行了研究. 不同研究者的角度、出发点和研究方向均不相同. 例如:北京大学第三版《高等代数》教材(高等教育出版社,王萼芳 石生明修订)中就提到了范德蒙德行列式在行列式计算和多项式根的存在性问题中的应用. 在一些高校的学报中我们也可以找到许多范德蒙德行列式的应用. 如:徐杰在《范德蒙德行列式的应用》(职校论坛,2009)中探讨了应用范德蒙德行列式证明向量的线性相关性问题;张文治、赵艳在《范德蒙德行列式应用三则》(北华航天工业学院学报,2007)中给出了构造范德蒙德行列式计算缺项行列式;程伟健、贺冬冬在《范德蒙德行列式在微积分中的应用》(大学数学,2004)中研究了利用范德蒙德行列式求高阶无穷小和证明K 阶导数极限存在问题等等. 综上所述,虽然国内外对范德蒙德行列式的应用研究比较多,但是对应用方法技巧的总结、归纳还比较欠缺和零散,系统性、规范性不足. 针对这种情况,本文较为系统的探讨范德蒙德行列式的应用,并对方法和技巧做出了总结.2. 范德蒙德行列式的概念及其性质定义 形如12322221231111123111...1........................n n n n n n na a a a a a a a a a a a ----的行列式,称为n 阶范德蒙德(V andermonde )行列式,记为n D .范德蒙德行列式构造独特、形式优美,并且有独特的性质. 下面将给出范德蒙德行列式的各种性质.首先,范德蒙德行列式拥有普通行列式的所有性质.(1)行列互换,行列式不变;(2)以一个数乘行列式的一行(列),相当于用这数乘此行列式;(3)行列式某一行(列)是两组数的和,则此行列式等于两个行列式的和; (4)如果行列式中两行(列)成比例,则行列式为零; (5)把一行(列)的倍数加到另一行(列),行列式不变; (6)行列式中两行(列)的位置,行列式符号改变.其次,我们给出范德蒙德行列式的五个更特别的性质. 性质1 对任意的(2)n n ≥,123222212311111123111...1......()..................n n n i j j i nn n n n na a a a D a a a a a a a a a a ≤<≤----==-∏,并且0n D =的充要条件是12,,...,n a a a 这n 个数中至少有两个相等,其中∏表示同类因子的乘积.证明: 对n 进行数学归纳. 当2n =时,211211n D a a a a ==-,结果正确. 假设对于1n -结论成立,即111()n i j j i n D a a -≤<≤-=-∏.则对于n 阶的情况有,在n D 中第n 行减去第1n -行的1a 倍,第1n -行减去第2n -行的1a 倍,以此类推,由下向上依次减去上一行的1a 倍,有2131122221231311212122123131111...10 0..................0...n n n nn n n n n n nna a a a a a D a a a a a a a a a a a a a a a a a a ---------=------=2131122221231311212122123131.....................n n nn n n n n n nna a a a a a a a a a a a a a a a a a a a a a a a ---------------=1232222213111232222123111...1...()()...().....................n n n n n n n na a a a a a a a a a a a a a a a a a -------.后面这是一个1n -阶的范德蒙德行列式,根据归纳法假设,它等于所有可能差(2)i j a a j i n -≤<≤的乘积,而包含1a 的差全在前面出现了. 因之,结论对n 阶范德蒙德行列式也成立. 根据数学归纳法,可知 1()n i j j i nD a a ≤<≤=-∏.由n D =1()i j j i na a ≤<≤-∏,可知0n D =的充要条件是12,,...,n a a a 这n 个数中至少有两个相等,证毕.注 2.1 因为T n n D D =,所以范德蒙德行列式还可以写成211112122221333211...1...1..................1...n n n n nnna a a a a a a a a a a a ----,行列式的值不变.性质2 若将范德蒙德行列式n D 顺时针旋转90 ,可得1211112222(1)1233312...1...1...1..................1n n n n n n n n n nnna a a a a a D a a a a a a --------=, 则有(1)(1)2(1)n n nn DD -=-.证明:因为T n n D D =,所以2111121222(1)21333211 (1)...1..................1...n n Tn n n n nnna a a a a a D D a a a a a a ----==,交换行列式的第1列与第n 列,则根据行列式的性质(6),行列式的值变为原来的-1倍,即有12111122221233312...1 (1)...1..................1n n n n n nnna a a a a a D a a a a a a ----=-, 再交换所得行列式的第2列和第1n -列,行列式变为原来的2(1)-倍,即有121111222221233312...1 (1)(1)...1..................1n n n n n n n n n nnna a a a a a D a a a a a a --------=-, 依次进行下去,得到最终的行列式12111122221233312...1...1...1..................1n n n n n n n n nnna a a a a a a a a a a a --------, 这样进行了(1)2(1)n n --次,于是1211112222(1)12233312...1...1(1)...1..................1n n n n n n n n n n n nnna a a a a a D a a a a a a ---------=-,结论得到证明.性质3 若将范德蒙德行列式n D 逆时针旋转90 ,可得(2)nD =212111121222211111 (1)...1 (1)...n n n nnn n n n n n n n n n n n a a a a a a a a a a a a --------------,有(1)(2)2(1)n n nn D D -=-.事实上,与性质2 的证明类似,依次交换行列式的两行,我们容易得到性质3 的结果.性质4 若将范德蒙德行列式n D 旋转180 ,可得(3)nD =111112122121211111............ (1)1...11n n n n n n n n n n nn n n n n a a a a a a a a a a a a -------------, 有(3)nn D D =.事实上,类似于性质2和性质3的证明,连续进行两次性质2 或性质3 的变换,就可以得到性质4 的结果.性质 5 n 阶准范德蒙1232222123(4)111112311111231231111n n nk k k k n k k k k nnnnnnx x x x x x x x D x x x x x x x x x x x x ----++++=1212,,...,1()n k n ki j p p p p p p j i nx x x x x --≤<≤=-∑∏,(1,2,,1)k n =- ,其中12,,,n k p p p - 是1,2,,n 中()n k -个数的一个正序排列,12,,,n kp p p -∑表示对所有()n k -阶排列求和.证明:在行列式中增补第(1)k +行和(1)n +列相应的元素. 考虑1n +阶范德蒙德行列式123222221231111111231231111112312311111()n n k k k k k n n kkkkknk k k k k nnnnnnnx x x x x x x x x xD x x x x x xx x x x x x x x x xx x x x x-----++++++=,按第1n +列展开,有11,12,11,11,111()1...()...()()inn n n i n n n n i j j i nD x A xA x A x A x x x x x x +++++++≤<≤=++++=---∏,其中,1(1,2,...,1)i n A i n +=+分别是21,,,...,n x x x 的代数余子式. 于是(4)(1)(1)1,1(1)n i ni n D A +++++=-. (1)对于11,12,11,11,111()1...()...()()inn n n i n n n n i j j i nD x A xA x A x A x x x x x x +++++++≤<≤=++++=---∏,由根与系数的关系(Vieta 定理)有12121,1,,...,1(1)...()n kn kn ii n p p p i j p p p j i nA x x x x x ---++≤<≤=--∑∏,由(1)式,可知1212(4),,...,1()n k n kni j p p p p p p j i nD x x x x x --≤<≤=-∑∏.3. 关于范德蒙德行列式应用的探讨前面介绍了范德蒙德行列式的概念及其性质,接下来我们将从行列式计算,向量空间理论,线性变换理论,多项式理论和微积分问题五个方面探讨范德蒙德行列式的应用.3.1 范德蒙德行列式在行列式计算中的应用范德蒙德行列式在行列式计算问题中起着举足轻重的作用. 利用范德蒙德行列式计算行列式已经被确立为一种特殊的方法被广泛使用. 下面我们来看几个例子:例1 计算行列式12322221232222123123111...1...........................n n n n n n nnnnnnx x x x x x x x D x x x x x x x x ----=.解:法1 构造1n +阶范德蒙德行列式1232222212312222212311111123123111...11......()...........................n n n n n n n n nn n n n n nnnnnnnx x x x x x x x x xD x x x x x x x x x x xx x x x x+----------=,则行列式D 为1()n D x +中元素1n x -的余子式,将行列式1()n D x +按1n +列展开得11,12,11,1()1...nn n n n n D x A xA x A +++++=+++,其中1n x -的系数为21,1,1,1(1)n n n n n n n A M M D ++++=-==-.又111()()...()()n n i j j i nD x x x x x x x +≤<≤=---∏,由根与系数的关系有1n x-的系数是1ni i x =-∑,因此在1()n D x +中1n x -的系数为11()nij i i i j nx x x =≤<≤--∑∏,所以11()nij i i i j nD x x x =≤<≤=--∑∏.法2 由范德蒙德行列式的性质 5,1212,,...,1()n k n ki j p p p p p p j i nD x x x x x --≤<≤=-∑∏,这里11()nij i i i j nD x x x =≤<≤=--∑∏.例2 证明n 阶循环行列式123121112122341.........()()...()..................n n n n n n n a a a a a a a a a a a a f f f a a a a εεε---=, 其中112()...n n f x a a x a x -=+++,12,,...,n εεε是所有的n 次单位根.证明:由于12,,...,n εεε是所有的n 次单位根,其所构成的n 阶范德蒙德行列式12322221231111123111...1......0..................n n n n n n nεεεεεεεεεεεε----≠,令123121123222211212311112341123...111...1................................................n nn n n n n n n n n n na a a a a a a a D a a a a a a a a εεεεεεεεεεεε-------=⋅,再由行列式的乘法,D 的第i 行第j 列的元素是2112311......i i n ij n i n i j n jj n i jd a a a a a εεεε----+-+-+=++++++,1,2,...,i n =,规定n k k a a +=.由于22cossin,(1,2,...,)m m m i m n ππεππ=+=,所以1mm εε=.于是(2)(1)(1)23111111......jj i j i j i ij n i n i n n i d a a a a a εεεε----+-+-+=++++++.又11nε=,因而(1)11,,1,2,...,j i ij j d d i j n ε-==.而右端的数恰好为行列式111231222221231311111231111...100...0 00...0. 00...0....................................nn n n n n nna a a a εεεεεεεεεεεε---- 的第i 行第j 列的元素,即上面的行列式也等于D ,且原循环行列式的值为11121...n a a a , 由行列式D 的形状可知:1112...(),1,2,...,n j j n jj a a a a f j n εεε-=+++==.于是再根据行列式的性质有1232341(1)(2)2345212121.........(1)()()...()..................n n n n nn a a a a a a a a a a a a f f f a a a a εεε---=-.通过对上述例题的分析,可归纳出构造和利用范德蒙德行列式来计算行列式的一些技巧:① 观察要计算的行列式是否具有范德蒙德行列式的的某些结构特征; ② 通过适当的方法构造范德蒙德行列式;③ 结合范德蒙德行列式以及题目的要求进行行列式的求解;④ n 阶循环行列式的解法以多项式理论为基础,结合范德蒙德行列式进行求解,方法简便易行,具有一定的实用价值.3.2 范德蒙德行列式在向量空间理论中的应用向量空间有时也称为线性空间,它是线性代数最基本的概念之一,也是我们在高等代数的学习中接触到的第一个抽象的概念. 向量空间与其子空间的关系问题,向量空间中向量的线性相关性问题都是向量空间研究的重点和难点,对逻辑推理有较高的要求. 对于判断、证明、计算向量空间中相应问题多往往比较难. 但将其与行列式适当结合,特别是与范德蒙德行列式相结合时,题目就会变得容易理解和掌握,如下面几个例子:例3 设V 是数域F 上的n 维向量空间,则V 不能写成它的有限个真子空间的并.证明:对n 进行数学归纳. 当1n =时,显然成立.设1n >时,令123,,,...,n a a a a 是V 的一组基,设1*12{...|}n n S a ka k a k F V -=+++∈⊂, 其中*F 是F 中元素的集合, 令*112:,...n n F S k e ke k e ϕ-→→+++,其中12,,...,n e e e 是单位向量, 则易证ϕ是双射,从而S 中有无穷多个不同的元素.设i V (1,2,...i t =)为V 的真子空间,则S 中的元素在i V 中的个数小于n . 否则,若,1,2,...,j i V j n β∈=,111121112........................................n n n nn n n a k a k a a k a k aββ--⎧=+++⎪⎨⎪=+++⎩,即211111121222222133333211...1...1 (1)...n n n n nn nnn a k k k a k k k a k k k a k k k ββββ----⎛⎫⎛⎫⎛⎫⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,则由,,1,2,...,,i j k k i j n i j ≠=≠知123,,,...,n a a a a 的系数行列式为范德蒙德行列式, 由范德蒙德行列式的性质 1知系数行列式非零,故,1,2,...,j k a V j n ∈=.进而,1,2,...,i V V i t ==矛盾, 从而S 中只有有限多个元素在1ti i V = ,即V 不能写成它有限个真子空间的并的形式.例4 设V 是数域F 上的n 维向量空间,任给正整数m n ≥,则在V 中存在m 个向量,其中任取n 个向量都线性无关.证明:因为n V F ≅,所以只需在n F 中考虑即可. 取211(1,,,...,)n a c c c -=,222122(1,,(),...,())n a c c c -=, .......................................... 21(1,,(),...,())m m n m m a c c c -=.令111222333212121211()...()1()...()1()...()...............1()...()nnnk k k n k k k n k k k n n k k k n c c c c c c D cc ccc c----=,121...,n k k k m ≤≤≤≤≤c为任意常数.因为111222333212121211()...()1()...()1()...()...............1()...()nnnk k k n k k k n k k k n n k k k n c c c c c c D cc ccc c----=是范德蒙德行列式,由范德蒙德行列式的性质1知n 0D ≠,所以12,,...,nk k k a a a 线性无关. 再由n V F ≅,所以结论成立.在向量空间理论中,我们经常会碰到需要用范德蒙德行列式转化的问题,通过转化我们很容易地得到所需要的结论. 而这就要求我们充分掌握范德蒙德行列式以及它的结构特征,达到灵活的使用.3.3 范德蒙德行列式在线性变换理论中的应用线性变换反映了线性空间中元素之间的一种最基本的联系,它是线性函数的推广.线性变换与行列式、矩阵联系密切. 利用行列式,尤其是范德蒙德行列式,来解决线性变换的特征值与特征向量问题能达到事半功倍的效果.例5 如果12,,...,s λλλ是线性变换的全部两两不同的特征值,(1,2,...)ii V i s λα∈=,则当12...0s ααα+++=时,必有12...0s ααα====.证明:注意到(1)i i i i s αλα=≤≤,对等式12...0s ααα+++=左右两边同时逐次作用,得112222211221111122 0...0 0s s s s s s s s s λαλαλαλαλαλαλαλαλα---+++=⎧⎪+++=⎪⎨⎪⎪+++=⎩, 用矩阵表示为()21111212222112333211 (1)...,,...,(0,0,...,0)1..................1...s s s s s sss λλλλλλαααλλλλλλ----⎛⎫ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭. (2)矩阵211112122221333211...1 (1)..................1...s s s s sss B λλλλλλλλλλλλ----⎛⎫ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭的行列式是范德蒙德行列式,并且由于12,,...,s λλλ两两不同,从而B 是可逆矩阵. 在(2)式两边右乘1B -,得()12,,...,(0,0,...,0)s ααα=,所以12...0s ααα====.例6 设数域F 上的n 维向量空间V 的线性变换σ有n 个互异的特征根12,,...,n λλλ则:(i )与σ可交换的V 的线性变换都是21,,,...,n e σσσ-的线性组合,其中e 为恒等变换;(ii )21,,,,...,n V αασασασα-∀∈线性无关的充要条件是1nii αα==∑,其中(),1,2,...,i i i i n σαλα==.证明:(i )设δ是与σ可交换的线性变换,且(),1,2,...,i i i i n σαλα==, 则{|}ii V k k F λα=∈是δ的不变子空间.令21121...n n xe x x x δσσσ--=++++且(),1,2,...,i i i k i n σαα==,则有下方程组21111211121212221221121.......................................n n n n n nn n n n k x x x x k x x x x k x x x x λλλλλλλλλ------⎧=+++⎪=+++⎪⎨⎪⎪=+++⎩ , (3) 可知(3)的系数行列式是范德蒙德行列式,且系数行列式1()i j j i nD λλ≤<≤=-∏,因为12,,...,n λλλ互异,由范德蒙德行列式的性质 1知0D ≠.于是方程组(3)有唯一解,所以δ是21,,,...,n e σσσ-的线性组合. (ii )先证明充分性. 因为1nii αα==∑,所以21111212222121123333211 (1)...(,,,...,)(,,...,)1..................1...n n n n n n n nnλλλλλλασασασαααααλλλλλλ-----=.且2111121222213331211...1...()01..................1...n n n i j j i nn n nnλλλλλλλλλλλλλλ---≤<≤-=-≠∏,因而211112122221333211...1...1..................1...n n n n n nnλλλλλλλλλλλλ----是可逆矩阵. 又由12,,...,n ααα是V 的一组基,可知21,,,...,n ασασασα-线性无关. 再证必要性.设12,,...,n e e e 是分别属于12,,...,n λλλ的特征向量,则12,,...,n e e e 构成V 的一组基,因而有1122...n n k e k e k e α=+++. 若0,1,2,...,i k i n ≠=则i i k e 是σ的属于i λ的特征向量,故结论成立. 若存在{1,2,...,}j n ∈使0j k ≠,不妨设12,,...,r k k k 全不为零, 而1...0r n k k +===,因而有1122...r r k e k e k e α=+++,则211111111212222222212112333333321......(,,,...,)(,,...,).....................n n n n r n rr rr rr r k k k k k k k k e e e k k k k k k k k λλλλλλασασασαλλλλλλ-----⎛⎫ ⎪ ⎪⎪= ⎪ ⎪ ⎪⎝⎭.利用范德蒙德行列式的性质 1可知21111111121222222221333333321...........................n n n n rr rr rr r k k k k k k k k A k k k k k k k k λλλλλλλλλλλλ----⎛⎫ ⎪ ⎪⎪= ⎪ ⎪ ⎪⎝⎭有一个r 阶子式不为零,所以秩(A )=r ,从而21(,,,...,)n r ασασασα-=秩, 又因为21,,,...,n ασασασα-线性无关,所以21(,,,...,)n n ασασασα-=秩.而r n <,矛盾. 所以1nii αα==∑,其中(),1,2,...,ii i i nσαλα==.在高等代数中,线性变换一直是最难的部分之一,题目的变化也很多. 在这些题目中,我们巧妙地运用范德蒙德行列式来使复杂的问题得到解决.3.4 范德蒙德行列式在多项式理论中的应用多项式是一类最常见、最简单的函数,它的应用非常广泛. 虽然多项式在整个高的代数中相对独立,然而却为高等代数的基本内容提供了理论依据. 研究多项式、多项式根的存在性问题、多项式求根问题是多项式理论中的重难点. 而多项式的求根问题又与行列式相关联,巧妙应用它们之间的联系,会起到化繁为简的作用. 例7 设01()n n f x c c x c x =+++ ,若()f x 至少有n+1个不同的根,则()0f x =. 证明:121,,,n x x x + 为()f x 的n+1个不同的根,则有齐次线性方程组20112112012222201121100n n nn n n n n n c c x c x c x c c x c x c x c c x c x c x +++⎧++++=⎪++++=⎪⎨⎪⎪++++=⎩. (4) 将01,,,n c c c 看作方程组(4)的未知量.因为方程组(4)的系数行列式D 是范德蒙行列式,且1()0i j i j nD x x ≤<≤=-≠∏,由克莱姆法则知方程组(4)只有零解,从而有010n c c c ==== ,即()f x 是零多项式.例8 设12,,,n a a a 是数域F 中互不相同的数,12,,,n b b b 是数域F 中任一组给定的不全为零的数,则存在唯一的数域F 上次数小于n 的多项式()f x ,使(),1,2,,i i f a b i n == .证明:设1011()n n f x c c x c x --=+++ , 由(),1,2,,i i f a b i n == ,知21011211112101222122210121n n n n n n n n n n c c a c a c a b c c a c a c a b c c a c a c a b------⎧++++=⎪++++=⎪⎨⎪⎪++++=⎩ . (5) 因为12,,,n a a a 互不相同,所以方程组(5)的系数行列式21111212222133312111()01...1n n n i j i j nn nnna a a a a a D a a a a a a a a ---≤<≤-==-≠∏.由克莱姆法则知方程组(5)有唯一解,即存在唯一的数域F 上次数小于n 的多项式1011()n n f x c c x c x--=+++ ,使得(),1,2,,i i f a b i n == .在多项式理论中,涉及到求根问题的有很多. 在分析有些题目时,范德蒙德行列式是能够起到关键的作用. 主要应用在多项式组成的方程组中,系数组成的行列式是范德蒙德行列式. 若系数行列式不为零(即范德蒙德行列式的性质 1),则由克莱姆法则知方程组只有零解. 熟练有效地运用范德蒙德行列式,对我们最终解决问题会有直接的帮助.3.5 范德蒙德行列式在微积分中的应用无穷大量、无穷小量、高阶导数和极限是微积分的主要内容. 这些概念的正确理解和掌握对学好微积分是必要的. 在解决这类问题的时候,有时巧妙地构造范德蒙德行列式变换形式,可以使问题得到容易理解的解答.例9 设f(x )在区间I 上n 阶可导(2)n ≥,若对x I ∀∈,0|()|f x M ≤,()|()|n n f x M ≤(0,n M M 是正常数).证明:若存在1n -个正常数121,,...,n M M M -,对x I ∀∈,()|()|(1,2,...,1)k k f x M k n ≤=-.证明:设121,,,,0,()n i i j a a a I a a a i j -∈≠≠≠ 且, 由泰勒公式,对1,2,...,1i n ∀=-,()()11()()()()!!k n n kni ii k fx ff x a f x a a k n ξ==+=++∑,由此得()()11()()()()!!k n n k nii i k fx fa f x a f x a k n ξ===+--∑,所以有()()101()|()||||()||()|||2,!!!k n n k nii i n k fx fA a f x a f x a M M k n n ξ==≤+++≤+∑其中11||m ax n ii n A a ≤≤-=.令1()1()()!kn k ii k a fx A x k ===∑,(x I ∈,1,2,...,1)i n =-, (6)则0|()|2!i n A A x M M n ≤+,(x I ∀∈,1,2,...,1)i n =-.由于方程组(6)的系数行列式D 为231111123122222311111...2!3!(1)!...2!3!(1)!..................2!3!(1)!n n n n n n n a a a a n a a a a D n a a a a n --------=--211112122221121333211111...1......1...1!2!...(1)!...............1...n n n n n n n n a a a a a a a a a a a a n a a a --------=-右边的行列式为121,,,n a a a - 的范德蒙德行列式,由0,()i i j a a a i j ≠≠≠知0D ≠,由克莱姆法则知,存在与x 无关的常数()()()121,,...,k k k n λλλ-,使得 1()()1()(),,1,2,...,1n k k i i i fx A x x I k n λ-==∀∈=-∑,由此推得x I ∀∈,1,2,...,1k n =-11()()()0011|()||||()|||(2)!n n k k k ii ik i i A fx A x M M M n λλ--==≤≤+=∑∑.例10 设函数f(x)在x=0附近有连续的n 阶导数,且'()(0)0,(0)0,...,(0)0n f f f≠≠≠,若121,,...,n p p p +是一组两两互异的实数,证明:存在惟一的一组实数121,,...,n λλλ+,使得当0h →时,11()(0)n i i i f p h f λ+=-∑是比n h 高阶的无穷小.证明:由题设的条件,可得()i f p h ,1,2,...,1i n =+在0x =处带有皮亚诺余项的麦克劳林展开式为:()110()(0)(),!k knk nk p h f p h fo h k ==+∑(1q )()220()(0)(),!kknk nk p h f p h fo h k ==+∑(2q ).........................()110()(0)(),!k knk nn n k p h f p h fo h k ++==+∑(1n q +)112211()()...()n n q q q λλλ++⨯+⨯++⨯,得111()11111()(0)(1)(0)()(0)()!n n nn k k kn ii i ii i i k i f p h f f p fh o h k λλλ+++====-=-++∑∑∑∑.当0h →时,若11()(0)n i i i f p h f λ+=-∑为比n h 高阶的无穷小,则有121112211222112211112211...1...0...0 0n n n n n n n n n n p p p p p p p p p λλλλλλλλλλλλ++++++++++=⎧⎪+++=⎪⎪+++=⎨⎪⎪+++=⎪⎩, 这是以121,,...,n λλλ+为未知数的线性方程组,其系数行列式有123122221231111231111...1......()0..................n n j i i j n nn nn n p p p p D p p p p p p p p p p ++≤<≤++==-≠∏,所以上述方程组有惟一的解,即存在唯一的一组实数121,,...,n λλλ+,使得当0h →时,11()(0)n i i i f p h f λ+=-∑为比n h 高阶的无穷小.例11 设f(x)至少有k 阶导数,且对某个实数α有()lim ()0,lim ()0k x x x f x x f x αα→∞→∞==. (7)试证:()lim ()0,0,1,2,...,i x x f x i k α→∞==,其中(0)()()fx f x =.证明:由条件(7)知,要证明()lim ()0i x x f x α→∞=,只要将()()i f x 写成()f x 与()()k f x 的线性组合的形式即可,利用泰勒公式,21'"(1)()()()()()...()()2!(1)!!k kk k m mmmf x m f x m f x f x fx fk k ξ--+=+++++- (8)其中,1,2,...,m x x m m k ξ<<+=.这是关于'"(1)(),(),...,()k f x f x f x -的线性方程组,其系数行列式为21211111...2!(1)!2212...2!(1)! (1)...2!(1)!k k k k D kkkk ----=-212121111 (1)122 (21133)...31!2!...(1)!...............1...k k k k kkk ---=-,后一行列式是范德蒙德行列式,且有212121111 (1)122...21!2!...(1)!133...3 (1)...k k k k kkk---=-,所以D =1. 于是可从方程组(8)把'"(1)(),(),.()k f x f x f x-写成()(1,2,...,)f x m m k +=与()()(1,2,...,)k m fm k ξ=的线性组合. 只需证明()lim ()lim ()0,(1,2,..,)k m x x x f x m x fm k ααξ→∞→∞+===.事实上,设x t x k ≤≤+,于是()()()lim ()lim ()()lim ()lim ()0,(0,)i i i x x x x x x x ft t ft t ft i k tt ααααα→∞→∞→∞→∞====.在此式中分别令,0t x m i =+=和令,m t i k ξ==,则得()lim ()lim ()0,(1,2,..,)k m x x x f x m x fm k ααξ→∞→∞+===.通过对以上例题的分析可以总结利用范德蒙德行列式解决微积分问题的方法: ① 首先要应用泰勒公式,写出函数在某点的近似解;② 根据构造函数在某点的泰勒展开形式,构造范德蒙德行列式;③结合范德蒙德行列式和题目本身进行求解.4. 结束语范德蒙德行列式为问题的求解提供了十分有效地手段. 对范德蒙德行列式的应用,不仅需要对范德蒙德行列式的形式、特点及性质熟练掌握,而且要能灵活的应用. 范德蒙德行列式应用中,构造范德蒙德行列式是解决问题的难点和关键点. 要巧妙地构造范德蒙德行列式进行解题,必须对高等数学的基础知识熟练掌握,要善于将知识衔接起来. 达到这样的境界非一日之功,因此只有打好高等数学的基础,不断地分析解决典型的题目,找出内在的规律,日积月累,对范德蒙德行列式的应用才能得到进一步的掌握.参考文献:[1] 北京大学数学系集合与代数教研室前代数小组.高等代数[M].北京:高等教育出版社,2003.[2] 华东师范大学数学系.数学分析[M]. 北京:高等教育出版社,2001.[3] 裴礼文.数学分析中的典型问题与方法[M].北京:高等教育出版社,2006.[4] 邹应.数学分析习题及其解答[M].武汉:武汉大学出版社,2001.[5] 章乐.几道考研试题的推广[J].大学数学,2003.[6] 牛莉.线性代数[M].北京:中国水利水电出版社,2005.[7] 吴良森,毛羽辉,宋国栋,魏木生,数学分析习题精解[M].北京:科学出版社,2002.[8] 易大义, 陈道琦. 数值分析引论[M].杭州: 浙江大学出版社, 1998.。
线性代数简史线性代数是高等代数的一个分支,是研究具有线性关系的代数量的一门学科。
历史上,线性代数中的第一个问题是关于解线性方程组的问题,而线性方程组理论的发展又反过来促进了作为工具的矩阵论和行列式理论的创立与发展,这些内容已成为我们线性代数教材的主要部分。
此外,近现代数学分析与几何学等数学分支的要求也促进了线性代数的进一步发展。
在线性代数中最重要的内容就是行列式和矩阵。
虽然表面上看,行列式和矩阵不过是一种语言或速记,但从数学史上来看,优良的数学符号和生动的概念是数学思想产生的动力和钥匙。
行列式:行列式的概念最初是由十七世纪日本数学家关孝和提出来的,他在1683年写了一部叫做《解伏题之法》的著作,标题的意思是“解行列式问题的方法”,书里对行列式的概念和它的展开已经有了清楚的叙述。
欧洲第一个提出行列式概念的是德国的数学家、微积分学奠基人之一--莱布尼兹(Leibnitz)。
1693 年4 月,莱布尼茨在写给洛比达的一封信中使用并指出了行列式,并给出方程组的系数行列式为零的条件。
1750 年,瑞士数学家克莱姆 (G.Cramer,1704‐1752) 在其著作《线性代数分析导引》中,对行列式的定义和展开法则给出了比较完整、明确的阐述,并给出了现在我们所称的解线性方程组的克莱姆法则。
1764年,法国数学家贝祖 (E.Bezout,1730‐1783) 将确定行列式每一项符号的方法进行了系统化;对给定了含n个未知量的n个齐次线性方程,贝祖证明了系数行列式等于零是该方程组有非零解的条件。
在行列式的发展史上,第一个对行列式理论做出连贯的逻辑的阐述,即把行列式理论与线性方程组求解相分离的人,是法国数学家范德蒙 (Vandermonde,1735‐1796) 。
范德蒙自幼在父亲的指导下学习音乐,但对数学有浓厚的兴趣,后来终于成为法兰西科学院院士。
特别地,他给出了用二阶子式和它们的余子式来展开行列式的法则。
1772 年,拉普拉斯在论文《对积分和世界体系的探讨》中证明了范德蒙提出的一些规则,推广了他的展开行列式的方法,用r行中所含的子式和它们的余子式的集合来展开行列式,这个方法现在仍然以他的名字命名。
线代1996年第三题范德蒙(原创实用版)目录1.范德蒙和他的线代问题2.1996 年第三题的背景和重要性3.线代问题的核心概念和方法4.范德蒙的解决方法和贡献5.范德蒙的线代问题对现代数学的影响正文范德蒙和他的线代问题范德蒙(Vandermonde)是一位法国数学家,他在线性代数领域有着重要的贡献。
线性代数是数学的一个重要分支,它研究的是向量、矩阵、线性方程组等概念。
范德蒙的贡献主要在于他提出了一个有名的线代问题,这个问题后来被称为“范德蒙问题”。
1996 年第三题的背景和重要性1996 年,国际数学奥林匹克竞赛(IMO)的第三题就是基于范德蒙问题提出的。
这道题目要求参赛者解决一个线性方程组,这个线性方程组的解是一个正整数解。
这道题目的难度非常高,它需要参赛者熟练掌握线性代数的知识,包括矩阵的性质、行列式、线性方程组等。
这个问题的解决方法对理解线性代数的基本概念和方法有着重要的意义。
线代问题的核心概念和方法要理解范德蒙问题,我们需要了解线性代数的一些核心概念和方法。
首先,线性代数研究的是向量和矩阵,向量是具有大小和方向的量,矩阵则是具有特定行和列的一个数表。
其次,线性方程组是线性代数的一个基本概念,它是一个包含多个线性方程的问题,每个线性方程中的变量都具有一次方。
最后,行列式是矩阵的一个重要性质,它用于判断矩阵是否可逆,以及求解线性方程组等问题。
范德蒙的解决方法和贡献范德蒙问题最早是由范德蒙在 18 世纪提出的,他提出了一种解决线性方程组的方法,这个方法被称为“范德蒙法”。
范德蒙法的基本思想是,通过构造一个新的矩阵,将原线性方程组转化为一个容易求解的形式。
这个方法对后来的线性代数研究产生了深远的影响,它成为了解决线性方程组的基本方法之一。
范德蒙的线代问题对现代数学的影响范德蒙的线代问题不仅对线性代数的研究有着重要的意义,而且对现代数学的发展也有着深远的影响。
它不仅推动了线性代数领域的研究,而且对其他数学领域,如微积分、概率论、统计学等也产生了重要的影响。
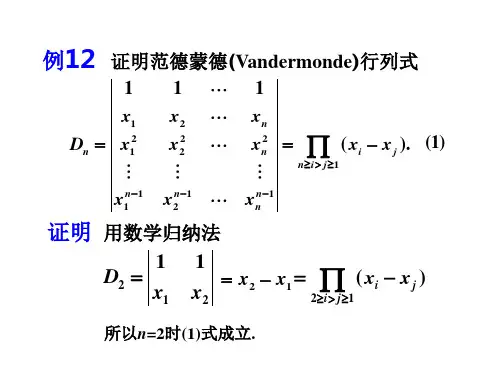
范德蒙德行列式的证明及其应用摘要:介绍了n阶范德蒙行列式的定义,用递推法和拉普拉斯定理两种方法证明了范德蒙行列式,辅以实例研究了它在高等代数中的一些应用.向量空间理论用来解决线性问题;在线性变换理论、多项式理论和微积分理论中,主要用它构造线性方程组,进而应用克拉默法则或相关定理判断根的情况;在行列式计算中,主要运用范德蒙行列式的结论简化n阶行列式的计算过程.探究范德蒙行列式的历史及相关应用,为更进一步钻研其相关性质与应用奠定了良好的基础.关键词:范德蒙德行列式;向量空间;线性变换;应用1引言行列式本身有着长远的历史发展过程.它的理论最早可追溯到十七世纪末,在十九世纪末,其理论体系已基本形成.1683年,定义行列式概念的是日本数学家关孝和.同一年,德国数学家莱布尼茨首先开始使用指标数的系数集合来表示有三个未知数的三个一次方程组的系数.他这种解决方程组的思维方式为行列式理论的深入研究工作打下了坚实地基础.1771年,范德蒙创造性的在深入研究行列式理论的基础上,尝试解线性方程组.他这种勇于创新、敢于探索的精神为大家所认可,被公认为行列式的奠基人.他以现在被大家所熟悉的拉格朗日著作中的相关知识为理论基础,进行了反复的钻研,为后来研究群的概念奠定了良好的基础.第一个阐述行列式的数学家便是范德蒙.他运用自己的聪明才智、活跃的思维、批判的科研态度给出了现代代数书中二阶子式及余子式的定义,经过推理,演绎这一系列严谨的过程,完善了行列式的概念,并给出了行列式的数学符号记录.1772年,皮埃尔-西蒙.拉普拉斯在范德蒙著作和自身灵感的启示下,思维方法发生了变化,得出了子类型的概念.自此起,人们对行列式展开了单独的研究.人们为了深入了解行列式理论的本质特征,在19世纪展开了更深层次的研究.柯西积极吸收前人的劳动成果的同时,首次给出了行列式的系统理论.包括双重组标记法、行列式的乘法定理等.1832年至1833年,问卡尔.雅可给出了一个特殊的行列式的计算结果.基于此,1839年,卡塔兰发现了Jacobian行列式.范德蒙行列式整齐、完美的结构形式让我们体验到数学之美.简单探索它的应用,感悟数学的魅力.如果我们能够深入探索范德蒙行列式并灵活运用它,未来将更广泛的应用在数学各个领域.2范德蒙行列式的定义及证明2.1定义行列式1121121111---n nn n na a a a a a(1)称为n 阶的范德蒙(Vandermonde )行列式.由范德蒙行列式的定义,我们可以得出结论:对任意的(2)n n ≥阶范德蒙行列式等于n a a a ,,21这n 个数的所有可能的差)1(n i j a a j i ≤<≤-的乘积. 2.2范德蒙德行列式的证明 2.2.1用递推法证明12112211120011111221111a a a a a a a a a a D n n n n n n n n r a r r a r r a r n n n n n -----------−−−−−−→−---)()()()()()(12132312221133122123121a a a a a a a a a a a a a a a a a a a a a a a a n n n n n n n n c ---------−−−→−---展开按上式112312)())((----=n n D a a a a a a仿上做法,有2224231)())((-----=n n n D a a a a a a D 再递推下去,直到11=D .故)()()())()(())((112242311312j i ni j n n n n n a a a a a a a a a a a a a a a a D -=-------=∏≤<≤-2.2.2用Laplace 定理证明 已知在n 级行列式 nnnj n in ij i nj a a a a a a a a a D 111111=中,除第i 行(或第j 列)的元素ij a 以外,行列式中其余元素全是零,则由Laplace 定理得:此行列式等于ij a 与它的代数余子式ij A 的乘积ij ij A a D =,在113121122322213211111----=n nn n n nnn a a a a a a a a a a a a D中,从最后一行开始,每一行减去它相邻前一行的1a 倍,得)()()(0)()()(0011111213231222113312211312a a a a a a a a a a a a a a a a a a a a a a a a D n n n n n n n n n ---------=---根据上述定理)()()()()()(1213231222113312211312a a a a a a a a a a a a a a a a a a a a a a a a D n n n n n n n n n ---------=---把每列的公因子提出来,得223223211312111)())((------=n nn n nn n a a a a a a a a a a a a D等式右边的第二个因子是1-n 阶行列式,用1-n D 表示,则上式中111312)())((----=n n n D a a a a a a D同样地,可以得到2224231)())((-----=n n n D a a a a a a D此处2-n D 是一个2-n 阶范德蒙行列式,一直继续下去,得)()())(())((122311312-------=n n n n n a a a a a a a a a a a a D)(1j i ni j a a -=∏≤<≤3范德蒙德行列式的应用3.1在向量空间理论中的应用在解析几何中,直观上我们经常认为一维、二维、三维向量空间是有意义的.当3>n 时,就没有直接的现实意义,但在高等代数这门课程中,n 维向量空间却是很常见的.当涉及线性相关问题时,通常我们通过构造同构映射的方法,将其转化为范德蒙行列式的问题,进而利用该行列式是否为零判断线性相关性.例1.设V 是数域F 上的n 维向量空间,任给正整数n m ≥,则在V 中存m 个向量,其中任取n 个向量都线性无关]7[.证明:因为n F F ≅,所以只须在n F 中考虑.取)3,,3,3,1(121-=n a))3(,,3,1(2122-=n a))3(,,3,1(1m n m m a -=令.1,)3()3(31)3()3(31)3()3(3121121212222111m k k k D n k n k k k n k k k n k n nnnk≤≤≤≤≤=--- 121212)3()3(31)3()3(31)3()3(31222111---=n k k k n k k k n k k k n n n nD 是范德蒙行列式 且0≠n D ,所以n k k k a a a ,,,21 线性无关.3.2在线性变换中的应用线性变换是代数学中的一个重要概念,它的抽象性使我们在掌握这个概念时比较困难.此时,我们可以应用线性变换的定义及性质,考虑构造新函数,运用方程思想解决此类问题.例2.设数域F 上的n 维向量V 的线性变换σ有个互异的特征值n λλλ,,,21 ,则与σ可交换的V 的线性变换是12,,,,-n e σσσ 的线性组合,这里e 为恒等变换.证明:由题意,由于σ是n 维向量V 上的线性变换,由线性变换的定义得n i i i i ,,2,1,)( ==αλασ,假设{}F k k V i ∈=|αλ是δ的不变子空间.根据不变子空间的特点,δ是与σ可交换的线性变换.令112210--++++=n n x x x e x σσσδ 且n i k i i i ,,2,1,)( ==αασ,则有以下方程组⎪⎪⎩⎪⎪⎨⎧+++=+++=+++=------111012121021111101n n n n nn n n n x x x k x x x k x x x k λλλλλλ (2) 由于线性方程组的系数矩阵的行列式)(j 1j i ni D λλ-∏=≤<≤,所以方程组(2)有唯一解,即就是12,,,,-n e σσσ 这n 个向量线性无关,题目得证. 3.3多项式理论中的应用在多项式理论中,许多题目涉及求根问题.一般情况下,我们可以用综合除法解决这类问题,但是在不知道多项式函数最高次项系数和常数项系数的条件下,我们可根据题意列出线性方程组.通过计算该线性方程组对应的系数矩阵的行列式是否为零判断根的情况,进而得出结论.例 3.设n n x c x c c x f +++= 110)(.若()f x 至少有1+n 个不同的根,则0)(=x f .证明:取121,,,+n x x x 为()f x 的1+n 个不同的根.则有由齐次线性方程组⎪⎪⎩⎪⎪⎨⎧=++++=++++=++++++000121211022222101212110n n n n n nn n n x c x c x c c x c x c x c c x c x c x c c (3) 其中n c c c ,,,10 看作未知量.且0)(1≠-∏=≤<≤j i ni j x x D .由于该方程组的等式右端的数均为零,由变形后的定理得:此方程组的解全为零.从而010====n c c c .即)(x f 是零多项式. 3.4微积分中的应用例4.设)(y f 在],[b a 上连续,在),(b a 内存在2阶导数]2[.证明:在b x a <<上有)(21)()()()(''c a b a f b f a x a f x f f=-----.这里),(b a c ∈证明:在],[b a 上构造函数)(1)(1)(1)(1)(2222b f b b x f x x a f a a y f y y y F =是范德蒙行列式,而函数)(y F 满足中值定理条件:因)()()(y F x F a F ==.由中值定理,在),(b a 内存在b x x x a <<<<21,使0)()(2''1''==x F x F .故存在),(21x x c ∈,使0)(''=c F .即就是0)(1)(1)(1)(200)(222''''==b f b b x f x x a f a ac f c F .按行列式定义展开,即得所证. 3.5行列式计算中的应用涉及行列式计算问题时,经常运用行列式的性质解决问题,但其复杂多变的形式给行列式的计算增加了难度.对于具体的行列式,我们可以根据它的性质和定义解决.但对于那些结构特殊的、抽象的行列式,可通过观察、归纳总结,我们可以用特殊的方法迅速解决问题. (1)用提取公因式计算行列式例5.计算nn n n n n n D 222333222111= 解:由观察得到:该行列式中每行元素都分别是同一个数的不同方幂,并且其方幂次数从左至右依次增加,但它的次数是由1递加至n ,由行列式的相关性质,得1212121333122211111321---⨯⨯⨯⨯=n n n n n n n n D仔细观察,我们在右边的行列式中,从第2行开始,每行的1都写成该行中这个自然数的零次幂的形式,则它为n 阶范德蒙行列式,故)]1([)2()24)(23)(1()13)(12(!--------=n n n n n D n!1!2)!2()!1(! --=n n n (2)对换行列式中每一行(或每一列)的次序例6.计算1111)()()1()1(1111n b b b n b n b b b b b D n nn nn nn ------=---+ 分析:遇到这类问题,我们经常考虑运用行列式的六条性质来解决.为此,我们可以调换该行列式的次序,将它化为标准形式.解:把1+n 行依次与上面的每一行交换至第1行,第n 行依次与上面的每一行交换至第2行,以此类推,由自然数排列的逆序原则,共经过2)1(12)2()1(+=+++-+-+n n n n n 次交换 得到1+n 阶范德蒙行nn nn n n n n n n b b b n b b b n b b b D)()1()()1(1111)1(1112)1(1-------=---++)]1([)]1(2)[()2)(1()1(2)1(--------------=+n b n b b b b n b b b b b n n !1k nk =∏=(3)用拆行(列)计算行列式n 阶行列式中的i 行(列)由两个互异元素构成,且任意相邻两行(列)都含有共同元素,那么我们可以利用行列式的初等变换原则,通过消去一些分行中某一元素的方法,巧妙运用范德蒙行列式结论.例7.计算4阶行列式3424332332223121244233222211432111111111a a a a a a a a a a a a a a a a a a a a D ++++++++++++=分析:观察此行列式,我们可以看出:该行列式满足拆项行(列)计算行列式的特点,因此我们可以用该方法来解决这个问题.解:消去此行列式第二行每一项中的数字1,得:342433233222312124423322221143211111a a a a a a a a a a a a a a a a a a a a ++++++++ (4) 消去行列式 (4)第三行中加号前的元素,得:34243323322231212423222143211111a a a a a a a a a a a a a a a a ++++ (5)再从行列式(5)中消去第4行中与第三行一样的元素得:343332312423222143211111aaaaa a a aa a a a因为该行列式为4阶范德蒙行列式,故)(11114134333231242322214321j i i j a a a a a a a a a a a a a a -∏==≤<≤ (4)用加边法计算行列式行列式的各行(或列)有明显范德蒙行列式定义的特点,但共同元素的方幂并不是按连续的自然数的顺序依次增加,此时我们可以考虑用加边法.例8.计算4级行列式444422221111d c b a d c b a d c b a D =分析:D 不是范德蒙德行列式,但具有该行列式的特点,可考虑构造5级的范德蒙德行列式,再利用范德蒙德行列式的结果,间接求出D 的值. 解:构造5阶范德蒙行列式33333222225a11111x d c b a x d c b a x d c b D =按第五列展开得45534523525155x A x A x A x A A D ++++=其中3x 的系数为D D A -=-=+5445)1( 又利用范德蒙行列式的结果得))()()(())()()()()((5d x c x c d b x b d b c a x a d a c a b D ----⨯------= ])([))()()()()((34 ++++-⨯------=x d c b a x c d b d b c a d a c a b其中3x 的系数为))()()()()()((d c b a c d b d b c a d a c a b D +++------=故))()()()()()((d c b a c d b d b c a d a c a b D +++------=4结束语范德蒙德行列式还可以应用于数学其他科目上.例如:在数学分析中,我们可以用它来构造高阶无穷小量,在线性代数中,我们可以用它来解决向量组线性相关性的证明问题.范德蒙行列式广泛的作用更加激发了我们深入探索它的欲望.我们希望在掌握相关的基础课程和基本理论之上,研究范德蒙行列式,用科学技术指导实践,更好的服务社会,促进经济发展.参考文献:[1]范臣君.范德蒙行列式在构造高阶无穷小的应用[J].吉林师范大学学报,2015.2(1) [2]万勇,李兵.线性代数[M].:复旦大学出版社,2006. [3]何江妮.范德蒙德行列式的证明及其应用[J].科教文化.[4]Kenneth C .Louden .Compiler Construction Principles and Practice[M].:机械工业出版社,2002.[5]徐杰.范德蒙行列式的应用[J].科技信息,2009(17).[6]SERGE Lang.Linear Algebra(2nd ed)[M].NeW York:Columbia University,1988. [7]刘彦信.高等代数(第三版)[M].西北工业大学出版社,2004.[8]北京大学数学系几何与代数教研室代数小组.高等代数(第三版)[M].:高等教育出版社,2003.[9]北京大学数学系几何与代数教研室代数小组.高等代数(第三版)[M].:高等教育出版社,2003.Proof of Fandemengde Determinant and its Application Abstract : This paper introduces the definition of n-order Vandermondedeterminant. We proved Vandermonde determinant by recurisive method and Laplasse theorem , and explored its application in the higher algebra by some examples.Vector space theory is used to solve linear problem; It was used to structure linear equcations in linear transformation theory, polynomial theory and calculus theory , and judge the situation of root by Cramers rule or related theorem; In the calculation process of determinant calculation,It is maily used to simplify the n-order determinant. It laid a good foundation for further studying its properties and application by exploring the history of Vandermonde determinant and related applications.Keywords: fandemeng determinant; vectort space; linear trasformation; application。
范德蒙范德蒙(Vandermonde,AlexandreTheophile法国数学家,1735~1796)范德蒙1735年生于巴黎。
蒙日的好友。
1771年成为巴黎科学院院士。
1796年1月1日逝世。
范德蒙在高等代数方面有重要贡献。
他在1771年发表的论文中证明了多项式方程根的任何对称式都能用方程的系数表示出来。
他不仅把行列式应用于解线性方程组,而且对行列式理论本身进行了开创性研究,是行列式的奠基者。
他给出了用二阶子式和它的余子式来展开行列式的法则,还提出了专门的行列式符号。
他具有拉格朗日的预解式、置换理论等思想,为群的观念的产生做了一些准备工作。
在高等代数中,一次方程组(即线性方程组)发展成为线性代数理论;而—、二次方程发展成为多项式理论。
前者是向量空间、线性变换、型论、不变量论和张量代数等内容的一门近世代数分支学科,而后者是研究只含有一个未知量的任意次方程的一门近世代数分支学科。
作为大学课程的高等代数,只研究它们的基础。
1683年关孝和(日本人)最早引入行列式概念(一说为莱布尼兹)。
关于行列式理论最系统的论述,则是雅可比1841年的《论行列式的形成与性质》一书。
在逻辑上,矩阵的概念先于行列式的概念;而在历史上,次序正相反。
凯莱在1855年引入了矩阵的概念,定义了矩阵的运算,零矩阵和单位矩阵,逆矩阵等等,在1858年发表了关于这个课题的第一篇重要文章《矩阵论的研究报告》。
19世纪,行列式和矩阵受到人们极大的关注,出现了千余篇关于这两个课题的文章。
但是,它们在数学上并不是大的改革,而是速记的一种表达式。
不过已经证明它们是高度有用的工具。
在牛顿幂和公式的影响下,对称函数开始引起人们的普遍关注。
1771年,法国著名数学家范德蒙(A.T.Vandermonde,1753~1796)在他的文章中提出重要的定理:“根的任何有理对称函数都可以用方程的系数表示出来”。
他还首次构造了对称函数表。
至此,人们对对称函数的兴趣就更加浓厚了,许多著名数学家如华林(E.Waring,1734~1798)、欧拉、克莱姆(G.Cramer,1704~1752)、拉格朗日(grange,1736~1813)、柯西(A.L.Cauchy,1789~1857)、希尔奇(M.Hirsch,1765~1851)等都在对称函数的研究中取得了重要结果。
范德蒙公式
范德蒙公式是一种经典的经济学理论,它被广泛应用于全球范围内的经济分析中。
范德蒙公式是由著名的经济学家约翰·范德蒙在1870年提出的,它表明了投资的有效性。
范德蒙公式的核心思想是,投资的有效性取决于资本收益率(或投资回报率)和资本投资的金额。
换句话说,资本的投资回报率越高,资本投资会产生越多的有效投资。
范德蒙公式的公式是:投资回报率=资本收益率(或投资回报率)/资本投资,这个公式被广泛用于投资决策中,因为它可以帮助投资者评估投资的有效性。
范德蒙公式也可以用来帮助企业分析投资项目的有效性。
投资者可以使用范德蒙公式来预测投资的未来收益,以及投资项目的有效性。
企业可以根据范德蒙公式来估算投资项目的收益和投资回报率,这样就可以更好地控制和管理风险。
此外,范德蒙公式还可以用于投资组合管理中,帮助投资者确定投资组合中各项投资的比例,从而最大化投资回报率。
投资者可以通过改变投资组合中不同投资的比例来调整投资回报率。
总的来说,范德蒙公式是一种非常有用的经济学理论,它可以帮助投资者和企业通过评估投资的有效性,最大化投资回报率,从而获
得最大的收益。
范德蒙公式的使用可以帮助投资者更好地管理风险,使投资收益最大化。
Alexandre-Théophile VandermondeBorn: 28 Feb 1735 in Paris, FranceDied: 1 Jan 1796 in Paris, FranceArticle by:J J O'Connor and E F RobertsonMarch 2001Edited by XiaJingbo, mail to: xjb@ Alexandre-Theophile Vandermonde's father was a medical doctor who was originally from Landrices but had spent 12 years in the Orient. He had set up a medical practice in Paris and was working there as a doctor when his son Alexandre-Théophile was born. He did not encourage his son to follow a medical profession but rather encouraged him to take up a career in music. Certainly he was not interested in mathematics when he was young. Alexandre-Théophile was awarded his bachelier on 7 September 1755 and his licencie on 7 September 1757.His first love was music and his instrument was the violin. He pursued a music career and he only turned to mathematics when he was 35 years old. It was Fontaine des Bertins whose enthusiasm for mathematics rubbed off on Vandermonde. Perhaps surprisingly he was elected to the Académie des Sciences in 1771 with little evidence of his mathematical genius other than his first paper which, although he was not a member at the time, was read to the Academy in November 1770. However, he did make quite a remarkable contribution to mathematics in this paper and three further papers which he presented to the Academy between 1771 and 1772. These four papers represent his total mathematical output and we will discuss their content below together with the views of a number of historians of mathematics on his contribution.Vandermonde's election to the Académie des Sciences did motivate him to work hard for the Academy and to publish other works on science and music. In 1777 he published the results of experiments he had carried out with Bézout and the chemist Lavoisier on low temperatures, in particular investigating the effects of a very severe frost which had occurred in 1776. Ten years later he published two papers on manufacturing steel, this time joint work with Monge and Bertholet. The aimof this research was to improve the steel used for bayonets but experimenting with different mixtures of iron and carbon. That he work closely with Monge reflected the fact that the two were very close friends, in fact he so close that he was known as femme de Monge.In 1778 Vandermonde presented the first of a two part work on the theory of music to the Académie des Sciences. The second part was presented two years later. This work Système d'harmonie applicable à l'état actuel de la musique did not propose a mathematical theory of music as one mighthave expected from someone who was an expert in both fields. On the contrary the aim of the work was to put forward the idea that musicians should ignore all theory of music and rely solely on their trained ears when judging music. As one might expect this proved a controversial work with musicians being sharply divided as to whether they agreed with Vandermonde or not. Despite the opposition of many musicians at first, the ideas put forward by Vandermonde gained favour over the years and by the beginning of the nineteenth century the Académie des Sciences had moved music from the mathematical area to the arts area. It is worth repeating that it is strange that a mathematician of the highest rank should have argued against music as a mathematical art, a position it had held since the days of ancient Greece.Positions which Vandermonde held include director of the Conservatoire des Arts et Métiers in 1782 and chief of the Bureau de l'Habillement des Armées in 1792. In the same year of 1792 he sat with Lagrange on a committee of the Académie des Sciences which had to examine the violon harmonique, a newly invented musical instrument. He was involved with the École Normale, which was founded in October 1794, and was on the team designing a course in political economy. His friend Monge was also involved with the École Normale as were Lagrange and Laplace. However the establishment only operated for six months after it opened in the Muséum d'Histoire Naturelle in January 1795 before being closed down.Like Monge, Vandermonde was a strong supporter of the Revolution which began with the storming of the Bastille on 14 July 1789. The politics of Revolution in France long before this event had been so exciting for Vandermonde that it diverted him from a possible longer mathematical and scientific career. However the truth of the matter is that he suffered from poor health all his life and, but for this, he might well have been able to be highly involved in politics yet continue with mathematical and scientific activities.Perhaps the name of Vandermonde is best known today for the Vandermonde determinant. While it is certainly true that he made a major contribution to the theory of determinants, yet nowhere in his four mathematical papers does this determinant appear. It is rather strange, therefore, that this determinant should be named after him and several authors have puzzled over the fact for some time. Lebesgue's conjecture in [3] (first published in 1940) that it resulted for someone misreading Vandermonde's notation, and therefore believing that this determinant was in his work, seems the most likely.Vandermonde's four mathematical papers, with their dates of publication by the Académie des Sciences, were Mémoire sur la résolution des équations (1771), Remarques sur des problèmes de situation (1771), Mémoire sur des irrationnelles de différens ordres avec une application au cercle (1772), and Mémoire sur l'élimination (1772).The first of these four papers presented a formula for the sum of the m th powers of the roots of an equation. It also presented a formula for the sum of the symmetric functions of the powers of such roots. Neither of these were new having appeared in Waring's work shortly before but, although he was aware of this Vandermonde claimed, rightly in my [EFR] opinion, that his approach was sufficiently different to make publication of these results for a second time worthwhile. The paper also shows that if n is a prime less than 10 the equation x n - 1 = 0 can be solved in radicals. Jones writes in [1]:- ... Vandermonde's real and unrecognised claim to fame was lodged in his first paper, in which he approached the general problem of the solubility of algebraic equations through a study of functions invariant under permutations of the roots of the equation.Kronecker claimed in 1888 that the study of modern algebra began with this first paper of Vandermonde. Cauchy states quite clearly that Vandermonde had priority over Lagrange for this remarkable idea which eventually led to the study of group theory.In his second paper Vandermonde considered the problem of the knight's tour on the chess board. This paper is an early example of the study of topological ideas. Vandermonde considers the intertwining of the curves generated by the moving knight and his work in this area marks the beginning of ideas which would be extended first by Gauss and then by Maxwell in the context of electrical circuits.In his third paper Vandermonde studied combinatorial ideas. He defined the symbol[p]n = p(p-1)(p-2)(p-3)...(p-n+1)and[p]-n = 1/(p+1)(p+2)(p+3)...(p+n).He gave an identity for the expansion of [x + y]n and also proved thatπ/2 = [1/2]1/2.[-1/2]-1/2It is interesting to note that at this time no notation existed for n! yet with his notation Vandermonde had defined something more general. Clearly[n]n = n!The final of Vandermonde's four papers studied the theory of determinants. Muir [4] claims that because of this paper Vandermonde was:-The only one fit to be viewed as the founder of the theory of determinants.The reason for this strong claim by Muir is that, although mathematicians such as Leibniz had studied determinants earlier than Vandermonde, all earlier work had simply used the determinant as a tool to solve linear equations. Vandermonde, however, thought of the determinant as a function and gaveproperties of the determinant function. He showed the effect of interchanging two rows and of interchanging two columns. From this he deduced that a determinant with two identical rows or two identical columns is zero. Finally he gave a remarkably clever notation for determinants which has not survived.References for Alexandre-TheophileVandermonde1.P S Jones, Biography in Dictionary of Scientific Biography (New York 1970-1990).Articles:2.H Lebesgue, L'oeuvre mathématique de Vandermonde, Thales, recueil des travaux del'Institut d'histoire des sciences IV (1937-39), 28-42.3.H Lebesgue, L'oeuvre mathématique de Vandermonde, Enseignement Math. (2) 1 (1956),203-223.4.T Muir, History of determinants V olume 3 (1920).5.J H Przytycki, History of the knot theory from Vandermonde to Jones, in XXIVth NationalCongress of the Mexican Mathematical Society (México City, 1992), 173-185.6.J J Tattersall, Who put the 'C' in A-T Vandermonde?, Historia Math.15 (4) (1988),361-367.7.J J Tattersall, Vandermonde's contributions to the early history of combinatorial theory,Eleventh British Combinatorial Conference, Ars Combin.25 (1988), C, 195-203.。