材料力学作业
- 格式:docx
- 大小:881.60 KB
- 文档页数:28
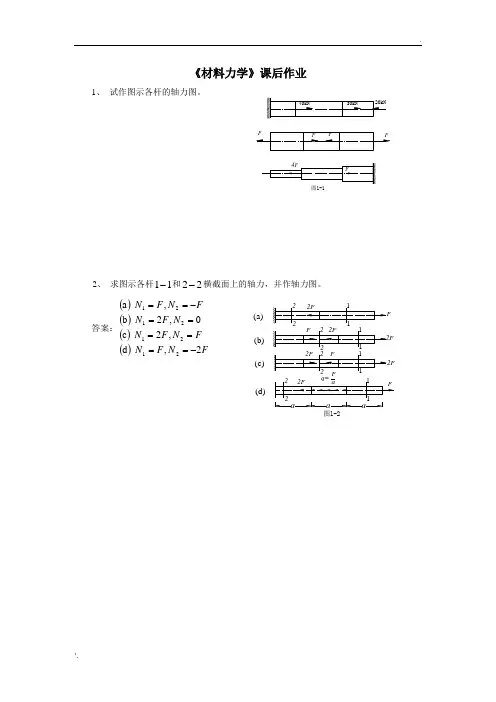

一、单选题(共 10 道试题,共 20 分。
)V1. 如图:A. AB. BC. CD. D正确答案:C 满分:2 分2.材料的持久极限与试件的()无关A.材料B.变形形式C.循环特征D.最大应力正确答案:D 满分:2 分在相同的交变载荷作用下,构件的横向尺寸增大,其()。
A.工作应力减小,持久极限提高;B.工作应力增大,持久极限降低;C.工作应力增大,持久极限提高;D.工作应力减小,持久极限降低。
正确答案:D 满分:2 分4.圆截面杆受扭转作用,横截面任意一点(除圆心)的切应力方向()A.平行于该点与圆心连线B.垂直于该点与圆心连线C.不平行于该点与圆心连线D.不垂直于该点与圆心连线正确答案:B 满分:2 分在以下措施中()将会降低构件的持久极限A.增加构件表面光洁度;B.增加构件表面硬度;C.加大构件的几何尺寸;D.减缓构件的应力集中正确答案:C 满分:2 分6. 如图2:A. AB. BC. CD. D正确答案:A 满分:2 分7.截面上的切应力的方向()A.平行于截面B.垂直于截面C.可以与截面任意夹角D.与截面无关正确答案:A 满分:2 分8. 如图3:A. AB. BC. CD. D正确答案:A 满分:2 分9. 如图1:A. AB. BC. CD. D正确答案:C 满分:2 分10.脆性材料的破坏应力是()A.比例极限B.弹性极限C.屈服极限D.强度极限正确答案:D 满分:2 分二、判断题(共 40 道试题,共 80 分。
)V1.拉伸(压缩)和弯曲组合变形时中性轴一定不过截面的形心。
A.错误B.正确正确答案:B 满分:2 分2.. 用力法解超静定问题时,由于有标准形式的正则方程,故不需要考虑静力平衡、变形几何和物理关系三个方面。
A.错误B.正确正确答案:A 满分:2 分3.当受力构件内最大工作应力低于构件的持久极限时,通常构件就不会发生疲劳破坏的现象。
A.错误B.正确正确答案:B 满分:2 分4.力法的正则方程是解超静定问题的变形协调方程。
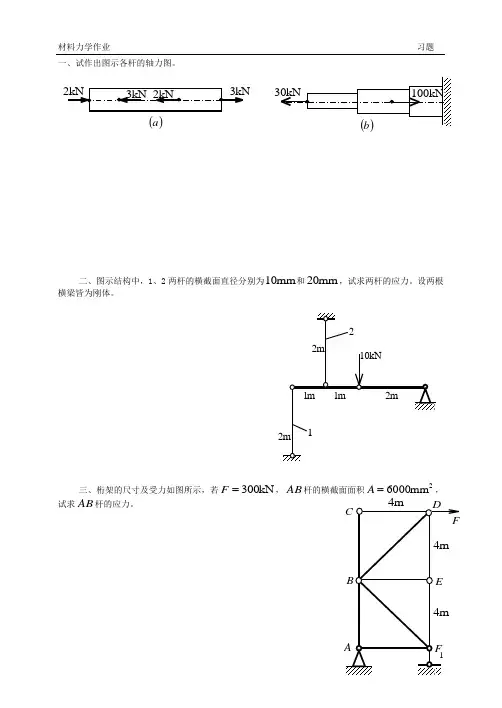
一、试作出图示各杆的轴力图。
二、图示结构中,1、2两杆的横截面直径分别为mm 10和mm 20,试求两杆的应力。
设两根横梁皆为刚体。
三、桁架的尺寸及受力如图所示,若kN 300=F ,AB杆的横截面面积2mm 6000=A ,试求AB杆的应力。
()a四、在图示简易吊车中,BC 为钢杆,AB为木杆。
木杆AB的横截面面积21cm 100=A ,许用应力[]MPa 71=σ;钢杆BC 的横截面面积22cm 6=A ,许用应力[]MPa 1602=σ。
试求许可吊重[]F 。
五、在低碳钢拉伸实验用的力与变形曲线及应力应变曲线中分别标出p F 、s F 、b F 和p σ、s σ、b σ,并回答在εσ-曲线中的p σ、s σ、b σ是否是构件中的真实应力,如果不是请另绘出强化阶段与颈缩阶段真实应力曲线的大致形状。
六、像矿山升降机钢缆这类很长的拉杆,应考虑其自重的影响。
设材料单位体积的重量为γ,许用应力为[]σ。
钢缆下端所受拉力为F ,且钢缆截面不变。
试求钢缆的允许长度及其总伸长。
钢缆横截面面积为A 。
B七、图示结构中,AB 为刚体,杆1、杆2、杆3的材料和横截面面积均相同,在杆AB 的中点C 作用铅垂方向的载荷F,试计算C 点的水平位移和铅垂位移。
已知:kN 20=F ,2321mm 100====A A A A ,mm 1000=l ,GPa 200=E 。
八、设横梁ABCD为刚体。
横截面面积为2mm 36.76的钢索绕过无摩擦的滑轮。
设kN 20=P ,试求钢索内的应力和C九、图示结构中,AB 为刚体,1、2杆的抗拉(压)刚度均为EA 。
试求两杆的轴力。
十、图示杆系的两杆同为钢杆,GPa200=E,C 061105.12-⨯=α。
两杆的横截面面积同为2cm 10=A 。
若AC 杆的温度降低C 200,而AB 杆的温度不变,试计算两杆的轴力。
十一、图示支架中的三根杆件材料相同,杆1的横截面面积为2mm 200,杆2的横截面面积为2mm 300,杆3的横截面面积为2mm 400。
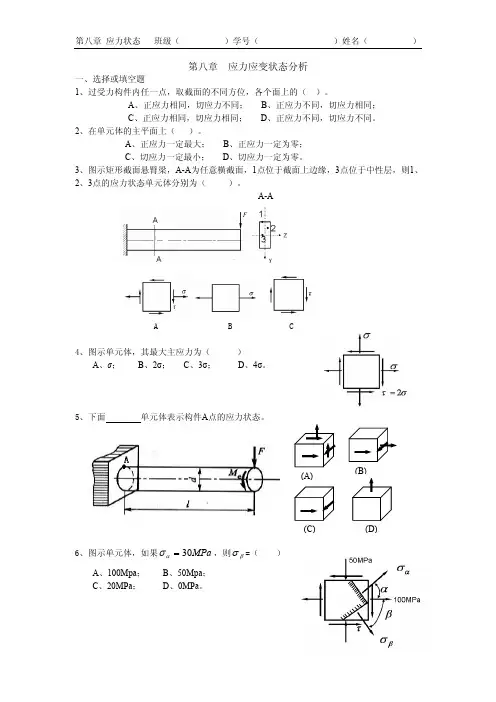
第八章 应力应变状态分析一、选择或填空题1、过受力构件内任一点,取截面的不同方位,各个面上的( )。
A 、正应力相同,切应力不同;B 、正应力不同,切应力相同;C 、正应力相同,切应力相同;D 、正应力不同,切应力不同。
2、在单元体的主平面上( )。
A 、正应力一定最大;B 、正应力一定为零;C 、切应力一定最小;D 、切应力一定为零。
3、图示矩形截面悬臂梁,A-A 为任意横截面,1点位于截面上边缘,3点位于中性层,则1、2、3点的应力状态单元体分别为( )。
A-AA B C4、图示单元体,其最大主应力为( )A 、σ;B 、2σ;C 、3σ;D 、4σ。
5、下面 单元体表示构件A 点的应力状态。
6、图示单元体,如果MPa 30=ασ,则βσ=( ) A 、100Mpa ; B 、50Mpa ; C 、20MPa ; D 、0MPa 。
(C)7、图示单元体应力状态,沿x 方向的线应变εx 可表示为( )A 、Eyσ; B 、)(1y x E μσσ−;C 、)(1x y E μσσ− ;D 、Gτ。
8、图示应力圆对应于单元体( )。
9、已知单元体及应力圆如图所示,σ1所在主平面的法线方向为( )。
A 、n 1;B 、 n 2;C 、n 3;D 、n4。
二、计算题1、已知应力状态如图所示,试用解析法计算图中指定截面上的正应力和切应力。
2、试画图示应力状态的三向应力圆,并求主应力、最大正应力和最大切应力。
3、边长为20mm的钢立方块置于刚性模中,在顶面受力F=14kN作用。
已知材料的泊松比为0.3,求立方体各个面上的正应力。
4、图示矩形截面梁某截面上的弯矩和剪力分别为M=10 kN.m,Q=120 kN。
试绘出截面上1、2、3、4各点的应力状态单元体,并求其主应力。
第九章 强度理论一、选择题或填空题 1、在冬天严寒天气下,水管中的水会受冻而结冰。
根据低温下水管和冰所受力情况可知( )。
A 、冰先破裂而水管完好;B 、水管先破裂而冰完好;C 、冰与水管同时破裂;D 、不一定何者先破裂。

第一章 绪 论一、选择题1 构件的强度是指( ),刚度是指( ),稳定性是指( )。
A. 在外力作用下构件抵抗变形的能力B. 在外力作用下构件保持其原有的平衡状态的能力C. 在外力作用下构件抵抗破坏的能力2 根据均匀性假设,可认为构件的( )在各点处相同。
A. 应力B. 应变C. 材料的弹性常数D. 位移 3 下列结论中正确的是( )A. 内力是应力的代数和B. 应力是内力的平均值C. 应力是内力的集度D. 内力必大于应力 4 下列说法中,正确的是( )A. 内力随外力的改变而改变。
B. 内力与外力无关。
C. 内力在任意截面上都均匀分布。
D. 内力在各截面上是不变的。
5 图示两单元体虚线表示其A. α,α 受力后的变形情况,两单元体切应变γ ( )、计算题1、如图所示,在杆件的斜截面m-m 上,任一点A 处的应力p =120 MPa ,其方位角θ=20°,试求B. 0,α C. 0,-2αD. α,2α二该点处的正应力σ与切应力τ。
2、已知杆内截面上的内力主矢为F R 与主矩M 如图所示,且均位于x-y 平面内。
试问杆件截面上 、板件ABCD 的变形如图中虚线A’B’C’D’所示。
试求棱边AB 与AD 的平均正应变以及A 点处直存在哪种内力分量,并确定其大小。
图中之C 点为截面形心。
3角BAD 的切应变。
第二章 拉伸与压缩一、选择题和填空题1、轴向拉伸杆件如图所示,关于应力分布正确答案是_________。
A 1-1、2-2面上应力皆均匀分布;B 1-1面上应力非均匀分布,2-2面上应力均匀分布;C 1-1面上应力均匀分布,2-2面上应力非均匀分布;D 1-1、2-2面上应力皆非均匀分布。
2、图示阶梯杆AD 受三个集中力作用,设AB 、BC 、CD 段的横截面积分别为3A 、2A 、A ,则三段的横截面上。
A 轴力和应力都相等B 轴力不等,应力相等C 轴力相等,应力不等D 轴力和应力都不等3、在低碳钢拉伸曲线中,其变形破坏全过程可分为4个变形阶段,它们依次是 、 、 、 。


材料力学作业4 单项选择题第1题下列哪项措施不能提高压杆稳定性:___。
A、减小压杆支撑间的长度B、减弱压杆的约束条件C、选择合理的截面形状D、合理选用压杆的材料答案:B第2题下列哪项措施可以提高构件的疲劳强度:___。
A、减缓应力集中B、增加构件尺寸C、降低表面质量答案:A第3题下列哪项措施不能提高构件的抗冲击能力:___。
A、减小构件的刚度B、增加构件的弹性模量C、增加构件的体积答案:B第4题下图所示的连续梁的静不定次数为___。
A、1B、2C、3D、4答案:B判断题第5题构件在发生疲劳破坏前,会出现明显的塑性变形。
答案:错误第6题构件外形的变化不会改变构件的持久极限。
答案:错误第7题虚位移表示这种位移是由其他原因引起,且和梁上的原有载荷相关。
答案:错误第8题在虚功原理中,与材料性质也是相关的。
答案:错误第9题对于既是外力静不定又是内力静不定的情况,应当同时接触外多余约束和内多余约束,才能形成静定基。
答案:正确第10题轴向受压的细长直杆当压力过大时,可能突然变弯,失去原直线形式的平衡状态,此状态称为失稳。
答案:正确第11题杆愈细长,其临界力越小,愈容易失稳。
答案:正确第12题杆端的约束愈强,压杆的临界压力就愈低。
答案:错误第13题压杆的柔度愈大,其愈容易失稳。
答案:正确第14题机器设备中零件的工作应力随时间作随机性变化,,这种应力称为交变应力。
答案:错误第15题交变应力作用下材料抵抗疲劳破坏的能力,称为疲劳强度。
答案:正确填空题第16题两根尺寸和材料均相同的细长压杆,弹性模量=200Gpa,直径d=80mm。
下端固定,上端与刚性很大的横梁固连,压杆长度L=1.2m,则细长压杆的临界力为___。
答案:689kN第17题变形固体的功能原理为:外力功=___。
答案:变形能第18题对于任何弹性体,其外力功 = ___广义力 X 广义位移。
答案:0.5第19题列出两个常用的结构位移变形能法:___和___。

材料力学作业解答1.弹簧的力学行为弹簧是一种具有弹性的材料,它可以在受力时发生弹性形变,并且能够恢复到原始形状。
弹簧的力学行为可以通过胡克定律来描述。
根据胡克定律,弹簧的形变与施加在它上面的力成正比,即F=k*x,其中F是施加在弹簧上的力,k是弹簧的弹性系数,x是弹簧的形变量。
2.弹簧的应变能和弹性势能当弹簧被拉伸或压缩时,它会储存一定量的应变能。
弹簧的应变能可以通过下式计算:U=(1/2)*k*x^2,其中U是弹簧储存的应变能,k是弹簧的弹性系数,x是弹簧的形变量。
3.伸长弹簧的应变能假设一个弹簧的弹性系数为k,它被拉伸或压缩x长度。
根据胡克定律,施加在弹簧上的力可以通过F = k * x计算得到。
通过积分力在形变路径上的关系,可以得到弹簧的应变能。
假设初始长度为L,拉伸后的长度为L+x,则弹簧的伸长应变能可以计算如下:U = ∫[0, L+x] F(x)dx = ∫[0, x] k * x dx = (1/2) k * x^24.剪切应力和剪切应变剪切应力是作用于物体上的横截面内的剪切力与该横截面上的面积之比。
剪切应变是物体在受到剪切应力时产生的形变。
剪切应力和剪切应变之间的关系可以通过剪切弹性模量来描述。
剪切弹性模量G可以通过下式计算:G=τ/γ,其中τ是剪切应力,γ是剪切应变。
5.弯曲应力和弯曲应变弯曲应力是作用于物体上的弯曲力与该物体的横截面想对距离之比。
弯曲应变是物体在受到弯曲应力时产生的形变。
弯曲应力和弯曲应变之间的关系可以通过弯曲弹性模量来描述。
弯曲弹性模量E可以通过下式计算:E=σ/ε,其中σ是弯曲应力,ε是弯曲应变。
6.斯特拉因准则斯特拉因准则描述了材料在达到破坏点之前的应力和应变行为。
根据斯特拉因准则,当材料达到其屈服点时,应力和应变之间的关系可以通过单一的线性方程来描述。
这个线性方程表明了在屈服点之前,应力与应变之间的比例关系。
7.杨氏模量和泊松比杨氏模量是一种描述材料刚度的量度,它可以表示应力与应变之间的比例关系。

绪 论一、 是非题1.1 材料力学主要研究杆件受力后变形与破坏的规律。
( ) 1.2 内力只能是力。
( )1.3 若物体各点均无位移,则该物体必定无变形。
( ) 1.4 截面法是分析应力的基本方法。
( ) 二、选择题1.5 构件的强度是指( ),刚度是指( ),稳定性是指( )。
A. 在外力作用下构件抵抗变形的能力B. 在外力作用下构件保持其原有的平衡状态的能力C. 在外力作用下构件抵抗破坏的能力1.6 根据均匀性假设,可认为构件的( )在各点处相同。
A. 应力 B. 应变C. 材料的弹性常数D. 位移1.7 下列结论中正确的是( ) A. 内力是应力的代数和 B. 应力是内力的平均值 C. 应力是内力的集度 D. 内力必大于应力参考答案:1.1 √ 1.2 × 1.3 √ 1.4 × 1.5 C,A,B 1.6 C 1.7 C轴向拉压一、选择题1. 等截面直杆CD 位于两块夹板之间,如图示。
杆件与夹板间的摩擦力与杆件自重保持平衡。
设杆CD 两侧的摩擦力沿轴线方向均匀分布,且两侧摩擦力的集度均为q ,杆CD 的横截面面积为A ,质量密度为ρ,试问下列结论中哪一个是正确的? (A) q gA ρ=;(B) 杆内最大轴力N max F ql =; (C) 杆内各横截面上的轴力N 2gAlF ρ=;(D) 杆内各横截面上的轴力N 0F =。
2. 低碳钢试样拉伸时,横截面上的应力公式N F A σ=适用于以下哪一种情况? (A) 只适用于σ≤p σ; (B) 只适用于σ≤e σ; (C)3. 在A 和B和点B 的距离保持不变,绳索的许用拉应力为[]σ取何值时,绳索的用料最省? (A) 0; (B) 30; (C) 45; (D) 60。
4. 桁架如图示,载荷F 可在横梁(刚性杆)DE 为A ,许用应力均为[]σ(拉和压相同)。
求载荷F 的许用值。
以下四种答案中哪一种是正确的?(A)[]2A σ; (B) 2[]3Aσ;(C) []A σ; (D) 2[]A σ。
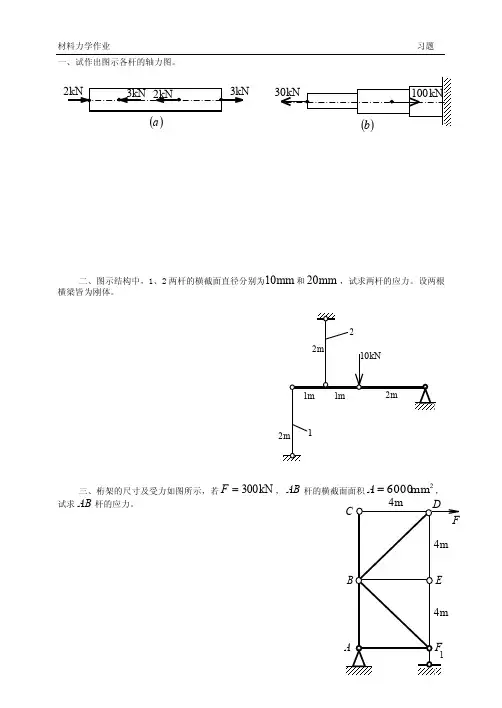
一、试作出图示各杆的轴力图。
二、图示结构中,1、2两杆的横截面直径分别为mm 10和mm 20,试求两杆的应力。
设两根横梁皆为刚体。
三、桁架的尺寸及受力如图所示,若kN 300=F ,AB杆的横截面面积2mm 6000=A ,试求AB 杆的应力。
()a四、在图示简易吊车中,BC 为钢杆,AB 为木杆。
木杆AB 的横截面面积21cm 100=A ,许用应力[]MPa 71=σ;钢杆BC 的横截面面积22cm 6=A ,许用应力[]MPa 1602=σ。
试求许可吊重[]F 。
五、在低碳钢拉伸实验用的力与变形曲线及应力应变曲线中分别标出p F 、s F 、b F 和p σ、s σ、b σ,并回答在εσ-曲线中的p σ、s σ、b σ是否是构件中的真实应力,如果不是请另绘出强化阶段与颈缩阶段真实应力曲线的大致形状。
六、像矿山升降机钢缆这类很长的拉杆,应考虑其自重的影响。
设材料单位体积的重量为γ,许用应力为[]σ。
钢缆下端所受拉力为F ,且钢缆截面不变。
试求钢缆的允许长度及其总伸长。
钢缆横截面面积为A 。
B七、图示结构中,AB 为刚体,杆1、杆2、杆3的材料和横截面面积均相同,在杆AB 的中点C 作用铅垂方向的载荷F,试计算C 点的水平位移和铅垂位移。
已知:kN20=F ,2321mm 100====A A A A ,mm 1000=l ,GPa 200=E 。
八、设横梁ABC D 为刚体。
横截面面积为2mm 36.76的钢索绕过无摩擦的滑轮。
设kN 20=P ,试求钢索内的应力和C九、图示结构中,AB 为刚体,1、2杆的抗拉(压)刚度均为EA 。
试求两杆的轴力。
十、图示杆系的两杆同为钢杆,GPa200=E ,C 061105.12-⨯=α。
两杆的横截面面积同为2cm 10=A 。
若AC 杆的温度降低C 200,而AB杆的温度不变,试计算两杆的轴力。
十一、图示支架中的三根杆件材料相同,杆1的横截面面积为2mm 200,杆2的横截面面积为2mm 300,杆3的横截面面积为2mm 400。
24木架受力如图所示,已知两立柱横截而均为100mmX 100mm 的正方形。
试求:(1)绘左.右立柱的轴力图:(2)求左.右立柱上.中、下三段内横截而上的正应力。
解:(1)求立柱各节点的 受力为了求岀ACEG 立柱(左立 柱)和BDFH 立柱(右立柱)中 的内力和应力,首先对各杆受力 进行分析如卜-图24a 所示,并求 出数值。
取AB 为研究对象,由平衡 方程工® (尸)=0,F, x 1 — x 2 = 0 ①工"0, 几+几一片=0② 联合①和②解得,图 2-4aF ;=F ;=5KNaF AF 2=6KNFi=10KNJ F BFcF zDDF A =8KNF EF Glm/ / / / /4 ----------- ---------------lmlm lmF DF H又由牛顿第三左律得,L\=F;=5KN、F R=F;=5KN°AC-5xlO ,N 100 x 100//?/??2=—0・5MPa :同理可得,Fc=F ;=9KN 、F D =F ;)=3KN ;件=F ;=4KN,F F =F ; = \2KN °(2) 绘左、右立柱的轴力图取左立柱(ACEG 立柱)为研究对象。
采用截面法,画受力图如图2-4b 所示,求得 N AC =_©=—5(KN);鼻=_F\_F(・=-5-9 = -14(KN);□ = _© _ F C + Fg = _5 _9 + 4 = _10(KN)。
同理又取右立柱(BDFH 立柱)为研究对象。
采用截而法求得 N BD =_F B =—5(KN); G = ~F B + 耳=一5 + 3 = —2(KN):N HI = _F R + Fp _ F F =—5 + 3_12 = _14(KN)°画轴力图如图左立柱所示和如图右立柱所示。
图右立柱(3)求左、右立柱上、中.下三段内横截而上的正应力 N 由轴向拉压正应力汁算公式b =—得,A 左立柱上.中、下正应力:F&5KN A ' rN AC 图 4-2b图左立柱2-9图示的构架中,AB 为刚性杆,CD 杆的刚度为EA,试求:(1) CD 杆的伸长;(2) C 、B 两点的位移。
材料力学作业Company number:【0089WT-8898YT-W8CCB-BUUT-202108】第一章 绪论1. 试求图示结构m-m 和n-n 两截面上的内力,并指出AB 和BC 两杆的变形属于何类基本变形。
2. 拉伸试样上A ,B 两点的距离l 称为标距。
受拉力作用后,用变形仪量出两点距离的增量为mm l 2105-⨯=∆。
若l 的原长为l =100mm ,试求A 与B 两点间的平均应变m ε。
第二章 轴向拉伸和压缩与剪切 一、选择题1.等直杆受力如图,其横截面面积A=1002mm ,则横截面mk上的正应力为( )。
(A)50MPa(压应力); (B)40MPa(压应力); (C)90MPa(压应力); (D)90MPa(拉应力)。
2.低碳钢拉伸经过冷作硬化后,以下四种指标中哪种得到提高( ): (A)强度极限; (B)比例极限;(C)断面收缩率; (D)伸长率(延伸率)。
3.图示等直杆,杆长为3a ,材料的抗拉刚度为EA ,受力如图。
杆中点横截面的铅垂位移为( )。
(A)0;(B)Pa/(EA);(C)2 Pa/(EA);(D)3 Pa/(EA)。
4.图示铆钉联接,铆钉的挤压应力bs σ是( )。
(A )2P/(2d π); (B )P/2dt;(C)P/2bt; (D)4p/(2d π)。
5.铆钉受力如图,其压力的计算有( )(A )bs σ=p/(td);(B)bs σ=p/(dt/2);(C)bs σ=p/(πdt/2);(D)bs σ=p/(πdt/4)。
6.图示A 和B 的直径都为d,则两面三刀者中最大剪应力为( )(A)4bp/(2d απ); (B)4(αb +)P/(2d απ); (C)4(a b +)P/(2b d π); (D)4αP/(2b d π). 7.图示两木杆(I 和II )连接接头,承受轴向拉力作用,错误的是( ).(A )1-1截面偏心受拉; (B )2-2为受剪面;(C )3-3为挤压面; (D )4-4为挤压面。
2-3求下列结构中指定杆的应力。
已知(b)图中杆的横截面面积A1=850 mm2,A2=600 mm2,A3=500 mm2。
(1)图(a)为开槽拉杆,两端受力F=10 kN,b=4mm,h=20mm,h0=10mm;2-6图示短柱,上段为钢制,截面尺寸为100×100mm2,钢的弹性模量E s=200GPa,下段为铝制,截面尺寸为200×200mm2,E a=70GPa。
当柱顶受F力作用时,柱子总长度减少了0.4mm,试求F值(注:不计杆的自重)。
2-11图示结构中,AB为刚性杆,AD为钢杆,面积A1=500mm2,弹性模量E1=200GPa;CG为铜杆,面积A2=1500mm2,弹性模量E2=100GPa;BE为木杆,面积A3=3000mm2,弹性模量E3=10GPa。
当G点受力F=60kN作用时,求该点的竖直位移ΔG。
2-13图示结构,CD 杆为刚性杆,C 端铰接于墙壁上,AB 杆为钢杆,直径d =30mm ,容许应力[]170MPa σ=,弹性模量52.010MPa E =⨯。
试求结构的容许荷载F 。
2-14图示正方形砖柱,顶端受集中力16kN F =作用,柱边长为0.4m ,砌筑在高为0.4m的正方形块石底脚上。
已知砖的容重3116kN m g ρ=,块石容重3220kN m g ρ=。
地基容许应力[]0.08MPa σ=。
试设计正方形块石底脚的边长a 。
2-17图示AB杆为刚性杆,长为3a。
A端铰接于墙壁上,在C、B两处分别用同材料、同面积的1、2两杆拉住。
在D点受力F作用,求1、2两杆的应力。
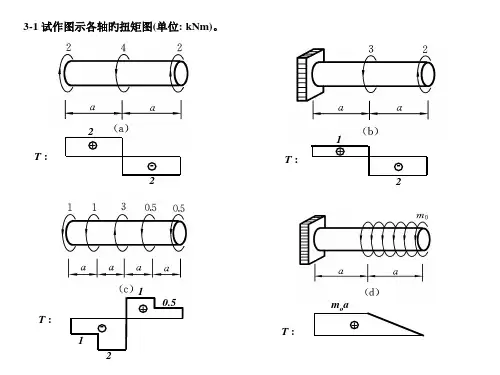
设弹性模量为E,3-1试作下列各杆的扭矩图。
10N·m 90N·m 500N·m/m(d)3-2一直径d=60mm的圆杆,两端受外力偶矩2kN mT=⋅的作用而发生扭转。
试求横截面上1,2,3点处的切应力和最大切应变。
(80GPaG=)。
T3-6图示圆轴AC,AB段为实心,直径为50mm;BC段为空心,外径为50mm,内径G 。
材料⼒学作业习题第⼆章轴向拉伸与压缩1、试求图⽰各杆1-1和2-2横截⾯上的轴⼒,并做轴⼒图。
(1)(2)2、图⽰拉杆承受轴向拉⼒F =10kN ,杆的横截⾯⾯积A =100mm 2。
如以α表⽰斜截⾯与横截⾯的夹⾓,试求当α=10°,30°,45°,60°,90°时各斜截⾯上的正应⼒和切应⼒,并⽤图表⽰其⽅向。
3、⼀⽊桩受⼒如图所⽰。
柱的横截⾯为边长200mm 的正⽅形,材料可认为符合胡克定律,其弹性模量E =10GPa 。
如不计柱的⾃重,试求:(1)作轴⼒图;(2)各段柱横截⾯上的应⼒; (3)各段柱的纵向线应变;(4)柱的总变形。
4、(1)试证明受轴向拉伸(压缩)的圆截⾯杆横截⾯沿圆周⽅向的线应变d ε,等于直径⽅向的线应变d ε。
(2)⼀根直径为d =10mm 的圆截⾯杆,在轴向拉⼒F 作⽤下,直径减⼩0.0025mm 。
如材料的弹性摸量E =210GPa ,泊松⽐ν=0.3,试求轴向拉⼒F 。
(3)空⼼圆截⾯钢杆,外直径D =120mm,内直径d =60mm,材料的泊松⽐ν=0.3。
当其受轴向拉伸时, 已知纵向线应变ε=0.001,试求其变形后的壁厚δ。
5、图⽰A和B两点之间原有⽔平⽅向的⼀根直径d=1mm的钢丝,在钢丝的中点C加⼀竖直荷载F。
已知钢丝产⽣的线应变为ε=0.0035,其材料的弹性模量E=210GPa,钢丝的⾃重不计。
试求:(1) 钢丝横截⾯上的应⼒(假设钢丝经过冷拉,在断裂前可认为符合胡克定律);(2) 钢丝在C点下降的距离?;(3) 荷载F的值。
6、简易起重设备的计算简图如图所⽰.⼀直斜杆AB应⽤两根63mm×40mm×4mm不等边⾓钢组[σ=170MPa。
试问在提起重量为P=15kN的重物时,斜杆AB是否满⾜强度成,钢的许⽤应⼒]条件?7、⼀结构受⼒如图所⽰,杆件AB,AD均由两根等边⾓钢组成。
已知材料的许⽤应⼒[σ=170MPa,试选择杆AB,AD的⾓钢型号。
材料力学作业Company number:【WTUT-WT88Y-W8BBGB-BWYTT-19998】材料力学作业绪论一、名词解释1.强度:构件应有足够的抵抗破坏的能力。
2.刚度:构件应有足够的抵抗变形的能力。
3.稳定性:构件应有足够的保持原有平衡形态的能力。
4.变形:在外力作用下,构件形状和尺寸的改变。
5.杆件:空间一个方向的尺寸远大于其他两个方向的尺寸,这种弹性体称为杆或杆件。
6.板或壳:空间一个方向的尺寸远小于其他两个方向的尺寸,且另两个尺寸比较接近,这种弹性体称为板或壳。
7.块体:空间三个方向具有相同量级的尺度,这种弹性体称为块体。
二、简答题1.答:根据空间三个方向的几何特性,弹性体大致可分为:杆件;板或壳;块体。
2.答:单杆3.答:材料力学的任务就是在满足强度、刚度和稳定性的要求下,为设计既经济又安全的构件,提供必要的理论基础和计算方法。
4.答:均匀性假设;连续性假设;各项同性假设。
5.答:轴向拉伸或轴向压缩;剪切;扭转;弯曲。
6.答:杆件长度方向为纵向,与纵向垂直的方向为横向。
7.答:就杆件外形来分,杆件可分为直杆、曲杆和折杆;就横截面来分,杆件又可分为等截面杆和变截面杆等;实心杆、薄壁杆等。
8.答:若构件横截面尺寸不大或形状不合理,或材料选用不当,将不能满足强度、刚度、稳定性。
如果加大横截面尺寸或选用优质材料,这虽满足了安全要求,却多使用了材料,并增加了成本,造成浪费。
因此,在设计时,满足强度、刚度和稳定性的要求下,为设计既经济又安全的构件,提供必要的理论基础和计算方法。
第一章 轴向拉伸和压缩一、名词解释1.内力:物体内部某一部分与另一部分间相互作用的力称为内力。
2.轴力:杆件任意横截面上的内力,作用线与杆的轴线重合,即垂直于横截面并通过其形心。
这种内力称为轴力。
3.应力:△A 上分布内力的合力为F ∆。
因而得到点的应力0limA Fp A∆→∆=∆。
反映内力在点的分布密度的程度。
4.应变:单位长度的伸长来衡量杆件的变形程度为应变。
5.正应力:作用线垂直于横截面的应力称为正应力。
6.切应力:作用线位于横截面内的应力称为剪应力或切应力。
7.伸长率:试样拉断后,试样长度由原来的l 变为1l ,用百分比表示的比值8.断面收缩率:原始横截面面积为A 的试样,拉断后缩颈处的最小截面面积变为1A ,用百分比表示的比值 9.许用应力:极限应力的若干分之一。
用[]σ表示。
10.轴向拉伸:杆产生沿轴线方向的伸长,这种形式称为轴向拉伸。
11.冷作硬化:把试样拉到超过屈服极限的点,然后逐渐卸除拉力,在短期内再次加载,则应力和应变大致上沿卸载时的斜直线变化。
在第二次加载时,其比例极限(亦即弹性阶段)得到了提高,但塑性变形和伸长率却有所降低,这种现象称为冷作硬化。
二、简答题1.答:作用于杆件上的外力合力的作用线与杆件轴线重合。
2.答:杆件变形是沿轴线方向的伸长或缩短。
3.答:归纳为以下三个步骤:截开-----假想在欲求内力截面处,把构件截成两部分。
代替------留下其中一部分,用作用于截面上的内力代替弃去部分对留下部分的作用。
平衡------建立留下部分的平衡方程,由已知的外力求出横截面上未知的内力。
4.答:内力是物体内部某一部分与另一部分间相互作用的力,而应力是描述内力分布密度的程度,即单位面积上的力。
内力常用单位是N ,应力常用单位是MPa 。
5.答:极限应力是屈服极限、强度极限的统称。
许用应力是极限应力的若干分之一。
6.答:变形是在外力作用下,构件形状和尺寸的改变,有量纲。
应变是单位长度的伸长来衡量杆件的变形程度,无量纲。
7.答:对没有明显屈服极限的塑性材料,可以将产生%塑性应变时的应力作为屈服指标,并用来表示,称为名义屈服应力。
8.答:低碳钢在整个拉伸试验过程中,其工作段的伸长量与载荷的关系大致可分为以下四个阶段:弹性阶段---应力与应变成正比;屈服阶段---当应力增加到某一数值时,应变有非常明显的增加,而应力先是下降,然后作微小的波动,在曲线上出现接近水平线的小锯齿形线段;强化阶段---过屈服阶段后,材料又恢复了抵抗变形的能力,要使它继续变形必须增加拉力,这种现象称为材料的强化。
在强化阶段中,试样的横向尺寸有明显的缩小;颈缩阶段。
灰口铸铁拉伸时的应力一应变关系是一段微弯曲线,没有明显的直线部分。
它在较小的拉应力下就被拉断,没有屈服和缩颈现象,拉断前的应变很小,伸长率也很小。
9.答:外力分析;内力计算;强度计算。
10.答:在比例极限内,正应力与正应变成正比。
11.答:屈服极限s σ、名义屈服应力0.2σ、强度极限b σ。
12.答:弹性模量E 、泊松比和剪切弹性模量。
13.答:当应力不超过比例极限时,横向应变ε'与轴向应变ε之比的绝对值是一个常数,即εενεε''==-。
这个比例系数称为材料的泊松比。
14.答:伸长率δ和断面收缩率ψ。
15.答:根据圣维南原理,外力作用处产生应力集中,因此,只适用于离外力作用端稍远处。
16.平面假设。
三、计算题1.解:应用截面法10N F =,2N F F =,3N F F =2.解:应用截面法122N N F F kN ==3.解:应用截面法1N F F =,22N F F =,3N F F =-4.解:应用截面法12N F F =-,2N F F =5.解:应用截面法150N F kN =-,290N F kN =- 0x F =∑,12cos45cos300N N FF +=6.解:解得:10.448N F F =,20.366N F F =-轴向拉伸为正,压缩为负7.解:31248501035.5175N F Mpa A σπ⨯⨯===⨯ 得:max 35.5Mpa σ= 8.解:受力分析得:0x F =∑,12cos30cos750N N FF +=0y F =∑,12sin30cos150N N FF F ---=∴1103.5N BC F Mpa Aσ==9.解:(1)312010201000N ACF Mpa A σ-⨯===-,0CD Mpa σ=,0.01N ACF l l mm EA ∆==-,0N CD F ll mm EA∆==, 0.01N DB F ll mm EA∆==-,0.02AB AC CD DB l l l l mm ∆=∆+∆+∆=- 10.解:32401031.8404N ACF Mpa A σπ⨯===⨯,324010127204N CB F Mpa A σπ⨯===⨯, 根据胡可定律,E σε=,得41.5910AC AC E σε-==⨯,46.3610BC BC Eσε-==⨯ 11.解:0x F =∑,12305N N F F +⨯=0y F =∑2405N F F ⨯+=,解得:245N F F =-,143N F F = AB 杆:[]160014084F A kN σ==⨯=BC 杆:[]230000 3.5105c F A kN σ==⨯=因此,114[]1123N F F kN ==,224[]845N F F kN =-=,取[]84F kN = 第二章剪切一、名词解释1.剪切:大小相等、方向相反,作用线相距很近的两个横向力作用时,杆件将产生剪切变形。
2.剪力:在剪切面上有与外力大小相等,方向相反的内力,这个内力叫剪力。
3.剪切面:发生剪切变形的截面。
4.挤压面:挤压力的作用面。
5.挤压应力:由挤压力而引起的应力。
6.挤压力:在接触面上的压力,称为挤压力。
二、简答题1.答:切应力与横截面平行,正应力垂直于横截面。
2.答:不相同。
挤压面是真实的挤压作用面,计算挤压面是挤压面的正投影作为计算面积。
3.挤压是在构件相互接触的表面上,因承受较大的压力作用,使接触处的局部区域发生显着的塑性变形或被压碎。
压缩是外力沿杆件轴线作用,使构件产生压缩变形。
4.答:连接件上的剪切面沿外力方向、挤压面与外力方向垂直。
5.答:满足剪切强度和挤压强度条件。
剪切的强度条件可表示为[]QA ττ=≤,挤压强度条件可表达为bsbs bs bs[]F A σσ=≤ 6.答:过直径平面正投影作为计算面积。
7.答:均匀分布在挤压平面上。
三、计算题 1.解:[]QA ττ=≤,40d mm ≥== 2.解:0M =∑,0M QD -=,10000Q N =,3.解:[]FA σσ=≤,得34d mm≥,[]QA ττ=≤,10.4[]Q t mm d πτ≥= 4.解:322410==105.8Mpa<[]174Q A ττπ⨯=⨯,5.解:3250.210==320Mpa 1024Q Aτπ⨯=⨯⨯6.解:0CM =∑,0A R a Fb -=得:1000A FbR N a==0y F=∑,0C A R R F --=,得:1200C R N =第三章扭转一、名词解释1.扭转:大小相等、方向相反,作用在垂直于杆轴平面内的力偶Me 时,杆件将产生扭转变形,即杆件的横截面绕其轴相对转动。
2.扭矩:圆轴上有作用面垂直于杆轴的外力偶作用,杆件的横截面上也只有作用于该平面上的内力偶,即为扭矩。
3.扭转角:在杆件两端垂直于杆轴线的平面内作用一对大小相等,方向相反的外力偶。
两个横截面之间相对转过一个角度,这个转角称为扭转角。
4.剪切胡克定律:切应力不超过材料剪切比例极限的线弹性范围,G τγ=,这个关系式称为材料的剪切胡克定律。
5.单位长度扭转角:d d xφ表示单位长度扭转角,公式为:P d d T x GI φ=。
二、简答题1.答:成立。
切应力互等定理具有普遍意义,在非纯剪切的情况下同样适用。
2.答:在切应力作用下,单元体截面沿切应力方向错动,产生切应变。
3.答:切应力线性分布,中心处切应力为零,最外边缘最大。
4.答:从强度方面考虑,空心圆截面轴的壁厚是愈薄愈好。
5.答:PTlGI φ=,其单位是弧度。
6.答:在扭矩一定的情况下,P GI越大,单位长度的扭转角愈小,P GI 反映了圆轴抵抗扭转变形的能力,P GI 称为圆轴的抗扭刚度。
7.答:切应力线性分布,中心处切应力为零,最外边缘最大。
8.答:右手螺旋法则:右手四指并拢弯曲指向扭矩的转动方向,若伸开拇指的方向与横截面的外法线方向一致,则扭矩为正,反之为负。
9.答:最大切应力τmax 相同,max t T W τ=与材料无关。
扭转角不相同,PTl GI φ=与材料有关。
10.答:(b )对提高轴的承载能力有利。
11.I p 可以,W p 不能,因为p p I W R=三、计算题1. 解:据截面沿指定截面i-i(i=123)将杆截为两段,考虑任一段的平衡即可得该指定截面上的扭矩:13.T kN m =,为正扭矩,232.T T kN m ==-,为负扭矩。