当前位置：文档之家 › 第五章 多重共线性(计量经济学-北京大学,岳昌君)

第五章 多重共线性(计量经济学-北京大学,岳昌君)

  • 格式：ppt
  • 大小：239.50 KB
  • 文档页数：24

下载文档原格式

  / 24

合集下载

计量经济学多重共线性分析

计量经济学多重共线性分析

➢收集整理实验数据 ➢建立线性回归模型 ➢检验多重共线性 ➢用逐步回归法克服多重共线性
收集整理实验数据
1978年至2011年我国税收收入与国民生产总值情况
（来源于中国统计年鉴）
建立线性回归模型
➢ 用普通最小二乘法估计模型
利用实验数据分别建立Y关于X1、X2、X3的散点图 （SCAT Xi Y）
建立线性回归模型
2.8134 -0.1091 0.9979 0.613
t值
(-1.644)
(18.427) (-1.997)
用逐步回归法克服多重共线性
➢逐步回归
第一步：在初始模型中引入X1，模型拟合优度提高， 但是参数符号不合理，且变量没有通过了t检验，故去 掉C、X1
Y=24023.76+4.1804X2 (-1.1194) (116.4316) R2=0.9978 D.W.=0.6285
检验多重共线性
➢检验简单相关系数
进一步选择Covariance Analysis的Correlation，得到变 量之间的偏相关系数矩阵，观察偏相关系数。
可以发现，Y与X1、X2、X3的相关系数都在0.9以 上，但输出结果中，解释变量X1、X3的回归系数 却无法通过显著性检验。认为解释变量之间存在多 重共线性。
用逐步回归法克服多重共线性
➢找出最简单的回归形式
分别作Y与X1、X2、X3间的回归（LS Y C Xi ）
用逐步回归法克服多重共线性
➢找出最简单的回归形式
分别作Y与X1、X2、X3间的回归（LS Y C Xi ）
用逐步回归法克服多重共线性
➢找出最简单的回归形式
分别作Y与X1、X2、X3间的回归（LS Y C Xi ）
计量经济学多重共线性分析
多重共线性

多重共线性


解决方法
解决方法
（1）排除引起共线性的变量 找出引起多重共线性的解释变量，将它排除出去，以逐步回归法得到最广泛的应用。 （2）差分法 时间序列数据、线性模型：将原模型变换为差分模型。 （3）减小参数估计量的方差：岭回归法（Ridge Regression）。 （4）简单相关系数检验法
谢谢观看
简介
简介
对线性回归模型 基本假设之一是自变量，之间不存在严格的线性关系。如不然，则会对回归参数估计带来严重影响。为了说 明这一点，首先来计算线性回归模型参数的 LS估计的均方误差。为此。重写线性回归模型的矩阵形式为 其中服从多元正态分布，设计矩阵 X是的，且秩为 p。这时，参数的 LS估计为，而回归系数的 LS估计为。 注意到由此获得的 LS估计是无偏的，于是估计的均方误差为 其中是的特征根。显然，如果至少有一个特征根非常接近于零，则就很大，也就不再是的一个好的估计。由 线性代数的理论知道，若矩阵的某个特质根接近零，就意味着矩阵 X的列向量之间存在近似线性关系。 如果存在一组不全为零的数，使得 则称线性回归模型存在完全共线性；如果还存在随机误差 v，满足，使得 则称线性回归模型存在非完全共线性。 如果线性回归模型存在完全共线性，则回归系数的 LS估计不存在，因此，在线性回归分析中所谈的共线性 主要是非完全共线性，也称为复共线性。判断复共线性及其严重程度的方法主要有特征分析法(analysis of eigenvalue)，条件数法 (conditional numbers)和方差扩大因子法(variance inflation factor)。
产生原因
产生原因
主要有3个方面： （1）经济变量相关的共同趋势 （2）滞后变量的引入 （3）样本资料的限制
影响
影响
第五章 多重共线性(计量经济学,南开大学)

第五章 多重共线性(计量经济学,南开大学)


例如，为了估计汽车需求的价格弹性和收入弹性，得到销售量、平均价格、消 费者收入的时间序列数据。设定回归式：
ln(Yt ) 1 2 ln P t 3 ln I t ut
由于在时间序列数据中价格Pt、收入It 一般都具有高度共线的趋势。因此，直接 估计上面的回归式将存在问题。由于在同一式点上，价格与收入的相关程度不高， 可以先利用截面数据估计出收入弹性 ，再利用这一估计结果修改原回归式，变 ˆ 为： 3
R 2 /(k 1) F ~ F (k 1, n k ) 2 (1 R ) /(n k )
可以采用类似的方法检验：
F
R2 ) j /( k 1 (1 R j ) /(n k 1)
2
~ F (k 1, n k )
选择显著水平α ，计算F 统计量的值，与F分布表中的临界值进行比较，若F检验值 小于临界值，则多重共线性不显著，反之，则多重共线性显著。
第三节 多重共线性的探查和解决
一、多重共线性的探查 由于多重共线性使一种普遍现象，而多重共线性的程度影响了参数估计结果， 因此我们关心的是共线性的程度，而不是共线性是否存在。
在双边量回归模型中，可以直接对解释变量的相关系数进行显著性检验，以确 定线性相关的程度（此时相关系数的平方等于样本决定系数）。而对于多于两个结 束变量的回归模型，则不能利用俩俩相关系数来检验。 对于有多个变量的回归模型，可以采用辅助回归的方法，分别以k-1个解释变量 中的第i个对其他变量进行回归，可得到k-2个回归方程的判定系数： R22，R32，…，Rk2。假定这些判定系数中Rj2最大且接近1，则变量Xj 与其他解释变量 中的一个或多个有较高相关程度，因此回归方程出现高度多重共线性。 可以进行F 检验确定其显著性： 根据第三章的结果，检验R2显著性的F检验值为：
计量经济学：多重共线性

计量经济学：多重共线性

计量经济学：多重共线性多重共线性52=.53085123 第四章专门讨论古典假定中⽆多重共线性假定被违反的情况，主要内容包括多重共线性的实质和产⽣的原因、多重共线性产⽣的后果、多重共线性的检测⽅法及⽆多重共线性假定违反后的处置⽅法。

第⼀节什么是多重共线性⼀、多重共线性的含义第三章讨论多元线性回归模型的估计时，强调了假定⽆多重共线性，即假定各解释变量之间不存在线性关系，或者说各解释变量的观测值之间线性⽆关。

在计量经济学中所谓的多重共线性(Multi-Collinearity)，不仅包括解释变量之间精确的线性关系，还包括解释变量之间近似的线性关系。

从数学意义上去说明多重共线性，就是对于解释变量k X 、、X X 32，如果存在不全为0的数k λλλ,2,1 ，能使得n ,2, ,1i 033221 ==++++ki k i i X X X λλλλ ( 4.1 )则称解释变量k X X X ,,,32 之间存在着完全的多重共线性。

⽤矩阵表⽰，解释变量的数据矩阵为X=213112232223111k k nnkn X X X X X X X X X ??（4.2）当Rank(X )在实际经济问题中，完全的多重共线性并不多见。

常见的情形是解释变量k X X X ,,,32 之间存在不完全的多重共线性。

所谓不完全的多重共线性，是指对于解释变量k X 、、X X 32，存在不全为0的数k λλλ,2,1 ，使得n ,2, ,1i 033221 ==+++++i ki k i i u X X X λλλλ（4.3）其中,i u 为随机变量。

这表明解释变量k X 、、X X 32只是⼀种近似的线性关系。

如果k 个解释变量之间不存在完全或不完全的线性关系，则称⽆多重共线性。

若⽤矩阵4表⽰，这时X 为满秩矩阵，即Rank(X )=k 。

需要强调，解释变量之间不存在线性关系，并⾮不存在⾮线性关系，当解释变量存在⾮线性关系时，并不违反⽆多重共线性假定。

第五章 多重共线性(计量经济学-北京大学,岳昌君)

第五章 多重共线性(计量经济学-北京大学,岳昌君)

4
§2 多重共线性的来源
一、解释变量受同一因素的影响 时间序列数据： 1、经济发展;2、政治事件 3、偶然事件;4、时间趋势 二、解释变量中含有当期和滞后变量 I t 1 2 rt 3Yt 4Yt 1 ut Y2 Y3 Y1 , Yn ; Y n Y1 Y2 有多重共线性。 Yn 1
5
§3 多重共线性的影响
一、完全共线性 ˆ X Y ˆ无唯一解 ( X X ) ˆ 的方差是无穷大。 i
6
二、“不完全”多重共线性
ˆ的解不稳定。 ˆ 的方差非常大。 1、 i ˆ 2.8 ˆ 1 1 0.9 2 2 例如： 0.9 1 ˆ 2.9 ˆ 2 3 3 ˆ 2.8 ˆ 3.5678 0.99 1 2 2 0.99 ˆ ˆ 1 2 . 9 6 . 4322 3 3 ˆ 2.8 ˆ 40 .5743 0.999 1 2 2 0.999 2.9 ˆ ˆ 1 51 . 4257 3 3
观察结果（共线性诊断）：1、最大条件指数 37.1>30，说明中等相关；2、与最大条件指数在 一行的4个变量的方差比例都大于0.5，说明这4个 变量就是一个具有中等相关的变量集。
14
五、F检验
例如：X2，X3，X4相互回归
1、 X2—X3，X4；若F >F ，则有多重共线性； 否则的话，就没有。 2、 X3—X2，X4；若F >F ，则有多重共线性； 否则的话，就没有。
t 1 t t 1 t
第5章多重共线性

第5章多重共线性

先验信息：在此之前的研究成果 所提供的信息。
利用某些先验信息，将信息重叠 的一些变量合为一个变量，从而 消除共线性。
接例1
假如认为消费对财富的变化率是对收 入的相应变化率的1/10，即a3=1/10a2 ， 如何解决多重共线性？
将a3=1/10a2 带入模型，可得 Y=a1+a2(X2+0.1X3)+ut 此时解释变量只有一个：X2+0.1X3，此
注意：
较高的简单相关系数只是多重共线性存在的 充分条件，而不是必要条件。特别是在多于 两个解释变量的回归模型中，有时较低的简 单相关系数也可能存在多重共线性。因此并 不能简单地依据相关系数进行多重共线性的 准确判断。
二、综合判断法
R2 (或R2）大，F值大；t 值小，说明模型存在多重共线性
这是因为：R2和F值大，表明总离差中95%（假定R2 0.95） 是由回归解释的，各解释变量对Y的联合线性作用显著。 在此前提下，若各个t值很小，说明各解释变量之间存在共线 性，对Y的独立作用不能分辨，故t检验不显著。
eg
Yi 1 2 X 2i 3 X 3i i
完全多重共线性 1+2 X 2i 3 X 3i 0
近似多重共线性
1 +2 X 2i 3 X 3i vi 0
例子1 消费与收入、财富的例子
可支配收入与家庭财富之间有明 显的共线性关系，他们的相关系 数高达0.9989.
Std. Error t-Statistic
0.342045
-5.576888
0.042746
1.074892
0.765767
8.433867
0.091660
4.477646
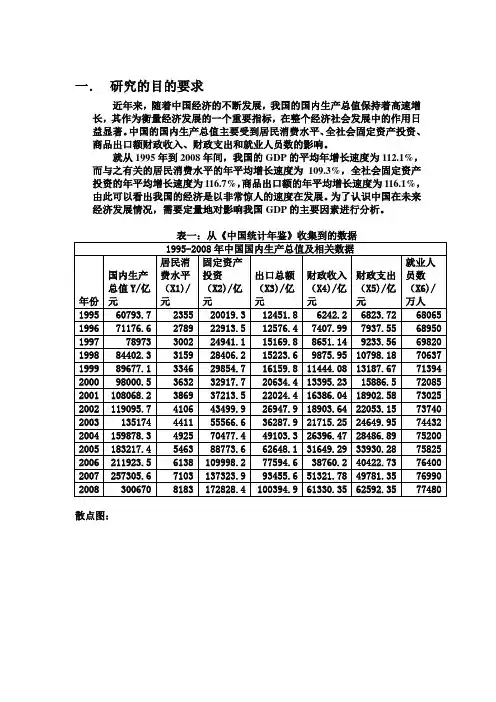
计量经济学多重共线性

计量经济学多重共线性

一．研究的目的要求近年来，随着中国经济的不断发展，我国的国内生产总值保持着高速增长，其作为衡量经济发展的一个重要指标，在整个经济社会发展中的作用日益显著。

中国的国内生产总值主要受到居民消费水平、全社会固定资产投资、商品出口额财政收入、财政支出和就业人员数的影响。

就从1995年到2008年间，我国的GDP的平均年增长速度为112.1%，而与之有关的居民消费水平的年平均增长速度为109.3%，全社会固定资产投资的年平均增长速度为116.7%，商品出口额的年平均增长速度为116.1%，由此可以看出我国的经济是以非常惊人的速度在发展。

为了认识中国在未来经济发展情况，需要定量地对影响我国GDP的主要因素进行分析。

散点图：利用EViews软件，输入Y、X1、X2、X3、X4、X5、X6等数据，采用这些数据对模型进行OLS回归，结果如下：由此可见，该模型的R2=0.999909，Adjusted R-squared=0.999832可决系数异常高，F检验值12865.89，明显显著。

但是当α=0.05时查表的T值万为2.365，不仅X3的T检验不显著，而且X5系数的符号与预期的相反，这表明很可能存在严重的多重共线性。

二、相关分析令国内生产总值为Y,居民消费水平为X1,固定资产投资为X2,出口总额为X3,财政收入为X4,财政支出为X5,就业人员数为X6,有e-views软件可以得到各变量之间的相关系数：表三由相关系数矩阵可以看出，各解释变量相互之间的相关系数很高，证实确实存在严重的多重共线性。

三、修正多重共线性1、判定系数法：2、采用逐步回归的办法，去检验和解决多重共线的问题。

分别做Y对X1、X2、X3、X4、X5、X6的一元线性回归，根据比较系数由大到小排序为：x4、x1、x5、x2、x3、x6X5、x2导致不显著，删最后修正严重多重共线性的回归结果为Y = 2434.07753 + 1.728188114*X4 + 17.97396022*X1 + 0.4320065441*X3随机解释变量问题：检验内生性：第一步：X1 = 1156.103781 + 0.4979871065*X1(-1) + 0.005053326594*X3 + 0.04818665208*X4X3 = -50406.28441 + 1.161928962*X3(-1) + 23.11627169*X1 - 2.273365012*X4X4 = -11019.22777 + 0.5056267614*X4(-1) + 4.854749225*X1 +0.06574184046*X3第二步：Y = 6347.819234 + 16.24766676*X1 + 0.4428944999*X3 + 1.876605301*X4 + 7.026642473*E1Y = 7149.553219 + 15.97797479*X1 + 0.5300464217*X3 + 1.744257955*X4 - 0.176056636*E3Y = 45699.73211 - 1.456575031*X1 + 0.4044678757*X3 + 3.685902148*X4 - 2.36392959*E4X4有内生性工具变量法：第一阶段：X4 = -792.8862088 + 1.249459681*X4(-1)第二步：Y = 15755.17718 + 11.99382105*X1 + 0.2558015318*X3 + 2.738892206*X4F。

多重共线性资料

多重共线性资料

• 完全多重共线性容易发现，不完全多重共线性具有 隐弊性，客易造成严重后果，常常需要检验不完全 多重共线性。
直接观察回归结果
• 拟合优度R²很大(一般大于0.8），但模型全部或部 分参数估计值不显著(t值小)。
• 参数估计量的显著性与经济理论不符。 • 模型新增变量后，拟合优度增加，但原有参数估计
7.356574
1988
14.79707
29.50232
8.951532
1989
15.38405
30.6203
8.071457
1990
17.27538
34.60292
9.852538
• . reg Y x1 x2
• Source | SS df MS
Number of obs = 21
• -------------+------------------------------
97
24
120
129
30
150
152
样本向量X2与X3*的相关系数为0.9959
进口额yt
国内产值x1t
存货额x2t
国内消费x3t
15.9
149.3
4.2
16.4
19.0
┇
108.1
直接回归得：
Yˆt 10.1300.051X1t 0.587X2t 0.287X3t R2 0.992
国内产值与进口反 额关 有系 相，显然不济 符含 合义 经。
例如数据：1.00
11.00
100
2.00
19.00
80
3.00
28.00
4.00
42.00
60
5.00
第5章 多重共线性的情形及其处理

第5章 多重共线性的情形及其处理


§5.2 多重共线性的诊断
以下用SPSS软件诊断例3.2中国民航客运量一例中的多重共线性问题。
Coefficients a Standar dized Coeffici ents Beta 2.447 -2.485 -.083 .531 .564 t 2.532 4.152 -4.478 -3.510 5.354 8.440 Sig. .030 .002 .001 .006 .000 .000
(Constant) X1 X2 X3 X4 X5
Unstandardized Coefficients Std. B Error 450.909 178.078 .354 .085 -.561 .125 -7.E-03 .002 21.578 4.030 .435 .052
Collinearity Statistics Tolera nce VIF .001 .001 .315 .018 .040 1963 1741 3.171 55.5 25.2
a. Dependent Variable: Y
§5.2 多重共线性的诊断
二、特征根判定法 （一）特征根分析 根据矩阵行列式的性质，矩阵的行列式等于其 特征根的连乘积。因而，当行列式|X′X|≈0时, 矩 X X 阵X′X至少有一个特征根近似为零。反之可以证明， X X 当矩阵X′X至少有一个特征根近似为零时，X 的列 X X X 向量间必存在复共线性，证明如下：
ɶ ɶ x12 ⋯ x1n ɶ ɶ x22 ⋯ x2 n
2 ( x1i − x1 ) ∑ X ′X = ∑ ( x − x )( x − x ) 2i 2 1i 1 L11 L12 X ′X = 可以简记为 L21 L22
∑ ( x − x )( x − x ) ∑( x − x )
[精品]第四讲 多重共线性

[精品]第四讲 多重共线性

第五讲 多重共线性本讲分为两个部分：第一部分是对相关性问题的研究，作为多重共线性问题的基础，第二部分则是对多重共线性问题展开讨论。

第一部分：相关理论 1．相关理论相关分析是研究变量间相互关系的最基本方法。

从相关分析中引出的相关系数是回归分析的一个基本统计量。

掌握它有助于对经济问题和经济计量模型的分析与理解。

1.1 相关的定义与分类定义：相关（correlation ）指两个或两个以上变量间相互关系的程度或强度。

分类：①按强度分完全相关：变量间存在函数关系。

例，圆的周长，L = 2πr 。

高度相关（强相关）：变量间近似存在函数关系。

例，我国家庭收入与支出的关系。

弱相关：变量间有关系但不明显。

例，近年来我国耕种面积与产量。

零相关：变量间不存在任何关系。

例，某班学生的学习成绩与年龄。

2004006008001020304050YX121020304050YX0.51.01.52.02.53.02.02.53.03.54.04.5YX完全相关 高度相关、线性相关、正相关 弱相关②按变量个数分按形式分：线性相关, 非线性相关 简单相关：指两个变量间相关按符号分：正相关, 负相关, 零相关 复相关（多重相关和偏相关）：指三个或三个以上变量间的相关。

05010015020050100150200250YX 121020304050Y X-4-224-4-224YX非线性相关 负相关 零相关因非线性相关可以转化为线性相关处理，而复相关又可看作是简单相关基础上的拓展，所以后面重点介绍简单线性相关。

1.2 简单线性相关的度量用简单线性相关系数，简称相关系数（correlation coefficient ）度量两个变量间的线性相关强度，用表示。

的随机变量表达式是=)()()(t t t t y D x D y ,x Cov 。

的统计表达式是=∑∑∑===----Tt y t Tt x t Tt y t x t y Tx Ty x T 12121)(1)(1))((1μμμμ=∑∑∑===----T t y t T t x t Tt y t x t y x y x 12121)()())((μμμμ其中T ，总体容量；x t , y t ，变量的观测值；μx ,μy ，变量观测值的均值。

计量经济学多重共线性

计量经济学多重共线性


3、减小参数估计量的方差
多重共线性的主要后果是参数估计量具 有较大的方差，所以 采取适当方法减小参数估计量的方差， 虽然没有消除模型中的多重共线性，但确 能消除多重共线性造成的后果。 例如： ①增加样本容量，可使参数估计量的方 差减小。
*②岭回归法（Ridge Regression）
70年代发展的岭回归法，以引入偏误为代价减小 参数估计量的方差，受到人们的重视。 具体方法是：引入矩阵D，使参数估计量为
多重共线性使参数估计值的方差增大，1/(1-r2) 为方差膨胀因子(Variance Inflation Factor, VIF)
相关系数平方 方差膨胀因子 0 1 0.5 2 0.8 5 表 4.3.1 方差膨胀因子表 0.9 0.95 0.96 0.97 10 20 25 33 0.98 50 0.99 100 0.999 1000
1 ˆ var( 1 ) 2 ( X X )11 2 x12i x 2i ( x1i x 2i ) 2 2 2 x 2i

1 ( x1i x 2i ) 2
2 / x12i
2 x12i x 2i
1 2 x1i 1 r 2
2
i=1,2,…,n
其中ci不全为0，vi为随机误差项，则称为 近似共线 性（approximate multicollinearity）或交互相 关(intercorrelated)。
注意： 完全共线性的情况并不多见，一般出现 的是在一定程度上的共线性，即近似共线 性。

产生多重共线性的主要原因：
求出X1与X2的简单相关系数r，若|r|接近1，则说 明两变量存在较强的多重共线性。
(2)对多个解释变量的模型，采用综合统计检验法 若 在OLS法下：R2与F值较大，但t检验值较小， 说明各解释变量对Y的联合线性作用显著，但各解 释变量间存在共线性而使得它们对Y的独立作用不 能分辨，故t检验不显著。

多重共线性问题


§4.1 多重共线性问题 农民消费函数主要回归计算结果
-223.33 0.8129 0.0039 -0.1478 0.0068 94.62
57.127 0.1025 0.0008 0.1495 0.0291 41.10
-3.91 7.93 5.04 -0.99 0.23 2.30
132.52 5.49
（三）岭回归估计 称由关系式
所确定的估计量：为线性源自归模型的岭回归估计，其中是待定常数。
§4.3 多重共线性模型的岭回归估计
1. 2. 矩阵
有特征根
矩阵
有特征根
逆运算矩阵有较小特征根的情形得到改善
3. 岭回归估计是线性估计量
4. 岭回归估计是有偏估计量
§4.3 多重共线性模型的岭回归估计
5. 岭回归估计的均方误差
167.13 32.42 22.91
§4.1 多重共线性问题
多重共线性问题发生的原因
——很多宏观经济总量随着经济周期的波动，呈现出几乎同步 增长或削减的趋势，它们的数据向量极易出现近似线性相关的 现象。 ——还有一些经济行为不仅需要某些变量作为其解释因素，同 时还需要它们的滞后值变量也作为其解释因素。由于变量与它 的滞后变量几乎总是同方向发生变化，模型也容易存在多重共 线性问题 。
§4.2 多重共线性问题的检测
方差扩大化因子检测（以 为例） 方差的因子分解 受三方面因素的影响 ：
其中 为以下模型的拟合
检测临界指标：
§4.3 多重共线性模型的岭回归估计
——线性无偏估计类整体不再适用于多重共线性模型
——岭回归估计是具有较小均方误差的线性有偏估计量 （一）均方误差
对于无偏估计量 对于有偏估计量
逐一求得全部 个组合变量

多重共线性问题课件

多重共线性通常出现在多元回归分析 中，当两个或多个自变量之间存在高 度相关或完全相关时，会导致模型估 计的参数不稳定。
多重共线性的表现形式
相关性矩阵
通过计算自变量之间的相关性矩阵，可以发现高度相关的自变量 。
特征值
在多重共线性情况下，某些特征值的绝对值会接近于0，这表明自 变量之间存在高度相关。
方差膨胀因子
数据收集阶段预防
总结词
在数据收集阶段，预防多重共线性的关键是保证 数据的准确性和完整性，以及合理的数据样本量 。
总结词
在数据收集阶段，可以通过增加样本量来降低多 重共线性的影响。
详细描述
数据的质量直接关系到模型的准确性和可靠性， 因此需要确保数据的准确性和完整性。此外，合 理的数据样本量可以降低随机误差的影响，提高 模型的稳定性和可靠性。
多重共线性问题的
03
诊断
特征值诊断法
总结词
通过计算模型中自变量的特征值来判断是否存在多重共线性问题。
详细描述
特征值诊断法是通过计算自变量的特征值来判断自变量之间的相关性。如果自变量的特征值接近于零 ，说明该自变量与其他自变量高度相关，存在多重共线性问题。
条件指数法
总结词
通过计算自变量之间的条件指数来判断 是否存在多重共线性问题。
VS
详细描述
条件指数是一种衡量自变量之间相关性的 指标，如果条件指数大于一定阈值，说明 自变量之间存在多重共线性问题。
方差膨胀因子法
总结词
通过计算自变量的方差膨胀因子来判 断是否存在多重共线性问题。
详细描述
方差膨胀因子是衡量自变量对因变量 影响的放大程度，如果方差膨胀因子 大于一定阈值，说明自变量之间存在 多重共线性问题。
Байду номын сангаас

第五章多重共线性


第三节 多重共线性的检验
１．R2 较高，而显著t 统计量较少时，可能存在多重共
线性问题。 ２．当增加或剔除一个解释变量，或者改变一个观测值时， 回归系数的估计值发生较大变化，认为回归方程存在严重 的多重共线性。 ３．一些重要的解释变量在回归方程中没有通过显著性检 验时，可初步判断存在着严重的多重共线性。 ４．有些解释变量的回归系数所带符号与定性分析结果违 背时，可能存在多重共线性问题。 ５．解释变量间的相关系数较大时。 多重共线性是一个程度问题而不是有无的问题，是测度它 在任一具体样本中显现的程度。
可见每个因素都与服 装需求高度相关，而 且解释变量之间也是 高度相关的。
（2）建立一元回归模型 相关系数检验表明，收入与服装需求的相关性最强。所 以，以Y＝a＋bX＋μ作为最基本的模型。 （3）将其余变量逐个引入模型。 LS Y C X 则 X[0.1179] R2[0.9956] 引 入 P1 ： LS Y C X P1 则 X[0.1262(8.57)] P1[0.0378(-0.57)] R2[0.9958] 引 入 P0 ： LS Y C X P0 则 X[0.1030(5.67)] P0[0.0857(0.83)] R2[0.9960] 引入K：LS Y C X K 引入P1，P0：LS Y C X P1 P0 引入P1，P0，K：LS Y C X P1 P0 K

2 1 r12
2、无法正确反映每个解释变量对被解释变量的单独影响。
在多重共线性的情况下，解释变量的相关性将无法“保持其它变 量不变”，从而也难以分离出每个解释变量的单独影响。 各个回归系数的值很难精确估计，甚至可能出现符号错误的现象。
3、t检验的可靠性降低。
可能使原来显著的值变成不显著的，即容易将有重要影响的变量 误认为不显著的变量。

多重共线性——精选推荐

多重共线性多重共线性湖北⽂理学院湖北襄阳王茂林5.3（2）（1）检验含有时间趋势变量的回归⽅程中的时间趋势是否是多余的变量。

该检验为检验模型是否存在拟合过度，去掉时间变量，对模型进⾏t检验，得如下结果：LOG（Y）=-7.092248+LOG(X1)*0.6483+LOG(X2)*0.5737+T1*0.012841T统计值 -1.3921 2.2769 2.1701 0.3624p值 0.1761 0.0316 0.0397 0.7201R2=0.9984T=28显然，根据模型的估计和t检验结果，我们不能拒绝时间趋势变量T1 的系数为0，所以该变量为多余的变量（3）采⽤拉姆齐检验模型ＯＬＳ估计的拟合值和残差：(⼀)以残差为纵坐标，解释变量为横坐标作图：由图可以看出两变量的关系，得到辅助回归⽅程：Ct=a+a1Yt+a2Ct*Ct+f，我们可以得到|：由上的 Ct=19.35826+0.010433*Ct*Ct+0.071817*T1T值 14.60049 5.603946 3.467508P 值 0.0000 0.00000 0.0018R2=0.9996 T=28我们的待假设检验为H0：a2=0 H1: a2!=0由T检验可知，Ct*Ct系数估计值t检验的p值为0.00000，所以我们可以拒绝原假设，该模型的确存在拟合不⾜的情况。

（6）各个参数的值可能偏⼤也可能偏⼩--------------------------------------------------------------------------------------------------------------------------------------5.4（1）导⼊数据后，我们对数据进⾏估计：由上可知：显著性检验数表明，各个模型均不符合要求。

（2）两种模型的显著性检验均达不到要求，故不能⽤来反映中国通货膨胀的动态调整。

多重共线性

多重共线性城乡居民消费水平研究-解多重共线性一、文献综述长期以来，我国一直受到商品短缺的困扰，必须采取配给制的方式来限制居民的消费选择自由；随着供求关系的变化，人们的消费取向正在发生根本性的变化。

因此，了解当前城乡居民消费水平及其影响因素，对于把握我国不同群体消费需求的变化，引导生产、引导消费，开拓市场，发展循环经济，构建和谐社会具有重要意义。

影响消费的因素很多，如价格水平、利率水平、收入水平、消费偏好、家庭财产、风俗习惯、制度模式等。

其中，收入是影响消费的最重要因素。

改革开放以来,我国居民的收入水平在不断提高,居民消费情况也有明显变化。

在居民总体收入逐渐增加的同时,居民的收入差距也有所扩大,形成了高、中、低不同阶层的收入与消费群体。

根据国家统计局的调查资料显示,不同消费群体之间的消费与投资倾向已有很大差异,受此影响,社会消费结构也已发生了较大变化。

如今生活宽裕的高收入居民,十分关注生活质量的提高,消费倾向也出现明显变化,投资意识日益高涨。

调查显示,越来越多的高收入居民,在消费时追求精神消费和服务消费,教育、文化、通信、保健、住宅等成为消费热点,追求时尚化与个性化日趋明显。

高收入家庭的投资是社会民间投资中极为重要的部分,在国民经济运行中的作用不可低估.中等收入群体占到城镇家庭总数的60%以上,收入占到居民收入总数的50%多,是我国消费的主体部分,他们的消费行为对我国整体消费状况的影响是最大的,对这一层次居民消费的启动将直接关系到我国经济启动的成败。

这一消费群体的消费特征表现为对未来收入与支出不良预期的影响.所以基于这个问题的重要性，决定研究城乡居民的消费水平及其影响因素。

二、数据的初步分析数据的收集来源于2021年中华人民共和国国家统计局公布的年度数据，并选取城乡居民消费水平、城乡居民家庭人均可支配收入、职工平均工资、人均国内生产总值、城乡居民消费价格指数、城乡新建住房面积来研究其对城镇居民消费水平的影响。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

24
5
§3 多重共线性的影响
一、完全共线性 ˆ X Y ˆ无唯一解 ( X X ) ˆ 的方差是无穷大。 i
6
二、“不完全”多重共线性
ˆ的解不稳定。 ˆ 的方差非常大。 1、 i ˆ 2.8 ˆ 1 1 0.9 2 2 例如： 0.9 1 ˆ 2.9 ˆ 2 3 3 ˆ 2.8 ˆ 3.5678 0.99 1 2 2 0.99 ˆ ˆ 1 2 . 9 6 . 4322 3 3 ˆ 2.8 ˆ 40 .5743 0.999 1 2 2 0.999 2.9 ˆ ˆ 1 51 . 4257 3 3
10
三、方差膨胀因子(VIF)
第j个回归系数的方差 VIF j 自变量不相关时第j个回归系数的方差 1 ; 2 1 Rj 其中R 2 j 是自变量X j 对模型中其余自变量 线性回归模型的R 2。 矩阵X X的特征值。 一般地，若VIF 10，表明模型中有很强的 共线性问题。
11
四、SAS中的检验
2
例子
Yi 1 2 X 2i 3 X 3i ui 样本为 Y 0 1 2 X1 1 1 1 X2 1 0 1 X3 0 1 0
则X 1 X 2 X 3 0 ˆ X 由正规方程组的表达式( X X ) Y 1 X X 1 0 1 0 1 1 1 1 1 1 0 1 1 0 0 3 1 2 1 0 2 2 0 1 0 1
观察结果（共线性诊断）：1、最大条件指数 37.1>30，说明中等相关；2、与最大条件指数在 一行的4个变量的方差比例都大于0.5，说明这4个 变量就是一个具有中等相关的变量集。
14
五、F检验
例如：X2，X3，X4相互回归
1、 X2—X3，X4；若F >F ，则有多重共线性； 否则的话，就没有。 2、 X3—X2，X4；若F >F ，则有多重共线性； 否则的话，就没有。
1；则可以变换模型为Y AK L1 e u
Y K u A e L L 四、估计方法： 1、混合估计； 2、岭回归；
18

§4 多重共线性的处理
五、SAS中逐步回归方法 1、变量选择问题： 回归关系式Y Yt X 1，X 2， ，X m 解释变量因入太少，则预测时偏差大； 解释变量因入太多，也会影响预测精度； “最优”回归方程：从 { X 1，X 2， ，X m }中选出
7
二、“不完全”多重共线性
2、由于后果 （方差大），置信区间 1 将要宽很多 3、由于后果1，一个、多个系数的t值检验不显著 4、虽然一个或多个系数的t值统计上不显著， 但是R 2仍然可能很大。 5、OLS 估计量及其标准误对数据的小小变化 也会是敏感的。
8
§4 多重共线性的检验
Kenenta: 1 、多重共线性是一个程度问题，而不是有无的问题 2、多重共线性是对被假定为非随机的解释变量的情 况而言，所以它是一种样本而非总体特征。 一、观察回归结果 1、R 2很大，而 | t | 值很小。 2、添加新的解释变量R 2增加，而 | t | 值减小。
4
§2 多重共线性的来源
一、解释变量受同一因素的影响 时间序列数据： 1、经济发展;2、政治事件 3、偶然事件;4、时间趋势 二、解释变量中含有当期和滞后变量 I t 1 2 rt 3Yt 4Yt 1 ut Y2 Y3 Y1 , Yn ; Y n Y1 Y2 有多重共线性。 Yn 1
Proc reg data=data1; model y=x1 x2 x3 x4 / vif collin;
12
四、SAS中的检验结果
Parameter Estimaes
variable INTERCEP X1 X2 X3 X4 DF 1 1 1 1 1 Parameter Estimate 62.4 1.55 0.510 0.102 -0.144 Standard Error 70.1 0.745 0.724 0.755 0.709 T for H0 Parameter=0 0.891 2.08 0.705 0.135 -0.203 Prob>|T| 0.3991 0.0708 0.5009 0.8959 0.8441 Variance Inflation 0.0000 38.49 254.42 46.868 282.51
3、 X4—X3，X2；若F >F ，则有多重共线性； 否则的话，就没有。
15
§4 多重共线性的处理
一、样本处理 1、增加样本容量n； 2、增加精度，比如字长； 3、使用混合数据ห้องสมุดไป่ตู้时间 截面）
16
§4 多重共线性的处理
二、解释变量的处理 1、删除引起共线性的变量； 2、逐步回归； 3、解释变量加工： 例如：Yt 1 2 X t 3 X t 1 ut ˆ 0. 7 X 0 . 4 X u ˆ Y
ˆ有无穷多解。 r( X X ) 2,
3
二、不完全共线性
虽然解释变量之间 不存在完全共线性，但 是一些解释变量之间高度相关。例如：
X2 10 15 18 24 30 X3 50 75 90 120 150 X3* 52 75 97 129 152
样本向量X2与X3*的相关系数为0.9959。
23
§4 多重共线性的处理
(3)计算量适中的选择法：不计算所有可能回归子集 如MINR、MAXR等； 例如 : proc reg data data23; model y x1 - x4/selection rsquare best 2 run; 其中best 2要求每种变量的个数输出二个最佳的回归子集。 cp ;
观察结果（参数）：1、4个自变量的方差膨 胀因子（VIF）均大于10，最大为283.51， 这表明变量有严重的多重共线性。2、R2大， |t|小。
13
四、SAS中的检验结果
Collinearity Diagnostics (intercept adjusted)
Number 1 2 3 4 Eigenvalue 2.236 1.576 0.186 0.002 Condition Index 1.000 1.191 3.461 37.12 Var Prop X1 0.0026 0.0043 0.0635 0.9296 Var Prop X2 0.0006 0.0004 0.0021 0.9969 Var Prop X3 0.0015 0.0005 0.0465 0.9471 Var Prop X4 0.0005 0.0005 0.0007 0.9983
2 * * 选择子集A { X 1*，X 2 ， ，X L }
nL 使得J ( A) ESS ( A)达到最小； nL
20
§4 多重共线性的处理
(3)C p 统计量最小
* * 选择子集A { X 1*，X 2 ， ，X L }
ESS ( A) 使得C p ( A) 2 L n达到最小； ESS（n m） (4) AIC或BIC准则
t 1 t t 1 t
令Z t 0.7 X t 0.4 X t 1 Yt 1 2 Z t t 4、主分量法。
17
§4 多重共线性的处理
三、模型处理 1、差分：Yt 1 2 X 2t 3 X 3t ut Yt 2 X 2t 3 X 3t ut 2、环比指数 增长率； 3、利用约束条件：Y AK L e u
22
§4 多重共线性的处理
(2)计算量最大的全子集方法 通过计算所有可能回归子集按最优选择的 标准的回归方程。
2 包括标准R 2 ( RSQUARE)，C（ CP ）， R ( ADJRSQ) P
例如 : proc reg data data23; model y x1 - x4/selection rsquare cp aic rmse adjreq; run;
9
二、条件数
max 条件数：k ; 其中是矩阵X X的特征值。 min
因为X X是实对称正定阵，所以是实数，并且大于0
i 条件指数：ki min
一般地，ki 20 ~ 30，存在多重共线性。 10 ~ 30弱相关 k： 30 ~ 100中等相关 100 强相关
* * { X 1*，X 2 ， ，X L }使得选中的对Y都显著，
没有选中的对Y都不显著。
19
§4 多重共线性的处理
1、最优选择的标准： (1)均方误差S 2最小（Root MSE）
* * 选择子集A { X 1*，X 2 ， ，X L }
ESS ( A) 使得S ( A) 达到最小； nL (2)预测均方误差最小
第五章 多重共线性
1
§1 含义
一、多重共线性（multicolli nearity） 回归模型中的一些或全部解释变量（样本向量） 之间存在“完全”的线性关系。 即，对向量X 1 , X 2 , X k , 存在不全为0的 一组常数1 , 2 , k 使得
1 X 1 2 X 2 k X k 0
* * 选择子集A { X 1*，X 2 ， ，X L }
2L 使得AIC ( A) Ln ( ESS ( A)) n Lln( n) 或ＢIC ( A) Ln ( ESS ( A)) 达到最小； n ２ (5)修正Ｒ 准则：使得R２达到最大。
21
§4 多重共线性的处理
3、选择“最优”子集回归的方法 选择“最优”子集回归的方法有8种，三类。 (1)选择“最优”子集的简便方法 逐步筛选法（STEPWISE） ; 向前引入法（FORWARD） ; 向后剔除法（BACKWARD） ; 例如 : proc reg data data23; model y x1 - x4/selection stepwise sle 0.10 sls 0.10