人教版八年级数学第十八章测试卷试题及答案

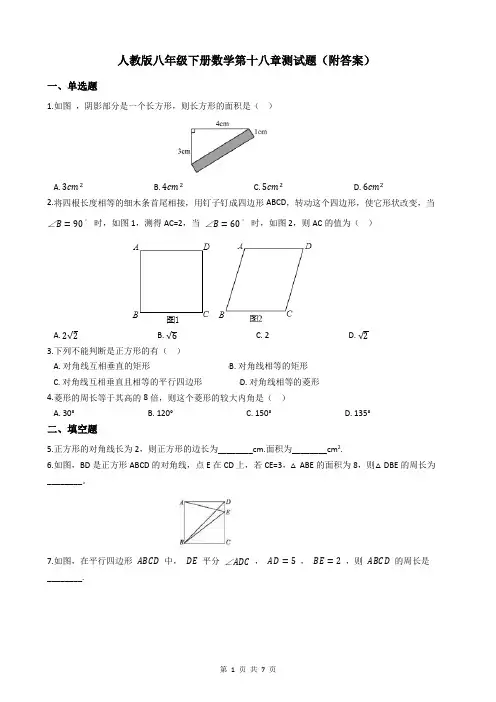
人教版八年级下册数学第十八章测试题（附答案）一、单选题1.如图，阴影部分是一个长方形，则长方形的面积是（）A. 3cm2B. 4cm2C. 5cm2D. 6cm22.将四根长度相等的细木条首尾相接，用钉子钉成四边形ABCD，转动这个四边形，使它形状改变，当∠B=90°时，如图1，测得AC=2，当∠B=60°时，如图2，则AC的值为（）A. 2√2B. √6C. 2D. √23.下列不能判断是正方形的有（）A. 对角线互相垂直的矩形B. 对角线相等的矩形C. 对角线互相垂直且相等的平行四边形D. 对角线相等的菱形4.菱形的周长等于其高的8倍，则这个菱形的较大内角是（）A. 30°B. 120°C. 150°D. 135°二、填空题5.正方形的对角线长为2，则正方形的边长为________cm.面积为________cm2.6.如图，BD是正方形ABCD的对角线，点E在CD上，若CE=3，△ABE的面积为8，则△DBE的周长为________。

7.如图，在平行四边形ABCD中，DE平分∠ADC，AD=5，BE=2，则ABCD的周长是________.8.如图，正方形ABCD的边长为10cm，E是AB上一点，BE=4cm，P是对角线AC上一动点，则PB+PE的最小值是________cm.9.若一个正方形的面积为a2+a+ 14，则此正方形的周长为________.10.如图为等边△ABC与正方形DEFG的重叠情形，其中D、E两点分别在AB、BC上，且BD=BE.若AB=3，DE=1，则△EFC的面积为________.11.如图,在平面直角坐标系中,O为坐标原点,A（1,3）,B（2,1）,直角坐标系中存在点C,使得O,A,B,C四点构成平行四边形,则C点的坐标为________.12.菱形的面积是16，一条对角线长为4，则另一条对角线的长为________.13.已知▱ABCD的对角线AC，BD相交于点O，△AOD是等边三角形，且AD=4，则AB的长为________.14.如图，边长为4的菱形ABCD中，∠ABC＝30°，P为BC上方一点，且S△PBC=14S菱形ABCD，则PB＋PC的最小值为________.三、解答题15.如图，点O是平行四边形ABCD的对角线交点，AD>AB，E,F是AB边上的点，且EF=1 2AB；G,H是BC边上的点，且GH=13BC，若S1,S2分别表示ΔEOF和ΔGOH的面积，求S1:S2的比。

【精选】人教版八年级下册数学第十八章《平行四边形》测试卷（含答案）一、选择题(每题3分，共30分)1．已知在▱ABCD中，∠B＋∠D＝200°，则∠B的度数为( ) A．100° B．160° C．80° D．60°2．【2022·广东】如图，在△ABC中，BC＝4，点D，E分别为AB，AC的中点，则DE＝( )A.14B.12C．1 D．2(第2题) (第4题) (第5题) (第8题) 3．【2022·河北】依据所标数据，下列一定为平行四边形的是( )4．【教材P44例2改编】【2021·恩施州】如图，在▱ABCD中，AB＝13，AD＝5，AC ⊥BC，则▱ABCD的面积为( )A．30 B．60 C．65 D.65 25．【教材P53例1改编】如图，在矩形ABCD中，对角线AC，BD交于点O，∠AOB ＝60°，AB＝5，则BD的长为( )A．20 B．15 C．10 D．56．【2021·河南】关于菱形的性质，以下说法不正确．．．的是( )A．四条边相等 B．对角线相等C．对角线互相垂直 D．是轴对称图形7．下列命题中，是真命题的为( )A．一组对边平行，另一组对边相等的四边形是平行四边形B．对角线互相垂直的四边形是菱形C．对角线相等的四边形是矩形D．一组邻边相等的矩形是正方形8．如图，已知在菱形ABCD中，对角线AC与BD交于点O，∠BAD＝120°，AC＝4，则该菱形的面积是( )A．16 3 B．16 C．8 3 D．89．【2022·青岛】如图，O为正方形ABCD对角线AC的中点，△ACE为等边三角形．若AB＝2，则OE的长度为( )A.62B. 6 C．2 2 D．2 3(第9题) (第10题) (第11题) (第13题)10．【教材P68复习题T13拓展】【2022·恩施州】如图，在四边形ABCD中，∠A＝∠B＝90°，AD＝10 cm，BC＝8 cm，点P从点D出发，以1 cm/s的速度向点A运动，点M从点B同时出发，以相同的速度向点C运动，当其中一个动点到达端点时，两个动点同时停止运动．设点P的运动时间为t(单位：s)，下列结论正确的是( )A．当t＝4时，四边形ABMP为矩形B．当t＝5时，四边形CDPM为平行四边形C．当CD＝PM时，t＝4D．当CD＝PM时，t＝4或6二、填空题(每题3分，共24分)11．如图，在▱ABCD中，AB＝5，AC＝8，BD＝12，则△COD的周长是________．12．在Rt△ABC中，∠C＝90°，AC＝5，BC＝12，则斜边上的中线CD＝________. 13．【2021·益阳】如图，已知四边形ABCD是平行四边形，从①AB＝AD，②AC ＝BD，③∠ABC＝∠ADC中选择一个作为条件，补充后使四边形ABCD成为菱形，则其选择是________(限填序号)．14．如图，平行四边形ABCD的三个顶点的坐标分别为A(1，1)，B(4，1)，D(2，3)，要把顶点A平移到顶点C的位置，则其平移方式可以是：先向右平移________个单位长度，再向上平移________个单位长度．(第14题) (第15题) (第16题) (第17题) 15．【2022·哈尔滨】如图，菱形ABCD的对角线AC，BD相交于点O.点E在OB 上，连接AE，点F为CD的中点，连接OF.若AE＝BE，OE＝3，OA＝4，则线段OF的长为________．16．如图，在矩形ABCD中，E是BC边上一点，AE＝AD，DF⊥AE于点F，连接DE，AE＝5，BE＝4，则DF＝________.17．【2022·苏州】如图，在平行四边形ABCD中，AB⊥AC, AB＝3, AC＝4，分别以A，C为圆心，大于12AC的长为半径画弧，两弧相交于点M，N，过M，N两点作直线，与BC交于点E，与AD交于点F，连接AE，CF.则四边形AECF的周长为________．18．以正方形ABCD的边AD为边作等边三角形ADE，则∠BEC的度数是____________．三、解答题(19，20题每题8分，21，22题每题12分，其余每题13分，共66分)19．【2022·桂林】如图，在▱ABCD中，点E和点F是对角线BD上的两点，且BF ＝DE.(1)求证：BE＝DF；(2)求证：△ABE≌△CDF.20．【2021·郴州】如图，四边形ABCD中，AB＝DC，将对角线AC向两端分别延长至点E，F，使AE＝CF, 连接BE，DF.若BE＝DF，证明：四边形ABCD是平行四边形．21．【教材P55练习T2改编】【2021·长沙】如图，▱ABCD的对角线AC，BD相交于点O，△OAB是等边三角形，AB＝4.(1)求证：▱ABCD是矩形；(2)求AD的长．22．【2021·十堰】如图，已知△ABC中，D是AC的中点，过点D作DE⊥AC交BC于点E，过点A作AF∥BC交ED的延长线于点F，连接AE，CF.(1)求证：四边形AECF是菱形；(2)若CF＝2，∠FAC＝30°，∠B＝45°，求AB的长．23．如图，正方形ABCD中，E是BC上的一点，连接AE，过B点作BH⊥AE，垂足为点H，延长BH交CD于点F，连接AF.(1)求证：AE＝BF；(2)若正方形的边长是5，BE＝2，求AF的长．24．【2022·北京八中模拟】在▱ABCD中，AB≠AD，对角线AC，BD交于点O，AC ＝10，BD＝16.点M，N在对角线BD上，点M从点B出发以每秒1个单位长度的速度向点D运动，到达点D时停止运动，同时点N从点D出发，运动至点B后立即返回，点M停止运动的同时，点N也停止运动，设运动时间为t 秒(t＞0)．。

人教版八年级数学下册第十八章测试卷及答案一.选择题(共10小题,每小题3分,共30分)1.下面的性质中,平行四边形不一定具有的是( )A．对角互补 B．邻角互补C．对角相等 D．对边相等2.如图,D,E分别是△ABC的边AB,AC上的点,且AD＝DB,AE＝EC.若DE＝4,则BC的长为( )A．2 B．4 C．6 D．83. 如图,在菱形ABCD中,下列结论错误的是( )A．AC＝BD B．AC⊥BD C．AB＝AD D．∠1＝∠24. 如图,在平行四边形ABCD中,已知∠ODA＝90°,AC＝10 cm,BD＝6 cm,则AD的长为( )A．4 cm B．5 cm C．D．8 cm5.四边形ABCD的对角线AC与BD相交于点O,下列四组条件中,一定能判定四边形ABCD为平行四边形的是( )A．AD∥BC B．OA＝OC,OB＝ODC．AD∥BC,AB＝DC D．AC⊥BD6.如图,在矩形ABCD中,AD＝6,对角线AC与BD相交于点O,AE⊥BD,垂足为E,且DE＝3BE,则AE的长为( )A．2 B．．3 D．7.如图,四边形ABCD 的两条对角线相交于点O,且互相平分．添加下列条件后,不能判定四边形ABCD为菱形的是( )A．AC⊥BD B．AB＝ADC．AC＝BD D．∠ABD＝∠CBD8.如图,四边形ABCD是正方形,延长AB到点E,使AE＝AC,则∠BCE的度数是( )A．67.5° B．22.5° C．30° D．45°9.如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC,AD＝＝2,则四边形OCED的面积为( )A．．4 C．．810. 如图,在四边形ABCD中,∠A＝∠B＝90°,AD＝10 cm,BC＝8 cm,点P从点D出发,以1 cm/s的速度向点A运动,点M从点B同时出发,以相同的速度向点C运动,当其中一个动点到达端点时,两个动点同时停止运动．设点P的运动时间为t(单位:s),下列结论正确的是( )A．当t＝4时,四边形ABMP为矩形B．当t＝5时,四边形CDPM为平行四边形C．当CD＝PM时,t＝4D．当CD＝ PM时,t＝4或6二．填空题(共8小题,每小题3分,共24分)11.在四边形ABCD中,AB＝DC,请添加一个条件,使四边形ABCD成为平行四边形,你所添加的条件为__________．12. ．如图,在菱形ABCD中,对角线AC＝6,BD＝10,则菱形ABCD的面积为________．13.若以A(－0.5,0),B(2,0),C(0,1)三点为顶点画平行四边形,则第四个顶点不可能在第________象限．14.如图,E,F是正方形ABCD的对角线AC上的两点,若AC＝8,AE＝CF＝2,则四边形BEDF的周长是________．15.如图,BD为正方形ABCD的对角线,BE平分∠DBC,交DC于点E,延长BC到点F,使CF＝CE,连接DF.若CE ＝1 cm,则BF＝__________cm．16.如图,连接四边形ABCD各边中点,得到四边形EFGH,还要添加______________条件,才能保证四边形EFGH是矩形．17.如果一个平行四边形的一个内角的平分线分它的一边为1:2两部分,那么称这样的平行四边形为"协调平行四边形",称该边为"协调边"．当协调边为6时,这个平行四边形的周长为________．18.如图,正方形ABCD的边长为1,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,…,以此类推,第n个正方形的面积为________．三．解答题(共7小题, 66分)19．(8分) 如图,在▱ABCD中,E为AD延长线上的一点,F为CB延长线上的一点,且DE＝BF,连接AF,CE.求证:四边形AFCE是平行四边形．20．(8分) 如图,在▱ABCD中,点E,F分别在边CB,AD的延长线上,且BE＝DF,EF分别与AB,CD交于点G,H.求证AG＝CH.21．(8分) 如图,在▱ABCD中,点E和点F是对角线BD上的两点,且BF＝DE.(1)求证:BE＝DF；(2)求证:△ABE≌△CDF.22．(8分) 在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.(1)求证AF＝DC；(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论．23．(10分)如图,正方形ABCD的边长为4,E,F分别为DC,BC的中点．(1)求证△ADE≌△ABF；(2)求△AEF的面积．24．(10分)如图,在正方形ABCD中,点E,F分别在BC和CD上,且BE＝DF,连接EF.(1)求证:AE＝AF；(2)过点E作EM∥AF,过点F作FM∥AE,求证:四边形AEMF是菱形．25．(14分)如图,在矩形ABCD中,AB＝3,BC＝4.点M,N在对角线AC上,且AM＝CN,E,F分别是AD,BC的中点．(1)求证:△ABM≌△CDN；(2)点G是对角线AC上的点,∠EGF＝90°,求AG的长．参考答案1-5ADAAB 6-10CCBAD11. AB ∥DC(答案不唯一)_12. 3013. 三15.(216.AC ⊥BD(答案不唯一)　17. 16或2018. 2n －1　19.证明:∵四边形ABCD 是平行四边形,∴AD ∥BC,AD ＝BC,∴AE ∥CF. 又∵DE ＝BF,∴AD ＋DE ＝BC ＋BF,即AE ＝CF,∴四边形AFCE 是平行四边形20．证明:∵四边形ABCD 是平行四边形,∴AD ＝BC,AD ∥BC,∠A ＝∠C.∴∠F ＝∠E.∵BE ＝DF,∴AD ＋DF ＝CB＋BE,即AF ＝CE.在△AGF 和△CHE 中, {∠A ＝∠CAF ＝CE ∠F ＝∠E ∴△AGF ≌△CHE(ASA)．∴AG ＝CH.21. 证明:(1)∵BF ＝DE,∴BF －EF ＝DE －EF,即BE ＝DF.(2)∵四边形ABCD 为平行四边形,∴AB ＝CD,且AB ∥CD.∴∠ABE ＝∠CDF.在△ABE 和△CDF 中, {AB ＝CD∠ABE ＝∠CDF BE ＝DF∴△ABE ≌△CDF(SAS)．22. 证明:(1)∵四边形ABCD 是正方形,∴AB ＝AD,∠B ＝∠D ＝90°.又∵BE ＝DF,∴Rt△ABE≌Rt△ADF(SAS),∴AE ＝AF(2)∵EM ∥AF,FM ∥AE,∴四边形AEMF 是平行四边形．又由(1)知AE ＝AF,∴▱AEMF 是菱形23. (1)证明:∵四边形ABCD 为正方形,∴AB ＝AD ＝DC ＝CB,∠D ＝∠B ＝90°.∵E,F 分别为DC,BC 的中点,∴DE ＝12DC,BF ＝12BC.∴DE ＝BF.在△ADE 和△ABF 中, {AD ＝AB∠D ＝∠B DE ＝BF ∴△ADE ≌△ABF(SAS)．(2)解:由题易知△ABF,△ADE,△CEF 均为直角三角形,且AB ＝AD ＝4,DE ＝BF ＝CE ＝CF ＝12×4＝2,∴S △AEF ＝S 正方形ABCD －S △ADE －S △ABF －S △CEF ＝4×4－12×4×2－12×4×2－12×2×2＝6.24. (1)证明:∵AF ∥BC,∴∠AFE ＝∠DBE.∵E 是AD 的中点,∴AE ＝DE.在△AFE 和△DBE 中, {∠AFE ＝∠DBE∠FEA ＝∠BED AE ＝DE ∴△AFE ≌△DBE(AAS)．∴AF ＝BD.∵AD 是BC 边上的中线,∴DC ＝BD.∴AF ＝DC.(2)解:四边形ADCF 是菱形．证明:由(1)得AF ＝DC,又∵AF ∥BC,∴四边形ADCF 是平行四边形．∵AC ⊥AB,AD是斜边BC 上的中线,∴AD ＝12BC ＝DC.∴四边形ADCF 是菱形．25.解:(1)∵四边形ABCD 是矩形,∴AB ∥CD,AB ＝CD,∴∠MAB ＝∠NCD.在△ABM 和△CDN 中,{AB ＝CD∠MAB ＝∠NCDAM ＝CN ∴△ABM ≌△CDN(SAS)(2)如图,连接EF,交AC 于点O.∵四边形ABCD 是矩形,∴AD ＝BC,∠ABC ＝90°,∵AB ＝3,BC ＝4,∴AC ＝5,∵E,F 分别是AD,BC 的中点,∴AE ＝BF ＝CF,∴四边形ABFE 是矩形,∴EF ＝AB ＝3.在△AEO 和△CFO 中,{∠EOA ＝∠FOC∠EAO ＝∠FCO AE ＝CF ∴△AEO ≌△CFO(AAS),∴EO ＝FO,AO ＝CO,∴O 为EF,AC 中点．∵∠EGF ＝90°,OG ＝12EF ＝32,∴AG ＝AO －OG ＝1或AG ＝AO ＋OG ＝4,∴AG 的长为1或4。

人教版八年级数学下册第十八章《平行四边形》综合测试卷一、单选题(共30分)1．如图，在四边形ABCD 中，AB ∥CD ，要使四边形ABCD 是平行四边形，下列可添加的条件不正确的是（ ）A ．AD =BCB ．AB =CDC ．AD ∥BC D ．∥A =∥C 2．如图，在∥ABCD 中，连接AC ，∥ABC ＝∥CAD ＝45°，AB ＝2，则BC 的长是( )A 2B ．2C ．2D ．43．如图，在长方形ABCD 中无重叠放入面积分别为216cm 和212cm 的两张正方形纸片，则图中空白部分的面积为（ ）2cmA ．1683-B ．1283-+C ．843-D ．423- 4．如图，已知平行四边形ABCD 的对角线AC ，BD 交于点O ，且AC =8，BD =10，则边AB 的长可以是（ ）A ．1B ．8C ．10D ．125．在平面直角坐标系中，A ，B ，C 三点的坐标分别为(0,0)，(0,4)，(1,1)，以这三点为平行四边形的三个顶点，则第四个顶点不可能在（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限 6．如图，矩形ABCD 和矩形CEFG ，AB ＝1，BC ＝CG ＝2，CE ＝4，点P 在边GF 上，点Q 在边CE 上，且PF ＝CQ ，连结AC 和PQ ，M ，N 分别是AC ，PQ 的中点，则MN 的长为（ ）A ．3B ．6C 37D 17 7．如图，菱形ABCD 对角线AC ，BD 交于点O ，15ACB ∠=︒，过点C 作CE AD ⊥交AD 的延长线于点E ．若菱形ABCD 的面积为4，则菱形的边长为（ ）A ．22B ．2C ．2D ．48．如图，在ABC 中，90A ∠=，D 是AB 的中点，过点D 作BC 的平行线，交AC 于点E ，作BC 的垂线交BC 于点F ，若AB CE =，且DFE △的面积为1，则BC 的长为（ ）A ．25B ．5C ．5D ．10 9．如图，在矩形ABCD 内有一点F ，FB 与FC 分别平分∥ABC 和∥BCD ，点E 为矩形ABCD 外一点，连接BE ，CE ．现添加下列条件：∥EB ∥CF ，CE ∥BF ；∥BE =CE ，BE =BF ；∥BE ∥CF ，CE ∥BE ；∥BE =CE ，CE ∥BF ，其中能判定四边形BECF 是正方形的共有( )A ．1个B ．2个C ．3个D ．4个 10．在平面直角坐标系中，长方形OACB 的顶点O 在坐标原点，顶点A 、B 分别在x 轴、y 轴的正半轴上，OA ＝3，OB ＝4，D 为边OB 的中点，若E 为x 轴上的一个动点，当∥CDE 的周长最小时，求点E 的坐标（ ）A ．（一3，0）B ．（3，0）C ．（0，0）D ．（1，0）二、填空题(共24分)11．在菱形ABCD 中，∥BAD ＝72°，点F 是对角线AC 上（不与点A ，C 重合）一动点，当ADF 是等腰三角形时，则∥AFD 的度数为_____．12．如图，在ABC 中，点M 为BC 的中点，AD 平分,BAC ∠且BD AD ⊥于点D ，延长BD 交AC 于点,N 若12,18AB AC ==，则MD =_______________________．13．如图，在Rt ∥ABC 中，∥ABC ＝90º，D 、E 、F 分别为AB 、BC 、CA 的中点，若BF ＝6，则DE ＝_____．14．平行四边形ABCD 的周长为60cm ，对角线AC 、BD 相交于点O ，∥AOB 的周长比∥BOC 的周长为8cm ，则AB 的长为_____cm ．15．如图，在平行四边形ABCD 中，BF 平分∥ABC ，交AD 于点F ，CE 平分∥BCD ，交AD 于点E ，AB =8，BC =12，则EF 的长为__________．16．如图在Rt △ABC 中，∥ACB ＝90°，AC ＝4，BC ＝3，D 为斜边AB 上一点，以CD 、CB 为边作平行四边形CDEB ，当AD ＝_____，平行四边形CDEB 为菱形．17．如图，在平行四边形ABCD 中，AB ＝10，AD ＝6，AC ∥BC ．则BD ＝_____．18．如图所示,在ΔABC 中,点D 是BC 的中点,点E ,F 分别在线段AD 及其延长线上,且DE ＝DF ,给出下列条件:∥BE ∥EC ;∥BF∥EC ;∥AB ＝AC∥从中选择一个条件使四边形BECF 是菱形,你认为这个条件是____(只填写序号).三、解答题(共66分)19．如图，在ABCD 中，对角线AC 与BD 相交于点O ，点,E F 分别为,OB OD 的中点，连接,AE CF ．求证：AE CF ．20．如图，∥ABCD 的对角线AC 、BD 交于点O ，E 、F 是对角线AC 上两点，AE ＝CF ．求证：四边形DEBF 是平行四边形．21．如图，将∥ABCD 的边AB 延长至点E ，使BE=AB ，连接DE 、EC 、BD 、DE 交BC 于点O ．（1）求证：∥ABD∥∥BEC ；（2）若∥BOD=2∥A ，求证：四边形BECD 是矩形．22．如图，在ABC ∆中，AD 是高，E F 、分别是AB AC 、的中点．（1）EF 与AD 有怎样的位置关系？证明你的结论；（2）若6,4BC AD ==，求四边形AEDF 的面积．23．如图，等边AEF ∆的顶点E ，F 在矩形ABCD 的边BC ，CD 上，且45CEF ∠=． 求证：矩形ABCD 是正方形．24．如图，在正方形ABCD 中，点E 、F 分别在边BC 和CD 上，且BE CF =，连接AE 、BF ，其相交于点G ，将BCF △沿BF 翻折得到BC F '△，延长FC '交BA 延长线于点H ．（1）求证：AE BF =；（2）若3AB =，2EC BE =，求BH 的长．25．如图，在▱ABCD 中，AE∥BC ，AF∥CD ，垂足分别为E ，F ，且BE=DF （1）求证：▱ABCD 是菱形；（2）若AB=5，AC=6，求▱ABCD 的面积．26．如图，在矩形ABCD 中，AB ＝15，E 是BC 上的一点，将∥ABE 沿着AE 折叠，点B 刚好落在CD 边上点G 处；点F 在DG 上，将∥ADF 沿着AF 折叠，点D 刚好落在AG 上点H 处，且CE ＝45BE ， （1）求AD 的长；（2）求FG 的长27．如图，BD是∥ABC的角平分线，过点作DE//BC交AB于点E，DF//AB交BC于点F．（1）求证：四边形BEDF是菱形；（2）若∥ABC＝60°，∥ACB＝45°，CD＝6，求菱形BEDF的边长．28．（1）如图1，正方形ABCD中，E为边CD上一点，连接AE，过点A作AF∥AE 交CB的延长线于F，猜想AE与AF的数量关系，并说明理由；（2）如图2，在（1）的条件下，连接AC，过点A作AM∥AC交CB的延长线于M，观察并猜想CE与MF的数量关系，并说明理由；（3）解决问题：王师傅有一块如图所示的板材余料，其中∥A=∥C=90°，AB=AD．王师傅想切一刀后把它拼成正方形．请你帮王师傅在图3中画出剪拼的示意图．参考答案：1．A2．C3．B4．B5．C6．C7．A8．A9．D10．D11．108°或72°12．313．614．1915．416．7517．1318．∥22．（1）EF 垂直平分AD ；（2）6AEDF S 四边形． 24．5．25．S 平行四边形ABCD =24 26．（1）AD = 9；（2）FG =7.5 27．（2）628．（1）AE=AF （2）CE=MF ，。

人教版八年级数学下册第十八章测试题（附答案）学校:___________姓名：___________班级：___________考号：___________评卷人得分一、选择题AC与BD交于点O，下列条件不能判定这个四边形是平行四边形的是（）A．OA=OC，OB=OD B．AD∥BC，AB∥DCC．AB=DC，AD=BC D．AB∥DC，AD=BC2.如图，△ABC和△ADE都是等腰直角三角形，∠BAC=∠DAE=90°，四边形ACDE是平行四边形，连接CE交AD于点F，连接BD交CE于点G，连接BE．下列结论中：①CE=BD；②△ADC是等腰直角三角形；③∠ADB=∠AEB；④CD•AE=EF•CG；一定正确的结论有（）A．1个 B．2个 C．3个 D．4个3.如图，在菱形ABCD中，对角线AC与BD相交于点O，OE⊥AB，垂足为E，若∠ADC=130°，则∠AOE的大小为（）A．75° B．65° C．55° D．50°4.如果四边形内的一个点到四条边的距离相等，那么这个四边形一定有（）A．一组邻边相等 B．一组对边平行 C．两组对边分别相等 D．两组对边的和相等5.长方形的一条对角线的长为10cm，一边长为6cm，它的面积是（）A．60cm2 B．64cm2 C．24cm2 D．48cm26.已知▱ABCD的周长为32，AB=4，则BC=（）A．4 B．12 C．24 D．287.在□ABCD中，对角线AC、BD相交于O，下列说法一定正确的是（）A．AC=BD B． AC⊥BD C．AO=DO D．AO=CO8.如图，在菱形ABCD中，AB=2，∠BAD=60°，E是AB的中点，P是对角线AC上的一个动点，则PE+PB的最小值为（）A． 1 B．3C． 2 D．59.如图，下列条件之一能使平行四边形ABCD是菱形的为（）①AC ⊥BD ②∠BAD=90° ③AB=BC ④AC=BD A ．①③ B ．②③ C ．③④ D ．①②③10.如图，将宽为1cm 的纸条沿BC 折叠，使∠CAB=45°，则折叠后重叠部分的面积为（ ）A ．32cm 2 B ．3 cm 2 C ．2 cm 2 D ．22 cm 211.如图，已知正方形ABCD 的边长为2，E 是边BC 上的动点，BF ⊥AE 交CD 于点F ，垂足为点G ，连接CG ，下列说法：①AG＞GE ；②AE=BF；③点G 运动的路径长为π；④CG 的最小值5﹣1．其中正确的说法有（ ）个．A ．4B ．3C ．2D ．112.已知▱ABCD 的周长为32，AB=4，则BC=（ ） A 、4 B 、12 C 、24 D 、28评卷人 得分二、填空题13.如图，把一张矩形纸片ABCD 沿对角线BD 折叠，使C 点落在C'，且BC'与AD 交于E 点，若,40=∠ABE 则=∠ADB °14.如图，在边长为6的正方形ABCD 中，E 是边CD 的中点，将△ADE 沿AE 对折至△AFE ，延长EF 交BC 于点G ，连接AG ，则BG= ．15.如图．边长为1的两个正方形互相重合，按住其中一个不动，将另一个绕顶点A 顺时针旋转45°，则这两个正方形重叠部分的面积是 ．16.如图，在菱形ABCD中，点A在x轴上，点B的坐标为（4，1），点D的坐标为（0，1），则点C的坐标为________。

人教版八年级数学下册第十八章-平行四边形章节测评考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、如图，菱形OABC在平面直角坐标系中的位置如图所示，∠AOC＝45°，OA C的坐标为（）A．，1）B．（1，1）C．（1D．，1）2、如图菱形ABCD，对角线AC，BD相交于点O，若BD＝8，AC＝6，则AB的长是（）A．5 B．6 C．8 D．103、如图，已知P 是AOB ∠平分线上的一点，60AOB ︒∠=，PD OA ⊥，M 是OP 的中点，4cm DM =，如果C 是OB 上一个动点，则PC 的最小值为（ ）A ．8cmB ．5cmC ．4cmD ．2cm4、顺次连接矩形各边中点得到的四边形是（ ）A ．平行四边形B ．矩形C ．菱形D ．正方形5、如图所示，公路AC 、BC 互相垂直，点M 为公路AB 的中点，为测量湖泊两侧C 、M 两点间的距离，若测得AB 的长为6km ，则M 、C 两点间的距离为（ ）A ．2.5kmB ．4.5kmC ．5kmD ．3km6、如图，已知四边形ABCD 和四边形BCEF 均为平行四边形，∠D ＝60°，连接AF ，并延长交BE 于点P ，若AP ⊥BE ，AB ＝3，BC ＝2，AF ＝1，则BE 的长为（ ）A ．5B ．C ．D ．7、如图，在菱形ABCD中，AB＝5，AC＝8，过点B作BE⊥CD于点E，则BE的长为（）A．125B．245C．6 D．4858、如图，在平面直角坐标系中，点A是x轴正半轴上的一个动点，点C是y轴正半轴上的点，BC AC⊥于点C．已知16AC=，6BC=．点B到原点的最大距离为（）A．22 B．18 C．14 D．109、如图，已知在正方形ABCD中，10AB BC CD AD====厘米，90A B C D∠=∠=∠=∠=︒，点E在边AB 上，且4AE=厘米，如果点P在线段BC上以2厘米/秒的速度由B点向C点运动，同时，点Q在线段CD上以a厘米/秒的速度由C点向D点运动，设运动时间为t秒．若存在a与t的值，使BPE与CQP全等时，则t的值为（）A．2 B．2或1.5 C．2.5 D．2.5或210、已知三角形三边长分别为7cm，8cm，9cm，作三条中位线组成一个新的三角形，同样方法作下去，一共做了五个新的三角形，则这五个新三角形的周长之和为（）A ．46.5cmB ．22.5cmC ．23.25cmD ．以上都不对第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分）1、如图，在直角三角形ABC 中，∠B =90°，点D 是AC 边上的一点，连接BD ，把△CBD 沿着BD 翻折，点C 落在AB 边上的点E 处，得到△EBD ，连接CE 交BD 于点F ，BG 为△EBD 的中线．若BC =4，△EBG 的面积为3，则CD 的长为____________2、如图，在▱ABCD 中，BC ＝3，CD ＝4，点E 是CD 边上的中点，将△BCE 沿BE 翻折得△BGE ，连接AE ，A 、G 、E 在同一直线上，则AG ＝______，点G 到AB 的距离为______．3、如图，在ABC 中，2AB AC ==，90BAC ∠=︒，M ，N 为BC 上的两个动点，且MN AM AN +的最小值是________．4、一个三角形三边长之比为4∶5∶6，三边中点连线组成的三角形的周长为30cm ，则原三角形最大边长为_________cm ．5、如图，在长方形ABCD 中，9DC =．在DC 上找一点E ，沿直线AE 把AED 折叠，使D 点恰好落在BC上，设这一点为F，若ABF的面积是54，则FCE△的面积=______________．三、解答题（5小题，每小题10分，共计50分）1、如图，正方形网格中的每个小正方形边长都是1，每个小格的顶点叫做格点，以格点为顶点分别按下列要求画三角形．（1）在图1中，画一个三边长都是有理数的直角三角形；（2）在图2中，画一个以BC为斜边的直角三角形，使它们的三边长都是无理数且都不相等；（3）在图3中，画一个正方形，使它的面积是10．2、如图，在Rt△ABC中，∠ACB＝90°．（1）作AB的垂直平分线l，交AB于点D，连接CD，分别作∠ADC，∠BDC的平分线，交AC，BC于点E，F（尺规作图，不写作法，保作图痕迹）；（2）求证：四边形CEDF是矩形．3、如图：在Rt ABC中，90∠=，点O为AB的中点，点P为直线BC上的动点（不与点A︒ACB︒∠=，30∆，连接BQ．B，C重合），连接OC，OP，以OP为边在OC的上方作等边OPQ（1）OBC是________三角形；=；（2）如图1，当点P在边BC上时，运用（1）中的结论证明CP BQ（3）如图2，当点P在CB的延长线上时，（2）中的结论是否依然成立？若成立，请加以证明，若不成立，请说明理由．4、如图，在▱ABCD中，对角线AC，BD交于点O，E是BD延长线上一点，且△ACE是等边三角形．（1）求证：四边形ABCD是菱形；（2）若∠AED＝2∠EAD，AB＝a，求四边形ABCD的面积．5、已知：如图，30∠=︒，45B∠=︒，AD是BC上的高线，CE是AB边上的中线，DG CE于G．ACDAB=，求线段AC的长；（1）若6（2）求证：CG EG．---------参考答案-----------一、单选题1、B【解析】【分析】作CD⊥x轴，根据菱形的性质得到OC=OA Rt△OCD中，根据勾股定理求出OD的值，即可得到C点的坐标．【详解】：作CD⊥x轴于点D，则∠CDO=90°，∵四边形OABC是菱形，OA∴OC=OA又∵∠AOC=45°，∴∠OCD=90°-∠AOC=90°-45°=45°，∴∠DOC=∠OCD，∴CD=OD，在Rt△OCD中，OC CD2+OD2=OC2，∴2OD2=OC2=2，∴OD2=1，∴OD=CD=1（负值舍去），则点C的坐标为（1，1），故选：B．【点睛】此题考查了菱形的性质、等腰直角三角形的性质以及勾股定理，根据勾股定理和等腰直角三角形的性质求出OD=CD=1是解决问题的关键．2、A【解析】【分析】由菱形的性质可得OA=OC=3，OB=OD=4，AO⊥BO，由勾股定理求出AB．【详解】解：∵四边形ABCD是菱形，AC=6，BD=8，∴OA=OC=3，OB=OD=4，AO⊥BO，在Rt△AOB中，由勾股定理得：5AB=，故选：A．【点睛】本题考查了菱形的性质、勾股定理等知识；熟练掌握菱形对角线互相垂直且平分的性质是解题的关键．3、C【解析】【分析】根据题意由角平分线先得到OPD △是含有30角的直角三角形，结合直角三角形斜边上中线的性质进而得到OP ，DP 的值，再根据角平分线的性质以及垂线段最短等相关内容即可得到PC 的最小值．【详解】解：∵点P 是∠AOB 平分线上的一点，60AOB ∠=︒， ∴1302AOP AOB ∠=∠=︒，∵PD ⊥OA ，M 是OP 的中点，4cm DM =∴28cm OP DM ==， ∴14cm 2PD OP ==∵点C 是OB 上一个动点∴当PC OB ⊥时，PC 的值最小，∵OP 平分∠AOB ，PD ⊥OA ，PC OB ⊥∴PC 最小值4cm PD ==，故选C ．【点睛】本题主要考查了角平分线的性质、含有30角的直角三角形的选择，直角三角形斜边上中线的性质、垂线段最短等相关内容，熟练掌握相关性质定理是解决本题的关键．4、C【解析】【分析】如图，矩形ABCD 中，利用三角形的中位线的性质证明111,,,,222EF BD EF BD GH BD GH BD FG AC ∥∥，再证明四边形ABCD 是平行四边形，再证明,EF FG 从而可得结论.【详解】解：如图，矩形ABCD 中，,AC BD ∴=,,,E F G H 分别为四边的中点，111,,,,222EF BD EF BD GH BD GH BD FG AC ∥∥， ,,EF GH EF GH ∥∴ 四边形ABCD 是平行四边形，11,,,22AC BD EF BD FG AC === ,EF FG ∴= ∴ 四边形EFGH 是菱形．故选C ．【点睛】本题考查的是矩形的性质，菱形的判定，三角形的中位线的性质，熟练的运用三角形的中位线的性质解决中点四边形问题是解本题的关键.5、D【解析】【详解】根据直角三角形斜边上的中线性质得出CM ＝12AB ，即可求出CM ．【解答】解：∵公路AC，BC互相垂直，∴∠ACB＝90°，∵M为AB的中点，AB，∴CM＝12∵AB＝6km，∴CM＝3km，即M，C两点间的距离为3km，故选：D．【点睛】本题考查了直角三角形的性质，解题关键是掌握直角三角形斜边上的中线的性质：直角三角形斜边上的中线等于斜边的一半．6、D【解析】【分析】过点D作DH⊥BC，交BC的延长线于点H，连接BD，DE，先证∠DHC=90º，再证四边形ADEF是平行四边形，最后利用勾股定理得出结果．【详解】过点D作DH⊥BC，交BC的延长线于点H，连接BD，DE，∵四边形ABCD是平行四边形，AB=3，∠ADC=60º，∴CD=AB=3，∠DCH=∠ABC=∠ADC=60º，∵DH⊥BC，∴∠DHC =90º，∴∠ADC +∠CDH =90°，∴∠CDH =30°，在Rt △DCH 中，CH =12CD =32，DH ，∴222223(2)192BD BH DH =+=++=， ∵四边形BCEF 是平行四边形，∴AD =BC =EF ，AD ∥EF ，∴四边形ADEF 是平行四边形，∴AF ∥DE ，AF =DE =1，∵AF ⊥BE ，∴DE ⊥BE ，∴22219118BE BD DE =-=-=， ∴BE =故选D ．【点睛】本题考查了平行四边形的判定与性质，勾股定理，解题的关键是熟练运用这些性质解决问题．7、B【解析】【分析】根据菱形的性质求得BD 的长，进而根据菱形的面积等于12AC BD CD BE ⋅=⋅，即可求得BE 的长【详解】解：如图，设,AC BD 的交点为O ，四边形ABCD 是菱形AC BD ∴⊥，142AO CO AC ===，DO BO =，5CD AB == 在Rt AOB 中，5AB =，4AO =3BO ∴26BD BO ∴== 菱形的面积等于12AC BD CD BE ⋅=⋅1168242255AC BD BE CD ⋅⨯∴==⨯= 故选B【点睛】本题考查了菱形的性质，掌握菱形的性质，求得BD 的长是解题的关键．8、B【解析】【分析】首先取AC的中点E，连接BE，OE，OB，可求得OE与BE的长，然后由三角形三边关系，求得点B到原点的最大距离．【详解】解：取AC的中点E，连接BE，OE，OB，∵∠AOC＝90°，AC＝16，∴OE＝CE12=AC＝8，∵BC⊥AC，BC＝6，∴BE=10，若点O，E，B不在一条直线上，则OB＜OE+BE＝18．若点O，E，B在一条直线上，则OB＝OE+BE＝18，∴当O，E，B三点在一条直线上时，OB取得最大值，最大值为18．故选：B【点睛】此题考查了直角三角形斜边上的中线的性质以及三角形三边关系．此题难度较大，注意掌握辅助线的作法，注意掌握数形结合思想的应用．9、D【解析】【分析】根据题意分两种情况讨论若△BPE≌△CQP，则BP=CQ，BE=CP；若△BPE≌△CPQ，则BP=CP=5厘米，BE=CQ=6厘米进行求解即可.解：当2a =，即点Q 的运动速度与点P 的运动速度都是2厘米/秒，若△BPE ≌△CQP ，则BP =CQ ，BE =CP ，∵AB =BC =10厘米，AE =4厘米，∴BE =CP =6厘米，∴BP =10-6=4厘米，∴运动时间t =4÷2=2（秒）；当2a ≠，即点Q 的运动速度与点P 的运动速度不相等，∴BP ≠CQ ，∵∠B =∠C =90°，∴要使△BPE 与△OQP 全等，只要BP =PC =5厘米，CQ =BE =6厘米，即可．∴点P ，Q 运动的时间t =252 2.5BP ÷=÷=（秒）.综上t 的值为2.5或2.故选：D ．【点睛】本题主要考查正方形的性质以及全等三角形的判定，解决问题的关键是掌握正方形的四条边都相等，四个角都是直角；两边及其夹角分别对应相等的两个三角形全等．同时要注意分类思想的运用．10、C【解析】【分析】如图所示，8cm AB =，9cm BC =，7cm AC =，DE ，DF ，EF 分别是三角形ABC 的中位线，GH ，GI ，HI 分别是△DEF 的中位线，则14.5cm 2DE BC ==，14cm 2EF AB ==，1 3.5cm 2DF AC ==，即可得到△DEF 的周长==12cm DE DF EF ++，由此即可求出其他四个新三角形的周长，最后求和即可．解：如图所示，8cm AB =，9cm BC =，7cm AC =，DE ，DF ，EF 分别是三角形ABC 的中位线，GH ，GI ，HI 分别是△DEF 的中位线， ∴14.5cm 2DE BC ==，14cm 2EF AB ==，1 3.5cm 2DF AC ==， ∴△DEF 的周长==12cm DE DF EF ++，同理可得：△GHI 的周长==6cm HI HG GI ++，∴第三次作中位线得到的三角形周长为3cm ，∴第四次作中位线得到的三角形周长为1.5cm∴第三次作中位线得到的三角形周长为0.75cm∴这五个新三角形的周长之和为1263 1.50.75=23.25cm ++++，故选C ．【点睛】本题主要考查了三角形中位线定理，解题的关键在于能够熟练掌握三角形中位线定理．二、填空题1【解析】【分析】由折叠的性质可得，BD CE ⊥，4BE BC ==，12CF CE =，由勾股定理可得，CE =得，26BCD BDE BEG S S S ===△△△，求得CF 的长度，即可求解．【详解】解：由折叠的性质可得，BD CE ⊥，4BE BC ==，12CF CE =，BCD BDE △≌△ ∴BCE 为等腰直角三角形，F 为CE 的中点，BCD BDE SS = ∴12BF CF EF CE ===由勾股定理可得，CE∴12BF CF EF CE ====∵BG 为△EBD 的中线，△EBG 的面积为3∴26BCD BDE BEG S S S ===△△△162BCD S BD CF =⨯=△，解得BD =∴DF BD BF =-=由勾股定理得：CD =【点睛】此题考查了折叠的性质，勾股定理以及直角三角形的性质，解题的关键是灵活利用相关性质进行求解．2、【解析】【分析】根据折叠性质和平行四边形的性质可以证明△ABG≌△EAD，可得AG=DE=2，然后利用勾股定理可得求出AF的长，进而可得GF的值．【详解】解：如图，GF⊥AB于点F，∵点E是CD边上的中点，∴CE=DE=2，由折叠可知：∠BGE=∠C，BC=BG=3，CE=GE=2，在▱ABCD中，BC=AD=3，BC∥AD，∴∠D+∠C=180°，BG=AD，∵∠BGE+∠AGB=180°，∴∠AGB=∠D，∵AB∥CD，∴∠BAG=∠AED，在△ABG和△EAD中，AGB DBAG AED BG AD∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ABG≌△EAD（AAS），∴AG=DE=2，∴AB=AE=AG+GE=4，∵GF⊥AB于点F，∴∠AFG=∠BFG=90°，在Rt△AFG和△BFG中，根据勾股定理，得AG2-AF2=BG2-BF2，即22-AF2=32-（4-AF）2，解得AF=118，∴GF2=AG2-AF2=4-12164=13564，∴GF，故答案为2．【点睛】本题考查了折叠的性质、平行四边形的性质、勾股定理等知识，证明△ABG≌△EAD是解题的关键．3【解析】【分析】过点A作AD//BC，且AD＝MN，连接MD，则四边形ADMN是平行四边形，作点A关于BC的对称点A′，连接AA′交BC于点O，连接A′M，三点D、M、A′共线时，AM AN最小为A′D的长，利用勾股定理求A′D的长度即可解决问题．【详解】解：过点A作AD//BC，且AD＝MN，连接MD，则四边形ADMN 是平行四边形，∴MD ＝AN ，AD ＝MN ，作点A 关于BC 的对称点A ′，连接A A ′交BC 于点O ，连接A ′M ， 则AM ＝A ′M ，∴AM ＋AN ＝A ′M ＋DM ，∴三点D 、M 、A ′共线时，A ′M ＋DM 最小为A ′D 的长， ∵AD //BC ，AO ⊥BC ，∴∠DA A '＝90°，∵2AB AC ==，90BAC ∠=︒，，∴BC＝BO＝CO ＝AO ，∴AA '=在Rt△AD A '中，由勾股定理得：A 'D =∴AM AN +【点睛】本题主要考查了等腰三角形的性质，平行四边形的判定与性质，勾股定理等知识，构造平行四边形将AN转化为DM是解题的关键．4、24【解析】【分析】由三边长之比得到三角形的三条中位线之比，再由这三条中位线组成的三角形周长求出三中位线长，推出边长，再比大小判断即可．【详解】∵ 如图，H、I、J分别为BC，AC，AB的中点∴12HI AB=，12IJ BC=，12HJ AC=又∵30HI IJ HJ++=∴60AB BC AC++=∵AB：AC：BC=4：5：6，即BC边最长∴660=244+5+6BC=⨯故填24．【点睛】本题考查了三角形中位线的性质，即三角形的中位线平行于第三边且等于第三边的一半．5、6【解析】【分析】根据三角形的面积求出BF，利用勾股定理列式求出AF，再根据翻折变换的性质可得AD=AF，然后求出CF，设DE=x，表示出EF、EC，然后在Rt△CEF中，利用勾股定理列方程求解和三角形的面积公式解答即可．【详解】解：∵四边形ABCD是矩形∴AB=CD=9，BC=AD∵12•AB•BF＝54，∴BF=12．在Rt△ABF中，AB=9，BF=12，由勾股定理得，15AF=．∴BC=AD=AF=15，∴CF=BC-BF=15-12=3．设DE=x，则CE=9-x，EF=DE=x．则x2=（9-x）2+32，解得，x=5．∴DE=5．∴EC=DC-DE=9-5=4．∴△FCE的面积=1122CF CE⨯⨯=×4×3=6．【点睛】本题考查了翻折变换的性质，矩形的性质，三角形的面积，勾股定理，熟记各性质并利用勾股定理列出方程是解题的关键．三、解答题1、（1）见解析；（2）见解析；（3）见解析【分析】（1）如图，AB =4，BC =3，5AC =，利用勾股定理逆定理即可得到△ABC 是直角三角形；（2）如图，AB =AC =BC ==△ABC 是直角三角形；（3）如图，AB BC CD AD =====AC =222AC AB BC =+，∠ABC =90°，即可得到四边形ABCD 是正方形，10ABCD SAB BC =⋅=．【详解】解：（1）如图所示，AB =4，BC =3，5AC =，∴222AC AB BC =+，∴△ABC 是直角三角形；（2）如图所示，AB ==AC =BC =∴222AC AB BC =+，∴△ABC 是直角三角形；（3）如图所示，AB BC CD AD ==== AC =∴222AC AB BC =+，∴∠ABC =90°，∴四边形ABCD 是正方形，∴10ABCDS AB BC =⋅=．【点睛】 本题主要考查了有理数与无理数，正方形的判定，勾股定理和勾股定理的逆定理，熟知相关知识是解题的关键．2、（1）见解析（2）见解析【分析】（1）利用垂直平分线和角平分线的尺规作图法，进行作图即可．（2）利用直角三角形斜边中线性质，以及角平分线的性质直接证明CED ∠与EDF ∠都是90︒，最后加上90ACB ∠=︒，即可证明结论．【详解】（1）答案如下图所示：分别以A 、B 两点为圆心，以大于2AB 长为半径画弧，连接弧的交点的直线即为垂直平分线l ，其与AB 的交点为D ，以点D 为圆心，适当长为半径画弧，分别交DA 于点M ，交CD 于点N ，交BD 于点T ，然后分别以点M ，N 为圆心，大于2MN 为半径画弧，连接两弧交点与D 点的连线交AC 于点E ，同理分别以点T ，N 为圆心，大于2TN 为半径画弧，连接两弧交点与D 点的连线交BC 于点F ． （2）证明：D 点是AB 与其垂直平分线l 的交点，D ∴点是AB 的中点，CD ∴是Rt △ABC 上的斜边的中线，2AB CD AD ∴==， DE 、DF 分别是∠ADC ，∠BDC 的角平分线，12CDE ADE ADC ∴∠=∠=∠，12CDF CDB ∠=∠，EDF CDE CDF ∠=∠+∠，11190222EDF ADC CDB ADB ∴∠=∠+∠=∠=︒ ， CD AD CDE ADE DE DE =⎧⎪∠=∠⎨⎪=⎩， ()CDE ADE SAS ∴∆∆≌，1902CED AED AEC ∴∠=∠=∠=︒， 在四边形CEDF 中，90ACB CED EDF ∠=∠=∠=︒，∴四边形CEDF 是矩形．【点睛】本题主要是考查了尺规作图、直角三角形斜边中线性质以及矩形的判定，熟练利用直角三角形斜边中线性质，找到三角形全等的判定条件，并且选择合适的矩形判定条件，是解决本题的关键．3、（1）等边；（2）见解析；（3）成立，理由见解析【分析】（1）根据含30度角的直角三角形的性质，直角三角形斜边上的中线等于斜边的一半可证明12BC OC OB AB ===，即可证明△OBC 是等边三角形； （2）先证明COP BOQ ∠=∠，即可利用SAS 证明COP BOQ ≌，得到CP BQ =；（3）先证明COP BOQ ∠=∠，即可利用SAS 证明COP BOQ ≌，得到CP BQ =．【详解】（1）∵∠ACB =90°，∠A =30°，O 是AB 的中点， ∴12BC OC OB AB ===， ∴△OBC 是等边三角形，故答案为：等边；（2）由（1）可知，OB OC =，60BOC ∠=︒， OPQ 是等边三角形，OP OQ ∴=，60POQ ∠=︒，60COP BOP BOQ ∴∠=︒-∠=∠，即COP BOQ ∠=∠，在COP 和BOQ △中OC OB COP BOQ OP OQ =⎧⎪∠=∠⎨⎪=⎩， ()COP BOQ SAS ∴≌，CP BQ ∴=；（3）成立，CP BQ =证明：由（1）可知，OB OC =，60BOC ∠=︒， OPQ 是等边三角形，OP OQ ∴=，60POQ ∠=︒，60COP BOP BOQ ∴∠=︒+∠=∠，即COP BOQ ∠=∠，在COP 和BOQ △中OC OB COP BOQ OP OQ =⎧⎪∠=∠⎨⎪=⎩， ()COP BOQ SAS ∴≌，CP BQ ∴=．【点睛】本题主要考查了等边三角形的性质与判定，全等三角形的性质与判定，含30度角的直角三角形的性质，直角三角形斜边上的中线，熟练掌握等边三角形的性质与判定条件是解题的关键．4、（1）见解析；（2）正方形ABCD的面积为2a【分析】（1）由等边三角形的性质得EO⊥AC，即BD⊥AC，再根据对角线互相垂直的平行四边形是菱形，即可得出结论；（2）证明菱形ABCD是正方形，即可得出答案．【详解】（1）证明：∵四边形ABCD是平行四边形，∴AO＝OC，∵△ACE是等边三角形，∴EO⊥AC（三线合一），即BD⊥AC，∴▱ABCD是菱形；（2）解：∵△ACE是等边三角形，∴∠EAC＝60°由（1）知，EO⊥AC，AO＝OC∴∠AEO＝∠OEC＝30°，△AOE是直角三角形，∵∠AED＝2∠EAD，∴∠EAD＝15°，∴∠DAO＝∠EAO﹣∠EAD＝45°，∵▱ABCD是菱形，∴∠BAD＝2∠DAO＝90°，∴菱形ABCD 是正方形，∴正方形ABCD 的面积＝AB 2＝a 2．【点睛】本题考查了菱形的判定与性质、正方形的判定与性质、平行四边形的性质、等边三角形的性质等知识，证明四边形ABCD 为菱形是解题的关键．5、（1）（2）见解析【分析】（1）根据30°角所对直角边等于斜边的一半，得到AD =3，根据等腰直角三角形，得到CD =AD =3，根据勾股定理，得到AC 的长即可；（2）根据斜边上的中线等于斜边的一半，得到DE =DC ，根据等腰三角形三线合一性质，证明即可．【详解】（1）AD BC ⊥90ADB ADC ∴∠=∠=︒30B ∠=︒，6AB =132AD AB ∴== 45ACD ∠=︒45CAD ∴∠=︒3AD CD ∴==AC ∴=（2）连接DE90ADB ∠=︒，AE BE =12ED AB ∴=， 12AD AB =，AD CD =， ED CD ∴=，GD EC ⊥，EG CG ∴=．【点睛】 本题考查了30°角的性质，等腰直角三角形的性质，斜边上中线的性质，等腰三角形三线合一性质，熟练掌握性质是解题的关键．。

人教版数学八年级下册第18章平行四边形达标检测卷4份第18章单元测试（1）班级姓名成绩一、选择题（3′×10=30′）1．下列性质中，平行四边形具有而非平行四边形不具有的是（）．A．内角和为360° B．外角和为360° C．不确定性 D．对角相等2．□ ABCD中，∠A=55°，则∠B、∠C的度数分别是（）．A．135°，55° B．55°，135° C．125°，55° D．55°，125°3．下列正确结论的个数是（）．①平行四边形内角和为360°；②平行四边形对角线相等；③平行四边形对角线互相平分；④平行四边形邻角互补．A．1 B．2 C．3 D．44．平行四边形中一边的长为10cm，那么它的两条对角线的长度可能是（）．A．4cm和6cm B．20cm和30cm C．6cm和8cm D．8cm和12cm 5．在□ABCD中，AB+BC=11cm，∠B=30°，S ABCD=15cm2，则AB与BC的值可能是（）．A．5cm和6cm B．4cm和7cm C．3cm和8cm D．2cm和9cm 6．在下列定理中，没有逆定理的是（）．A．有斜边和一直角边对应相等的两个直角三角形全等;B．直角三角形两个锐角互余;C．全等三角形对应角相等;D．角平分线上的点到这个角两边的距离相等.7．下列说法中正确的是（）．A．每个命题都有逆命题 B．每个定理都有逆定理C．真命题的逆命题是真命题 D．假命题的逆命题是假命题8．一个三角形三个内角之比为1：2：1，其相对应三边之比为（）．A．1：2：1 B．1：1 C．1：4：1 D．12：1：29．一个三角形的三条中位线把这个三角形分成面积相等的三角形有（）个． A．2 B．3 C．4 D．510．如图所示，在△ABC中，M是BC的中点，AN平分∠BAC，BN⊥AN．若AB=•14，•AC=19，则MN的长为（）．A．2 B．2.5 C．3 D．3.5二、填空题（3′×10=30′）11．用14cm长的一根铁丝围成一个平行四边形，短边与长边的比为3：4，短边的比为________，长边的比为________．12．已知平行四边形的周长为20cm，一条对角线把它分成两个三角形，•周长都是18cm，则这条对角线长是_________cm．13．在□ABCD中，AB的垂直平分线EF经过点D，在AB上的垂足为E，•若□ABCD•的周长为38cm，△ABD的周长比□ABCD的周长少10cm，则□ABCD的一组邻边长分别为______．14．在□ABCD中，E是BC边上一点，且AB=BE，又AE的延长线交DC的延长线于点F．若∠F=65°，则□ABCD的各内角度数分别为_________．15．平行四边形两邻边的长分别为20cm，16cm，两条长边的距离是8cm，•则两条短边的距离是_____cm．16．如果一个命题的题设和结论分别是另一个命题的______和_______，•那么这两个命题是互为逆命题．17．命题“两直线平行，同旁内角互补”的逆命题是_________．18．在直角三角形中，已知两边的长分别是4和3，则第三边的长是________．19．直角三角形两直角边的长分别为8和10，则斜边上的高为________，斜边被高分成两部分的长分别是__________．20．△ABC的两边分别为5，12，另一边c为奇数，且a+b+•c•是3•的倍数，•则c•应为________，此三角形为________三角形．三、解答题（6′×10=60′）21．如右图所示，在□ABCD中，BF⊥AD于F，BE⊥CD于E，若∠A=60°，AF=3cm，CE=2cm，求ABCD的周长．22．如图所示，在□ABCD 中，E 、F 是对角线BD 上的两点，且BE=DF.求证：（1）AE=CF ；（2）AE ∥CF ．23．如图所示，□ABCD 的周长是，AB 的长是DE ⊥AB 于E ，DF ⊥CB 交CB•的延长线于点F ，DE 的长是3，求（1）∠C 的大小；（2）DF 的长．24．如图所示，□ABCD 中，AQ 、BN 、CN 、DQ 分别是∠DAB 、∠ABC 、∠BCD 、•∠CDA 的平分线，AQ 与BN 交于P ，CN 与DQ 交于M ，在不添加其它条件的情况下，试写出一个由上述条件推出的结论，并给出证明过程（要求：•推理过程中要用到“平行四边形”和“角平分线”这两个条件）．FCDAEB25．已知△ABC的三边分别为a，b，c，a=n2-16，b=8n，c=n2+16（n>4）.求证：∠C=90°．26．如图所示，在△ABC中，AC=8，BC=6，在△ABE中，DE⊥AB于D，DE=12，S =60，•求∠C的度数．△ABE27．已知三角形三条中位线的比为3：5：6，三角形的周长是112cm，•求三条中位线的长．28．如图所示，已知AB=CD，AN=ND，BM=CM，求证：∠1=∠2．29．如图所示，△ABC的顶点A在直线MN上，△ABC绕点A旋转，BE⊥MN于E，•CD•⊥MN于D，F为BC中点，当MN经过△ABC的内部时，求证：（1）FE=FD；（2）当△ABC继续旋转，•使MN不经过△ABC内部时，其他条件不变，上述结论是否成立呢？30．如图所示，E是□ABCD的边AB延长线上一点，DE交BC于F，求证：S△ABF=S ．△EFC答案:一、1．D 2．C 3．C 4．B 5．A 6．C 7．A 8．B 9．C 10．C二、11．3cm 4cm 12．8 13．9cm和10cm 14．50°，130°，50°，130°• •15．10 16．结论题设 17．同旁内角互补，两直线平行18．5．．13 直角三、21．□ABCD的周长为20cm 22．略24．略23．（1）∠C=45°（2）DF=225．•略 26．∠C=90° 27．三条中位线的长为：12cm；20cm；24cm 28．提示：连结BD，取BD•的中点G，连结MG，NG29．（1）略（2）结论仍成立．提示：过F作FG⊥MN于G 30．略第18章单元测试（2）班级姓名成绩一、选择题（3′×10=30′）1．下列判断四边形是平行四边形的是（）．A．两组角相等的四边形; B．对角线平分的四边形; C．一组对边相等，一组对角相等的四边形; D．两组对边分别相等的四边形2．根据下列条件，能作出平行四边形的是（）．A．两组对边长分别是3cm和7cm;B．相邻两边的边长分别是2cm和4cm，一条对角线长是7cm;C．一条边长为6cm，另一条对角线长为10cm，一条边长为8cm;D．一条边长为7cm，两条对角线长为6cm和8cm3．如图1所示，在□ABCD中，EF∥GH∥AB，MN∥BC，则图中的平行四边形的个数为（• ）．A．12个 B．16个 C．14个 D．18个(1) (2) (3) 4．已知下列四个命题：①一组对边平行且相等的四边形；②两组对角分别相等的四边形；③对角线相等的四边形；④对角线互相平分的四边形．•其中能判断是平行四边形的命题个数为（）．A．1个 B．2个 C．3个 D．4个5．以不共线的三点为平行四边形的其中三个顶点作平行四边形，•一共可作平行四边形的个数是（）．A．2个 B．3个 C．4个 D．5个6．平行四边形的一边为32，则它的两条对角线长不可能是（）．A．20和40 B．30和50 C．40和50 D．20和607．如图2所示，EF过□ABCD对角线的交点O，分别交AD于E，交BC于点F，若OE=5，四边形CDEF的周长为25，则□ABCD的周长为（）．A．20 B．30 C．40 D．508．在□ABCD中，∠A：∠B：∠C：∠D的值可以是（）．A．1：2：3：4 B．1：3：4：2 C．1：1：2：2 D．3：4：3：49．已知O为□ABCD对角线的交点，且△AOB的周长为1，则□ABCD的面积为（） A．1 B．2 C．3 D．410．已知O为□ABCD对角线的交点，且△AOB的周长比△BOC的周长多23，则CD-AD•的值为（）．A．23B．32C．2 D．3二、填空题（3′×10=30′）11．□ABCD中，∠A：∠B=7：2，则∠C=______．12．如图3所示，在□ABCD中，CM⊥AD于M，CN⊥AB于N，若∠B=50°，则∠MCN=_____．13．若平行四边形的周长为40cm，对角线AC、BD•相交于点O，•△BOC•的周长比△AOB的周长大2cm，则AB=________．14．若平行四边形的周长为56cm，相邻两边的长度比为3：4，则四边形的四边长分别为_____________．15．如果□ABCD和□ABEF有公共边AB，那么四边形DCEF是_________．16．四边形ABCD中，∠ADC=∠ABC，要判断这个四边形是平行四边形，•只需判断出__________即可，根据是________________．17．已知一个四边形的边长依次分别为a，b，c，d，且a2+b2+c2+d2=2ac+2bd，•则此四边形为___________．18．过平行四边形对角线的交点，且与一组边平行的直线将平行四边形分成的两个四边形________平行四边形．（填“是”或“不是”）19．四边形ABCD中，AC、BD交于点O，且OA=OC，OB=•OD，•∠ABC=•80•°，•则∠ADC=_____．20．已知：四边形ABCD中，AD∥BC，要使四边形ABCD为平行四边形，•需要增加条件________．（只需填写一个你认为正确的即可）三、解答题（共60′）21．（6′）如右图所示，在□ABCD中，AE、CF分别是∠DAB、∠BCD的平分线，求证：四边形AFCE是平行四边形．22．（6′）如右图所示，O为等边△ABC内任意一点，OD∥BC，OE∥AC，OF∥AB，•并且D、E、F分别在AB、BC、AC上，求证：OD+OE+OF=BC．23．（8′）如下图所示，已知平行四边形ABCD的周长是36cm，由钝角顶点D向AB、•BC引两条高DE、DF，且，cm，求平行四边形ABCD的面积．24．（8′）如下图所示，□ABCD中，AE⊥BC，AF⊥DC，垂足分别为E、F，∠ADC=•60•°，BE=2，CF=1，连结DE，求△DEC的面积．25．（8′）求证：顺次连结四边形各边中点所得的四边形是平行四边形．26．（8′）如右图所示，△ABC中，CD是△ABC的角平分线，AE⊥CD于E，F为AC的中点，试问EF∥BC吗？为什么？27．（8′）已知□ABCD中，E、F分别是BC、CD的中点，AE、AF分别交BD于M、N.求证：BM=MN=ND．28．（8′）已知如下图所示，在□ABCD中，∠A=60°，E、F分别是AB、CD•的中点，•且AB=2AD．（1）求证：EF：（2）试判断EF与BD的位置关系？答案:一、1．D 2．A 3．D 4．C 5．B 6．A 7．B 8．D 9．D 10．A二、11．140° 12．50° 13．9cm 14．12cm，16cm，12cm，16cm 15．•平行四边形16．∠BAD=∠BCD 两组对角分别相等，则四边形是平行四边形 17．•平行四边形 •18．是 19．80° 20．AB∥DC三、21．略 22．略 23．2 24．．提示：连结AC 26．略27．略28．（1）提示：连结DE （2）EF⊥BD第18章单元测试（3）一、选择题.(每小题4分，共32分)1.一个平行四边形的两条对角线的长分别为8和10，则这个平行四边形边长不可能是（）A.2B.5C.8D.102.如图，在菱形ABCD中，对角线AC与BD相交于点O，OE⊥AB，垂足为E，若∠ADC=130°，则∠AOE的大小为（）A.75°B.65°C.55°D.50°第2题图第3题图3.如图，在矩形ABCD中，AB=2，BC=4，对角线AC的垂直平分线分别交AD、AC于点E、O，连接CE，则CE的长为（）A.3B.3.5C.2.5D.2.84. 下列命题中，真命题是（）A.对角线相等的四边形是矩形B.对角线互相垂直的四边形是菱形C.对角线互相平分的四边形是平行四边形D.对角线互相垂直平分的四边形是正方形5.如图，CD是△ABC的中线，点E，F分别是AC、DC的中点，EF=2，则BD=（）A.2B.3C.4D.6第5题图第6题图第7题第8题6.如图所示，将□ABCD折叠，使顶点D恰好落在AB边上的点M处，折痕为AN,那么对于结论：①MN∥BC，②MN=AM，下列说法正确的是（）A.①②都对B.①②都错C.①对②错D.①错②对7.如图所示，在正方形ABCD中，点E、F分别在CD，BC上，且BF=CE,连接BE,AF相交于点G,则下列结论不正确的是（）A.BE=AFB.∠DAF=∠BECC.∠AFB+∠BEC=90°D.AG⊥BE8. 如图，矩形ABCD中，O为AC中点，过点O的直线分别与AB、CD交于点E、F，连结BF交AC于点M，连结DE、BO,若∠COB=60°，FO=FC,则下列结论：①FB垂直平分OC；②△EOB≌△CMB；③DE=EF；④S△AOE ∶S△BCM=2∶3.其中正确结论的个数是（）A.4个B.3个C.2个D.1个二、填空题.(每小题4分，共32分)9.如图，在平行四边形ABCD中，∠B=110°，延长AD至F，延长CD至E，连接EF，则∠E+∠F= .第9题图第10题图10.如图所示，在R t△ABC中，∠C=90°，DE垂直平分AC，DF⊥BC，当△ABC满足条件时，四边形DECF是正方形.（要求：①不再添加任何辅助线；②只填一个符合要求的条件）11.如图，DE为△ABC的中位线，点F在DE上，且∠AFB=90°，若AB=8，BC=10，则EF的长为 .第11题图第12题图12. 如图，正方形ABCO的顶点C、A分别在x轴、y轴上，BC是菱形BDCE 的对角线，若∠D=60°，BC=2，则点D的坐标是 .13.已知一个平行四边形的一条对角线将其分为两个全等的等腰直角三角形，且这条对角线的长为6，则另一条对角线的长为 .14. 如图，菱形ABCD的面积为120cm2，正方形AECF的面积为50cm2，则菱形的边长为 cm.15.如图，已知点P是正方形ABCD的对角线BD上一点，PE⊥BC于E，PF⊥CD于F，连接PA、EF.则线段PA与EF之间的大小关系是 .第15题图第16题图16.如图，E是正方形ABCD的边CD的中点，AE的垂直平分线分别交AE、BC于H、G，若CG=7，BC=8，则GH等于 .三、解答题.(共56分)17.（8分）如图所示，一根长2.5m的木棍（AB）斜靠在与地面（OM）垂直的墙（ON）上，此时OB的距离为0.7m，设木棍的中点为P.若木棍顶端A沿墙下滑，且底端B沿地面向右滑行.（1）如果木棍的顶端A沿墙下滑0.4 m，那么木棍的底端B向外移动了多少距离？（2）请判断木棍滑动的过程中，点P到点O的距离是否变化，并简述理由.18.（8分）如图，在正方形ABCD中，对角线AC,BD相交于点O，E,F分别在OD,OC上，且DE=CF，连接DF,AE,AE的延长线交DF于点M.求证：AM⊥DF.19.（8分）如图，在平行四边形ABCD中，AE是BC边上的高，将△ABE沿BC方向平移，使点E与点C重合，得到△GFC.（1）求证：BE=DG；（2）若∠B=60°，当AB与BC满足什么数量关系时，四边形ABFG是菱形？证明你的结论.20.（8分）如图，在四边形ABCD中，AD∥BC，∠B=90°，AD=18cm，BC=21cm，点P从点A出发沿AD边向D以1cm/s的速度运动，点Q从点C出发沿CB边向B以2cm/s的速度运动，如果P、Q分别从A、C同时出发，设运动时间为t s.求：（1）当t为何值时，四边形ABQP为矩形？（2）当t为何值时，四边形PQCD为平行四边形？21.（12分）(2016·湖北十堰)如图，将矩形纸片ABCD（AD＞AB）折叠，使点C刚好落在线段AD上，且折痕分别与边BC，AD相交，设折叠后点C，D的对应点分别为G,H，折痕分别与边BC,AD相交于点E,F.（1）判断四边形CEGF的形状，并证明你的结论；（2）若AB=3，BC=9，求线段CE的取值范围.22.（12分）如图①，菱形ABCD对角线AC,BD的交点O是四边形EFGH 对角线FH的中点，四个顶点A,B,C,D分别在四边形EFGH的边EF，FG，GH,HE 上.（1）求证：四边形EFGH是平行四边形；（2）如图②，若四边形EFGH是矩形，当AC与FH重合时，已知ACBD=2，且菱形ABCD的面积是20，求矩形EFGH的长与宽.答案第十八章达标检测卷一、选择题(每题3分，共30分)1．如图，▱ABCD中，AC＝3 cm，BD＝5 cm，则边AD的长可以是() A．3 cm B．4 cm C．5 cm D．6 cm2．如图，D，E分别是△ABC的边AB，AC上的点，且AD＝DB，AE＝EC.若DE ＝4，则BC的长为()A．2 B．4 C．6 D．83．如图，在▱ABCD中，AE平分∠BAD，若CE＝3 cm，AB＝4 cm，则▱ABCD的周长是()A．20 cm B．21 cm C．22 cm D．23 cm4．下列命题中，真命题是()A．对角线相等的四边形是矩形B．对角线互相垂直的四边形是菱形C．对角线互相平分的四边形是平行四边形D．对角线互相垂直平分的四边形是正方形5．若顺次连接四边形ABCD四边的中点，得到的图形是一个矩形，则四边形ABCD 一定是()A．矩形B．菱形C．对角线相等的四边形D．对角线互相垂直的四边形6．如图，在矩形ABCD中，对角线AC，BD相交于点O，过点O的直线EF分别交AB，CD于点E，F，若图中阴影部分的面积为6，则矩形ABCD的面积为()A．12 B．18 C．24 D．307．平行四边形ABCD的对角线交于点O，有五个条件：①AC＝BD，②∠ABC ＝90°，③AB＝AC，④AB＝BC，⑤AC⊥BD，则下列哪个组合可判定这个四边形是正方形？()A．①②B．①③C．①④D．④⑤8．如图，正方形ABCD的边长为4，点E在对角线BD上，且∠BAE＝22.5°，EF⊥AB，垂足为F，则EF的长为()A．1 B. 2 C．4－2 2 D．3 2－49．如图，在菱形ABCD中，AB＝2，∠A＝120°，P，Q，K分别为线段BC，CD，BD上的任意一点，则P K＋Q K的最小值为()A．1 B. 3 C．2 D.3＋110．如图，依次连接第一个矩形各边的中点得到一个菱形，再依次连接菱形各边的中点得到第二个矩形，按照此方法继续下去．若第一个矩形的面积为1，则第n个矩形的面积为()A.14 B.14n－1C.14n D.14n＋1二、填空题(每题3分，共30分)11．如图，在▱OABC中，点O为坐标原点，点A的坐标为(3，0)，点B的坐标为(4，2)，则点C的坐标为__________．12．如图，在菱形ABCD中，对角线AC＝6，BD＝10，则菱形ABCD的面积为________．13．如图，在正方形ABCD中，点F为CD上一点，BF与AC交于点E，若∠CBF＝20°，则∠AED等于________．14．如图，在矩形ABCD中，对角线AC，BD相交于点O，DE⊥AC于点E，∠EDC:∠EDA＝1:2，且AC＝10，则EC的长度是________．15．如图，平行四边形ABCD的对角线AC，BD相交于点O，E，F分别是线段AO，BO的中点．若AC＋BD＝30 cm，△OAB的周长为23 cm，则EF的长为__________．16．如图，在▱ABCD中，点E为BC边上一点(不与端点重合)，若AB＝AE，且AE平分∠DAB，则有下列结论：①∠B＝60°；②AC＝BC；③∠AED＝∠ACD；④△ABC≌△EAD.其中正确的是__________(在横线上填所有正确结论的序号)．17．如图，在菱形纸片ABCD中，∠A＝60°，折叠菱形纸片ABCD，使点C落在DP(P为AB的中点)所在的直线上的点C′处，得到经过点D的折痕DE.则∠DEC的大小为________．18．菱形ABCD在平面直角坐标系中的位置如图所示，其中点A的坐标为(1，0)，点B的坐标为(0，3)，动点P从点A出发，沿A→B→C→D→A→B→…的路径，在菱形的边上以每秒0.5个单位长度的速度移动，移动到第2 020 s 时，点P的坐标为__________．19．如图，四边形ABCD为矩形，过点D作对角线BD的垂线，交BC的延长线于点E，取BE的中点F，连接DF，DF＝4.设AB＝x，AD＝y，则x2＋(y－4)2的值为________．20．正方形ABCD的边长是4，点P是AD边的中点，点E是正方形边上的一点，若△PBE是等腰三角形，则腰长为____________________．三、解答题(21题8分，26题12分，其余每题10分，共60分)21．如图，在▱ABCD中，AE平分∠BAD，CF平分∠BCD，分别交CD，AB于点E，F.求证AE＝CF.22．如图，正方形ABCD的边长为4，E，F分别为DC，BC的中点．(1)求证△ADE≌△ABF；(2)求△AEF的面积．23．如图，在平行四边形ABCD中，边AB的垂直平分线交AD于点E，交AB于点G，交CB的延长线于点F，连接AF，BE.(1)求证△AGE≌△BGF；(2)试判断四边形AFBE的形状，并说明理由．24．如图，在矩形ABCD中，对角线AC的垂直平分线EF分别交AD，AC，BC 于点E，O，F，连接CE和AF.(1)求证：四边形AECF为菱形；(2)若AB＝4, BC＝8，求菱形AECF的周长．25．如图，在平行四边形ABCD中，AB＝3 cm，BC＝5 cm，∠B＝60°，G是CD 的中点，E是边AD上的动点，EG的延长线与BC的延长线交于点F，连接CE，DF.(1)求证：四边形CEDF是平行四边形．(2)①当四边形CEDF是矩形时，求AE的长；②当四边形CEDF是菱形时，求AE的长．26．如图，在正方形ABCD外侧作直线AP，点B关于直线AP的对称点为E，连接BE，DE，其中DE交直线AP于点F.(1)依题意补全图①；(2)若∠P AB＝20°，求∠ADF的度数；(3)如图②，若45°＜∠P AB＜90°，用等式表示线段AB，EF，FD之间的数量关系，并证明．答案一、1.A 2.D 3.C 4.C5．D 点拨：运用三角形的中位线定理和矩形的性质解答．6．C 点拨：根据题意易知△COF 的面积与△AOE 的面积相等，阴影部分的面积为矩形面积的四分之一．7．C8．C 点拨：由题易得∠ABD ＝∠ADB ＝45°，再求出∠DAE 的度数．根据三角形的内角和定理求∠AED ，从而得到∠DAE ＝∠AED ，再根据等角对等边得到AD ＝DE ，然后求出正方形的对角线BD ，再求出BE ，进而在等腰直角三角形中利用勾股定理求出EF 的长．9．B10．B 点拨：第一个矩形的面积为1，易知第二个矩形的面积为14，第三个矩形的面积是116……故第n 个矩形的面积为14n －1. 二、11.(1，2) 12.30 13.65° 14.2.515．4 cm16．①③④ 点拨：∵四边形ABCD 为平行四边形，∴AB ∥CD ，AD ＝BC ，AD ∥BC .∴∠DAE ＝∠AEB .∵AE 平分∠DAB ，∴∠DAE ＝∠BAE .∴∠BAE ＝∠AEB .∴AB ＝BE .又AB ＝AE ，∴AB ＝AE ＝BE .∴△ABE 为等边三角形．∴∠B ＝∠BAE ＝60°.∴∠B ＝∠DAE .∵∠BAC ＝∠BAE ＋∠EAC ＝60°＋∠EAC ＞∠B ，∴BC ＞AC .在△ABC 和△EAD 中，⎩⎨⎧AB ＝EA ，∠ABC ＝∠EAD ，BC ＝AD ，∴△ABC ≌△EAD (SAS )．∴∠BAC＝∠AED.∵AB∥CD，∴∠BAC＝∠ACD.∴∠AED＝∠ACD.故正确的是①③④.17．75°点拨：如图，连接BD，由菱形的性质及∠A＝60°，得到三角形ABD为等边三角形．由P为AB的中点，利用等腰三角形三线合一的性质得到∠ADP＝30°.由题意易得∠ADC＝120°，∠C＝60°，进而求出∠PDC＝90°，由折叠的性质得到∠CDE＝∠PDE＝45°，利用三角形的内角和定理即可求出∠DEC＝75°.18．(0，3)19．16点拨：∵四边形ABCD是矩形，AB＝x，AD＝y，∴CD＝AB＝x，BC＝AD＝y，∠BCD＝90°.又∵BD⊥DE，点F是BE的中点，DF＝4，∴BF＝DF＝EF＝4.∴CF＝BF－BC＝4－y.在Rt△DCF中，DC2＋CF2＝DF2，即x2＋(4－y)2＝42＝16，∴x2＋(y－4)2＝16.20．25或52或652三、21.证明：∵四边形ABCD为平行四边形，∴AD＝BC，∠D＝∠B，∠BAD＝∠BCD.又∵AE平分∠BAD，CF平分∠BCD，∴∠DAE＝12∠BAD，∠BCF＝12∠BCD.∴∠DAE＝∠BCF.在△DAE和△BCF中，⎩⎨⎧∠D ＝∠B ，DA ＝BC ，∠DAE ＝∠BCF ，∴△DAE ≌△BCF (ASA )．∴AE ＝CF .22．(1)证明：∵四边形ABCD 为正方形，∴AB ＝AD ＝DC ＝CB ，∠D ＝∠B ＝90°.∵E ，F 分别为DC ，BC 的中点，∴DE ＝12DC ，BF ＝12BC .∴DE ＝BF .在△ADE 和△ABF 中，⎩⎨⎧AD ＝AB ，∠D ＝∠B ，DE ＝BF ，∴△ADE ≌△ABF (SAS )．(2)解：由题易知△ABF ，△ADE ，△CEF 均为直角三角形，且AB ＝AD ＝4，DE ＝BF ＝CE ＝CF ＝12×4＝2，∴S △AEF ＝S 正方形ABCD －S △ADE －S △ABF －S △CEF ＝4×4－12×4×2－12×4×2－12×2×2＝6.23．(1)证明：∵四边形ABCD 是平行四边形，∴AD ∥BC .∴∠AEG ＝∠BFG .∵EF 垂直平分AB ，∴EF ⊥AB ，AG ＝BG .在△AGE 和△BGF 中，⎩⎨⎧∠AEG ＝∠BFG ，∠AGE ＝∠BGF ，AG ＝BG ，∴△AGE ≌△BGF (AAS )．(2)解：四边形AFBE 是菱形．理由如下：∵△AGE ≌△BGF ，∴AE ＝BF .∵AD ∥BC ，∴四边形AFBE 是平行四边形．又∵EF ⊥AB ，∴四边形AFBE 是菱形．24．(1)证明：∵EF 是AC 的垂直平分线，∴AO ＝OC ，∠AOE ＝∠COF ＝90°.∵四边形ABCD 是矩形，∴AD ∥BC .∴∠EAO ＝∠FCO .在△AEO 和△CFO 中，⎩⎨⎧∠EAO ＝∠FCO ，AO ＝CO ，∠AOE ＝∠COF ，∴△AEO ≌△CFO (ASA )．∴OE ＝OF .∵OA ＝OC ，∴四边形AECF 是平行四边形．又∵EF ⊥AC ，∴四边形AECF 是菱形．(2)解：设AF ＝x .∵EF 是AC 的垂直平分线，∴AF ＝CF ＝x ，∴BF ＝8－x .在Rt △ABF 中，由勾股定理得：AB 2＋BF 2＝AF 2，即42＋(8－x )2＝x 2，解得x ＝5.∴AF ＝5.∴菱形AECF 的周长为20.25．(1)证明：∵四边形ABCD 是平行四边形，∴CF ∥ED .∴∠FCG ＝∠EDG .∵G 是CD 的中点，∴CG ＝DG .在△FCG 和△EDG 中，⎩⎨⎧∠FCG ＝∠EDG ，CG ＝DG ，∠CGF ＝∠DGE ，∴△FCG ≌△EDG (ASA )．∴FG ＝EG .∵CG ＝DG ，∴四边形CEDF 是平行四边形．(2)解：①∵四边形ABCD 是平行四边形，∴∠CDA ＝∠B ＝60°，DC ＝AB ＝3 cm ，BC ＝AD ＝5 cm .∵四边形CEDF 是矩形，∴∠CED ＝90°.在Rt △CED 中，易得ED ＝12CD ＝1.5 cm ，∴AE ＝AD －ED ＝3.5(cm)．故当四边形CEDF 是矩形时，AE ＝3.5 cm.②若四边形CEDF 是菱形，则CE ＝ED .由①可知∠CDA ＝60°，∴△CED 是等边三角形．∴DE ＝CD ＝3 cm.∴AE ＝AD －DE ＝5－3＝2(cm)．故当四边形CEDF 是菱形时，AE ＝2 cm.点拨：在判定三角形全等时，关键是选择恰当的判定条件，有时还需添加适当的辅助线构造全等三角形．同时全等三角形也为平行四边形、矩形、菱形的判定构筑了重要的平台和保障．26．解：(1)如图①所示．(2)如图②，连接AE.∵点E是点B关于直线AP的对称点，∴∠P AE＝∠P AB＝20°，AE＝AB.∵四边形ABCD是正方形，∴AE＝AB＝AD，∠BAD＝90°.∴∠AED＝∠ADE，∠EAD＝∠DAB＋∠BAP＋∠P AE＝130°.∴∠ADF＝180°－130°2＝25°.(3)EF2＋FD2＝2AB2.证明：如图③，连接AE，BF，BD，由轴对称和正方形的性质可得EF＝BF，AE ＝AB＝AD，易得∠ABF＝∠AEF＝∠ADF，又∵∠BAD＝90°，∴∠ABF＋∠FBD＋∠ADB＝90°.∴∠ADF＋∠ADB＋∠FBD＝90°.∴∠BFD＝90°.在Rt△BFD中，由勾股定理得BF2＋FD2＝BD2；在Rt△ABD中，由勾股定理得BD2＝AB2＋AD2＝2AB2，∴EF2＋FD2＝2AB2.。

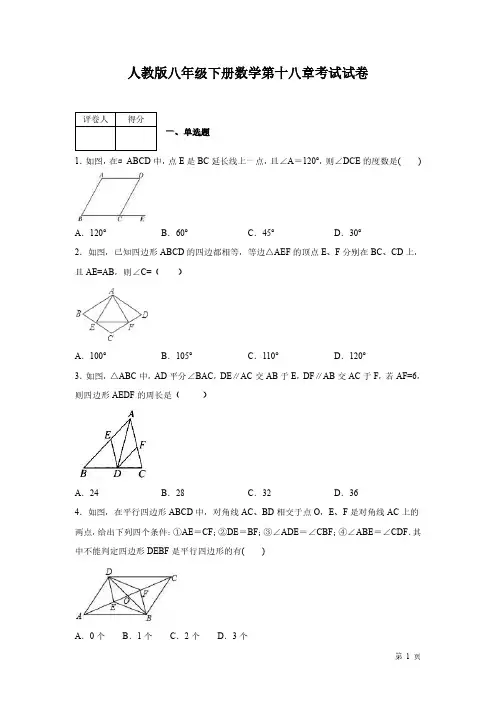
人教版八年级下册数学第十八章考试试卷评卷人得分一、单选题1．如图，在▱ABCD中，点E是BC延长线上一点，且∠A＝120°，则∠DCE的度数是()A．120°B．60°C．45°D．30°2．如图，已知四边形ABCD的四边都相等，等边△AEF的顶点E、F分别在BC、CD上，且AE=AB，则∠C=（）A．100°B．105°C．110°D．120°3．如图，△ABC中，AD平分∠BAC，DE∥AC交AB于E，DF∥AB交AC于F，若AF=6，则四边形AEDF的周长是（）A．24B．28C．32D．364．如图，在平行四边形ABCD中，对角线AC、BD相交于点O，E、F是对角线AC上的两点，给出下列四个条件：①AE＝CF；②DE＝BF；③∠ADE＝∠CBF；④∠ABE＝∠CDF．其中不能判定四边形DEBF是平行四边形的有()A．0个B．1个C．2个D．3个5．矩形具有而平行四边形不一定具有的性质是()A ．对角线互相垂直B ．对角线相等C ．对角线互相平分D ．对角相等6．菱形的周长为8cm ，高为1cm ，则菱形两邻角度数比为（）A ．4：1B ．5：1C ．6：1D ．7：17．如图，在周长为12的菱形ABCD 中，AE =1，AF =2，若P 为对角线BD 上一动点，则EP +FP 的最小值为（）A ．1B ．2C ．3D ．48．如图，平行四边形ABCD 中，对角线AC 与BD 相交于点O ，且AB ⊥AC ，AB=3，OC=4，则BD 的长为（）A ．4B ．5C ．10D ．12评卷人得分二、填空题9．如图，在矩形ABCD 中，横向阴影部分是矩形，另一阴影部分是平行四边形．依照图中标注的数据，计算图中空白部分的面积，已知a ＝2b ＝6c ，其面积是__________．(用含c 的代数式表示)10．在平行四边形ABCD 中，5AB =，6BC =，若AC BD =，则平行四边形ABCD 的面积为________．11．如图，平行四边形ABCD 的对角线AC 、BD 交于一点O ，AB=11，△OCD 的周长为27，则AC+BD=_________．12．在四边形ABCD中，对角线AC、BD交于点O，从①AB=CD；②AB∥CD；③OA=OC；④OB=OD；⑤AC=BD；⑥∠ABC＝90°这六个条件中，可选取三个推出四边形ABCD是矩形，如①②⑤→四边形ABCD是矩形．请再写出符合要求的两个：__________________；__________________．13．如图，直线AE∥BD，点C在BD上．若AE＝5，BD＝8，三角形ABD的面积为16，则三角形ACE的面积为________．14．如图，在Rt△ABC中，∠ACB＝90°，将边BC沿斜边上的中线CD折叠到CB′，若∠B ＝50°，则∠ACB′＝______.15．如图是一张长方形纸片ABCD，已知AB=8，AD=7，E为AB上一点，AE=5，现要剪下一张等腰三角形纸片（△AEP），使点P落在长方形ABCD的某一条边上，则等腰三角形AEP的底边长是_____________．16．在研究了平行四边形的相关内容后，老师提出这样一个问题：“四边形ABCD中，AD∥BC，请添加一个条件，使得四边形ABCD是平行四边形”．经过思考，小明说“添加AD=BC”，小红说“添加AB=DC”．你同意________的观点，理由是________.评卷人得分三、解答题17．如图，四边形ABCD中，BD垂直平分AC，垂足为点F，E为四边形ABCD外一点，且∠ADE=∠BAD，AE⊥AC．（1）求证：四边形ABDE是平行四边形；（2）如果DA平分∠BDE，AB=5，AD=6，求AC的长．18．如图，在△ABC中，AB＝6cm，AC＝10cm，AD平分∠BAC，BD⊥AD于点D，BD的延长线交AC于点F，E为BC的中点，求DE的长．19．如图，平行四边形ABCD的对角线AC、BD，相交于点O，EF过点O且与AB、CD 分别相交于点E、F，求证：AE=CF．20．如图，在平行四边形ABCD中，点E.F分别在AB、CD上，AE=CF，连接AF，BF，DE，CE，分别交于H、G.求证：(1)四边形AECF是平行四边形。

人教版八年级数学下册第十八章达标测试卷一、选择题(本题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合要求的)1．如图，菱形ABCD中，∠D＝150°，则∠1＝( )A．30°B．25°C．20°D．15°(第1题) (第2题) (第4题)2．如图，▱ABCD中，对角线AC，BD交于点O，点E是BC的中点．若OE＝3 cm，则AB的长为( )A．12 cm B．9 cm C．6 cm D．3 cm3．下列四组条件中，不能判定四边形ABCD是平行四边形的是( ) A．AB＝DC，AD＝BC B．AB∥DC，AD∥BCC．AB∥DC，AD＝BC D．AB∥DC，AB＝DC4．如图，在Rt△ABC中，∠B＝90°，BC＝12，AB＝5，则斜边上的中线BO长是( ) A．2.5 B．4 C．6 D．6.55．如图，在菱形ABCD中，∠B＝60°，AB＝4，则以AC为一边的正方形ACEF的周长为( )A．14 B．15 C．16 D．17(第5题) (第7题) (第8题)6．下列说法中，正确的个数有( )①对顶角相等；②两直线平行，同旁内角相等；③对角线互相垂直的四边形为菱形；④对角线互相垂直平分且相等的四边形为正方形．A ．1个B ．2个C ．3个D ．4个7．如图，已知在菱形ABCD 中，对角线AC 与BD 交于点O ，∠BAD ＝120°，AC ＝4，则该菱形的面积是( )A ．16 3B ．16C ．8 3D ．88．将五个边长都为2 cm 的正方形按如图所示方式摆放，点A ，B ，C ，D 分别是四个正方形的中心，则图中四块阴影部分面积的和为( )A ．2 cm 2B ．4 cm 2C ．6 cm 2D ．8 cm 29．如图，在矩形ABCD 中，AD ＝3AB ，点G ，H 分别在AD ，BC 上，连接BG ，DH ，且BG ∥DH ，若四边形BHDG 为菱形，则AG AD＝( ) A.45 B.35 C.49 D.38(第9题) (第10题) (第11题)10．如图，在正方形纸片ABCD 中，对角线AC ，BD 交于点O ，折叠纸片使得AD 落在BD 上，点A 恰好与BD 上的点F 重合．展开后，折痕DE 分别交AB ，AC 于E ，G ，连接FG ，EF ，下列结论：①∠AGD ＝112.5°；②AD ∶AE ＝2∶1；③S △AGD ＝S △OGD ；④四边形AEFG 是菱形；⑤BE ＝2OG ，其中正确结论的个数是( )A．2 B．3 C．4 D．5二、填空题(本题共6小题，每小题3分，共18分)11．如图，▱ABCD中，AC，BD相交于点O，若AD＝6，AC＋BD＝16，则△BOC的周长为________．12．如图，四边形ABCD是对角线互相垂直的四边形，且OB＝OD，请你添加一个适当的条件：____________，使四边形ABCD成为菱形(只需添加一个即可)．(第12题) (第14题) (第16题)13．若以A(－0.5，0)，B(2，0)，C(0，1)三点为顶点画平行四边形，则第四个顶点不可能在第________象限．14．如图，BD为正方形ABCD的对角线，BE平分∠DBC，交DC于点E，延长BC到点F，使CF＝CE，连接DF.若CE＝1 cm，则BF＝__________．15．矩形ABCD中，AB＝3，AD＝4，P是AD上一动点，PE⊥AC于E，PF⊥BD于F，则PE＋PF的值为________．16．如图，在边长为1的菱形ABCD中，∠DAB＝60°.连接对角线AC，以AC为边作第二个菱形ACEF，使∠FAC＝60°.连接AE，再以AE为边作第三个菱形AEGH，使∠HAE＝60°，…，按此规律所作的第n个菱形的边长是________．三、解答题(本题共6小题，共52分．解答应写出文字说明、证明过程或演算步骤) 17．(8分)如图，在▱ABCD中，点E，F分别在边CB，AD的延长线上，且BE＝DF，EF分别与AB，CD交于点G，H.求证：AG＝CH.18.(8分)如图，正方形ABCD中，E是BC上的一点，连接AE，过B点作BH⊥AE，垂足为点H，延长BH交CD于点F，连接AF.(1)求证：AE＝BF；(2)若正方形的边长是5，BE＝2，求AF的长．19．(8分)如图，▱ABCD的对角线AC与BD相交于点E，点G为AD的中点，连接CG，CG的延长线交BA的延长线于点F，连接FD.(1)求证：AB＝AF；(2)若AG＝AB，∠BCD＝120°，判断四边形ACDF的形状，并证明你的结论．20．(8分)如图，在四边形ABCD中，AB∥DC，AB＝AD，对角线AC，BD交于点O，AC平分∠BAD，过点C作CE⊥AB交AB的延长线于点E，连接OE.(1)求证：四边形ABCD是菱形；(2)若AE＝5，OE＝3，求线段CE的长．21．(10分)如图，在△ABC中，AB＝AC，AD为∠BAC的平分线，AN为△ABC的外角∠CAM的平分线，CE⊥AN，垂足为E.(1)求证：四边形ADCE是矩形；(2)连接DE，试判断四边形ABDE的形状，并说明理由；(3)△ABC再添加一个什么条件时，可使四边形ADCE是正方形，并证明你的结论．22．(10分)我们给出如下定义：顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形．(1)如图①，在四边形ABCD中，点E，F，G，H分别为边AB，BC，CD，DA的中点，求证：中点四边形EFGH是平行四边形；(2)如图②，点P是四边形ABCD内一点，且满足PA＝PB，PC＝PD，∠APB＝∠CPD，点E，F，G，H分别为边AB，BC，CD，DA的中点，判断中点四边形EFGH的形状，并说明理由；(3)若改变(2)中的条件，使∠APB＝∠CPD＝90°，其他条件不变，直接写出中点四边形EFGH的形状(不必证明)．答案一、1.D 2.C 3.C 4.D 5.C 6.B7．C 8.B9．C 10．B 二、11.14 12．OA ＝OC (答案不唯一)13．三 14．(2＋2)cm 15.12516．(3)n －1 三、17.证明：∵四边形ABCD 是平行四边形，∴AD ＝BC ，AD ∥BC ，∠A ＝∠C .∴∠F ＝∠E .∵BE ＝DF ，∴AD ＋DF ＝CB ＋BE ，即AF ＝CE .在△AGF 和△CHE 中，⎩⎨⎧∠A ＝∠C ，AF ＝CE ，∠F ＝∠E ，∴△AGF ≌△CHE (ASA)．∴AG ＝CH .18．(1)证明：∵四边形ABCD 是正方形，∴AB ＝BC ，∠ABE ＝∠BCF ＝90°.∴∠BAE ＋∠AEB ＝90°.∵BH ⊥AE ，∴∠BHE ＝90°.∴∠AEB ＋∠EBH ＝90°.∴∠BAE ＝∠EBH .在△ABE 和△BCF 中，⎩⎨⎧∠BAE ＝∠CBF ，AB ＝BC ，∠ABE ＝∠BCF ，∴△ABE ≌△BCF (ASA)．∴AE ＝BF .(2)解：由(1)得△ABE ≌△BCF ，∴BE＝CF.∵正方形的边长是5，BE＝2，∴DF＝CD－CF＝CD－BE＝5－2＝3.在Rt△ADF中，由勾股定理得AF＝AD2＋DF2＝52＋32＝34. 19．(1)证明：∵四边形ABCD是平行四边形，∴BF∥CD，AB＝CD.∴∠AFC＝∠DCG.∵易得GA＝GD，∠AGF＝∠DGC，∴△AGF≌△DGC(AAS)．∴AF＝CD.∴AB＝AF.(2)解：四边形ACDF是矩形．证明：∵由(1)得AF＝CD，AF∥CD，∴四边形ACDF是平行四边形．∵四边形ABCD是平行四边形，∴∠BAD＝∠BCD＝120°.∴∠FAG＝60°.∵AB＝AG＝AF，∴△AGF是等边三角形．∴AG＝GF.∵△AGF≌△DGC，∴FG＝CG.又∵AG＝GD，∴AD＝CF.∴四边形ACDF是矩形．20．(1)证明：∵AB∥CD，∴∠OAB＝∠DCA.∵AC平分∠BAD，∴∠OAB＝∠DAC，∴∠DCA＝∠DAC，∴CD＝AD.∵AB＝AD，∴AB＝CD.又∵AB∥CD，∴四边形ABCD是平行四边形，∵AD＝AB，∴四边形ABCD是菱形．(2)解：由(1)知四边形ABCD是菱形，∴AO＝CO，∵CE⊥AB，∴∠AEC＝90°，∴AC＝2OE＝6.在Rt△ACE中，CE＝AC2－AE2＝11.21．(1)证明：在△ABC中，∵AB＝AC，AD为∠BAC的平分线，∴AD⊥BC，∠BAD＝∠CAD＝12∠BAC，∴∠ADC＝90°.∵AN为△ABC的外角∠CAM的平分线，∴∠MAN＝∠CAN＝12∠CAM，∴∠DAE＝∠DAC＋∠CAN＝12∠BAC＋12∠CAM＝12×180°＝90°.∵CE⊥AN，∴∠AEC＝90°，∴四边形ADCE是矩形．(2)解：四边形ABDE是平行四边形．理由：由(1)知，四边形ADCE是矩形，则AE＝CD，AE∥CD.∵AB＝AC，AD为∠BAC的平分线，∴BD＝CD，∴AE＝BD.又∵AE∥BD，∴四边形ABDE是平行四边形．(3)解：当∠BAC＝90°时，四边形ADCE是正方形．证明：∵∠BAC＝90°，AB＝AC，AD为∠BAC的平分线，∴AD＝CD＝BD.又∵四边形ADCE是矩形，∴四边形ADCE是正方形．22．(1)证明：如图①，连接BD.∵点E，H分别为边AB，DA的中点，∴EH∥BD，EH＝12 BD.∵点F，G分别为边BC，CD的中点，∴FG∥BD，FG＝12 BD.∴EH∥FG，EH＝FG.∴中点四边形EFGH是平行四边形．(2)解：中点四边形EFGH是菱形．理由：如图②，连接AC，BD.∵∠APB＝∠CPD，∴∠APB＋∠APD＝∠CPD＋∠APD，即∠BPD＝∠APC.在△APC和△BPD中，⎩⎨⎧PA ＝PB ，∠APC ＝∠BPD ，PC ＝PD ，∴△APC ≌△BPD (SAS)．∴AC ＝BD .∵点E ，F ，G 分别为边AB ，BC ，CD 的中点，∴EF ＝12AC ，FG ＝12BD .∴EF ＝FG . 又由(1)中结论知中点四边形EFGH 是平行四边形， ∴中点四边形EFGH 是菱形．(3)解：中点四边形EFGH 是正方形．。

人教版八年级下册数学第十八章平行四边形一、选择题（每小题3分，共30分）1．菱形和矩形一定都具有的性质是()A．对角线相等B．对角线互相垂直C．对角线互相平分且相等D．对角线互相平分2．能够判定一个四边形是矩形的条件是()A．对角线互相平分且相等B．对角线互相垂直平分C．对角线相等且互相垂直D．对角线互相垂直3．已知正方形的边长为4cm，则其对角线长是()A．8cm B．16cm C．32cm D．4cm4．在矩形ABCD中，AB=3，BC=4，则点A到对角线BD的距离为()A．B．2C．D．5．如图，▱ABCD中，CE⊥AB，垂足为E，如果∠A=115°，则∠BCE等于()A．65°B．25°C．30°D．15°6．如图，在正方形ABCD中∠DAE=25°，AE交对角线BD于E点，那么∠BEC等于()A．45°B．60°C．70°D．75°7．四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是()A．AB∥DC，AD∥BC B．AB=DC，AD=BC C．AO=CO，BO=DO D．AB∥DC，AD=BC8．如图，菱形ABCD中对角线相交于点O，且OE⊥AB，若AC=8，BD=6，则OE的长是()A．2.5B．5C．2.4D．不确定9．如图，在△ABC中，D，E，F分别为BC，AC，AB边的中点，AH⊥BC于H，FD=8，则HE等于()A．20B．16C．12D．810．如图，△ABC中，AB=AC，点D、E分别是边AB、AC的中点，点G、F在BC边上，四边形DEFG是正方形．若DE=2cm，则AC的长为()A．cm B．4cm C．cm D．cm二、填空题（每小题3分，共18分）11．菱形的两条对角线分别长10cm，24cm，则菱形的边长为cm，2．面积为cm12．如图，菱形ABCD的边长是2cm，E是AB的中点，且DE丄AB，则菱形ABCD2．的面积为cm13．如图，▱ABCD的对角线AC，BD相交于点O，点E，F分别是线段AO，BO的中点．若AC+BD=24厘米，△OAB的周长是18厘米，则EF=厘米．14．如图，在平面直角坐标系中，四边形AOBC是菱形．若点A的坐标是（3，4），则菱形的周长为，点B的坐标是．15．如图，四边形ABCD是正方形，P在CD上，△ADP旋转后能够与△ABP′重合，若AB=3，DP=1，则PP′=．16．如图，在正方形ABCD的外侧，作等边△ADE，则∠AEB=．三、解答题（共52分）17．如图，点D、E、F分别是△ABC各边中点．求证：四边形ADEF是平行四边形．18．如图，BD是菱形ABCD的对角线，点E、F分别在边CD、DA上，且CE=AF．求证：BE=BF．19．如图，正方形ABCD的对角线AC、BD相交于点O，∠OCF=∠OBE．求证：OE=OF．20．已知：如图，在Rt△ABC中，∠ACB=90°，CD平分∠ACB，DE⊥BC，DF⊥AC，垂足分别为E、F，求证：四边形CFDE是正方形．21．已知：如图，在△ABC中，AB=AC，AD⊥BC，垂足为点D，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E，（1）求证：四边形ADCE为矩形；（2）当△ABC满足什么条件时，四边形ADCE是一个正方形？并给出证明．参考答案一、选择题（每小题3分，共30分）1．菱形和矩形一定都具有的性质是()A．对角线相等B．对角线互相垂直C．对角线互相平分且相等D．对角线互相平分考点：菱形的性质；矩形的性质．分析：根据矩形的对角线的性质（对角线互相平分且相等），菱形的对角线性质（对角线互相垂直平分）可解．解答：解：菱形的对角线互相垂直且平分，矩形的对角线相等且平分．菱形和矩形一定都具有的性质是对角线互相平分．故选：D．点评：此题主要考查矩形、菱形的对角线的性质．熟悉菱形和矩形的对角线的性质是解决本题的关键．2．能够判定一个四边形是矩形的条件是()A．对角线互相平分且相等B．对角线互相垂直平分C．对角线相等且互相垂直D．对角线互相垂直考点：矩形的判定．分析：根据矩形的判定定理逐一进行判定即可．解答：解：A、对角线互相平分且相等的四边形是矩形，故正确；B、对角线互相垂直平分的是菱形，故错误；C、对角线相等且互相垂直的四边形不一定是矩形，故错误；D、对角线互相垂直的四边形不一定是矩形，故错误，故选A．点评：本题主要考查了对矩形定义和判定的理解．矩形的判定定理有：（1）有一个角是直角的平行四边形是矩形．（2）有三个角是直角的四边形是矩形．（3）对角线互相平分且相等的四边形是矩形．3．已知正方形的边长为4cm，则其对角线长是()A．8cm B．16cm C．32cm D．4cm考点：勾股定理．分析：作一个边长为4cm的正方形，连接对角线，构成一个直角三角形如下图所示：由勾2=AB2+BC2，求出AC的值即可．股定理得AC解答：解：如图所示：四边形ABCD是边长为4cm的正方形，在Rt△ABC中，由勾股定理得：AC==4cm．所以对角线的长：AC=4cm．故选：D．点评：本题主要考查勾股定理的应用，应先构造一个直角三角形，在直角三角形中斜边的平方等于两直角边的平方和，作图可以使整个题变得简洁明了4．在矩形ABCD中，AB=3，BC=4，则点A到对角线BD的距离为()A．B．2C．D．考点：矩形的性质．分析：本题只要根据矩形的性质，利用面积法来求解．×3×4=6，解答：解：因为BC=4，故AD=4，AB=3，则S△DBC=×5AE，故×5AE=6，AE=．又因为BD==5，S△ABD=故选A．点评：本题考查矩形的性质，矩形具有平行四边形的性质，又具有自己的特性，要注意运用矩形具备而一般平行四边形不具备的性质．5．如图，▱ABCD中，CE⊥AB，垂足为E，如果∠A=115°，则∠BCE等于()A．65°B．25°C．30°D．15°考点：平行四边形的性质．分析：由平行四边形的性质得出邻角互补，求出∠B，再由角的互余关系求出∠BCE即可．解答：解：∵四边形ABCD是平行四边形，∴AD∥BC，∴∠A+∠B=180°，∴∠B=180°﹣115°=65°，∵CE⊥AB，∴∠BEC=90°，∴∠BCE=90°﹣∠B=90°﹣65°=25°；故选：B．点评：本题考查了平行四边形的性质、角的互余关系；熟练掌握平行四边形的性质，并能进行推理计算是解决问题的关键．6．如图，在正方形ABCD中∠DAE=25°，AE交对角线BD于E点，那么∠BEC等于()A．45°B．60°C．70°D．75°考点：正方形的性质．分析：首先证明△AED≌△CED，即可证明∠ECD=∠DAE=25°，从而求得∠BEC，再根据三角形内角和定理即可求解．解答：解：在△AED和△CED中，，∴△AED≌△CED，∴∠ECD=∠DAE=25°，又∵在△DEC中，∠CDE=45°，∴∠CED=180°﹣25°﹣45°=110°，∴∠BEC=180°﹣110°=70°．故选：C．点评：此题主要考查了正方形的性质，正确理解，证明△AED≌△CED是解题的关键．7．四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是()A．AB∥DC，AD∥BC B．AB=DC，AD=BCC．AO=CO，BO=DO D．AB∥DC，AD=BC考点：平行四边形的判定．分析：根据平行四边形判定定理进行判断．解答：解：A、由“AB∥DC，AD∥BC”可知，四边形ABCD的两组对边互相平行，则该四边形是平行四边形．故本选项不符合题意；B、由“AB=DC，AD=BC”可知，四边形ABCD的两组对边相等，则该四边形是平行四边形．故本选项不符合题意；C、由“AO=CO，BO=DO”可知，四边形ABCD的两条对角线互相平分，则该四边形是平行四边形．故本选项不符合题意；D、由“AB∥DC，AD=BC”可知，四边形ABCD的一组对边平行，另一组对边相等，据此不能判定该四边形是平行四边形．故本选项符合题意；故选D．点评：本题考查了平行四边形的判定．（1）两组对边分别平行的四边形是平行四边形．（2）两组对边分别相等的四边形是平行四边形．（3）一组对边平行且相等的四边形是平行四边形．（4）两组对角分别相等的四边形是平行四边形．（5）对角线互相平分的四边形是平行四边形．8．如图，菱形ABCD中对角线相交于点O，且OE⊥AB，若AC=8，BD=6，则OE的长是()A．2.5B．5C．2.4D．不确定考点：菱形的性质；勾股定理．分析：根据菱形的性质可得AC⊥DB，AO=AC，BO=BD，然后利用勾股定理计算出AB长，再根据菱形的面积公式得到S菱形ABCD=×8×6=24，进而得到△AOB的长，然后根据直角三角形的面积计算出EO长即可．解答：解：∵四边形ABCD是菱形，∴AC⊥DB，AO=AC，BO=BD，∵AC=8，BD=6，×8×6=24，∴AO=4，BO=3，S菱形ABCD=，∴AB==5，S△AOB=6∵•AB•EO=×AO×BO，∴5EO=4×3，EO=，故选：C．点评：此题主要考查了菱形的性质、面积，以及勾股定理，关键是掌握菱形的四条边都相等；菱形的两条对角线互相垂直，并且每一条对角线平分一组对角．9．如图，在△ABC中，D，E，F分别为BC，AC，AB边的中点，AH⊥BC于H，FD=8，则HE等于()A．20B．16C．12D．8考点：三角形中位线定理；直角三角形斜边上的中线．分析：利用三角形中位线定理知DF=AC；然后在直角三角形AHC中根据“直角三角形斜边上的中线等于斜边的一半”即可将所求线段EH与已知线段DF联系起来了．解答：解：∵D、F分别是AB、BC的中点，∴DF是△ABC的中位线，∴DF=AC（三角形中位线定理）；又∵E是线段AC的中点，AH⊥BC，∴EH=AC，∴EH=DF=8．故选D．点评：本题综合考查了三角形中位线定理、直角三角形斜边上的中线．三角形的中位线平行于第三边且等于第三边的一半．10．如图，△ABC中，AB=AC，点D、E分别是边AB、AC的中点，点G、F在BC边上，四边形DEFG是正方形．若DE=2cm，则AC的长为()A．cm B．4cm C．cm D．cm考点：三角形中位线定理；等腰三角形的性质；勾股定理；正方形的性质．专题：计算题．分析：根据三角形的中位线定理可得出BC=4，由AB=AC，可证明BG=CF=1，由勾股定理求出CE，即可得出AC的长．解答：解：∵点D、E分别是边AB、AC的中点，∴DE=BC，∵DE=2cm，∴BC=4cm，∵AB=AC，四边形DEFG是正方形．∴△BDG≌△CEF，∴BG=CF=1，∴EC=，∴AC=2cm．故选D．点评：本题考查了相似三角形的判定、勾股定理、等腰三角形的性质以及正方形的性质，是基础题，比较简单．二、填空题（每小题3分，共18分）11．菱形的两条对角线分别长10cm，24cm，则菱形的边长为13cm，面积为120cm2．考点：菱形的性质．分析：根据菱形的对角线性质，得出两条对角线的一半为5与12．然后可用勾股定理求出其边长．利用菱形的面积公式：对角线之积的一半进行计算．解答：解：根据题意可得AC=10cm，BD=24cm，∵四边形ABCD是菱形，∴AO=AC，BO=BD，AC⊥BD，∵AC=10cm，BD=24cm，∴AO=5cm，BO=12cm，∴AB==13cm，2）．面积：AC•BD=×10×24=120（cm故答案为：13；120．点评：此题主要考查了菱形的性质，以及勾股定理的应用，关键是掌握菱形四边相等，对角线互相垂直平分．12．如图，菱形ABCD的边长是2cm，E是AB的中点，且DE丄AB，则菱形ABCD2．的面积为2cm考点：菱形的性质；勾股定理．分析：因为DE丄AB，E是AB的中点，所以AE=1cm，根据勾股定理可求出DE的长，菱形的面积=底边×高，从而可求出解．解答：解：∵E是AB的中点，∴AE=1cm，∵DE丄AB，∴DE==cm．2．∴菱形的面积为：2×=2cm故答案为：2．点评：本题考查菱形的性质，四边都相等，菱形面积的计算公式以及勾股定理的运用等．13．如图，▱ABCD的对角线AC，BD相交于点O，点E，F分别是线段AO，BO的中点．若AC+BD=24厘米，△OAB的周长是18厘米，则EF=3厘米．考点：三角形中位线定理；平行四边形的性质．分析：根据平行四边形的性质可知OA=AC，OB=BD，结合AC+BD=24厘米，△OAB 的周长是18厘米，求出AB的长，利用三角形中位线定理求出EF的长．解答：解：∵▱ABCD的对角线AC，BD相交于点O，∴点O是AC、BD的中点，∵AC+BD=24厘米，∴OB+0A=12厘米，∵△OAB的周长是18厘米，∴AB=18﹣12=6厘米，∵▱ABCD的对角线AC，BD相交于点O，点E，F分别是线段AO，BO的中点，∴AB=2EF，∴EF=6÷2=3厘米，故答案为：3．点评：本题主要考查了三角形中位线定理以及平行四边形的性质的知识，解答本题的关键是求出AB的长，此题难度不大．14．如图，在平面直角坐标系中，四边形AOBC是菱形．若点A的坐标是（3，4），则菱形的周长为20，点B的坐标是（5，0）．考点：菱形的性质；坐标与图形性质．分析：过A作AE⊥x轴于点E，根据勾股定理可求出OA的长，进而可求出菱形的周长，再由菱形的性质可得AO=AC=BO=BC=5，即可求出点B的坐标．解答：解：过A作AE⊥x轴于点E，∵点A的坐标是（3，4），∴OE=3，AE=4．∴AO==5，∵四边形AOBC是菱形，∴AO=AC=BO=BC=5，∴菱形的周长=4AB=20，点B的坐标是（5，0），故答案为：20，（5，0）．点评：此题主要考查了菱形的性质，解题的关键是利用勾股定理求出OA的长，是2015届中考常见题型，比较简单．15．如图，四边形ABCD是正方形，P在CD上，△ADP旋转后能够与△ABP′重合，若AB=3，DP=1，则PP′=2．考点：旋转的性质．分析：由正方形的性质得出AB=AD=3，∠ABC=∠D=∠BAD=90°，由勾股定理求出AP，再由旋转的性质得出△ADP≌△ABP′，得出AP′=AP=，∠BAP′=∠DAP，证出△PAP′是等腰直角三角形，得出PP′=AP，即可得出结果．解答：解：∵四边形ABCD是正方形，∴AB=AD=3，∠ABC=∠D=∠BAD=90°，∴AP==，∵△ADP旋转后能够与△ABP′重合，∴△ADP≌△ABP′，∴AP′=AP=，∠BAP′=∠DAP，∴∠PAP′=∠BAD=90°，∴△PAP′是等腰直角三角形，∴PP′=AP=2；故答案为：2．点评：本题考查了旋转的性质、勾股定理、全等三角形的性质、等腰直角三角形的性质；熟练掌握正方形和旋转的性质是解决问题的关键．16．如图，在正方形ABCD的外侧，作等边△ADE，则∠AEB=15°．考点：正方形的性质；等边三角形的性质．专题：计算题分析：由四边形ABCD为正方形，三角形ADE为等比三角形，可得出正方形的四条边相等，三角形的三边相等，进而得到AB=AE，且得到∠BAD为直角，∠DAE为60°，由∠BAD+∠DAE求出∠BAE的度数，进而利用等腰三角形的性质及三角形的内角和定理即可求出∠AEB的度数．解答：解：∵四边形ABCD为正方形，△ADE为等边三角形，∴AB=BC=CD=AD=AE=DE，∠BAD=90°，∠DAE=60°，∴∠BAE=∠BAD+∠DAE=150°，又∵AB=AE，∴∠AEB==15°．故答案为：15°．点评：此题考查了正方形的性质，以及等边三角形的性质，利用了等量代换的思想，熟练掌握性质是解本题的关键．三、解答题（共52分）17．如图，点D、E、F分别是△ABC各边中点．求证：四边形ADEF是平行四边形．考点：三角形中位线定理；平行四边形的判定．专题：证明题．分析：根据三角形的中位线定理可得DE∥AC，EF∥AB，再根据两组对边分别平行的四边形是平行四边形证明即可．解答：证明：∵D、E分别为AB、BC的中点，∴DE∥AC，∵E、F分别为BC、AC中点，∴EF∥AB，∴四边形ADEF是平行四边形．点评：此题主要考查了三角形的中位线定理，勾股定理以及平行四边形的判定定理，关键是掌握三角形中位线定理：三角形的中位线平行于第三边，并且等于第三边的一半．18．如图，BD是菱形ABCD的对角线，点E、F分别在边CD、DA上，且CE=AF．求证：BE=BF．考点：菱形的性质；全等三角形的判定与性质．专题：证明题．分析：根据菱形的性质可得AB=BC，∠A=∠C，再证明△ABF≌△CBE，根据全等三角形的性质可得BF=BE．解答：证明：∵四边形ABCD是菱形，∴AB=BC，∠A=∠C，∵在△ABF和△CBE中，，∴△ABF≌△CBE（SAS），∴BF=BE．点评：此题主要考查了菱形的性质，以及全等三角形的判定与性质，关键是掌握菱形的四条边都相等．19．如图，正方形ABCD的对角线AC、BD相交于点O，∠OCF=∠OBE．求证：OE=OF．考点：正方形的性质；全等三角形的判定与性质．专题：证明题．分析：根据正方形的性质及全等三角形的判定得到△OCF≌△OBE，从而可得到结论．解答：证明：∵四边形ABCD是正方形，∴AC⊥BD，即∠AOB=∠BOC=90°，∴BO=OC，∵∠OCF=∠OBE，∴△OCF≌△OBE，∴OE=OF．点评：本题利用了正方形的性质（正方形的四个角都是直角，对角线互相垂直平分且相等），还利用了全等三角形的判定．20．已知：如图，在Rt△ABC中，∠ACB=90°，CD平分∠ACB，DE⊥BC，DF⊥AC，垂足分别为E、F，求证：四边形CFDE是正方形．考点：正方形的判定；角平分线的性质；矩形的判定与性质．专题：证明题．分析：由题意可得，四边形CFDE是矩形，根据角平分线的性质得到DE=DF，根据有一组邻边相等的矩形是正方形，四边形CFDE是正方形．解答：证明：∵∠ACB=90°，DE⊥BC，DF⊥AC，∴四边形CFDE是矩形．又∵CD平分∠ACB，DE⊥BC，DF⊥AC，∴DE=DF．∴四边形CFDE是正方形（有一组邻边相等的矩形是正方形）．点评：本题是考查正方形的判别方法，判别一个四边形为正方形主要根据正方形的概念，途经有两种：①先说明它是矩形，再说明有一组邻边相等；②先说明它是菱形，再说明它有一个角为直角．21．已知：如图，在△ABC中，AB=AC，AD⊥BC，垂足为点D，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E，（1）求证：四边形ADCE为矩形；（2）当△ABC满足什么条件时，四边形ADCE是一个正方形？并给出证明．考点：矩形的判定；角平分线的性质；等腰三角形的性质；正方形的判定．专题：证明题；开放型．分析：（1）根据矩形的有三个角是直角的四边形是矩形，已知CE⊥AN，AD⊥BC，所以求证∠DAE=90°，可以证明四边形ADCE为矩形．（2）根据正方形的判定，我们可以假设当AD=BC，由已知可得，DC=BC，由（1）的结论可知四边形ADCE为矩形，所以证得，四边形ADCE为正方形．解答：（1）证明：在△ABC中，AB=AC，AD⊥BC，∴∠BAD=∠DAC，∵AN是△ABC外角∠CAM的平分线，∴∠MAE=∠CAE，∴∠DAE=∠DAC+∠CAE=180°=90°，又∵AD⊥BC，CE⊥AN，∴∠ADC=∠CEA=90°，∴四边形ADCE为矩形．（2）当△ABC满足∠BAC=90°时，四边形ADCE是一个正方形．理由：∵AB=AC，∴∠ACB=∠B=45°，∵AD⊥BC，∴∠CAD=∠ACD=45°，∴DC=AD，∵四边形ADCE为矩形，∴矩形ADCE是正方形．∴当∠BAC=90°时，四边形ADCE是一个正方形．点评：本题是以开放型试题，主要考查了对矩形的判定，正方形的判定，等腰三角形的性质，及角平分线的性质等知识点的综合运用．。

第十八章综合测试一、选择题（每小题5分，共30分）1.如图18-10，在菱形ABCD 中，M ，N 分别在AB ，CD 上，且AM CN =，MN 与AC 交于点O ，连接BO ，若28DAC ∠=︒，则OBC ∠的度数为（ ）A .28︒B .52︒C .62︒D .72︒2.如图18-11，在矩形ABCD 中，AB BC ＜，AC ，BD 相交于点O ，则图中等腰三角形的个数是（ ） A .8B .6C .4D .23.如图18-12，在菱形ABCD 中，3AB =，60ABC ∠=︒，则对角线AC =（ ）A .12B .9C .6D .34.已知ABC △的各边长度分别为3 cm ，4 cm ，5 cm ，则连接各边中点的三角形的周长为（ ） A .2 cmB .7 cmC .5 cmD .6 cm5.如图18-13，在ABC △中，AB AC =，点D ，E 分别是边AB ，AC 的中点，点G ，F 在BC 边上，四边形DEFG 是正方形.若 2 cm DE =，则AC 的长为（ ）A .B .4 cmC .D .6.如图18-14，将n 个边长都为2的正方形按如图18-14所示摆放，点1A ，2A …，n A 分别是正方形的中心，则这n 个正方形重叠部分的面积之和是（ ）A .nB .1n -C .114n -⎛⎫ ⎪⎝⎭D .14n二、填空题（每小题6分，共24分）7.如图18-15，在矩形ABCD 中，对角线AC ，BD 相交于点O ，点E ，F 分别是AO ，AD 的中点，若8AC =，则EF =________.8.已知正方形的边长为4 cm ，则其对角线长是________.9.如图18-16，在四边形ABCD 中，对角线 AC BD ⊥，E ，F ，G ，H 分别是各边的中点，若 4 cm AC =，6 cm BD =，则四边形EFGH 的面积是________2cm .10.如图18-17，菱形ABCD 的对角线AC ，BD 相交于点O ，且8AC =，6BD =，过点O 作OH AB ⊥，垂足为点H ，则点O 到边AB 的________.三、解答题（共46分）11.（11分）如图18-18，在平行四边形ABCD 中，点E ，F 分别在AD ，BC 上，且AE CF =.求证：BE DF =.12.（11分）如图18-19，在ABC △中，AD 是BC 边上的中线，E 是AD 的中点，过点A 作BC 的平行线交BE 的延长线于点F ，连接CF . （1）求证：AF DC =；（2）若AB AC ⊥，试判断四边形ADCF 的形状，并证明你的结论.13.（12分）如图18-20，四边形ABCD 的对角线AC ，BD 交于点O ，BE AC ⊥于E ，DF AC ⊥于F ，点O 既是AC 的中点，又是EF 的中点.（1）求证：BOE DOF △≌△； （2）若12OA BD =，则四边形ABCD 是什么特殊四边形？说明理由.14.（12分）如图18-21，在平行四边形ABCD中，O为对角线BD的中点，过点O的直线EF分别交AD，BC于E，F两点，连接BE，DF.△≌△；（1）求证：DOE BOF等于多少度时，四边形BFDE为菱形？请说明理由.（2）当DOE第十八章综合测试答案解析1.【答案】C【解析】因为四边形ABCD 为菱形，且AM CN =，可证得AOM CON △≌△，所以OA OC =.因为AB CB =，所以OB AC ⊥，所以90BOC ∠=︒.又因为28DAC ∠=︒，所以28BCO ∠=︒，所以=62OBC ∠︒. 2.【答案】C【解析】因为四边形ABCD 是矩形，所以AO BO CO DO ===.所以ABO △，BCO △，DCO △，ADO △都是等腰三角形. 3.【答案】D【解析】因为四边形ABCD 是菱形，所以AB BC =.又因为60ABC ∠=︒，所以ABC △为等边三角形，所以3AC AB ==. 4.【答案】D【解析】如答图18-1，D ，E ，F 分别是ABC △的三边的中点，则12DE AC =，12DF BC =，12EF AB =，所以DEF △的周长16cm 2DE DF EF AC BC AB =++-++=（）（）.15.【答案】D【解析】因为点D ，E 分别是边AB ，AC 的中点，所以12DE BC =.因为 2 cm DE =，所以 4 cm BC =. 因为A B A C =，四边形DEFG 是正方形，可证得BDG CEF △≌△.所以1 c m B G C F ==，所以c mEC =.所以AC =. 6.【解析】B【解析】因为正方形的边长为2，所以每个正方形的面积是4，因为每个重叠的部分正好是正方形面积的14，所以每个重叠的部分的面积是1.当1个正方形重叠时有()1n -个重叠的部分，所以这n 个正方形重叠部分的面积之和是1n -. 7.【解析】2【解析】因为四边形ABCD 为矩形，所以8BD AC ==.所以4OD =.又因为EF 为AOD △的中位线，所以122EF OD ==.8.【答案】【解析】如答图18-2，四边形ABCD 是边长为4 cm 的正方形，在Rt ABC △中，由勾股定理，得AC ==，所以对角线的长为AC =.9.【答案】6【解析】因为E ，F ，G ，H 分别是四边形ABCD 各边的中点，所以EH BD ∥，且12EH B D =，FG BD ∥，且12FG BD =.所以EH FG ∥，EH FG =.同理EF HG ∥，EF HG =.又因为AC BD ⊥，所以四边形EFGH 是矩形.所以四边形EFGH 的面积()21111466cm 2222EF EH AC BD =⨯=⨯=⨯⨯⨯=. 10.【答案】125【解析】因为8AC =，6BD =，所以4AO =，3BO =.所以5AB =.因为1122AO BO AB OH ⋅=⋅，所以125OH =. 11.【答案】证明：因为四边形ABCD 是平行四边形，所以AD BC ∥，AD BC =. 又因为AE CF =，所以DE BF =，DE BF ∥. 所以四边形DEBF 是平行四边形. 所以BE DF =.12.【答案】（1）证明：因为AF BC ∥，所以AFE DBE ∠=∠. 因为E 是AD 的中点，所以AE DE =. 在AFE △和DBE △中，AFE DBE ∠=∠，FEA BED ∠=∠，AE DE =，所以AFE DBE △≌△.所以AF BD =.因为AD 是BC 边上的中线，所以BD DC =. 所以AF DC =.（2）解：四边形ADCF 是菱形。

人教版数学八年级下册第十八章测试卷姓名：分数：第十八章卷（3）一、选择题1．如图，已知矩形ABCD中，R、P分别是DC、BC上的点，E、F分别是AP、RP的中点，当P在BC上从B向C移动而R不动时，那么下列结论成立的是（）A．线段EF的长逐渐增大B．线段EF的长逐渐减小C．线段EF的长不改变D．线段EF的长不能确定2．已知一个直角梯形，一腰长为6，这腰与一底所成的角为30°，那么另一腰的长是（）A．1.5 B．3 C．6 D．93．如图所示，将一张正方形纸片对折两次，然后在上面打3个洞，则纸片展开后是（）A．B．C．D．4．在平行四边形ABCD中，∠A：∠B：∠C=2：3：2，则∠D=（）A．36°B．108°C．72° D．60°5．如果等边三角形的边长为3，那么连接各边中点所成的三角形的周长为（）A．9 B．6 C．3 D．6．菱形具有而矩形不一定具有的性质是（）A．对角线互相垂直B．对角线相等C．对角线互相平分D．对角互补7．四边形ABCD中，AD∥BC．要判别四边形ABCD是平行四边形，还需满足条件（）A．∠A+∠C=180°B．∠B+∠D=180°C．∠B+∠A=180°D．∠A+∠D=180°8．如图，已知E，F分别为平行四边形ABCD边AD，AB上的两点，则图形中与△BEC的面积相等的三角形有（）A．2个B．3个C．4个D．5个二、填空题9．如图，在平行四边形ABCD中，DB=DC，∠C=70°，AE⊥BD于E，则∠DAE=度．10．如图，点E、F在▱ABCD的对角线BD上，要使四边形AECF是平行四边形，还需添加一个条件．（只需写出一个结论，不必考虑所有情况）．11．如图所示，工人师傅做铝合金窗框分下面三个步骤进行：(1)先截出两对符合规格的铝合金窗料（如图①所示），使AB=CD，EF=GH．(2)摆放成如图②的四边形，则这时窗框的形状是，根据的数学道理是．(3)将直尺紧靠窗框的一个角（如图③），调整窗框的边框，当直角尺的两条直角边与窗框无缝隙时（如图④，说明窗框合格，这时窗框是，根据的数学道理是．。

八年级数学第十八章试卷班级_______________ 姓名___________分数___________一、选择题：（每小题3分，共30分）1、在□ABCD 中，∠A ：∠B:∠C:∠D 的值可以是（ ） A 、1：2：3：4 B 、1:2：2:1 C 、2:2：1：1 D 、2：1：2：12、菱形和矩形一定都具有的性质是（ )A 、对角线相等B 、对角线互相垂直C 、对角线互相平分D 、对角线互相平分且相等3、平行四边形的一边长是10cm ，那么这个平行四边形的两条对角线的长可以是( ）A.4cm 和6cm B 。

6cm 和8cm C.8cm 和10cm D.10cm 和12cm4、四边形ABCD 的对角线AC 、BD 交于点O,能判定它是正方形的是（ ）A 、AO ＝OC ，OB ＝OD B 、AO ＝BO ＝CO ＝DO ，AC ⊥BD C 、AO ＝OC ，OB ＝OD,AC ⊥BD D 、AO ＝OC ＝OB ＝OD 5、给出下列四个命题⑴一组对边平行的四边形是平行四边形⑵一条对角线平分一个内角的平行四边形是菱形 ⑶两条对角线互相垂直的矩形是正方形⑷顺次连接四边形四边中点所得的四边形是平行四边形。

其中正确命题的个数为（ ）A 、1个B 、2个C 、3个D 、4个6、下列矩形中按虚线剪开后,能拼成平行四边形，又能拼成直角三角形的是（ ）A BC D7、如图,过矩形ABCD 的四个顶点作对角线AC 、BD 的平行线，分别相交于E 、F 、G 、H 四点，则四边形EFGH 为（ ） A 。

平行四边形 B 、矩形 C 、菱形 D. 正方形8、如图，如果□ABCD 的对角线AC 、BD 相交于点O ,那么图中的全等三角形共有（ ）A 。

1对 B.2对 C.3对 D 。

4对9、如图，大正方形中有2个小正方形，如果它们的面积分别是S 1、S 2,那么S 1、S 2的大小关系是（ ）A 。

S 1 〉 S 2 B.S 1 = S 2C 。

人教版数学八年级下期第十八章平行四边形最值问题训练一、选择题1.如图，在菱形ABCD中，∠ABC=60∘，E为BC边的中点，M为对角线BD上的一BM最小值的是（）个动点．则下列线段的长等于AM+12A. ADB. AEC. BDD. BES矩形2.如图，在矩形ABCD中，AB=4，AD=3，矩形内部有一动点P，满足S△PAB=13，则点P到A、B两点的距离之和PA+PB的最小值（ ）ABCDA. 4B. 42C. 22D. 23.如图，菱形ABCD的两条对角线长分别为AC=6，BD=8，点P是BC边上的一动点，则AP的最小值为( )A. 4B. 4.8C. 5D. 5.54.如图，正方形ABCD的边长为4，E点是BC上一点，F是AB上一点，P是AC上一动点，且BE=1，AF=2，则PE+PF的最小值是（ ）A. 4B. 15C. 5D. 175.如图，矩形ABCD中，AB=8，BC=6，点E，F，G，H分别在矩形ABCD各边上，且AE=CG，BF=DH，则四边形EFGH周长的最小值为（ ）A. 10B. 43C. 20D. 876.如图，矩形ABCD中，∠BOC＝120°，BD＝12，点P是AD边上一动点，则OP的最小值为（）A. 3B. 4C. 5D. 6二、填空题7.如图：菱形ABCD中，AB=2，∠B=120°，E是AB的中点，P是对角线AC上的一个动点，则PE+PB的最小值是____．8.如图,在边长为6的菱形ABCD中, ∠ DAB＝120°,E,F分别为边CD、CB上的动点,且CE+CF= 6,则线段EF长的最小值是 .9.如图，在边长为1的菱形ABCD中，∠ABC＝60°，将△ABD沿射线BD的方向平移得到△A'B'D'，分别连接A'C，A'D，B'C，则A'C+B'C的最小值为______．10.填空如图，在菱形ABCD中，∠B＝45°，BC＝23，E，F分别是边CD，BC上的动点，连接AE，EF，G，H分别为AE，EF的中点，连接GH，则GH的最小值为____．11.如图，在边长为4的菱形ABCD中，∠A=60°，M是AD边的中点，点N是AB边上一动点，将△AMN沿MN所在的直线翻折得到△A′MN，连接A′B，则线段A′B 长度的最小值是_____________．12.如图，将边长为4的正方形ABCD纸片沿EF折叠，点C落在AB边上的点G处，点D与点H重合，CG与EF交于点P，取GH的中点Q，连接PQ，则▵GPQ的周长最小值是_________.三、解答题13.如图，在等腰直角三角形ABC中，∠ACB=90°，AC=BC=4，D是AB的中点，E，F分别是AC，BC上的点(点E不与端点A，C重合)，且AE=CF，连接EF并取EF的中点O，连接DO并延长至点G，使GO=OD，连接DE，DF，GE，GF．(1)求证：四边形EDFG是正方形；(2)四边形EDFG面积的最小值为________．14.如图，点O为▱ABCD的对角线AC，BD的交点，∠BCO=90°，∠BOC=60°，BD=8，点E是OD上的一动点，点F是OB上的一动点（E，F不与端点重合），且DE=OF，连接AE，CF．（1）求线段EF的长；（2）若△OAE的面积为S1，△OCF的面积为S2，S1+S2的值是否发生变化？若不变，求出这个不变的值；若变化，请说明随着DE的增大，S1+S2的值是如何发生变化的？（3）求AE+CF的最小值．15.如图，在△ABC中，AC＝9，AB＝12，BC＝15，P为BC边上一动点，PG⊥AC于点G，PH⊥AB于点H．（1）求证：四边形AGPH是矩形；（2）是否存在点P，使得GH最短？若存在，请求出最小值，若不存在，请说明理由．16.如图，在正方形ABCD中，E是边AB上的一动点（不与点A、B重合），连接DE，点A关于直线DE的对称点为F，连接EF并延长交BC于点G，连接DG，过点E作EH⊥DE交DG的延长线于点H，连接BH．（1）求证：GF=GC；（2）用等式表示线段BH与AE的数量关系，并证明．（3）若正方形ABCD的边长为4，取DH的中点M，请直接写出线段BM长的最小值.17.已知菱形ABCD的两条对角线分别为6和8，M、N分别是边BC、CD的中点，P是对角线BD上的动点（不含B、D）．（1）证明无论动点P在何处，四边形PMCN的面积总是固定值，这个固定值是多少？（2）试探究动点P在何处时，四边形PMCN的周长最小，最小值是多少？18.如图，正方形ABCD中，以B为顶点的交AD于E，交CD于F，延长DC使得CG=AE.（1）证明：△ABE≌△CBG；（2）若EF=5，AE=2，求AB的长度.（3）在（2）条件下，若P为线段BF上一动点，求PG+PC最小值.参考答案1.B2.B3.B4.D5.C6.A7.38.339.310.6211.23−212.2+2513.解：（1）连接DC,∵O是EF的中点,GO=OD,∴四边形EDFG是平行四边形,∵△ABC为等腰直角三角形,∠ACB=90°,D是AB的中点,∴∠A=∠DCF=45°,AD=CD,在△ADE和△CDF中,AE=CF,∠A=∠DCFAD=CD∴△ADE≌△CDF,∴DE=DF,∠ADE=∠CDF,∴四边形EDFG是菱形,∵∠ADE+∠EDC=90°,∴∠EDC+∠CDF=∠EDF=90°,∴四边形EDFG是正方形;（2）4.14.解：（1）∵四边形ABCD是平行四边形，∴OD=OB，∵DE=OF，BD=4；∴EF=OD=12（2）S1+S2的值不变，理由如下：如图所示，连结AF，∵四边形ABCD是平行四边形，∴AO=OC，∴S△AOF=S△COF，∵DE=OF，∴S △ADE =S △COF ，∴S 1+S 2=S △AEF =S △AOD ，∵∠BCO =90°，∠BOC =60°，∴∠DAC =90°，∠AOD =60°，∴AO =12OD =2，在Rt △AOD 中，AD =3AO =23，∴S 1+S 2=S △AOD =12AD •OA =12×23×2=23；（3）当DE =OE 时，AE +CF 的值最小，此时E 为OD 的中点，∵∠OAD =90°，∴AE =12OD =2，同理CF =2，∴AE +CF 的最小值=4．15.（1）证明∵AC =9 AB =12 BC =15，∴AC 2=81，AB 2=144，BC 2=225，∴AC 2+AB 2=BC 2，∴∠A =90°．∵PG ⊥AC ，PH ⊥AB ，∴∠AGP =∠AHP =90°，∴四边形AGPH 是矩形；（2）存在．理由如下：连结AP ．∵四边形AGPH 是矩形，∴GH =AP ．∵当AP ⊥BC 时AP 最短．根据三角形面积有12×9×12=12×15•AP ．∴AP =365，.∴GH=36516.证明：（1）如图1，连接DF，∵四边形ABCD是正方形，∴DA=DC，∠A=∠C=90°，∵点A关于直线DE的对称点为F，∴△ADE≌△FDE，∴DA=DF=DC，∠DFE=∠A=90°，∴∠DFG=90°，在Rt△DFG和Rt△DCG中，∵DF=DCDG=DG，∴Rt△DFG≌Rt△DCG（HL），∴GF=GC；（2）BH=2AE，理由是：证法一：如图2，在线段AD上截取AM，使AM=AE，∵AD=AB，∴DM=BE，由（1）知：∠1=∠2，∠3=∠4，∵∠ADC=90°，∴∠1+∠2+∠3+∠4=90°，∴2∠2+2∠3=90°，∴∠2+∠3=45°，即∠EDG=45°，∵EH⊥DE，∴∠DEH=90°，△DEH是等腰直角三角形，∴∠AED+∠BEH=∠AED+∠1=90°，DE=EH，∴∠1=∠BEH，在△DME和△EBH中，∵DM=BE∠1=∠BEH DE=EH，∴△DME≌△EBH，∴EM=BH，Rt△AEM中，∠A=90°，AM=AE，∴EM=2AE，∴BH=2AE；证法二：如图3，过点H作HN⊥AB于N，∴∠ENH=90°，由方法一可知：DE=EH，∠1=∠NEH，在△DAE和△ENH中，∵∠A=∠ENH ∠1=∠NEH DE=EH，∴△DAE≌△ENH，∴AE=HN，AD=EN，∵AD=AB，∴AB=EN=AE+BE=BE+BN，∴AE=BN=HN，∴△BNH是等腰直角三角形，∴BH=2HN=2AE.（3）22.17.解：（1）如图所示：∵M、N分别是边BC、CD的中点，∴MN∥BD．∴△PMN的面积=△BMN的面积=△CMN的面积，∴四边形PMCN的面积=1菱形ABCD的面积=6；4（2）如图所示：作M关于BD的对称点Q，连接NQ交BD于P，连接MP，此时MP+NP的值最小，∵四边形ABCD是菱形，∴AC⊥BD，∠QBP=∠MBP，即Q在AB上，∵MQ⊥BD，∴AC∥MQ，∵M为BC中点，∴Q为AB中点，∵N为CD中点，四边形ABCD是菱形，∴BQ∥CD，BQ=CN，∴四边形BQNC是平行四边形，∴NQ=BC，∵四边形ABCD是菱形，∴CP=AP=3，BP=PD=4，在Rt△BPC中，由勾股定理得：BC=5，即NQ=5，∴MP+NP=QP+NP=QN=5，∴四边形PMCN周长最小值是10．18.证明：（1）∵四边形ABCD是正方形，∴AB=BC，∠A=∠BCD=90°，∴∠A=∠BCG=90°，∵AE=CG，∴△ABE≌△CBG；（2）设AB=x，∵四边形ABCD是正方形，∴AB=AD=CD=x，∵AE=2，AE=CG，∴DE=x-2，CG=2，由（1）知△ABE≌△CBG，∴BE=BG，∠ABE=∠CBG，∵∠EBF=45°，∴∠ABE+∠CBF=45°，∴∠ABE+∠CBG=45°，即∠GBF=45°，∴∠EBF=∠GBF，∵BF=BF，∴△EBF≌△GBF，∴EF=GF=5，∴FC=GF-CG=5-2=3，∴DF=x-3，在RT△DEF中，由勾股定理得，DE2+DF2=EF2，∴（x-2）2+（x-3）2=52，解得x=6或-1（舍去），即AB的长度是6；（3）连接EG，EC，如图，由（2）知△EBF≌△GBF，∴点E与点G关于BF对称，连接EC，则EC与BF的交点即为点P，此时PG+PC最小，且最小值是PG+PC=PE+PC=EC，在Rt△CDE中，由勾股定理得：CD2+DE2=EC2，由（2）知CD=AB=6，DE=6-2=4，∴EC2=62+42=52，∴EC=213，即PG+PC的最小值是213.。

人教版数学八年级下册第十八章测试卷一．选择题（共10小题）1．以三角形的一条中位线和第三边上的中线为对角线的四边形是（）A．梯形B．平行四边形C．菱形D．矩形2．如图，是屋架设计图的一部分，点D是斜梁AB的中点，立柱BC、DE垂直于横梁AC，AB=4m，∠A=30°，则DE等于（）A．1m B．2m C．3m D．4m3．若平行四边形的一边长为5，它的两条对角线的长可能是（）A．4和3 B．4和8 C．4和6 D．2和124．菱形相邻两角的比为1：2，那么它们的较长对角线与边长的比为（）A．2：3 B．C．2：1 D．5．如图，△ABC周长为1，连接△ABC三边中点构成第二个三角形，再连接第二个三角形三边中点构成第三个三角形，以此类推，第2016个三角形的周长为（）A．22016B．22017 C．D．6．在Rt△ABC中，∠C=90°，AB=16cm，点D为AB的中点，则CD的长为（）A．2cm B．4cm C．6cm D．8cm7．如图，平行四边形ABCD中，AB=6cm，AD=10cm，点P在AD 边上以每秒1cm 的速度从点A向点D运动，点Q在BC边上，以每秒4cm的速度从点C出发，在CB间往返运动，两个点同时出发，当点P到达点D时停止（同时点Q也停止），在运动以后，以P、D、Q、B四点组成平行四边形的次数有（）A．1 次B．2次 C．3次 D．4次8．如图，一根木棍斜靠在与地面（OM）垂直的墙（ON）上，设木棍中点为P，若木棍A端沿墙下滑，且B沿地面向右滑行．在此滑动过程中，点P到点O的距离（）A．变小B．不变C．变大D．无法判断9．如图，△ABC中，CD⊥AB于D，且E是AC的中点．若AD=6，DE=5，则CD 的长等于（）A．5 B．6 C．7 D．810．平面直角坐标系中，四边形ABCD的顶点坐标分别是A（﹣3，0），B（0，2），C（3，0），D（0，﹣2），则四边形ABCD是（）A．矩形B．菱形C．正方形D．平行四边形二．填空题（共5小题）11．如图，△ABC中，AD是中线，AE是角平分线，CF⊥AE于F，AB=10，AC=6，则DF的长为．12．已知平行四边形ABCD的周长为44，过点A作AE⊥直线BC于E，作AF⊥直线CD于点F，若AE=5，AF=6，则CE+CF的值为．13．用20cm长的铁丝围成一个平行四边形，使长边比短边长2cm，则它的长边长为，短边长为．14．在直角三角形中，斜边上的中线为3，那么斜边长为．15．如图，在Rt△ABC中，CD是斜边AB上的中线，若AB=2，则CD=．三．解答题（共7小题）16．已知：如图，∠ABC=∠ADC=90°，E、F分别是AC、BD的中点．求证：EF⊥BD．17．在△ABC中，AD=BF，点D，E，F分别是AC，BC，BA延长线上的点，四边形ADEF为平行四边形．求证：AB=AC．18．已知：如图，A，B，C，D在同一直线上，且AB=CD，AE=DF，AE∥DF．求证：四边形EBFC是平行四边形．19．如图，在Rt△ABC中，∠ACB=90°，点E，F分别是边AC，AB的中点，延长BC到点D，使2CD=BC，连接DE．（1）如果AB=10，求DE的长；（2）延长DE交AF于点M，求证：点M是AF的中点．20．△ABC的中线BD、CE相交于O，F，G分别是BO、CO的中点，求证：EF∥DG，且EF=DG．21．如图，∠ACB=∠ADB=90°，M、N分别为AB、CD的中点．求证：MN⊥CD．22．如图，AD是△ABC的中线，AE∥BC，BE交AD于点F，交AC于G，F是AD 的中点．（1）求证：四边形ADCE是为平行四边形；（2）若EB是∠AEC的角平分线，请写出图中所有与AE相等的边．参考答案与试题解析一．选择题（共10小题）1．以三角形的一条中位线和第三边上的中线为对角线的四边形是（）A．梯形B．平行四边形C．菱形D．矩形【解答】解：如右图：∵D、E、F分别是三角形的三边的中点∴DF∥AC，EF∥AB∵AE、AD分别在AC、AB上∴DF∥AE，EF∥AD∴四边形是平行四边形．故选B．2．如图，是屋架设计图的一部分，点D是斜梁AB的中点，立柱BC、DE垂直于横梁AC，AB=4m，∠A=30°，则DE等于（）A．1m B．2m C．3m D．4m【解答】解：∵点D是斜梁AB的中点，立柱BC，DE垂直于横梁AC，∴点E是AC的中点，∴DE是直角三角形ABC的中位线，根据三角形的中位线定理得：DE=BC，又∵在Rt△ABC中，AB=4m，∠A=30°，∴BC=AB=2m．故DE=BC=1m，故选：A．3．若平行四边形的一边长为5，它的两条对角线的长可能是（）A．4和3 B．4和8 C．4和6 D．2和12【解答】解：如图，过点C作CF∥BD，交AB延长线于点F，∴四边形BFCD为平行四边形，∴CF=BD，∴在△AFC中：AC﹣CF＜AF＜AC+CF，即AC﹣BD＜2AB＜AC+BD，∵AB=5，∴选项中只有D中的数据能满足此关系：8﹣4=4＜5×2＜8+4=12，故选B．4．菱形相邻两角的比为1：2，那么它们的较长对角线与边长的比为（）A．2：3 B．C．2：1 D．【解答】解：如图在菱形ABCD中，连接AC、BD交于点O，∵∠ADC=2∠DAB，∠ADC+∠DAB=180°，∴∠DAB=60°，∴∠DAO=30°，∠AOD=90°，'设OD=a，则AD=2a，OA=a，∴AC=2OA=2a，∴AC：AD=2a：2a=：1，故选D．5．如图，△ABC周长为1，连接△ABC三边中点构成第二个三角形，再连接第二个三角形三边中点构成第三个三角形，以此类推，第2016个三角形的周长为（）A．22016B．22017 C．D．【解答】解：根据三角形中位线定理可得第二个三角形的各边长都等于最大三角形各边的一半，那么第二个三角形的周长=△ABC的周长1×=，第三个三角形的周长为=△ABC的周长×=（）2，第2016个三角形的周长═（）2015．故选D．6．在Rt△ABC中，∠C=90°，AB=16cm，点D为AB的中点，则CD的长为（）A．2cm B．4cm C．6cm D．8cm【解答】解：∵∠C=90°，点D为AB的中点，∴CD=AB=8cm，故选：D．7．如图，平行四边形ABCD中，AB=6cm，AD=10cm，点P在AD 边上以每秒1cm 的速度从点A向点D运动，点Q在BC边上，以每秒4cm的速度从点C出发，在CB间往返运动，两个点同时出发，当点P到达点D时停止（同时点Q也停止），在运动以后，以P、D、Q、B四点组成平行四边形的次数有（）A．1 次B．2次 C．3次 D．4次【解答】解：∵四边形ABCD为平行四边形，∴PD∥BQ．若要以P、D、Q、B四点组成的四边形为平行四边形，则AP=BQ．设运动时间为t．当0＜t＜时，AP=t，PD=10﹣t，CQ=4t，BQ=10﹣4t，∴10﹣t=10﹣4t，方程无解；当＜t＜5时，AP=t，PD=10﹣t，BQ=4t﹣10，∴10﹣t=4t﹣10，解得：t=4；当5＜t＜时，AP=t，PD=10﹣t，CQ=4t﹣20，BQ=30﹣4t，∴10﹣t=30﹣4t，解得：t=；当＜t＜10时，AP=t，PD=10﹣t，BQ=4t﹣30，∴10﹣t=4t﹣30，解得：t=8．综上所述：当运动时间为4秒、秒或8秒时，以P、D、Q、B四点组成的四边形为平行四边形．故选C．8．如图，一根木棍斜靠在与地面（OM）垂直的墙（ON）上，设木棍中点为P，若木棍A端沿墙下滑，且B沿地面向右滑行．在此滑动过程中，点P到点O的距离（）A．变小B．不变C．变大D．无法判断【解答】解：在木棍滑动的过程中，点P到点O的距离不发生变化，理由是：连接OP，∵∠AOB=90°，P为AB中点，AB=2a，∴OP=AB=a，即在木棍滑动的过程中，点P到点O的距离不发生变化，永远是a；故选B．9．如图，△ABC中，CD⊥AB于D，且E是AC的中点．若AD=6，DE=5，则CD 的长等于（）A．5 B．6 C．7 D．8【解答】解：∵△ABC中，CD⊥AB于D，∴∠ADC=90°．∵E是AC的中点，DE=5，∴AC=2DE=10．∵AD=6，∴CD===8．故选D．10．平面直角坐标系中，四边形ABCD的顶点坐标分别是A（﹣3，0），B（0，2），C（3，0），D（0，﹣2），则四边形ABCD是（）A．矩形B．菱形C．正方形D．平行四边形【解答】解：如图所示：∵A（﹣3，0）、B（0，2）、C（3，0）、D（0，﹣2），∴OA=0C，OB=OD，∴四边形ABCD为平行四边形，∵BD⊥AC，∴四边形ABCD为菱形，故选：B二．填空题（共5小题）11．如图，△ABC中，AD是中线，AE是角平分线，CF⊥AE于F，AB=10，AC=6，则DF的长为2．【解答】解：延长CF交AB于点G，∵AE平分∠BAC，∴∠GAF=∠CAF，∵AF垂直CG，∴∠AFG=∠AFC，在△AFG和△AFC中，，∴△AFG≌△AFC（ASA），∴AC=AG，GF=CF，又∵点D是BC中点，∴DF是△CBG的中位线，∴DF=BG=（AB﹣AG）=（AB﹣AC）=2．故答案为：2．12．已知平行四边形ABCD的周长为44，过点A作AE⊥直线BC于E，作AF⊥直线CD于点F，若AE=5，AF=6，则CE+CF的值为2+或22+11．．【解答】解：①如图1中，当∠BAD是钝角时，设AB=a，BC=b，∵四边形ABCD是平行四边形，∴AB=CD=a，•BC•AE=•CD•AF，∴6a=5b ①∵a+b=22 ②由①②解得a=10，b=12，在Rt△ABE中，∵∠AEB=90°，AB=10，AE=5，∴BE===5，∴EC=12﹣5，在Rt△ADF中，∵∠AFD=90°．AD=12，AF=6．∴DF===6，∵6＞10，∴CF=DF﹣CD=6﹣10，∴CE+CF=EC+CF=2+．②如图2中，当∠BAD是锐角时，由①可知：DF=6，BE=5，∴CF=10+6，CE=12+5，∴CE+CF=22+11．故答案为：2+或22+11．13．用20cm长的铁丝围成一个平行四边形，使长边比短边长2cm，则它的长边长为6cm，短边长为4cm．【解答】解：设平行四边形的两边分别为xcm，（x﹣2）cm，由题意2[x+（x﹣2）]=20，解得x=6，∴平行四边形的两边分别为6cm，4cm，故答案为6cm，4cm．14．在直角三角形中，斜边上的中线为3，那么斜边长为6．【解答】解：∵直角三角形斜边上的中线长为3，∴斜边长是6．故答案为：6．15．如图，在Rt△ABC中，CD是斜边AB上的中线，若AB=2，则CD=1．【解答】解：在Rt△ABC中，∵CD是斜边AB上的中线，AB=2，∴CD=AB=1，故答案为1．三．解答题（共7小题）16．已知：如图，∠ABC=∠ADC=90°，E、F分别是AC、BD的中点．求证：EF⊥BD．【解答】证明：如图，连接BE、DE，∵∠ABC=∠ADC=90°，E是AC的中点，∴BE=DE=AC，∵F是BD的中点，∴EF⊥BD．17．在△ABC中，AD=BF，点D，E，F分别是AC，BC，BA延长线上的点，四边形ADEF为平行四边形．求证：AB=AC．【解答】证明：∵四边形ADEF是平行四边形，∴AD=EF AD∥EF，∴∠2=∠3，又∵AD=BF，∴BF=EF，∴∠1=∠3，∴∠1=∠2，∴AB=AC．18．已知：如图，A，B，C，D在同一直线上，且AB=CD，AE=DF，AE∥DF．求证：四边形EBFC是平行四边形．【解答】证明：连接AF，ED，EF，EF交AD于O．∵AE=DF，AE∥DF．∴四边形AEDF为平行四边形，∴EO=FO，AO=DO，又∵AB=CD，∴AO﹣AB=DO﹣CD，∴BO=CO，又∵EO=FO，∴四边形EBFC是平行四边形．19．如图，在Rt△ABC中，∠ACB=90°，点E，F分别是边AC，AB的中点，延长BC到点D，使2CD=BC，连接DE．（1）如果AB=10，求DE的长；（2）延长DE交AF于点M，求证：点M是AF的中点．【解答】解：（1）连接CF，在Rt△ABC中，F是AB的中点，∴CF=AB=5，∵点E，F分别是边AC，AB的中点，∴EF∥BC，EF=BC，∵2CD=BC，∴EF=CD，EF∥CD，∴四边形EDCF是平行四边形，∴DE=CF=5；（2）如图2，∵四边形EDCF是平行四边形，∴CF∥DM，∵点E是边AC的中点，∴点M是AF的中点．20．△ABC的中线BD、CE相交于O，F，G分别是BO、CO的中点，求证：EF∥DG，且EF=DG．【解答】证明：连接DE，FG，∵BD、CE是△ABC的中线，∴D，E是AB，AC边中点，∴DE∥BC，DE=BC，同理：FG∥BC，FG=BC，∴DE∥FG，DE=FG，∴四边形DEFG是平行四边形，∴EF∥DG，EF=DG．21．如图，∠ACB=∠ADB=90°，M、N分别为AB、CD的中点．求证：MN⊥CD．【解答】证明：如图，连接CM、DM，∵∠ACB=∠ADB=90°，M为AB的中点，∴CM=AB，DM=AB，∴CM=DM=AB，∵N为CD的中点，∴MN⊥CD．22．如图，AD是△ABC的中线，AE∥BC，BE交AD于点F，交AC于G，F是AD 的中点．（1）求证：四边形ADCE是为平行四边形；（2）若EB是∠AEC的角平分线，请写出图中所有与AE相等的边．【解答】（1）证明：∵AD是△ABC的中线，∴BD=CD，∵AE∥BC，∴∠AEF=∠DBF，在△AFE和△DFB中，，∴△AFE≌△DFB（AAS），∴AE=BD，∴AE=CD，∵AE∥BC，∴四边形ADCE是平行四边形；（2）图中所有与AE相等的边有：AF、DF、BD、DC．理由：∵四边形ADCE是平行四边形，∴AE=DC，AD∥EC，∵BD=DC，∴AE=BD，∵BE平分∠AEC，∴∠AEF=∠CEF=∠AFE，∴AE=AF，∵△AFE≌△DFB，∴AF=DF，∴AE=AF=DF=CD=BD．。

初中数学人教版八年级下学期第十八章测试卷一、单选题（共6题；共12分）1. ( 2分) 在四边形ABCD中，∠A:∠B:∠C:∠D的比例依次如下,其中能使四边形ABCD是平行四边形的是( )A. 1:2:3:4B. 2:2:3:3C. 2:3:3:2D. 2:3:2:32. ( 2分) 如图,已知△ABC与△CDA关于点O成中心对称,过点O任作直线EF分别交AD,BC于点E,F,则下则结论:①点E和点F,点B和点D是关于中心O的对称点;②直线BD必经过点O;③四边形ABCD是中心对称图形;④四边形DEOC与四边形BFOA的面积必相等;⑤△AOE与△COF成中心对称.其中正确的个数为（）A. 2B. 3C. 4D. 53. ( 2分) 如图，在等腰梯形ABCD中，AD∥BC，AD=5，AB=6，BC=8，且AB∥DE，则△DEC的周长是（）.A. 3B. 12C. 15D. 194. ( 2分) 如图,矩形A BCD的对角线AC,BD相交于点O,CE//BD,DE//AC.若AC=4,则四边形CODE的周长是( ).A. 4B. 6C. 8D. 105. ( 2分) 如图，菱形ABCD中，边CD的中垂线交对角线BD于点E，交CD于点F，连结AE.若∠ABC＝50°，则∠AEB的度数为（）A. 30°B. 40°C. 50°D. 60°6. ( 2分) 已知平行四边形ABCD中，对角线AC、BD相交于O.则下列说法准确的是（）A. 当OA=OC时，平行四边形ABCD为矩形B. 当AB=AD时，平行四边形ABCD为正方形C. 当∠ABC=90°时，平行四边形ABCD为菱形D. 当AC⊥BD时，平行四边形ABCD为菱形二、填空题（共2题；共2分）7. ( 1分) 在四边形ABCD中，对角线AC,BD相交于点O,若OA=OC,要使四边形ABCD成为平行四边形，则可添加的条件为________(填一个即可)8. ( 1分) 如图,菱形中，对角线AC,BD交于点O,E为AD边中点，菱形ABCD的周长为28,则OE的长等于________.三、解答题（共1题；共5分）9. ( 5分) 如图,D,E分别是△A BC的边AB,AC的中点,点O是OA BC内部任意一点，连接OB,0C，点G,F分别是OB ,OC的中点，顺次连接点D,G,F,E.求证:四边形DGFE是平行四边形.四、综合题（共3题；共26分）10. ( 6分) 如图，在菱形ABCD中，对角线AC，BD交于点O，过点A作AE⊥BC于点E，延长BC至F，使CF＝BE，连接DF．（1）求证：四边形AEFD是矩形；（2）若AC＝10，∠ABC＝60°，则矩形AEFD的面积是________．11. ( 10分) 如图，在正方形ABCD中，点E是BC的中点，连接DE，过点A作AG⊥ED交DE于点F，交CD于点G．（1）证明：△ADG≌△DCE；（2）连接BF，证明：AB＝FB．12. ( 10分) 如图，AC是矩形ABCD的对角线，过AC的中点O作EF⊥AC，交BC于点E，交AD于点F，连接AE，CF.（1）求证：四边形AECF是菱形；（2）若AB=2，BC=4，求四边形AECF的面积.答案解析部分一、单选题1.【答案】D【考点】平行四边形的判定【解析】【解答】A、由∠A:∠B:∠C:∠D=1:2:3:4，没有角相等，不能判定四边形是平行四边形，故A 错误；B、由∠A:∠B:∠C:∠D=2:2:3:3，没有角相等，不能判定四边形是平行四边形，故A错误；C、、由∠A:∠B:∠C:∠D=2:2:3:3，虽然有两组角相等，但它们是邻角，不能判定四边形是平行四边形，故C错误；D、、由∠A:∠B:∠C:∠D=2:3:2:3，两组对角分别相等，能判定四边形是平行四边形，故D正确.故选D.【分析】两组对角分别相等的四边形是平行四边形，据此逐一判断即可.2.【答案】D【考点】平行四边形的判定与性质【解析】【解答】△ABC与△CDA关于点O对称，则AB=CD、AD=BC，所以四边形ABCD是平行四边形，因此点O就是▱ABCD的对称中心，则有：（1）点E和点F；B和D是关于中心O的对称点，符合题意；（2）直线BD必经过点O，符合题意；（3）四边形ABCD是中心对称图形，符合题意；（4）四边形DEOC 与四边形BFOA的面积必相等，符合题意；（5）△AOE与△COF成中心对称，符合题意；其中正确的个数为5个，故答案为：D．【分析】由于△ABC与△CDA关于点O对称，那么可得到AB=CD、AD=BC，即四边形ABCD是平行四边形，由于平行四边形是中心对称图形，且对称中心是对角线交点，可根据上述特点对各结论进行判断．3.【答案】C【考点】平行四边形的判定与性质【解析】【解答】∵AD∥BC，AB∥DE，∴ABED是平行四边形，∴DE=CD=AB=6，EB=AD=5，∴EC=8-5=3，则△DEC的周长=DE+DC+EC=6+6+3=15.故答案为：C【分析】根据两组对边分别平行可证四边形ABED是平行四边形，从而可得DE=CD=AB=6，EB=AD=5，继而求出CE的长，利用△DEC的周长=DE+DC+EC计算即可.4.【答案】C【考点】菱形的判定与性质，矩形的性质【解析】【解答】解：∵CE//BD,DE//AC，∴四边形CODE是平行四边形，在矩形A BCD中，AC =4,∴OD=OC=12AC=2，∴四边形CODE是菱形，∴四边形CODE的周长：4OC=8.故选:C.【分析】利用两组对边分别平行可证四边形CODE是平行四边形，根据矩形的性质可得OC=OD=12AC=2，利用一组邻边相等的平行四边形可证四边形CODE是菱形，利用菱形的性质即可求出结论.5.【答案】C【考点】菱形的性质【解析】【解答】如图，连接CE.∵四边形ABCD是菱形，∴AB＝BC，∠ABD＝∠DBC＝12∠ABC＝25 °，AB∥CD，∴∠BDC＝∠ABD＝25 °，∵点E在线段CD的中垂线上，∴EC＝ED，∴∠ECD＝∠EDC＝25 °，∴∠BEC＝∠ECD+∠EDC＝50°.在△ABE与△CBE中，{AB=CB∠ABE=∠CBEBE=BE，∴△ABE≌△CBE（SAS），∴∠AEB＝∠CEB =50 °.故答案为：C.【分析】连接CE.根据菱形的性质以及平行线的性质可得AB＝BC，∠ABD＝∠DBC，∠BDC＝∠ABD＝25 °，利用线段中垂线的性质得出EC＝ED，那么∠ECD＝∠EDC＝25 °，点F垂直平分DC∠BEC＝∠ECD ＋∠EDC＝50 °.利用SAS证明△ABE≌△CBE，即可得出∠AEB＝∠CEB＝50 °.6.【答案】D【考点】菱形的判定，矩形的判定，正方形的判定【解析】【解答】∵平行四边形对角线互相平分，∴OA=OC而对角线相等的平行四边形是矩形，∴OA=OC不能判定平行四边形ABCD为矩形，故A错误；∵邻边相等的平行四边形是菱形，∴当AB=AD时，平行四边形ABCD是菱形，故B错误；∵有一个角是直角的平行四边形是矩形∴当∠ABC=90°时，平行四边形ABCD为矩形，故C错误；∵对角线互相垂直的平行四边形是菱形∴当AC⊥BD时，平行四边形ABCD为菱形，故D正确.故答案为：D.【分析】A. 根据平行四边形的性质和对角线相等的平行四边形是矩形进行判断；B. 根据邻边相等的平行四边形是菱形进行判断；C. 根据有一个角是直角的平行四边形是矩形进行判断；D. 根据对角线互相垂直的平行四边形是菱形进行判断.二、填空题7.【答案】答案不唯一如：OB=OD等【考点】平行四边形的判定【解析】【解答】解：条件：OB=OD.∵OA=OC，OB=OD，∴四边形ABCD是平行四边形.故答案为：OB=OD.【分析】根据对角线互相平分的四边形是平行四边形进行解答即可.8.【答案】3.5【考点】直角三角形斜边上的中线，菱形的性质【解析】【解答】∵四边形ABCD是菱形，∴AC⊥BD，AD=1×28=7，4∵E为AD的中点，∴OE=1AD=3.5.2故答案为：3.5.【分析】由于菱形的四边相等，对角线互相垂直，可得AD的长，AC⊥BD，结合E是AD的中点，则由直角三角形斜边的中线等于斜边的一半可知OE的长.三、解答题9.【答案】解：证明：如图，连接OA，∵D、E分别是AB和AC的中点，∴DE∥BC，DE=1BC，2BC，同理GF∥BC，GH=12∴DE∥GF，DE=GF，∴四边形DGFE是平行四边形.【考点】三角形中位线定理，平行四边形的判定【解析】【分析】由三角形的中位线定理可得DE平行等于BC的一半，GF平行等于BC的一半，因此可得DE和GH平行且相等，则四边形DGFE是平行四边形.四、综合题10.【答案】（1）证明：∵四边形ABCD是菱形，∴AD∥BC，AD＝BC，∵CF＝BE，∴BC＝EF，∴AD∥EF，AD＝EF，∴四边形AEFD是平行四边形，∵AE⊥BC，∴∠AEF＝90°，∴平行四边形AEFD是矩形（2）50√3【考点】菱形的性质，矩形的判定与性质【解析】【解答】（2）∵AB＝CD，BE＝CF，∠AEB＝∠DFC＝90°，∴Rt△ABE≌Rt△DCF （HL），∴矩形AEFD的面积＝菱形ABCD的面积，∵∠ABC＝60°，∴△ABC是等边三角形，∵AC＝10，∴AO＝1AC＝5，AB＝10，BO＝5 √3，2∴矩形AEFD的面积＝菱形ABCD的面积＝1×10×10 √3＝50 √3，2故答案为：50 √3．【分析】（1）根据菱形的性质得到AD∥BC且AD＝BC，等量代换得到BC＝EF，推出四边形AEFD是平行四边形，根据矩形的判定定理即可得到结论；（2）根据全等三角形的判定定理得到Rt△ABE≌Rt△DCF （HL），求得矩形AEFD的面积＝菱形ABCD的面积，根据等腰三角形的性质得到结论．11.【答案】（1）证明：∵四边形ABCD是正方形，∴∠ADG＝∠C＝90°，AD＝DC，又∵AG⊥DE，∴∠DAG+∠ADF＝90°＝∠CDE+∠ADF，∴∠DAG＝∠CDE，∴△ADG≌△DCE（ASA）；（2）解：如图所示，延长DE交AB的延长线于H，∵E是BC的中点，∴BE＝CE，又∵∠C＝∠HBE＝90°，∠DEC＝∠HEB，∴△DCE≌△HBE（ASA），∴BH＝DC＝AB，即B是AH的中点，又∵∠AFH＝90°，∴Rt△AFH中，BF＝1AH＝AB．2【考点】正方形的性质【解析】【分析】（1）利用正方形的性质可得∠ADG＝∠C＝90°，AD＝DC，再利用AG⊥DE得DAG+∠ADF 90°＝∠CDE+∠ADF，则有∠DAG＝∠CDE，从而可证△ADG≌△DCE；（2）延长DE交AB的延长线于H，易得△DCE≌△HBE，利用全等三角形的对应边相等可得DH＝DC＝AB，然后利用直角三角形斜边上的中线等于是斜边的一半证得BF＝1AH＝AB，故得证。

第十八章平行四边形单元测试卷题号一二三总分得分一、选择题(每题3分,共30分)1.直角三角形中,两直角边长分别是12和5,则斜边上的中线长是( )A.34B.26C.8.5D.6.52.如图,矩形ABCD的两条对角线相交于点O,∠AOD=60°,AD=4,则AC 的长是( )A.4B.8C.4错误!未找到引用源。

D.8错误!未找到引用源。

3.一个菱形的周长为8 cm,高为1 cm,这个菱形相邻两角的度数之比为( )A.3∶1B.4∶1C.5∶1D.6∶14.下列命题错误．．的是( )A.对角线互相垂直平分的四边形是菱形B.平行四边形的对角线互相平分C.矩形的对角线相等D.对角线相等的四边形是矩形5.若顺次连接四边形ABCD四边的中点,得到的图形是一个矩形,则四边形ABCD一定是( )A.矩形B.菱形C.对角线相等的四边形D.对角线互相垂直的四边形6.如图,在矩形ABCD中,对角线AC,BD相交于点O,过O的直线EF分别交AB,CD于点E,F,若图中阴影部分的面积为6,则矩形ABCD的面积为( )A.12B.18C.24D.307.平行四边形ABCD的对角线交于点O,有五个条件:①AC=BD,②∠ABC=90°,③AB=AC,④AB=BC,⑤AC⊥BD,则下列哪个组合可判定这个四边形是正方形( )A.①②B.①③C.①④D.④⑤8.如图,已知E是菱形ABCD的边BC上一点,且∠DAE=∠B=80°,那么∠CDE的度数为( )A.20°B.25°C.30°D.35°9.如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BA E=22.5°,EF⊥AB,垂足为F,则EF的长为( )A.1B.错误!未找到引用源。

C.4-2 错误!未找到引用源。

D.3 错误!未找到引用源。

-410.如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上的M点处,延长BC,EF交于点N.有下列四个结论:①DF=CF;②BF⊥EN;③△BEN是等边三角形;④S.其中,将正确结论的序号全部选对的是( )△BEF=3S△DEFA.①②③B.①②④C.②③④D.①②③④二、填空题(每题3分,共30分)11.如图,在平行四边形ABCD中,点E,F分别在边BC,AD上,请添加一个条件__________,使四边形AECF是平行四边形(只填一个即可).12.如图,在周长为20的平行四边形ABCD中,AB<AD,AC与BD交于点O,OE⊥BD,交AD于点E,则△ABE的周长为__________.13.如图,已知AB=BC=CD=AD,∠DAC=30°,那么∠B=__________.14.如图,在矩形ABCD中,对角线AC,BD相交于O,DE⊥AC于E,∠EDC∶∠EDA=1∶2,且AC=10,则EC的长度是__________.15.如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E,F,G,H分别为AD,AB,BC,CD的中点.若AC=8,BD=6,则四边形EFGH的面积为__________.16.如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB的中点)所在的直线上的点C'处,得到经过点D的折痕DE.则∠DEC的大小为__________.17.正方形ABCD的边长是4,点P是AD边的中点,点E是正方形边上的一点,若△PBE是等腰三角形,则腰长为__________.18.已知:如图,正方形ABCD中,对角线AC和BD相交于点O.E,F分别是边AD,DC上的点,若AE=4 cm,CF=3 cm,且OE⊥OF,则EF的长为____cm.19.菱形ABCD在直角坐标系中的位置如图所示,其中点A的坐标为(1,0),点B的坐标为(0,错误!未找到引用源。

人教版八年级数学第十八章测试卷试.一. 单选题（共10题；共18分）1 •如图•在学习〃四边形〃一章时，小明的书上有一图因不小心被滴上墨水，看不淸所印的字，请问被墨迹 遮盖了的文字应是（）2•如图，RtA ABC 中，ZC 二90°, AC 二& AB=10, D 、E 分别为 AC 、AB 中点，连接 DE,则 DE 长为（）3•已知四边形ABCD 是平行四边形，下列结论中错误的是（）A.当AB= 它是菱形B.当丄3D 时，它是菱形C.当Z ABC = 90°时，它是矩形D.当= 时，它是正方形 4•如图，平行四边形ABCD 的对角线交于点E,已知AB=5cm. △ ABE 的周长比△ BEC 的周长小3cm,则AD 5•如图，在四边形PBCD 中，E 是3C 边的中点，连接DE 并延长，交.3的延长线于点F ，AB=BF •添加一个条件使四边形是平行四边形，你认为下面四个条件中可选择的是（）6•如图，正方形ABCD 的面积为&菱形AECF 的而积为4,则EF 的长是（）B.梯形C.矩形D.菱形B.3C.8D. 5C. 3cmD. 2cmA ・AD = ECB ・CD = BF C. ZZC D. ZF=厶 CDFA.四边形 A.4 的长度为（）B. 5cm(01/1A. 4B./5C. 2D. 17. 以下四个条件中可以判泄四边形是平行四边形的有（）① 两组对边分别平行：② 两组对边分別相等；③ 有一组对边平行且相等；④ 对角线相等.A.1个B.2个C.3个D.4个8. 如图，E 、F 分别是正方形ABCD 的边CD 、AD 上的点，且CE=DF, AE 、BF 相交于点0,下列结论①AE=BF ； ②AE 丄BF ：③A0=0E ；④= S 四边形DE0F 中，错误的有（）9•如图，两张等宽的纸条交叉重叠在一起，重叠的部分为四边形ABCD,若测得A, C 之间的距离为12cm, 点B. D 之间的距离为16m,则线段AB 的长为（）10•如图，将矩形ABCD 沿对角线AC 剪开，再把AACD 沿CA 方向平移得到△AGS ,连结AD 】,BQ •若 Z ACB = 30\ AB = 1, CCi=x, A ACD 与△ A/iD 】重叠部分的而积为s,则下列结论：①△ A 】AD 岸△ CC 】B ： ②当x = 2时，四边形ABCxDx 是菱形：③当x=2时，△ BDD 】为等边三角形：@s = <x<2）。