吉林省白城市第一中学2017_2018学年高一数学下学期期末考试试题20-含答案

白城一中2017-2018学年下学期期末考试高一英语试卷第Ⅰ卷（选择题共90分）第一部分：听力(共两节，满分30分)第一节（共5小题；每小题1.5分，满分7.5分）听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1. When does the rainy season start?A. In JanuaryB. In February.C. In November2. what's wrong with the man's food?A. it's hotB. it's salty.C. it's tasteless3. What is Jennifer learning in school now?A. To make sculptures.B. To take picturesC. To draw.4. Which room has the man finished decorating?A. The living roomB. The bathroomC. The kitchen.5. Where are the speakers？A. At a hospitalB. In a classroomC. At a ball field第二节（共15小题；每小题1.5分，满分22.5分）听下面5段对话或独白。

每段对话或独白后有几个小题，从题中所给的A、B、C三个选项中选出最佳选项并标在试卷的相应位置。

听每段对话或独白前，你将有时间阅读各个小题，每小题5秒钟；听完后，各小题将给出5秒钟的作答时间。

每段对话或独白读两遍。

听第6段材料，回答第6至7题。

6. Where does Sam suggest going？A. To a theater.B. To a restaurant.C. To a coffee shop.7. How does Rita feel about the plan?A. Excited.B. Indifferent.C. Disappointed听第7段材料，回答第8-9题。

白城一中2017-2018学年度下学期期末考试高一生物试题本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟。

第Ⅰ卷选择题(共60分)一、选择题（本题包括40小题，每小题1.5分。

每小题只有一个选项符合题意）1．在孟德尔的豌豆杂交实验中，叙述错误的是A. 豌豆是自花传粉、闭花受粉植物，所以自然状态下一般都是纯种B. 豌豆种皮的黄色和子叶的绿色是一对相对性状C. F2的3:1性状分离比一定依赖于雌雄配子的随机结合D. 孟德尔在研究杂交实验时需要考虑雌蕊和雄蕊的发育程度2. 基因分离定律的实质是A．性染色体分离B．同源染色体上等位基因分离C．性状分离D．一条染色体上染色单体分离3.对于进行有性生殖的生物体来说，维持每种生物前后代体细胞中染色体数目恒定的生理作用是A. 有丝分裂和无丝分裂B. 减数分裂和受精作用C. 无丝分裂和减数分裂D. 细胞分裂和细胞分化4. 猪的卵原细胞中含有20对同源染色体，它产生的卵细胞中染色体有A. 10条B. 20条C. 40条D. 60条5.下列有关DNA与RNA的叙述,正确的是A. 禽流感病毒同时含有DNA和RNAB. DNA和RNA都是松鼠的遗传物质C. 乳酸菌中既有DNA，也有RNAD. DNA中有氢健，RNA没有6.用秋水仙素诱发基因突变和诱导多倍体，起作用的时间分别是A．有丝分裂的间期和中期 B．有丝分裂的间期和分裂期C．有丝分裂的前期和前期 D．有丝分裂的间期和间期7.从理论上分析，下列叙述中不正确的是A．二倍体×四倍体→三倍体 B．二倍体×二倍体→二倍体C．三倍体×三倍体→三倍体 D．二倍体×六倍体→四倍体8．要把两个不同物种的优良性状集中在一起，应采用的育种方法是A. 杂交育种B. 单倍体育种C. 诱变育种D. 基因工程育种9．下列关于育种的叙述中，正确的是A．用物理因素诱变处理可提高突变率B．诱变育种和杂交育种均可产生新的基因C．三倍体植物不能由受精卵发育而来D．用花药作材料培育出的植株均是单倍体10．下列有关人体细胞分裂的叙述，正确的是A. 减数分裂与有丝分裂相比基因突变和基因重组的概率增加B. 减数分裂的各个时期发生基因突变的概率相同C. 减数第二次分裂细胞中无同源染色体，染色体数都为23个D. 减数第一次分裂后期与减数第二次分裂后期细胞中都有两个染色体组11．通过分析，发现甲、乙两个生物细胞中DNA碱基总量完全相同，且4种碱基的量也分别相同。

2017-2018学年吉林省白城一中高一（下）期末数学试卷一、选择题：（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的，将正确答案的选项填涂在答题卡上）1．（5分）过点（1，0）且与直线x﹣2y﹣2＝0平行的直线方程是（）A．x﹣2y﹣1＝0B．x﹣2y+1＝0C．2x+y﹣2＝0D．x+2y﹣1＝0 2．（5分）在△ABC中，a、b、c分别是∠A、∠B、∠C的对边，且，则∠A等于（）A．60°B．30°C．120°D．150°3．（5分）已知某个几何体的三视图如图，根据图中标出的尺寸（单位：cm），可得这个几何体的体积是（）A．B．C．2000cm3D．4000cm34．（5分）直线x cosα+y+b＝0的倾斜角的取值范围是（）A．[0，π）B．C．D．5．（5分）空间四边形SABC中，SB⊥AC，SB＝AC＝2，E、F分别是SC、AB的中点，那么EF＝（）A．1B．C．D．6．（5分）下列结论正确的是（）A．当x＞0且x≠1时，lgx+≥2B．当x＞0时，+≥2C．当x≥2时，x+的最小值为2D．当0＜x≤2时，x﹣无最大值7．（5分）已知m、n是不同的直线，α、β是不重合的平面，则下列命题正确的是（）A．若α∥β，m⊂α，n⊂β，则m∥nB．若m⊂α，n⊂α，m∥β，n∥β，则α∥βC．若a⊂α，b⊂β，a∥b，则α∥βD．m、n是两异面直线，若m∥α，m∥β，且n∥α，n∥β，则α∥β8．（5分）设△ABC的三个内角A，B，C成等差数列，其外接圆半径为1，且有sin A﹣sin C+cos（A﹣C）＝，则此三角形的面积为（）A．B．C．或D．或9．（5分）在圆x2+y2＝5x内，过点（，）有n条弦的长度成等差数列，最小弦长为数列的首项a1，最大弦长为a n，若公差d∈[，]，那么n的取值集合为（）A．{4，5，6，7}B．{4，5，6}C．{3，4，5，6}D．{3，4，5} 10．（5分）已知数列{a n}的前n项之和S n＝n2﹣4n+1，则|a1|+|a2|+…+|a10|的值为（）A．61B．65C．67D．6811．（5分）已知数列{a n}满足a1＝0，a n+1＝（n＝1，2，3，…），则a2008等于（）A．0B．C．D．12．（5分）若直线y＝x+b与曲线有公共点，则b的取值范围是（）A．B．C．D．二、填空题：本大题共4小题，每小题5分，共20分.将正确答案写在答题卡的相应位置上. 13．（5分）已知△ABC中，c＝，a＝1，a cos B＝b cos A，则△ABC面积为14．（5分）点M（x，y）是不等式组表示的平面区域Ω内的一动点，且不等式2x﹣y+m≥0总成立，则m的取值范围是．15．（5分）长方体共顶点的三个侧面积分别为、、，则它的外接球表面积为．16．（5分）已知（x0，y0）是x+y＝2k﹣1与圆x2+y2＝k2+2k﹣3的公共点，则当k＝时，x0y0最小．三、解答题：（本大题共6小题，共70分.解答应写出文字说明，证明过程或演算步骤，解答过程书写在答题纸的相应位置.）17．（10分）已知两条直线l1：x+my+6＝0，l2：（m﹣2）x+3y+2m＝0m为何值时，l1与l2①相交；②平行；③垂直．18．（12分）在△ABC中，a，b，c分别是∠A、∠B、∠C的对边，且b sin A＝cos B．（1）求∠B的大小；（2）若b＝3，sin C＝2sin A，求a及c．19．（12分）已知数列{log2（a n﹣1）}（n∈N*）为等差数列，且a1＝3，a3＝9．（Ⅰ）求数列{a n}的通项公式；（Ⅱ）证明++…+＜1．20．（12分）如图，在棱长为1的正方体ABCD﹣A1B1C1D1中，E是BC的中点，平面B1ED 交A1D1于F（1）指出F在A1D1上的位置，并证明．（2）求直线A1C与B1F所成角的余弦值．21．（12分）已知数列{a n}的前n项和为S n，且S n＝n﹣5a n﹣85，n∈N*（1）证明：{a n﹣1}是等比数列；（2）求数列{S n}的通项公式．请指出n为何值时，S n取得最小值，并说明理由（参考数据15＝﹣14.85）22．（12分）已知圆C：x2+（y﹣3）2＝4，一动直线l过A（﹣1，0）与圆C相交于P、Q 两点，M是PQ中点，l与直线m：x+3y+6＝0相交于N．（Ⅰ）求证：当l与m垂直时，l必过圆心C；（Ⅱ）当时，求直线l的方程；（Ⅲ）探索是否与直线l的倾斜角有关，若无关，请求出其值；若有关，请说明理由．2017-2018学年吉林省白城一中高一（下）期末数学试卷参考答案与试题解析一、选择题：（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的，将正确答案的选项填涂在答题卡上）1．（5分）过点（1，0）且与直线x﹣2y﹣2＝0平行的直线方程是（）A．x﹣2y﹣1＝0B．x﹣2y+1＝0C．2x+y﹣2＝0D．x+2y﹣1＝0【考点】I8：两条直线平行与倾斜角、斜率的关系；IG：直线的一般式方程与直线的性质．【解答】解：设直线方程为x﹣2y+c＝0，又经过（1，0），∴1﹣0+c＝0故c＝﹣1，∴所求方程为x﹣2y﹣1＝0；故选：A．2．（5分）在△ABC中，a、b、c分别是∠A、∠B、∠C的对边，且，则∠A等于（）A．60°B．30°C．120°D．150°【考点】HR：余弦定理．【解答】解：根据，可得．由余弦定理可得b2+c2﹣a2＝2bc•cos A，∴cos A＝，故三角形的内角A＝150°，故选：D．3．（5分）已知某个几何体的三视图如图，根据图中标出的尺寸（单位：cm），可得这个几何体的体积是（）A．B．C．2000cm3D．4000cm3【考点】L!：由三视图求面积、体积．【解答】解：如图，几何体是四棱锥，一个侧面PBC⊥底面ABCD，底面ABCD是正方形，．故选：B．4．（5分）直线x cosα+y+b＝0的倾斜角的取值范围是（）A．[0，π）B．C．D．【考点】I2：直线的倾斜角．【解答】解：由题意，直线方程可化为：y＝﹣x cosα﹣b∴直线的斜率为﹣cosα∴cosα∈[﹣1，1]设直线x cosα+y+b＝0的倾斜角为β∴tanβ∈[﹣1，1]∴β∈故选：D．5．（5分）空间四边形SABC中，SB⊥AC，SB＝AC＝2，E、F分别是SC、AB的中点，那么EF＝（）A．1B．C．D．【考点】MK：点、线、面间的距离计算．【解答】解：取SA中点G，连结EG、FG、EF，∵SB⊥AC，SB＝AC＝2，E、F分别是SC、AB的中点，∴EG∥AC，且GE＝AC＝1，GF∥SB，且GF＝SB＝1，∴∠EGF＝90°，∴EF＝＝．故选：B．6．（5分）下列结论正确的是（）A．当x＞0且x≠1时，lgx+≥2B．当x＞0时，+≥2C．当x≥2时，x+的最小值为2D．当0＜x≤2时，x﹣无最大值【考点】7F：基本不等式及其应用．【解答】解：A中，当0＜x＜1时，lgx＜0，lgx+≥2不成立；由基本不等式B正确；C中“＝”取不到；D中x﹣在0＜x≤2时单调递增，当x＝2时取最大值．故选：B．7．（5分）已知m、n是不同的直线，α、β是不重合的平面，则下列命题正确的是（）A．若α∥β，m⊂α，n⊂β，则m∥nB．若m⊂α，n⊂α，m∥β，n∥β，则α∥βC．若a⊂α，b⊂β，a∥b，则α∥βD．m、n是两异面直线，若m∥α，m∥β，且n∥α，n∥β，则α∥β【考点】LP：空间中直线与平面之间的位置关系；LQ：平面与平面之间的位置关系．【解答】解：由m、n是不同的直线，α、β是不重合的平面，知：在A中，若α∥β，m⊂α，n⊂β，则m与n平行或异面，故A错误；在B中，若m⊂α，n⊂α，m∥β，n∥β，则α与β平行或相交，故B错误；在C中，若a⊂α，b⊂β，a∥b，则α与β平行或相交，故C错误；在D中，m、n是两异面直线，若m∥α，m∥β，且n∥α，n∥β，则由面面平行的判定定理得α∥β，故D正确．故选：D．8．（5分）设△ABC的三个内角A，B，C成等差数列，其外接圆半径为1，且有sin A﹣sin C+cos（A﹣C）＝，则此三角形的面积为（）A．B．C．或D．或【考点】GP：两角和与差的三角函数．【解答】解：△ABC的三个内角A，B，C成等差数列，则：A+C＝2B，解得：B＝，故A+C＝，所以：C＝，其外接圆半径为1，且有sin A﹣sin C+cos（A﹣C）＝，所以＝，整理得：，则：或，解得：，①当时，＝．②当时，＝．故选：C．9．（5分）在圆x2+y2＝5x内，过点（，）有n条弦的长度成等差数列，最小弦长为数列的首项a1，最大弦长为a n，若公差d∈[，]，那么n的取值集合为（）A．{4，5，6，7}B．{4，5，6}C．{3，4，5，6}D．{3，4，5}【考点】82：数列的函数特性；84：等差数列的通项公式．【解答】解：圆x2+y2＝5x的圆心为C，半径为r＝过点P最短弦的弦长为a1＝2 ＝4过点P最长弦长为圆的直径长a n＝5，∴4+（n﹣1）d＝5，d＝，∵d∈[，]，∴，∴4≤n≤7．故选：A．10．（5分）已知数列{a n}的前n项之和S n＝n2﹣4n+1，则|a1|+|a2|+…+|a10|的值为（）A．61B．65C．67D．68【考点】8E：数列的求和．【解答】解：当n＝1时，S1＝a1＝﹣2，当n≥2时，a n＝S n﹣S n﹣1＝（n2﹣4n+1）﹣[（n﹣1）2﹣4（n﹣1）+1]＝2n﹣5，故a n＝，据通项公式得a1＜a2＜0＜a3＜a4＜…＜a10∴|a1|+|a2|+…+|a10|＝﹣（a1+a2）+（a3+a4+…+a10）＝S10﹣2S2＝102﹣4×10+1﹣2（﹣2﹣1）＝67．故选：C．11．（5分）已知数列{a n}满足a1＝0，a n+1＝（n＝1，2，3，…），则a2008等于（）A．0B．C．D．【考点】8H：数列递推式．【解答】解：依题意，a1＝0，a2＝＝﹣，a3＝，a4＝∴数列{a n}是一个以3为周期的周期数列∴a2008＝a669×3+1＝a1＝0故选：A．12．（5分）若直线y＝x+b与曲线有公共点，则b的取值范围是（）A．B．C．D．【考点】J9：直线与圆的位置关系．【解答】解：如图所示：曲线y＝3﹣，即y﹣3＝﹣，平方可得（x﹣2）2+（y﹣3）2＝4（1≤y≤3，0≤x≤4），表示以A（2，3）为圆心，以2为半径的一个半圆．由圆心到直线y＝x+b的距离等于半径2，可得＝2，∴b＝1+2，或b＝1﹣2．结合图象可得1﹣2≤b≤3，故选：C．二、填空题：本大题共4小题，每小题5分，共20分.将正确答案写在答题卡的相应位置上.13．（5分）已知△ABC中，c＝，a＝1，a cos B＝b cos A，则△ABC面积为【考点】HP：正弦定理．【解答】解：∵a cos B＝b cos A，∴由正弦定理可得：sin A cos B＝sin B cos A，可得：sin（A﹣B）＝0，∵0＜A＜π，0＜B＜π，可得：﹣π＜A﹣B＜π，∴A﹣B＝0，可得：a＝b＝1，∴cos A＝＝＝，可得：sin A＝，∴S△ABC＝bc sin A＝＝．故答案为：．14．（5分）点M（x，y）是不等式组表示的平面区域Ω内的一动点，且不等式2x﹣y+m≥0总成立，则m的取值范围是m≥3．【考点】7C：简单线性规划．【解答】解：若2x﹣y+m≥0总成立⇔m≥y﹣2x总成立即可，设z＝y﹣2x，即求出z的最大值即可，作出不等式组对应的平面区域如图：由z＝y﹣2x得y＝2x+z，平移直线y＝2x+z，由图象可知当直线经过点C（0，3）时，直线的截距最大，此时z最大，此时z＝3﹣0＝3，∴m≥3，故答案为：m≥315．（5分）长方体共顶点的三个侧面积分别为、、，则它的外接球表面积为9π．【考点】LG：球的体积和表面积；LR：球内接多面体．【解答】解：因为一个长方体相邻的三个面的面积分别是、、，设长方体的一个顶点上的三条棱长分别是a，b，c则①÷②×③得：b＝，则a＝1，c＝∴长方体的一个顶点上的三条棱长分别是1、、，且它的8个顶点都在同一个球面上，所以长方体的对角线就是确定直径，长方体的体对角线的长是：＝3球的半径是：R＝这个球的表面积：S＝4 π（）2＝9π故答案为：9π16．（5分）已知（x0，y0）是x+y＝2k﹣1与圆x2+y2＝k2+2k﹣3的公共点，则当k＝2﹣时，x0y0最小．【考点】J9：直线与圆的位置关系．【解答】解：直线x+y＝2k﹣1，圆x2+y2＝k2+2k﹣3，则圆心（0，0）到直线的距离为d＝≤，解得2﹣≤k≤2+，又圆x2+y2＝k2+2k﹣3，∴k2+2k﹣3＞0，解得k＜﹣3，或k＞1；∴k的取值范围为2﹣≤k≤2+；由，得x0y0＝[（2k﹣1）2﹣（k2+2k﹣3）]＝k2﹣3k+2＝（k﹣1）2+，∴当k＝2﹣时，x0y0取得最小值．故答案为：2﹣．三、解答题：（本大题共6小题，共70分.解答应写出文字说明，证明过程或演算步骤，解答过程书写在答题纸的相应位置.）17．（10分）已知两条直线l1：x+my+6＝0，l2：（m﹣2）x+3y+2m＝0m为何值时，l1与l2①相交；②平行；③垂直．【考点】II：直线的一般式方程与直线的平行关系；IJ：直线的一般式方程与直线的垂直关系．【解答】解：①当l1和l2相交时，1×3﹣（m﹣2）m≠0，由1×3﹣（m﹣2）m＝0，m2﹣2m﹣3＝0，∴m＝﹣1，或m＝3，∴当m≠﹣1且m≠3时，l1和l2相交．②∵m＝0时，l1不平行l2，l1∥l2⇔，解得m＝﹣1．③l1⊥l2 时，1×（m﹣2）+m×3＝0，m＝，∴当m＝时，l1⊥l2．18．（12分）在△ABC中，a，b，c分别是∠A、∠B、∠C的对边，且b sin A＝cos B．（1）求∠B的大小；（2）若b＝3，sin C＝2sin A，求a及c．【考点】HR：余弦定理．【解答】解：（1）由及正弦定理，得，所以，所以；（2）由sin C＝2sin A及得c＝2a，由b＝3及余弦b2＝a2+c2﹣2ac cos B，得9＝a2+c2﹣ac，∴；19．（12分）已知数列{log2（a n﹣1）}（n∈N*）为等差数列，且a1＝3，a3＝9．（Ⅰ）求数列{a n}的通项公式；（Ⅱ）证明++…+＜1．【考点】8E：数列的求和．【解答】（I）解：设等差数列{log2（a n﹣1）}的公差为d．由a1＝3，a3＝9得2（log22+d）＝log22+log28，即d＝1．所以log2（a n﹣1）＝1+（n﹣1）×1＝n，即a n＝2n+1．（II）证明：因为＝＝，所以++…+＝+++…+＝＝1﹣＜1，即得证．20．（12分）如图，在棱长为1的正方体ABCD﹣A1B1C1D1中，E是BC的中点，平面B1ED 交A1D1于F（1）指出F在A1D1上的位置，并证明．（2）求直线A1C与B1F所成角的余弦值．【考点】L2：棱柱的结构特征；LM：异面直线及其所成的角．【解答】解：（1）以A为原点建立空间直角坐标系A﹣xyz．∵面ABCD∥面A1B1C1D1，面B1EDF∩面A1B1C1D1＝B1F，面B1EDF∩面ABCD＝DE∴B1F∥DE又∵D（0，1，0），E（1，，0），B1（1，0，1）设F（0，y，1），则＝（﹣1，y，0），＝（﹣1，，0）∴即∴∴F为A1D1的中点（2）A1（0，0，1），C（1，1，0），则＝（1，1，﹣1），∴A1C与B1F所成角的余弦值为（12分）21．（12分）已知数列{a n}的前n项和为S n，且S n＝n﹣5a n﹣85，n∈N*（1）证明：{a n﹣1}是等比数列；（2）求数列{S n}的通项公式．请指出n为何值时，S n取得最小值，并说明理由（参考数据15＝﹣14.85）【考点】8H：数列递推式．【解答】证明：（1）当n＝1时，a1＝S1＝1﹣5a1﹣85，解得a1＝﹣14，则a1﹣1＝﹣15．∵当n≥2时，S n﹣1＝（n﹣1）﹣5a n﹣1﹣85，∴a n＝S n﹣S n﹣1＝1﹣5a n+5a n﹣1，∴6a n＝5a n﹣1+1，即a n﹣1＝（a n﹣1﹣1），∴{a n﹣1}是首项为﹣15，公比为的等比数列．解：（2）∵a n﹣1＝﹣15•（）n﹣1，∴S n＝n﹣5[1﹣15•（）n﹣1]﹣85＝n+75•（）n﹣1﹣90．由a n＝1﹣15•（）n﹣1＞0，即15•（）n﹣1＜1，解得n＞log+1≈15.85．∴当n≤15时，a n＜0；当n≥16时，a n＞0．故n＝15时，S n取得最小值．22．（12分）已知圆C：x2+（y﹣3）2＝4，一动直线l过A（﹣1，0）与圆C相交于P、Q 两点，M是PQ中点，l与直线m：x+3y+6＝0相交于N．（Ⅰ）求证：当l与m垂直时，l必过圆心C；（Ⅱ）当时，求直线l的方程；（Ⅲ）探索是否与直线l的倾斜角有关，若无关，请求出其值；若有关，请说明理由．【考点】J9：直线与圆的位置关系．【解答】解：（Ⅰ）∵直线l与直线m垂直，且，∴k l＝3，又k AC＝3，所以当直线l与m垂直时，直线l必过圆心C；（Ⅱ）①当直线l与x轴垂直时，易知x＝﹣1符合题意，②当直线l与x轴不垂直时，设直线l的方程为y＝k（x+1），即kx﹣y+k＝0，因为，所以，则由CM＝＝1，得，∴直线l：4x﹣3y+4＝0．从而所求的直线l的方程为x＝﹣1或4x﹣3y+4＝0；（Ⅲ）因为CM⊥MN，∴，当直线l与x轴垂直时，易得，则，又，∴，当直线l的斜率存在时，设直线l的方程为y＝k（x+1），则由，得N（，），则，∴＝，综上，与直线l的斜率无关，且．。

白城一中2017-2018学年度下学期期末考试高一化学试题（本试卷满分100分，时间90分钟）可能用到的相对原子质量：H:1 C:12 N:14 O:16 S:32 Na:23 Mg:24 Al:27 Fe:56 Cu:64 K:39 Zn:65 Cl:35.5 Mn:55第Ⅰ卷（ 选择题部分 共50分 ）一、选择题（本题共16小题，每小题2分，共32分。

每小题只有一个．．．．选项符合题意） 1. 关于电解质强弱及非电解质的组合完全正确的是:A B C D 强电解质 NaCl H 2SO 4 CaCO 3 HNO 3 弱电解质 HF BaSO 4 HClO CH 3COOH 非电解质Cl 2CO 2C 2H 5OHH 2O2. 下列溶液一定呈中性的是: A. pH=7的溶液B. c(H +)=c(OH －)=10-6mol/L 溶液C. 使石蕊试液呈紫色的溶液D. 酸与碱恰好完全反应生成正盐的溶液 3.向平底烧瓶中放入氢氧化钡固体()228Ba OH H O ⎡⎤⋅⎣⎦和氯化铵固体,塞紧瓶塞,在瓶底和木板间滴少量水,一会儿,就会发现瓶内固态物质减小,有液体生成,瓶壁变冷,小木板上因少量水结冰冻结,而将烧瓶黏住,这时打开瓶塞,散发出来的气体有氨味,这是自发地发生了反应:()()()24282? Ba OH H O s NH Cl s ⋅+()()()232210BaCl s NH g H O l ++下列结论正确的是( )A.该反应是一个熵减小的反应B. 吸热反应在常温下一定不能进行C.该反应0H ∆>,0H T S ∆-∆<D.能自发进行的反应一定能迅速发生反应 4.下列操作中，能使电离平衡H 2OH +＋OH －，向右移动且溶液呈酸性的是:A. 向水中加入NaHSO 4溶液B. 向水中加入Al 2(SO 4)3固体C. 向水中加入Na 2CO 3溶液D. 将水加热到100℃，使pH ＝65.在密闭容器中进行反应：X （g ）+3Y （g （g ），有关下列图象的说法正确的是（ ）A．依据图a可判断正反应为吸热反应B．在图b中，虚线可表示压强增大C．若正反应的△H＜0，图c可表示升高温度使平衡向逆反应方向移动D．由图d中气体平均相对分子质量随温度的变化情况，可推知正反应的△H＞06.取c(H+)均为0.01 mol/L的盐酸和醋酸各100mL分别稀释2倍后，再分别加入0.03g锌粉，在相同条件下充分反应，有关叙述正确的是（）①醋酸与锌反应放出氢气多②盐酸和醋酸分别与锌反应放出的氢气一样多③盐酸与锌反应放出氢气多④盐酸和醋酸分别与锌反应的速度一样大⑤醋酸与锌反应速率大⑥盐酸与锌反应速率大A．①⑥B．②⑤C．③④D．①⑤7.甲醇是一种重要的化工原料，广泛应用于化工生产，也可以直接用作燃料．已知：CH3OH（l）+O2（g）=CO（g）+2H2O（g）△H1=﹣443.64kJmol﹣12CO（g）+O2（g）=2CO2（g）△H2=﹣566.0kJmol﹣1下列说法或热化学方程式正确的是（）A． CO的燃烧热为566.0 kJmol﹣1B． 2 mol CO和1 mol O2的总能量比2 mol CO2的总能量低C．完全燃烧20g甲醇，生成二氧化碳和水蒸气时放出的热量为908.3 kJD． 2CH3OH（l）+3O2（g）=2CO2（g）+4H2O（g）△H=﹣1453.28 kJmol﹣18. 已知25℃，醋酸、次氯酸、碳酸、亚硫酸的电离平衡常数如右表：A．将0.1mol/L的醋酸加水不断稀释，c(CH3COO—)终减小B．少量CO2通入NaClOCO2+H2O+2ClO—=CO32—+2HClOC．少量的SO2通入Ca(ClO)2为：SO 2+H 2O+Ca 2++2ClO —=CaSO 3↓+2HClOD ．25℃，等浓度的CH 3COONa 、NaClO 、Na 2CO 3和Na 2SO 3 溶液中，碱性最强的是NaClO 9. 25℃时，某溶液中由水电离出的c （OH －）=1×10－13mol/L ，该溶液中一定不能大量共存的离子组是:A. NH 4+、Fe 3+、SO 42－、Cl－B. CO 32－、PO 43－、K + 、Na +C. Na +、SO 42－、NO 3－ 、Cl －D. HPO 42－、 Na +、 HSO 3－、K +10. 下列错误操作中，能造成中和滴定结果偏低的是( ) A ．用滴定管量取标准液时，开始时平视，滴定后仰视 B ．盛标准液的滴定管尖嘴部分有气泡未排出就开始滴定C ．往锥形瓶中加待测液时，对滴定管读数，开始时仰视，滴定后平视D ．振荡时锥形瓶中液滴飞溅出来11.用CO 合成甲醇的反应为：CO （g ）+2H2（g 3OH （g ）△H ＜0．按照相同的物质的量投料，测得CO 在不同温度下的平衡转化率与压强的关系如图所示．下列说法正确的是（ ）A ．温度：T 1＞T 2＞T 3B ．正反应速率：v （a ）＞v （c ） v （b ）＞v （d ）C ．平衡常数：K （a ）＞K （b ） K （b ）=K （d ）D ．平均摩尔质量：M （a ）＞M （c ） M （b ）＜M （d ）12. 25℃时,浓度均为0.21mol L -⋅的3NaHCO 与23Na CO 溶液中,下列判断不正确的是( )A.均存在电离平衡和水解平衡B. ()c OH -前者大于后者 C.存在的粒子种类相同D.分别加入NaOH 固体,恢复到原温度, ()23c CO -均增大13．下列结论正确的是( )①粒子半径：K +>Al 3+>S 2->Cl -②酸性：H 2SO 4>H 3PO 4>H 2CO 3>HCl0 ③离子的还原性：S 2-> I -> Cl ->Br - ④氧化性：Cl 2>S>Se>Te ⑤金属性：Be<Mg<Ca<K ⑥非金属性：O>N>P>Si ⑦氢化物的稳定性：HF>HCl>H 2S>PH 3>SiH 4 A ．②③⑤⑦ B ．②⑥⑦ C ．②③④⑤⑥⑦ D ．②④⑥ 14. 有一反应: 2A B2C ,其中A 、B 、C 均为气体,下图中的曲线是该反应在不同温度下的平衡曲线, x 轴表示温度, y 轴表示B 的转化率,图中有a 、b 、c 三点,如图所示,则下列描述正确的是( )A.该反应是放热反应B. b 点时混合气体的平均摩尔质量不再变化C. 1T 时若由a 点达到平衡,可以采取增大压强的方法D. c 点v (正)< v (逆)15.25 ℃在等体积的①pH=0的H 2SO 4溶液，②0.05 mol ·L －1的Ba(OH)2溶液，③pH = 10的Na 2S 溶液，④pH=5的NH 4NO 3溶液中，发生电离的水的物质的量之比是: A ．1∶10∶1010∶109B ．1∶5∶5×109∶5×109C ．1∶20∶1010∶109D ．1∶10 ∶104∶10916．下列各组热化学方程式中，化学反应的ΔH 前者大于后者的是( ) ①C(s)＋O 2(g)===CO 2(g) ΔH 1 C(s)＋12O 2(g)===CO(g) ΔH 2②S(s)＋O 2(g)===SO 2(g) ΔH 3 S(g)＋O 2(g)===SO 2(g) ΔH 4 ③H 2(g)＋12O 2(g)===H 2O(l) ΔH 52H 2(g)＋O 2(g)===2H 2O(l) ΔH 6 ④CaCO 3(s)===CaO(s)＋CO 2(g) ΔH 7 CaO(s)＋H 2O(l)===Ca(OH)2(s) ΔH 8A ．①B ．④C ．②③④D ．①②③二、选择题（本题共6小题，每小题3分，共18分。

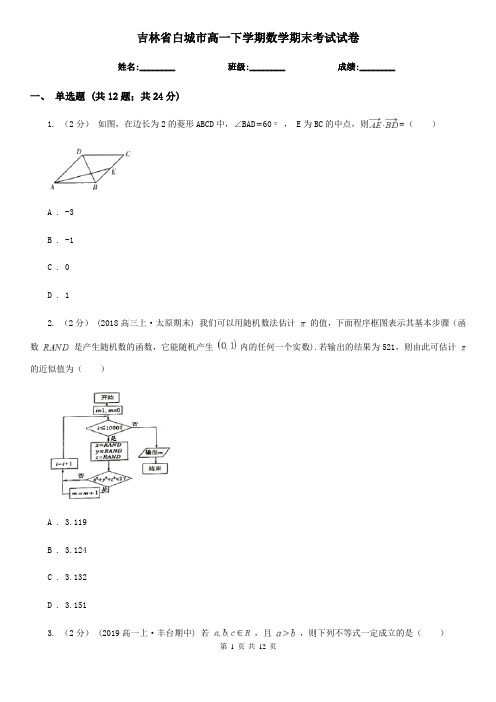
吉林省白城市高一下学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共24分)1. （2分）如图，在边长为2的菱形ABCD中，∠BAD60， E为BC的中点，则（）A . -3B . -1C . 0D . 12. （2分） (2018高三上·太原期末) 我们可以用随机数法估计的值，下面程序框图表示其基本步骤（函数是产生随机数的函数，它能随机产生内的任何一个实数).若输出的结果为521，则由此可估计的近似值为（）A . 3.119B . 3.124C . 3.132D . 3.1513. （2分） (2019高一上·丰台期中) 若，且，则下列不等式一定成立的是（）A .B .C .D .4. （2分） (2018高二上·武邑月考) 若△ABC中，sinA:sinB:sinC=2:3:4，那么cosC=（）A .B .C .D .5. （2分） (2018高三上·西安模拟) 若为对立事件，其概率分别为，则的最小值为（）A . 10B . 9C . 8D . 66. （2分） (2017高三下·新县开学考) 已知表示的平面区域为D，若∀（x，y）∈D，2x+y≤a 为真命题，则实数a的取值范围是（）A . [5，+∞）B . [2，+∞）C . [1，+∞）D . [0，+∞）7. （2分）(2018·梅河口模拟) 下图为射击使用的靶子，靶中最小的圆的半径为1，靶中各圆的半径依次加1，在靶中随机取一点，则此点取黑色部分（7环到9环）的概率是（）A .B .C .D .8. （2分） (2016高一下·抚顺期末) 已知回归直线的斜率的估计值是1.23，样本点的中心为（4，5），则回归直线的方程是（）A . =1.23x+4B . =1.23x﹣0.08C . =1.23x+0.8D . =1.23x+0.089. （2分） (2016高三上·平罗期中) 若数列{an}满足a1=2，an+1= （n∈N*），则该数列的前2014项的乘积等于（）A . 3B . ﹣6C . 2D . 110. （2分） (2016高一下·红桥期中) 若△ABC的内角A，B，C满足 = = ，则cosB=（）A .B .C . ﹣D . ﹣11. （2分） (2019高二上·洛阳期中) 若，则的最小值为（）A .B .C .D .12. （2分）在直角梯形ABCD中，AB∥CD，∠ABC=90°，AB=2BC=2CD，则cos∠DAC=（）A .B .C .D .二、填空题 (共4题；共6分)13. （1分）绵阳南山中学实验学校2016年高考实现“高考冠军”三联冠，特别是文科补习生平均涨分102.45，理科补习生平均涨分121.32．现从2016年补习生中随机选出45名学生，得到其所涨分数的茎叶图如图所示，若将涨分由低到高编为1﹣45号，再用系统抽样的方法从中抽取9名学生，则这9名学生所涨分数在[111，144]内的有________名．14. （2分） (2018高一下·北京期中) 下面茎叶图记录了在某项体育比赛中，九位裁判为一名选手打出的分数情况，则去掉一个最高分和一个最低分后，所剩数据的平均值为________，方差为________.15. （2分）如图所示的流程图的运行结果是________16. （1分） (2016高一下·江阴期中) 把1，3，6，10，15，21，…这些数叫做三角形数，这是因为用这些数目的点可以排成一个正三角形（如图）．则第8个三角形数是________．三、解答题 (共6题；共57分)17. （10分）绵阳二诊后，某学校随机抽査部分学生的政治成绩进行统计分析，己知统计出的成绩频率分布直方图如图，数据的分组依次为[20，40），[40，60），[60，80），[80，100），己知低于60 分的人数是6人．（I）求x与被抽查的学生人数n；（Ⅱ）现从被抽查低于60分的学生中随机选取2人进行访谈，求这2人在同一分数组的概率．18. （10分） (2016高一下·成都期中) 已知 =（cosα，sinα）， =（cosβ，sinβ），其中0＜α＜β＜π．（1）求证：与互相垂直；（2）若k 与﹣k 的长度相等，求β﹣α的值（k为非零的常数）．19. （10分） (2016高二下·玉溪期中) 已知函数f（x）=cos2x+2 sinxcosx﹣sin2x．（1）求f（x）的最小正周期和值域；（2）在△ABC中，角A，B，C所对的边分别是a，b，c，若且a2=bc，试判断△ABC的形状．20. （2分） (2018高二下·长春期末) 市某机构为了调查该市市民对我国申办年足球世界杯的态度，随机选取了位市民进行调查，调查结果统计如下：支持不支持合计男性市民女性市民合计附：，其中 .（1）根据已知数据，把表格数据填写完整；（2）利用（1）完成的表格数据回答下列问题：（i）能否在犯错误的概率不超过的前提下认为支持申办足球世界杯与性别有关；（ii）已知在被调查的支持申办足球世界杯的男性市民中有位退休老人，其中位是教师，现从这位退休老人中随机抽取人，求至多有位老师的概率.21. （10分） (2018高一下·六安期末) 数列满足，，为其前项和.数列为等差数列，且满足， .（1）求数列，的通项公式；（2）设，数列的前项和为，证明： .22. （15分）若一元二次方程kx2+3kx+k﹣3=0的两根都是负数，求k的取值范围．参考答案一、单选题 (共12题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题；共6分)13-1、14-1、15-1、16-1、三、解答题 (共6题；共57分)17-1、18-1、18-2、19-1、19-2、20-1、20-2、21-1、21-2、22-1、。

吉林省白城市高一下学期数学期末联考试卷姓名:________ 班级:________ 成绩:________一、选择题:本大题共12小题,每小题5分,共60分。

(共12题；共60分)1. （5分）如果AC＜0，且BC＜0，那么直线Ax＋By＋C＝0不通过（）．A . 第一象限B . 第二象限C . 第三象限D . 第四象限2. （5分）设的内角所对边的长分别为,若,则角（）A .B .C .D .3. （5分）设为单位向量，若向量满足，则的最大值是（）A . 1B .C . 2D . 24. （5分） (2017高一下·牡丹江期末) 在正方体中，是棱的中点，是侧面内的动点，且平面，记与平面所成的角为，下列说法正确的是个数是（）①点F的轨迹是一条线段② 与不可能平行③ 与是异面直线④ ⑤当与不重合时，平面不可能与平面平行A . 2B . 3C . 4D . 55. （5分） (2019高一下·邢台月考) 若等差数列中，，则为（）A . 8B . 6C . 4D . 36. （5分）如图，正方体ABCD—A1B1C1D1的棱长为2，动点E、F在棱A1B1上。

点Q是CD的中点，动点P 在棱AD上，若EF=1，DP=x，A1E=y(x,y大于零)，则三棱锥P-EFQ的体积（）A . 与x，y都有关；B . 与x，y都无关；C . 与x有关，与y无关；D . 与y有关，与x无关；7. （5分）(2018·河北模拟) 已知点为双曲线的右顶点，过的直线与的两条渐近线分别交于，两点.若，分别在第一、第四象限内，且，则的方程为（）A .B .C .D .8. （5分） (2018高三上·大连期末) 某四棱锥的三视图如图所示，则该四棱锥的外接球半径为（）A . 1B .C .D .9. （5分）已知角的顶点在坐标原点，始边与轴的正半轴重合，，角的终边与单位圆交点的横坐标是，角的终边与单位圆交点的纵坐标是，则的值为（）A .B .C .D .10. （5分）圆x2+y2﹣2x﹣1=0关于直线x﹣y+3=0对称的圆的方程是（）A . （x+3）2+（y﹣4）2=2B . （x﹣3）2+（y+4）2=2C .D .11. （5分）设等差数列的公差不等于0，且其前n项和为。

2017—2018学年度第二学期教学质量检查高一数学考生注意：本卷共三大题，22小题，满分150分，时间120分钟.不准使用计算器.参考公式：用最小二乘法求线性回归方程a x b yˆˆˆ+=的系数公式： ()()()∑∑∑∑====-⋅⋅-=---=n i i ni ii ni i ni i ixn x yx n yx x x y y x xb1221121ˆ，x b y aˆˆ-=. 一、选择题：本大题共12小题，每小题5分，共60分． 每小题各有四个选择支，仅有一个选择支正确．请把正确选择支号在答题卡中的相应位置涂黑． 1.︒135sin 的值是（ ） A.22B.22-C.23-D.23 2.已知向量),4(),1,(x b x a ==ρρ，若5=⋅b a ρρ，则x 的值为（ ）A.1B.2C.1±D.53.若圆22240x y x y ++-=关于直线20x y a -+=对称，则a 的值为( ) A.3- B. 1- C. 0 D. 44.为了调查某班级的作业完成情况，将该班级的52名同学随机编号01～52，用系统抽样．．．．的方法抽取一个容量为4的样本，已知05、18、44号同学在样本中，那么样本中还有一位同学的编号应该是（ ） A.29 B.30 C.31 D.325.已知α是第四象限角，且tan 2α=-，则sin 2α=（ ） A.25-B. 25C.45-D. 456.要得到曲线3sin(2)5y x π=-，只需把函数3sin 2y x =的图象（ ）A ．向左平移5π个单位 B ．向右平移5π个单位 C ．向左平移10π个单位 D ．向右平移10π个单位7.运行如右图所示的程序框图，则输出的结果S 为（ ） A ．1- B ．0 C ．21 D ．23-7第题图否2019?n <8.从集合{2,3,4,5}中随机抽取一个数a ，从集合{4,6,8}中随机抽取一个数b ，则向量(,)m a b =u r与 向量(1,2)n =r平行的概率为（ ）A.16B.14C.13D.129.过原点的直线l 与圆4)2()1(22=-+-y x 相交所得的弦长为32，则直线l 的斜率为（ ）A. 2B. 1C.43 D.1210.如图，圆C 内切于扇形AOB ，3AOB π∠=，若在扇形AOB 内任取一点，则该点在圆C 外的概率为（ ） A ．14B.13C.23D.3411.已知0ω>，函数()sin()4f x x πω=+在42ππ（，）上单调递减，则ω的取值范围是（ ） A ． (0,2] B ．1(0,]2 C ．13[]22， D ．5[1]2， 12.设2,1OA OB ==u u u r u u u r ，0OA OB ⋅=u u u v u u u v ，OP OA OB λμ=+u u u v u u u v u u u v，且1=+μλ，则向量OA 在OP u u u v 上的投影的取值范围( ) A.]2,552(-B.]2,552(C. ]2,554(-D. ]2,554( 二、填空题：本大题共4小题，每小题5分，共20分．请把答案填在答题卡的相应位置上． 13.在空间直角坐标系中，点)4,3,2(P 到y 轴的距离为________.14.已知,a b r u r 为单位向量，且,a b r r 所成角为3π，则2a b +r r 为_________.15.某校为了了解学生的课外阅读情况，随机调查了50名学生，得到他们在某天阅读时间及人数的数据，结果用条形图表示（如右图），根据条形图可知 这50名学生在这天平均每人的课外阅读时间为 小时.16.已知sin 2cos y θθ=+，且θπ∈（0,），则当y 取得最大值时sin θ= .0.511.5220151050小时人数第15题图第10题图三、解答题：本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．必须把解答过程写在答题卡相应题号指定的区域内，超出指定区域的答案无效． 17．(本小题10分)已知平面向量)2,1(=a ，),1(k -=．（1）当k 为何值时，向量a 与b a ρρ+2垂直；（2）当1=k 时，设向量与的夹角为θ，求θtan 及θ2cos 的值．18．(本小题12分)近年来，我国许多省市雾霾天气频发，为增强市民的环境保护意识，某市面向全市征召n 名义务宣传志愿者，成立环境保护宣传组织.现把该组织的成员按年龄分成5组：第1组[20，25)，第2组[25，30)，第3组[30，35)，第4组[35，40)，第5组[40，45]，得到的频率分布直方图如图所示，已知第2组有70人.)（1）求该组织中志愿者人数；（2）若从第3，4，5组中用分层抽样的方法抽取6名志愿者参加某社区的宣传活动，然后在这6名志愿者中随机抽取2名志愿者介绍宣传经验，求第3组至少有一名志愿者被抽中的概率.19．(本小题12分)某企业为了对新研发的一批产品进行合理定价，将产品按事先拟定的价格进行试销，得到一组销售数据()(),1,2,6i i x y i =⋯，如表所示：已知80y =.（1）求表格中q 的值；（2）已知变量,x y 具有线性相关关系，试利用最小二乘法原理，求产品销量y 关于试销单价x 的线性回归方程ˆˆˆybx a =+ ( 参考数据：662113050,271i i i i i x y x ====∑∑)；（3）用（2）中的回归方程得到与i x 对应的产品销量的估计值记为i yˆ)6,...,2,1(=i ， 当ˆ1i i y y -≤时，称(),i i x y 为一个“理想数据”.试确定销售单价分别为6,5,4时有哪些是“理想数据”.20.(本小题12分)设函数()2π2sin 24f x x x ⎛⎫=+⎪⎝⎭.（1）请把函数)(x f 的表达式化成)2||,0,0()sin()(πϕωϕω<>>++=A b x A x f 的形式，并求)(x f 的最小正周期；（2）求函数)(x f 在]2,4[ππ∈x 时的值域．21.(本小题12分)在平面内，已知点(1,1)A ，圆C ：22(3)(5)4x y -+-=，点P 是圆C 上的一个动点，记线段PA 的中点为Q . （1）求点Q 的轨迹方程；（2）若直线:2l y kx =+与Q 的轨迹交于M N ，两点，是否存在直线l ，使得10OM ON •=u u u u r u u u r（O为坐标原点），若存在，求出k 的值；若不存在，请说明理由.22．(本小题12分)已知1≥a ，1)cos (sin cos sin )(-++-=x x a x x x f . （1）求当1=a 时，)(x f 的值域； （2）若函数)(x f 在3[0,]4π内有且只有一个零点，求a 的取值范围.2017—2018学年度第二学期教学质量检查 高一数学参考答案及评分标准二、填空题(每小题5分,满分20分)13.52 14．7； 15．0.95； 16．5三、解答题 17．（本小题满分10分）解:（1）Θ与2+a b r r 垂直，得2+0a a b ⋅=r r r（） 即22+=0a a b r r rg……………………2分 即10120k -+= ……………………3分解得92k =-． ……………………4分（2）依题意，10102521||||cos =⨯+-==b a θ， ……………………6分因为[0,]θπ∈ sin 10θ∴==……………………7分 sin tan 3cos θθθ∴== ……………………8分 54110121cos 22cos 2-=-⨯=-=∴θθ ……………………10分18．（本小题满分l2分）解: (1)由题意：第2组的人数：7050.07n =⨯⨯，得到：=200n ， 故该组织有200人.……………………3分(2)第3组的人数为0.3200=60⨯， 第4组的人数为0.2200=40⨯，第5组的人数为0.1200=20⨯. ∵第3，4，5组共有120名志愿者，∴利用分层抽样的方法在120名志愿者中抽取6名志愿者，每组抽取的人数分别为：第3组：606=3120⨯；第4组：406=2120⨯；第5组：206=1120⨯. ……………………5分 记第3组的3名志愿者为1A ，2A ，3A ，第4组的2名志愿者为1B ，2B ， 第5组的1名志愿者为C .则从6名志愿者中抽取2名志愿者有：()12A A ，，()13A A ，，()11A B ，，()12A B ，，()1A C ，，()23A A ，，()21A B ，,()22A B ，,()2A C ，,()31A B ，,()32A B ，,()3A C ，,()12B B ，,()1B C ，,()2B C ，， 共有15种.……………………8分其中第3组的3名志愿者为1A ，2A ，3A ，至少有一名志愿者被抽中的有：()12A A ，，()13A A ，，()11A B ，，()12A B ，，()1A C ，，()23A A ，，()21A B ，,()22A B ，,()2A C ，,()31A B ，,()32A B ，,()3A C ， 共有12种.……………………10分则第3组的为至少有一名志愿者被抽中的概率为124155P ==. ……………………12分 [用间接法求解亦可以给满分] 19. （本小题满分l2分） 解：（1）66880838490+++++=q y Θ，又80y =Q ，75=∴q . ……………………3分（2）4567891362x +++++==， ……………………4分2133050680241327162b ∧-⨯⨯∴==-⎛⎫- ⎪⎝⎭……………………6分 ()138041062a ∧∴=--⨯= ……………………7分 4106y x ∧∴=-+ ……………………8分（3）4106y x ∧=-+Q1111410690,909001y x y y ∧∧∴=-+=-=-=<，所以()()11,4,90x y =是“理想数据”；2222410686,=868421y x y y ∧∧=-+=--=>，所以()()22,5,84x y =不是“理想数据”; 3333410682,838211y x y y ∧∧=-+=-=-==，所以()()33,6,83x y =是“理想数据”.所以所求的“理想数据”为)90,4( ，)83,6(. ……………………12分20. （本小题满分l2分） 解: （1）()2ππ2sin 1cos 242f x x x x x ⎛⎫⎛⎫=+-=-+⎪ ⎪⎝⎭⎝⎭π1sin22sin 213x x x ⎛⎫=+=-+ ⎪⎝⎭， ……………………4分∴函数()f x 最小正周期为22T ππ== ……………………5分 (2) ππ,42x ⎡⎤∈⎢⎥⎣⎦Q∴ππ2π2,363x ⎡⎤-∈⎢⎥⎣⎦， ……………………7分 ∴π1sin 2[,1]32x ⎛⎫-∈ ⎪⎝⎭ ∴π2sin 2[1,2]3x ⎛⎫-∈ ⎪⎝⎭……………………10分 ∴()[2,3]f x ∈……………………11分 ∴函数()f x 的值域是[2,3]……………………12分21. （本小题满分l2分）（1）解：设点(),Q x y 、()00,P x y .Q 点P 在圆C 上，∴2200(3)(5)4x y -+-=. ① ……………………1分又Q PA 中点为点Q∴002121x x y y =+⎧⎨=+⎩………………… 3分可得021x x =-，021y y =-代入①得22(2)(3)1x y -+-=∴点Q 的轨迹方程为22(2)(3)1x y -+-= …………………… 4分 （2）假设存在直线l ，使得6=•OM ，设()11,M x y ，()22,N x y ，由222(2)(3)1y kx x y =+⎧⎨-+-=⎩ 得22(1)(24)40k x k x +-++= …………………… 6分因为直线与Q 的轨迹交于两点所以22=(24)16(1)0k k ∆+-+> 得403k <<② …………………… 7分 且121222244,11k x x x x k k ++==++ …………………… 8分又212121212(1)2()4OM ON x x y y k x x k x x +=+•++=+u u u u r u u u r222424(1)24=1011k k k k k+=+⨯+⨯+++ …………………… 9分∴2410k k +-= 解得2k =-± …………………… 10分因为2k =--②， …………………… 11分所以存在直线l ：(22y x =-++，使得=10OM ON •u u u u r u u u r……………………12分22. （本小题满分l2分）解：（1）当1=a 时，1cos sin cos sin )(-++-=x x x x x f ，令x x t cos sin +=，则]2,2[-∈t ，21cos sin 2-=t x x ，22)1(21121)(--=-+--=t t t t g ， 当1=t 时，0)(max =t g ，当2-=t 时，223)(min --=t g ， 所以)(x f 的值域为]0,223[--……………………4分 （2）1)cos (sin cos sin )(-++-=x x a x x x f ，令sin cos t x x =+，则当3[0,]4x π∈时，t ∈，21sin cos 2t x x -=， 2221111()1()2222t h t at t a a -=-+-=--++， …………………… 5分)(x f 在3[0,]4π内有且只有一个零点等价于()h t 在[0,1)I 内有且只有一个零点，)2,1[无零点.因为1≥a ， ……………………6分 ∴()h t 在[0,1)内为增函数，①若()h t 在[0,1)内有且只有一个零点，)2,1[无零点，故只需10(1)01(0)0020302a h h h ⎧⎪->⎧>⎪⎪-⎪≤⇒≤⎨⎨⎪⎪>⎩->得423>a ；……………………10分 ②若2为()h t 的零点，)2,1[内无零点，则0232=-a ，得423=a ， 经检验，423=a 不符合题意. 综上，423>a . ……………………12分。

吉林省白城市高一下学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题；共24分)1. （2分）(2017·自贡模拟) 设集合A={x|x2﹣3x＜0}，B={x||x|＞2}，则A∩B=（）A . （2，3）B . （﹣2，3）C . （0，2）D . （﹣2，0）2. （2分）已知全集U=R，集合A＝{1,2,3,4,5｝,B＝[3，十），则图中阴影部分所表示的集合为（）A . {0，1，2}B . {0，1}，C . {1，2}D . ｛1｝3. （2分） (2018高一上·舒兰期中) 函数定义域为（）A .B .C .D .4. （2分） (2019高一上·浠水月考) 关于函数的最值的说法正确的是（）A . 既没有最大值也没有最小值B . 没有最小值，只有最大值C . 没有最大值，只有最小值D . 既有最小值0，又有最大值5. （2分）设f(x)是定义在R的偶函数，对任意x R，都有f(x-2)=f(x+2)，且当x[-2, 0]时，f(x)=．若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0(a>1)恰有3个不同的实数根，则实数a的取值范围是（）A . (1, 2)B . (2,+)C . (1,)D . (, 2)6. （2分）记实数中的最大数为max{} , 最小数为min{}，则max{min{}}= （）A .B . 1C . 3D .7. （2分） (2015高一下·衡水开学考) 某几何体的三视图如图所示（单位：cm），则该几何体的体积是（）A . 8cm3B . 12cm3C .D .8. （2分） (2015高三上·房山期末) 如图是一个几何体的三视图，则该几何体的体积等于（）A .B .C . 1D .9. （2分） (2019高一上·成都月考) 已知函数在上是减函数，则实数的取值范围是（）A .B .C .D .10. （2分） f (x)＝(n∈Z)是偶函数，且y＝f(x)在(0，＋∞)上是减函数，则n＝（）.A . 1B . 2C . 1或2D . 311. （2分）如图所示的直观图的平面图形ABCD是（）A . 任意梯形B . 直角梯形C . 任意四边形D . 平行四边形12. （2分） (2015高一上·柳州期末) 在平面直角坐标内A，B两点满足：①点A，B都在函数y=f（x）的图象上；②点A，B关于原点对称，则称A，B为函数y=f（x）的一个“黄金点对”．则函数f（x）= 的“黄金点对”的个数为（）A . 0个B . 1个C . 2个D . 3个二、填空题 (共4题；共4分)13. （1分） (2016高一上·东海期中) 若a=log 2，b=log ，c=（）0.3 ，则，a，b，c的大小关系为________．14. （1分）(2018·临川模拟) 已知三棱锥的各顶点在一个表面积为的球面上，球心在上，平面， ,则三棱锥的体积为________.15. （1分） (2019高一上·淄博期中) 已知函数，若，则 ________.16. （1分） (2019高三上·苏州月考) 已知，，则________.三、解答题 (共6题；共55分)17. （5分）已知集合A={x|x2﹣2x﹣15≤0}，B={x|m﹣2＜x＜2m﹣3}，且B⊆A，求实数m的取值范围．18. （10分） (2017高一上·濉溪期末) 已知函数f（x）=ax+ +c是奇函数，且满足f（1）= ，f（2）= ．（1）求a，b，c的值；（2）试判断函数f（x）在区间（0，）上的单调性并证明．19. （10分）已知函数（a、b是常数且a＞0，a≠1）在区间[﹣，0]上有ymax=3，ymin= ;（1）试求a和b的值．（2）又已知函数f（x）=lg（ax2+2x+1）①若f（x）的定义域是R，求实数a的取值范围及f（x）的值域；②若f（x）的值域是R，求实数a的取值范围及f（x）的定义域．20. （10分） (2016高一上·高青期中) 已知函数f（x）的定义域为[﹣2，2]，若对于任意的x，y∈[﹣2，2]，都有f（x+y）=f（x）+f（y），且当x＞0时，有f（x）＞0（1）证明：f（x）为奇函数；（2）若f（1）=3求f（x）在[﹣2，2]上的值域．21. （10分）(2017·合肥模拟) [选修4-5：不等式选讲]已知函数．（1）求函数f（x）的定义域；（2）若当x∈[0，1]时，不等式f（x）≥1恒成立，求实数a的取值范围．22. （10分） (2019高二下·深圳期中) 选修4-5：不等式选讲设函数 .（1）解不等式；（2），恒成立，求实数的取值范围.参考答案一、选择题 (共12题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题；共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题；共55分) 17-1、18-1、18-2、19-1、19-2、20-1、20-2、21-1、21-2、22-1、22-2、。

吉林省白城市高一下学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共24分)1. （2分）已知圆C：， Q是x轴上的一点，QM,QN分别切圆C于M,N两点，且，则直线MN的斜率为（）A . 2B .C . 1D .2. （2分） (2018高一下·伊春期末) 经过点A（2，3）且与直线垂直的直线方程为（）A .B .C .D .3. （2分）若α，β，γ表示平面，m，n表示直线，则下列命题中，正确的是（）A . m⊂α，n⊂α，m∥β，n∥β，则α∥βB . 若α⊥γ，β⊥γ，则α∥βC . 若α∥β，m⊂α，n⊂β，则m∥nD . 若α∥β，m⊂α，则m∥β4. （2分） (2019高一上·兰州期末) 半径为的半圆卷成一个圆锥，则它的体积为（）.A .B .C .D .5. （2分）左面的三视图所示的几何体是（）A . 六棱台B . 六棱柱C . 六棱锥D . 六边形6. （2分） (2019高二下·湖南期中) 曲线 : ( 为参数)上的点到曲线 :(t为参数)上的点的最短距离为（）A . 1B . 2C . 3D . 47. （2分）“”是“直线与直线互相平行”的（）A . 充分不必要条件B . 必要不充分条件C . 充分必要条件D . 既不充分也不必要条件8. （2分） (2019高二上·汇川期中) 正方体ABCD—A′B′C′D′中，AB的中点为M，DD′的中点为N，则异面直线B′M与CN所成角的大小为（）A . 0°B . 45°C . 60 °D . 90°9. （2分）直三棱柱ABC﹣A1B1C1中，底面是正三角形，三棱往的高为，若P是△A1B1C1中心，且三棱柱的体积为，则PA与平面ABC所成的角大小是（）A .B .C .D .10. （2分）双曲线-=1的渐近线与圆（x-3）2+y2=r2（r＞0）相切，则r=（）A .B . 2C . 3D . 611. （2分）(2017·兰州模拟) 已知一正方体截去两个三棱锥后，所得几何体的三视图如图所示，则该几何体的体积为（）A . 8B . 7C .D .12. （2分）设圆上有且仅有两个点到直线的距离等于1，则圆半径r的取值范围是（）A .B .C .D .二、填空题 (共4题；共4分)13. （1分） (2018高二上·寻乌期末) 已知，若且，则的取值范围为________．14. （1分） (2018高一下·虎林期末) 已知直线l的斜率为1，与两坐标轴围成三角形的面积为4，则直线l 的方程为________ 。

吉林省白城市高一下学期期末数学考试试卷（理科）姓名:________班级:________成绩:________一、 选择题 (共 12 题；共 24 分)1. （2 分） 下列函数中，既是奇函数，又是增函数是（ ）A . f（x）=x|x|B . f（x）=﹣x3C . f（x）=D . f（x）=2. （2 分） 函数的零点所在的区间是 （ ）A. B. C. D. 3. （2 分） (2016 高二上·平原期中) 设 m、n 是两条不同的直线，α、β 是两个不同的平面，则下列命题中 正确的是（ ） A . 若 m∥n，m∥α，则 n∥α B . 若 α⊥β，m∥α，则 m⊥β C . 若 α⊥β，m⊥β，则 m∥α D . 若 m⊥n，m⊥α，n⊥β，则 α⊥β4.（2 分）(2016 高一下·长春期中) 在△ABC 中，内角 A，B，C 所对的边分别是 a，b，c，若 3a=2b，则 的值为（ ）第 1 页 共 11 页A.﹣B. C.1D.5. （2 分） 已知等比数列{an}中，a3=2，a4a6=16，则 A.2 B.4 C.8 D . 16=（ ）6. （2 分） (2017 高一下·黄冈期末) 从点（2，3）射出的光线沿斜率 k= 线所在的直线方程为（ ）的方向射到 y 轴上，则反射光A . x+2y﹣4=0B . 2x+y﹣1=0C . x+6y﹣16=0D . 6x+y﹣8=07. （2 分） (2016 高二上·开鲁期中) 若 α，β 为锐角，且满足 cosα= 的值为（ ），cos（α+β）=，则 sinβA.﹣B.C.第 2 页 共 11 页D. 8. （2 分） 若动点 A（x1 ， y2）、B（x2 ， y2）分别在直线 l1：x+y﹣11=0 和 l2：x+y﹣1=0 上移动，则 AB 中点 M 所在直线方程为（ ） A . x﹣y﹣6=0 B . x+y+6=0 C . x﹣y+6=0 D . x+y﹣6=0 9. （2 分） (2017 高一下·黄冈期末) 已知某几何体的三视图如图所示，其中，正（主）视图，侧（左）视 图均是由三角形与半圆构成，俯视图由圆与内接三角形构成，根据图中的数据可得此几何体的体积为（ ）A. B.C.D.10. （2 分） (2017 高一下·黄冈期末) 将正偶数集合{2，4，6，…}从小到大按第 n 组有 2n 个偶数进行分组： {2，4}，{6，8，10，12}，{14，16，18，20，22，24}，…，则 2018 位于（ ）组．A . 30第 3 页 共 11 页B . 31 C . 32 D . 3311. （2 分） (2017 高一下·黄冈期末) 已知实数 x，y 满足 A . [﹣1， ]，则 ω=的取值范围是（ ）B . [﹣ ， ]C . [﹣ ，1）D . [﹣ ，+∞）12. （2 分） (2017 高一下·黄冈期末) 在正方体 ABCD﹣A1B1C1D1 中，E 是棱 CC1 的中点，F 是侧面 BCC1B1 内的动点，且 A1F∥平面 D1AE，则 A1F 与平面 BCC1B1 所成角的正切值 t 构成的集合是（ ）A . {t|}B . {t|≤t≤2}C . {t|2}D . {t|2}二、 填空题 (共 4 题；共 4 分)第 4 页 共 11 页13. （1 分） (2016 高一上·灌云期中) 已知函数 f（x）=，若 f（x）=3，则 x=________．14. （1 分） (2018 高一下·珠海月考) 已知，________.，,则15. （1 分） (2019 高一下·大庆月考)中， 、 、 成等差数列，∠B=30°，，那么 b =________.16. （1 分） 第三象限角的集合表示为________．三、 解答题 (共 6 题；共 65 分)17. （5 分） 已知△ABC 中 A（3，2）、B（﹣1，5），C 点在直线 3x﹣y+3=0 上，若 S△ABC=10，求△ABC 外接 圆的方程．18. （10 分） (2020·江西模拟) 已知椭圆 ： 轴长的 倍.过点，且它的焦距是短（1） 求椭圆 的方程.（2） 若 ， 是椭圆 上的两个动点（ ， 两点不关于 轴对称）， 为坐标原点， ，的斜率分别为 ， ，问是否存在非零常数 ，使当时，的面积 为定值？若存在，求的值；若不存在，请说明理由.19. （15 分） 在平面直角坐标系中，O 为坐标原点，A、B、C 三点满足=+．（1） 求证：A、B、C 三点共线；（2） 求的值；（3） 已知 A（1，cosx）、B（1+cosx，cosx），x∈[0， ]，f（x）=•﹣（2m+ ）| |的最小值为﹣ ，求实数 m 的值．20.（10 分）(2020·榆林模拟) 已知动圆过定点，且与直线第 5 页 共 11 页相切，动圆圆心的轨迹为 ，过 作斜率为的直线 与 交于两点线 与 交于两点．，过分别作 的切线，两切线的交点为 ，直（1） 证明：点 始终在直线 上且；（2） 求四边形的面积的最小值．21. （10 分） (2017 高一下·黄冈期末) 某投资公司计划投资 A，B 两种金融产品，根据市场调查与预测，A产品的利润 y1 与投资金额 x 的函数关系为 y1=18﹣，B 产品的利润 y2 与投资金额 x 的函数关系为 y2=（注：利润与投资金额单位：万元）．（1） 该公司已有 100 万元资金，并全部投入 A，B 两种产品中，其中 x 万元资金投入 A 产品，试把 A，B 两种 产品利润总和表示为 x 的函数，并写出定义域；（2） 在（1）的条件下，试问：怎样分配这 100 万元资金，才能使公司获得最大利润？其最大利润为多少万 元？22.（15 分）(2017 高一下·黄冈期末) 已知曲线 f（x）=（x＞0）上有一点列 Pn（xn ，yn）（n∈N*），过点 Pn 在 x 轴上的射影是 Qn（xn ， 0），且 x1+x2+x3+…+xn=2n+1﹣n﹣2．（n∈N*）（1） 求数列{xn}的通项公式；（2） 设四边形 PnQnQn+1Pn+1 的面积是 Sn ， 求 Sn；（3） 在（2）条件下，求证： ++…+＜4．第 6 页 共 11 页一、 选择题 (共 12 题；共 24 分)1-1、 2-1、 3-1、 4-1、 5-1、 6-1、 7-1、 8-1、 9-1、 10-1、 11-1、 12-1、二、 填空题 (共 4 题；共 4 分)13-1、 14-1、 15-1、参考答案第 7 页 共 11 页16-1、三、 解答题 (共 6 题；共 65 分)17-1、18-1、18-2、第 8 页 共 11 页19-1、 19-2、第 9 页 共 11 页19-3、20-1、20-2、21-1、第 10 页 共 11 页21-2、22-1、22-2、22-3、第11 页共11 页。