条件logistic回归模型的SAS计算程序

利用SAS宏程序进行单因素Logistic回归分析在做单因素logistic回归时，如果有十几个自变量，每个自变量都运行一遍程序，然后把sas结果黏贴到word里再修改，最后合并生成一个汇总的数据，无疑是件很麻烦的事情，所以我编了一段程序，可以自动的汇总生成报表，省了很多事啊！欢迎大家共同交流宏程序如下：%macro log1(data,yy,xx,num); /*data=分析数据集，yy=应变量，xx=自变量，num=自变量个数%do i=1 %to #%let var_=%sysfunc(scan(&xx,&i,’ ‘));ods output ParameterEstimates=&var_.1 OddsRatios=&var_.2;proc logistic data=&data desc ;model &yy=&var_; run;data &var_.1(drop=i);set &var_.1;i=_n_;if i=1 then delete; run;data &var_ (drop=effect df);merge &var_.1 &var_.2;run;proc delete data=&var_.1 &var_.2;run;%end;data log1;set &xx;proc print noobs data=log1;proc delete data=log1 &xx;run;%mend;测试一下：%log1(factor,tw1,sex agegroup b4 b5 b6 b7 b10 b11 b12 b32a b32b b32c b32d,13);效果显示如下，（sas9.2自动生成html格式结果，stype选择journal）以上程序注意，logistic回归增加了desc选项，表示取2的概率。

[SAS] Logistic回归程序代码和输出结果基于贝叶斯判别的房地产信用评级研究本文首先采用Logistic回归法筛选出4个财务指标作为评价函数的计量参数，再构造Bayes判别算法建立信用评估模型，将其应用于某些房地产企业的实际数据分析，并评估其评判效果。

程序代码data LOGIT;input g x1-x10 @@ ; /* 输入数据和对应的变量名称，指定数据是按顺序对应变量(@@) */cards;1 76.02 112.16 52.65 16.24 4.17 88.54 -1.93 98.07 -58.63 -1.931 50.15 53.55 6.18 5.81 0.77 6.91 5.89 105.89 18.21 5.891 35.94 8.04 0.25 12.89 0.04 11.54 0.25 100.25 3.56 0.252 36.03 65.44 5.07 4.71 0.77 -4.21 2.42 102.42 47.27 2.422 76.95 86.32 -6.38 14.28 -0.51 101.50 -6.18 93.82 34.19 -6.182 36.36 37.91 6.01 10.78 0.87 -11.03 6.20 106.20 43.43 6.202 45.44 46.41 -1.09 14.04 -0.14 82.45 130.53 230.53 -82.56 130.532 48.80 43.19 6.97 11.15 0.94 20.58 8.62 108.62 7.67 8.622 21.09 45.85 6.10 13.79 0.00 32.70 6.86 106.86 -91.48 6.862 26.38 1.14 16.25 7.98 2.26 -31.83 15.26 115.26 63.42 15.262 32.61 26.18 8.51 22.08 1.45 10.71 8.89 108.89 6.14 8.892 25.16 57.63 20.94 23.88 3.44 -0.98 30.46 130.46 60.45 30.462 48.47 39.56 8.23 10.76 1.06 7.67 8.56 108.56 45.65 8.563 52.05 75.95 24.12 13.18 2.50 -7.47 24.90 124.90 18.17 24.903 86.92 14.00 4.55 10.96 0.38 -23.56 -79.83 20.17 36.01 -79.833 39.96 41.87 7.10 12.04 -0.12 8.20 3.24 103.24 5.98 3.241 65.00 29.00 1.50 2.00 0.16 54.55 -0.63 99.37 -58.34 -0.632 66.20 30.52 21.51 23.18 1.77 16.29 23.42 123.42 31.15 23.42…………;proc logistic data=LOGIT des; /* 选择Logistic回归模型对这个数据进行分析，对因变量设置des概率 */model g=x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 /selection=stepwise slentry=0.15 slstay=0.15; /* 指定因变量和自变量，逐步选择变量，设置stepwise显著性水平0.15*/run;输出结果SAS 系统 2012年05月26日星期六下午12时31分22秒 1The LOGISTIC ProcedureModel InformationData Set W ORK.LOGITResponse Variable gNumber of Response Levels 3Model cumulative logitOptimization Technique Fisher's scoringNumber of Observations Read 48Number of Observations Used 48Response ProfileOrdered TotalValue g Frequency1 3 132 2 313 1 4Probabilities modeled are cumulated over the lower Ordered Values.Stepwise Selection ProcedureStep 0. Intercepts entered:Model Convergence StatusConvergence criterion (GCONV=1E-8) satisfied.-2 Log L = 80.949。

只能控制少数因素（分层因素过多 ，每个格子中的样本例数太少）
定量资料需要分组，信息丢失 不能对因素作用大小进行定量分析
（交互作用）
二、Logistic 回归原理
y
01
经过数理统计学家证明：把疾病概率 P 转换成
y
=
log2lxn
1
p
p
，会使该回归方程的统计性能更好一些。而且，
在经过转换以后，
...... px11 ...... 1 px11 p x1 0
1 x1 1 x1
1 px10
e 11
= e 10
= e1
假设建立了如下的logistic回归方程：
Logit P = α + βx
x 为二分变量，当暴露时，取值为1；
不暴露时，取值为0。
所以暴露时,
Logit(P1) = α + β， 比值(odds) = exp(α + β )
变化对似然比的影响，来检验增加/减少的自 变量是否对应变量有统计学上的显著意义。
检验统计量： G = -2 [ Ln (Lk－1) - Ln (Lk) ] Ln ((Lk－1)为不包含检验变量时模型的对数 似然值 Ln (Lk)为包含检验变量时模型的对数似然值
当检验一个变量时则G服从自由度为1的 χ2 分 ∞到+∞，而且这
些
ln1
p
p
值都可以和在大于
0
小于
1
范围内的
P
值相对
应。统计学中，常把
ln
1
p
p
称为
Logit
变换。
Logistic 回归方程：
ln 1
p
p

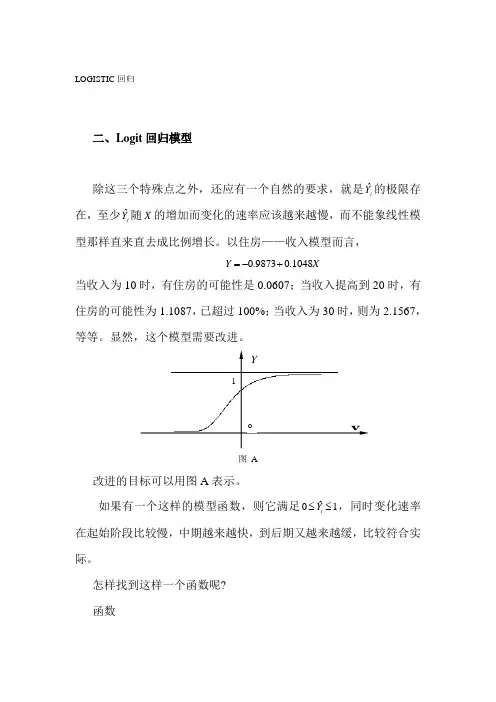
LOGISTIC 回归二、Logit 回归模型除这三个特殊点之外，还应有一个自然的要求，就是i Y ˆ的极限存在，至少iY ˆ随X 的增加而变化的速率应该越来越慢，而不能象线性模型那样直来直去成比例增长。

以住房——收入模型而言，XY 1048.09873.0+-=当收入为10时，有住房的可能性是0.0607；当收入提高到20时，有住房的可能性为1.1087，已超过100%；当收入为30时，则为2.1567，等等。

显然，这个模型需要改进。

图 A改进的目标可以用图A 表示。

如果有一个这样的模型函数，则它满足ˆ01iY ≤≤，同时变化速率在起始阶段比较慢，中期越来越快，到后期又越来越缓，比较符合实际。

怎样找到这样一个函数呢? 函数1o1()11xx xe f x e e-==++ 具有此性质 原来是i i i X X Y E P 10)|1(ββ+===如果改进为)(1011)|1(i X i i eX Y E P ββ+-+===则01i P ≤≤，并且i P 在X →±∞时变化越来越缓。

记01i i Z X ββ=+，则iZ i eP -+=11 111ii i Z Q P e =-=+ iii Z Z Z i i e e e P P =++=--111i i iiX Z P P 1011nββ+==-这就得到了我们需要的Logit 模型函数，原来是对它取了对数，故名Log it 。

这个函数不是i P 与i X 呈线性关系，而是iiP P -11n与i X 呈线性关系。

当X →±∞时， 10<<i P 。

i P 与i X 的关系曲线正是上图表示的S 形曲线。

将自变量扩充为多元，加上随机项，就得到一般的Logit 回归模型：i i iiX P P εβ+'=-11n如果我们从这个模型中得到β的估计βˆ，就可以估计出第i 个样本有(或无)的可能性iP ˆ。

但是又产生一个新问题，我们如何得到βˆ呢? 如果从原来的二值选择数据出发，我们连回归模型都建立不起来。

费雪信息矩阵(Fisher information
•
matrix)
E( 2l )
1 pi pi
rs i pi (1 pi ) r s
i
(pi / pi (1
i )2
pi )
xir
xis
{X TWX }rs
• 这里
W
diag{( pi
i
)2
/
pi (1
pi )}
• 当 i g( pi ) 是逻辑连系函数时
逻辑回归模型
:
pi
1
1 e(0
1 xi
)
0 1xi
1 e e0 1xi
而事件不发生的概率 1 pi
1
1
e
0 1xi
e0 1xi
1
1 e0
1 xi
则事件不发生的概率与事件不发生的概率之比
p e i
0 1xi
1 pi
2. log istic回归模型
p
e0 1x 1 e0 1x
p
e 0 1x
model y x1 x2 x3 / LACKFIT scale aggregate;
run;
4.信息测量指标(Information Measures)
AIC (aKAIKE' S inf ormation criterion)指标
AIC 2LLS 2(K S) n
其中, K为自变量数目, S 响应变量类别数1, n样本容量, LLS 所设模型的极大似然估计的对数.
3.HOSMER-Lemeshow拟合优度指标
HL 指标(用于变量多 )
H0 : 观测值 预测值.
G
HL
Yg ng pˆ g

复习：
医学研究者经常关心的问题
哪些因素导致了人群中有的人患胃癌而有的人不患胃癌? 哪些因素导致了手术后有的人感染，而有的人不感染？ 哪些因素导致了某种治疗方法出现治愈、显效、好转、无效等不
同的效果?
是回归分析问题: Y=f(x)
复习：
回归分析的分类
一个 因变 量y
连续型因变量 (y) --- 线性回归分析 分类型因变量 (y) ---Logistic 回归分析 生存时间因变量 (t) ---生存风险回归分析 时间序列因变量 (t) ---时间序列分析
log
it(
p)
In
p 1
p
0.9099＋0.8856x1
0.5261x2
用编程法作二分类logisitc回归
Proc logistic data=sasuser.eg9_1 descend; freq f; model y=x1 x2 /selection=stepwise sle=0.05 sls=0.05;
态分析； 等方差 Equal variance：指自变量的取值不同时，因变量Y的总体变异保
持不变（用总体方差 2 表示）。
复习：
回归分析的分类
一个 因变 量y
连续型因变量 (y) --- 线性回归分析 分类型因变量 (y) ---Logistic 回归分析 生存时间因变量 (t) ---生存风险回归分析 时间序列因变量 (t) ---时间序列分析
多个因变量 (y1,y2…yk)
路径分析 结构方程模型分析
复习：
线性回归分析
研究一个正态随机变量Y与一个或多个自变量X1，X2，X3，…，Xm 间的 线性关系。其回归方程为：Yˆ b0 b1X1 b2 X2 bmXm

SA S软件计算条件L og istic回归的方法比较娄冬华,于浩[摘要]　在病因学研究中,常用1:1配对的L ogistic回归来探讨危险因素的作用,SA S软件中作条件L ogistic回归的方法很多,本文介绍几种常用方法,对几种方法作出比较,发现使用SA S软件的宏程序可以很方便地解决此问题。

[关键词]　条件L ogistic回归;宏程序[中图分类号]O21214 [文献标识码]A [文章编号]100328507(2003)0620769202THE COM PAR ING OF S OM E M ETHOD S T O CALCULATE COND IT I ONAL LOGIST I C REGRESSI ON IN USING SAS S OFT W ARE1L OU D ong2hua,YU H ao1Ep id e m iology and B iostatistics D ep art m ent N anj ing M ed ical U nivari2 ate,N anj ing,2100291Abstract:In study of disease cau se,w e often u se1:1m atch ing to study the risk facto r1T here is m any m ethods to calcu late conditi onal logistic regressti on in SA S softw are,th is paper take som e m ethods and compare them1T he resu lt is that u sing m acro p rocedu re in SA S softw are can easily so lve th is questi on1Key words:Conditi onal logistic regressi on;M acro p rocedu re SA S软件(Statistical A nalysis System)是当前国际上最流行的、最具权威性的统计分析软件。

MODEL语句

第二种形式为： model events/trails=independents<\options>; 该模型称为事件/试验模型，即样本资料是分 组的或样本来自于分组试验的结果。 该模型等式左边必须指定分组试验次数的变量， 相当于模型中trails； 以及试验中某事件发生次数的变量，相当于模 型中的events，用“/”分开。
GISTIC过程
一般格式： proc logistic<options>; model dependent=independents</options>; by variables; freq variable; weight variable; output<out=sas-data-set>keyword=names;

逻辑斯蒂回归与LOGISTIC过程
本节我们将介绍因变量为属性变量，且只 有是或不是两个取值的回归模型。 在实际工作中，我们经常遇到这样的问题： 给定家庭收入、食品支出额、人口数以及收入 最高者的年龄，问该家庭是否购买了住房？给 定企业的财务数据，问该企业破产或陷于财务 困难的可能性有多大？再比如，在信贷过程中， 银行非常关心一笔贷款是否能按时收回，即借 款单位是否会违约。

OUTPUT语句
一般格式： output out=sas-data-set keyword=names; output语句创建一个新的SAS数据集，它包括输入 数据集中的所有变量，以及规定的统计量。常见 的统计量有： （1）p=：计算因变量的预测概率； （2）xbeta= ：计算对数单位的预测值。

逻辑斯蒂函数

逻辑斯蒂函数又称增长函数，是由美国学 者皮尔和瑞德在研究果蝇的繁殖中提出的，其 一般表达式为：

如前所述，逻辑回归是一种用于解决 二元分类问题的机器学习算法，基于 逻辑函数拟合数据来预测事件发生的 概率。它在处理具有连续特征的数据 集时表现良好，并且可以用于预测概 率。
比较
支持向量机和逻辑回归在处理分类问 题时各有优缺点。SVM的优点在于其 强大的分类能力和对高维数据的处理 能力，尤其在处理线性可分的数据集 时表现优秀。而逻辑回归在处理具有 连续特征的数据集和预测概率方面表 现良好，且对于非线性数据集的处理 能力较强。
与决策树算法的比较
决策树算法
决策树算法是一种基于树的机器学习算法，通过递归地将数据集划分为更小的子集来构建 模型。它能够处理分类和回归问题，并且易于理解和解释。
逻辑回归
逻辑回归是一种用于解决二元分类问题的机器学习算法。它基于逻辑函数，通过拟合数据 来预测事件发生的概率。逻辑回归在处理具有连续特征的数据集时表现良好，并且可以用 于预测概率。
比较
决策树算法和逻辑回归在处理分类问题时各有优缺点。决策树算法可以处理更复杂的数据 集，但可能过拟合数据。逻辑回归在处理具有连续特征的数据集时表现良好，并且可以用 于预测概率，但可能不适用于具有大量特征的数据集。
与支持向量机算法的比较
支持向量机算法
逻辑回归
支持向量机（SVM）是一种监督学习 算法，用于分类和回归分析。它通过 找到能够将不同类别的数据点最大化 分隔的决策边界来实现分类。SVM对 于非线性数据集的处理能力有限，且 对于大规模数据集可能效率较低。
通过将自变量代入逻辑函数中，可以得到因变量的预测概率值，进而判断 其所属类别。
02 SASlogistic逻辑回归的 实现
SASlogistic逻辑回归的步骤
数据准备
对数据进行清洗、整理和转换， 确保数据的质量和可用性。

[SAS] Logistic回归程序代码和输出结果基于贝叶斯判别的房地产信用评级研究本文首先采用Logistic回归法筛选出4个财务指标作为评价函数的计量参数，再构造Bayes判别算法建立信用评估模型，将其应用于某些房地产企业的实际数据分析，并评估其评判效果。

程序代码data LOGIT;input g x1-x10 @@ ; /* 输入数据和对应的变量名称，指定数据是按顺序对应变量(@@) */cards;1 76.02 112.16 52.65 16.24 4.17 88.54 -1.93 98.07 -58.63 -1.931 50.15 53.55 6.18 5.81 0.77 6.91 5.89 105.89 18.21 5.891 35.94 8.04 0.25 12.89 0.04 11.54 0.25 100.25 3.56 0.252 36.03 65.44 5.07 4.71 0.77 -4.21 2.42 102.42 47.27 2.422 76.95 86.32 -6.38 14.28 -0.51 101.50 -6.18 93.82 34.19 -6.182 36.36 37.91 6.01 10.78 0.87 -11.03 6.20 106.20 43.43 6.202 45.44 46.41 -1.09 14.04 -0.14 82.45 130.53 230.53 -82.56 130.532 48.80 43.19 6.97 11.15 0.94 20.58 8.62 108.62 7.67 8.622 21.09 45.85 6.10 13.79 0.00 32.70 6.86 106.86 -91.48 6.862 26.38 1.14 16.25 7.98 2.26 -31.83 15.26 115.26 63.42 15.262 32.61 26.18 8.51 22.08 1.45 10.71 8.89 108.89 6.14 8.892 25.16 57.63 20.94 23.88 3.44 -0.98 30.46 130.46 60.45 30.462 48.47 39.56 8.23 10.76 1.06 7.67 8.56 108.56 45.65 8.563 52.05 75.95 24.12 13.18 2.50 -7.47 24.90 124.90 18.17 24.903 86.92 14.00 4.55 10.96 0.38 -23.56 -79.83 20.17 36.01 -79.833 39.96 41.87 7.10 12.04 -0.12 8.20 3.24 103.24 5.98 3.241 65.00 29.00 1.50 2.00 0.16 54.55 -0.63 99.37 -58.34 -0.632 66.20 30.52 21.51 23.18 1.77 16.29 23.42 123.42 31.15 23.42…… ……;proc logistic data=LOGIT des; /* 选择Logistic回归模型对这个数据进行分析，对因变量设置des概率 */model g=x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 /selection=stepwise slentry=0.15 slstay=0.15; /* 指定因变量和自变量，逐步选择变量，设置stepwise显著性水平0.15*/run;输出结果SAS 系统 2012年05月26日星期六下午12时31分22秒 1The LOGISTIC ProcedureModel InformationData Set WORK.LOGITResponse Variable gNumber of Response Levels 3Model cumulative logitOptimization Technique Fisher's scoringNumber of Observations Read 48Number of Observations Used 48Response ProfileOrdered TotalValue g Frequency1 3 132 2 313 1 4Probabilities modeled are cumulated over the lower Ordered Values.Stepwise Selection ProcedureStep 0. Intercepts entered:Model Convergence StatusConvergence criterion (GCONV=1E-8) satisfied.-2 Log L = 80.949Residual Chi-Square TestChi-Square DF Pr > ChiSq13.0922 8 0.1087NOTE: No (additional) effects met the 0.05 significance level for entry into the model.Analysis of Maximum Likelihood EstimatesStandard WaldParameter DF Estimate Error Chi-Square Pr > ChiSqIntercept 3 1 -0.9904 0.3248 9.2980 0.0023Intercept 2 1 2.3979 0.5222 21.0830 <.0001SAS 系统2012年05月26日星期六下午12时31分22秒 2The LOGISTIC ProcedureModel InformationData Set WORK.LOGITResponse Variable gNumber of Response Levels 3Model cumulative logitOptimization Technique Fisher's scoringNumber of Observations Read 48Number of Observations Used 48Response ProfileOrdered TotalValue g Frequency1 3 132 2 313 1 4Probabilities modeled are cumulated over the lower Ordered Values.Stepwise Selection ProcedureStep 0. Intercepts entered:Model Convergence StatusConvergence criterion (GCONV=1E-8) satisfied.-2 Log L = 80.949Residual Chi-Square TestChi-Square DF Pr > ChiSq13.0922 8 0.1087Step 1. Effect x4 entered:Model Convergence StatusConvergence criterion (GCONV=1E-8) satisfied.Score Test for the Proportional Odds AssumptionChi-Square DF Pr > ChiSq4.7698 1 0.0290SAS 系统2012年05月26日星期六下午12时31分22秒 3The LOGISTIC ProcedureModel Fit StatisticsInterceptIntercept andCriterion Only CovariatesAIC 84.949 83.246SC 88.691 88.859-2 Log L 80.949 77.246Testing Global Null Hypothesis: BETA=0Test Chi-Square DF Pr > ChiSqLikelihood Ratio 3.7032 1 0.0543Score 3.7112 1 0.0540Wald 3.2133 1 0.0730Residual Chi-Square TestChi-Square DF Pr > ChiSq10.0282 7 0.1870NOTE: No effects for the model in Step 1 are removed.Step 2. Effect x6 entered:Model Convergence StatusConvergence criterion (GCONV=1E-8) satisfied.Score Test for the Proportional Odds AssumptionChi-Square DF Pr > ChiSq5.0078 2 0.0818Model Fit StatisticsInterceptIntercept andCriterion Only CovariatesAIC 84.949 81.703SC 88.691 89.187-2 Log L 80.949 73.703Testing Global Null Hypothesis: BETA=0Test Chi-Square DF Pr > ChiSqLikelihood Ratio 7.2465 2 0.0267Score 6.9374 2 0.0312Wald 6.1144 2 0.0470SAS 系统2012年05月26日星期六下午12时31分22秒 4The LOGISTIC ProcedureResidual Chi-Square TestChi-Square DF Pr > ChiSq7.4184 6 0.2839NOTE: No effects for the model in Step 2 are removed.Step 3. Effect x5 entered:Model Convergence StatusConvergence criterion (GCONV=1E-8) satisfied.Score Test for the Proportional Odds AssumptionChi-Square DF Pr > ChiSq6.0306 3 0.1101Model Fit StatisticsInterceptIntercept andCriterion Only CovariatesAIC 84.949 80.027SC 88.691 89.383-2 Log L 80.949 70.027Testing Global Null Hypothesis: BETA=0Test Chi-Square DF Pr > ChiSqLikelihood Ratio 10.9224 3 0.0122Score 9.5728 3 0.0226Wald 8.8338 3 0.0316Residual Chi-Square TestChi-Square DF Pr > ChiSq3.7605 5 0.5844Step 4. Effect x4 is removed:Model Convergence StatusConvergence criterion (GCONV=1E-8) satisfied.Score Test for the Proportional Odds AssumptionChi-Square DF Pr > ChiSq1.4638 2 0.4810SAS 系统2012年05月26日星期六下午12时31分22秒 5The LOGISTIC ProcedureModel Fit StatisticsInterceptIntercept andCriterion Only CovariatesAIC 84.949 78.987SC 88.691 86.471-2 Log L 80.949 70.987Testing Global Null Hypothesis: BETA=0Test Chi-Square DF Pr > ChiSqLikelihood Ratio 9.9625 2 0.0069Score 8.5919 2 0.0136Wald 8.0936 2 0.0175Residual Chi-Square TestChi-Square DF Pr > ChiSq4.6568 6 0.5885NOTE: No effects for the model in Step 4 are removed.NOTE: No (additional) effects met the 0.15 significance level for entry into the model.Summary of Stepwise SelectionEffect Number Score WaldStep Entered Removed DF In Chi-Square Chi-Square Pr > ChiSq1 x4 1 1 3.7112 0.05402 x6 1 2 3.3464 0.06743 x5 1 3 3.6124 0.05734 x4 1 2 0.9037 0.3418Analysis of Maximum Likelihood EstimatesStandard WaldParameter DF Estimate Error Chi-Square Pr > ChiSqIntercept 3 1 -0.2253 0.4165 0.2927 0.5885Intercept 2 1 3.7752 0.8090 21.7733 <.0001x5 1 -0.7061 0.2951 5.7259 0.0167x6 1 -0.0203 0.00878 5.3502 0.0207Odds Ratio EstimatesPoint 95% WaldEffect Estimate Confidence Limitsx5 0.494 0.277 0.880x6 0.980 0.963 0.997SAS 系统2012年05月26日星期六下午12时31分22秒 6The LOGISTIC ProcedureAssociation of Predicted Probabilities and Observed ResponsesPercent Concordant 72.7 Somers' D 0.459Percent Discordant 26.8 Gamma 0.462Percent Tied 0.5 Tau-a 0.236Pairs 579 c 0.730。

204 SAS 统计分析与应用从入门到精通111()(()()2211a d b c e L e e βββ=++ 类似于非条件Logistic 回归分析的参数估计，就可以得到β的最大似然估计如下：ˆln(cbβ= 适用于配对比例对照资料的条件Logistic 回归模型的一般形式如下： log ()ln 1P it P x Pβ==- 11.2.2 条件Logistic 回归的SAS 程序用于条件Logistic 回归分析的过程步一般借用生存数据风险回归分析的PHREG 过程步。

使用PHREG 过程步时，要注意数据的输入方法和过程步语句的写法。

PHREG 过程步的一般格式如下：Proc phreg data= ;Model 因变量*截尾变量=协变量/ ties=risklimits selection= sle= sls details; Strata 分组变量;Run;其语句格式解释如下。

MODEL 语句：用于指定模型的结构，适用于生存时间有右截尾的情况，且生存时间变量作为模型的因变量，协变量作为模型的自变量。

TIES ：用来选择处理生存时间结点的方法，每一种方法使用了不同的公式来计算最大似然值。

RISKLIMITS ：指令输出危险比的95%置信区间，供选择的有：backward 、forward 、stepwise 、score 。

SLE ：指定协变量进入模型的显著水平，缺省值是0.05。

SLS ：指定协变量停留在模型中的显著水平，缺省值是0.05。

DETAILS ：指令输出逐步回归过程中每一步的详细分析结果。

STRATA ：指定用于分组计算的分组变量。

如果分组变量的数值不符合分组要求，则在变量后面的括号内列出分组的端点值。

例11-6 某研究机构为了研究胃癌与饮酒的相关关系，收集了病例对照资料如表11-9所示，其中D 和D '分别表示患有胃癌和未患有胃癌，E 和E '分别表示饮酒和不饮酒。

模型选择与灵活性
R提供了多种Logistic回归变种，如glm()函数， 且定制性更强。
并行计算与性能
R在并行计算方面有优势，适合处理大规模数据集。
THANKS FOR WATCHING
感谢您的观看
Logistic回归
Logistic回归是一种用于解决分类问题的统计方法。它使用逻辑函数将线性回归 的输出转换为概率，从而可以预测一个事件发生的概率。在Logistic回归中，自 变量可以是连续的或分类的，因变量只能是二元分类结果。
02 Logistic回归基础
定义和原理
定义
Logistic回归是一种用于解决二分类 问题的统计方法，通过构建逻辑函数 来预测事件发生的概率。
泛化能力
模型的泛化能力是指在新数据上的预测性能。为了提高模型 的泛化能力，需要避免过拟合，并确保模型具有足够的代表 性。
外部验证
可以使用独立的验证集对模型进行外部验证，以评估模型的 泛化能力。外部验证可以帮助我们了解模型在实际应用中的 表现。
06 SAS的Logistic回归与其 他软件的比较
与SPSS的比较
结果准误、显著性等。
预测准确度
02
根据模型预测结果与实际结果的对比，评估模型的预测准确度。
模型解释性
03
理解自变量对因变量的影响程度和方向，以及模型的可解释性。
04 案例分析
数据来源和预处理
数据来源
本案例所使用的数据集来源于某大型银行的历史客户数据。数据集包含了客户的基本信息、信用历史、收入状况、 贷款申请信息等。
数据转换
对分类变量进行适当的编码，如将分类变量转换 为虚拟变量。
3
数据探索
了解数据的分布和特征，为后续建模提供依据。

使用条件：应变量Y是一个二值变量，取值为0和1自变量X1，X2，……，Xm。

P表示在m个自变量作用下事件发生的概率。

图像：程序：data ceshi; input x1-x18 y; cards; ……; proc logistic des; model y=x1-x18/selection=stepwise; run;例：三种药物drug取值0-2, 病情程度degree 分重-轻两类（0-1）；因变量response为治疗效果的效与无效(1-0)Data ex12_1;Input drug degree response count;Datalines;0 1 1 380 1 0 640 0 1 100 0 0 821 1 1 951 1 0 181 0 1 501 0 0 352 1 1 882 1 0 262 0 1 342 0 0 37;Proc logistic data=ex12_1 descending;Freq count;Class drug/param=ref descending;Model response=drug degree/rsq scale=n aggregate;Run;Rsq显示R2Scale, SCALE= specifies method to correct overdispersion,指定参数，=n表示不需要修正。

Aggregate计算卡方检验统计量Class 语句将分类变量化成虚拟变量，三种药用两个虚拟变量表示。

The LOGISTIC ProcedureModel InformationData Set WORK.EX12_1Response Variable responseNumber of Response Levels 2Frequency Variable countModel binary logitOptimization Technique Fisher's scoringNumber of Observations Read 12Number of Observations Used 12Sum of Frequencies Read 577Sum of Frequencies Used 577Response ProfileOrdered TotalValue response Frequency1 1 3152 0 262Probability modeled is response=1.Class Level InformationDesignClass Value Variablesdrug 2 1 01 0 10 0 0Model Convergence StatusConvergence criterion (GCONV=1E-8) satisfied. Deviance and Pearson Goodness-of-Fit Statistics Criterion Value DF Value/DF Pr > ChiSq Deviance 0.3749 2 0.1874 0.8291 Pearson 0.3689 2 0.1844 0.8316模型拟合集优度检验，Number of unique profiles: 6Model Fit StatisticsInterceptIntercept andCriterion Only CovariatesAIC 797.017 641.326SC 801.375 658.757-2 Log L 795.017 633.326R-Square 0.2444 Max-rescaled R-Square 0.3268The LOGISTIC ProcedureTesting Global Null Hypothesis: BETA=0Test Chi-Square DF Pr > ChiSqLikelihood Ratio 161.6907 3 <.0001Score 148.1598 3 <.0001Wald 118.1394 3 <.0001检验模型全部系数为0，拒绝则模型有意义Type 3 Analysis of EffectsWaldEffect DF Chi-Square Pr > ChiSqdrug 2 95.0859 <.0001degree 1 47.4607 <.0001Analysis of Maximum Likelihood EstimatesStandard WaldParameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -1.9594 0.2229 77.2441 <.0001drug 2 1 1.8342 0.2406 58.0936 <.0001drug 1 1 2.2850 0.2479 84.9472 <.0001degree 1 1.3806 0.2004 47.4607 <.0001参数估计与检验Odds Ratio EstimatesPoint 95% WaldEffect Estimate Confidence Limitsdrug 2 vs 0 6.260 3.906 10.033drug 1 vs 0 9.826 6.044 15.974degree 3.977 2.685 5.891Association of Predicted Probabilities and Observed Responses Percent Concordant 72.2 Somers' D 0.568Percent Discordant 15.4 Gamma 0.649Percent Tied 12.4 Tau-a 0.282Pairs 82530 c 0.784铸铁冶炼，要对铁加热heat和水中热处理（soaking time），n 表示铸铁块数，r 表示没有准备好轧制的铁块数。

利用SAS宏程序进行单因素Logistic回归分析在做单因素logistic回归时，如果有十几个自变量，每个自变量都运行一遍程序，然后把sas结果黏贴到word里再修改，最后合并生成一个汇总的数据，无疑是件很麻烦的事情，所以我编了一段程序，可以自动的汇总生成报表，省了很多事啊！欢迎大家共同交流宏程序如下：%macro log1(data,yy,xx,num); /*data=分析数据集，yy=应变量，xx=自变量，num=自变量个数%do i=1 %to &num;%let var_=%sysfunc(scan(&xx,&i,’ ‘));ods output ParameterEstimates=&var_.1 OddsRatios=&var_.2;proc logistic data=&data desc ;model &yy=&var_; run;data &var_.1(drop=i);set &var_.1;i=_n_;if i=1 then delete; run;data &var_ (drop=effect df);merge &var_.1 &var_.2;run;proc delete data=&var_.1 &var_.2;run;%end;data log1;set &xx;proc print noobs data=log1;proc delete data=log1 &xx;run;%mend;测试一下：%log1(factor,tw1,sex agegroup b4 b5 b6 b7 b10 b11 b12 b32a b32b b32c b32d,13);效果显示如下，（sas9.2自动生成html格式结果，stype选择journal）以上程序注意，logistic回归增加了desc选项，表示取2的概率。

回归分析与REG 过程前面我们介绍了相关分析，并且知道变量之间线性相关的程度可以通过相关系数来衡量。

但在实际工作中，仅仅知道变量之间存在相关关系往往是不够的，还需要进一步明确它们之间有怎样的关系。

换句话说，实际工作者常常想知道某些变量发生变化后，另一个相关变量的变化程度。

例如，第六章中已经证明消费和收入之间有很强的相关关系，而且也知道，消费随着收入的变化而变化，问题是当收入变化某一幅度后，消费会有多大的变化？再比如，在股票市场上，股票收益会随着股票风险的变化而变化。

一般来说，收益和风险是正相关的，也就是说，风险越大收益就越高，风险越小收益也越小，著名的资本资产定价模型（CAPM ）正说明了这种关系。

现在的问题是当某个投资者知道了某只股票的风险后，他能够预测出这只股票的平均收益吗？类似这类通过某些变量的已知值来预测另一个变量的平均值的问题正是回归分析所要解决的。

第一节 线性回归分析方法简介一、回归分析的含义及其所要解决的问题“回归”(Regression)这一名词最初是由19世纪英国生物学家兼统计学家F.Galton(F.高尔顿)在一篇著名的遗传学论文中引入的。

高尔顿发现，虽然有一个趋势：父母高，儿女也高；父母矮，儿女也矮，但给定父母的身高，儿女辈的平均身高却趋向于或者“回归”到全体人口的平均身高的趋势。

这一回归定律后来被统计学家K.Pearson 通过上千个家庭成员身高的实际调查数据进一步得到证实，从而产生了“回归”这一名称。

当然，现代意义上的“回归”比其原始含义要广得多。

一般来说，现代意义上的回归分析是研究一个变量（也称为因变量Dependent Variable 或被解释变量Explained Variable ）对另一个或多个变量（也称为自变量Independent Variable 或Explanatory Variable ）的依赖关系，其目的在于通过自变量的给定值来预测因变量的平均值或某个特定值。

条件logistic回归模型的SAS计算程序
宇传华;徐勇勇
【期刊名称】《中国卫生统计》
【年(卷),期】1997(014)005
【摘要】条件ｌｏｇｉｓｔｉｃ回归模型的ＳＡＳ计算程序第四军医大学卫生统计学教研室宇传华徐勇勇病例－对照研究资料的条件ｌｏｇｉｓｔｉｃ回归模型计算比较复杂，常需借助统计软件进行计算，国际通用软件ＳＡＳ（６．０４版本）有ＬＯＧＩＳＴＩＣ和ＰＨＲＥＧ两个过程步能较...
【总页数】2页(P50-51)
【作者】宇传华;徐勇勇
【作者单位】第四军医大学卫生统计学教研室;第四军医大学卫生统计学教研室【正文语种】中文
【中图分类】R195.4
【相关文献】
1.秩和比综合评价法的SAS计算程序
2.基于PSASP综合计算程序的阿勒泰地区电网调度经济运行分析
3.二分类、多分类Logistic回归模型SAS程序实现的探讨
4.秩和比综合评价法的SAS计算程序
5.模糊状态风险分析的广义Logistic回归理论与应用(4)——广义无条件与条件Logistic回归模型
因版权原因，仅展示原文概要，查看原文内容请购买。