散射与截面

飞机雷达散射截面(rcs)公式
飞机雷达散射截面（Radar Cross Section，RCS）是描述目标对雷达波的散射能力的重要参数。

在雷达系统中，RCS公式是用来计算目标散射的电磁波能量的数学表达式。

RCS公式通常是基于目标的几何形状、材料特性和入射波的频率等因素进行建模的。

RCS公式可以用来预测目标在雷达系统中的探测性能，以及设计隐身技术和电磁干扰技术。

它对于军事和民用航空领域都具有重要意义。

RCS公式的一般形式如下：
RCS = σ A.
其中，σ表示目标的散射截面，A表示目标的有效面积。

散射截面σ是描述目标对入射电磁波的反射能力的参数，通常是一个与频率有关的函数。

目标的有效面积A则是描述目标在雷达波束中所占的实际面积。

RCS公式的具体形式会根据目标的几何形状和材料特性而有所
不同。

对于复杂的目标，RCS公式可能需要进行数值模拟或实验测
量来获得准确的数值。

在现代雷达技术中，研究人员不断努力寻求降低目标的RCS，
以实现隐身和减少雷达探测距离。

因此，RCS公式的研究和应用对
于提高雷达系统的性能具有重要意义。

总之，飞机雷达散射截面（RCS）公式是描述目标对雷达波的散
射能力的重要数学表达式，对于雷达技术和隐身技术具有重要意义。

碰撞截面为
(d 1+d 2 )2 /4
• 刚性球的碰撞截面是以(d 1+d 2 ) /2 为半径的圆,可
以从下面的图清
)
红球和两个蓝球 恰好能相碰
两个蓝球和 红球都能相碰
两个蓝球和红 球都不能相碰
刚性分子碰撞截面可比喻为古代战争用的盾牌，而被 碰撞的其它视为质点的 B分子可比喻为箭。
引入碰撞截面概念:
图表示视作质点的 B 分子束平行射向静止的 A 分子
时，B 分子的轨迹线.A 分子的质心在O。
由图可见，B 分子在接近 A 分子时受到 A 的作用而 使轨迹线发生偏折。
定义“偏折角”:它是 B 分子射向 A 分子时的轨迹线 与离开A 分子时的轨迹线间的交角。
偏折角随 B 分子与 O 点间垂直距离 b 增大而减小。
所有射向圆外区域的 B 分子都不会发生偏折，因而 都不会被散射。
圆的面积 d 2 称为分子散射截面，也称分子
碰撞截面。
在距离 d 恰正开始 不偏折,
d —分子有效直径
碰撞截面中最简单的情况是刚球势的碰撞截面 。
不管两同种分子相对速率多大，分子有效直径总等于 刚球的直径 。
对于有效直径分别为d1、d2的两刚球分子间的碰撞，其
在距离恰正开始不偏折不管两同种分子相对速率多大分子有效直径总等于刚球的直径的两刚球分子间的碰撞其碰撞截面为刚性分子碰撞截面可比喻为古代战争用的盾牌而被碰撞的其它视为质点的b分子可比喻为箭
§3.6.1 碰撞（散射）截面
第二章曾经对分子碰撞过程利用下图做较为直观而又 十分简单的定性分析， 在分析中假定两分子作对心碰撞。 实际上两分子作对心碰撞概率非常小, 大量发生的是非对心碰撞。 下面讨论非对心碰撞。
在距离d 恰正 开始不偏折

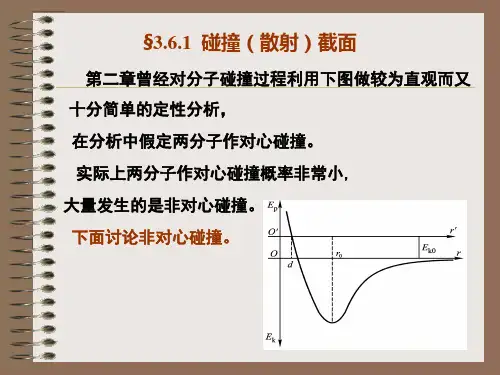
康普顿散射光子能量及微分截面的测量[实验目的]1.理解康普顿散射及微分截面的概念；2.熟练掌握康普顿散射光子及微分截面的计算；3.掌握康普顿散射微分截面测量方法。

[实验内容]1.利用康普顿散射谱仪测量康普顿散射微分截面及散射光子的能量。

2.在同一坐标中作出康普顿散射微分截面及散射光子的能量的理论值与实验值，并比较。

[实验原理]1、康普顿散射康普顿效应是射线与物质相互作用的三种效应之一。

康普顿效应是入射光子与物质原子中的核外电子产生非弹性碰撞而被散射。

散射时，入射光子把部分能量转移给电子，使它脱离原子成为反冲电子，而散射光子的能量和运动方向发生变化。

如图一所示，其中h ν是入射γ光子的能量，h ν'是散射γ光子的能量，θ是散射角，e 是反冲电子，Φ是反冲角。

图1 康普顿散射示意图由于发生康普顿散射的γ光子能量比电子的束缚能要大的多，所以入射γ光子与原子中的电子作用时，可以把电子的束缚能忽略，看成是自由电子，并视为散射发生以前电子是静止的，动能为0，只有静止能量m 0C 2，散射后，电子获得速度V，此时电子的能量m E =,动量为mmv = , 其中β＝V ／c ，c 为光速。

用相对论的能量和动量守恒定律就可以得到：eE 反冲电子20m m c h h νν'+=…………………………………………(1)'cos cos h h c c ννφθ=+∙ (2)'sin sin h cνθφ= (3)由(1)(2)(3)式可得出：20'1(1cos )h h h m c νννθ=+- (4)其中h ν/c 是入射γ光子的动量，h ν'/c 是散射γ光子的动量，此式就表示散射γ光子能量与入射γ光子能量及散射角的关系。

2、康普顿散射的微分截面康普顿散射的微分截面的意义是：一个能量为h ν的入射γ光子与一个电子作用后被散射到θ方向单位立体角里的几率。

记作()d d σθΩ。

电磁散射分层媒质上的电偶极子理想导电圆柱对平面波的散射理想导电圆柱对柱面波的散射理想导电球对平面波的散射理想导电球对球面波的散射散射矩阵与散射截面61散射矩阵与散射截面散射体波源观察点散射矩阵散射矩阵散射体波源观察点10logdbsm定义
第6章
电磁散射
散射矩阵与散射截面
理想导电圆柱对平面波的散射 理想导电圆柱对柱面波的散射 理想导电球对平面波的散射 理想导电球对球面波的散射

an H (ka) ( j ) J n (ka) 0

J n (ka ) an ( j ) (2) H n (ka )
n
故得到
★ 讨论： ① 远区散射场
J n (ka ) (2) E ( j ) H n (k )e jn (2) H n (ka ) n
xLeabharlann es 1 (2) e jkz cos an H n (k sin )e jn k 0sin n
ei es 边界条件： ( )
a
0
an
§6.3 理想导电圆柱对柱面波的散射
问题：如图所示，一半径为a 的无限长理想
导体圆柱沿z 轴放置，附近放置一根无限长 的线电流 I，计算导体圆柱的散射场。 1. 无限长线源的场 位于 ( 0 ,0 ) 的无限长的线源的位函数满足方程
e
jkx
a

0
(Ei E S )
a
0
a

n
(2) an H n (ka )e jn 0
★ 平面波→基本柱面波函数展开 r (ex cos ey sin ) ez z jk r ， 平面波： e k k (ex cos k ey sin k ) ez kz

卢瑟福散射截面公式推导卢瑟福散射截面公式是描述入射粒子在靶核上散射的经典物理公式。

推导卢瑟福散射截面公式的过程如下：1. 假设入射粒子为α粒子，靶核为一个单个原子核。

2. 假设入射粒子以速度v0垂直入射，入射角度为θ。

3. 假设入射粒子与靶核之间的相互作用力为库仑力。

4. 根据库仑力的性质，入射粒子在靶核附近会受到库仑力的作用，从而发生散射。

5. 根据经典力学的原理，入射粒子的受力方向与速度方向垂直，所以入射粒子会在靶核周围的一个圆环上散射。

6. 假设靶核的原子序数为Z，靶核的核半径为R，入射粒子的质量为m，入射粒子的电荷为e，根据库仑力的表达式，可以得到入射粒子受到的库仑力大小为F = (Ze^2)/(4πε0r^2)，其中r为入射粒子与靶核的距离。

7. 假设入射粒子在靶核处的速度为v，根据动能定理，可以得到入射粒子的动能为E = (1/2)mv^2。

8. 由于入射粒子与靶核之间的相互作用力是保守力，所以根据机械能守恒定律，可以得到入射粒子的动能在散射过程中保持不变，即E = (1/2)mv^2 = (1/2)m(v0^2)。

9. 将入射粒子受到的库仑力与入射粒子的动能相等，可以得到(Ze^2)/(4πε0r^2) = (1/2)mv0^2。

10. 将入射粒子的速度v表示为v = v0/sin(θ)，可以得到(Ze^2)/(4πε0r^2) = (1/2)m(v0^2)sin^2(θ)。

11. 将库仑力的表达式转化为力的大小与方向的分量形式，可以得到(Ze^2)/(4πε0r^2) = (1/2)mv0^2sin^2(θ) = (1/2)mv0^2(1 - cos^2(θ))。

12. 将动能表达式中的速度v0替换为速度v = v0/sin(θ)，可以得到(Ze^2)/(4πε0r^2) = (1/2)m(v^2)sin^2(θ) = (1/2)m(v^2)(1 - cos^2(θ))。

13. 根据几何关系，可以得到散射角度θ与散射粒子的偏转角度Δφ之间的关系为tan(Δφ/2) = tan(θ/2)。

弹性散射，否则称为非弹性散射。
入射粒子流密度N ：单位时间内通过与入射粒子运动方向垂直的单位面积的入 射粒子数，用于描述入射粒子流强度的物理量，故又称为 入射粒子流强度。
散射截面：
设单位时间内散射到（，）方向面积元ds上（立体角d内）的粒子数为dn，显 然
ds dn d
r2 dn N
处设的r 散射体时系，V的(r波) 函数0 ，。方程（5）变为
2 k 2 0
（6）
令
r
（7）
将（6）式写成
2
r 2
k 2

L情形下，此方程简化为
2 k 2 0
r 2
（8）
此方程类似一维波动方程，我们知道： 对于一维势垒或势阱的散射情况
综合之，则有：
dn Nd
或
dn q( ,)Nd
（1）
比例系数q(，)的性质：
q(，)与入射粒子和靶粒子（散射场）的性质，它们之间的相互作用，以及 入射粒子的动能有关，是，的函数。
q(，)具有面积的量纲
[q]


dn Nd

L2
故称q(，)为微分散射截面，简称为截面或角分布
如果在垂直于入射粒子流的入射方向取面积q(，)，则单位时间内通过此截
面q(，)的粒子数恰好散射到(，)方向的单位立体角内。
q( ,)N dn
d
（2）
总散射截面：
2
Q q(,)d q(,)sindd
（3）
00
[由注（] 2）式知，由于N、dn 可通过实验测定，故而求得 q( ,) 。
k x Aeikx Beikx
k x ceikx

粒子物理学中的反应截面与散射过程粒子物理学是研究物质的微观结构以及其相互作用的学科，其中的反应截面和散射过程是重要的概念和研究方向。

本文将介绍粒子物理学中的反应截面和散射过程的基本概念、应用以及与实验数据的关系。

一、反应截面概念及计算方法粒子物理学中的反应截面（cross section）是描述粒子与其他粒子之间相互作用概率的物理量。

在散射过程中，当一个粒子与另一个粒子相互作用时，它们之间发生的相互作用的横截面就是反应截面。

反应截面常用单位是平方厘米（cm^2）。

计算反应截面的方法基本上是通过实验测量得到。

实验中，通过调节入射粒子的能量和方向，观察散射粒子在某一角度上的强度，并结合相关理论模型进行数据分析，从而计算出反应截面。

其中，理论模型可以是量子力学、量子场论等粒子物理学的基本原理。

二、反应截面的应用反应截面在粒子物理学中有广泛的应用。

首先，反应截面是研究粒子与粒子之间相互作用机制的重要手段。

通过实验测量不同粒子的反应截面，可以推断出相互作用的本质，了解粒子之间的力和力的传递以及粒子的内部结构等信息。

其次，反应截面的研究对于粒子探测技术的发展也有重要意义。

在实验中，通过测量入射粒子与探测器之间的相互作用，可以根据反应截面推断出探测器对不同粒子的探测效率，进而优化探测器的设计和性能。

此外，反应截面还可以用于天体物理学的研究。

宇宙中存在大量的粒子和能量交换现象，通过粒子物理学中反应截面的研究，可以推断出宇宙中粒子的产生和相互作用情况，进而帮助解释宇宙中的物理现象。

三、散射过程及其研究方法散射过程是粒子物理学中常见的一种现象，它描述了两个或多个粒子相互作用后改变运动方向和能量的过程。

通过研究散射过程，可以揭示粒子之间的相互作用力、内部结构以及它们的动力学特性。

研究散射过程的方法可以是理论计算和实验测量相结合。

理论方面，基于量子力学和量子场论等基本原理，可以建立起一系列描述粒子散射的数学模型，通过计算这些模型得到的散射截面等参数，来解释实验结果。

S P
测量散射截面的原理

实验中选择 Is Ip I I
* s
* p

可作Ps与Va关系图 及QL与 V a 的关系图
实验结果与分析

Ps与Va关系图
实验结果与分析

QL与 V a 的关系图
量子原理分析


引入了电子的波函数及气体原子对电子作用而 形成的三维势阱 采用分波法，得其散射截面为

经典物理下的散射几率与散射截面的关系 ：
L P L ) 1e x p ( ) s(

1 其中λ为平均自由程， n
Q n
即为总散射截面
测量散射截面的原理

直流测量冉绍 1 S IP (IS IP)
IP(IS IP) QL ln I (I I ) P P S
冉绍尔-汤森实验的 散射截面研究
——苏 阳
实验背景

在经典的分子运动规律下由于电子与气体分 子都是被看作是刚性球，散射截面只和原子 体积的大小有关。

冉绍尔-汤森效应中发现电子与气体原子之间 的散射不遵守经典规律，散射截面同电子能 量有关，随着电子速度的减小散射截面的变 化趋势会有改变。
实验原理
4 2 Q 2 ( 2 l 1 )s i n l k l 0

在低能散射下，合理调整势阱参数，就会出现 共振透射现象 ，此时即达到了总有效散射截 面极小的情况
Thank
U

Leabharlann 作业如何计算散射截面
张宏浩
2—>n散射的微分截面
分母的通量因子是Lorentz不变量，它可以用在质心系两粒子的 总能量sqrt(s)和其中一个粒子的3动量p_a^{cm}来表达：
因此，2到n的微分散射截面又可写为
特别地，对于末态只有两个粒子，即a+b—>1+2散射的 情况，二体末态相空间积分测度为
将其代入微分散射截面公式得
2到2的微分散射截面公式也可用Mandelstam变量t来 表达，其中
特别地，对于2到2的弹性散射，t的变化范围是：
更特别地，对于2到2的弹性散射，且初态两粒子的静质量相同时，t的变换范围是
证明：
例1：标量型相互作用下暗物质的成对湮灭【振幅不依赖于散射角度】
张宏浩等，Nuclear Physics B 854 (2012) 350–374

k cot(δ o ) 。对于左侧项，相对于 K ' 中的 Vo，可以忽略 E。同时相对于 K 中的 Vo，可以忽略 EB。
于是 K ~ K ，由于(5.8)， 左侧项可设为等于 − κ 。注意这一系列的近似已经使我们可以利用 束缚态问题中的色散关系（5.8）来进行散射计算。因此，(5.14)可以写为：
n + 1H → 2 H + γ (2.23MeV )
该反应的逆反应是利用一定能量的电子产生外部的轫致辐射从而在 H 上引发( γ , n)反应，这 2 已经得到应用。 H 除了基态以外，没有其它的稳定态。它在～2.30 MeV 能量上存在一个虚态。
2
需要强调的是学生应该牢记对于氢核(n, γ ) 的反应截面是 0.33 巴。尽管与当前散射问题 的讨论无关，但对于北美核能的开发却具有重要意义。水对中子的吸收很高，因此不能建造以 235 天然铀为燃料、轻水作为慢化剂的临界堆。美国采用的方法是浓缩天然铀使 U 的浓度达到 3% 235 （ U 的天然丰度是 0.07%） 。而加拿大则采用重水作为慢化剂，因为重水的中子吸收截面比轻 水低三个量级，使用重水作为慢化剂的反应堆利用天然铀即可达到临界条件。 利用氘核的数据，我们考虑将中子——质子的相互作用势简化为最简单的形式——球形势 阱。势由两个参数决定，阱深 Vo 和力程 ro 。
22.54 中子与物质的相互作用及应用（2004 年春季） 第五讲（2004 年 2 月 19 日） 中子——质子散射
参考文献： M. A. Preston, Physics of the Nucleus (Addison–Wesley, Reading, 1962). E. Segre, Nuclei and Particles (W. A. Benjamin, New York, 1965), Chap. X. 我们在本讲继续讨论低能中子与氢核的散射问题，它的散射截面在很宽能量范围内的测量 结果都是 20.4 巴。我们的目的是将上一讲中讨论的势散射理论应用到这个问题中。我们很快就 会看到 s-波近似（低能时的反应条件）在中子能量为 1～1000eV 时是非常适用的。以方势阱来 表达 n－p 相互作用，我们考虑关于它的两个计算。氘核的束缚态问题，即波动方程在 E<0 时的 解，使我们可以对势阱的宽度和深度设置界限；而散射态的解，即 E>0 时的解则提供给我们相 移或者等价的散射长度。该计算得到的反应截面值 2.3 巴与实验值相去甚远。原因在于我们没 有考虑 n-p 反应的自旋相关特性。 中子和质子的自旋可以形成迥异的两种自旋组态——平行 （三 重态）或者反平行（单态）——都会对散射长度有影响。考虑到这些因素之后的计算值就会与 实验室相当接近。结论是 n-p 应是与自旋相关的，且氢核对于中子具有异常大的散射截面实际 上与核力在这一方面的特点有关。 氘核的束缚态 氘核是两种核子所能形成的唯一稳定束缚态。 换句话说， 双中子和双质子都是不稳定的 （由 于不相容原理） 。氘核是由于低能中子被氢核所俘获形成，该反应释放出能量为 2.23 MeV 的 γ：

康普顿散射知识点康普顿散射是一种重要的物理过程，它在粒子物理和核物理领域有着广泛的应用。

本文将介绍康普顿散射的基本概念、原理和相关知识点。

一、康普顿散射的基本概念康普顿散射是指入射光子与物质中的自由电子相互作用后发生能量和动量的转移，结果产生散射光子和散射电子的过程。

它是一种经典的弹性散射过程，解释了X射线的散射现象。

康普顿散射是由美国物理学家康普顿于1923年首次提出的。

二、康普顿散射的原理康普顿散射的原理可以用光子的波粒二象性来解释。

光子既有粒子性又有波动性，当X射线入射到物质中时，它会与物质中的电子相互作用。

根据量子力学的原理，散射光子和散射电子的相互作用可以看作是一个光子作用于一个自由电子。

三、康普顿散射的关键参数康普顿散射的关键参数包括散射角度、散射截面和康普顿波长。

散射角度是入射光子和散射光子之间的夹角，可以通过散射角度的测量来确定康普顿散射的特性。

散射截面是描述康普顿散射概率的物理量，它与散射介质、能量和散射角度有关。

康普顿波长是入射光子的波长和散射光子的波长之差，它与入射光子的能量和散射角度有关。

四、康普顿散射与能谱测量康普顿散射在γ射线能谱测量中有着重要的应用。

由于康普顿散射的能量和角度的关系，在能谱中会出现特定的峰位，这些峰位可以用于测量γ射线的能量。

通过测量康普顿散射的能谱，可以得到入射光子的能量信息。

五、康普顿散射的应用康普顿散射在核物理、医学影像以及安全检查等领域都有着广泛的应用。

在核物理实验中，康普顿散射可以用于测量粒子的能量和角度分布。

在医学上，康普顿散射成像技术可以用于肿瘤的检测和诊断。

在安全检查领域，康普顿散射技术可以用于爆炸品的检测和辐射剂量的测量。

六、康普顿散射的局限性康普顿散射虽然在许多应用中具有重要的地位，但也存在一些局限性。

康普顿散射的散射截面较大，因此在散射过程中会有许多能量和动量的损失。

另外，在康普顿散射过程中，散射的光子能量会降低，因此要精确测量入射光子的能谱是有一定挑战的。

散射中心特征引言散射是物理学中一种重要的现象，在各个领域都有广泛的应用。

散射中心特征是描述散射现象的关键指标，它能够提供有关被散射物体的结构和性质的信息。

本文将深入探讨散射中心特征的相关概念、性质以及应用。

什么是散射中心特征散射中心特征是指在散射过程中，被散射物体表现出来的一些特殊性质。

散射中心特征包括散射截面、相位移、散射幅度等。

通过研究散射中心特征，可以了解散射过程中的能量转移、波的传播以及被散射物体的结构信息。

散射截面散射截面是描述散射现象中能量传递的一个重要指标。

它表示入射波在单位面积上被散射的能量。

散射截面可以用数学公式表示，并用于计算在不同方向上的散射能量。

散射截面的大小与入射波的频率、散射物体的形状和尺寸有关。

常用的散射截面包括雷诺兹散射截面、米尔斯散射截面等。

相位移相位移是描述散射过程中波的传播和干涉现象的一个重要参数。

在散射过程中，入射波和散射波之间存在相位差，相位差的大小和变化规律可以反映出散射物体的性质。

相位移可以通过测量入射波和散射波的相位差来获得，也可以通过数学模型进行计算。

散射幅度散射幅度是指入射波与散射波之间振幅的差异。

散射幅度可以用来描述散射过程中波的强度变化和振幅的增减。

测量散射幅度可以通过测量入射波和散射波的幅度来获得，也可以通过数学模型进行计算。

散射幅度的大小和变化规律与散射物体的大小、形状以及物质特性有关。

散射中心特征的应用散射中心特征在各个领域都有广泛的应用。

以下是几个常见的应用示例：无损检测散射中心特征可以用于无损检测，通过测量入射波和散射波的特征参数，可以判断被测物体是否存在缺陷或损伤。

无损检测广泛应用于材料科学、工程结构等领域，能够提高产品质量和安全性。

生物医学散射中心特征在生物医学领域中也有重要的应用。

通过测量散射中心特征，可以了解生物组织的结构和性质，对于疾病的诊断和治疗具有重要意义。

例如，散射中心特征可以用于测量血液中的红细胞数量和大小，进而判断患者的健康状况。

⎧− 3V0 , r ≤ a V r =⎨ r>a ⎩ 0,
()
。
（1’）
解：自旋为 1 2 的二全同粒子体系的总波函数必须是交换反对称的， s 波（ l = 0 ）波函 数是两粒子空间坐标的对称函数，所以自旋波函数必须是反对称的，即为自旋单态，因 此，体系总自旋为 0 ，亦即，
σ 1 ⋅ σ 2 = −3 ，
f (θ ) = −
2u h2 K
2
∫
∞
0
r 'V ( r ' ) sin Kr ' dr ' ， K = 2k sin
4u 2 h4 K 2
θ
2
，
（1） （2）
q (θ ) = f (θ ) =
a
∫
∞
0
r 'V ( r ' ) sin Kr ' dr '
2
，
（a） ∫ r ' ( −V0 ) sin Kr ' dr ' = −
−
亦即：h2 " 来自 + V (r )u = 0 2u
，
（3）
u " + k 02 u = 0 , r ≤ a u" = 0 , r>a
(E → 0 )
，
（3’）
其中：
k 0 = 6uV0 h = 3mV0 h
，
（4）
m 为粒子质量， μ = m 2 为两粒子体系的约化质量。
方程（3’）满足边界条件 u (0 ) = 0 的解为：
r≤a ⎧ A sin k 0 r , ⎪ ⎛ r ⎞ u (r ) = ⎨ C⎜ 1− ⎟ ⎜ ⎟, r >a ⎪ ⎩ ⎝ a0 ⎠

粒子物理学中的反应截面与散射过程粒子物理学作为物理学的一个重要分支，研究的是基本粒子的结构、相互作用和性质。

在粒子物理学中，反应截面与散射过程是两个核心概念，它们对理解微观世界的运作机制起着关键作用。

1. 反应截面反应截面是指一个粒子与另一个粒子进行相互作用并发生某种物理过程的概率面积。

通俗地说，反应截面可以理解为粒子之间发生碰撞时发生特定反应的可能性大小。

反应截面通常用σ表示，单位是平方米（或以barn为单位，1 barn = $10^{-28}$ 平方米）。

在粒子物理的实验中，反应截面是一个重要的物理量，可以用来描述粒子之间相互作用的强弱程度。

研究反应截面可以帮助科学家更深入地理解基本粒子之间的相互作用规律，揭示微观世界的奥秘。

2. 散射过程散射是指一个粒子与另一个粒子发生碰撞后改变原有运动方向的物理过程。

在粒子物理学中，散射是一种常见的反应形式，可以通过研究散射过程来获取粒子的相互作用信息。

散射过程包括前向散射和后向散射。

前向散射是指碰撞后粒子保持运动方向不变或保持在一个角度范围内散射；后向散射是指碰撞后粒子改变运动方向，并向碰撞线的反方向散射。

通过研究散射过程，科学家可以推断出粒子的相互作用力，揭示物质微观结构和性质。

散射过程也是粒子物理学实验中常用的手段，可以通过散射实验获取大量粒子信息，并验证理论模型的有效性。

总结在粒子物理学中，反应截面与散射过程是两个重要的概念，它们对研究基本粒子的相互作用和性质起着关键作用。

通过研究反应截面和散射过程，科学家可以深入探索微观世界的奥秘，理解基本粒子之间的相互作用规律，推动物理学的发展和进步。

希望本文内容能够帮助读者更好地理解粒子物理学中的重要概念，激发对科学的浓厚兴趣。

（4）
令
k2

2E 2
V
(r)

2 2
U
(r)
方程（4）改写为
2 [k 2 V (r)] 0
（5）
由于实验观测是在远离靶的地方进行的，从微观角度看，可以认为r 。因 此，在计算时q( ,) ，仅需考虑 r 处的散射粒子的行为，即仅需考虑 r
三、分波法
讨论粒子在中心力场中的散射。 粒子在辏力场中的势能为U (r)，状态方程
2 [k 2 V (r)] 0
（3-1）
取沿粒子入射方向并通过散射中心的轴线为极轴z，显然与无关，按照§3.3.的 讨论，对于具有确定能量的粒子，方程（3-1）的特解为
Rl (r)Ylm ( , ) 由于现在与无关(m=0)，所以，方程（1）的特解可写成
知道了散射振幅 f ( ,) ，也就能求出微分散射截面，f ( ,) 的具体形式通过求 schrödinger方程（5）的解并要求在 r 时具有渐近形式（9）而得出。
下面介绍两种求散射振幅或散射截面的方法——分波法，玻恩近似方法。 分波法是准确的求散射理论问题的方法，即准确的散射理论。
综合Nd
（1）
比例系数q(，)的性质：
q(，)与入射粒子和靶粒子（散射场）的性质，它们之间的相互作用，以及 入射粒子的动能有关，是，的函数。
q(，)具有面积的量纲
[q]


dn Nd


L2
故称q(，)为微分散射截面，简称为截面或角分布

i 2
(ik11*
ik1* )
k N
（10）
散射波的几率流密度
Jr