第 4 章 神经计算基本方法(BP神经网络MATLAB仿真程序设计)例子

在Matlab中实现神经网络的方法与实例神经网络是一种模拟人类大脑神经系统的计算模型，它能够通过学习数据的模式和关联性来解决各种问题。

在计算机科学和人工智能领域，神经网络被广泛应用于图像识别、自然语言处理、预测等任务。

而Matlab作为一种功能强大的科学计算软件，提供了一套完善的工具箱，可以方便地实现神经网络的建模和训练。

本文将介绍在Matlab中实现神经网络的方法与实例。

首先，我们会简要介绍神经网络的基本原理和结构，然后详细讲解在Matlab中如何创建并训练神经网络模型，最后通过几个实例展示神经网络在不同领域的应用。

一、神经网络的原理和结构神经网络模型由神经元和它们之间的连接构成。

每个神经元接收输入信号，并通过权重和偏置进行加权计算，然后使用激活函数对结果进行非线性变换。

这样，神经网络就能够模拟复杂的非线性关系。

常见的神经网络结构包括前馈神经网络（Feedforward Neural Network）和循环神经网络（Recurrent Neural Network）。

前馈神经网络是最基本的结构，信号只能向前传递，输出不对网络进行反馈；而循环神经网络具有反馈连接，可以对自身的输出进行再处理，适用于序列数据的建模。

神经网络的训练是通过最小化损失函数来优化模型的参数。

常用的训练算法包括梯度下降法和反向传播算法。

其中，梯度下降法通过计算损失函数对参数的梯度来更新参数；反向传播算法是梯度下降法在神经网络中的具体应用，通过反向计算梯度来更新网络的权重和偏置。

二、在Matlab中创建神经网络模型在Matlab中，可以通过Neural Network Toolbox来创建和训练神经网络模型。

首先，我们需要定义神经网络的结构，包括输入层、隐藏层和输出层的神经元数量，以及每个神经元之间的连接权重。

例如，我们可以创建一个三层的前馈神经网络模型：```matlabnet = feedforwardnet([10 8]);```其中，`[10 8]`表示隐藏层的神经元数量分别为10和8。

bp神经网络及matlab实现分类：算法学习2012-06-20 20:56 66399人阅读评论(28) 收藏举报网络matlab算法functionnetworkinput本文主要内容包括： (1) 介绍神经网络基本原理，(2) 实现前向神经网络的方法，(3) Matlab实现前向神经网络的方法。

第0节、引例本文以Fisher的Iris数据集作为神经网络程序的测试数据集。

Iris数据集可以在找到。

这里简要介绍一下Iris数据集：有一批Iris花，已知这批Iris花可分为3个品种，现需要对其进行分类。

不同品种的Iris花的花萼长度、花萼宽度、花瓣长度、花瓣宽度会有差异。

我们现有一批已知品种的Iris花的花萼长度、花萼宽度、花瓣长度、花瓣宽度的数据。

一种解决方法是用已有的数据训练一个神经网络用作分类器。

如果你只想用C#或Matlab快速实现神经网络来解决你手头上的问题，或者已经了解神经网络基本原理，请直接跳到第二节——神经网络实现。

第一节、神经网络基本原理1. 人工神经元( Artificial Neuron )模型人工神经元是神经网络的基本元素，其原理可以用下图表示：图1. 人工神经元模型图中x1~xn是从其他神经元传来的输入信号，wij表示表示从神经元j到神经元i的连接权值，θ表示一个阈值 ( threshold )，或称为偏置( bias )。

则神经元i的输出与输入的关系表示为：图中 yi表示神经元i的输出，函数f称为激活函数 ( Activation Function )或转移函数 ( Transfer Function ) ，net称为净激活(net activation)。

若将阈值看成是神经元i的一个输入x0的权重wi0，则上面的式子可以简化为：若用X表示输入向量，用W表示权重向量，即：X = [ x0 , x1 , x2 , ....... , xn ]则神经元的输出可以表示为向量相乘的形式：若神经元的净激活net为正，称该神经元处于激活状态或兴奋状态(fire)，若净激活net为负，则称神经元处于抑制状态。

BP神经网络实验详解（MATLAB实现）BP（Back Propagation）神经网络是一种常用的人工神经网络结构，用于解决分类和回归问题。

在本文中，将详细介绍如何使用MATLAB实现BP神经网络的实验。

首先，需要准备一个数据集来训练和测试BP神经网络。

数据集可以是一个CSV文件，每一行代表一个样本，每一列代表一个特征。

一般来说，数据集应该被分成训练集和测试集，用于训练和测试模型的性能。

在MATLAB中，可以使用`csvread`函数来读取CSV文件，并将数据集划分为输入和输出。

假设数据集的前几列是输入特征，最后一列是输出。

可以使用以下代码来实现：```matlabdata = csvread('dataset.csv');input = data(:, 1:end-1);output = data(:, end);```然后，需要创建一个BP神经网络模型。

可以使用MATLAB的`patternnet`函数来创建一个全连接的神经网络模型。

该函数的输入参数为每个隐藏层的神经元数量。

下面的代码创建了一个具有10个隐藏神经元的单隐藏层BP神经网络：```matlabhidden_neurons = 10;net = patternnet(hidden_neurons);```接下来，需要对BP神经网络进行训练。

可以使用`train`函数来训练模型。

该函数的输入参数包括训练集的输入和输出，以及其他可选参数，如最大训练次数和停止条件。

下面的代码展示了如何使用`train`函数来训练模型：```matlabnet = train(net, input_train, output_train);```训练完成后，可以使用训练好的BP神经网络进行预测。

可以使用`net`模型的`sim`函数来进行预测。

下面的代码展示了如何使用`sim`函数预测测试集的输出：```matlaboutput_pred = sim(net, input_test);```最后，可以使用各种性能指标来评估预测的准确性。

计算智能实验报告实验名称：BP神经网络算法实验班级名称： 2010级软工三班专业：软件工程姓名：李XX学号： XXXXXX2010090一、实验目的1）编程实现BP神经网络算法；2）探究BP算法中学习因子算法收敛趋势、收敛速度之间的关系；3）修改训练后BP神经网络部分连接权值，分析连接权值修改前和修改后对相同测试样本测试结果，理解神经网络分布存储等特点。

二、实验要求按照下面的要求操作，然后分析不同操作后网络输出结果。

1）可修改学习因子2）可任意指定隐单元层数3）可任意指定输入层、隐含层、输出层的单元数4）可指定最大允许误差ε5）可输入学习样本（增加样本）6）可存储训练后的网络各神经元之间的连接权值矩阵；7）修改训练后的BP神经网络部分连接权值，分析连接权值修改前和修改后对相同测试样本测试结果。

三、实验原理1 明确BP神经网络算法的基本思想如下：在BPNN中，后向传播是一种学习算法，体现为BPNN的训练过程，该过程是需要教师指导的；前馈型网络是一种结构，体现为BPNN的网络构架反向传播算法通过迭代处理的方式，不断地调整连接神经元的网络权重，使得最终输出结果和预期结果的误差最小BPNN是一种典型的神经网络，广泛应用于各种分类系统，它也包括了训练和使用两个阶段。

由于训练阶段是BPNN能够投入使用的基础和前提，而使用阶段本身是一个非常简单的过程，也就是给出输入，BPNN会根据已经训练好的参数进行运算，得到输出结果2 明确BP神经网络算法步骤和流程如下：1初始化网络权值2由给定的输入输出模式对计算隐层、输出层各单元输出3计算新的连接权及阀值，4选取下一个输入模式对返回第2步反复训练直到网络设输出误差达到要求结束训练。

四、实验内容和分析1．实验时建立三层BP神经网络，输入节点2个，隐含层节点2个，输出节代码：P=[0.0 0.0 1.0 1.0;0.0 1.0 0.0 1.0];%输入量矩阵T=[0.0 1.0 1.0 0.0];%输出量矩阵net=newff(minmax(P),T,[2 1],{'tansig','purelin'},'traingd');%创建名为net的BP神经网络inputWeights=net.IW{1,1};%输入层与隐含层的连接权重inputbias=net.b{2};%输入层与隐含层的阈值net.trainParam.epochs=5000;%网络参数：最大训练次数为5000次net.trainParam.goal=0.01;%网络参数：训练精度为0.001 net.trainparam.lr=0.5;%网络参数：学习设置率为0.5net.trainParam.mc=0.6; %动量[net,tr]=train(net,P,T); %训练A=sim(net,P); %仿真E=T-A; %误差MSE=mse(E); %均方误差训练次数5000，全局误差0.0083642．输入测试样本为可见网络性能良好，输出结果基本满足识别要求。

BP神经⽹络（原理及MATLAB实现）⼈⼯神经⽹络概述：⼈⼯神经元模型：神经⽹络的分类：按照连接⽅式，可以分为：前向神经⽹络 vs. 反馈（递归）神经⽹络；按照学习⽅式，可以分为：有导师学习神经⽹络 vs. ⽆导师学习神经⽹络；按照实现功能，可以分为：拟合（回归）神经⽹络 vs. 分类神经⽹络。

数据归⼀化：将数据映射到[0, 1]或[-1, 1]区间或其他的区间。

数据归⼀化的原因：1.输⼊数据的单位不⼀样，有些数据的范围可能特别⼤，导致的结果是神经⽹络收敛慢、训练时间长。

2.数据范围⼤的输⼊在模式分类中的作⽤可能会偏⼤，⽽数据范围⼩的输⼊作⽤就可能会偏⼩。

3.由于神经⽹络输出层的激活函数的值域是有限制的，因此需要将⽹络训练的⽬标数据映射到激活函数的值域。

例如神经⽹络的输出层若采⽤S形激活函数，由于S形函数的值域限制在(0,1)，也就是说神经⽹络的输出只能限制在(0,1)，所以训练数据的输出就要归⼀化到[0,1]区间。

4.S形激活函数在(0,1)区间以外区域很平缓，区分度太⼩。

例如S形函数f(X)在参数a=1时，f(100)与f(5)只相差0.0067。

归⼀化算法：1.y = ( x - min )/( max - min )；2.y = 2 * ( x - min ) / ( max - min ) - 1。

部分函数：参数对BP神经⽹络性能的影响：隐含层神经元节点个数激活函数类型的选择学习率初始权值与阈值交叉验证训练集测试集验证集留⼀法MATLAB实现程序：1 %% I. 清空环境变量2 clear all3 clc45 %% II. 训练集/测试集产⽣6 %%7 % 1. 导⼊数据8 load spectra_data.mat910 %%11 % 2. 随机产⽣训练集和测试集12 temp = randperm(size(NIR,1));13 % 训练集——50个样本14 P_train = NIR(temp(1:50),:)';15 T_train = octane(temp(1:50),:)';16 % 测试集——10个样本17 P_test = NIR(temp(51:end),:)';18 T_test = octane(temp(51:end),:)';19 N = size(P_test,2);2021 %% III. 数据归⼀化22 [p_train, ps_input] = mapminmax(P_train,0,1);23 p_test = mapminmax('apply',P_test,ps_input);2425 [t_train, ps_output] = mapminmax(T_train,0,1);2627 %% IV. BP神经⽹络创建、训练及仿真测试28 %%29 % 1. 创建⽹络30 net = newff(p_train,t_train,9);3132 %%33 % 2. 设置训练参数34 net.trainParam.epochs = 1000;35 net.trainParam.goal = 1e-3;36 net.trainParam.lr = 0.01;3738 %%39 % 3. 训练⽹络40 net = train(net,p_train,t_train);4142 %%43 % 4. 仿真测试44 t_sim = sim(net,p_test);4546 %%47 % 5. 数据反归⼀化48 T_sim = mapminmax('reverse',t_sim,ps_output);4950 %% V. 性能评价51 %%52 % 1. 相对误差error53 error = abs(T_sim - T_test)./T_test;5455 %%56 % 2. 决定系数R^257 R2 = (N * sum(T_sim .* T_test) - sum(T_sim) * sum(T_test))^2 / ((N * sum((T_sim).^2) - (sum(T_sim))^2) * (N * sum((T_test).^2) - (sum(T_test))^2)); 5859 %%60 % 3. 结果对⽐61 result = [T_test' T_sim' error']6263 %% VI. 绘图64 figure65 plot(1:N,T_test,'b:*',1:N,T_sim,'r-o')66 legend('真实值','预测值')67 xlabel('预测样本')68 ylabel('⾟烷值')69 string = {'测试集⾟烷值含量预测结果对⽐';['R^2=' num2str(R2)]};70 title(string)运⾏效果截图：。

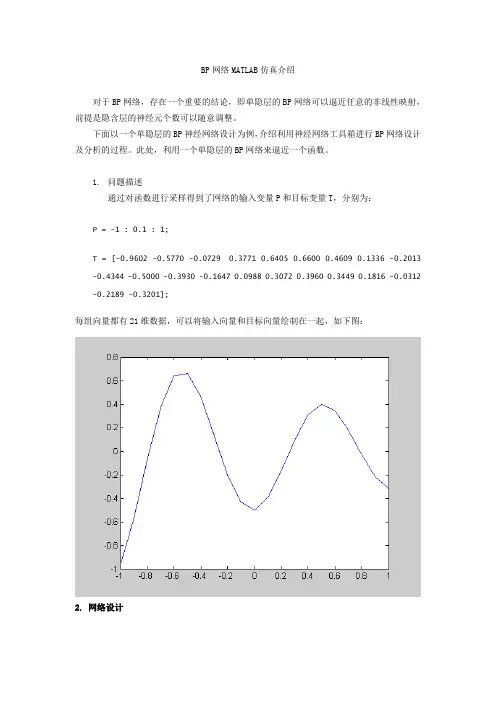
BP网络MATLAB仿真介绍对于BP网络，存在一个重要的结论，即单隐层的BP网络可以逼近任意的非线性映射，前提是隐含层的神经元个数可以随意调整。

下面以一个单隐层的BP神经网络设计为例，介绍利用神经网络工具箱进行BP网络设计及分析的过程。

此处，利用一个单隐层的BP网络来逼近一个函数。

1.问题描述通过对函数进行采样得到了网络的输入变量P和目标变量T，分别为：P = -1 : 0.1 : 1;T = [-0.9602 -0.5770 -0.0729 0.3771 0.6405 0.6600 0.4609 0.1336 -0.2013 -0.4344 -0.5000 -0.3930 -0.1647 0.0988 0.3072 0.3960 0.3449 0.1816 -0.0312 -0.2189 -0.3201];每组向量都有21维数据，可以将输入向量和目标向量绘制在一起，如下图：2. 网络设计网络的输入层和输出层的神经元个数均为1，根据隐含层设计经验，解决该问题的网络的隐层神经元个数应该在3~8之间。

下面设计一个隐含层神经元数目可变的BP网络，通过误差对比，确定最佳的隐含层神经元个数，并检查隐含层神经元个数对网络性能的影响。

网络设计及训练代码如下：P = -1 : 0.1 : 1;T = [-0.9602 -0.5770 -0.0729 0.3771 0.6405 0.6600 0.4609 0.1336 -0.2013 -0.4344 -0.5000 -0.3930 -0.1647 0.0988 0.3072 0.3960 0.3449 0.1816 -0.0312 -0.2189 -0.3201];s = 3 : 8; % S表示隐层数目的可选项res = 1 : 6;for i = 1 : 6% 隐含层神经元的传递函数为tansig，输出层神经元的传递函数为logsig% 目标函数在[-1, 1]间，刚好满足tansig的输出要求。

%清空环境变量clcclear%读取数据num = xlsread('C:\Users\Administrator\Desktop\模型训练matlab\正样本标记.xls',1,'C3:AN52');num1= xlsread('C:\Users\Administrator\Desktop\模型训练matlab\负样本标记.xls',1,'C3:AN52');训练数据输入fu_input=[num1(:,1),num1(:,3),num1(:,5),num1(:,7),num1(:,10),num1(:,12),num1(:,14) ,num1(:,16),num1(:,18),num1(:,20),num1(:,24),num1(:,26),num1(:,33),num1(:,35),num1 (:,37)];zheng_input=[num(:,1),num(:,3),num(:,5),num(:,7),num(:,10),num(:,12),num(:,14),num (:,16),num(:,18),num(:,20),num(:,24),num(:,26),num(:,33),num(:,35),num(:,37)];Input=[fu_input; zheng_input];训练数据输出a1=ones(50,1)*1;a2=ones(50,1)*0;output=[a1;a2];save data1.mat bsave data2.mat aload data1load data2%节点个数inputnum=100;hiddennum=50;outputnum=100;%训练数据和预测数据input_train=Input;output_train=output;input_test=a(:,91:137);output_test=b(:,91:137);%将训练样本输入输出数据归一化[inputn,inputps]=mapminmax(input_train);[outputn,outputps]=mapminmax(output_train);[pn,minp,maxp,tn,mint,maxt]=premnmx(input,output); %将数据归一化NodeNum1 =20; % 隐层第一层节点数NodeNum2=40; % 隐层第二层节点数TypeNum = 1; % 输出维数TF1 = 'tansig';TF2 = 'tansig';TF3 = 'tansig';net=newff(minmax(pn),[NodeNum1,NodeNum2,TypeNum],{TF1 TF2 TF3},'traingdx');%网络创建traingdmnet.trainParam.show=50;net.trainParam.epochs=50000; %训练次数设置net.trainParam.goal=1e-5; %训练所要达到的精度net.trainParam.lr=0.01; %学习速率net=train(net,pn,tn);p2n=tramnmx(ptest,minp,maxp);%测试数据的归一化an=sim(net,p2n);[a]=postmnmx(an,mint,maxt) %数据的反归一化，即最终想得到的预测结果plot(1:length(t),t,'o',1:length(t)+1,a,'+');title('o表示预测值--- *表示实际值')grid onm=length(a); %向量a的长度t1=[t,a(m)];error=t1-a; %误差向量figureplot(1:length(error),error,'-.')title('误差变化图')grid on%构建BP神经网络net=newff(inputn,outputn,[20,12],{'tansig','purelin'},'traingdx'); net.trainParam.epochs=1000;net.trainParam.lr=0.01;net.trainParam.goal=0.00000001;%BP神经网络训练net=train(net,inputn,outputn);%测试样本归一化inputn_test=mapminmax('apply',input_test,inputps);%BP神经网络预测an=sim(net,inputn_test);%%网络得到数据反归一化BPoutput=mapminmax('reverse',an,outputps);d=BPoutput>cfigure(1)%plot(d,':og');scatter(1:(137-90),d,'rx');hold on;%plot(output_test,'-*');scatter(1:(137-90),output_test,'o');legend('预测输出','期望输出','fontsize',12);title('BP网络预测输出','fontsize',12);xlabel('样本','fontsize',12);xlabel('优化前输出的误差','fontsize',12);figure(2)error=d-output_test;plot(1:(137-90),error);xlabel('样本','fontsize',12);ylabel('优化前输出的误差','fontsize',12);%save net net inputs outputs-----精心整理，希望对您有所帮助!。

MATLAB下BP神经网络的设计开发BP网络在神经网络工具箱中的仿真本文利用Matlab6.5神经网络工具箱，以一组动态冲击实验数据为例建立网络模型。

实验数据共有13组，将其中对曲线形状有关键性影响的10组数据作为网络的训练数据，另外3组作为测试数据用以验证网络的预测性能。

①BP网络的建立在建立BP神经网络时，首先要根据应用的问题确定网络结构，即选择网络的层数和隐层节点数。

由于本例中实验数据较少，采用最基本的两层网络就可以很好地逼近未知函数了。

隐层节点数的选择在神经网络的应用中一直是一个复杂的问题：隐层节点数过多，将导致网络的预测能力不够，并容易导致网络陷入局部极小值难以跳出；隐层节点数过少，网络训练不出来，或不能识别以前没有的样本，且容错性差。

在设计中，比较实际的做法是通过对不同神经元数的网络进行训练、对比，找出网络效果最好时的隐层节点数。

在本例中，经大量的训练、对比，最终取中间隐层节点数为10。

另一方面，BP隐层传递函数采用正切Sigmoid 函数tansig，可以逼近任意非线性函数；输出层神经元则采用线性函数purelin，可以把输出值释放到任意值。

至此，一个1-10-1的神经网络模型建立完毕。

②BP网络的训练Matlab神经网络工具箱为用户提供了三种可用于BP网络的训练函数，它们是：trainbp、trainbpx和trainlm。

它们用法类似，采用不同的学习规则。

trainlm训练函数使用Levenberg-Marquardt算法，是三种规则中迭代次数最少、训练速度最快的一个，缺点是该算法在每次迭代时的计算量比其他算法大，故需要大量的存储空间，对于参数很大的应用是不实用的，考虑到待处理问题的参数较小，因此采用trainlm训练函数。

目标误差设为0.01，最大训练步数设为10 000。

设定好参数之后开始训练网络，训练结果显示：网络在训练了32次之后达到目标误差0.01，训练停止。

③BP网络的测试由于初始值取随机值，每次训练得到的结果都不相同，经多次训练得到最好的结果，并记录下此时的权值和阈值。

close allclearecho onclc% NEWFF——生成一个新的前向神经网络% TRAIN——对BP 神经网络进行训练% SIM——对BP 神经网络进行仿真pause% 敲任意键开始clc% 定义训练样本矢量% P 为输入矢量sqrs=[0.0000016420520 0.0000033513140 0.0000051272540 0.0000069694860 0.0000088776310 0.0000139339960 -0.0000594492310 -0.0001080022920 -0.0001476714860 ...0.0000112367340 0.0002021567880 0.0008695337800 -0.0001189929700 -0.0000912336690 0.0002160472130 0.0006358522040 0.0012365884200 0.0049930394010 ]./0.001657904949 ;sqjdcs=[0.0000399039272 0.0000805129702 0.0001218448339 0.0001639173001 0.0002067504102 0.0003172835720 0.0000421189848 0.0000870310694 0.0001350858140 ...0.0001866997652 0.0002423599348 0.0004033628719 0.0000394450224 0.0000830935373 0.0001317612004 0.0001864881262 0.0002486249700 0.0004497441812 ]./0.000533286;sqglmj=[0.0000068430669 0.0000147605347 0.0000240097285 0.0000349372747 0.0000480215187 0.0000954580176 0.0000005804238 0.0000011640375 0.0000017508228 ...0.0000023407605 0.0000029338317 0.0000044301058 0.0000030813582 0.0000071511410 0.0000126615618 0.0000203910217 0.0000318028637 0.0001118629438 ]./0.000034868299 ;s1=[0.0001773503110 0.0003553133430 0.0005338922010 0.0007130899610 0.0008929096590 0.0013452002950 0.0005747667510 0.0012111415700 0.0019195724060 ...0.0027130110200 0.0036077110840 0.0064386221260 0.0005056929850 0.0010189193420 0.0015398201520 0.0020685403470 0.0026052286500 0.0039828224110 ]./0.00275071;%s2=[25.9167875445 24.0718476818 22.2364947192 20.4105777318 18.5939487791 14.0920619223 990.2535888432 1040.4661104131 1096.3830297389 1159.029******* ...% 1229.6925839338 1453.3788619676 164.1136642277 142.4834641073 121.6137611080 101.4436832756 81.9180522413 35.6044841634];glkyl=[1 1 1 1 1 1 2 2 2 2 2 2 3 3 3 3 3 3];glhyl=[2 4 6 8 10 15 2 4 6 8 10 15 2 4 6 8 10 15 ];P=[sqrs;sqjdcs;sqglmj;s1]; %输入数据矩阵T=[glkyl;glhyl]; %目标数据矩阵echo onclcpauseclc% 创建一个新的前向神经网络net=newff(minmax(P),[20,2],{'tansig','purelin'});pauseclcecho offclcdisp('1. L-M 优化算法TRAINLM'); disp('2. 贝叶斯正则化算法TRAINBR'); choice=input('请选择训练算法(1,2):');figure(gcf);if(choice==1)echo onclc% 采用L-M 优化算法TRAINLMnet.trainFcn='trainlm';pauseclc% 设置训练参数net.trainParam.epochs = 500;net.trainParam.goal = 1e-6;net=init(net);% 重新初始化pauseclcelseif(choice==2)echo onclc% 采用贝叶斯正则化算法TRAINBRnet.trainFcn='trainbr';pauseclc% 设置训练参数net.trainParam.epochs = 500;randn('seed',192736547);net = init(net);% 重新初始化pauseclcendnet.trainParam.epochs = 500; net.trainParam.goal = 1e-6; net.trainFcn='trainoss';% 调用相应算法训练BP 网络[net,tr]=train(net,P,T);pauseclc% 对BP 网络进行仿真A = sim(net,P);% 计算仿真误差E = T - A;MSE=mse(E)pauseclc。

BP神经网络的设计实例BP神经网络（Backpropagation Neural Network）是一种常用的人工神经网络方法，其具有在模式识别、分类、预测等领域具有较好的性能和应用广泛度。

本文将通过一个MATLAB编程的实例，详细介绍BP神经网络的设计过程。

首先，我们需要定义神经网络的结构。

一个BP神经网络的结构通常包括输入层、隐藏层和输出层。

输入层的节点数与输入数据的特征个数相对应，而输出层的节点数则根据具体问题的输出类别个数而定。

隐藏层的节点数一般根据经验确定，可以根据具体问题的复杂程度来调整。

接下来，我们需要初始化神经网络的参数。

这包括各个层之间的连接权重和阈值。

权重和阈值可以随机初始化，通常可以取一个较小的随机数范围，例如(-0.5,0.5)。

这里需要注意的是，随机初始化的权重和阈值如果过大或过小可能导致网络无法正常训练，进而影响预测结果。

然后，我们需要定义神经网络的激活函数。

激活函数通常是一个非线性函数，它的作用是为了引入非线性特征，增加神经网络的拟合能力。

常用的激活函数有sigmoid函数、tanh函数等。

在MATLAB中，可以通过内置函数sigmf和tansig来定义这些激活函数。

接着，我们需要定义神经网络的前向传播过程。

前向传播是指将输入数据通过神经网络，计算得到输出结果的过程。

具体操作可以按照以下步骤进行：1.输入数据进入输入层节点；2.将输入层节点的输出值乘以与隐藏层节点连接的权重矩阵，然后求和，此时得到隐藏层节点的输入值；3.将隐藏层节点的输入值通过激活函数进行激活，得到隐藏层节点的输出值；4.重复上述步骤，将隐藏层节点的输出值乘以与输出层节点连接的权重矩阵，然后求和，此时得到输出层节点的输入值；5.将输出层节点的输入值通过激活函数进行激活，得到输出层节点的输出值。

最后，我们需要定义神经网络的反向传播过程。

反向传播是为了根据输出误差来调整各个层之间的权重和阈值，使得预测结果更接近真实值。

MA TLAB神经网络算法实例讲解【附源代码】例1 采用动量梯度下降算法训练BP 网络。

训练样本定义如下：输入矢量为p =[-1 -2 3 1-1 1 5 -3]目标矢量为t = [-1 -1 1 1]解：本例的MA TLAB 程序如下：close allclearecho onclc% NEWFF——生成一个新的前向神经网络% TRAIN——对BP 神经网络进行训练% SIM——对BP 神经网络进行仿真pause% 敲任意键开始clc% 定义训练样本% P 为输入矢量P=[-1, -2, 3, 1; -1, 1, 5, -3];% T 为目标矢量T=[-1, -1, 1, 1];pause;clc% 创建一个新的前向神经网络net=newff(minmax(P),[3,1],{'tansig','purelin'},'traingdm') % 当前输入层权值和阈值inputW eights=net.IW{1,1}inputbias=net.b{1}% 当前网络层权值和阈值layerW eights=net.LW{2,1}layerbias=net.b{2}pauseclc% 设置训练参数net.trainParam.show = 50;net.trainParam.lr = 0.05;net.trainParam.mc = 0.9;net.trainParam.epochs = 1000;net.trainParam.goal = 1e-3;pauseclc% 调用TRAINGDM 算法训练BP 网络[net,tr]=train(net,P,T);pauseclc% 对BP 网络进行仿真A = sim(net,P)% 计算仿真误差E = T - AMSE=mse(E)pauseclcecho off例2 采用贝叶斯正则化算法提高BP 网络的推广能力。

BP神经网络的仿真实验一、实验目的学会用matlab的神经网络工具箱（Nntool）来完成神经网络可逼近函数的功能。

二、实验任务设计一个两层的BP神经网络。

输入范围为[－1 1]，样本输入x和目标输出y为：x=-1:0.01:1；y=（1－x2）1/2训练该网络使输出在区间[-1 1] 内逼近该函数。

三、实验要求：通过仿真画出y=（1－x2）1/2 和在样本输入x的情况下神经网络输出的图形，分析你所设计的神经网络的逼近性能如何？四、实验步骤及结果1实验步骤1) 在Matlab的命令窗口下键入Nntool，2) 我们就进入了神经网络工具箱的Network/Data Manager窗口：2）点击Network/Data Manager窗口下部的New Network，3）进入Create New Network窗口，4）该窗口的每一个设置参数如图所示：3）输入神经网络的输入向量和目标向量：在Matlab命令窗口中定义好所需要的输入向量和目标向量，再传送到工具箱中，具体操作为在命令窗口键入以下命令行：>> x=-1:0.01:1;>> y=sqrt(1-x.^2);这样就定义好了输入向量和目标向量。

点击Network/Data Manager窗口下的Import 按钮，进入Import or Load to Network/Data Manager窗口：由于数据来自于工作空间，所以Source项取默认值；如果数据来自于disk，则选择Load from disk file。

在Select a variable中选择想要传送的数据x，再在destination项中键入名字x，同时import as中的选项被激活了，选择其中的Inputs，最后点击Import，这样就完成了输入向量从工作空间向工具箱的传送，在Network/Data Manager窗口下的Inputs列表中出现了新输入的输入向量的名字x；同理可以输入目标向量y。