第8章讲义材料分析方法

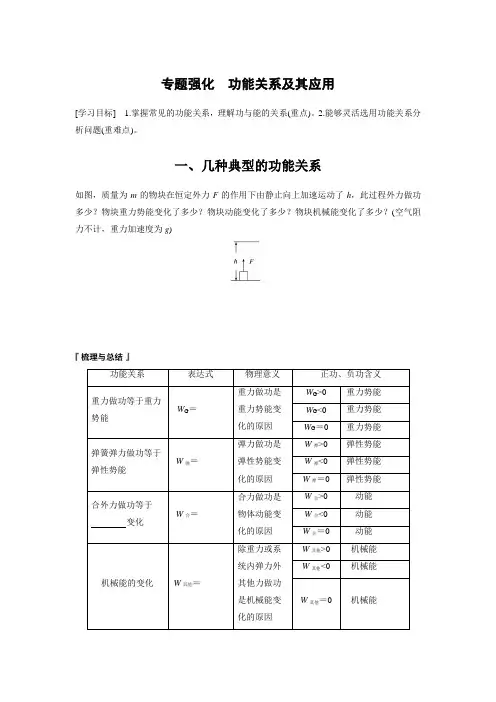
专题强化功能关系及其应用[学习目标] 1.掌握常见的功能关系，理解功与能的关系(重点)。

2.能够灵活选用功能关系分析问题(重难点)。

一、几种典型的功能关系如图，质量为m的物块在恒定外力F的作用下由静止向上加速运动了h，此过程外力做功多少？物块重力势能变化了多少？物块动能变化了多少？物块机械能变化了多少？(空气阻力不计，重力加速度为g )________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ 功能关系表达式物理意义正功、负功含义重力做功等于重力势能_________W G＝______重力做功是重力势能变化的原因W G>0重力势能_____W G<0重力势能_____W G＝0重力势能_____弹簧弹力做功等于弹性势能_______ W弹＝______弹力做功是弹性势能变化的原因W弹>0弹性势能_____W弹<0弹性势能_____W弹＝0弹性势能_____合外力做功等于变化W合＝______合力做功是物体动能变化的原因W合>0动能_____W合<0动能_____W合＝0动能_____机械能的变化W其他＝______ 除重力或系统内弹力外其他力做功是机械能变化的原因W其他>0机械能_____W其他<0机械能_____W其他＝0机械能_____一对滑动摩擦力做功与内能增加量F f l 相对＝Q (l 相对指相对路程)滑动摩擦力与 的乘积等于产生的热量功和能一样吗？二者有何关系？________________________________________________________________________ ________________________________________________________________________ 例1 (2023·贵阳市期末)质量为m 的物体在升降机中，随升降机竖直向上以大小为14g (g 为重力加速度)的加速度做匀减速直线运动，上升高度为h ，在此过程中，物体的机械能( ) A ．增加14mghB ．减少14mghC ．增加34mghD ．减少34mgh例2 (多选)(2023·临汾市高一期末)如图所示，在竖直平面内有一半径为R 的34圆弧轨道，半径OA 水平、OB 竖直，一个质量为m 的小球自A 点的正上方P 点由静止开始自由下落，小球沿圆弧轨道到达最高点B 时恰好对轨道没有压力，已知AP ＝2R ，重力加速度为g ，则小球从P 到B 的运动过程中( )A ．重力做功mgRB ．机械能减少12mgRC ．合外力做功mgRD ．克服摩擦力做功mgR二、热量的产生与摩擦力做功如图，质量为M 、长为l 0的木板静止放置于光滑地面上，一质量为m 的物块以速度v 0从左端冲上木板，物块和木板间的滑动摩擦力大小为F f 。

第八章海浪第一节概述一、波浪（Wave）要素1、波峰――波面的最高点。

2、波谷――波面的最低点。

3、波高（H）――相邻波峰与波谷之间的垂直距离。

4、波幅（a）――波高的一半，a=H/2。

5、波长（λ）――相邻两波峰或相邻两波谷之间的水平距离。

6、波陡（δ）――波高与波长之比，δ＝H/λ。

7、周期（T）――相邻的两波峰或两波谷相继通过一固定点所需要的时间。

8、频率（f）――周期的倒数，f＝1/T。

9、波速（C）――波峰或波谷在单位时间内的水平位移（波形传播的速度），C＝λ/ T。

10、波峰线――通过波峰垂直于波浪传播方向的线。

11、波向线――波形传播的方向线，垂直于波峰线。

二、波浪的分类1、按周期或频率分类海浪大部分能量集中在周期4～12s的范围内，属重力波范围。

最常见的重力波是风浪和涌浪。

2、按成因分类1）风浪和涌浪风浪（Wind Wave）――风的直接作用所引起的水面波动。

（无风不起浪）涌浪（Swell）――风浪离开风区传至远处，或者风区里风停息后所遗留下来的波浪。

（无风三尺浪）2）海啸（Tsunami，又称地震波）――由于海底或海岸附近发生地震或火山爆发所形成的海面异常波动。

特点：周期长，波长长，波速大，在外海坡度很小，当传至近岸时，波高剧增。

世界上常受海啸袭击的国家和地区有：日本、菲律宾、印度尼西亚、加勒比海、墨西哥沿岸、地中海。

3）风暴潮（Storm Surge）――由强烈的大气扰动（强台风、强锋面气旋、寒潮大风等）引起的海面异常上升现象。

主要原因：海面气压分布不均匀――气压每下降1hPa，海面约升高1cm；大风――风暴向岸边移动时，受强风牵引海水涌向岸边，海面升高，升高幅度与风速的平方成正比。

我国风暴潮多发区：莱州湾、渤海湾、长江口至闽江口、汕头至珠江口、雷州湾和海南岛东北角，其中莱州湾、汕头至珠江口是严重多发区。

4）内波（Internal Wave）――密度相差较大的水层界面上的波动。

第八章 19世纪文学（三）19世纪后期的文学呈多元化：30年代的批判现实主义文学（主潮）、自然主义文学、巴黎公社文学。

非理性的具有现代特征的形式主义文学第一节概述一、19世纪后期文学的基本特征1.三种基本思想并存。

①马克思的科学社会主义，它明确提出必须推翻资本主义制度，建立社会主义。

②传统的人道主义思想。

③叔本华、尼采、柏格森的非理性学说，对世界感到失望和无所适从，只好退回内心强调“意志”。

2.开始“退回内心”。

（19世纪后期欧洲文学开始出现“向内转”的趋势）。

3.越来越重视文学技巧。

批判现实主义文学注重心理分析与内心独白；形式主义文学则注重象征和隐喻，讲究交感和对应。

二、多元文学的发展概况自然主义、巴黎公社文学、唯美主义文学、象征主义文学、批判现实主义文学。

（一）现实主义文学19世纪后期文学的主导潮流，不再局限于资本主义发达国家，而是扩展到封建专制的国家；对罪恶的根源的追问；对人类心灵关注加强。

（1）法国莫泊桑1、世界文坛三大“短篇小说之王”之一。

中短篇小说300余篇、长篇小说6部；中短篇小说是莫泊桑的最高成就，所表现的生活可以拼贴成法国社会风俗画。

福楼拜的学生，受福楼拜影响。

2、代表作《羊脂球》（成名作、具有爱国主义思想。

）最富现实意义长篇小说：《漂亮朋友》3、特点（1）普法战争称为主要题材。

（2）展现小职员的生活与精神世界。

（3）以诺曼底农村生活为背景（4）展现人的神秘精神状态4、艺术成就（1）文字简洁，结构严密（2）用平淡的口吻叙述故事（3）语言朴实无华都德：《柏林之围》《最后一课》（2）英国梅瑞狄斯：《利益主义者》哈代（3）德国主流是现实主义文学冯达诺：德国文学史上现实主义创始人，《艾菲·布利斯特》（4）中欧和南欧以反对压迫争取民族解放为主挪威：易卜生（5）俄国19世纪后期现实主义文学成就最高的国家列夫·托尔斯泰契诃夫：《小公务员之死》《变色龙》《套中人》1、契诃夫的创作特点：（1）多选取普通生活，自然的反映善恶（2）不动声色的叙述态度（3）契诃夫的小说没有大篇幅的景物描写2、《套中人》中别里科夫的典型形象和社会意义：⑴契诃夫在短篇小说《套中人》中塑造了一个旧制度的卫道士，新事物的反对者的典型――中学希腊语教员别里科夫。

正保远程教育旗下品牌网站 美国纽交所上市公司(NYSE:DL)
自考365 中国权威专业的自考辅导网站
官方网站： 高等教育自学考试辅导《护理学研究》第八章第二节讲义1
量性研究资料的统计学分析方法
一、计量资料的统计学分析方法
二、计数资料的统计学分析方法
三、等级资料常用的统计学分析方法
四、统计表和统计图
量性研究资料的统计分析包括两个方面：
①统计描述：即描述数据的分布规律和特征，常用均数、标准差、中位数、率、构成比等统计指标，以及统计表、统计图等进行描述。

②统计推断：即由样本信息推断总体特征，常用t 检验、方差分析、χ2检验、秩和检验等比较组间有无差异，以及相关分析、回归分析等探讨变量之间的关联性。

统计学分析方法的选择取决于研究目的、科研设计类型和资料类型。

计量资料的统计学分析方法
（一）统计描述
正态分布：均数±标准差
偏态分布：中位数、四分位数间距
1.均数。

材料分析方法总结材料分析是一门重要的科学技术，它在工程、材料科学、地质学、化学等领域都有着广泛的应用。

在材料分析中，我们需要运用各种方法来对材料的成分、结构、性能进行分析，以便更好地理解和利用材料。

本文将对常见的材料分析方法进行总结，希望能够对相关领域的研究者和工程师有所帮助。

首先，光学显微镜是材料分析中常用的方法之一。

通过光学显微镜，我们可以观察材料的形貌、颗粒大小、晶粒结构等信息。

这对于金属、陶瓷、塑料等材料的分析都非常有帮助。

同时，透射电子显微镜和扫描电子显微镜也是常用的分析工具，它们可以提供更高分辨率的图像，帮助我们观察材料的微观结构。

除了显微镜，X射线衍射也是一种常用的材料分析方法。

通过X射线衍射，我们可以确定材料的晶体结构和晶格参数，从而了解材料的晶体学性质。

X射线衍射在材料科学、地质学和化学领域都有着广泛的应用，是一种非常有效的分析手段。

此外，光谱分析也是材料分析中常用的方法之一。

光谱分析包括紫外可见吸收光谱、红外光谱、拉曼光谱等，它们可以用于分析材料的组成、结构和性能。

光谱分析在材料科学、化学和生物学领域都有着重要的应用，是一种非常有力的分析工具。

在材料分析中，热分析也是一种常用的方法。

热分析包括热重分析、差热分析、热膨胀分析等，它们可以用于研究材料的热稳定性、热分解过程、相变行为等。

热分析在材料科学、化学工程和材料加工领域都有着广泛的应用，是一种非常重要的分析手段。

最后，表面分析也是材料分析中不可或缺的方法。

表面分析包括扫描电子显微镜、原子力显微镜、X射线光电子能谱等，它们可以用于研究材料的表面形貌、化学成分和电子结构。

表面分析在材料科学、电子工程和纳米技术领域都有着重要的应用，是一种非常有效的分析手段。

综上所述，材料分析是一门重要的科学技术，它涉及到多个领域的知识和技术。

在材料分析中，我们可以运用光学显微镜、X射线衍射、光谱分析、热分析和表面分析等方法来对材料进行分析，从而更好地理解和利用材料。

第8章《幂的运算》考点+易错知识梳理重难点分类解析考点1 运用幂的基本性质进行运算【考点解读】掌握幂的基本性质是解决问题的关键，要根据算式的特点确定运算的顺序，并选择幂的基本性质进行正确计算，不要混淆同底数幂的乘法、积的乘方以及幂的乘方. 例1 (2017·江西)下列运算正确的是( )A. 5210()a a -=B. 22236a a a =gC. 23a a a -+=-D. 623623a a a -÷=-分析: 5210()a a -=，故选项A 正确；23236a a a =g，故选项B 错误；2a a a -+=-，故选项C 错误；624623a a a -÷=-，故选项D 错误.答案:A【规律·技法】根据合并同类项、幂的乘方及同底数幂的乘法的定义解答. 【反馈练习】1.下列计算正确的是( )A. 224x x x +=B. 3332x x x -=C. 236x x x =g D. 236()x x =点拨:正确应用各类计算法则计算. 2.计算:201320111(3)()3-⨯-= .点拨:应用积的乘方的逆运算，把2013(3)-折分成20112(3)(3)-⨯-.考点2 运用零指数、负整数指数幂的意义进行运算【考点解读】明确零指数、负整数指数幂的规定，同时区分一些形式上相似而实质上不一样的算式，如03与03-，12-与12--等. 例2 计算0112()2-+的结果是 . 分析:0112()1232-+=+=.答案:3 【规律·技法】本题考查了0次幂和负整数指数幂的意义，解答本题的关键是熟记相关法则. 【反馈练习】3.计算018()2---的结果是( )A. 7-B. 7C. 172D. 9 点拨:018()8172---=-=. 4.计算2133-⨯的结果是( )A. 3B. 3-C. 2D. 2- 点拨: 1133-=. 考点3 用科学记数法表示数【考点解读】要善于总结用科学记数法表示数的一般性规律，如:40.000110-=，50.0000110-=，60.00000110-=，70.000000110-=等.例3 (2017·济宁)某桑蚕丝的直径为0.000 016 m ，将0.000 016用科学记数法表示是() A. 41.610-⨯ B. 51.610-⨯ C. 61.610-⨯ D. 61610-⨯ 分析:绝时值小于1的正数也可以利用科学记数法表示，一般形式为10na -⨯，与较大数的科学记数法不同的是其所使用的是负整数幂，指数由原数左边起第一个不为零的数字前面0的个数所决定，则50.000016 1.610-=⨯.答案:B【规律·技法】用科学记数法表示较小的数，一般形式为10na -⨯，其中110a ≤<，n 由原数左边起第一个非零数字前面0的个数所决定. 【反馈练习】5.生物学家发现了一种病毒，其长度为0.000 000 32 mm ，数据0.000 000 32用科学记数法表示正确的是( )A. 73.210⨯ B. 53.210-⨯ C. 73.210-⨯ D. 83.210-⨯ 点拨:确定科学记数法表示较小的数的一般形式10na -⨯中a 和n 的值.6.蜜蜂建造的蜂巢既坚固又省料，其厚度约为0.000 073 m ，将0.000 073用科学记数法表示为 .点拨:确定科学记数法表示较小的数的一般形式10na -⨯中a 和n 的值.考点4 幂的相关运算【考点解读】熟练掌握有关幂的运算法则. 例4 下列运算正确的是( )A. 320a a -=B. 23a a a =gC. 432a a a ÷= D. 325()a a =分析:32a a a -=，故选项A 不正确；23a a a =g ，故选项B 正确；43a a a ÷=，故选项C 不正确；326()a a =，故选项D 不正确.答案:B【规律·技法】本题考查了同底数幂的除法、合并同类项、同底数幂的乘法、幂的乘方，这些运算很容易混淆，一定要记准不同的运算法则. 【反馈练习】7.下列计算结果正确的是( )A. 842a a a ÷=B. 236a a a =g C. 248()a a = D. 236(2)8a a -= 点拨mnm na a a-÷=；m n m na a a+⨯= ；()m n mna a=(m ，n 是整数).8.下列运算正确的是( )A. 5210()a a = B. 1644x x x ÷=C. 224235a a a +=D. 3332b b b =g点拨m n m na a a-÷=；m n m na a a+⨯= ；()m n mna a=(m ，n 是整数).易错题辨析易错点 1 运用同底数幂的乘法法则计算时，漏掉了指数是“1”的因式例1计算: 32m m m ∙g . 错误解答: 32325m m m mm +∙==g s.错因分析:本题错在忽视最后一个因式m 的指数是1，误认为它的指数是0. 正确解答:323216m m m mm ++∙==g .易错辨析:单个字母的指数是1而不是0，只不过指数为1时可以省略不写，但不能认为指数是0.易错点2 运算法则使用不当例2计算:(1) 43(3)xy -; (2) 22(3)a b . 错误解答:(1) 4312(3)3xy xy -=-. (2) 2242(3)6a b a b =.错因分析:积的乘方是将积中的每一个因式分别乘方，而(1)中只将最后一个因式乘方，忽略了3-，x 两个因式的乘方，而(2)中错误地将乘方的次数乘以系数了. 正确解答:(1) 43312(3)27xy x y -=-. (2) 2242(3)9a b a b =.易错辨析:运用积的乘方法则时，要注意不能遗漏因式.易错点3 错用合并同类项法则例3计算: 3223()()x x +.错误解答: 32236612()()x x x x x +=+=.错因分析:本题错在将合并同类项法则与同底数幂乘法法则相混淆，错解中既运用了合并同类项法则，又运用了同底数幂相乘的法则.本题实际上是合并同类项，利用合并同类项法则将系数相加作为和的系数，字母和字母指数不变. 正确解答:3223666()()2x x x x x +=+=. 易错辨析:正确区分合并同类项与同底数幕乘法.易错点4 错用同底数幂除法法则例4计算:62x x ÷. 错误解答: 62623x x xx ÷÷==.错因分析:上面的解法用错了法则，同底数幂相除，底数不变，指数相减，而不是相除. 正确解答: 62624x x xx -÷==.易错辨析:同底数幕除法法则为mnm na a a -÷= (其中m ，n 是整数)，注意m n -不能写成m n ÷.易错点5 运算中符号出错例5 计算:62()()y y -÷-. 错误解答:626244()()()()y y y y y --÷-=-=-=-.错因分析: 44444()(1)(1)y y y y -=-=-=g g . 正确解答:626244()()()()y y y y y --÷-=-=-=.易错辨析:当n 为奇数时，()nna a -=-;当n 为偶数时，()nna a -=.反馈练习1.给出下列算式:①43272()()a a c a c --=-g ；②326()a a -=-；③3342()a a a -÷=；④633()()a a a -÷-=-.其中正确的有( )A. 4个B. 3个C. 2个D. 1个 点拨:注意运算的顺序，正确运用法则运算.2.若20.3a =-，23b -=-，21()3c -=-，01()3d =-，则( )A. a b c d <<<B. b a d c <<<C. a d c b <<<D. c a d b <<<点拨:分别计算出,,,a b c d 的值，比较即可.3.给出下列各式:①523[()]a a --g；②43()a a -g ；③2332()()a a -g ；④43[()]a --.其中计算结果为12a -的有( )A.①和③B.①和②C.②和③D.③和④点拨:注意“偶次方”和“奇次方”的符号处理. 4.计算: 23()()p p --=g ；231()2a b -= . 点拨:正确运用法则计算，最后结果化为最简形式.5.计算: 2018201952()()25-⨯-= . 点拨:把20192()5-分解为201822()()55--g 即可。

8．4列联表独立性分析案例[读教材·填要点]1．列联表一般地，对于两个因素X和Y，X的两个水平取值：A和A(如吸烟和不吸烟)，Y也有两个水平取值：B和B(如患肺癌和不患肺癌)，我们得到下表中的抽样数据，这个表格称为2×2列联表.2．χ2公式χ2＝n ad－bc2a ＋b c＋d a＋c b＋d.3．独立性检验的概念用随机变量χ2研究两变量是否有关的方法称为独立性检验．4．独立性检验的步骤要判断“X与Y有关系”，可按下面的步骤进行：(1)提出假设H0：X与Y无关；(2)根据2×2列联表及χ2公式，计算χ2的值；(3)查对临界值，作出判断．其中临界值如表所示：表示在H0成立的情况下，事件“χ2≥x0”发生的概率．5．变量独立性判断的依据(1)如果χ2>10.828时，就有99.9%的把握认为“X与Y有关系”；(2)如果χ2>6.635时，就有99%的把握认为“X与Y有关系”；(3)如果χ2>2.706时，就有90%的把握认为“X与Y有关系”；(4)如果χ2≤2.706时，就认为没有充分的证据显示“X与Y有关系”，但也不能作出结论“H0成立”，即X与Y没有关系．[小问题·大思维]1．利用χ2进行独立性分析，估计值的准确度与样本容量有关吗？提示：利用χ2进行独立性分析，可以对推断的正确性的概率作出估计，样本容量n越大，这个估计值越准确．如果抽取的样本容量很小，那么利用χ2进行独立性检验的结果就不具有可靠性．2．在χ2运算后，得到χ2的值为29.78，在判断因素相关时，P(χ2≥6.64)≈0.01和P(χ2≥7.88)≈0.005，哪种说法是正确的？提示：两种说法均正确．P(χ2≥6.64)≈0.01的含义是在犯错误的概率不超过0.01的前提下认为两因素相关；而P(χ2≥7.88)≈0.005的含义是在犯错误的概率不超过0.005的前提下认为两因素相关．[例1]数据：[解] 由列联表中的数据，得χ2的值为χ2＝－2254×1 379×54×1 579≈68.033>6.635.因此，有99%的把握认为每一晚打鼾与患心脏病有关系．解决一般的独立性分析问题，首先由所给2×2列联表确定a，b，c，d，a＋b＋c＋d 的值，然后代入随机变量的计算公式求出观测值χ2，将χ2与临界值x0进行对比，确定有多大的把握认为两个分类变量有关系．1．某大型企业人力资源部为了研究企业员工工作积极性和对待企业改革态度的关系，经过调查得到如下列联表：系？解：由列联表中的数据，得 χ2＝－294×95×86×103≈10.759>6.635，∴有99%的把握认为工作态度与支持企业改革之间有关系．[例2] (1)(2)若饮用干净水得病5人，不得病50人，饮用不干净水得病9人，不得病22人．按此样本数据分析这种疾病是否与饮用水有关，并比较两种样本在反映总体时的差异．[解] (1)假设H 0：传染病与饮用水无关．把表中数据代入公式，得χ2＝－2146×684×518×312≈54.21，因为当H 0成立时，χ2≥10.828的概率约为0.001，所以我们有99.9%的把握认为该地区这种传染病与饮用不干净水有关．(2)依题意得2×2列联表：此时，χ2＝－214×72×55×31≈5.785.由于5.785＞2.706，所以我们有90%的把握认为该种疾病与饮用不干净水有关．两个样本都能统计得到传染病与饮用不干净水有关这一相同结论，但(1)中我们有99.9%的把握肯定结论的正确性，(2)中我们只有90%的把握肯定．独立性分析的步骤：要推断“X与Y是否有关”可按下面的步骤进行：①提出统计假设H0：X与Y无关；②根据2×2列联表与χ2计算公式计算出χ2的值；③根据两个临界值，作出判断．2．为了探究学生选报文、理科是否与对外语的兴趣有关，某同学调查了361名高二在校学生，调查结果如下：理科对外语有兴趣的有138人，无兴趣的有98人，文科对外语有兴趣的有73人，无兴趣的有52人．是否有90%的把握认为“学生选报文、理科与对外语的兴趣有关”？解：根据题目所给的数据得到如下列联表：χ2＝－2211×150×236×125≈1.871×10－4.因为1.871×10－4<2.706，所以没有90%的把握认为“学生选报文、理科与对外语的兴趣有关”．[例3] 为了比较注射A，B两种药物后产生的皮肤疱疹的面积，选200只家兔做试验，将这200只家兔随机地分成两组，每组100只，其中一组注射药物A，另一组注射药物B.下表1和表2分别是注射药物A和药物B后的试验结果．(疱疹面积单位：mm2) 表1：注射药物A后皮肤疱疹面积的频数分布表表2：注射药物B 后皮肤疱疹面积的频数分布表完成下面2×2列联表，并回答是否有99%的把握认为“注射药物A 后的疱疹面积与注射药物B 后的疱疹面积有差异”．表3：[解]χ2＝－2100×100×105×95≈24.56>6.635.因此，有99%的把握认为“注射药物A 后的疱疹面积与注射药物B 后的疱疹面积有差异”．在绘制列联表时，应对问题中的不同数据分成不同的类别，然后列表．要注意列联表中各行、各列中数据的意义及书写格式．3．已知某班n 名同学的数学测试成绩(单位：分，满分100分)的频率分布直方图如图所示，其中a ，b ，c 成等差数列，且成绩在[90,100]内的有6人．(1)求n 的值；(2)规定60分以下为不及格，若不及格的人中女生有4人，而及格的人中，男生比女生少4人，借助独立性检验分析是否有90%的把握认为“本次测试的及格情况与性别有关”？附：χ2＝a ＋bc ＋d a ＋cb ＋d解：(1)依题意得⎩⎪⎨⎪⎧＋0.025＋c ＋2b ＋a ＝1，2b ＝a ＋c ，解得b ＝0.01.因为成绩在[90,100]内的有6人， 所以n ＝60.01×10＝60.(2)由于2b ＝a ＋c ，而b ＝0.01，可得a ＋c ＝0.02，则不及格的人数为0.02×10×60＝12，及格的人数为60－12＝48，设及格的人中，女生有x 人，则男生有x －4人， 于是x ＋x －4＝48，解得x ＝26，故及格的人中，女生有26人，男生有22人． 于是本次测试的及格情况与性别的2×2列联表如下：结合列联表计算可得χ2＝30×30×48×12＝1.667<2.706，故没有90%的把握认为“本次测试的及格情况与性别有关”.性别与患色盲是否有关？你所得到的结论在什么范围内有效？[解] 由题意作2×2列联表如下：法一：由列联表中数据可知，在调查的男人中，患色盲的比例是38480≈7.917%，女人中患色盲的比例为6520≈1.154%，由于两者差距较大，因而我们可以认为性别与患色盲是有关系的．法二：由列联表中所给的数据可知，a＝38，b＝442，c＝6，d＝514，a＋b＝480，c＋d＝520，a＋c＝44，b＋d＝956，n＝1 000，代入公式得χ2＝－2480×520×44×956≈27.1.由于χ2≈27.1>6.635，所以我们有99%的把握即在犯错误不超过0.01的前提下认为性别与患色盲有关系．这个结论只对所调查的480名男人和520名女人有效．1．下面是2×2列联表：则表中a，b的值分别为A．94,96 B．52,50C．52,54 D．54,52解析：选C ∵a＋21＝73，∴a＝52.又∵a＋2＝b，∴b＝54.2．下列关于χ2的说法中正确的是( )A．χ2在任何相互独立问题中都可以用于检验是否相关B．χ2的值越大，两个事件的相关性越大C．χ2是用来判断两个相互独立事件相关与否的一个统计量，它可以用来判断两个事件是否相关这一类问题D．χ2＝n ad－bca ＋b c＋d a＋c b＋d答案：C3．对于因素X与Y的随机变量χ2的值，下列说法正确的是( )A．χ2越大，“X与Y有关系”的可信程度越小B．χ2越小，“X与Y有关系”的可信程度越小C．χ2越接近于0，“X与Y没有关系”的可信程度越小D．χ2越大，“X与Y没有关系”的可信程度越大解析：选B χ2越大，“X与Y没有关系”的可信程度越小，则“X与Y有关系”的可信程度越大．即χ2越小，“X与Y有关系”的可信程度越小．4．若由一个2×2列联表中的数据计算得χ2的观测值为4.013，那么在犯错误的概率不超过________的前提下，认为两个变量之间有关系．解析：因为4.013>3.841，所以在犯错误的概率不超过0.05的前提下，认为两个变量之间有关系．答案：0.055．某矿石粉厂当生产一种矿石粉时，在数天内即有部分工人患职业性皮肤炎，在生产季节开始，随机抽取75名车间工人穿上新防护服，其余仍穿原用的防护服，生产进行一个月后，检查两组工人的皮肤炎患病人数如下：解析：χ2＝－275×28×15×88≈13.826>6.635.故有99%的把握说，新防护服比旧防护服对预防工人职业性皮炎有效．答案：99%6．为了解某班学生喜爱打篮球是否与性别有关，对本班50人进行了问卷调查得到了如下的列联表：已知在全部50人中随机抽取1人抽到爱打篮球的学生的概率为35.(1)请将上面的列联表补充完整；(2)是否有99%的把握认为喜爱打篮球与性别有关；请说明理由． 附参考公式：χ2＝n ad －bc 2a ＋bc ＋d a ＋cb ＋d，其中n ＝a ＋b ＋c ＋d .解：(1)列联表补充如下：(2)∵χ2＝－230×20×25×25≈8.333>6.635，∴有99%的把握认为喜爱打篮球与性别有关．一、选择题1．有两个因素X 与Y 的一组数据，由其列联表计算得χ2≈4.523，则认为X 与Y 有关系是错误的可信度为( )A ．95%B ．90%C ．5%D ．10%解析：选C ∵χ2≥3.841.∴X 与Y 有关系的概率为95%，∴X 与Y 有关系错误的可信度为5%.2．通过随机询问110名性别不同的大学生是否爱好某项运动，得到如下的列联表：计算得，χ2＝－260×50×60×50≈7.8.附表：A．在犯错误的概率不超过0.1% 的前提下，认为“爱好该项运动与性别有关”B．在犯错误的概率不超过0.1% 的前提下，认为“爱好该项运动与性别无关”C．有99%以上的把握认为“爱好该项运动与性别有关”D．有99%以上的把握认为“爱好该项运动与性别无关”解析：选C 根据独立性分析的思想方法，正确选项为C.3．某高校“统计初步”课程的老师随机调查了选该课的一些学生情况，具体数据如下表：为了分析主修统计中的数据，得到χ2＝－223×27×20×30≈4.84，所以断定主修统计专业与性别有关系，这种判断出错的可能性为( )A．0.025 B．0.05C．0.975 D．0.95解析：选B ∵χ2≈4.84>3.841，所以我们有95%的把握认为主修统计专业与性别无关，即判断出错的可能性为0.05.4．已知P(x2≥2.706)＝0.10，两个因素X和Y，取值分别为{x1，x2}和{y1，y2}，其样本频数分别是a＝10，b＝21，c＋d＝35.若在犯错误的概率不超过0.1的前提下，认为X与Y有关系，则c等于( )A．5 B．6C．7 D．8解析：选A 经分析，c＝5.二、填空题5．班级与成绩2×2列联表：表中数据m，n，p，解析：m＝10＋7＝17，n＝35＋38＝73，p＝7＋38＝45，q＝m＋n＝90.答案：17,73,45,906．在吸烟与患肺病是否相关的判断中，有下面的说法：①若χ2>6.64，则在犯错误的概率不超过0.01的前提下，认为吸烟与患肺病有关系，那么在100个吸烟的人中必有99人患有肺病；②从独立性分析可知在犯错误的概率不超过0.01的前提下，认为吸烟与患肺病有关系时，若某人吸烟，则他有99%的可能患有肺病；③从独立性分析可知在犯错误的概率不超过0.05的前提下，认为吸烟与患肺病有关系时，是指有5%的可能性使得推断错误．其中说法正确的是________．解析：χ2是检验吸烟与患肺病相关程度的量，是相关关系，而不是确定关系，是反映有关和无关的概率，故说法①不正确；说法②中对“确定容许推断犯错误概率的上界”理解错误；说明③正确．答案：③7．统计推断，当________时，在犯错误的概率不超过0.05的前提下认为事件A与B 有关；当________时，认为没有充分的证据显示事件A与B是有关的．解析：当k>3.841时，就有在犯错误的概率不超过0.05的前提下认为事件A与B有关，当k＜2.706时认为没有充分的证据显示事件A与B是有关的．答案：k>3.841 k＜2.7068．某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中，随机抽取了100名电视观众，相关的数据如下表所示：由表中数据直观分析，收看新闻节目的观众是否与年龄有关：________(填“是”或“否”)．解析：因为在20至40岁的58名观众中有18名观众收看新闻节目，而大于40岁的42名观众中有27名观众收看新闻节目，即ba ＋b ＝1858，dc ＋d ＝2742，两者相差较大，所以，经直观分析，收看新闻节目的观众与年龄是有关的．答案：是 三、解答题9．某市对该市一重点中学2018年高考上线情况进行统计，随机抽查得到表格：解：对于上述四个科目，分别构造四个随机变量 χ21，χ22，χ23，χ24. 由表中数据可以得到： 语文：χ21＝－2201×43×204×40＝7.294>6.64，数学：χ22＝－2201×43×201×43＝30.008>6.64，英语：χ23＝－2201×43×200×44＝24.155>6.64，综合科目： χ24＝－2201×43×201×43＝17.264>6.64.所以有99%的把握认为语文、数学、英语、综合科目上线与总分上线有关系，数学上线与总分上线关系最大．10．一次对人们休闲方式的调查中共调查了124人，其中女性70人，男性54人，女性中有43人主要的休闲方式是看电视，另外27人主要的休闲方式是运动；男性中有21人主要的休闲方式是看电视，另外33人主要的休闲方式是运动．(1)根据以上数据建立一个2×2列联表；(2)能否在犯错误的概率不超过0.05的前提下认为性别与休闲方式有关系？ 解：(1)2×2列联表如下：(2)χ2＝－270×54×64×60≈6.201.因为6.201>3.841，所以有理由认为假设休闲方式与性别无关是不合理的，即在犯错误的概率不超过0.05的前提下认为休闲方式与性别有关．。

【考点1】目标之间的关系【考点2】工程总目标确定原则【考点3】三大目标控制的任务和措施【考点4】签发工程暂停令的情形【考点5】巡视【考点6】平行检验【考点7】旁站【考点8】见证取样【考点9】信息化第一节建设工程监理工作内容任何建设工程都有质量、造价、进度三大目标。

（一）建设工程三大目标之间的关系从建设单位角度出发，往往希望建设工程的质量好、投资省、工期短（进度快），但在工程实践中，几乎不可能同时实现上述目标。

1.三大目标之间的对立关系建设工程三大目标之间存在着矛盾和对立的一面。

【对立：鱼和熊掌不可兼得】2.三大目标之间的统一关系【统一：并不相互制约，而是相互促进】（二）建设工程三大目标的确定与分解从不同角度将建设工程总目标分解成若干分目标、子目标及可执行目标。

从而形成“自上而下层层展开、自下而上层层保证”的目标体系。

1.建设工程总目标的分析论证分析论证建设工程总目标，应遵循下列基本原则：（1）确保建设工程质量目标符合工程建设强制性标准。

在追求建设工程质量、造价和进度三大目标间最佳匹配关系时，应确保建设工程质量目标符合工程建设强制性标准。

（2）定性分析与定量分析相结合。

（3）不同建设工程三大目标可具有不同的优先等级。

在“质量优、投资省、工期短”之间寻求最佳匹配。

2.建设工程总目标的逐级分解为了有效地控制建设工程三大目标，需要逐级分解建设工程总目标，按工程参建单位、工程项目组成和时间进展等制定分目标、子目标及可执行目标，形成如图8-1所示建设工程目标体系。

（三）建设工程三大目标控制的任务和措施3.三大目标控制措施为了有效地控制建设工程项目目标，应从组织、技术、经济、合同等多方面采取措施。

【至少一题】（1）组织措施组织措施是其他各类措施的前提和保障，包括：建立健全实施动态控制的组织机构、规章制度和人员，明确各级目标控制人员的任务和职责分工，改善建设工程目标控制的工作流程；建立建设工程目标控制工作考评机制，加强各单位（部门）之间的沟通协作；加强动态控制过程中的激励措施，调动和发挥员工实现建设工程目标的积极性和创造性等。