五年级第三单元 小数除法知识点整理
- 格式:docx
- 大小:12.72 KB
- 文档页数:1

第三单元《小数除法》知识点
9.小数除法的意义:已知两个因数的积与其中的一个因数,求另一个因数的运算。
如:0.6÷0.3表示已知两个因数的积0.6,一个因数是0.3,求另一个因数是多少。
10.小数除以整数的计算方法:小数除以整数,按整数除法的方法去除,商的小数点要和被除数的小数点对齐。
整数部分不够除,商0,点上小数点。
如果有余数,要添0再除。
11.除数是小数的除法的计算方法:先将除数和被除数扩大相同的倍数,使除数变成整数,再按“除数是整数的小数除法”的法则进行计算。
注意:如果被除数的位数不够,在被除数的末尾用0补足。
12.在实际应用中,小数除法所得的商也可以根据需要用“四舍五入”法保留一定的小数位数,求出商的近似数。
13.除法中的变化规律:
①商不变性质:被除数和除数同时扩大或缩小相同的倍数(0除外),商不变。
②除数不变,被除数扩大(缩小),商随着扩大(缩小)。
③被除数不变,除数缩小,商反而扩大;被除数不变,除数扩大,商反而缩小。
14.循环小数:一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现,这样的小数叫做循环小数。
循环节:一个循环小数的小数部分,依次不断重复出现的数字。
如6.3232……的循环节是32.简写作6.32。
15.小数部分的位数是有限的小数,叫做有限小数。
小数部分的位数是无限的小数,叫做无限小数。
小数分为有限小数和无限小数。

西师版数学五年级上册第三单元小数除法的知识点整理
1、除数是整数的小数除法(按整数除法的方法计算)
2、除数是小数的除法(把除数转换成整数计算)
3、商的近似值(用到四舍五入法)
4、循环小数
(1)循环小数:一个小数,从小数部分的某一位起,一个数字或几个数字依次不断地重复出
现,这样的小数叫做循环小数。
(2)循环节:循环小数的小数部分依次不断地重复出现的一个数字或几个数字叫做这个循环
小数的循环节。
(3)有限小数
小数按小数部分的位数来分分为:{
无限小数
有限小数:小数部分的位数是有限的小数。
无限小数:小数部分的位数是无限的小数。
纯循环小数:循环节是从十分位开始的循环小数。
混循环小数:循环节不是从十分位开始的循环小数。
5、问题解决。
(1)去尾数法
(2)进一法
(3)三步解决问题。

人教版五年数学上册第三单元《小数除法》知识点+练习,课前预习用第三单元《小数除法》知识点1. 小数除法的计算方法(1)除法的意义:已知两个因数的积与其中的一个因数,求另一个因数的运算。
(2)小数除以整数的计算方法:小数除以整数,按整数除法的方法去除,商的小数点要和被除数的小数点对齐。
整数部分不够除,商写上0,点上小数点。
如果有余数,要添0再除。
(3)除数是小数的除法的计算方法:先将除数和被除数扩大相同的倍数,使除数变成整数,再按“除数是整数的小数除法”的法则进行计算。
易错点:如果被除数的位数不够,在被除数的末尾用0补足。
2. 除法中的变化规律①商不变性质:被除数和除数同时扩大或缩小相同的倍数(0除外),商不变。
②除数不变,被除数扩大,商随着扩大。
③被除数不变,除数缩小,商扩大。
3. 商的近似数(1)准确数与近似数①准确数:在日常生活和生产实际所遇到的数中,有时可以得到完全准确的数,他们精确,没有误差。
如:五(1)班有学生46人,这里的46是准确数。
②近似数:由于实际中常常不需要用精确的数描述一个量,或不可能得到精确的数。
如:中国约有13亿人,这里的13就是近似数。
(2)有效数字:一个近似数精确到哪一位,从左边第一个不是零的数算起,到这一位数字上,所有的数字,都叫做这个数的有效数字。
例如:0.6166≈0.62,有两个有效数字:6、2。
(3)求商的近似数:一般先除到比需要保留的小数位数多一位,再按照“四舍五入”法取商的近似值。
易错点:其中小数末尾的“0”不能去掉。
4. 循环小数&用计算器探索规律(1)循环小数:一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现,这样的小数叫做循环小数。
(2)循环节:一个循环小数的小数部分,依次不断重复出现的数字。
如6.3232……的循环节是32。
(3)小数部分的位数是有限的小数,叫做有限小数。
小数部分的位数是无限的小数,叫做无限小数。
5. 解决问题(1)进一法:在取近似数的时候,不管省略部分最高位上的数字是几,都向前进1。
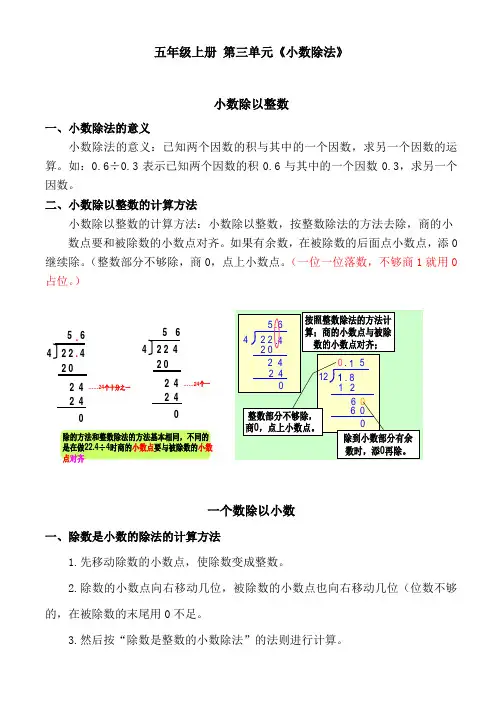
五年级上册第三单元《小数除法》小数除以整数一、小数除法的意义小数除法的意义:已知两个因数的积与其中的一个因数,求另一个因数的运算。
如:0.6÷0.3表示已知两个因数的积0.6与其中的一个因数0.3,求另一个因数。
二、小数除以整数的计算方法小数除以整数的计算方法:小数除以整数,按整数除法的方法去除,商的小数点要和被除数的小数点对齐。
如果有余数,在被除数的后面点小数点,添0继续除。
(整数部分不够除,商0,点上小数点。
(一位一位落数,不够商1就用0占位。
)一个数除以小数一、除数是小数的除法的计算方法1.先移动除数的小数点,使除数变成整数。
2.除数的小数点向右移动几位,被除数的小数点也向右移动几位(位数不够的,在被除数的末尾用0不足。
3.然后按“除数是整数的小数除法”的法则进行计算。
二、除法中的变化规律除法中的变化规律:①商不变性质:被除数和除数同时扩大或缩小相同的倍数(0除外),商不变。
②除数不变,被除数扩大(缩小),商随着扩大(缩小)。
③被除数不变,除数缩小,商反而扩大;被除数不变,除数扩大,商反而缩小。
三:商和被除数的大小关系被除数除以一个小于1的除数时,商会比被除数大;被除数除以一个大于1的除数时,商会比被除数小。
商的近似数一:准确数与近似数准确数:在日常生活和生产实际所遇到的数中,有时可以得到完全准确的数,他们精确,没有误差。
如:五(1)班有学生46人,这里的46是准确数。
近似数:由于实际中常常不需要用精确的数描述一个量,或不可能得到精确的数。
如:中国约有13亿人,这里的13就是近似数。
二:有效数字有效数字:一个近似数精确到哪一位,从左边第一个不是零的数算起,到这一位数字上,所有的数字,都叫做这个数的有效数字。
例如:0.6166≈0.62,有两个有效数字:6、2。
三:商的近似数求出商的近似数,一般先除到比需要保留的小数位数多一位,在按照“四舍五入”法取商的近似值。
循环小数循环小数:一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现,这样的小数叫做循环小数。

小数除法知识点归纳 1、小数除法的意义:已知两个因数的积与其中的一个因数,求另一个因数的运算。
如:0.6÷0.3 表示已知两个因数的积 0.6 与其中的一个因数 0.3,求另一个因数的运算。
2、小数除以整数的计算方法(P16):小数除以整数,按整数除法的方法去除。
商的小数点要和被除数的小数点对齐。
整数部分不够除,商 0,点上小数点。
如果有余数,要添 0 再除。
3、(P21)除数是小数的除法的计算方法:先将除数和被除数扩大相同的倍数,使除数变成整数,再按"除数是整数的小数除法"的法则进行计算。
注意:如果被除数的位数不够,在被除数的末尾用 0 补足。
3、(P23)在实际应用中,小数除法所得的商也可以根据需要用"四舍五入"法保留一定的小数位数求出商的近似数。
4、(P24、25)除法中的变化规律:①商不变性质:被除数和除数同时扩大或缩小相同的倍数( 0除外),商不变。
②除数不变,被除数扩大,商随着扩大。
被除数不变,除数缩小,商扩大。
③被除数不变,除数缩小,商扩大。
5、(P28)循环小数:一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现,这样的小数叫做循环小数。

小数除法知识点归纳 1、小数除法的意义:已知两个因数的积与其中的一个因数,求另一个因数的运算。
如:0.6÷0.3 表示已知两个因数的积 0.6 与其中的一个因数 0.3,求另一个因数的运算。
2、小数除以整数的计算方法(P16):小数除以整数,按整数除法的方法去除。
商的小数点要和被除数的小数点对齐。
整数部分不够除,商 0,点上小数点。
如果有余数,要添 0 再除。
3、(P21)除数是小数的除法的计算方法:先将除数和被除数扩大相同的倍数,使除数变成整数,再按"除数是整数的小数除法"的法则进行计算。
注意:如果被除数的位数不够,在被除数的末尾用 0 补足。
3、(P23)在实际应用中,小数除法所得的商也可以根据需要用"四舍五入"法保留一定的小数位数求出商的近似数。
4、(P24、25)除法中的变化规律:①商不变性质:被除数和除数同时扩大或缩小相同的倍数( 0除外),商不变。
②除数不变,被除数扩大,商随着扩大。
被除数不变,除数缩小,商扩大。
③被除数不变,除数缩小,商扩大。
5、(P28)循环小数:一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现,这样的小数叫做循环小数。

小数除法知识点归纳
1、小数除法的意义:已知两个因数的积与其中的一个因数,求另一个因数的运算。
如:0.6÷0.3 表示已知两个因数的积0.6 与其中的一个因数0.3,求另一个因数的运算。
2、小数除以整数的计算方法(P16):小数除以整数,按整数除法的方法去除。
商的小数点要和被除数的小数点对齐。
整数部分不够除,商0,点上小数点。
如果有余数,要添0 再除。
3、(P21)除数是小数的除法的计算方法:先将除数和被除数扩大相同的倍数,使除数变成整数,再按"除数是整数的小数除法"的法则进行计算。
注意:如果被除数的位数不够,在被除数的末尾用0 补足。
3、(P23)在实际应用中,小数除法所得的商也可以根据需要用"四舍五入"法保留一定的小数位数求出商的近似数。
4、(P24、25)除法中的变化规律:①商不变性质:被除数和除数同时扩大或缩小相同的倍数( 0除外),商不变。
②除数不变,被除数扩大,商随着扩大。
被除数不变,除数缩小,商扩大。
③被除数不变,除数缩小,商扩大。
5、(P28)循环小数:一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现,这样的小数叫做循环小数。
循环节:一个循环小数的小数部分,依次不断重复出现的数字。
如
6.3232…… ……的循环节是32.
6、小数部分的位数是有限的小数,叫做有限小数。
小数部分的位数是无限的小数,叫做无限小数。

小数除法知识点归纳总结一、小数除法的概念小数除法是指在除法中除数或被除数中至少有一个是小数的除法。
小数除法的基本概念是“将被除数分成若干等分,每一份与除数相乘”。
例如,计算0.6 ÷ 0.2时,可以理解为将0.6分成若干等分,每一份的大小是0.2,这样就可以得到3份。
二、小数除法的步骤小数除法的计算步骤与整数除法的步骤类似,主要包括以下几个步骤:1. 将小数除法的题目写成竖式。
2. 确定被除数和除数的位置,按小数点对齐。
3. 逐位相除,将商的小数点位置与被除数对齐。
4. 若有余数,可以继续进行除法运算,直到商的位数足够或者出现循环小数为止。
三、小数除法的相关性质小数除法有一些重要的性质,掌握这些性质有助于学生更好地理解和运用小数除法。
1. 小数除法的商的小数位数与被除数、除数的小数位数有关,商的小数位数等于被除数的小数位数减去除数的小数位数,即商的小数位数=被除数的小数位数-除数的小数位数。
2. 小数除法中的余数也是小数的形式,它与被除数和除数的小数部分有关。
3. 小数除法中,如果被除数和除数中有负数,计算方法和整数除法类似,只是需要注意符号的处理。
四、小数除法的解决问题方法小数除法在解决实际问题时有着广泛的应用,主要包括以下几种类型的问题:1. 小数除以整数的问题:例如,某船油箱可装油15.3吨,如果已经装了3/5油,问已经装了多少吨油?2. 小数除以小数的问题:例如,如果一台机器一小时生产零件0.08个,要生产3000个零件,需要多少小时?3. 小数除法与实际问题的结合:例如,小明每天花费篮球训练时间的1/3练习投篮,每天练习投篮时间为0.75小时,问他每天练习篮球训练多长时间?在解决这些问题时,需要根据问题的要求,进行小数除法的运算,并根据实际情况给出答案。
五、小数除法与其他运算的关系小数除法与加法、减法、乘法有着密切的关系,掌握这些关系有助于学生更全面地理解小数运算。
1. 小数除法与小数乘法的关系:小数除法可以理解为小数乘法的逆运算,即被除数乘以除数等于商。

五年级知识梳理里小数除法的方法,手抄报。
五年级小数除法知识梳理手抄报
一、小数除法的意义:小数除法的意义与整数除法的意义相同,是已知两个因数的积与其中的一个因数,求另一个因数的运算。
二、小数除以整数的计算方法:小数除以整数,按整数除法的方法去除。
商的小数点要和被除数的小数点对齐。
整数部分不够除,商写上0,点上小数点。
如果除到被除数的末尾仍有余数,就在余数末尾添0,再继续除。
三、除数是小数的除法的计算方法:先将除数和被除数扩大相同的倍数,使除数变成整数,再按“除数是整数的小数除法”进行计算。
四、循环小数:一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现,这样的小数叫做循环小数。
五、小数部分的位数是有限的小数叫做有限小数。
小数部分的位数是无限的小数叫做无限小数。

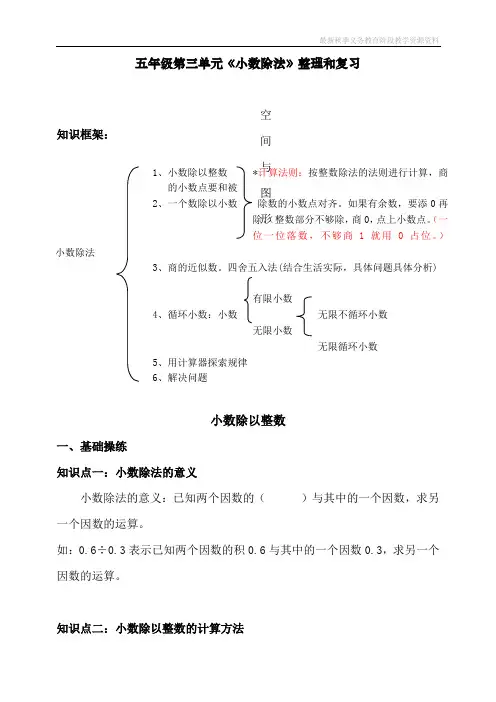
五年级第三单元《小数除法》整理和复习知识框架:小数除以整数一、基础操练知识点一:小数除法的意义小数除法的意义:已知两个因数的( )与其中的一个因数,求另一个因数的运算。
如:0.6÷0.3表示已知两个因数的积0.6与其中的一个因数0.3,求另一个因数的运算。
知识点二:小数除以整数的计算方法1、小数除以整数*计算法则:按整数除法的法则进行计算,商的小数点要和被 2、一个数除以小数 除数的小数点对齐。
如果有余数,要添0再除。
(整数部分不够除,商0,点上小数点。
(一位一位落数,不够商1就用0占位。
)空间与图形3、商的近似数。
四舍五入法(结合生活实际,具体问题具体分析)有限小数4、循环小数:小数 无限不循环小数 无限小数无限循环小数 5、用计算器探索规律 6、解决问题小数除法小数除以整数的计算方法:小数除以整数,按整数除法的方法去除,商的小数点要和被除数的小数点对齐。
整数部分不够除,商写上0,点上小数点。
如果有余数,要添0再除。
【练习】58.89÷13 96÷15 0.465÷15 16.32÷51二、感悟与实践例题1:学校买了13盒白粉笔和10盒彩色粉笔,共付64.5元。
每盒白粉笔2.5元,每盒彩色粉笔多少元?变式练习:一支钢笔的价钱是一支圆珠笔价钱的4倍。
王小东买了一支钢笔和3支圆珠笔,一共花了17.5元。
钢笔和圆珠笔的单价各是多少元?例题2:服装厂做校服。
原来每套服装用布2.2米,现在每套用布节省0.2米。
原来做800套这种服装的布,现在可以做多少套?变式练习:工程队要铺设一条长4.8千米的地下管道,计划用15天完成,实际每天比计划多铺设3.2千米,实际多少天完成任务?变式练习:西平乡修一条长2.1千米的河堤,前15天平均每天修0.086千米。
余下的要9天完成,平均每天修多少千米?三、巩固练习练习1一、口算。
23.6÷10=10÷4=0.36÷3=8.4÷2=40÷50= 6.6÷33 =二、填空。
第三单元小数除法知识点归纳1. 小数的定义和表示方式小数是指整数之间的数,可以用分数表示,也可以用小数表示。
小数的表示方式有有限小数和无限循环小数两种形式。
有限小数是指小数部分有限个数位的小数,例如 0.5、0.25 等。
无限循环小数是指小数部分有限个数位后会无限重复的小数,例如0.333…、0.666… 等。
2. 小数的除法运算规则小数的除法运算规则与整数除法类似,但需要注意小数点的处理。
下面是小数除法的运算规则:•将除数和被除数按照小数点对齐。
•从被除数的左侧开始,依次做除法运算,计算商的整数部分。
•将商的整数部分写在结果的整数部分上,余数写在小数点下方。
•将余数后面的位数补零,继续进行除法运算,直到除尽或达到所要求的精度。
3. 小数的进位和退位在小数除法运算过程中,可能会产生进位或退位的情况。
进位是指商的整数部分计算得到的结果比原先的估算结果大1。
退位是指商的整数部分计算得到的结果比原先的估算结果小1。
进位和退位的判断规则如下:•如果商的小数部分大于等于5,进位;如果小于5,退位。
4. 小数的循环节和循环节长度无限循环小数的小数部分会无限重复,在计算中,我们通常使用循环节表示循环部分,并用循环节长度来表示循环的位数。
循环节是指从小数部分的某位开始重复出现的位数。
例如,无限循环小数0.666… 的循环节是 6,循环节长度为 1。
5. 解决无限循环小数的方法为了方便计算和表示,我们通常使用有理数来表示无限循环小数。
有理数是指可以表示为两个整数的比值的数。
有理数的表示方式是用分数,分子是循环节,分母是循环节长度减去1个9。
例如,无限循环小数0.666… 可以表示为分数 2/3。
6. 小数除法中的特殊情况小数除法中可能会遇到一些特殊情况,例如除数为0、被除数为0等。
这些情况需要单独处理。
•如果除数为0,除法运算无意义,结果为无穷大。
•如果被除数为0,除法运算结果为0。
7. 小数除法的练习和应用小数除法是数学学习中的重要内容,需要通过大量的练习来熟练掌握运算规则。
五年级上册数学笔记第三单元:小数除法1、除数是整数的小数除法的计算方法:(1)按照整数除法的计算方法计算,商的小数点要和被除数的小数点对齐。
(2)如果除到被除数的末位仍有余数,要在余数后面添“0”继续除。
(3)如果被除数的整数部分不够除,要先在个位上商0,点上小数点后再继续除。
2、小数除法的验算方法同整数除法的验算方法相同,即:用商和除数相乘,看积是否等于被除数。
3、判断除法算式的商与1的大小关系,关键是看被除数与除数的大小关系:被除数大于除数,则商大于1;被除数小于除数,则商小于1;被除数等于除数,则商等于1.4、商的变化规律:(1)商不变的性质:在除法中,被除数和除数同时乘以或除以相同的数(0除外),商的大小不变,这叫做商不变的性质。
(2)在除法中,被除数不变,除数乘几(0除外),商就除以几;反之相反,除数除以几,商就乘以几。
(相反)(3)在除法中,除数不变,被除数乘几或除以几(0除外),商也要乘几或除以几。
(相同)5、一个数除以小数的计算方法:根据商不变的性质,把除数转化为整数,除数扩大多少倍,被除数也要扩大相同的倍数。
当被除数的位数不够时,用“0”补足,再按照除数是整数的小数除法的方法计算。
6、商与被除数的大小比较:(1)一个数除以1,仍的原数。
(2)一个非0的数除以大于1的数,商比原数小。
(3)一个非0的数除以小于1的数,商比原数大。
7、商的近似数:小数除法取商的近似数时有两种情况,(1)除不尽的时候;(2)除得尽,但是商的位数比较多,根据实际情况保留小数位数,如价钱、人数、个数等。
求商的近似数的一般方法:先看需要保留几位小数,计算到比保留的小数位数多一位,再将最后一位“四舍五入”。
(近似数末尾有“0”的,0不能去掉)8、循环小数:一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现,这样的小数叫做循环小数。
像5.3333…和7.14545…都是循环小数。
一个循环小数的小数部分,依次不断重复出现的数字,叫做这个循环小数的循环节。
小学五年级数学小数除法知识点总结,附练习题及答案小数除法知识点1.小数除法的意义:与整数除法的意义相同,是已知两个因数(乘数)的积与其中一个因数,求另个因数的运算。
2.小数除法的计算法则:(1)除数是整数:①按照整数除法的法则去除;②商的小数点要和被除数的小数点对齐(重点!);③每一位商都要写在被除数相同数位的上面;④如果除到末尾仍有余数,在被除数的个位数的右边点上小数点,再在被除数的后面添上“0”继续除,直到除尽为止。
⑤除得的商的哪一数位上不够商,就在那一位上写0占位。
(2)除数是小数:①先看除数中有几位小数,就把除数和被除数的小数点向右移动相同的位置(也就是扩大相同的倍数),使除数变成整数,当被除数数位不够时,用0补足;②然后按照除数是整数的小数除法计算。
3、商不变的规律:被除数扩大a倍(或缩小),除数也扩大(或缩小)a倍,商不变。
简言之,被除数和除数同时扩大或者同时缩小相同的倍数,商不变。
4、被除数不变,除数扩大(或缩小)a倍,商缩小(或扩大)a倍。
被除数扩大(或缩小)a倍,除数不变,商扩大(或缩小)a倍。
5、被除数比除数大的,商大于1。
被除数比除数小的,商小于1。
6、一个数(0除外)除以1,商等于原来的数。
(一个数除以1,还等于这个数)一个数(0除外)除以大于1的数,商比原来的数小。
一个数(0除外)除以小于1的数,商比原来的数大。
0除以一个非零的数还得0。
0不能作除数。
7、近似值相关知识点:(1)求商的近似值:计算时要比保留的小数多一位。
求积的近似值:计算出整个积的值后再去近似值。
(2)取商的近似值的方法:“四舍五入”法、“进一法”和“去尾法”在解决问题的时候,可以根据实际情况选择“进一法”和“去尾法”取商的近似值。
(3)保留商的近似值,小数末尾的0不能去掉。
8、循环小数相关知识点:(1)小数分类:可以分为无限小数和有限小数。
小数部分的位数是有限的小数,叫做有限小数。
小数部分是无限的小数叫做无限小数。
第三单元小数除法
1、小数除法的意义:已知两个因数的积与其中的一个因数,求另一个因数的运算。
如:0.6÷0.3表示已知两个因数的积0.6与其中的一个因数0.3,求另一个因数的运算。
2、小数除以整数的计算方法:小数除以整数,按整数除法的方法去除。
商的小数点要和被除数的小数点对齐。
整数部分不够除,商0,点上小数点。
如果有余数,要添0再除。
3、除数是小数的除法的计算方法:先将除数和被除数扩大相同的倍数,使除数变成整数,再按“除数是整数的小数除法”的法则进行计算。
注意:如果被除数的位数不够,在被除数的末尾用0补足。
4、在实际应用中,小数除法所得的商也可以根据需要用“四舍五入”法保留一定的小数位数,求出商的近似数。
5、除法中的变化规律:
①商不变:被除数和除数同时扩大或缩小相同的倍数(0除外),商不变。
②除数不变,被除数扩大,商随着扩大。
③被除数不变,除数缩小,商扩大。
6、循环小数:一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现,这样的小数叫做循环小
数。
@ 循环节:一个循环小数的小数部分,依次不断重复出现的数字。
如6.3232……的循环节是32.
7、小数部分的位数是有限的小数,叫做有限小数。
小数部分的位数是无限的小数,叫做无限小数。
第三单元小数除法
1、小数除法的意义:已知两个因数的积与其中的一个因数,求另一个因数的运算。
如:0.6÷0.3表示已知两个因数的积0.6与其中的一个因数0.3,求另一个因数的运算。
2、小数除以整数的计算方法:小数除以整数,按整数除法的方法去除。
商的小数点要和被除数的小数点对齐。
整数部分不够除,商0,点上小数点。
如果有余数,要添0再除。
3、除数是小数的除法的计算方法:先将除数和被除数扩大相同的倍数,使除数变成整数,再按“除数是整数的小数除法”的法则进行计算。
注意:如果被除数的位数不够,在被除数的末尾用0补足。
4、在实际应用中,小数除法所得的商也可以根据需要用“四舍五入”法保留一定的小数位数,求出商的近似数。
5、除法中的变化规律:
①商不变:被除数和除数同时扩大或缩小相同的倍数(0除外),商不变。
②除数不变,被除数扩大,商随着扩大。
③被除数不变,除数缩小,商扩大。
6、循环小数:一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现,这样的小数叫做循环小
数。
@ 循环节:一个循环小数的小数部分,依次不断重复出现的数字。
如6.3232……的循环节是32.
7、小数部分的位数是有限的小数,叫做有限小数。
小数部分的位数是无限的小数,叫做无限小数。
五年级数学知识点:小数除法知识点五年级数学知识点:小数除法知识点1、小数除法的意义:已知两个因数的积与其中的一个因数,求另一个因数的运算。
如:0.6÷0.3 表示已知两个因数的积 0.6 与其中的一个因数 0.3,求另一个因数的运算。
2、小数除以整数的计算方法(P16):小数除以整数,按整数除法的方法去除。
商的小数点要和被除数的小数点对齐。
整数部分不够除,商 0,点上小数点。
如果有余数,要添 0 再除。
3、(P21)除数是小数的除法的计算方法:先将除数和被除数扩大相同的倍数,使除数变成整数,再按除数是整数的小数除法的法则进行计算。
注意:如果被除数的位数不够,在被除数的末尾用 0 补足。
4、(P23)在实际应用中,小数除法所得的商也可以根据需要用四舍五入法保留一定的小数位数求出商的近似数。
5、(P24、25)除法中的变化规律:①商不变性质:被除数和除数同时扩大或缩小相同的倍数( 0除外),商不变。
②除数不变,被除数扩大,商随着扩大。
被除数不变,除数缩小,商扩大。
③被除数不变,除数缩小,商扩大。
6、(P28)循环小数:一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现,这样的小数叫做循环小数。
循环节:一个循环小数的小数部分,依次不断重复出现的数字。
如 6.3232…… ……的循环节是 32.7、小数部分的位数是有限的小数,叫做有限小数。
小数部分的位数是无限的小数,叫做无限小数。
针对练习用竖式计算下面各题。
(1)68.8÷4=(2)85.44÷16=(3)67.5÷15=(4)289.9÷18=(5)101.7÷9=(6)243.2÷64=(7)16.8÷28=(8)15.6÷24=(9)0.138÷15=(10)1.35÷27=(11)0.416÷32=(12)3.64÷52=(13)91.2÷3.8=(14)0.756÷0.18=(15)51.3÷0.27=(16)26÷0.13=(17)210÷1.4=(18)2.688÷0.56=(19)10.625÷25=(20)126÷45=(21)10÷25=(22)2.7÷7.5=(23)15÷0.06=(24)25.6÷0.032=小数除法知识点就先到这儿了,我会持续为大家更新最新的内容,希望大家学有所成。
第三单元小数除法
1、小数除法的意义:已知两个因数的积与其中的一个因数,求另一个因数的运算。
如:0.6÷0.3表示已知两个因数的积0.6与其中的一个因数0.3,求另一个因数的运算。
2、小数除以整数的计算方法:
小数除以整数,按整数除法的方法去除。
商的小数点要和被除数的小数点对齐。
整数部分不够除,商0,点上小数点。
如果有余数,要添0再除。
3、除数是小数的除法的计算方法:先将除数和被除数扩大相同的倍数,使除数变成整数,再按“除数是整数的小数除法”的法则进行计算。
注意:如果被除数的位数不够,在被除数的末尾用0补足。
4、在实际应用中,小数除法所得的商也可以根据需要用“四舍五入”法保留一定的小数位数,求出商的近似数。
5、除法中的变化规律:
①商不变性质:被除数和除数同时扩大或缩小相同的倍数(0除外),商不变。
②除数不变,被除数扩大,商随着扩大。
③被除数不变,除数缩小,商扩大。
6、循环小数:一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现,这样的小数叫做循环小数。
循环节:一个循环小数的小数部分,依次不断重复出现的数字。
如
6.3232……的循环节是32
7、小数部分的位数是有限的小数,叫做有限小数。
小数部分的位数是无限的小数,叫做无限小数。