当前位置：文档之家 › (化工原理)第二节 沉降过程

(化工原理)第二节 沉降过程

  • 格式：ppt
  • 大小：5.29 MB
  • 文档页数：3

下载文档原格式

  / 3

合集下载

第3章化工原理中的沉降与过滤

第3章化工原理中的沉降与过滤

ut
4d (P ) ur 2
3
R
在离心沉降时，如果颗粒与流体的相对运动 属于层流，阻力系数也符合斯托克斯定律：
ut
dP2 (P ) ur2
18
R
离心分离因数：
离心力 离心加速度 KC 重力 重力加速度
3、离心沉降的应用——旋风分离器
旋风分离器动画
文丘里除尘器动画
静电除尘器动画
例3-3：速溶咖啡粉（比重1.05）的直径为60μm， 被250℃热空气带入旋风分离器中，进入时切线速 度为20m/s，在器内的旋转半径为0.5m。求其径向 沉降速度。同样大小的颗粒在同温度的静止空气中 沉降时，其沉降速度应为多少？（设沉降处于层流 区）
9.807
2.66 106 m s 1
检验
Re
值：
Re
dPu0
15106 2.66106 1.005103
998.2
3.96105
1
计算结果表明，与假设相符，故算得的 u0 2.66106ms1 正确。
【例3-2】 某除尘室高2m、宽2m、长5m，用于矿石焙烧炉 的炉气除尘。矿尘的密度为4500kg·m-3，其形状近于圆球。
令 V q，Ve
A
A
qe
q2
2qqe
Kt
K 过滤常数
2、过滤常数的测定
t/q
q2
2qqe
Kt
t q
1 K
q
2 K
qe
α
t 与q线性相关 q
2qe/K
q
tga=1/K
【例 3-4】在100kPa 的恒压下过滤某悬浮液，温度 300 C ，过 滤面积为 40m2 ，并已知滤渣的比阻为11014 m/Kg，x 值 为 0.05Kg/m3 。过滤介质的阻力忽略不计，滤渣不可压缩，试

化工原理 沉降

化工原理 沉降
Ci进 Ci出 i 100% Ci进
Ci进、ci出为进、出口气体中粒径 dpi 的颗粒质量浓度g/m3
粒级效率可以准确表示旋风分离器的分离性能。 可以用 i ～ d pi d c 的函数曲线来表示粒级效率：
1.0 0.8 0.6
粒级效率
dc=d50:是粒级效
率恰为50％的颗
0.4
0.2
P P

—— 牛顿公式
沉降速度ut计算方法
计算ut时需先知道所在沉降区域──选择相应式计算。 试差法 设在层流区 计算ut 设在过渡区 no
Re判断
yes
结束
通常微小颗粒的沉降一般属层流区(Stokes区)
沉降速度的影响因素
（1）干扰沉降 发生于颗粒之间距离很小的情况下。多发生于非均 相物系的沉降过程（物系内部有两个以上相）。 当颗粒浓度↑，浮力 ↑ ── ut↓ （2）端效应（器壁效应） 容器壁对颗粒沉降有阻止作用 ，使实际沉降速度 ut<自由沉降速度。当D容器>100dp,可忽略影响。 （3）分子运动 当颗粒直径小到可与流体分子的平均自由程相比拟 时，颗粒可穿过快速运动的流体分子之间，沉降速 度可大于按斯托克斯定律的计算值。
Re<2， gd ——斯托克斯公式 u 18 ζ =24/Re，
2 P P t
过渡区(Allen区) ： 2<Re<500， ζ =18.5/Re 0.6
湍流区(Newton区) —— 颗粒较大时
500<Re<×105， ζ ≈0.44
u 1.74
t
d g
浮力
1 3 Fb g π dp g p 6
m
曳 力 FD Ap

化工原理课件 沉降

化工原理课件 沉降

t
1 8
1 8 1 .0 0 5 1 0 3
3
计算Rep，核算流型：
R epdpu95 10 61 .9 0 .0 75 9 7 1 0 1 0 3 3 998.20.92442
假设正确，计算有效。
（2）在20 ℃的空气中： 20 ℃空气的密度为1.205kg/m3，粘度为18.1×10-6 Pas
。 m3 / s
，实际上为避免已沉下的尘粒重新被扬起， 往往
u m/ s 取更低 u qV 。降尘室一般用于分离
的粗颗粒。
BH
u
u0.5m/s
dP 50m
• A—降尘室底面积， 。
m2
ABL
u m/ s u •
—颗粒的沉降速度， 。 应根据要分离的最小 颗粒直径 决定。
t
t
d P ,min
5.3.1 重力沉降设备
T↑，气体μ↑，阻力↑ ，除沉不利
T↑，液体μ↓，阻力 ↓，除沉有利
液体粘度约为气体粘度的50倍，故颗粒在液体中的沉降速度比在气体中的小很多。
5.2.2 静止流体中颗粒的自由沉降
3）当流体做水平运动时：
4）当流体以一定的速度向上运动时： 当u>ut时，颗粒向上运动 当u<ut时，颗粒向下运动 当u=ut时，颗粒悬浮在流体中
5.2.1 流体对固体颗粒的绕流
流体与固体颗粒之间的相对运动可分为以下三种情况：
①颗粒静止，流体对其做绕流；
②流体静止，颗粒作沉降运动；
③颗粒与流体都运动，但保持一定的相对运动。
FD
u
流体绕过颗粒的流动
5.2.1 流体对固体颗粒的绕流 （1）两种曳力—表面曳力和形体曳力
5.2.1 流体对固体颗粒的绕流

化工原理：沉降小结

化工原理：沉降小结

沉降 小结
一、 沉降
1. 定义：利用两相密度的差异，将分均相混合物以分离的单元操作
2. 重力沉降：
1）沉降速度
（斯区 Re<2）
2）沉降设备（降尘室）
生产能力V=u t .A 底 （仅与底面积有关，与高度无关） 3. 离心沉降
1）
沉降速度 Re<2）
2） 沉降设备（旋风分离器） （1） 分离性能 a. 临界直径 b. 分离效率
总效率
粒级效率 （2） 压力降
i
i C C C 0
0-=
η进
出
进,,,i i i i C C C -=η2
1/16D AB c =ζ
二、过滤
1.定义：在外力的作用下，使悬浮液通过多孔介质，将固体颗粒截
留，从而使悬浮液得以分离的单元操作
2.过滤基本方程
或
3.
恒压过滤
4.过滤常数K、q e、V e、θ由实验确定直线）
5.过滤设备
1）间歇操作（板框压滤机、叶压机等）
2）连续操作（转筒真空过滤机）。

化工原理第三章概述、重力沉降

化工原理第三章概述、重力沉降
u t 9 1 5 6 1 2 0 1 3 . 0 8 1 0 0 9 3 . 2 0 0 5 9 9 . 8 0 8 9 . 1 7 1 9 － 3 ( m 0 7 /s )
核算流型：
R d e p u t 9 1 5 6 0 1 .9 0 .7 0 1 9 1 5 3 0 7 3 0 9.2 9 0 8 .92 2 4
f(Res,)
【获取方法】当球形度一定时，阻力（曳力）系数ζ 获取方法有如下两种： （1）查取ζ－Re关系曲线图； （2）使用经验公式。
【步骤】（1）根据颗粒的球形度找到对应的 曲线； （2）根据Re找到曲线上的一点； （3）由该点查得ζ ；
s
S Sp
(球形度）
ζ－Re关系曲线图
何谓球形度
s
S Sp
dP ，流体的密度为ρ，则：
Fg
6
dP3Pg
Fb
6
dP3g
Fd A2 u2
dP 2
4
u2
2
当颗粒在流体中做匀速运动（a＝0）时，颗粒所 受合力为零，即：
6dP 3Pg 6dP 3gd 4P 22 u20
由此可解出沉降速度：
ut
4gdPP
3
——沉降速度基本计算式
（1）颗粒从静止开始作沉降运动时，分为加速和匀 速两个阶段； （2）对于小颗粒，加速阶段时间很短，通常忽略， 可以认为沉降过程是匀速的。
S——与物体相同体积的球体的表面积； SP——物体的表面积。
【定义】与物体相同体积的球体的表面积和物体的 表面积之比。
（1）此处的雷诺数Re是指：
Re d Pu
计算Re时，dP应为足以表征颗粒大小的长度（特 性尺寸），对球形颗粒而言，就是它的直径。

化工原理中的沉降与过滤

化工原理中的沉降与过滤

化工原理中的沉降与过滤引言在化工工艺中，沉降和过滤是常用的固液分离方法。

沉降是指根据固液颗粒的重力作用，通过静置使固体颗粒沉降到底部，而将悬浮液体分离出来。

过滤则是通过利用滤介质的孔隙或表面，将悬浮液体中的固体颗粒留下，而使液体通过，从而达到分离固液的目的。

本文将从理论和实际应用两个方面，对化工原理中的沉降与过滤进行介绍。

沉降原理沉降是基于固体颗粒的重力作用，通过静置使固体颗粒沉降到底部，从而实现固液分离的过程。

沉降速度取决于固体颗粒与液体的密度差和粒径大小。

根据Stokes定律，沉降速度与颗粒直径的平方成正比，与液体的粘度成反比。

沉降速度可由下式计算：v = (2/9) * (ρp - ρl) * g * (d^2) / μ其中，v为沉降速度，ρp为颗粒的密度，ρl为液体的密度，g为重力加速度，d为颗粒的直径，μ为液体的动力粘度。

过滤原理过滤是通过滤介质的孔隙或表面，将悬浮液体中的固体颗粒留下，而使液体通过，从而实现固液分离的过程。

滤介质常用的有滤纸、滤筒、滤板等，其孔隙大小决定了能够透过的颗粒大小。

根据Darcy定律，过滤速度与滤介质的孔隙直径的平方成正比，与液体的粘度成反比。

过滤速度可由下式计算：Q = (π/4) * (d^2) * (ΔP/μ) * A其中，Q为过滤速度，d为滤介质的孔隙直径，ΔP为过滤压差，μ为液体的动力粘度，A为过滤面积。

实际应用沉降的应用沉降在化工过程中被广泛应用，常见的应用场景包括：1.污水处理：污水中悬浮的固体颗粒通过沉降实现固液分离，从而达到净化水质的目的。

2.矿石提取：矿石中的有用矿物颗粒通过沉降分离出来，然后进行后续的加工和提取。

3.食品加工：在食品饮料生产中，一些颗粒物质需要通过沉降分离，以获得纯净的液体产品。

4.生物工程：在细胞培养和发酵工艺中，需要将细胞或发酵产物与培养基进行分离。

沉降是一种常用的分离方法。

5.药物制剂：在药物合成和制剂工艺中，沉降用于分离和提取所需的纯净物质。

化工原理 沉降与过滤


（三）压力损失
气体通过旋风分离器的压力损失，可用进 口气体动压的某一倍数表示为

式中的阻力系数用下式计算

ui
2
2
30bh D 2 d LH
四、旋液分离器
旋液分离器是利用离 心力的作用，使悬浮 液中固体颗粒增稠或 使粒径不同及密度不 同的颗粒进行分级。 与旋风分离器相似， 只是液体与颗粒的密 度差较小，为提高分 离的离心力和停留时 间，因此器身做的较 细长。
2、临界粒径dpc：
若在各种不同粒径的尘粒中，有一种粒径的 尘粒能满足L/u＝H/ut的条件，此粒径称为 重力降尘室能100％除去的最小粒径，或称 为临界粒径dpc 。
则某些粒径的尘粒，其沉降速度ut大于或等 于qVs/WL，则能全部分离出来。故与临界粒径 dpc相对应的临界沉降速度为utc＝qVs/WL 。
分散相或分散物质→非均相物系中，处于分散状态的物质，如悬浮液
中的固体颗粒、乳浊液中的液滴、泡沫液中的气泡；


连续相或分散介质→包围着分散物质且处于连续状态的流体。 根据连续相状态，非均相物质分为两类： 气态非均相物质：如含尘气体、含雾气体等。 液态非均相物质：如悬浮液、乳浊液等。
（二）非均相混合物的分离方式
注： a、由上式可知，当utc与dpc一定时，qVs与底 面积WL成正比，而与高度H无关。 b、当qVs一定时，dpc及utc与降尘室的底面积 WL成反比，而与高度H无关。
3、降尘室的形状：
由以上分析可知，降尘室的生产能力与其高度H无关， 宜做成扁平形。
若qVs不变，使H缩小1/2，则u变为原来的两倍（ qVs
连续式增稠器
絮凝剂
溶胶：液体中所含固体颗粒径大小会有差别，含

化工原理-沉降与过滤

叶滤机： τw = 2（V + Ve）Vw / KA2 板框压滤机： τw = 8（V + Ve）Vw / KA2
三、过滤过程计算
设计型：确定过滤面积 操作型：计算设备生产能力，或确定操作条件
确定恒压过滤面积：例4-6 已知：w、r、ε、Δp、qe=0、V悬、τ 、ρp 、ρ、
V2+2VVe=KA2τ →V、K、τ → V悬、φ、ε、r、Δp 、μ
第四章
第一节 概述
流体通过颗粒层的流动
均相混合物与非均相混合物 液-固 气-固
1、混合物的分类 两相流动物系 2、固定床
流体通过固定床的流动 3、单元操作的应用 固定床反应器 固体悬浮液的过滤
第二节 颗粒床层的特点
一、单颗粒的特性 （大小、形状、表面积） 球形颗粒 dp —球形颗粒直径 非球形颗粒 de —体积当量直径 Ψ —形状系数（球形度）
固体颗粒的流动输送 (气力输送)。 考察两相物系的相对运动应从流体对颗粒运动的阻力着手。
第二节 颗粒的沉降运动
一、流体对颗粒运动的阻力（曳力） 形体阻力 表面阻力 F d =ζ（ πdp2 / 4）ρu2/2
阻力（曳力）
式中阻力系数ζ是颗粒相对于流体运动的Ret的函数（可通过 实验测定），当Ret值在不同的范围时的ζ值： 层流区（斯托克斯区） 10-4< Ret < 2 过渡区(阿仑区) 湍流区(牛顿区) 2< Ret <500 ζ=24/ Ret ζ=18.5/ Ret0.5
沉降速度u t表示
* 因 μ气<μ液
,所以 u t 气体中>> u t 液体中
* 沉降速度的确定:
设一种流型 → u t → Ret → 看Ret是否在所设的流型区内

沉降过程与操作

学习情境4沉降过程与操作学习要求知识目标：1. 了解重力沉降及离心沉降基本知识。

2. 掌握旋风分离器、油水分离设备工作原理。

能力目标：1. 能使旋风分离器平稳运行。

2. 能使油水分离设备平稳运行。

学习情境4.1常压塔顶回流罐的油水分离【教学内容】化工生产中需要将混合物加以分离的情况横多，大致说来，混合物可分为两大类，即均相混合物和非均相混合物，详细内容下表。

均相：内部各处均匀不存在相界面的物系称为均相物系。

如溶液、混合气体及少量混合液体。

非均相：由具有不同物理性质（如密度和粒径）的分散物质和连续介质所组成的物系称非均相物系。

均相物系的分离属于传质内容，均相物系中的“固一固”物系不在讨论之列；非均相物系可以借助沉降、过滤、筛分等手段，利用物系中两相间的物性（如p或d）差，实现两相间的相对运动达到分离的目的。

这些属于机械分离，操作遵循流体力学的基本规律。

在非均相物系中，处于分散状态的物质称“分散相”；包围它的物质称“连续相”（即分散介质）。

沉降是将混合物置于力场中，在力场作用下，使分散相与连续相发生相对运动，密度大的物质定向地移向收集面，实现分离。

力场沉降类型物系重力场重力沉降自由沉降气一固、液一固气一液、液一液干扰沉降离心力场离心沉降同上电场电沉降电除尘器颗粒极微者电捕焦油器固一固物系往往要借助流体，使固固两相间的运动产生速度差。

在这里我们重点学习重力沉降，其沉降方向垂直向下。

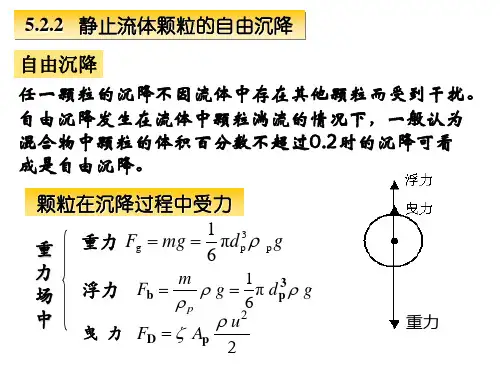
沉降速度㈠球形颗粒的自由沉降自由沉降一一颗粒沉降中不受外界的任何影响。

将一粒表面光滑的刚性球形颗粒置于静止的流体中，颗粒p S＞液体的p ,于是颗粒受到的力分别为：重力Fg、浮力Fb、阻力Fd,其作用方向如图示。

当颗粒和流体的种类确定后，仅于p s、d和p有关的重力及浮力便为常量；阻力则随着颗粒运动的速度的变化而变化。

直径为d的颗粒，所受三力表示为（向下为正）：j三力之和，使颗粒产生加速度： a =du/d 0图4-1受力分析从颗粒沉降达到等速阶段， 理论上讲需要很长的时间，但达到0.99u t 需时很短，固可以忽略加速段，认为颗粒始终在等速U t 下运动。

化工原理第三章1沉降解析


u Vs Hb
l lHb
Vs Vs Hb
lHb H Vs u0
Vs blu0 A0u0 ——降尘室的生产能力
• 说明
①含尘气体的最大处理量与某一粒径对应的，是指这一粒 径及大于该粒径的颗粒都能100%被除去时的最大气体量；
• 完全被分离出的最小颗粒直径
dmin
18Hu
gs L
4)常用沉降速度的计算
试差法
方法：
u0
假设沉降属于层流区
d 2s
18
Re0 du u0
Re0
u0为所求
Re0＜2
公式适 用为止
判断
艾伦公式
……
求u0
Re0＞2
例：试计算直径为30μm，密度为2000kg/m3的固体颗粒在空
气中做自由沉降时的沉降速度。空气的密度为1.2kg/m3，黏
度为0.0185mPa·s
a) 层流区或斯托克斯(stokes)定律区（10 –4＜Re0<2）
24
Re 0
u0
d 2s
18
——斯托克斯公式
b) 过渡区或艾伦定律区（Allen）（2＜Re0<500）
18.5
Re
0.6 0
u0 0.269
gd s
Re
0.6 0
——艾伦公式
c) 湍流区或牛顿定律区（Nuton）（500＜Re0＜ 2×105）
容器效应可忽略，否则需加以考虑。
u0'
1
u0 2.1
d
D
③颗粒形状的影响
球形度
s
S Sp
与物体相同体积的球体的表面积和物体的 表面积的比
对于球形颗粒，φs=1，颗粒形状与球形的差异愈大，球形度
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
布朗运动
沉降速度计算—试差法
四、沉降速度的计算
1、试差法
设Rep选公式 ut核算Rep判断
沉降速度计算—摩擦数群法
2、摩擦数群法
3
沉降速度计算—摩擦数群法
ζ是Ret的已知函数，则 ζRet2 也是Ret的已知函数。
ζ-Ret曲线转化为ζRet2Ret曲线
根据已知值,首先算出 ζRet2的值,再用ζRet2- Ret 曲线查出相应的Ret值,然 后根据Ret的定义式反算 出ut,即：
第二节 沉降过程
沉降速度
沉降速度
颗粒的沉降过程应分为两个阶段,起初为加速阶段,而后为等速 阶段
等速阶段里颗粒相对于流体的运动速度ut称为“沉降速度”， “终端速度”。
阻力系数 ζ
二、阻力系数 ζ
定义：颗粒与流体相对运动时的雷诺数
由Re、фs数，查图得ζ
阻力系数 ζ
阻力系数 ζ
气体在器内的运动情况
离心沉降-7
三、旋风分离器的性能 （分离效果、压强降）
（ 一）、临界粒径
旋风分离器中能被完全分离下来的最小颗粒直径。
临界粒径的计算式,可在如下简化条件之下 推导出来。
（1）进入旋风分离器的气流严格按螺旋形路线作等速运动,其 切向速度等于进口气速ui
(2) 颗粒向器壁沉降时,必须穿过厚度等于整个进气口宽度B的 气流层,方能到达壁面 而被分离。
作预除尘器使用。 多层降尘室虽能分离较细小的颗粒并节省地
面但出灰不便。
例3-2
例3-2
重力沉降设备–沉降槽
（二）、沉降槽 （过程）
1、沉降槽的构造与操作 又称增浓器或澄清器
重力沉降设备–沉降槽
浓悬浮液的沉聚过程 （自学） 连续沉降槽的直径,小者数米,大者可达
数百米。小槽可用木料或金属制造,大 槽要用混凝土砌筑。小槽耙的转速约 为1r.p.m.,大槽只有0.1r.p.m.左右。
离心沉降-4
在离心沉降时，如果颗粒与流体的相对运动属于滞 流，阻力系数也符合斯托克斯定律：
同一颗粒在同种介质中的离心沉降速度与重力沉降 速度的比值为
比与值重力Kc场也强就度是之颗比粒，所称在为位离置心上分的离惯因性数离心力场强度
离心沉降设备-旋风分离器
二、 旋风分离器的操作原理
结构

离心沉降设备-旋风分离器
重力沉降设备–分级器
（三）、分级器
重力沉降用于分离不同粒径的同种颗粒和不 同密度的颗粒所用设备称为分级器
例3-3
例3-3
例3-3
3-2-2 离心沉降-1
依靠惯性离心力的作用而实现的沉降过 程叫作离心沉降
一、惯性离心力作用下的沉降速度
离心沉降-2
平衡时颗粒在径向上相对于流体的速度 是它在此位置上的离心沉降速度
离心沉降-3
颗粒的离心沉降速度 ur与重力沉降速度 ut 具有相似的关系式，只是将重力场强度 g 改为惯性离心力场强度 uT²/R
区别：
离心力沉降速度ur 不是颗粒运动的绝对速度，而是 绝对速度在径向上的分量，且方向不是向下而是沿 半径向外；
离心沉降速度ur 本身就不是一个恒定的数值，而重 力沉降速度ut 则是不变的。
例3-1
例3-1
重力沉降设备–降尘室
二、重 力 沉 降设备
（一）、降尘室 （过程）
令 l——降尘室的长度,m ； H ——降尘室的高度,m； b ——降尘室的宽度,m； ut —— 颗粒的沉降速度,m;
u —— 气体在降尘室内水平通过的流速,m/s。
重力沉降设备–降尘室
颗粒沉降至室底所 需的时间为：
重力沉降设备–降尘室
如气体处理量为Vs
降尘室的生产能力只与其 沉降面积bl及颗粒 的沉降速度ut有 关,而与降尘室的高度无关。
重力沉降设备–降尘室
因此, 可将降尘室做成多层, 称为多层降尘室
重力沉降设备–降尘室
多层降尘室的生产能力为
Vs ≤（n+1)blut （n为隔板数）
降尘室特点
降尘室结构简单,阻力小, 但体积庞大,分离效率低, 只适用于分离直径在50μm以上的粗粒,一般
离心沉降-8
(3) 颗粒在滞流情况下作自由沉降，其径向沉降速度可用下式 计算
因ρ<<ρs ,故式中的ρ可以略去；又旋转半径R 可取平均值 Rm，则气流中的离心沉降速度为
离心沉降-9
颗粒到达器壁所需的沉降时间为
令气流的有效旋转圈数为Ne,它在器内 运行的距离便是2πRmNe,则停留时间为
离心沉降-10
若某种尺寸的颗粒所需的沉降时间θt恰 等于停留时间θ，该颗粒就是理论上能 被完全分离下来的最小颗粒。
离心沉降-11
临界粒径随分离器尺寸增大而增大,因此分离 效率随分离器尺寸增大而减小,所以当气体处 理量大时，常将若干个小尺寸的旋风分离器 并联使用(称为旋风分离器组),以维持较高的 除尘效率。
Ne的数值一般为0.5～3.0,但对标准旋 风分离器，可取Ne=5。
离心沉降-12
（二）、分离效率
旋风分离器的分离效率有两种表示法,一是 总效率,以η0代表；一是分效率,又称粒级效 率,以ηp代表。
总效率是指进入旋风分离器的全部颗粒中被 分离下来的质量分率,即：
C1——旋风分离器进口气体含尘浓度, g/m³； C2——旋风分离器出口气体含尘浓度, g/m³
曲线(φs=1.0)所示。该曲线可按Re值大 致分为三个区域,各区内的曲线可分别 用相应的关系式来表达
3
3
沉降速度
斯托克斯(Stokes)公式、艾仑(Allen)公 式及牛顿(Newton)公式
影响沉降速度的因素
三、影响沉降速度的因素
1、体积浓度 干扰沉降
2、器壁效应 3、颗粒形状
同一种固体物质，球形或近球形颗粒 比同体积的非球形颗粒的沉降要快一些 4、颗粒粒径
Goto Figure
沉降速度计算—摩擦数群法
令ζ与Ret-1相乘,得
ρ
3
可得ζRet-1- Ret图
由ζRet-1从图中查得 Ret,
用以根据沉降速度ut计 算
颗粒直径d
沉降速度计算—摩擦数群法
Back 14 Back 15
用K判断流型
将层流时的ut代入Ret,有
当Re<1时,在斯托克斯定律区的上限K值为2.62 当Re>1000，在牛顿定律区的下限K值为69.1 可根据K值选用相应的公式，避免试差法
离心沉降-13
粒级效率
C1i ——进口气体粒径在第i 小段范围内的颗粒的浓度，g/m3 Ci2 —— 出口气体中粒径在第i小段范围内的颗粒的浓度,g/m3