当前位置：文档之家 › 圆心角弧弦

圆心角弧弦

  • 格式：ppt
  • 大小：1.19 MB
  • 文档页数：116

下载文档原格式

  / 116

合集下载

圆心角弧弦弦心距之间的关系

圆心角弧弦弦心距之间的关系

圆心角弧弦弦心距之间的关系在我们探索圆的奇妙世界时，圆心角、弧、弦、弦心距这几个概念就像是打开这个神秘大门的钥匙。

它们之间存在着紧密而有趣的关系，让我们一起来揭开它们的神秘面纱。

首先，让我们来认识一下这几个重要的角色。

圆心角，顾名思义，是指顶点在圆心的角。

想象一下，从圆心出发的两条射线所夹的角，那就是圆心角。

弧呢，则是圆上任意两点间的部分。

弦则是连接圆上任意两点的线段。

而弦心距，是指圆心到弦的距离。

那么，它们之间到底有着怎样的关系呢？当在同圆或等圆中，圆心角的度数与它所对的弧的度数是相等的。

这就好像圆心角是弧的“指挥官”，圆心角有多大，它所对应的弧就有多长。

比如说，如果一个圆心角是 60 度，那么它所对的弧的度数也是60 度。

接下来，我们再看看弦和圆心角的关系。

在同圆或等圆中，如果两个圆心角相等，那么它们所对应的弦也相等。

这就好比两个“实力相当”的圆心角，它们“指挥”出的弦长度也是一样的。

不仅如此，圆心角还和弦心距有着密切的联系。

同样在同圆或等圆中，相等的圆心角所对应的弦心距也相等。

可以这样理解，当圆心角“发号施令”的力度一样时，圆心到弦的距离也是相同的。

反过来，如果两条弧相等，那么它们所对的圆心角也相等。

这就像是弧反过来给圆心角“反馈”，告诉圆心角自己的长度，从而让圆心角也有了对应的“表现”。

当两条弦相等时，它们所对的圆心角以及所对的弧也都相等。

弦就像是一个“传递者”，把相等的信息传递给了圆心角和弧。

同样，如果两条弦心距相等，那么对应的弦、对应的圆心角以及对应的弧也都相等。

弦心距在这里就像是一个“公正的裁判”，一旦它给出了相等的判定，其他相关的元素也就都平等了。

为了更好地理解这些关系，我们可以通过一些实际的例子来感受。

比如说，在一个半径为 5 厘米的圆中，如果有一个圆心角是 90 度，那么它所对的弧的长度就可以通过公式计算得出。

又或者已知一条弦的长度是 8 厘米，我们可以通过相关的关系求出对应的圆心角和弧的度数等等。

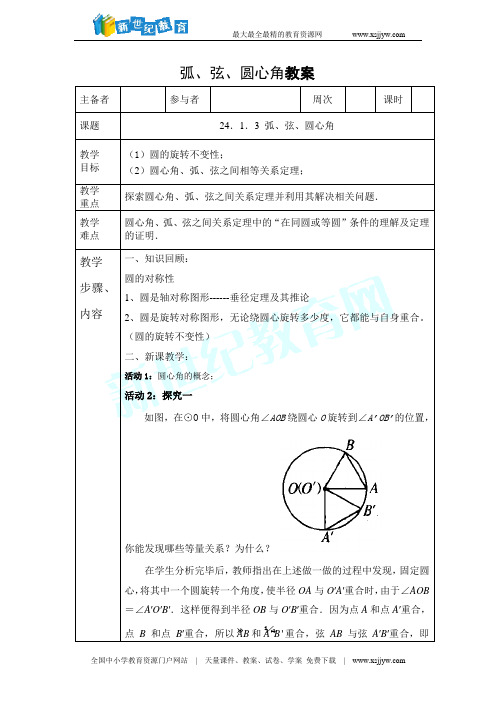
24.1.3弧弦圆心角(课件+教案+练习)-1

24.1.3弧弦圆心角(课件+教案+练习)-1

弧、弦、圆心角教案主备者参与者周次课时课题24．1．3 弧、弦、圆心角教学目标（1）圆的旋转不变性；（2）圆心角、弧、弦之间相等关系定理；教学重点探索圆心角、弧、弦之间关系定理并利用其解决相关问题．教学难点圆心角、弧、弦之间关系定理中的“在同圆或等圆”条件的理解及定理的证明．教学步骤、内容一、知识回顾：圆的对称性1、圆是轴对称图形------垂径定理及其推论2、圆是旋转对称图形，无论绕圆心旋转多少度，它都能与自身重合。

（圆的旋转不变性）二、新课教学：活动1：圆心角的概念；活动2：探究一如图，在⊙O中，将圆心角∠AOB绕圆心O旋转到∠A’OB’的位置，你能发现哪些等量关系？为什么？在学生分析完毕后，教师指出在上述做一做的过程中发现，固定圆心，将其中一个圆旋转一个角度，使半径OA与O′A′重合时，由于∠AOB ＝∠A′O′B′．这样便得到半径OB与O′B′重合．因为点A和点A′重合，点B和点B′重合，所以AB和''A B重合，弦AB与弦A′B′重合，即''AB A B =，AB =A ′B ′．思考：如图，在等圆中，如果∠AOB ＝∠A ′O ′ B ′， 你发现的等量关系是否依然成立？为什么？教师叙述步骤，同学们一起动手操作． 由已知条件可知∠AOB ＝∠A ′O ′B ′；由两圆的半径相等，可以得到∠OAB ＝∠OBA ＝∠O ′A ′B ′=∠O ′B ′A ′；由△AOB ≌△A ′O ′B ′，可得到AB ＝A ′B ′；由旋转法可知''AB A B =．进一步引导学生语言归纳圆心角、弧、弦之间相等关系定理： 在同圆和等圆中，相等的圆心角所对的弧相等，所对的弦也相等． 定理“在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等．”中，可否把条件“在同圆或等圆中”去掉？为什么？ 活动3：根据对上述定理的理解，你能证明下列命题是正确的吗？（1）在同圆或等圆中，如果两条弧相等，那么它们所对的圆心角相等，所对的弦相等；（2）在同圆或等圆中，如果两条弦相等，那么它们所对的圆心角相等，所对的优（劣）弧相等．师生活动设计：本问题由学生在思考的基础上讨论解决，可以证明上述命题是真命题．二、主体活动，巩固新知，进一步理解三量关系定理． 如图，AB 、CD 是⊙O 的两条弦．（1）如果AB=CD ，那么___________，_________________． （2）如果弧AB=弧CD ，那么____________，_____________．·AOBCDE（3）如果∠AOB=∠COD ，那么_____________，_________． （4）如果AB=CD ，OE ⊥AB 于E ，OF ⊥CD 于F ，OE 与OF 相等吗？为什么？ 活动4：课堂练习1．如图2，在⊙O 中，AB AC =，∠ACB ＝60°，求证∠AOB =∠AOC =∠BOC ．图2先让学生尝试〔证明〕∵ AB AC = ∴ AB =AC ，△ABC 是等腰三角形． 又 ∠ACB ＝60°，∴ △ABC 是等边三角形，AB =BC =CA ． ∴ ∠AOB =∠AOC =∠BOC ．2．如图，在⊙O 中，AB=AC ，∠C=75°，求∠A 的度数。

24.1.3弧,弦,圆心角(教案)

24.1.3弧,弦,圆心角(教案)
-弧和弦的分类：区分优弧、劣弧、半圆，以及直径和弦，让学生能够准确识别和运用。
举例：讲解圆心角与所对弧的关系时，可通过实际操作或动画演示，让学生直观地观察到当圆心角变化时，所对弧的长度也随之变化，强化这一重点知识。
2.教学难点
-弧、弦、圆心角的定义理解：学生对这些几何概念的理解可能存在困难，需要通过具体实例和直观演示来加深理解。
此外，学生在解决与弧、弦、圆心角相关的问题时，往往容易忽视圆心角与所对弧的关系。这说明我在讲解这个重点时，可能没有让学生充分理解和消化。为了帮助学生更好地掌握这个关系，我计划在接下来的课程中，设计更多具有针对性的练习题，并适时给予指导和反馈。
在课堂总结环节，我发现部分学生对今天的知识点仍然存在疑问。这提示我在今后的教学中，要更加重视课堂总结，及时解答学生的疑问，确保他们能够扎实掌握所学知识。
-圆心角与所对弧关系的应用：学生在运用这一性质解决实际问题时可能会感到困惑，需要通过大量练习和案例分析来提高应用能力。
-弧和弦的分类判定：学生在判断优弧、劣弧、半圆和弦时可能会混淆，需要通过对比分析和具体练习来突破。
举例：针对教学难点，教师可以通过以下方式帮助学生突破：
-设计互动环节，让学生动手操作圆规和直尺，在纸上画出不同类型的弧和弦，通过直观感受加深对概念的理解。
3.重点难点解析：在讲授过程中，我会特别强调圆心角与所对弧的关系以及弧和弦的分类这两个重点。对于难点部分，我会通过举例和比较来帮助大家理解。
（三）实践活动（用时10分钟）
1.分组讨论：学生们将分成若干小组，每组讨论一个与弧、弦、圆心角相关的实际问题。
2.实验操作：为了加深理解，我们将进行一个简单的实验操作，如使用圆规和直尺画出不同类型的弧和弦，演示圆心角与所对弧的关系。

弦弧圆心角关系定理

弦弧圆心角关系定理

弦弧圆心角关系定理
弦弧圆心角关系定理，又称为圆心角定理，是描述圆周上圆心角和弦长关系的定理。

其表述如下：
“在同一个圆中，圆心角所对应的的弧长是该圆上所有弦所对应的弦长之中最大的一段。

”
换言之，在同一个圆中，对于任意圆心角和其对应的弦，它们所对应的弧长都有大小关系。

即当圆心角相同时，对应的弧长越长，则对应的弦长越大；而当弧长相同时，对应的圆心角越大，则对应的弦长也越大。

这个定理的重要性在于，它将圆心角与弦长联系起来，使我们能够更加深入地理解圆的性质，并在相关问题的解决中提供便利。

同时也是许多几何证明中常用的定理之一。

人教版九年级数学上册24.1.3弧、弦、圆心角课件

人教版九年级数学上册24.1.3弧、弦、圆心角课件

的顺 的位序位置排置列关顺 关过，系序系点若，排，O列并并A作D，说说=O若明明BEC理理A，D由由=根A..BB据C于题，点意根E补据，全题交图意形补DC，全于探图点究形，AFB探, ，究 AB ，
C（D2的）位当置A关B 、系，CD并位说于明圆理心由O. 的异侧时，
连C交接D 的AOB位A于，置点关OB系G，，，并OC说，明理OD由..
D
F
C
∵ AD=BC ，
12
O
A
E
B
∴ 1 2 .
G
∴ 1 2，
解： AB交交∥∵AACBBDA于于D. =点点BGGC ，，，
证明：∵∵∵ ∴连OAA接E1DD==OBBAACC2B，，，，，OB ， OC ， OD ，
过点 O∴∴∴ ∵作O11E3OEA224BA，，，B，于点 E ，交交DDCC于于点点FF，, 交 AB 于点 G .
12
3 O4 E
G
B
∴
∴∴ ∴3DDDFFF4OOO，≌≌ CCCFFFOOO
， ， 90
，
已知 AB 是 O 的弦， C ， D 是 O 上位于弦 AB
例3 已知 AB 是 O 的弦， C ， D 是 O 上位于弦 AB
顺同 顺序侧序排的排两列同 列个，侧，点若的若，两AADD且个==点ABBCC，，，，且B根根，A据据，C题题，B意意，D作作四C图图，点，，在D探探圆四究究上点按在AABB逆圆，，时上CC针按DD逆时针
的顺 的CD位序位的置排置位列关顺 关C置D，系序系D关的若，排，3 系位列并并A，置D，说说4 =并关C若明明B说系C理理A明，，D由由=理根并..B由据说C∴∵题 .明，A意理根1B+补由据为全题 .2+图意O形∴ ∵ ∴补C的O，全直D探图113径+++究形1, 8，224A0++B探.，究CC3OOADDB，41,18800，,

圆心角弧弦弦心距关系定理及运用

圆心角弧弦弦心距关系定理及运用

结论1在同圆或等圆中，如果：①两个圆心角②两条弧③两条弦④两条弦的弦心距中，有任意一组量相等，那么其它各组量都相等。

结论2:称一段弧所对圆心角的度数为弧的度数。

即：圆心角度数=该圆心角所对弧的度数例1如图，已知AB、CD为O O的两条弦，AD二BC，求证AB= CD.A例2如图7-23，点0是/ EPF的平分线上的一点，以0为圆心的圆和角的两边分别交于点A、B和C、D.求证：AB=CD.变式1：变式2:例3如图，已知AB 和CD 是O O 的两条直径，弦CE //AB , EC 的度数为40°求/ BOC 的度数. L 1BMA P NDDE变式：已知：如图，AB和CD是两条直径，弦CE// AB,求证:1例4如图，在。

O中，弦AB所对劣弧为。

O的-，圆的半径为2cm,3例5如图，MN是半径为1的O O的直径，点A在O O上，/ AMN =30° B为AN弧的中点, P是直径MN上一动点，则PA+ PB的最小值为（）（A）2 2 (B) 2 (C)1(D)2OE例6如图，CD与EF为O O的弦，AB与之交于M、N,若AM=BN,/ 仁/2,求证：CD=EF作业：1. 如图，在半径为2cm的O O内有长为_的弦AB,求此弦所对的圆心角二此二的度数及AB上弦心距的长度。

2. 在O O中，弦AB的长恰好等于半径，求弦AB所对的圆心角度数。

3. O O的一条弦长与半径之比是，这条弦将圆周分成的两部分中，求其劣弧的度数：优弧的度数的比值。

4•如图，在O O中，D、E分别为半径OA、OB中点，C为AB中点,C5.如图，AB 是O O直径，AC 二CD,求证：OC// BD. AC 二CD。

圆的确定,圆心角、圆周角、弧、弦、弦心距之间的关系

儒洋教育学科教师辅导讲义6、多边形与圆如果一个圆经过一个多边形的各顶点，那么这个圆叫做这个多边形的外接圆，这个多边形叫做这个圆的内接多边形，提示：1、与圆的确定有关的两个图形一定要学生重点理解。

2、补充两个知识点：线段垂直平分线的性质和角平分线的性质3、和学生一起重点分析课本例题1和2，理解题目考察的细节和解题方法。

二、例题分析：1、以线段AB为弦的圆的圆心的轨迹是＿＿＿＿＿＿＿＿＿＿＿。

cm。

2、已知扇形的圆心角为120°，半径为2cm，则扇形的弧长是cm，扇形的面积是23、点和圆的位置关系有三种：点在圆，点在圆，点在圆；例1：已知圆的半径r等于5厘米，点到圆心的距离为d，（1）当d=2厘米时，有d r，点在圆（2）当d=7厘米时，有d r，点在圆（3）当d=5厘米时，有d r，点在圆4、下列四边形：①平行四边形，②菱形；③矩形；④正方形。

其中四个顶点一定能在同一个圆上的有（）A、①②③④B、②③④C、②③D、③④5、（07上海中考）小明不慎把家里的圆形玻璃打碎了，其中四块碎片如图所示，为配到与原来大小一样的圆形玻璃，小明带到商店去的一块玻璃碎片应该是（）A．第①块 B．第②块C．第③块 D．第④块6、三角形的外接圆的圆心是（），A．三条中线的交点B．三条高的交点C．三条角平分线的交点D．三条边的垂直平分线的交点7、直角三角形的两条直角边分别为5cm和12cm，则其外接圆半径长为。

（三）巩固练习1、圆是轴对称图形，其对称轴是任意一条的直线；圆是中心对称图形，对称中心为．2、三角形的外接圆的圆心——三角形的外心——三角形的交点；三角形的内切圆的圆心——三角形的内心——三角形的交点；3、三角形的外心一定在该三角形上的三角形（）（A）锐角三角形（B）钝角三角形（C）直角三角形（D）等腰三角形，第7题 （第2题） 7、如图，AB 和DE 是⊙O 的直径，弦AC ∥DE ，若弦BE=3，则弦CE=_______8、如图，OE ⊥AB 、OF ⊥CD ，如果OE=OF ，那么_______（只需写一个正确的结论）B A CEDOF（第8题） （第11题）9、已知，如图所示，点O 是∠EPF 的平分线上的一点，以O 为圆心的圆和角的两边分别交于点A 、Ｂ和C 、D 。

人教版数学九年级上册 弧、弦、圆心角


在同圆或等圆中，相等的圆心角所对的弧相等， 所对的弦也相等．
CB
D
O
A ①∠AOB = ∠COD
② AB CD ③ AB = CD
类比探究可得 弧、弦与圆心角关系定理的推论
在同圆或等圆中，如果两条弧相等，那么它们 所对的圆心角相等，所对的弦相等．
在同圆或等圆中，如果两条弦相等，那么它们 所对的圆心角相等，所对的
A
弧
圆心角
弦
想一想：圆心角、弧、弦之间有什么关系？
二 圆心角、弧、弦之间的关系 合作探究 观察：1. 将圆绕圆心旋转 180° 后，得到的 图形与原图形重合吗？由此你得到什么结论呢？
180° A
重合，
圆是中心对称图形
2. 把圆绕圆心旋转任意一个角度呢？仍与原来的圆 重合吗？
·
α
O
重合.圆是旋转对称图形，具有旋转不变性
在同圆中探究 问题1 在⊙O 中，如果圆心角∠AOB =∠COD，那么 AB
与 CD，弦 AB 与弦 CD 有怎样的数量关系？
因为将圆绕圆心旋转任一角度都能
与自身重合，所以可将 ⊙O 绕圆心
旋转，使点 A 与点 C 重合.
D
由于∠AOB =∠COD，
因此，点 B 与点 D 重合.
B
O·
D
C
（4）如果 AB = CD，OE⊥AB 于 E，OF⊥CD 于 F，那
么 OE 与 OF 相等吗？为什么？
解：OE = OF. 理由如下：
∵ OE⊥AB，OF⊥CD，
∴ AE 1 AB，CF 1 CD.
2
2
∵ AB = CD，∴ AE = CF.
∵ OA = OC，
A
E
B

公开课24.1.3圆心角、弧、弦、弦心距之间的关系


D
圆心角、弧、弦、弦心距之间的关系
在自己的圆内作两条长度相同的弦，量 一量它们所对的圆心角
D B C
O A
圆心角、弧、弦、弦心距之间的关系
两位同学作一条长度数相同的弦，看 一看它们所对的圆心角是否相同
B O A
O' B' A'
四、练习
如图，AB、CD是⊙O的两条弦． AOB COD AB = CD （1）如果AB=CD，那么___________ ，_________________ ．

1 C
A
2 O D
五、例题
例1 如图，在⊙O中， AB = 求证∠AOB=∠BOC=∠AOC
AC
,∠ACB=60°,
A
证明：
∵
AB =
AC
B
O
∴ AB=AC． 又∠ACB=60°， ∴ AB=BC=CA.
·
C
∴ ∠AOB＝∠BOC＝∠AOC.
你会做吗?
三, 如图，在⊙O中，AC=BD， 1 45 ,求∠2的度数。 解: ∵ AC=BD
B
AOE 180 3 35
75
︵ ︵ 1. 如图，在⊙ O 中， AB＝AC，∠B＝70°. 求 ∠C度数. ︵ ︵ ︵ 2.如图，AB是直径，BC＝CD＝DE， ∠BOC＝40°，求∠AOE的度数
第 1题
第 2题
3,如图:在圆O中，已知AC=BD，
试说明：（1）OC=OD
（已知）
图 23.1.5
∴ AC-BC=BD-BC （等式的性质） ∴ AB=CD
∴ ∠1=∠2=45° （在同圆中，相等的弧所对的 圆心角相等）
六、练习
如图，AB是⊙O 的直径，BC = CD ∠COD=35°，求∠AOE 的度数． 解：

圆心角,弦,弧的关系


③AB=A′B′
• 在同圆或等圆中,如果轮换下面三组条件: • ①两个圆心角,②两条弧,③两条弦,你能得出
什么结论?与同伴交流你的想法和理由.
A
A
B
●O
B
●O
●O′
A′
B′
⌒⌒
如由条件: ②AB=A′B′
可推出
A′
B′
①∠AOB=∠A′O′B′
③AB=A′B′
推论
• 在同圆或等圆中,如果①两个圆心角,② 两条弧,③两条弦中,有一组量相等,那么 它们所对应的其余各组量都分别相等.
7个金蛋你可以任选一个,如果出现“恭喜你”的字样， 你将直接过关;否则将有考验你的数学问题，当然你可以 自己作答,也可以求助你周围的老师或同学.
3
5
7
1
2
4
6
判断：
1、等弦所对的弧相等。 （× ）
2、等弧所对的弦相等。 （√ ）
3、圆心角相等，所对的弦相等。( ）
× 4、弦相等，所对的圆心角相等。（ ）
合，B与∴A⌒BB′重与合A⌒．'B' 重合，AB与A′B′重合．
AB A'B', ABA'B'.
三、定理
弧、弦与圆心角的关系定理
在同圆或等圆中，相等的圆心角所对的弧相等， 所对的弦也相等．
在同圆或等圆中，相等的弧所对的圆心角 _相__等__， 所对的弦___相_等____；
在同圆或等圆中，相等的弦所对的圆心角 __相__等__，所对的弧___相__等____．
A
A
B
●O
B
●O
●O′
A′
B′
如由条件: ③AB=A′B′
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
o
B
A
B' A'
o
B
A
B' A'
当∠AOB = ∠︵A'OB'︵时，
它们所对的弧 AB 和A'B' 、 弦AB 和A'B'.
o
B
A
这样，我们就得到下面的定理：
在同圆或等圆中，相等的圆心角所对的弧相等，所对 的弦也相等．
同样，还可以得到：
在同圆或等圆中，如果两条弧相等，那么它们所对的 圆心角_相__等__， 所对的弦__相__等____；
则垂线段OM 的长度,即圆心到弦的距离，叫弦 心距 , 图1中，OM为AB弦的弦心距。
1、判别下列各图中的角是不是圆心角，并说明 理由。
①
②
③
④
活动二 下面我们一起来观察一下圆心角与它所对的
弦、弧有什么关系？ A B 当∠AOB = ∠A'OB' 时，
它们︵所对︵的弧 AB 和A'B' 、
弦AB 和A'B' 相等吗？ 为什么？
在同圆或等圆中，如果两条弦相等，那么他们所对的 圆心角_相__等___，所对的弧__相__等_____．
同圆或等圆中， 两个圆心角、两 条弧、两条弦中 有一组量相等， 它们所对应的其 余各组量也相 等．
小练笔
如图，AB ，CD是⊙O的两条弦.
((12))如 如果果AA⌒BB==CC⌒DD
，那么 ，那么
ED C
A
O
B
1、顶点在 圆心上 的角叫做圆心角。 2、在 同圆或等圆 中，相等的圆心 角所对的弦 相等 ，所对的弧 相等 。
3、在同圆或等圆中，如果两条弧、两条 弦、两个圆心角中有一组量相等，那么其余 各组量也 相等 。
作业布置
1.如图,已知⊙O中,弦AB=CD ，求证：AD=BC
A
O
C
D
B
2．如图2，AB 和DE是⊙O的直径，弦 AC∥DE，若弦
，
.
，
.
(3) 如果∠AOB= ∠COD，那么
，
.
(4)如果AB=CD ，OE⊥AB ，OF⊥CD，垂足分别为 E，
F，OE与OF相等吗？为什么？
例3 如图，在⊙O中，A⌒B=A⌒C ，∠ACB=60 °.
求证：∠AOB= ∠BOC=∠AOC
A
O
B
C
︵ ︵︵ 2.如图，AB是⊙O的直径，BC = DC = DE ，∠COD=35 °， 求∠ AOE的度数。
24.1.3 弧、弦、圆心角
活动一：
剪一个圆形纸片，把它绕圆心旋转180°，所得 的图形与原图形重合吗？由此你能得到什么结论？
圆是中心对称图形，圆心就是它的对称中心 .
(1)顶点在圆心的角,叫圆心角，
如 ? AOB, B
圆心角 ? AOB 所对
的弧为 AB，所对的弦为AB；
M
O
A
过点O作弦AB的垂线, 垂足为M,
BE=3 ，则弦CE=________ ． C
E
D OE
A
O
B
A
B
D
C
3且.已AD知=点BED，，点E分C是别A是⌒B⊙的O中的点半，径求O证A：，OCBD=上C的E.点，
o
B
A
B' A'
o
B
A
B' A'
o
B
A
B' A'
o
B
A
B' A'oBAA Bo
C
D
A B
o
C
D
A B
o
C
D
A B
o
C
D
A B
o
C
D
A B
o
C
D
A B
o
C
D
A B
o
C
D
B' A'
o
B
A
B' A'
o
B
A
A B
o
C
D
B' A'
o
B
A
B' A'
o
B
A
B' A'
o
B
A
B' A'