四年级上册数学角的度量知识点整理

《角的度量》必考点：数角的个数
方法与线段类似，可以以一条线段为边，再找和它可以组合的角；也可以找到基础角，再数出由基础角组成的组合角。

方法一：
以AB为边，可以和AB构成角的有CB，DB，EB，3个角；以CB为边，可以和CB构成角的有DB，EB，有2个角；以DB为边，可以和DB构成角的有EB，有1个角。

一共有3+2+1=6个角。

方法二：按基本角的方法去数。

上图中的基本角是∠ABC，∠CBD，∠DBE，共3个基本角；其中包含两个基本角的是∠ABD，∠CBE，有2个。

包含三个基本角的是∠ABE，有1个。

一共有3+2+1=6个角。

规律：数角的方法可以采用数线段的方法，大角被分成几个小角，就从1一直加到几。

练习：
1.数一数，下图中一共有多少个角？
5＋4＋3＋2＋1=15（个）
2.数一数，下图中一共有多少个含有“☆”的角？
分类讨论：1个单角：1个
2个单角：2个
3个单角：2个
4个单角：1个
1+2+2+1=6（个）。

四年级上册数学角的度量笔记
一、认识度
度是计量角大小的单位，一条射线绕端点从一个位置旋转到另一个位置就形成了一个角。

角的大小和角两边的长短无关，和两条边叉开的大小有关。

二、认识量角器
量角器是用来量度角的工具，它的中心点与角的顶点重合，零刻度线与角的一条边重合。

角的另一条边所对的刻度就是这个角的度数。

三、如何用量角器量角
1.确定顶点与零刻度线对齐。

2.根据度数确定量角器的位置。

3.旋转量角器，让角的一条边与零刻度线重合，另一条边所对的
刻度就是角的度数。

四、如何找出一个角的角度
1.确定顶点与零刻度线对齐。

2.旋转量角器，让角的一条边与零刻度线重合，另一条边所对的
刻度就是角的度数。

3.如果找不到一个完整的刻度，可以沿着量角器边缘找出一个一
个的刻度，用点表示出来。

4.连接点与顶点，形成一个完整的角，所对的刻度就是这个角的
度数。

五、特殊角度的记忆
1.直角：90度
2.平角：180度
3.钝角：大于90度小于180度
4.锐角：小于90度
5.等腰直角三角形：两个锐角都是45度，一个直角是90度。

四年级数学角的度量知识点1. 角的定义及分类2. 角的度量单位：度和弧度3. 度数和弧度的换算4. 角的顶点、边和角度符号5. 直角、钝角和锐角6. 角度的比较和排列7. 互补角和补角8. 相邻角和对顶角9. 垂直角和同位角10. 角的相等性质和角平分线角是数学中重要的概念之一，它是由两个射线（或线段）通过一个共同的起点形成的部分。

根据角大小的不同，可将角分为不同的类型：直角、钝角、锐角等。

度数和弧度是角度量的两种单位，其中度数是指将一个圆周分为360份，而弧度是指将一个圆周分为2π份。

换算两种单位的公式为：1°=π/180，1弧度=180/π。

角的度数可以用角度符号来表示，通常用小写字母a、b、c等表示角的顶点。

在角度量中，还需要注意互补角、补角、相邻角、对顶角、垂直角以及同位角等概念。

同时，还需要了解角的相等性质和角平分线的概念，这些都是数学中基础的角度量知识点。

1. 角的定义及分类角的定义是由两条射线或线段共同确定的一对有向角。

根据角度的大小不同，它们可以被分类为直角，锐角和钝角等。

直角是90度的角，它可以用一个封闭的正方形来形象地表示。

锐角是小于90度的角，例如图中的∠BAC，它可以用一个封闭的等腰三角形来表示。

钝角是大于90度而小于180度的角，例如图中的∠BCD，它可以用一个封闭的等腰梯形来表示。

2. 角的度量单位：度和弧度角的度量单位有度和弧度两种，其中度是最常见的单位。

它的定义是将一个圆周分成360份，每份为1度。

弧度是指，圆的长度等于半径的弧所对应的圆心角。

例如，半径为r的圆的圆心角度数为θ，它所对应的弧长为s，则s=rθ。

同时，它也有一个常用的单位π（pi），圆的周长是2πr。

弧度的公式是：θ=弧长/半径，且通常用弧度符号来表示。

3. 度数和弧度的换算度数和弧度可以互相换算。

其换算公式为：1度=π/180弧度，1弧度=180/π度。

例如，若要将60度角转换为弧度，则应将其乘以π/180，即60π/180=π/3弧度。

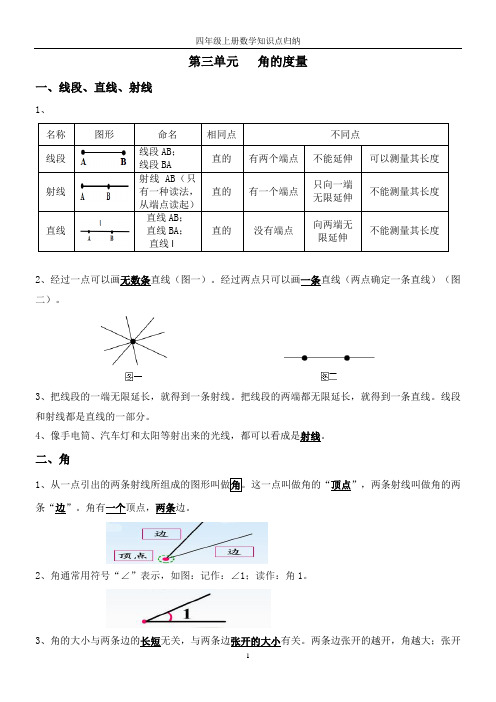
第三单元角的度量一、线段、直线、射线1、2、经过一点可以画无数条直线（图一）。

经过两点只可以画一条直线（两点确定一条直线）（图二）。

3、把线段的一端无限延长，就得到一条射线。

把线段的两端都无限延长，就得到一条直线。

线段和射线都是直线的一部分。

4、像手电筒、汽车灯和太阳等射出来的光线，都可以看成是射线。

二、角1、从一点引出的两条射线所组成的图形叫做角。

这一点叫做角的“顶点”，两条射线叫做角的两条“边”。

角有一个顶点，两条边。

2、角通常用符号“∠”表示，如图：记作：∠1；读作：角1。

3、角的大小与两条边的长短无关，与两条边张开的大小有关。

两条边张开的越开，角越大；张开名称图形命名相同点不同点线段线段AB；线段BA直的有两个端点不能延伸可以测量其长度射线射线AB（只有一种读法，从端点读起）直的有一个端点只向一端无限延伸不能测量其长度直线直线AB；直线BA；直线l直的没有端点向两端无限延伸不能测量其长度得越小，角就越小。

（放大镜不能把角放大。

）4、量角器就是度量角的工具。

角的计量单位是“度”，用“°”表示；如1度记做1°5、人们将圆平均分成360份，其中1份所对的角的大小就是1°；把半圆分成180等份，每一份所对的角的大小就是1°。

三、用量角器量角的方法：（1）把量角器的中心点与角的顶点重合，0°刻度线与角的一条边重合。

（2）角的另一边所对的量角器上的刻度，就是这个角的度数。

（量角时，角的一条边与内圈的0°刻度线重合，读内圈的度数；与外圈的0°刻度线重合，读外圈的度数。

）四、用量角器画角的方法：（如画65°的角）（1）画一条射线，作为角的顶点和一条边（2）使量角器的中心和射线的端点重合，0°刻度线和射线重合（3）在量角器（与0刻度线同圈的）65°刻度线的地方点一个点（4）以画出的射线的端点为端点，通过刚画的点，再画一条射线（5）画小弧线，标注五、角的分类：（1）平角：一条射线绕它的端点旋转半周，形成的角叫做平角。

四年级上册数学第三单元角的度量知识点
四年级上册数学第三单元《角的度量》知识点包括以下几个方面：
1. 角的基本定义：角是由两条射线从一个公共端点出发所形成的图形。

这个公共端点称为角的顶点，而这两条射线称为角的边。

2. 角的度量单位：角的度量单位是“度”，用符号“°”表示。

将一个圆平
均分成360份，每份所对的角的大小是1度。

3. 量角器的使用：用量角器测量角的大小时，需确保量角器的中心与角的顶点重合，0°刻度线与角的一边重合。

然后观察角的另一边所对着的刻度，即为该角的度数。

4. 角的分类：根据度数大小，角可以分为锐角（小于90°）、直角（等于90°）、钝角（大于90°且小于180°）、平角（等于180°）和周角（等于360°）。

5. 画指定度数的角：首先画一条射线，使量角器的中心和射线的端点重合，0°刻度线与射线重合。

然后在量角器上找到所画角的度数的地方点一个点。

最后以画出的射线的端点为端点，通过刚画的点，再画一条射线，即可完成。

以上是四年级上册数学第三单元《角的度量》的主要知识点，掌握这些知识点有助于更好地理解和学习角的度量。

角的度量一、角的定义1. 角的基本概念角是由两条射线共同确定的图形部分，射线称为角的边，它们的公共端点称为角的顶点。

2. 角的种类根据其度数的大小，角可以分为以下几种：•零角：度数为0°，两条射线重合，无法看出来的角。

•锐角：度数小于90°，尖角。

•直角：度数为90°的角，两条垂直的直线形成的角。

•钝角：度数大于90°，钝角是大于直角小于180°的角。

•平角：度数为180°，两条直线成一条直线。

二、角的计量1. 角的度量单位角的度量单位是度（°）。

一圆周的角度为360°。

2. 角的测量方法（1）使用量角器测量角度•将量角器其中一条边放在角的边上的顶点上。

•将量角器另一条边与坐标轴或放在图纸上的已知直线对齐。

•观察量角器刻度上所对应的角度值。

（2）使用圆规测量角度•将圆规的一只脚放在角的顶点上，另一只脚转到角的一边上，使圆规的另一只脚指向角的另一边。

•将这种位置转到已知角度的标志物上。

•在转到的角度上读出度数。

3. 角的度数关系（1）互补角两个角的度数之和为90°，则称这两个角为互补角。

（2）补角一个角的补角是与其互补角的角。

（3）对顶角两个相交直线上的两个相邻的角，互为对顶角。

（4）邻补角两个补角互为对顶角，则称这两个角为邻补角。

4. 角的比较大小（1）角的大小比较根据角的度数大小，角可以比较大小：•锐角 < 90°•直角 = 90°•钝角 > 90°（2）角的度数关系及比较根据角的大小关系，可以进行如下比较：•若角A > 角B，则称角A大于角B，记作 A > B。

•若角A < 角B，则称角A小于角B，记作 A < B。

•若角A = 角B，则称角A等于角B，记作 A = B。

三、角的运算1. 角的加法（1）角的和两个角的和是由这两个角的边所在直线作为边的角。

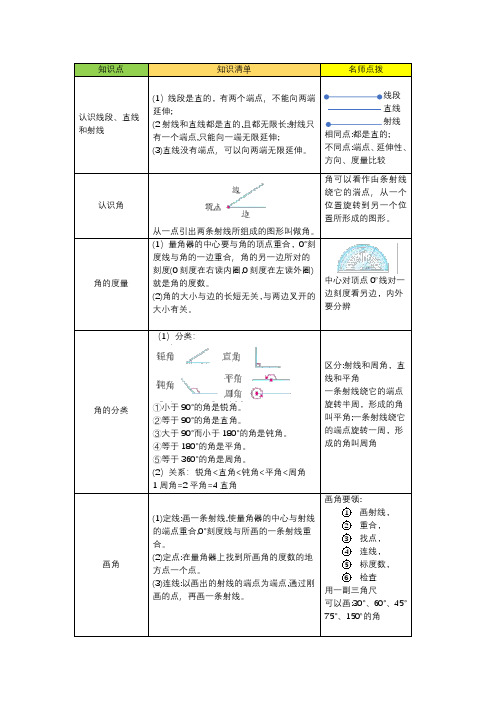
小学数学四年级角的度量知识点总结梳理汇总附练习题文章目录四年级数学角的度量知识点整理一、本节学习指导本节学习角的相关知识，同学们可以先回忆一下直线、斜线相关知识。

本节中我们要掌握角的表示、量角器的使用。

本节有配套免费学习视频。

二、知识要点1、直线、射线、角直线：向两端无限延伸的线，直线无端点。

射线：能像一个方向延伸的线，射线有一个端点。

线段：不能延伸的线，线段有两个端点。

角：具有公共端点的两条射线组成的图形叫做角。

这个公共端点叫做角的顶点，这两条射线叫做角的两条边。

（1）、直线和射线都可以无限延伸，因此无法量出长短。

（2）、线段可以量出长度。

（3）、线段有两个端点，直线没有端点，射线只有一个端点。

3、角的特征角有一个顶点，两条边，如下图角通常用符号“∠”来表示上图中的两个角表示为：∠1 ，∠2；读作：角 1 ，角24、角的大小比较：角的计量单位是“度”，符号“°”，把半圆平分成180等份，每一份所对的角的大小是l 度。

记做1°。

角大小的测量借助量角器，如下图。

测量方法：量角注意两对齐：量角器的中心和角的顶点对齐；量角器的0刻度线和角的一条边对齐。

做到两对齐后看角的另一条边对着刻度线几，这个角就是几度。

看刻度要分清内外圈。

这里我教大家一个小窍门：分清内外圈，紧跟0刻度；0刻度在外圈就看外圈的刻度。

0刻度在内圈就看内圈的刻度。

牢牢记住不忘记。

注意：角的大小与角的两边画出的长短没关系。

角的大小要看两条边叉开的大小，叉开得越大，角越大。

5、角的分类：锐角＜90°，直角=90°，90°＜钝角＜180°，平角=180°=2个直角，周角=360°=2个平角=4个平角6、画角步骤：以画65°的角为例（1）画一条射线，使量角器的中心和封线的端点重合，0 刻度线和射线重合。

（2）在量角器65°刻度线的地方点一个点。

（3）以画出的射线的端点为端点，通过刚画的点，再画一条射线。

《角的度量》必考知识点
角的定义：自一点引两条射线所成的图形叫角
角的符号：∠
角的分类：锐角、直角、钝角、平角、周角
锐角：大于0°小于90°的角叫做锐角
直角：等于90°的角叫做直角
钝角：大于90°小于180°的角叫做钝角
平角：等于180°的角叫做平角
周角：等于360°的角叫做周角
角的大小：角的大小与边的长短没关系，角的大小决定于角的两条边张开的程度。

三角形定义：由三条边首尾相接组成的封闭图形叫三角形
三角形内角和：三角形的内角和为180度
三角形外角：三角形的一个外角等于另外两个内角和
三角形的分类：
按角分：锐角三角形的三个角都小于90度
直角三角形有一个角等于90度
钝角三角形有一个角大于90度
按边分：不等腰三角形，等腰三角形（含等边三角形）注：锐角三角形和钝角三角形可统称为斜三角形。

小学四年级数学《角的度量》知识点整理及练习题（一）线的认识1、认识直线、线段与射线，会用字母正确读出直线、线段和射线：直线：可以向两端无限延伸；没有端点。

读作：直线AB或直线BA。

线段：不能向两端无限延伸；有两个端点。

读作：线段AB或线段BA。

射线：可以向一端无限延伸；有一个端点。

读作：射线AB（从端点读起。

）2、画直线：过一点可画无数条直线；过两个能画一条直线；过三点，如果三点在一条线上，经过三点只能画一条直线，如果这三点不在一条线上，那么经过三点不能画出直线。

3、明确两点之间的距离，线段比曲线、折线要短。

4、直线、射线可以无限延长。

因为直线没有端点，射线只有一个端点，所以不可以测量，没有具体的长度。

只有线段才能有具体的长度。

（二）旋转与角1、角的概念。

由一点引出两条射线所组成的图形叫做角。

角是由一个顶点和两条边组成的。

2、认识平角、周角：平角：角的两边在同一直线上，像一条直线，平角等于180°，等于两个直角。

周角：角的两边重合，(像一条射线），周角等于360°，等于两个平角，四个直角。

3、角的分类：小于90度的角叫做锐角；等于90度的角叫做直角；大于90度小于180度的角叫做钝角；等于180度的角叫做平角；大于180度小于270度叫做优角（此为补充内容）；等于360度的角叫做周角。

4、动手画平角、周角。

（三）角的度量1、认识度：将圆平均分成360份，其中1份所对的角叫做1度，记作1°，通常用1°作为度量角的单位。

2、认识量角器：量角器是把半圆平均分成180份，一份表示1度。

量角器上有中心点、0刻度线、内刻度线、外刻度线。

3、量角器的使用方法。

“两合一看”,“两合”是指中心点与角的顶点重合；0刻度线与角的一边重合。

“一看”就是要看角的另一边所对的量角器的刻度。

4、看角的度数时要注意是看外刻度还是内刻度。

交的开口向左看外刻度线，角的开口向右看内刻度线。

（四）画角1、用量角器画指定度数的角的方法。

四年级上册数学
角的度量重难点
一、射线、线段、直线
射线：射线有一个端点，没有端点的那一端可以无限延伸，不能量出长度。

像手电筒、汽车灯和太阳等射出来的光线，都可以近似地看成是射线。

线段：直的，有两个端点，有限长（可以度量）。

直线：直的，没有端点，可以无限延长。

注意：经过一点可以画无数条直线，经过两点只可以画一条直线
（两点确定一条直线）。

二、角的认识
从一点引出的（两条射线）所组成的图形叫做（角）。

角通常用符号（∠）来表示。

角有一个顶点，两条边。

1、角的大小与两条边的长短无关，与两条边的张开的大小有关，张开的越大，角越大。

2、放大镜不能把角放大。

三、角的分类
直角（等于90°）锐角（小于90°）
钝角（大于90°小于180°）平角（等于180°）
一条射线绕它的端点旋转半周，形成的角是平角。

周角（等于360°）
一条射线绕它的端点旋转1周，形成的角是周角。

锐角＜直角＜钝角＜平角＜周角
1周角＝2平角＝4直角。

《角的度量》知识点1.直线、射线、角直线：向两端无限延伸的线，直线无端点。

射线：能像一个方向延伸的线，射线有一个端点。

线段：不能延伸的线，线段有两个端点。

角：具有公共端点的两条射线组成的图形叫做角。

这个公共端点叫做角的顶点，这两条射线叫做角的两条边。

2.直线、射线与线段的联系和区别1）直线和射线都可以无限延伸，因此无法量出长短。

2）线段可以量出长度。

3）线段有两个端点，直线没有端点，射线只有一个端点。

3.角的特征角有一个顶点，两条边，如下图角通常用符号“∠”来表示4.角的大小比较：角的计量单位是“度”，符号“°”，把半圆平分成180 等份，每一份所对的角的大小是l 度。

记做1°，角大小的测量借助量角器，如下图。

测量方法：量角注意两对齐：量角器的中心和角的顶点对齐；量角器的0刻度线和角的一条边对齐。

做到两对齐后看角的另一条边对着刻度线几，这个角就是几度。

看刻度要分清内外圈。

这里我教大家一个小窍门：分清内外圈，紧跟0刻度；0刻度在外圈就看外圈的刻度。

0刻度在内圈就看内圈的刻度。

牢牢记住不忘记。

注意：角的大小与角的两边画出的长短没关系。

角的大小要看两条边叉开的大小，叉开得越大，角越大。

5.角的分类：锐角＜90°，直角=90°，90°＜钝角＜180°，平角=180°=2个直角，周角=360°=2个平角=4个平角6.画角步骤：以画65°的角为例（1）画一条射线，使量角器的中心和封线的端点重合，0 刻度线和射线重合。

（2）在量角器65°刻度线的地方点一个点。

（3）以画出的射线的端点为端点，通过刚画的点，再画一条射线。

《角的度量》练习题一．填空。

（26分）1. 线段有（）个端点，直线（）端点，射线有（）个端点。

2. 从一点引出两条（）所组成的图形叫做角。

这个点叫做角的（），这两条射线叫做角的两条（）。

3. 一条射线绕它的端点旋转半周，所形成的角叫做（）。

四年级数学《角的度量》知识点
四年级数学《角的度量》知识点
以下是店铺精心为大家分享的人教版四年级数学《角的度量》知识点欢迎大家参考学习。

1、认识度。

将圆平均分成360份，把其中的.1份所对的角叫做1度，记作1°，通常用1°作为度量角的单位。

2、认识量角器。

量角器是把半圆平均分成180份，一份表示1度。

量角器上有中心点、0刻度线、内刻度线、外刻度线。

3、量角器的使用方法。

“两合一看”,“两合”是指中心点与角的顶点重合;0刻度线与角的一边重合。

“一看”就是要看角的另一边所对的量角器的刻度。

4、看角的度数时要注意是看外刻度还是内刻度。

交的开口向左看外刻度线，角的开口向右看内刻度线。

通过店铺为大家分享的人教版四年级数学《角的度量》知识点希望对大家有所帮助。

下载全文。