基于Gompertz模型与回归分析模型控制测试质量的工程化方法(格式修改)[1]
- 格式:docx
- 大小:172.54 KB
- 文档页数:10

SYS PRACTICE 系统实践摘要:软件产品的缺陷可通过软件测试发现,软件测试直接影响软件质量,为更好开展软件测试,必须设法满足软件产品质量与测试过程的定量度量与预测需求。
基于此,论文将围绕基于模型的软件质量与测试过程评估开展研究,模型参数估计采用非线性回归最小二乘法,以此定量预估软件产品质量和测试过程,为测试活动的更好开展提供支持。
关键词:Gompertz模型;软件质量;软件测试;软件缺陷;过程评估一、研究思路结合相关研究和实践可以了解到,软件测试的最终目的是通过有限的物力、人力,高质量、高效率的完成测试。
对于软件测试来说,过度的测试将引发资源浪费问题,而不充分的测试则会引发很多问题。
如软件测试不足,软件隐藏错误催生的风险将由用户承担,如过度开展软件测试,很多宝贵的资源则会浪费。
因此,在软件测试的实践中,必须把握好软件测试的尺度,这种尺度的掌握需得到科学定义的定量描述工具支持,以此保证软件产品经理能够做出正确判断。
为实现软件测试尺度的定量描述,国内外相关学者开展大量研究,如基于软件缺陷进行度量、基于软件过程能力度指数控制图进行度量、基于软件缺陷状态跟踪图进行度量,但这类研究多围绕测试数据的定性判断展开,缺乏定量层面的研究。
因此,本文基于已有的测试数据,采用模型,定量分析和预测软件测试过程,以此定量评估软件产品质量,为测试任务是否应结束提供科学的判断依据[1]。
二、建模机理结合日常的软件测试实践进行分析可以发现,在软件测试的初始环节,由于不熟悉测试环境,测试人员一般仅开展基本功能测试,这种情况下软件测试日均发现的缺陷数减少,软件缺陷数增长在这一环节也较为缓慢。
随着逐渐进入状态,测试人员可实现对测试环境的熟练掌握,受不断增多的日均发现软件缺陷数影响,存在增长速度迅速加快的发现软件缺陷数。
随着软件测试的不断推进,受隐藏加深的软件缺陷影响,难度加大的测试使得一个缺陷发现需要执行较多的测试用例,这一过程中虽然缺陷数仍属于增长状态,但增长速度极慢,而对于有限的软件中隐藏缺陷来说,发现缺陷数的无限增长也会在这种情况下受到限制。

第25卷增2岩石力学与工程学报V ol.25 Supp.2 2006年10月Chinese Journal of Rock Mechanics and Engineering Oct.,2006基于Gompertz成长曲线的真空预压软土沉降规律分析吴起星,胡辉(暨南大学力学与土木工程系,广东广州 510632)摘要:对真空预压软土沉降变化规律进行分析,发现其与社会经济预测中的Gompertz成长曲线变化规律相似。
引入Gompertz成长曲线模型,采用3段估计法求解模型参数;同时,结合具体工程实例,对真空预压软土的表面累计沉降数据进行拟合和分析,并与双曲线模型和指数曲线模型进行比较。
研究结果表明,Gompertz成长曲线模型拟合曲线与实测曲线吻合良好,采用该模型进行真空预压软土沉降变化规律分析是可行的,并可根据所反映出的沉降发展变化趋势,作出沉降预测,计算工后沉降及确定卸荷时间。
与双曲线模型和指数曲线模型比较,Gompertz 成长曲线模型适应性较好,趋势预测准确性高。
最后指出应用Gompertz成长曲线模型进行分析时应注意抽真空的连续性、实测时间序列数据能等分成3组及保证实测沉降数据已进入弹塑性阶段等问题。
关键词:土力学;软土;真空预压;沉降;Gompertz成长曲线中图分类号:TU 447 文献标识码:A 文章编号:1000–6915(2006)增2–3600–07LAW ANALYSIS OF SOFT SOIL SETTLEMENT TREATED BY V ACUUM PRELOADING BASED ON GOMPERTZ GROWTH CURVEWU Qixing,HU Hui(Department of Mechanics and Civil Engineering,Jinan University,Guangzhou,Guangdong510632,China)Abstract:After the law of settlement change analysis of soft soil treated by vacuum preloading method,it is found that the law is similar to that of Gompertz Growth Curve used in socioeconomic prediction. Based on practical engineering examples,the values of parameters of Gompertz Growth Curve by three-segment estimation method are achieved,and the Gompertz Growth Curve Model is established to analyze the settlement data of soft soil treated by vacuum preloading method and compared with Hyperbolic Model and Index Curve Model. The analytical results of engineering practice indicate that the effect of fitting curves by using this method is good and this method is reasonable to analyze the law of settlement change of soft soil treated by vacuum preloading method. It also can be used for predicting soft soil settlement,calculating post-construction settlement and unloading time decision. Compared with Hyperbolic Model and Index Curve Model,Gompertz Growth Curve Model has good adaptability and precision in trend forecast. Last,some problems such as continuing evacuation,three equal segment measured data and elastic-plastic deformation of soil,are pointed out during application of Gompertz Growth Curve Model.Key words:soil mechanics;soft soil;vacuum preloading;settlement;Gompertz Growth Curve收稿日期:2006–05–18;修回日期:2006–07–19作者简介:吴起星(1972–),男,硕士,2002年于广西大学岩土工程专业获硕士学位,现为讲师、博士研究生,主要从事土工试验、原位测试及地基基础等方面的教学与研究工作。

Gompertz增长曲线方程参数估计若干问题的研究开题报告题目:Gompertz增长曲线方程参数估计若干问题的研究一、研究背景与意义随着经济社会的不断发展,人们对于生态环境、资源利用等方面的关注度不断提高,生物学研究也受到了越来越多的关注。
Gompertz增长曲线是描述生物种群在一定环境下生长变化规律的重要数学模型,其应用范围广泛,包括药物治疗、微生物生长、肿瘤生长等方面。
Gompertz增长曲线模型包含三个参数,分别是最大生长速率、最大可达个体数和生长速率下降的速率。
这些参数的准确评估对于生物学的研究具有重要意义,也是决策者在生产和管理方面所需要考虑的关键问题。
因此,本研究将围绕Gompertz增长曲线方程的参数估计方法开展深入研究,旨在提高生物学研究中参数估计的精确度和可靠性,为决策者提供更为科学的依据。
二、研究内容和方法1. Gompertz增长曲线模型概述介绍Gompertz增长曲线模型的基本形式及其在生物学领域中的应用。
2. 参数估计算法比较比较传统的参数估计算法、非线性最小二乘算法和贝叶斯统计方法等不同算法的优缺点,为后续研究提供基础。
3. 改进的Gompertz增长曲线参数估计方法研究基于参数估计算法的比较结果,提出一种改进的Gompertz增长曲线参数估计方法,包括正交实验设计、遗传算法等。
4. 数值模拟与实际数据分析通过数值模拟和实际数据分析,验证改进方法的可靠性与实用性。
三、预期结果与展望本研究将探讨Gompertz增长曲线参数估计方法的现状与未来发展,提出改进方法并进行实际数据分析,验证改进方法的可行性。
预计可提高生物学研究中参数估计的精度和可靠性,为决策者提供更为科学的依据。
四、参考文献[1] DeLury, D. B. (1947). On the estimation of biological populations. Biometrics, 3(4), 145-167.[2] Gompertz, B. (1825). On the nature of the function expressive of the law of human mortality, and on a new mode of determining the value of life contingencies. Philosophical Transactions of the Royal Society of London, 115, 513-585.[3] Höllrigl, T. (2011). Gompertz curve and logistic curve are competing models for incidence rates of female breast cancer in the United States. Journal of Applied Statistics, 38(5), 871-878.[4] Xu, K., DeGala, G. D., & Schmid, R. K. (1999). Parameter estimation and model selection for the Gompertz diffusion model. Technometrics, 41(1), 27-37.[5] Zurauskas, J., & Paliulis, D. (2007). A comparative study of the Gompertz and logistic models for fitting embryonic development data. Mathematical Biosciences and Engineering, 4(3), 529-547.。

最佳实践】量化项目管理案例:缺陷趋势预测利器之Gompertz模型收藏不知身为软件工程师的你,在写代码时是不是有过这样的经历:一方面对自己写的代码信心满满,一方面又非常希望知道自己开发的代码的质量到底多高。
如果代码真的没被测出bug来或者测出的bug较少时,反而有点担心——会不会还有隐藏的更深的bug没被发现?或者身为测试工程师的你,可能比开发人员担心的会更多:这些代码该不该再继续测试了?怎么就能断定当前的版本算是通过验收标准了,继而可以被客户和用户认可?是不是就可以把这个版本交付使用了呢?相信这是很多开发和测试人员都曾经经历过的。
无论是开发人员、测试人员,还是项目经理、高层管理人员,都已经为版本的交付日以继夜的加班工作,可不能在交付的时刻功亏一篑。
打击心情不说,加班加点不说,而且,谁该来为可能的返工和无休无止的变更买单呢。
所以,软件版本在发布时需要有一个判定的标准——没有预先定义的判定标准,就无法去判断版本是否已经达到了客户的要求。
不进行判断,或者是错误的判断,都很有可能会造成该项目资源安排的不合理,甚至造成资源的浪费,那么不管是精神上还是体力上,甚至进度上、成本上,都会给项目团队带来不小的打击。
CMMI四级的一个要求是量化的管理项目(详见量化项目管理QPM中文版)。
映射到缺陷预测活动中,也就是量化的管理缺陷。
量化的退出标准就是将类似“这个版本是否能够通过”这样的问题,形象地转变为“已经测出的bug数是否已经足够多,遗留的bug是否已经少到不会影响软件的交付”等等这样的表述。
这样,无论是理解上还是判断上都更加容易,版本发布标准也就变得不难理解了。
在决定发布版本之前,需要去统计这样几件事:我们已经发现了多少个bug;用量化的方法进行管理时,我们还有多少个bug没有发现;我们统计到的未发现的 bug数是否能达到客户的要求;如果无法满足客户的要求,那我们至少还需要发现多少个bug。
当这一系列问题都解决了以后,开发、测试人员是终于可以“收”工拿项目奖,还是需要返工加班、继续努力,也就一目了然了。


统计回归分析在产品质量控制中的应用在当今竞争激烈的市场环境中,产品质量是企业生存和发展的关键。
为了确保产品质量的稳定性和可靠性,企业需要采用有效的质量控制方法。
统计回归分析作为一种强大的数据分析工具,在产品质量控制中发挥着重要作用。
统计回归分析是一种用于研究变量之间关系的统计方法。
它通过建立数学模型,来描述自变量与因变量之间的定量关系。
在产品质量控制中,我们可以将影响产品质量的因素作为自变量,将产品质量的指标作为因变量,然后运用回归分析来揭示它们之间的内在联系。
例如,在一家汽车制造企业中,我们可能会关注汽车的油耗这一质量指标。
影响油耗的因素可能包括发动机排量、车辆重量、行驶速度、驾驶习惯等。
通过收集大量的相关数据,并进行回归分析,我们可以建立一个油耗与这些因素之间的数学模型。
这个模型可以帮助我们预测在不同的条件下汽车的油耗情况,从而为优化产品设计和改进生产工艺提供依据。
在产品质量控制中,统计回归分析主要有以下几个方面的应用:一、质量预测通过建立回归模型,我们可以根据已知的自变量值来预测产品质量指标的取值。
这对于企业提前了解产品质量状况、制定生产计划和质量控制策略非常有帮助。
例如,在电子产品生产中,我们可以根据零部件的质量参数、生产工艺参数等预测最终产品的合格率。
如果预测结果显示合格率可能较低,企业就可以及时采取措施,如加强原材料检验、调整生产工艺参数等,以提高产品质量。
二、因素分析回归分析可以帮助我们确定哪些因素对产品质量的影响最为显著。
这有助于企业在质量控制中抓住关键因素,有针对性地进行改进。
例如,在食品生产中,通过回归分析发现,原材料的新鲜度和加工温度对食品的口感和保质期影响最大。
那么企业就可以重点关注这两个因素,加强原材料采购管理和优化加工过程中的温度控制,从而提高产品质量。
三、质量改进基于回归分析的结果,企业可以制定质量改进措施。
当我们发现某个自变量对因变量的影响不符合预期时,可以通过调整该自变量的值来达到改进产品质量的目的。


霸王鸡生长曲线拟合及体重与体尺的相关性分析王飞;李笑春;吴科榜【摘要】[目的]研究霸王鸡体重生长发育规律及体重与体尺性状的相关性,为其科学饲养管理及选育提供理论依据.[方法]采用Logistic、Gompertz和Von Bertalanffy3种非线性模型对0~18周龄霸王鸡的体重数据进行生长曲线拟合与分析,同时对18周龄霸王鸡的体重与体尺性状进行相关分析与回归分析.[结果]以Gompertz模型对霸王鸡生长曲线的拟合效果最佳,拟合度(R2)达0.9989,极限体重1505.2 g,拐点体重553.7 g,拐点周龄为10周龄.霸王鸡的体重与各体尺性状之间均呈极显著正相关(P<0.01),其中,龙骨长与体重的相关性最高(r=0.9355),其次为胸深与体重的相关性(r=0.9119),而胸宽与体重的相关性最低(r=0.6795);经逐步回归分析后,霸王鸡生长曲线模型的自变量由7个减为4个(胸深、龙骨长、骨盆宽和胫围),最佳回归模型为:y=-1573.3470+57.9062x3+109.7107x4+66.4648x5+80.9203x7.[结论]在今后的实际生产中,应尽量满足霸王鸡前10周的营养供给,同时应加强对龙骨长、骨盆宽、胸深和胫围4个指标的选育,最大限度地提高霸王鸡的体重,以获取更高的经济效益.【期刊名称】《南方农业学报》【年(卷),期】2014(045)005【总页数】5页(P870-874)【关键词】霸王鸡;生长曲线模型;体重;体尺;相关分析【作者】王飞;李笑春;吴科榜【作者单位】海南大学农学院,海口 570228;海南大学农学院,海口 570228;海南大学农学院,海口 570228【正文语种】中文【中图分类】S831.89【研究意义】畜禽的生长发育一般都具有非线性特征,因此生产中可用非线性数学模型来描述其生长发育的变化规律。
在禽类上常用的非线性数学模型有Logistic、Gompertz和Von Bertalanffy,运用这些非线性数学模型对禽类生长曲线进行拟合分析,不仅可以动态了解禽类的生长过程,预测其生长规律,还可以指导饲养管理及提高选育效果。


Gompertz试验序列增长模型
陈昭宪
【期刊名称】《电子产品可靠性与环境试验》
【年(卷),期】1996(000)005
【摘要】电子元器件的可靠性增长过程,是一个TAAF的不断循环过程。
一般来说,一个成功的TAAF循环会使产品的可靠性得到一定的提高,若干个TAAF循环就会使产品的可靠性不断的增长。
1968年E.P Virene提出了可靠性增长的Gompertz 模型,该模型给出了产品可靠性随试验序列而增长的关系为R(K)=a×b^c~k式中k 为试验序列,a=(?)R(K)为产品的增长极限,b、C为产品的增长参数,它们满足关系式0<b、c<1。
采取该模型对试验数据进行数据处理时,需要将试验数据分成三组,即:【总页数】3页(P69-70,54)
【作者】陈昭宪
【作者单位】无
【正文语种】中文
【中图分类】TN606
【相关文献】
1.Gompertz增长模型在林产品产值预测中的应用 [J], 余永清;付顺华
2.Gompertz分布TFR模型简单步进应力加速寿命试验的统计分析 [J], 王蓉华;徐晓岭;刘皓宇;吴生荣
3.Gompertz分布TFR模型多步步进应力加速寿命试验的统计分析 [J], 王蓉华;徐晓岭;施宏伟
4.随机单种群Gompertz增长模型的稳定性 [J], 王凤筵
5.日元实际有效汇率、净出口比率与贸易条件——基于内生经济增长模型的时间序列分析 [J], 洪宇
因版权原因,仅展示原文概要,查看原文内容请购买。
航空航天科学技术科技创新导报 Science and Technology Innovation Herald7G om p er t z 模型是一种可靠性增长模型,适用于取得等间隔(时间、次数)的硬件或软件的可靠性增长数据,其增长有先快后慢和先慢后快之后再慢这两种情况。
对于高价值产品,在进行研制的过程中,每次试验的数量有限,并且每次试验后,会根据该次试验的结果,对产品进行改进后,再进行试验。
这种研制过程是比较适用Gomp er tz 模型对其的可靠性水平进行分析评估的。
同时,GJB 1407中明确表明:“一项成功的增长试验可以免去可靠性鉴定试验”,所以通过拟合G o mp e r t z 模型也可以有效地利用研制试验数据减少或免去可靠性鉴定试验。
但是,目前产品的可靠性要求基本上均是要求的某一置信度下的可靠度下限,而G o m p e r t z 模型经典的估计方法只给出了相应的点估计,文献[1]中虽然利用Be ye s方法给出可靠度下限的计算方法,但是计算相对复杂。
所以该文通过探讨G o m p e r t z 模型的可靠度下限求解方法,给出利用Gomp er tz模型的可靠性评估和验证方法。
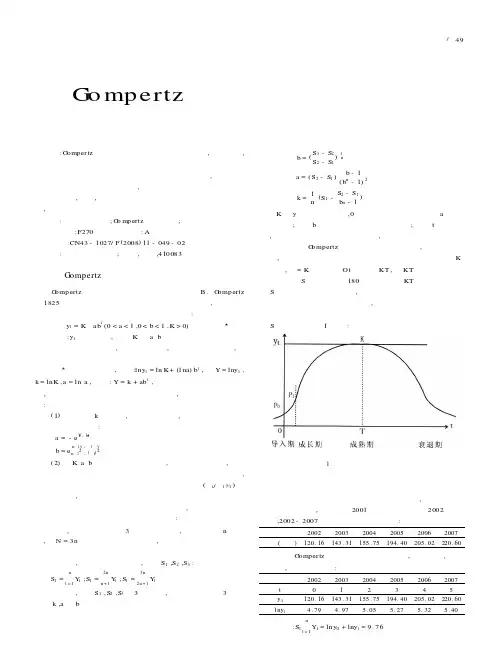
1 Gompertz模型及其点估计方法1.1 G om pertz模型Gomp er tz模型为:≤≥0 (1)其中:为时的可靠性;,,为增长后上限值;=0,,为起始值;为“起始值与上限值”之比;为试验周期序号(对应于时间);为增长速率。
1.2 模型求解Gomp er t z 模型最为经典的求解方法为Vir e ne 算法,该算法是由E.P.Vire ne 提出,是目前求解Gomp er tz模型的主要算法。
但是,为了后续的求取区间估计,所以该文介绍的为最小二乘估计方法。
设产品总的批次(或试验次数)为m 个,当产品不断地对出现的故障和问题进行改进时,就有)()1(0m R R <<< ,用G omp e r tz 模型拟合该过程,设)1()(-=t R t R g t ,=2,…,。
基于Gompertz增长模型的BUG预测基于Gompertz增长模型的BUG预测背景我们在⽇常的软件测试过程中会发现,在测试的初始阶段,测试⼈员对测试环境不很熟悉,因此⽇均发现的软件缺陷数⽐较少,发现软件缺陷数的增长较为缓慢;随着测试⼈员逐渐进⼊状态并熟练掌握测试环境后,⽇均发现软件缺陷数增多,发现软件缺陷数的增长速度迅速加快;但随着测试的进⾏,软件缺陷的隐藏加深,测试难度加⼤,需要执⾏较多的测试⽤例才能发现⼀个缺陷,尽管缺陷数还在增加,但增长速度会减缓,同时软件中隐藏的缺陷是有限的,因⽽限制了发现缺陷数的⽆限增长。
这种发现软件缺陷的变化趋势及增长速度是⼀种典型的‘S’曲线,满⾜Gompertz增长模型的应⽤条件。
模型表达式为:Y=a*b(c T)其中Y表⽰随时间T发现的软件缺陷总数,a是当T→∞时的可能发现的软件缺陷总数,即软件中所含的缺陷总数。
a*b是当T→0时发现的软件缺陷数,c表⽰发现缺陷的增长速度。
我们需要依据现有测试过程中发现的软件缺陷数量来估算出三个参数a,b,c的值,从⽽得到拟合曲线函数.实际使⽤1. 统计项⽬每天的累积BUG数,获得若⼲递增的数据2. 根据数据获得拟合曲线,计算出a,b,c的值,其中a为可能的软件缺陷总数3. 根据a,b,c的值,计算时间T,其中可按95%的a或者90%的a来计算需要发现95%/90%的bug所需要的时间4. T-已花费的时间=为了达到质量所仍需的天数原型代码如下(python)# coding: UTF-8import mathimport numpy as npfrom scipy.optimize import leastsq###采样点#project 1yi=np.array([2,4,4,6,12,15,21,27,39,45,50,54])#project 2yi=np.array([6,11,15,20,25,31,33,41,42,44,49,52,53])ti=np.array(xrange(1,yi.size+1))total=yi[-1]def func(p,t):a,b,c=preturn a*b**(c**t)def error(p,t,y,s):print sreturn func(p,t)-ydef extra(thread,a,b,c,total,day):expect=a*thread/100T=(math.log(math.log(expect/a)/math.log(b)))/math.log(c)if T>day:return T-dayelse:return 0#初始值p0=[1500,0.078,0.874]s="Test the number of iteration"para=leastsq(error,p0,args=(ti,yi,s))a,b,c=para[0]print 'a=',a,'b=',b,'c=',cprint '预期bug总数:',aprint '已发现bug总数:' ,totalprint '已发现bug占⽐:',total/aday=yi.sizeprint '已花费天数:' ,dayT=extra(95,a,b,c,total,day)print '为达到发现95的bug还需要%d天'%TT=extra(90,a,b,c,total,day)print '为达到发现90的bug还需要%d天'%Timport matplotlib.pyplot as pltplt.figure(figsize=(8,6))plt.scatter(ti,yi,color='red',label='Sample Point',linewidth=3)t=np.linspace(0,yi.size*2,1000)y=a*b**(c**t)plt.plot(t,y,color='orange',label='fitting Point',linewidth=2)plt.legend()plt.show()意义评估当前项⽬测试的程度评估可能线上问题的数⽬评估达到发布质量所额外需要的⼯时不⾜这个⽅法使⽤前提是产品的整个测试活动中测试能⼒保持相对稳定,⽐如分轮次提测或者测试⼈⼒投⼊时间不均匀,数值可能误差较⼤对测试过程中发现的缺陷只做数量上的处理,不做等级上的划分未来可以考虑优化这个预测模型或者采⽤更好的模型去判断测试退出时间点以及预测漏侧数量。
本文由黑涩哎贡献doc文档可能在WAP端浏览体验不佳。
建议您优先选择TXT,或下载源文件到本机查看。
Gompertz 模型在人口预测中的应用阎慧臻(大连工业大学信息科学与工程学院,辽宁大连 116034)摘要:摘要:Gompertz 模型是用来描述生物种群生长发育规律的数学模型,将 Gompertz 模型用于人类即为人口增长模型。
本文利用 Gompertz 模型对中国人口进行了预测,建立了人口预测公式。
通过与实际人口相比较,结果表明利用该预测公式进行人口预测是比较符合实际情况的。
关键词:Gompertz 模型;人口;预测关键词中图分类号:O29;Q141 文献标识码:A 中图分类号文献标识码 Application of Gompertz model in population prediction YAN Hui-zhen (School of Informational Science and Engineering,Dalian Polytechnic University,Dalian, 116034,China) Abstract:The Gompertz model can be used to describe the growth law of the biologypopulation , the population growth model can be obtained by applying the Gompertz model to the humanity . In this paper,the population of China has been predicted using Gompertz model,and the formula of population prediction has been pared with the actual population,we see that the results of population prediction using this formula conform to the real situation. Key words: gompertz model; population; prediction 0 引言人口预测就是根据现有的人口状况并考虑影响人口发展的各种因素,按照科学的方法,[1] 测算在未来某个时间的人口规模、水平和趋势。