SAS上机练习题(习题部分)(2)

sas测试题及答案1. SAS中，如何将一个数据集的所有变量的值增加10？A. data dataset; set dataset; +10; run;B. data dataset; set dataset; +10; quit;C. data dataset; set dataset; +10; run;D. data dataset; set dataset; +10;答案：C2. 在SAS中，如何创建一个新的数据集，并将原数据集中的变量`Var1`和`Var2`复制到新数据集中？A. data new_dataset; set old_dataset; Var1 =old_dataset.Var1; Var2 = old_dataset.Var2; run;B. data new_dataset; set old_dataset; Var1 = Var1; Var2 = Var2; run;C. data new_dataset / old_dataset; set old_dataset; Var1 = old_dataset.Var1; Var2 = old_dataset.Var2; run;D. data new_dataset; set old_dataset; Var1 = Var1; Var2 = Var2; quit;答案：A3. SAS中，如何使用`proc print`步骤打印数据集的前10行？A. proc print data=dataset firstobs=10;B. proc print data=dataset firstobs=1 obs=10;C. proc print data=dataset firstobs=10;D. proc print data=dataset firstobs=1 obs=10;答案：B4. 在SAS中，如何使用`if-then`语句来创建一个新的变量`NewVar`，当`Var1`大于10时，`NewVar`的值为`Var1`的两倍，否则为0？A. data dataset; set dataset; if Var1 > 10 then NewVar = 2 * Var1; else NewVar = 0; run;B. data dataset; set dataset; if Var1 > 10 then NewVar = 2 * Var1; NewVar = 0; run;C. data dataset; set dataset; if Var1 > 10 NewVar = 2 *Var1; else NewVar = 0; run;D. data dataset; set dataset; if Var1 > 10 then NewVar = 2 * Var1; else NewVar = 0; quit;答案：A5. SAS中，如何使用`proc means`步骤计算数据集中`Var1`的平均值？A. proc means data=dataset N mean of Var1;B. proc means data=dataset N mean Var1;C. proc means data=dataset N=mean Var1;D. proc means data=dataset N mean Var1;答案：D结束语：以上是SAS测试题及答案，希望能够帮助您更好地理解和掌握SAS编程的基础知识。

sas练习题（打印版）### SAS练习题（打印版）#### 一、基础数据操作1. 数据导入- 题目：使用SAS导入一个CSV文件，并列出前5个观测值。

- 答案：使用`PROC IMPORT`过程导入数据，并用`PROC PRINT`展示前5个观测。

2. 数据筛选- 题目：筛选出某列数据大于50的所有观测。

- 答案：使用`WHERE`语句进行筛选。

3. 数据分组- 题目：根据某列数据对数据集进行分组，并计算每组的均值。

- 答案：使用`PROC MEANS`过程和`BY`语句进行分组和计算。

4. 数据排序- 题目：按照某列数据的升序或降序对数据集进行排序。

- 答案：使用`PROC SORT`过程进行排序。

#### 二、描述性统计分析1. 单变量分析- 题目：计算某列数据的均值、中位数、标准差等统计量。

- 答案：使用`PROC UNIVARIATE`过程进行单变量描述性统计分析。

2. 频率分布- 题目：计算某列数据的频数和频率分布。

- 答案：使用`PROC FREQ`过程进行频率分布分析。

3. 相关性分析- 题目：计算两列数据的相关系数。

- 答案：使用`PROC CORR`过程计算相关系数。

#### 三、假设检验1. t检验- 题目：对两组独立样本的均值进行t检验。

- 答案：使用`PROC TTEST`过程进行t检验。

2. 方差分析- 题目：对多个组别数据进行方差分析。

- 答案：使用`PROC ANOVA`过程进行方差分析。

3. 卡方检验- 题目：对分类变量进行卡方检验。

- 答案：使用`PROC FREQ`过程和`CHI2TEST`选项进行卡方检验。

#### 四、回归分析1. 简单线性回归- 题目：使用一个自变量和一个因变量进行简单线性回归分析。

- 答案：使用`PROC REG`过程进行简单线性回归。

2. 多元线性回归- 题目：使用多个自变量和一个因变量进行多元线性回归分析。

- 答案：同样使用`PROC REG`过程，但包括多个自变量。

江西财经大学SAS软件技能测试试题二一、填空题（每小题2分，共20分。

）1．在SAS程序中，每一个完整的SAS语句都是以（）号结束的。

2．创建SAS数据集用（）步。

3．SAS软件使用（）窗口可以显示、修改、设置并存储SAS参数设置。

4．TITLES窗用以显示和让用户指定打印输出各页顶端的标题，共可以指定（）个标题。

5．DATA步建立SAS数据集时，常使用INPUT语句指定将要输入的变量及其类型。

在指定将输入（）型变量时，其后应用“$”符号。

6．SAS程序是由两种步骤（STEP）组成：它们是（）步和（）步。

7．在SAS程序中，经常要选择观测。

我们可以用选项（）保留原数据集中的观测，用选项（）删除原数据集中的观测。

8．INPUT语句中常用的数据读入的方式有四种。

其中有一方式是（）方式，它可以使字符型变量值中含有空格。

二、简答题（每小题10分，共20分）1．SAS系统软件有哪三个基本窗口？各有什么功能？2．请回答PUT语句、OUT和OUTPUT语句的作用。

1．试列举几种用SAS系统可以制作的统计图形，并回答在编程时各自用什么语句（或过程）或选项？2．DATA步中的INPUT语句有哪四种输入格式？3．请回答FILE和INFILE语句的作用。

3．三、编程或写出程序的运行结果（共60分）1．(10分)试用DATA步编辑一SAS数据集mydir.hw。

数据库mydir对应的路径是“c:\”。

要求按照下面的结果输出。

说明该数据集中有4个变量名分别为SEX、JOBCODE、FLIGHTS和DATE，其中SEX和JOBCODE是字符型变量，DATE 为日期型变量。

THIS IS A SAS_DATASET ABOUT FLIGHTSSEX JOBCODE FLIGHTS 日期F FA3 32886 01MAR99M FA2 28572 01MAR99F FA3 33104 02MAR99M FA3 32217 01MAR99F FA3 33419 04MAR99F FA2 28888 05MAR99F FA2 27787 08MAR99F FA1 23177 09MAR99F FA1 22454 03MAR99M FA1 22268 06MAR99M FA2 27808 07MAR99M FA2 27265 04MAR992.(续第1题，按要求写出过程)(15分)试用SET语句调用第１题的数据集mydir.hw 。

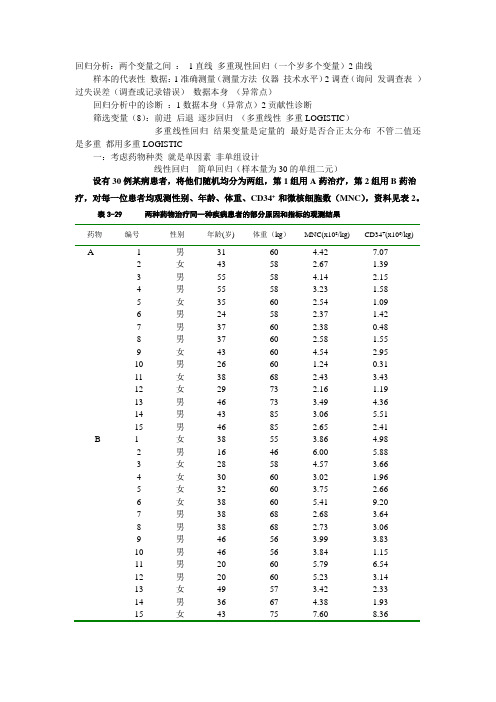
回归分析：两个变量之间：1直线多重现性回归（一个岁多个变量）2曲线样本的代表性数据：1准确测量（测量方法仪器技术水平）2调查（询问发调查表）过失误差（调查或记录错误）数据本身（异常点）回归分析中的诊断：1数据本身（异常点）2贡献性诊断筛选变量（8）：前进后退逐步回归（多重线性多重LOGISTIC）多重线性回归结果变量是定量的最好是否合正太分布不管二值还是多重都用多重LOGISTIC一：考虑药物种类就是单因素非单组设计线性回归简单回归（样本量为30的单组二元）设有30例某病患者，将他们随机均分为两组，第1组用A药治疗，第2组用B药治疗，对每一位患者均观测性别、年龄、体重、CD34+ 和微核细胞数（MNC），资料见表2。

表3-29 两种药物治疗同一种疾病患者的部分原因和指标的观测结果药物编号性别年龄(岁) 体重（kg）MNC(x108/kg) CD34+(x106/kg)A 1 男31 60 4.42 7.072 女43 58 2.67 1.393 男55 58 4.14 2.154 男55 58 3.23 1.585 女35 60 2.54 1.096 男24 58 2.37 1.427 男37 60 2.38 0.488 男37 60 2.58 1.559 女43 60 4.54 2.9510 男26 60 1.24 0.3111 女38 68 2.43 3.4312 女29 73 2.16 1.1913 男46 73 3.49 4.3614 男43 85 3.06 5.5115 男46 85 2.65 2.41B 1 女38 55 3.86 4.982 男16 46 6.00 5.883 女28 58 4.57 3.664 女30 60 3.02 1.965 女32 60 3.75 2.666 女38 60 5.41 9.207 男38 68 2.68 3.648 男38 68 2.73 3.069 男46 56 3.99 3.8310 男46 56 3.84 1.1511 男20 60 5.79 6.5412 男20 60 5.23 3.1413 女49 57 3.42 2.3314 男36 67 4.38 1.9315 女43 75 7.60 8.36请按要求实现如下的统计分析，并给出统计和专业结论。

习 题1、 下表为100头某品种猪的血红蛋白含量〔单位：g/100ml 〕资料，试将其整理成次数分布表，并绘制直方图和折线图。

13.4 13.8 14.4 14.7 14.8 14.4 13.9 13.0 13.0 12.8 12.5 12.3 12.1 11.8 11.0 10.1 11.1 10.1 11.6 12.0 12.0 12.7 12.6 13.4 13.5 13.5 14.0 15.0 15.1 14.1 13.5 13.5 13.2 12.7 12.8 16.3 12.1 11.7 11.2 10.5 10.5 11.3 11.8 12.2 12.4 12.8 12.8 13.3 13.6 14.1 14.5 15.2 15.3 14.6 14.2 13.7 13.4 12.9 12.9 12.4 12.3 11.9 11.1 10.7 10.8 11.4 11.5 12.2 12.1 12.8 9.5 12.3 12.5 12.7 13.0 13.1 13.9 14.2 14.9 12.4 13.1 12.5 12.7 12.0 12.4 11.6 11.5 10.9 11.1 11.6 12.6 13.2 13.8 14.1 14.7 15.6 15.7 14.7 14.0 13.9(提示：第一组下限取为9.1，组距i ＝0.7)2、 测得某肉品的化学成分的百分比方下〔单位：%〕，请绘制成圆图。

水 分 蛋白质 脂 肪 无机盐 其 它 62.0 15.317.21.83.73、 2001年调查四川省5个县奶牛的增长状况〔及2000年相比〕得如下资料〔单位：%〕，请绘成长条图。

双流县 名山县 宣汉县 青川县 泸定县 增长率〔%〕 22.613.818.231.39.54、 1-9周龄大型肉鸭杂交组合GW 和GY 的料肉比方下表所示，请绘制成线图。

周龄 1 2 3 4 5 6 7 8 9 GW 1.42 1.56 1.66 1.84 2.13 2.48 2.83 3.11 3.48 GY 1.471.711.801.972.312.913.023.293.57习 题1、随机抽测了10只兔的直肠温度，其数据为：38.7、39.0、38.9、39.6、39.1、39.8、38.5、39.7、39.2、38.4〔℃〕，确定该品种兔直肠温度的总体平均数0μ=39.5〔℃〕，试检验该样本平均温度及0μ是否存在显著差异？〔=t2.641 0.01<P <0.05〕2、11只60日龄的雄鼠在x 射线照射前后之体重数据见下表〔单位：g 〕：检验雄鼠在照射x 射线前后体重差异是否显著？〔=t 4.132 P <0.01〕3、某猪场从10窝大白猪的仔猪中，每窝抽出性别一样、体重接近的仔猪2头，将每窝两头仔猪随机地支配到两个饲料组，进展饲料比照试验，试验时间30天，增重结果见下表。

重庆医科大学--卫生统计学统计软件包SAS上机练习题（一）1、SAS常用的窗口有哪三个？请在三个基本窗口之间切换并记住这些命令或功能键。

2、请在PGM窗口中输入如下几行程序，提交系统执行，并查看OUTPUT窗和LOG窗中内容，注意不同颜色的含义；并根据日志窗中的信息修改完善程序。

3、将第2题的程序、结果及日志保存到磁盘。

4、试根据如下例1的程序完成后面的问题：表1 某班16名学生3门功课成绩表如下问题：1）建立数据集；2）打印至少有1门功课不及格同学的信息；(提示，使用if语句)参考程序：data a;input id sh wl bl;cards;083 68 71 65084 74 61 68085 73 75 46086 79 80 79087 75 71 68084 85 85 87085 78 79 75086 80 76 79087 85 80 82088 77 71 75089 67 73 71080 75 81 70118 70 54 75083 70 66 84084 62 73 65099 82 70 79;run;data b;set a;if sh<60 or wl<60 or bl<60then output;run;proc print data=b;var id sh wl bl;run;5、根据下列数据建立数据集表2 销售数据开始时间终止时间费用2005/04/28 25MAY2009 $123,345,0002005 09 18 05OCT2009 $33,234,5002007/08/12 22SEP2009 $345,60020040508 30JUN2009 $432,334,500提示：(格式化输入；数据之间以空格分隔，数据对齐；注意格式后面的长度应以前一个位置结束开始计算，如果读入错误，可试着调整格式的宽度；显示日期需要使用输出格式)开始时间，输入格式yymmdd10.终止时间，输入格式date10.费用，输入格式dollar12.参考程序：data a;input x1 yymmdd10. x2 date10. x3 dollar13.;cards;2005/04/28 25MAY2009 $123,345,0002005 09 18 05OCT2009 $33,234,5002007/08/12 22SEP2009 $345,60020040508 30JUN2009 $432,334,500;run;proc print;run;proc print;format x1 yymmdd10. x2 date9. x3 dollar13.;run;6、手机号码一编码规则一般是：YYY-XXXX-ZZZZ，其YYY为号段；XXXX一般为所在地区编码；ZZZZ为对应的个人识别编号。

1.SAS系统主要完成以数据为中心的四大功能，其中核心功能为:统计分析功能2.在SAS系统的组成模块中，能进行数据管理和数据加工、处理的模块……BASE模块3.SAS显示管理系统窗口中能够提交当前运行的SAS程序执行过程的窗口为：…………………………………………………………………PGM窗口4.如下一段SAS程序：DATA ;INPUT X @@;CARDS:2 3 4 9 1 ;RUN;模块当运行程序以后SAS系统会产生SAS数据集………………………………………( C )A. DATAB. NULLC. DATA1D.程序错误5．INPUT语句一般用来指定数据的读入方式，可以读取各种类型的数据包括字符型，现有如下的一段程序：DATA ONE;INPUT NAME $ SCORE;CARDS;Wanglin 85Zhang dong-feng 90;那么在第二个观测中读取到的NAME 为……………………………………………(B)A. Zhang dong-fengB. ZhangC. Zhang doD. Zhang dong6.假设变量X的值为5，有如下程序IF X<5 THENX=X+3;ELSEX=X-2;则执行程序以后变量X的值为………………………………………………………( B)A. 5B.3C.8D. 程序错误7．DATA TEST;DO I=1 TO 3;PUT I= ;END;RUN;程序结果在LOG窗口输出形式为……………………………………………………( A )A. I=1 I=2 I=3B.I=2 I=3 I=4C. 不显示D. I=3 I=2 I=18.假设变量X1=-10.253 X2=-5 则[SIGN(X1)+ABS(X2)]/INT(X1)的运算结果为………………………………………( B)A.-4B.-0.4C. 4D.0.5759.逻辑运算[(5<1)|(4<>2)]&(7>2)的结果为：……………………………………( 1 )10．以下几个统计量在UNIVARIATE过程中能求得到得而在MEANS过程中无法求得的是………………………………………………………………………………………( B )A. meanB. varC. Q1D.range11.SAS系统主要完成以数据为中心的四大功能，其中能够将Excel、Lotus、DBF、TXT等数据转化成SAS 数据集属于…………………………… (数据管理功能 )12. SAS数据集是关系型结构，分成两部分：描述部分和。

实验内容1试用产生标准正态分布的随机数normal(seed)产生参数为10的卡方分布随机数100个。

2根据数据集：（1）创建一个仅包含地区、销售的产品类型、销售数量和销售额的数据集。

（2）分别创建一个仅包含产品类型a100和产品类型a200和SAS数据集。

（3）选择一个人口在50000以上的部分子集。

3 以下数据来自7位同学的高考语文、数学和英语成绩，试用编程的方法计算出平均成绩在75以上的男同学的人数。

实验步骤：实验1：data a (drop=i) ;do i=1to100by1;z=normal(0)**2+normal(0)**2+normal(0)**2+normal(0)**2+normal(0)**2+no rmal(0)**2+normal(0)**2+normal(0)**2+normal(0)**2+normal(0)**2; output;end;结果如下：实验2：（1）data biao1;input region$ product$ quantity price; cards;es a100 150 3750so a100 410 10250es a100 350 8750so a100 710 17750es a100 750 18750so a100 760 19000es a100 150 3000so a100 410 8200es a100 350 7000so a100 710 14200es a100 750 15000so a100 760 152000es a200 165 4125so a200 425 10425es a200 365 9125ne a100 200 5000we a100 180 4500ne a100 600 15000we a100 780 19500ne a100 800 20000we a100 880 22000ne a100 200 4000we a100 180 3600ne a100 600 12000we a100 780 15600ne a100 800 16000we a100 880 17600ne a200 215 5375we a200 195 4875ne a200 615 15375;实验结果：（2）data biao2;input region$ citisize$ pop product$ saketype$ quantity price; cards;es s 25000 a100 r 150 3750so s 48000 a100 r 410 10250es m 125000 a100 r 350 8750so m 348000 a100 r 710 17750es l 62500 a100 r 750 18750so l 748000 a100 r 760 19000es s 25000 a100 s 150 3000so s 48000 a100 w 410 8200es m 125000 a100 w 350 7000so m 348000 a100 w 710 14200es l 62500 a100 w 750 15000so l 748000 a100 w 760 15200ne s 37000 a100 r 200 5000we s 32000 a100 r 180 4500ne m 237000 a100 r 600 15000we m 432000 a100 r 780 19500ne l 837000 a100 r 800 20000we l 93200 a100 r 880 22000ne s 37000 a100 w 200 4000we s 32000 a100 w 180 3600ne m 237000 a100 w 600 12000we m 432000 a100 w 780 15600ne l 837000 a100 w 800 16000we l 932000 a100 w 880 17600;data biao3;input region$ citisize$ pop product$ saketype$ quantity price; cards;es s 25000 a200 r 165 4125so s 48000 a200 r 425 10425es m 125000 a200 r 365 9125ne s 37000 a200 r 215 5375we s 32000 a200 r 195 4875ne m 237000 a200 r 615 15375;run;（3）data biao4;input region$ citisize$ pop product$ saketype$ quantity price; if pop <= 50000then delete;cards;es s 25000 a100 r 150 3750so s 48000 a100 r 410 10250es m 125000 a100 r 350 8750so m 348000 a100 r 710 17750es l 62500 a100 r 750 18750so l 748000 a100 r 760 19000es s 25000 a100 s 150 3000so s 48000 a100 w 410 8200es m 125000 a100 w 350 7000so m 348000 a100 w 710 14200es l 62500 a100 w 750 15000so l 748000 a100 w 760 15200es s 25000 a200 r 165 4125so s 48000 a200 r 425 10425es m 125000 a200 r 365 9125ne s 37000 a100 r 200 5000we s 32000 a100 r 180 4500ne m 237000 a100 r 600 15000we m 432000 a100 r 780 19500ne l 837000 a100 r 800 20000we l 93200 a100 r 880 22000ne s 37000 a100 w 200 4000we s 32000 a100 w 180 3600ne m 237000 a100 w 600 12000we m 432000 a100 w 780 15600ne l 837000 a100 w 800 16000we l 932000 a100 w 880 17600ne s 37000 a200 r 215 5375we s 32000 a200 r 195 4875ne m 237000 a200 r 615 15375；run;实验结果：实验3：data biao5;input sex$ yuwen shuxue yingyu @@;ave=sum(yuwen+shuxue+yingyu)/3;if ave>75 & sex='m'then n+1;else delete;cards;m 82 78 69 f 90 78 89 m 79 86 98 m 76 56 80 f 72 76 81 f 69 78 91 m 92 71 85;实验结果：。

6$6Ϟ 㒗д乬˄Ѡ˅㄀1乬data a;input x@@;cards;142.3 148.8 142.7 144.4 144.7 145.1 143.3 154.2 152.3 142.7 156.6 137.9 143.9 141.2 139.3 145.8 142.2 137.9 141.2 150.6 142.7 151.3 142.4 141.5 141.9 147.9 125.8 139.9 148.9 154.9 145.7 140.8 139.6 148.8 147.8 146.7 132.7 149.7 154.0 158.2 138.2 149.8 151.1 140.1 140.5 143.4 152.9 147.5 147.7 162.6 141.6 143.6 144.0 150.6 138.9 150.8 147.9 136.9 146.5 130.6 142.5 149.0 145.4 139.5 148.9 144.5 141.8 148.1 145.4 134.6 130.5 145.2 146.2 146.4 142.4 137.1 141.4 144.0 129.4 142.8 132.1 141.8 143.3 143.8 134.7 147.1 140.9 137.4 142.5 146.6 135.5 146.8 156.3 150.0 147.3 142.9 141.4 134.7 138.5 146.6 134.5 135.1 141.9 142.1 138.1 134.9 146.7 138.5 139.6 139.2 148.8 150.3 140.7 143.5 140.2 143.6 138.7 138.9 143.5 139.9 134.4 133.1 145.9 139.2 137.4 142.3 160.9 137.7 142.9 126.8;proc means data=a n mean median clm qrange std cv stderr maxdec=2;var x;proc univariate data=a normal;histogram x;var x;run;Џ㽕㒧The MEANS ProcedureAnalysis Variable : xN Mean Median Lower 95%CL for MeanUpper 95%CL for MeanQuartileRangeStdDevCoeff ofVariationStdError՟ Ёԡ 95%䯈ϟ䰤95%䯈Ϟ䰤ԡ 䯈䎱㋏ 䇃130 143.22142.75142.10144.337.80 6.43 4.490.56乥⿄㄀2乬data a2;do grp='⬆㒘','Э㒘';input id before after @@;cha=before-after;output;end;cards;1 6.11 6.00 1 6.90 6.932 6.81 6.83 2 6.40 6.353 6.48 4.49 3 6.48 6.414 7.59 7.28 4 7.00 7.105 6.42 6.30 5 6.53 6.416 6.94 6.64 6 6.70 6.687 9.17 8.42 7 9.10 9.058 7.33 7.00 8 7.31 6.839 6.94 6.58 9 6.96 6.9110 7.67 7.22 10 6.81 6.7311 8.15 6.57 11 8.16 7.6512 6.60 6.17 12 6.98 6.52;/* 䗄 㒳䅵*/proc means n mean std maxdec=2;class grp;var before after cha;run;proc ttest data=a2; /*ϸ㒘 䆩㗙䆩偠 㸔⏙㚚 䝛∈ Ⳍㄝ*/class grp;var before;proc ttest data=a2; /*⬆㒘䰡㚚 䝛 */paired before*after;where grp='⬆㒘'; /* ⬆㒘ⱘ ˈⳌ ѢDataℹЁⱘif䇁 */ run;proc ttest data=a2; /*Э㒘䰡㚚 䝛 */paired before*after;where grp='Э㒘';run;proc ttest data=a2; /*ϸ⾡䰡㚚 䝛 ⱘ Ⳍ ˈ⫼ */ class grp;var cha;run;Џ㽕㒧䗄 㒧grp N Obs V ariableN Mean Std Dev⬆㒘12 b efore after cha1212127.186.630.560.860.930.61 Э㒘12 b efore after cha1212127.116.960.150.780.750.21ϸ㒘 䆩㗙䆩偠 㸔⏙㚚 䝛∈ ⳌㄝT-TestsVariable Method Variances DF t ValuePr > |t|before PooledEqual220.220.8288beforeSatterthwaite Unequal21.80.220.8288唤 Ẕ偠Equality of VariancesVariable Method Num DFDen DFF ValuePr > F beforeFolded F11111.210.7525Equality of VariancesVariable Method Num DFDen DFF ValuePr > F chaFolded F11118.410.0014㄀3乬data a3;input x@@;if _n_<=11then grp='0 ';else if _n_<=20then grp='1 ';else grp='2 ';cards;8.0 9.0 5.8 6.3 5.4 8.5 5.6 5.4 5.5 7.2 5.6 8.5 4.3 11.0 9.0 6.7 9.0 10.5 7.7 7.711.3 7.0 9.5 8.5 9.6 10.8 9.0 12.6 13.9 6.5;/* 䗄 㒳䅵*/proc means n mean median std p25p75maxdec=2;class grp;var x;run;/*⾽ Ẕ偠ˈHẔ偠*/proc npar1way wilcoxon;class grp;var x;run;Kruskal-Wallis TestChi-Square 11.0991DF 2Pr > Chi-Square 0.0039㸼;; ⮒⮙ϡ 㸔⏙䪰㪱㲟ⱑ 䞣˄­mol/L˅՟ Ёԡ P25-p750 11 6.57 5.80 1.36 5.5-8.91 9 8.27 8.50 2.01 7.7-9.02 10 9.87 9.55 2.33 8.5-11.3Kruskal-Wallis Test˖H=11.0991ˈP=0.0039ㅔ㽕䇈䆹⮒⮙ ǃ ǃ 㸔⏙䪰㪱㲟ⱑ 䞣 ˄Ёԡ ˅ Ў˖ ˄ ˅ǃ ˄ ˅ǃ ˄ ˅ˈϡ ⏙䪰㪱㲟ⱑ 䞣ϡ ˄+ ˈ3 ˅ˈ 䞣䕗Ԣˈ 䞣䕗催DŽproc format ;value sexf 1='⬋'2=' ';value $ques1f 'A'=' ''B'='ϡ ''C'=' ';run ;data a;input id $ sex height weight money ques1$ ques2$;/*䅵ㅫBMI*/bmi=weight/((height/100)**2);/* ↡䕀 ↡*/ques1=upcase(ques1);/* A ǃB ǃC 䕀 ㄝ㑻 䞣ˈ ϔϾ 䞣Ёq Ё*/if ques1='A'then q=1;if ques1='B'then q=2;if ques1='C'then q=3;/* BMI ㄝ㑻 ˈ㒧 ϔϾ 䞣bmigrp Ё*/if bmi<18then bmigrp=" ⯺";else if bmi<25then bmigrp="ℷ ";else if bmi=<30then bmigrp="䍙䞡";else if bmi=<35then bmigrp="䕏 㙹㚪";else if bmi=<40then bmigrp="Ё 㙹㚪";else if bmi>40then bmigrp="䞡 㙹㚪";cards ;cnw1l01 1 179 70 5.7 a ABD EF cnw1l02 1 175 70 7.5 a ABE cnw1l03 2 157 47 4.5 a ABE cnw1l04 2 163 48 5 c AB DF cnw1l05 2 161 52 5 b ABF …………………………………………w7l03 1 175 66 10 A ABC EF cnw7l04 2 163 51 8 B AB D cnw7l05 2 165 57 4.9 A ABD cnw8l01 1 160 60 10 B ABE cnw8l02 2 154 50 4.3 A BE cnw8l03 2 160 60 7 A AB DEF ;run ;/*䅵ㅫ乥 ⱒ ↨*/proc freq data =a;tables sex ques1 bmigrp;format sex sexf. ques1 $ques1f.;run ;/*䅵ㅫϡ 㑻ⱘ ˄乥 ↨˅*/ proc freq data=a;tables sex*ques1;format sex sexf. ques1 $ques1f.;run;/* 䖯㸠⾽ Ẕ偠*/proc npar1way wilcoxon data =a;class sex;var q;format sex sexf.;run;/* 䗄⬋ ⫳ⱘBMI */proc means n mean std median p25p75maxdec=2;class sex;var bmi;format sex sexf.;run;/*↨䕗⬋ ⫳BMIⱘ */proc ttest;class sex;var bmi;format sex sexf.;run;Џ㽕㒧sex Frequency Percent CumulativeFrequencyCumulativePercent⬋ 5541.045541.047958.96134100.00Ϟ㸼 ⧚ 㒳䅵㸼( 乬⬹)՟ ⱒ ↨˄%˅⬋ 55 41.0479 58.96䅵 134 100.00ques1Frequency Percent CumulativeFrequencyCumulativePercent3425.373425.37ϡ 6145.529570.903929.10134100.00Ϟ㸼 ⧚ 㒳䅵㸼( 乬⬹)՟ ⱒ ↨˄%˅34 25.37ϡ 61 45.5239 29.10䅵 134 100.00bmigrp Frequency Percent CumulativeFrequencyCumulativePercent䍙䞡 10.7510.75⯺ 1511.191611.94ℷ 11888.06134100.00Ϟ㸼 ⧚ 㒳䅵㸼( 乬⬹)՟ ⱒ ↨˄%˅䍙䞡 1 0.75⯺ 15 11.19ℷ 118 88.06䅵 134 100.00FrequencyPercent Row Pct Col PctTable of sex by ques1ques1sex ϡ Total ⬋1611.9429.0947.062518.6645.4540.981410.4525.4535.905541.041813.4322.7852.943626.8745.5759.022518.6631.6564.107958.96Total3425.376145.523929.10134100.00⾽ Ẕ偠㒧Wilcoxon Scores (Rank Sums) for Variable qClassified by Variable sexsex N Sum ofScoresExpectedUnder H0Std DevUnder H0MeanScore⬋ 553515.03712.50205.59375063.909091795530.05332.50205.59375070.000000Wilcoxon Two-Sample TestStatistic 3515.0000Normal ApproximationZ -0.9582One-Sided Pr < Z 0.1690Two-Sided Pr > |Z| 0.3380t ApproximationOne-Sided Pr < Z 0.1699Two-Sided Pr > |Z| 0.3397Ϟ䴶ϝϾ㸼 ⧚ 㒳䅵㸼( 乬⬹)⚭ (%)ϡ (%) (%)刧⬋16(29.09) 25(45.45) 14(25.45) 5518(22.78) 36(45.57) 25(31.65) 79䅵34(25.37) 61(45.52) 39(29.10) 134Wilcoxon⾽ Ẕ偠: Z=0.9582ˈP=0.3380ㅔ㽕䇈 ˖29.09%ⱘ⬋⫳㸼⼎ д㣅䇁ⱘ⿃ Ӯ ˈ45.45%ⱘ㸼⼎ϡ ˈ25.45%ⱘ 㸼⼎⿃ Ӯ ˗㗠 ⫳ Ў˖ ˄22.78%˅ǃϡ ˄45.57%˅ǃ ˄31.65%˅DŽ⬋ ⫳ 㑻 䴽 д㣅䇁ⱘ⿃ ≵ ϡ ˄Z=0.9582ˈP=0.3380˅DŽ⬋ ⫳BMI↨䕗Analysis Variable : bmisex N Obs N Mean Std Dev Median25th Pctl75th Pctl⬋ 5555 21.01 2.0020.9619.8122.497979 19.77 1.5019.5618.8221.05 tẔ偠㒧T-TestsVariable Method Variances DF t Value Pr > |t|bmi Pooled Equal 132 4.09 <.0001bmi Satterthwaite Unequal 94.3 3.89 0.0002 唤 Ẕ偠Equality of VariancesVariable Method Num DF Den DF F Value Pr > Fbmi Folded F 5478 1.790.0186Ϟ䴶ϝϾ㸼 ⧚ 㒳䅵㸼( 乬⬹)Ёԡ P25-P75⯶⬋ 55 21.01 2.00 20.96 19.81-22.4979 19.77 1.50 19.56 18.82-21.05Satterthwaite t’Ẕ偠˖t’=3.89ˈP=0.0002ㅔ㽕䇈 ˖䇗 ⬋⫳55ҎˈBMI Ў21.01ˈЁԡ 20.96ˈ 2.00ˈ50%ⱘҎBMI䲚Ё 19.81-22.49П䯈˗䇗 ⫳79ҎˈBMI Ў19.77ˈЁԡ 19.57ˈ 1.50ˈ50%ⱘ ⫳BMI䲚Ё 18.82-21.05П䯈DŽ⬋ ⫳BMI ϡ ˈ⬋⫳BMI催Ѣ ⫳˄t’=3.89ˈP=0.0002˅DŽP132˖˄tẔ偠˅㄀2data a;input id control treat;cards;1 0.3550 0.27552 0.2000 0.25453 0.3130 0.18004 0.3630 0.18005 0.3544 0.31136 0.3450 0.29557 0.3050 0.2870;/* 䗄 㒳䅵*/proc means n mean std maxdec=4;var control treat;run;/*䜡 tẔ偠*/proc ttest;paired control*treat;run;Џ㽕㒧Variable N Mean Std Devcontrol treat 770.31930.25480.05710.0540 T-TestsDifference DF t Value Pr > |t|control - treat 6 2.200.0697⧚ 㒳䅵㸼㒘 ՟✻㒘 7 0.3193 0.0571䆩偠㒘7 0.25480.0540䜡 tẔ偠˖t=2.20ˈP=0.0697ㅔ㽕䇈 ˖㛥㔎⇻῵ 㒘˄䆩偠㒘˅㛥㒘㒛䩭⋉ⱘ 䞣 Ў0.2548ˈ ✻㒘 Ў0.3193ˈ 90%ⱘ ˄D=0.10˅䅸Ў㛥㔎⇻Ӯ䗴 㛥㒘㒛䩭⋉ 䞣䰡Ԣ˄t=2.20ˈP=0.0697˅DŽ(⊼ ˖ℸ㒧䆎 䖒 䗮 ⱘ95%ⱘ (D=0.05))P149㄀1乬data a;input grp$ @@;do i=1to4;input x@@;output;end;cards;0⬆17 16 16 151Э10 11 12 122ϭ11 9 8 9;/* 䗄 㒳䅵*/proc means n mean std maxdec=1;var x;class grp;run;/* */proc glm;class grp;model x=grp;means grp/snk hovtest;/*䗝乍hovtestˈ㽕∖䕧 Levene 唤 Ẕ偠㒧 */run; /* 唤 Ẕ偠Ⳃ 䩜 one-way ANOVA῵ */quit;Џ㽕㒧grp N Obs N Mean Std Dev0⬆ 4416.00.81Э 4411.3 1.02ϭ 449.3 1.3Source DF Type III SS Mean Square F Value Pr > Fgrp 296.1666666748.0833333345.55 <.0001Levene's Test for Homogeneity of x VarianceANOVA of Squared Deviations from Group Means Source DF Sum of Squares Mean Square F Value Pr > Fgrp2 1.01040.50520.540.5990Error98.37500.9306Levene 唤 Ẕ偠˖F=0.54ˈP=0.5990䇈 ϝ㒘䯈 ԧ 唤 DŽϸϸ↨䕗㒧Means with the same letterare not significantly different.SNK Grouping Mean NgrpA 16.000040⬆B 11.250041ЭC 9.250042ϭ⧚ 㒳䅵㸼㒘 ՟⬆ 4 16.0 0.8Э 4 11.3 1.0ϭ 4 9.3 1.3F=45.45ˈP<0.0001˗SNK-qẔ偠˖⬆Эϭϝ㒘ϸϸ↨䕗P<0.05ㅔ㽕䇈 ˖⬆ˈЭˈϭ3⾡ ⧚ 㑶㒚㚲≝䰡⥛ 㒳䅵 Н˄F=45.45ˈP<0.0001˅ˈSNK-q Ẕ偠 ⼎ϸϸП䯈 ϡⳌ ˄P<0.05˅ˈ⬆㒘 催˄16.0 mm/h˅ˈЭ㒘⃵П˄11.3 mm/h˅ˈϭ㒘 Ԣ˄9.3 mm/h˅DŽP149㄀3乬˄ 㒘 ˅data a;input block$ @@;do dose=0.2,0.4,0.8;input x@@;output;end;cards;1⬆ 106 116 1452Э42 68 1153ϭ 70 111 1334ϕ42 63 87;/*䅵ㅫ 䗄 㒳䅵䞣*/proc means n mean std;class dose;var x;run;/* 㒘䆒䅵ⱘ */proc glm;class block dose;model x=block dose;means dose/snk;run;quit;Џ㽕㒧 ˖dose N Obs N Mean Std Dev0.2 4465.030.40.4 4489.527.90.8 44120.025.2㒧Source DF Type III SS Mean Square F Value Pr > Fblock 36457.6666672152.55555623.77 0.0010dose 26074.0000003037.00000033.54 0.0006ϸϸ↨䕗㒧Means with the same letterare not significantly different.SNK Grouping Mean NdoseA 120.00040.8B 89.50040.4C 65.00040.2⧚ 㒳䅵㸼䲠▔㋴ 䞣՟0.2 4 65.0 30.40.4 4 89.5 27.90.8 4 120.0 25.2㒘 ˖F=33.54ˈP=0.0006˗ 䞣䯈ϸϸ↨䕗˖P<0.05ㅔ㽕䇈 ˖ϝ⾡䲠▔㋴ 䞣˄0.2ˈ0.4ˈ0.8˅ϟⱘXXX Ў65.0ǃ89.5ǃ120.0ˈ ℷ 哴 ㋏ⱘ ˄F=23.77ˈP=0.0010˅ ˈϝ⾡䲠▔㋴ϡ 䞣 XXX ˄F=33.54ˈP=0.0006˅ˈSNK-qẔ偠 ⼎ϸϸП䯈 㒳䅵 Н˄P<0.05˅ˈϨ䱣ⴔ 䞣ⱘ ˈ䆹 г DŽP149㄀4乬˄ ϕ 䆒䅵ⱘ ˅data a;do expdate=1to4;do no=1to4;input dose $ x@@;output;end;end;cards;C 32.7 A 11.2 B 23.2D 48.1B 26.2 D 31.8C 28.9 A 18.7A 14.0 C 14.0 D 27.5B 25.6D 33.2 B 16.5 A 21.2 C 40.2;/*䅵ㅫ 䗄 㒳䅵䞣*/proc means n mean std maxdec=1;class dose;var x;run;/* ϕ 䆒䅵ⱘ */proc glm;class expdate no dose;model x=expdate no dose;means dose/snk;run;quit;Џ㽕䕧 㒧dose N Obs N Mean Std DevA 4416.3 4.5B 4422.9 4.4C 4429.011.0D 4435.29.0㒧Source DF Type III SS Mean Square F Value Pr > Fexpdate 3175.142500058.3808333 3.17 0.1064no 3440.1525000146.71750007.98 0.0162dose 3786.5025000262.167500014.25 0.0039ϸϸ↨䕗㒧Means with the same letterare not significantly different.SNK Grouping Mean NdoseA 35.1504DB A 28.9504CB C 22.8754BC 16.2754A⧚ 㒳䅵㸼䞣⯶ ⯶A˖0.32 4 16.34.5B˖0.47 4 22.94.4C˖0.62 4 29.011.0D˖0.77 4 35.29.0˖F=14.25ˈP=0.0039ㅔ㽕䇈 ˖ 䆩偠ⷨお䞛⫼ ∈ ⱘ ϕ 䆒䅵ˈ䆩偠Ё 㗗 њ Ͼ䆩偠 ǃ ⾡㛄 ㋴ 䞣∈ ㄝϝϾ ㋴ˈ ϸϾ ㋴Ў䆩偠 ㋴DŽ㒣㒳䅵 ⼎ˈ њ䆩偠 ǃϡ 㒧 ⱘ ˈϡ 㛄 ㋴ 䞣∈ XXX 㒳䅵 Н˄㾕㸼XXˈF=14.25ˈP=0.0039˅ˈSNK-qẔ偠 䞡↨䕗 ⼎ˈA 䞣㒘˄0.32˅ϢD 䞣㒘˄0.77˅ǃC 䞣㒘˄0.62˅䯈 㒳䅵 Н˄P<0.05˅ˈB 䞣㒘˄0.47˅ϢD 䞣㒘˄0.77˅䯈 㒳䅵 Нˈ 䞣㒘䯈 㒳䅵 НDŽ⾽Ⳍ ˄ㄝ㑻Ⳍ ˅ ⼎ˈ䱣ⴔ㛄 ㋴ 䞣ⱘ ˈXXX ⱘ䍟 ˄s r=0.76ˈP=0.0006˅DŽif dose='A'then dose1=0.32;if dose='B'then dose1=0.47;if dose='C'then dose1=0.62;if dose='D'then dose1=0.77;proc corr spearman;var dose1 x;run;P168˖㄀1乬data a;do row=1to2;do col=1to2;input f@@; output;end;end;cards;25 629 3;proc freq;table row*col/chisq nopercent nocol; weight f;run;Џ㽕㒧 ˖Frequency Row PctTable of row by colcolrow 1 2Total 12580.65619.353122990.6339.3832 Total 54963 Statistics for Table of row by colStatistic DF Value ProbChi-Square 1 1.28070.2578Likelihood Ratio Chi-Square 1 1.30010.2542Continuity Adj. Chi-Square 10.59540.4403Mantel-Haenszel Chi-Square 1 1.26040.2616Phi Coefficient-0.1426 Contingency Coefficient0.1412Cramer's V-0.1426 WARNING: 50% of the cells have expected counts lessthan 5. Chi-Square may not be a valid test.Fisher's Exact TestCell (1,1) Frequency (F) 25Left-sided Pr <= F 0.2209Right-sided Pr >= F 0.9334Table Probability (P) 0.1543Two-sided Pr <= P 0.3020Sample Size = 63ㅔ㽕䇈 ˖⊼ Ϟ䴶ⱘ䄺 ĀWARNING: 50% of the cells have expected counts less than 5. Chi-Square may not be avalid test.āˈ䇈 Ẕ偠ϡ䗖⫼ˈℸ 䞛⫼Fisher㊒⹂Ẕ偠ˈFisher's Exact Test ջẔ偠˖P=0.3020ˈ䇈 䖬≵ 䎇 ⱘ⧚⬅䅸Ў⬆Эϸ⊩ⱘ ⥛ DŽP168˖㄀3乬data a;do row=1to2;do col=1to2;input f@@; output;end;end;cards;23 127 8;proc freq;table row*col/agree; /*䜡 */weight f;run;Џ㽕㒧 ˖McNemar's TestStatistic (S) 1.3158DF 1Pr > S 0.2513䇈 ˖䜡 Ẕ偠ˈ McNemar's Testˈ2F=1.3158ˈP=0.2513ˈ䖬ϡ㛑䅸Ў⬆Эϸ⾡ ⱘ DŽP184˖㄀2乬data a;input id before after;cha=before-after;cards;1 336 2582 371 2913 386 3004 364 2855 377 2986 292 3037 288 3128 304 2609 333 33910 302 290;proc means n mean std median clm maxdec=1; var before after cha;run;proc univariate;var cha;run;Џ㽕㒧 ˖Variable N Mean Std Dev Median Lower 95%CL for MeanUpper 95%CL for Meanbefore after cha101010335.3293.641.737.423.744.5334.5294.561.0308.5276.79.9362.1310.573.5Tests for Location: Mu0=0Test Statistic p ValueStudent's t t 2.966313Pr > |t| 0.0158Sign M 2Pr >= |M| 0.3438Signed Rank S 20.5Pr >= |S| 0.0352⧚ 㒳䅵㸼⒊㜆㜆 ԧ UU) ⱘ㊒ ˄10E9/L˅䞣՟ 95%CIUU 10 335.3 37.4 308.5-362.1UU 10 293.6 23.7 276.7-310.510 41.7 44.5 9.9-73.5䜡 ⾽ Ẕ偠˖S=20.5ˈP=0.0352ㅔ 䇈 ˖ ⒊㜆㜆 ԧ(UU) ⱘ㊒ Ў335.3ˈ Ў293.6ˈ ϟ䰡41.7(95%CI˖9.9-73.5)ˈ ㊒ 䰡Ԣ˄S=20.5ˈP=0.0352˅DŽP184˖㄀6乬data a;do row=0to3;do col=1to4;input f@@; output;end;end;cards;1 4 7 53 6 9 710 6 5 57 2 4 1;proc npar1way wilcoxon;class col;var row;freq f;run;Џ㽕㒧 ˖Wilcoxon Scores (Rank Sums) for Variable rowClassified by Variable colcol N Sum ofScoresExpectedUnder H0Std DevUnder H0MeanScore1 211182.50871.5090.58090056.3095242 18700.00747.0085.89903938.8888893 25912.501037.5095.53653836.5000004 18608.00747.0085.89903933.777778Average scores were used for ties.Kruskal-Wallis TestChi-Square 12.2366DF3Pr > Chi-Square 0.0066Kruskal-Wallis HẔ偠㒧 ˖2F=12.2366ˈP=0.0066ˈ䇈 4⾡⮒⮙ 㗙⯄⎆ 䝌 ㉦㒚㚲ⱘㄝ㑻 ϡ DŽ[ҢϞ䴶㸼Ёⱘ ⾽ ҹⳟ ˈ㄀ϔ⾡⮒⮙ 䝌 ㉦㒚㚲ⱘㄝ㑻Ⳍ Ѣ ϝ⾡ ˄䰇 ⿟ ˅DŽℸ䇈⊩ 㒳䅵 ]⊼ ˖ ⶹ䘧 ѯ⮒⮙П䯈ㄝ㑻 ϡ ˈ䳔㽕 ϸϸ↨䕗DŽ˄ ϸ㒘ⱘ ⾽ Ẕ偠ˈ ℷẔ偠∈ alpha˅。

实用实验1 数据文件建立与管理某航空公司38名职员性别和工资情况的调查数据，如下表所示，试在SPSS中进行如下操作：（1）定义变量，将gender定义为字符型变量，salary定义为数值型变量，在数据窗口录入数据，并保存数据文件，将其命名为“data1_1.sav”。

（2）打开文件data1_1.sav，练习增加一个个案，删除一个个案，增加一个变量、删除一个变量，以及个案和变量的复制、粘贴操作。

（3）将数据文件按性别分组；将数据文件按工资进行组距分组。

（4）查找工资大于40000美元的职工。

（5）按工资进行升序和降序排列，比较升序和降序排列结果有什么不同。

（6）练习数据的分类汇总操作，要求按照性别分类汇总样本的总数。

（7）练习数据选取操作，要求随机选取70%的数据。

（8）当工资大于40000美元时，职工的奖金是工资的20％；当工资小于40000美元时，职工的奖金是工资的10%，假设实际收入＝工资＋奖金，计算所有职工的实际收入，并将结果添加到income变量中。

实验2 数据特征的描述统计分析1.下表是一电脑公司某年连续120天的销售量数据(单位：台)。

试对其进行频数分析，计算均值、中位数、众数、四分位数,标准差、最大值、最小值、全距,偏度、峰度系数；画出直方图、茎叶图、箱线图；解释结果并说明其分布特征。

234 159 187 155 158 172 163 183 182 177 156 165 143 198 141 167 203 194 196 225 177 189 203 165 187 160 214 168 188 173 176 178 184 209 175 210161 152 149 211 206 196 196 234 185 189 196 172 150 161 178 168 171 174 160 153 186 190 172 207 228 162 223 170 208 165 197 179 186 175 213 176 153 163 218 180 192 175 197 144 178 191 201 181 166 196 179 171 210 233 174 179 187 173 202 182 154 164 215 233 168 175 198 188 237 194 205 195 174 226 180 172 211 190 200 172 187 189 188 1952.下表是某班同学月生活费资料，试对其进行描述分析，并对结果作出说明。