100以内的质数表和平方数

精心整理平方数的规律及100以内的整数平方表(1)完全平方数的个位数字只能是0,1,4,5,6,9.(没有2,3,7,8)两个整数的个位数字之和为10，则它们的平方数的个位数字相同.(2)奇数的平方的个位数字是奇数，十位数字是偶数.(3)如果完全平方数的十位数字是奇数,则它的个位数字一定是6；反之，如果完全平方数的个位数字是6，则它的十位数字一定是奇数.(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1.(5)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被5整除的数的平方为5n±1型,能被5整除的数的平方为5n型.,等..a×ab×b2×a×ba×ab×b2×a×b例：132=(10+3)2=102+32+2×10×3=100+9+60=169882=(90-2)2=902+22－2×90×2=8100+4－360=7744用处：①训练计算能力，使计算更快更准确；②估计某数的平方根所处的范围，在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到之间的所有质数是不是n的因子即可，超过的都不必检查了.例如，判定2431是否为质数，因为492=2401<2431<2500=502,所以49<<50,2+4+3+1=10不能被3整除,2341的个位既非0又非5,故只需检查7到47之间的所有质数能否整除2431即可，而53,59,61,67……等更大的质数都不用检查了，实际上2431=1117.③增加对数字的熟悉程度，比如162=256=28，322=1024=210，642=4096=212,另外一些特殊结构的数字应该牢记，如882=7744,112=121,222=484,(121和484从左到右与从右到左看是一样的)122=144,212=441,132=169,312=961,(a左右颠倒后a2也左右颠倒).。

(1)完全平方数的个位数字只能是0,1,4,5,6,9.(没有2,3,7,8)两个整数的个位数字之和为10，则它们的平方数的个位数字相同.(2)奇数的平方的个位数字是奇数，十位数字是偶数.(3)如果完全平方数的十位数字是奇数,则它的个位数字一定是6；反之，如果完全平方数的个位数字是6，则它的十位数字一定是奇数.(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1.(5)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被5整除的数的平方为5n±1型,能被5整除的数的平方为5n型.(8)平方数的形式具有下列形式16n,16n+1,16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4,6,7,9.(没有2,5,8)(10)如果质数p能整除a,但p的平方不能整除a,则a不是完全平方数.(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数.(12)一个正整数n是完全平方数的充分必要条件是n有奇数个因数(包括1和n).一个数如果是另一个整数的完全立方（即一个整数的三次方,或整数乘以它本身乘以它本身）,那么我们就称这个数为完全立方数,也叫做立方数，如0,1,8,27,64,125,216,343,512,729,1000等.如果正整数x,y,z满足不定方程x2+y2=z2 ,就称x,y,z为一组勾股数.x,y必然是一个为奇数另一个为偶数，不可能同时为奇数或同时为偶数.z和z2必定都是奇数.五组常见的勾股数：32+42=52；52+122=132；72+242=252；82+152=172；202+212=2929+16=25；25+144=169；49+576=625；64+225=289；400+441=841记忆技巧：(a+b)2= a2 + b2 + 2ab (a－b)2=a2 + b2 －2ab| | | | | |a×a b×b 2×a×b a×a b×b 2×a×b例：132=(10+3)2=102+32+2×10×3=100+9+60=169882=(90-2)2=902+22－2×90×2=8100+4－360=7744用处：①训练计算能力，使计算更快更准确；②估计某数的平方根所处的范围，在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到√n之间的所有质数是不是n的因子即可，超过√n的都不必检查了.例如，判定2431是否为质数，因为492=2401<2431<2500=502,所以49<√2431<50 ,2+4+3+1=10不能被3整除, 2341的个位既非0又非5,故只需检查7到47之间的所有质数能否整除2431即可，而53,59,61,67……等更大的质数都不用检查了，实际上2431=11×13×17.③增加对数字的熟悉程度，比如162=256=28，322=1024=210，642=4096=212 ,另外一些特殊结构的数字应该牢记，如882=7744,112=121,222=484,(121和484从左到右与从右到左看是一样的)122=144,212=441,132=169,312=961,(a左右颠倒后a2也左右颠倒).。

平方数的规律及100以内的整数平方表规律：(1)完全平方数的个位数字只能是0,1,4,5,6,9.(没有2,3,7,8)两个整数的个位数字之和为10，则它们的平方数的个位数字相同.(2)奇数的平方的个位数字是奇数，十位数字是偶数.(3)如果完全平方数的十位数字是奇数,则它的个位数字一定是6；反之，如果完全平方数的个位数字是6，则它的十位数字一定是奇数.(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1.(5)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被5整除的数的平方为5n±1型,能被5整除的数的平方为5n 型.(8)平方数的形式具有下列形式16n,16n+1,16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4,6,7,9.(没有2,5,8)(10)如果质数p能整除a,但p的平方不能整除a,则a不是完全平方数.(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数.(12)一个正整数n是完全平方数的充分必要条件是n有奇数个因数(包括1和n).一个数如果是另一个整数的完全立方（即一个整数的三次方,或整数乘以它本身乘以它本身）,那么我们就称这个数为完全立方数,也叫做立方数，如0,1,8,27,64,125,216,343,512,729,1000等.如果正整数x,y,z满足不定方程x2+y2=z2 ,就称x,y,z为一组勾股数.x,y必然是一个为奇数另一个为偶数，不可能同时为奇数或同时为偶数.z 和z2必定都是奇数.五组常见的勾股数：32+42=52；52+122=132；72+242=252；82+152=172；202+212=2929+16=25；25+144=169；49+576=625；64+225=289；400+441=841记忆技巧：(a+b)2= a2 + b2 + 2ab (a－b)2=a2 + b2 －2ab| | | | | |a×a b×b 2×a×b a×a b×b 2×a×b 例：132=(10+3)2=102+32+2×10×3=100+9+60=169882=(90-2)2=902+22－2×90×2=8100+4－360=7744 用处：①训练计算能力，使计算更快更准确；②估计某数的平方根所处的范围，在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到之间的所有质数是不是n的因子即可，超过的都不必检查了.例如，判定2431是否为质数，因为492=2401<2431<2500=502,所以49<<50 ,2+4+3+1=10不能被3整除, 2341的个位既非0又非5,故只需检查7到47之间的所有质数能否整除2431即可，而53,59,61,67……等更大的质数都不用检查了，实际上2431=1117.③增加对数字的熟悉程度，比如162=256=28，322=1024=210，642=4096=212 ,另外一些特殊结构的数字应该牢记，如882=7744, 112=121,222=484,(121和484从左到右与从右到左看是一样的)122=144,212=441,132=169,312=961,(a左右颠倒后a2也左右颠倒).1-20的平方数221-40的平方数341-60的平方数461-80的平方数581-100的平方数。

一．质数与合数的概念1．只有1和它本身两个因数的数，称为质数。

2．除了1和它本身，还有其他因数的数，称为合数。

0和1既不是质数，与不是合数。

二．100以内的质数表1~100中的质数是：2，3，5，7，11，13，17，19，23，29，31，37，41，43，47，53，59，61，67，71，73，79，83，89，97。

1~100中有25个质数，74个合数，其中1既不是质数与不是合数。

质数中有且仅有一个偶数，那就是2。

重难点：熟悉100以内的25个质数，并且灵活应用奇偶性，解决偶质数的相关应用。

题模一：100以内质数表例1.1.1只能被1和它本身整除的自然数叫做质数，如：2、3、5、7,等．那么，比40大并且比50小的质数是___________，小于100的最大的质数是___________．【答案】41、43、47；97【解析】本题考查100以内的常见质数．例 1.1.2爸爸和儿子岁数之和是一个两位数，这个两位数是一个质数，且数字之和为13，又已知爸爸比儿子大27岁，则儿子是________岁．【答案】20【解析】13495867=+=+=+，只有67为质数，故年龄和为67．由和差问题易知儿子20岁．例1.1.3五个连续自然数，每个数都是合数且都不超过60，则这五个连续自然数的和最大是（）．A．170B．250C．280D．285【答案】【解析】小于60的质数有59、53、47、43、41、……，所以连续的五个自然数且都是合数，最大的是58、57、56、55、54，它们的和是5455565758280++++=．例1.1.4已知p为50以内的一个两位质数，且21p+也是质数，则满足条件的所有p的和是________．【答案】104【解析】50以内的两位质数是11、13、17、19、23、29、31、37、41、43、47，满足条件的有11、23、29、41，和为11232941104+++=．例1.1.5有一类最简真分数满足以下条件：（1）分子与分母都是两位数的质数；（2）分母正好是分子这个质数逆序排列所成的质数．如1331就是满足上述条件的一个分数．那么满足数论第05讲_100以内的质数这两个条件的最简真分数有__________个，其中最大的一个是__________． 【答案】7997【解析】满足自身与其逆序数均为两位质数的有11；13、31；17、71；37、73；79、97．符合条件的最简真分数有有4个，最大的是7997． 题模二：偶质数性质与基本应用 例 1.2.1Let a 、b are prime numbers and the sum of these primes is 49．Then 11a b+=（ ）． A ．9449 B ．4994 C ．8645 D ．4586【答案】B【解析】根据奇偶性及2是质数中唯一的偶数易知两个质数分别为2和47，114994a b +=． 例1.2.2（1）两个质数的和是1999，那么这两个质数是多少？（2）若两个质数的差是35，那么它们的积是多少？【答案】（1）1997（2）74【解析】（1）通过奇偶分析易知两个质数必为一奇一偶，即一个为2，另一个为199921997-=． （2）通过奇偶分析易知两个质数必为一奇一偶，即一个为2，另一个为35237+=，它们的积是23774⨯=．例1.2.3三个互不相同的质数相加，和为52，这三个质数可能是多少？【答案】可能为（2，3,47）（2,43,7）（2,37,13）（2,31,19）【解析】小于50的质数有2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、发现只有一 个偶数2，所以一定包含2，另外两个为奇数，且和为50,5047350437=+=+、503713503119=+=+、．例1.2.4若两个不同的质数m 、n 满足2319m n +=，那么m n +=__________．【答案】7或8【解析】满足条件的有2m =，5n =或5m =，3n =，所以78m n +=或．例1.2.5若三个不同的质数的和是53，则这样的三个质数有__________组．【答案】11【解析】三个不同的质数的和是53，所以三个质数都必须是奇数．从最小的奇质数枚举如下：53374331337319315741511375172951929=++=++=++=++=++=++=++71729111329111923131723=++=++=++=++．共11组．例1.2.6三个数 p ， p + 3 ， p + 5 都是质数，它们的倒数之和是 ____ ． 【答案】5970【解析】可知p 一定是2，11159=25770++． 例1.2.7有6个数字a 、b 、c 、d 、p 、q ，满足abc bcd p q pq -=⨯⨯，c 和d 的奇偶性相同，且p 、q 、pq 都是质数，则abcd 最大是多少？【答案】9846【解析】c 和d 的奇偶性相同，故p q pq abc bcd ⨯⨯=-为偶数，p 、q 、pq 中必有偶数，只能是2p =，进而易得3q =，2323138abc bcd -=⨯⨯=．将问题转化为竖式，易知abcd最大是9846．例 1.2.8已知p 、q 为质数，并且存在两个正整数m 、n ，使得p m n =+，q mn =，则p qn m p q m n+=+_________． 【答案】313【解析】因为q mn =且q 为质数，所以m n 、中有一个为1．不妨设1m =，则q n =，1p m n q =+=+．又因为p 、q 为质数，故3,2,2p q n ===．代入得原式值为313． 题模三：质数与合数的应用提高例 1.3.1在1到100这100个正整数中，不能被2、3、5、7中任何一个数整除的数有__________个．【答案】22【解析】数论问题，不能被这些数整除的一定都是质数，1-100的质数去掉1、2、3、5、7还有22个．例1.3.2将正整数1，2，3，4，5，6，…，10000排成一行．若一个数不能表示成两个合数的和，则将此数划去．例如要划去1，但是因为844=+，8就不能划去．根据上面规定划掉所有能划掉的数之后，将剩下的数由小到大排列．这时从左数第2013个数是_______．【答案】2022【解析】从8开始往后的偶数可以拆成两个偶合数的和；从13开始的奇数可以拆成9+2n的形式（n 大于等于2），而1、2、3、4、5、6、7、9、11要划去，所以剩下的数列为8、10、12、13、14、15……，第2013项即为2022．例1.3.3小红、小明二人在讨论年龄，小红说：“我比你小，当你像我这么大时，我的年龄是个质数．”小明说：“当你长到我这么大时，我的年龄也是个质数．”小红说：“我发现现在咱俩的年龄和是个质数的平方．”那么小明今年____________岁．（小明今年年龄小于31岁，且年龄均为整数岁）【答案】16【解析】设小红x 岁，年龄差y ，则小明x y +岁．由题意知x y -为质数①，2x y +为质数②，2x y +为质数③的平方即年龄和，年龄和可能为4，9，25，49．经验证，年龄差为7，小红今年9岁，小明今年16岁．例1.3.4四个小三角形的顶点处有六个圆圈，如果在这些圆圈中分别填上六个质数，它们的和是20，而且每个小三角形顶点上的数之和相等．问这六个质数的积是多少？【答案】900【解析】设每个小三角形顶点上的数之和为x ，当计算题4个小三角形顶点上的数之和时，中间三个圆圈算了三次，减去两次后得到六个质数之和20，4220,10x x x -==，三个质数和为10，则这三个质数为2、3、5.六个圆圈分别填两个2、3、5.它们的积为900．随练1.1最小的质数是________，最小的自然数是________．【答案】2；0【解析】最小的质数是2，最小的自然数是0．随练1.2在31、37、51、57、71、77、91、97这8个数中，有几个合数？A．2个B．3个C．4个D．5个【答案】C【解析】在这8个数中，31、37、71、97是质数，51、57、77、91是合数，即一共有4个合数．正确答案是C．随练1.3三个连续自然数，每个数都是合数，则这三个连续自然数的和最小是（）．A．6B．27C．45D．720【答案】B【解析】列举可知，最小的三个数为8、9、10，所以这三个连续自然数的和最小是++=．891027随练1.4在20以内的质数中，加上2以后结果还是质数的，一共有（）个．A．8B．6C．4D．2【答案】C【解析】3、5、11、17符合要求，共4个．随练1.5两个质数的和是45，这两个质数的积是_______．【答案】86【解析】两质数必为一奇一偶，故一定有2，另一个为45243-=，两数之积为86．随练1.6从20以内的质数中选出6个，写在一个正方体的六个面上，使得两个向对面的和都相等，所选的6个数是________．【答案】5、7、11、13、17、19【解析】首先2不能入选，否则会出现有的和为奇数，有的和为偶数的情况，那么还剩下3、5、7、11、13、17、19这7个数，从中选择6个相当于剔除一个，由于这7个数的和为75，是3 的倍数，而选出的6个数的和也是3的倍数，所以被剔除的那个数应该也是3的倍数，只能是3，所以选出的6个数分别是5、7、11、13、17、19．随练1.7三个互不相同的质数相加，和为30，这三个质数的乘积最大是__________．【答案】374【解析】三个数的和是偶数，可以是三个偶数，或者一偶两奇．考虑质数中只有2是偶数，可知一定是一偶两奇，且偶数是2．另外两个奇数是5和23或11和17．所以这三个质数的乘积是2523230⨯⨯=，乘积最大是374．⨯⨯=或21117374随练 1.8一个两位质数的两个数字交换位置后，仍然是一个质数，请写出所有这样的质数．【答案】11、13、17、31、37、71、73、79、97【解析】列出备选的两位质数，十位数字是2、4、5、6、8的就不用罗列了．、、、、、、、、、．11131719313771737997观察这些数，只有19颠倒过来后是合数：91713=⨯，排除19，剩下的质数、、、、、、、、都满足要求．111317313771737997作业11~100这100个自然数中质数有25个，合数有________个．【答案】74【解析】1~100中，25个质数之外的75个数中，只有1不是合数，其他的都是．所以有74个合数．作业2a是100以内最大的质数，b是100以内最小的质数，那么a b+=__________．【答案】99【解析】97a =，2b =，所以99a b +=．作业3五个连续的自然数，每个数都是合数，这五个连续自然数的和最小是__________．【答案】130【解析】最小的连续五个合数是24、25、26、27、28，所以这五个连续自然数的和最小是130．作业4在横线上填入三个不同的质数，使等式成立________+________+________＝60，则共有________种不同的填法．【答案】3【解析】由奇偶性分析易知这三个质数必为2奇1偶，即必有2，只需将58表示为2个质数之和即可．5855311471741=+=+=+，共3种填法．作业5有一个质数是两位数，这两位上的数字相差6，则这个两位数的质数是．【答案】17或71【解析】各位必为偶数．分别试验1、7和3、9，17或71满足要求．作业6两个质数的和是19，则这两个质数的积是______．【答案】34【解析】由奇偶性可知必有2，另一个为19217-=，两数乘积为34．作业7当p 和3p +5都是质数时，55p +=_______．【答案】37【解析】当p 和3p +5奇偶性不同，而且都为质数，那么较小的数必须为2，所以55p +=37．作业8已知正整数p 、q 都是质数，并且7p q +与11pq +也都是质数，求p 、q 的值．【答案】23p q =⎧⎨=⎩或32p q =⎧⎨=⎩ 【解析】若p 、q 均为奇数则7p q +为大于2的偶数，与其为质数矛盾，故p 、q 必有偶数，即为2．当2p =时，q 、14q +、211q +均为质数，且讨论得此三数被3除的余数各不相同，因此q 只能为3，此时另两个均为17，满足条件；当2q =时，p 、72p +、211p +均为质数，同理可得p 也只能为3，此时另两个数分别为23和17，满足要求．综上，23p q =⎧⎨=⎩或32p q =⎧⎨=⎩． 作业9张中中小朋友手中有四张卡片，分别写有1、2、3、4；张右右小朋友手中也有四张卡片，分别写着5、6、7、9，两位小朋友将卡片放在一起适当组合恰好形成四个不同的两位质数（卡片不重复使用，也不得有剩余），请将四个质数的和求出．答：_________【答案】190【解析】2只能和9配，为29．4只能和7配，为47．进而另两个为61、53，总和为190． 作业10（1）两个质数的和是39，这两个质数的差是多少？（2）三个互不相同的质数相加，和为40，这三个质数分别是多少？【答案】（1）35（2）2、7、31【解析】（1）39=+奇数偶数．偶质数是2，所以奇质数是39237-=．这两个质数的差是37235-=（2）40是偶数，如果写成三个数相加的形式则有两种情况，40=++偶数偶数偶数，或偶数奇数奇数，第一种情况显然是不可能的（质数中只有2是偶数）．40=++所以可以确定出三个质数中有一个一定是2，剩下两个奇质数的和是38．通过简单的枚举可得，只有73138+=符合题意．所以这三个质数分别是：2，7，31．n-（n为质数）作业11有一种数，是以法国数学家梅森的名字命名的，它们就是形如21的梅森数，当梅森数是质数时就叫梅森质数，是合数时就叫梅森合数．例如：2213-=就是第一个梅森质数．第一个梅森合数是（）．A．4B．15C．127D．2047【答案】D【解析】可依次写出梅森数：2213-=，第二个梅森质数；-=，第一个梅森质数；32175-=，第四个梅森质数；11212047-=，第一个梅森-=，第三个梅森质数；7211272131合数．所以答案为D．也可以用排除法，梅森数一定为奇数，A选项排除．42115-=，4为合数，所以15不是梅森数，B选项排除．721127-=，127为质数，所以127为梅森质数，C选项排除．检验可知，D选项为梅森合数，所以答案为D．作业12在小于30的质数中，加3以后是4的倍数的是____________．【答案】5，13，17，29【解析】通过枚举法可得，5、13、17、29．作业13已知a,b,c只3个彼此不同的质数，若37+-最大是+⨯=，则a b ca b c___________．【答案】32【解析】223733132=⇒+=⇒=⇒=⇒+-=．c a b b a a b c作业14有些三位数，它的各位数字的乘积是质数，这样的三位数最大的为A，最小的为B．则A B-=__________．【答案】599【解析】由质数定义可知，质数只能写成1乘本身的形式，则说明三位数的三个数位上的数字有2个1，另一个为质数．则这样的三位数最大为711，最小为112，则-=-=．A B711112599作业15从1、2、3、4、5、6、7、8、9中选出8个数排成一个圆圈，使得相邻的两数之和都是质数．排好后可以从任意两个数字之间切开，按顺时针方向读这些八位数，其中可能读的最大的数是________________．【答案】98567432【解析】设首位为9，旁边可为8，下一位最大为5……这样进行下去，最大为98567432．。

知识图谱-100以内的质数100以内质数表偶质数性质与基本应用质数与合数的应用提高数论第02讲_100以内的质数错题回顾100以内的质数知识精讲一．质数与合数的概念1．只有1和它本身两个因数的数，称为质数。

2．除了1和它本身，还有其他因数的数，称为合数。

0和1既不是质数，与不是合数。

二．100以内的质数表1~100中的质数是：2，3，5，7，11，13，17，19，23，29，31，37，41，43，47，53，59，61，67，71，73，79，83，89，97。

1~100中有25个质数，74个合数，其中1既不是质数与不是合数。

质数中有且仅有一个偶数，那就是2。

三点剖析重难点：熟悉100以内的25个质数，并且灵活应用奇偶性，解决偶质数的相关应用。

题模精讲题模一100以内质数表例1.1、只能被1和它本身整除的自然数叫做质数，如：2、3、5、7,等．那么，比40大并且比50小的质数是___________，小于100的最大的质数是___________．答案：41、43、47；97解析：本题考查100以内的常见质数．例1.2、爸爸和儿子岁数之和是一个两位数，这个两位数是一个质数，且数字之和为13，又已知爸爸比儿子大27岁，则儿子是________岁．答案：20解析：，只有67为质数，故年龄和为67．由和差问题易知儿子20岁．例1.3、五个连续自然数，每个数都是合数且都不超过60，则这五个连续自然数的和最大是（）．A、170B、250C、280D、285答案：解析：小于60的质数有59、53、47、43、41、……，所以连续的五个自然数且都是合数，最大的是58、57、56、55、54，它们的和是．例1.4、已知为50以内的一个两位质数，且也是质数，则满足条件的所有的和是________．答案：104解析：50以内的两位质数是11、13、17、19、23、29、31、37、41、43、47，满足条件的有11、23、29、41，和为．例1.5、有一类最简真分数满足以下条件：（1）分子与分母都是两位数的质数；（2）分母正好是分子这个质数逆序排列所成的质数．如就是满足上述条件的一个分数．那么满足这两个条件的最简真分数有__________个，其中最大的一个是__________．答案：解析：满足自身与其逆序数均为两位质数的有11；13、31；17、71；37、73；79、97．符合条件的最简真分数有有4个，最大的是．题模二偶质数性质与基本应用例2.1、Let a、b are prime numbers and the sum of these primes is 49．Then （）．A、B、C、D、答案：B解析：根据奇偶性及2是质数中唯一的偶数易知两个质数分别为2和47，．例2.2、（1）两个质数的和是1999，那么这两个质数是多少？（2）若两个质数的差是35，那么它们的积是多少？答案：（1）1997（2）74解析：（1）通过奇偶分析易知两个质数必为一奇一偶，即一个为2，另一个为．（2）通过奇偶分析易知两个质数必为一奇一偶，即一个为2，另一个为，它们的积是．例2.3、三个互不相同的质数相加，和为52，这三个质数可能是多少？答案：可能为（2，3,47）（2,43,7）（2,37,13）（2,31,19）解析：小于50的质数有2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、发现只有一个偶数2，所以一定包含2，另外两个为奇数，且和为50,、．例2.4、若两个不同的质数m、n满足，那么__________．答案：7或8解析：满足条件的有，或，，所以．例2.5、若三个不同的质数的和是53，则这样的三个质数有__________组．答案：11解析：三个不同的质数的和是53，所以三个质数都必须是奇数．从最小的奇质数枚举如下：．共11组．例2.6、三个数p，p + 3 ，p + 5 都是质数，它们的倒数之和是 ____ ．答案：解析：可知p一定是2，．例2.7、有6个数字a、b、c、d、p、q，满足，c和d的奇偶性相同，且p、q、都是质数，则最大是多少？答案：解析：c和d的奇偶性相同，故为偶数，p、q、中必有偶数，只能是，进而易得，．将问题转化为竖式，易知最大是9846．例2.8、已知p、q为质数，并且存在两个正整数m、n，使得，，则_________．答案：解析：因为且为质数，所以中有一个为1．不妨设，则，．又因为p、q为质数，故．代入得原式值为．题模三质数与合数的应用提高例3.1、在1到100这100个正整数中，不能被2、3、5、7中任何一个数整除的数有__________个．答案：解析：数论问题，不能被这些数整除的一定都是质数，1-100的质数去掉1、2、3、5、7还有22个．例3.2、将正整数1，2，3，4，5，6，…，10000排成一行．若一个数不能表示成两个合数的和，则将此数划去．例如要划去1，但是因为，8就不能划去．根据上面规定划掉所有能划掉的数之后，将剩下的数由小到大排列．这时从左数第2013个数是_______．答案：2022解析：从8开始往后的偶数可以拆成两个偶合数的和；从13开始的奇数可以拆成9+2n的形式（n大于等于2），而1、2、3、4、5、6、7、9、11要划去，所以剩下的数列为8、10、12、13、14、15……，第2013项即为2022．例3.3、小红、小明二人在讨论年龄，小红说：“我比你小，当你像我这么大时，我的年龄是个质数．”小明说：“当你长到我这么大时，我的年龄也是个质数．”小红说：“我发现现在咱俩的年龄和是个质数的平方．”那么小明今年____________岁．（小明今年年龄小于31岁，且年龄均为整数岁）答案：16解析：设小红岁，年龄差，则小明岁．由题意知为质数①，为质数②，为质数③的平方即年龄和，年龄和可能为4，9，25，49．经验证，年龄差为7，小红今年9岁，小明今年16岁．例3.4、四个小三角形的顶点处有六个圆圈，如果在这些圆圈中分别填上六个质数，它们的和是20，而且每个小三角形顶点上的数之和相等．问这六个质数的积是多少？答案：900解析：设每个小三角形顶点上的数之和为，当计算题4个小三角形顶点上的数之和时，中间三个圆圈算了三次，减去两次后得到六个质数之和20，，三个质数和为10，则这三个质数为2、3、5.六个圆圈分别填两个2、3、5.它们的积为900．随堂练习随练1.1、最小的质数是________，最小的自然数是________．答案：2；0解析：最小的质数是2，最小的自然数是0．随练1.2、在31、37、51、57、71、77、91、97这8个数中，有几个合数？A、2个B、3个C、4个D、5个答案：C解析：在这8个数中，31、37、71、97是质数，51、57、77、91是合数，即一共有4个合数．正确答案是C．随练1.3、三个连续自然数，每个数都是合数，则这三个连续自然数的和最小是（）．A、6B、27C、45D、720答案：B解析：列举可知，最小的三个数为8、9、10，所以这三个连续自然数的和最小是．随练1.4、在20以内的质数中，加上2以后结果还是质数的，一共有（）个．A、8B、6C、4D、2答案：C解析：3、5、11、17符合要求，共4个．随练1.5、两个质数的和是45，这两个质数的积是_______．答案：86解析：两质数必为一奇一偶，故一定有2，另一个为，两数之积为86．随练1.6、从20以内的质数中选出6个，写在一个正方体的六个面上，使得两个向对面的和都相等，所选的6个数是________．答案：5、7、11、13、17、19解析：首先2不能入选，否则会出现有的和为奇数，有的和为偶数的情况，那么还剩下3、5、7、11、13、17、19这7个数，从中选择6个相当于剔除一个，由于这7个数的和为75，是3 的倍数，而选出的6个数的和也是3的倍数，所以被剔除的那个数应该也是3的倍数，只能是3，所以选出的6个数分别是5、7、11、13、17、19．随练1.7、三个互不相同的质数相加，和为30，这三个质数的乘积最大是__________．答案：374解析：三个数的和是偶数，可以是三个偶数，或者一偶两奇．考虑质数中只有2是偶数，可知一定是一偶两奇，且偶数是2．另外两个奇数是5和23或11和17．所以这三个质数的乘积是或，乘积最大是374．随练1.8、一个两位质数的两个数字交换位置后，仍然是一个质数，请写出所有这样的质数．答案：11、13、17、31、37、71、73、79、97解析：列出备选的两位质数，十位数字是2、4、5、6、8的就不用罗列了．观察这些数，只有19颠倒过来后是合数：，排除19，剩下的质数都满足要求．自我总结课后作业作业1、1~100这100个自然数中质数有25个，合数有________个．答案：74解析：1~100中，25个质数之外的75个数中，只有1不是合数，其他的都是．所以有74个合数．作业2、a是100以内最大的质数，b是100以内最小的质数，那么__________．答案：99解析：，，所以．作业3、五个连续的自然数，每个数都是合数，这五个连续自然数的和最小是__________．答案：130解析：最小的连续五个合数是24、25、26、27、28，所以这五个连续自然数的和最小是130．作业4、在横线上填入三个不同的质数，使等式成立________+________+________＝60，则共有________种不同的填法．答案：3解析：由奇偶性分析易知这三个质数必为2奇1偶，即必有2，只需将58表示为2个质数之和即可．，共3种填法．作业5、有一个质数是两位数，这两位上的数字相差6，则这个两位数的质数是．答案：17或71解析：各位必为偶数．分别试验1、7和3、9，17或71满足要求．作业6、两个质数的和是19，则这两个质数的积是______．答案：34解析：由奇偶性可知必有2，另一个为，两数乘积为34．作业7、当和+5都是质数时，_______．答案：37解析：当和+5奇偶性不同，而且都为质数，那么较小的数必须为2，所以37．作业8、已知正整数p、q都是质数，并且与也都是质数，求p、q的值．答案：或解析：若p、q均为奇数则为大于2的偶数，与其为质数矛盾，故p、q必有偶数，即为2．当时，q、、均为质数，且讨论得此三数被3除的余数各不相同，因此q只能为3，此时另两个均为17，满足条件；当时，p、、均为质数，同理可得p也只能为3，此时另两个数分别为23和17，满足要求．综上，或．作业9、张中中小朋友手中有四张卡片，分别写有1、2、3、4；张右右小朋友手中也有四张卡片，分别写着5、6、7、9，两位小朋友将卡片放在一起适当组合恰好形成四个不同的两位质数（卡片不重复使用，也不得有剩余），请将四个质数的和求出．答：_________答案：190解析：2只能和9配，为29．4只能和7配，为47．进而另两个为61、53，总和为190．作业10、（1）两个质数的和是39，这两个质数的差是多少？（2）三个互不相同的质数相加，和为40，这三个质数分别是多少？答案：（1）35（2）2、7、31解析：（1）．偶质数是2，所以奇质数是．这两个质数的差是（2）40是偶数，如果写成三个数相加的形式则有两种情况，，或，第一种情况显然是不可能的（质数中只有2是偶数）．所以可以确定出三个质数中有一个一定是2，剩下两个奇质数的和是38．通过简单的枚举可得，只有符合题意．所以这三个质数分别是：2，7，31．作业11、有一种数，是以法国数学家梅森的名字命名的，它们就是形如（n为质数）的梅森数，当梅森数是质数时就叫梅森质数，是合数时就叫梅森合数．例如：就是第一个梅森质数．第一个梅森合数是（）．A、4B、15C、127D、2047答案：D解析：可依次写出梅森数：，第一个梅森质数；，第二个梅森质数；，第三个梅森质数；，第四个梅森质数；，第一个梅森合数．所以答案为D．也可以用排除法，梅森数一定为奇数，A选项排除．，4为合数，所以15不是梅森数，B选项排除．，127为质数，所以127为梅森质数，C选项排除．检验可知，D选项为梅森合数，所以答案为D．作业12、在小于30的质数中，加3以后是4的倍数的是____________．答案：5，13，17，29解析：通过枚举法可得，5、13、17、29．作业13、已知a,b,c只3个彼此不同的质数，若，则最大是___________．答案：32解析：．作业14、有些三位数，它的各位数字的乘积是质数，这样的三位数最大的为A，最小的为B．则__________．答案：599解析：由质数定义可知，质数只能写成1乘本身的形式，则说明三位数的三个数位上的数字有2个1，另一个为质数．则这样的三位数最大为711，最小为112，则．作业15、从1、2、3、4、5、6、7、8、9中选出8个数排成一个圆圈，使得相邻的两数之和都是质数．排好后可以从任意两个数字之间切开，按顺时针方向读这些八位数，其中可能读的最大的数是________________．答案：98567432解析：设首位为9，旁边可为8，下一位最大为5……这样进行下去，最大为98567432．。

精心整理平方数的规律及100以内的整数平方表(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1.(5)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被5整除的数的平方为5n±1型,能被5整除的数的平方为5n型.(8)平方数的形式具有下列形式16n,16n+1,16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4,6,7,9.(没有2,5,8)(10)如果质数p能整除a,但p的平方不能整除a,则a不是完全平方数.(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数.精心整理精心整理(12)一个正整数n是完全平方数的充分必要条件是n有奇数个因数(包括1和n).一个数如果是另一个整数的完全立方（即一个整数的三次方,或整数乘以它本身乘以它本身）,那么我们就称这个数为完全立方数,也叫做立方数，如0,1,8,27,64,125,216,343,512,729,1000等.如果正整数x,y,z满足不定方程x2+y2=z2,就称x,y,z为一组勾股数.x,y必然是一个为奇数另一个为偶数，不可能同时为奇数或同时为偶数.z 和z2必定都是奇数.五组常见的勾股数：32+42=52；52+122=132；72+242=252；82+152=172；202+212=2929+16=25；25+144=169；49+576=625；64+225=289；400+441=841记忆技巧：(a+b)2=a2+b2+2ab(a－b)2=a2+b2－2ab||||||a×ab×b2×a×ba×ab×b2×a×b例：132=(10+3)2=102+32+2×10×3=100+9+60=169882=(90-2)2=902+22－2×90×2=8100+4－360=7744用处：①训练计算能力，使计算更快更准确；②估计某数的平方根所处的范围，在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到之间的所有质数是不是n的因子即可，超过的都不必检查了.例如，判定2431是否为质数，因为492=2401<2431<2500=502,所以49<<50,2+4+3+1=10不能被3整除,2341的个位既非0又非5,故只需检查7到47之间的所有质数能否整除2431即可，而53,59,61,67……等更大的质数都不用检查了，实际上2431=1117.③增加对数字的熟悉程度，比如162=256=28，322=1024=210，642=4096=212,另外一些特殊结构的数字应该牢记，如882=7744,112=121,222=484,(121和484从左到右与从右到左看是一样的)122=144,212=441,132=169,312=961,(a左右颠倒后a2也左右颠倒).精心整理。

平方数得规律及100以内得整数平方表规律：（１)完全平方数得个位数字只能就是０,１，4,5,6,9、(没有2，3，7，8）两个整数得个位数字之与为1０,则它们得平方数得个位数字相同、（2)奇数得平方得个位数字就是奇数,十位数字就是偶数、(3）如果完全平方数得十位数字就是奇数,则它得个位数字一定就是6;反之，如果完全平方数得个位数字就是6，则它得十位数字一定就是奇数、(4)偶数得平方就是４得倍数；奇数得平方就是4得倍数加1、(5)奇数得平方就是8n+1型;偶数得平方为８n或８n＋4型、（6）完全平方数得形式必为下列两种之一：3n，３ｎ+1、(7)不能被５整除得数得平方为5n±1型,能被5整除得数得平方为5n 型、(８）平方数得形式具有下列形式１6n,16n＋１,16n+4,1６n+９、(9）完全平方数得各位数字之与得个位数字只能就是０,1，3,4，６,7，９、(没有２,5，8）（10）如果质数ｐ能整除a,但ｐ得平方不能整除a,则a不就是完全平方数、(11）在两个相邻得整数得平方数之间得所有整数都不就是完全平方数、（12）一个正整数n就是完全平方数得充分必要条件就是n有奇数个因数（包括1与ｎ)、一个数如果就是另一个整数得完全立方（即一个整数得三次方，或整数乘以它本身乘以它本身)，那么我们就称这个数为完全立方数,也叫做立方数,如０,1，8,27，64,125,216,３4３,512，729，１0０0等、如果正整数x，ｙ，ｚ满足不定方程ｘ2+y２＝ｚ2,就称x，ｙ，z为一组勾股数、x，y必然就是一个为奇数另一个为偶数,不可能同时为奇数或同时为偶数、z与z2必定都就是奇数、五组常见得勾股数:32+42=52；5２+12２=132；72+2４2=２52；82+1５２＝172;２０2＋212=29２９＋16=25；25+14４=１69；４9＋5７6=6２5; 64+2２5＝２89；４００＋44１＝84１记忆技巧：(ａ+b)2＝a2＋ｂ２＋2ａb （ａ－b)2=a2 + ｂ2 －2ab｜｜| ｜| ｜ａ×a ｂ×b 2×a×b a×a b×b 2×a ×b例：132＝（10＋3)2=102＋３2+２×10×3=1０0＋9+６0=169 882=(90-２)2＝902+2２－2×９０×2=８1０0＋4—36０=７７4４用处：①训练计算能力，使计算更快更准确；②估计某数得平方根所处得范围，在判定某个较大得数n就是不就是质数时可以缩小其可能因子得筛选范围，只需检查3到之间得所有质数就是不就是n得因子即可，超过得都不必检查了、例如,判定2431就是否为质数,因为４92=240１<2431〈25０0=50２,所以4９＜＜5０，2+4+3＋1＝10不能被３整除，２341得个位既非0又非5，故只需检查7到４7之间得所有质数能否整除2431即可，而53,59，61,6７……等更大得质数都不用检查了，实际上２４31=1117、③增加对数字得熟悉程度，比如16２=2５6=28，３22＝10２4＝2１0,６42=４096=２1２,另外一些特殊结构得数字应该牢记，如８8２=774４，ﻫ１12=12１,2２２=484,（1２1与484从左到右与从右到左瞧就是一样得)ﻫ１２２＝144,21２=４41,１３2=169,３12=9６1,(a左右颠倒后ａ2也左右颠倒）、1—2０得平方数221－40得平方数341-60得平方数461－80得平方数581-100得平方数。

平方数的规律及以内的平方表Document serial number【KKGB-LBS98YT-BS8CB-BSUT-BST108】平方数的规律及100以内的整数平方表规律：(1)完全平方数的个位数字只能是0,1,4,5,6,9.(没有2,3,7,8)两个整数的个位数字之和为10，则它们的平方数的个位数字相同.(2)奇数的平方的个位数字是奇数，十位数字是偶数.(3)如果完全平方数的十位数字是奇数,则它的个位数字一定是6；反之，如果完全平方数的个位数字是6，则它的十位数字一定是奇数.(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1.(5)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被5整除的数的平方为5n±1型,能被5整除的数的平方为5n型.(8)平方数的形式具有下列形式16n,16n+1,16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4,6,7,9.(没有2,5,8)(10)如果质数p能整除a,但p的平方不能整除a,则a不是完全平方数.(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数.(12)一个正整数n是完全平方数的充分必要条件是n有奇数个因数(包括1和n).一个数如果是另一个整数的完全立方（即一个整数的三次方,或整数乘以它本身乘以它本身）,那么我们就称这个数为完全立方数,也叫做立方数，如0,1,8,27,64,125,216,343,512,729,1000等.如果正整数x,y,z满足不定方程x2+y2=z2,就称x,y,z为一组勾股数.x,y必然是一个为奇数另一个为偶数，不可能同时为奇数或同时为偶数.z和z2必定都是奇数.五组常见的勾股数：32+42=52；52+122=132；72+242=252；82+152=172；202+212=2929+16=25；25+144=169；49+576=625；64+225=289；400+441=841记忆技巧：(a+b)2=a2+b2+2ab(a－b)2=a2+b2－2ab||||||a×a b×b2×a×ba×ab×b2×a×b例：132=(10+3)2=102+32+2×10×3=100+9+60=169882=(90-2)2=902+22－2×90×2=8100+4－360=7744用处：①训练计算能力，使计算更快更准确；②估计某数的平方根所处的范围，在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到之间的所有质数是不是n的因子即可，超过的都不必检查了.例如，判定2431是否为质数，因为492=2401<2431<2500=502,所以49<<50,2+4+3+1=10不能被3整除,2341的个位既非0又非5,故只需检查7到47之间的所有质数能否整除2431即可，而53,59,61,67……等更大的质数都不用检查了，实际上2431=1117.③增加对数字的熟悉程度，比如162=256=28，322=1024=210，642=4096=212,另外一些特殊结构的数字应该牢记，如882=7744,112=121,222=484,(121和484从左到右与从右到左看是一样的)122=144,212=441,132=169,312=961,(a左右颠倒后a2也左右颠倒).。

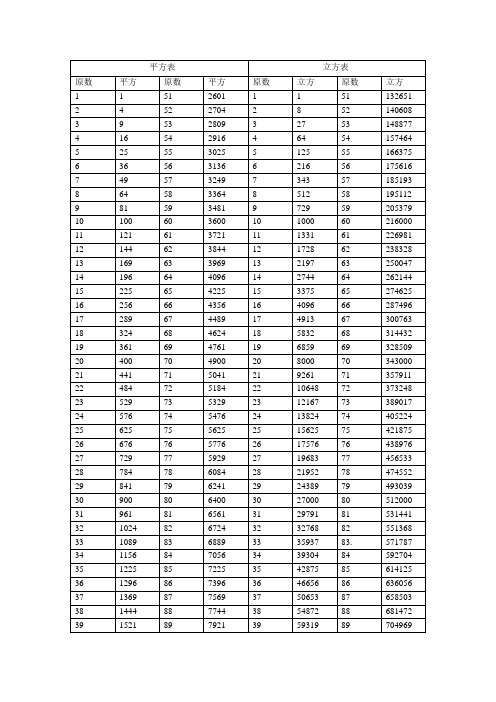
平方数的规律及100以内的整数平方表112=121122=144132=169142=196152=225162=256172=289182=324192=361202=400212=441222=484232=529242=576252=625262=676272=729282=784292=841302=900312=961322=1024332=1089342=1156352=1225362=1296372=1369382=1444392=1521402=1600412=1681422=1764432=1849442=1936452=2025462=2116472=2209482=2304492=2401502=2500512=2601522=2704532=2809542=2916552=3025562=3136572=3249582=3364592=3481602=3600612=3721622=3844632=3969642=4096652=4225662=4356672=4489682=4624692=4761702=4900712=5041722=5184732=5329742=5476752=5625762=5776772=5929782=6084792=6241802=6400812=6561822=6724832=6889842=7056852=7225862=7396872=7569882=7744892=7921902=8100912=8281922=8464932=8649942=8836952=9025962=9216972=9409982=9604992=98011002=10000规律：(1)完全平方数的个位数字只能是0,1,4,5,6,9.(没有2,3,7,8)两个整数的个位数字之和为10，则它们的平方数的个位数字相同.(2)奇数的平方的个位数字是奇数，十位数字是偶数.(3)如果完全平方数的十位数字是奇数,则它的个位数字一定是6；反之，如果完全平方数的个位数字是6，则它的十位数字一定是奇数.(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1.(5)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被5整除的数的平方为5n±1型,能被5整除的数的平方为5n型.(8)平方数的形式具有下列形式16n,16n+1,16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4,6,7,9.(没有2,5,8)(10)如果质数p能整除a,但p的平方不能整除a,则a不是完全平方数.(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数.(12)一个正整数n是完全平方数的充分必要条件是n有奇数个因数(包括1和n).一个数如果是另一个整数的完全立方（即一个整数的三次方,或整数乘以它本身乘以它本身）,那么我们就称这个数为完全立方数,也叫做立方数，如0,1,8,27,64,125,216,343,512,729,1000等.如果正整数x,y,z满足不定方程x2+y2=z2 ,就称x,y,z为一组勾股数.x,y必然是一个为奇数另一个为偶数，不可能同时为奇数或同时为偶数.z和z2必定都是奇数.五组常见的勾股数：32+42=52；52+122=132；72+242=252；82+152=172；202+212=2929+16=25；25+144=169；49+576=625；64+225=289；400+441=841记忆技巧：(a+b)2= a2 + b2 + 2ab (a－b)2=a2 + b2 －2ab| | | | | |a×a b×b 2×a×b a×a b×b 2×a×b例：132=(10+3)2=102+32+2×10×3=100+9+60=169882=(90-2)2=902+22－2×90×2=8100+4－360=7744用处：①训练计算能力，使计算更快更准确；②估计某数的平方根所处的范围，在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到之间的所有质数是不是n的因子即可，n超过的都不必检查了.例如，判定2431是否为质数，因为n2431492=2401<2431<2500=502,所以49<<50 ,2+4+3+1=10不能被3整除, 2341的个位既非0又非5,故只需检查7到47之间的所有质数能否整除2431即可，而53,59,61,67……等更大的质数都不用检查了，实际上2431=1117.×13×③增加对数字的熟悉程度，比如162=256=28，322=1024=210，642=4096=212 ,另外一些特殊结构的数字应该牢记，如882=7744,112=121,222=484,(121和484从左到右与从右到左看是一样的)122=144,212=441,132=169,312=961,(a左右颠倒后a2也左右颠倒).。