长沙市2018届高三统考文科数学试题

2018年长沙市一中高三数学（文、理）综合测试题（二）一、选择题（本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1．集合A 中有3个元素，集合B 中有2个元素，映射f ：A →B ，使B 中有且只有一个元素在A 中的原象为2个，这样的映射f 的个数为（ ） A ．4B ．5C ．6D ．82．已知直二面角α-l -β，直线a ⊂α，直线b ⊂β，且a 与l 不垂直，b 与l 不垂直，那么（ ）A ．a 与b 可以垂直，但不可以平行B ．a 与b 可以垂直，也可以平行C ．a 与b 不可以垂直，不可以平行D ．a 与b 不可以垂直，但可以平行3．某等差数列{a n }中，a 2+a 6+a 16为一个确定的常数，则其前n 项和S n 也为确定的常数的是（ ） A ．S 17B ．S 15C ．S 8D ．S 74．给定两个向量=（3,4），=（2,1），若+x ⊥-，则x =（ ） A ．-3B ．23C ．3D ．-23 5．下面三个论断：①命题“若a ，b 都是偶数，则a +b 是偶数”的逆否命题是“若a +b 不是偶数，则a ，b 都不是偶数”；②命题“若x 2+y 2=0，则x ，y 全为0”是命题“若x 2+y 2≠0，则x ，y 不全为0”的否命题；③条件p : |x +1|＞2，条件q : 5x –6＞x 2，则﹁p 是﹁q 的必要不充分条件.其中正确论断的个数是（ ） A ．3B ．2C ．1D ．0 6．已知（x ，y ）是右图中阴影部分内的点（含边界），若使目 标函数z =ax +y （a ＞0）取最大值的最优解有无穷多个，则 a 的值为（ ） A ．53B ．41 C ．35D ．47．已知直线kx y l =:和圆9)4()2(:22=-+-y x c ，若圆c上存在四个不同的点到直线l 的距离都是1，则实数k 的取值范围是（ ）A ．),43(+∞-B ．),43(+∞C ．)43,(-∞D ．)43,0()43,(⋃--∞8．（理）若4342lim 222=--+→x ax x x ，则a 的值是（ ） A ．0B ．1C ．-1D ．21（文）在(1+x )n 的展开式中，奇数项之和为A ，偶数项之和为B ，则(1-x 2)n 的值为（ ） A ．0B ．A ·BC ．A 2-B 2D ．A 2+B 29．（理）甲有1只放有x 个红球，y 个白球，z 个黄球的箱子（x ≥0，y ≥0，z ≥0，x +y +z =6），乙有1只放有3个红球，2个白球，1个黄球的箱子，两人各自从自己的箱子中任取一球，规定当两球同色时甲胜，异色时乙胜.并规定甲同取红、白、黄色球而胜的得分依次为1,2,3，则甲得分的期望的最大值是（ ） A ．21B ．43 C ．54 D ．52 （文）已知总体的个数是1013，现用系统抽样的方法从中抽取一个容量为50的样本，则首先应从总体中剔除（ ）个个体（利用随机数表），然后再按系数抽样的方法进行，在整个过程中每个个体被抽到的概率是（ ）A ．3，101050B ．3，101350C ．13，101050 D ．13，10135010．函数y =a sin x +3a cos x 的图象与|y |=2的图象在[32,3ππ-]上有且只有两个不同的公共点，则（ ） A ．|a |≥1B ．|a |＞1C ．|a |≥2D ．|a |＞211．将一张画有直角坐标系且两轴的长度单位相同的纸折叠一次，使点（2，0）与点（-2，4）重合，若点（7，3）与点（m ，n ）重合，则m +n 的值为（ ） A ．10B ．4C ．-4D ．-10 12．如右图，棱长为1的正方体容器ABCD -A 1B 1C 1D 1中，在A 1B ，A 1B 1，B 1C 1的中点E ，F ，G 处各有一小孔. 若此容器可以任意放置，小孔面积对容积影响忽略不 计，则最大容水量等于（ ） A ．5655B ．4847 C ．1211 D ．87 二、填空题：（本大题共4小题，每小题4分，共16分.把答案填在题中横线上.） 13．某企业去年销售收入1000万元，年成本分为年生产成本500万元与年广告成本200万元两部分.若利润的P %为国税，且年广告费超出年销售收入2%的部分也必须按P %1 A 1 A.14．已知F 1，F 2为椭圆E 的左，右焦点，抛物线C 以F 1为顶点，F 2为焦点，P 为E 与C的交点，若椭圆的离心率为e .且|1|=e |2PF |，则e =. 15．正三棱柱的侧面展开图是边长为2和4的矩形，则它的体积为.16．给出下列几个命题：（1）若|a ·b | = |a |·|b |，则a ∥b ；（2）平面α，β，直线a ，b .若a ⊂β，a ∥α，α⋂β=b ，且a 在平面α内的射影为a '，则a '∥b ；（3）AB =a ，c BC =，b CA =.若|a |=5，|b |=8，|c |=7，则a ·b =20；（4）s n 为等差数列{a n }的前n 项和，若s 6＜s 7，s 7＞s 8，则s 9＜s 6；（5）若凸多面体各个面都是六边形，则2F =V -2.其中真命题的序号是 .三、解答题（本大题共6小题，共74分.解答应写出文字说明，证明过程或演算步骤.）17．（本小题满分12分）设直线l 1的方向向量是a =（1+cos α，sin α），α∈（0，π），直线l 2的方向向量为b =（1-cos β，sin β），β∈（π，2π），直线l 3的方向向量为c =（1，0）.若l 1与l 3的夹角 为1θ，l 2到l 3的角为2θ，且621πθθ=-，求sin(4βαπ-+)的值.18．（本小题满分12分）如图，在正四棱柱ABCD -A 1B 1C 1D 1中，AA 1=21AB ，点E 、M 分别为A 1B 、C 1C 的中点.过点A 1，B ，M 三点 的平面A 1BMN 交C 1D 1于点N .（1）求证：EM ∥平面A 1B 1C 1D 1； （2）求二面角B -A 1N -B 1的正切值.A19．（本小题满分12分）设数列{a n }和{b n }满足a 1=b 1=6，a 2=b 2=4，a 3=b 3=3，且数列{a n +1-a n }（n ∈N *）是等差数列，数列{b n -2}是等比数列.（1）求数列{a n }，{b n }的通项公式； （2） 是否存在k ∈N *，使a k -b k ∈（0，21）？若存在，求出k 值；若不存在，说明理由.20．（本小题满分12分）（理）计算机中用的是二进制数，只用两个数码：0和1.如二进制数中110101=1×25+1×24+0×23+1×22+0×21+1×20等于十进制中的53.在制造电子计算机时，每个数码要用一个设备，如果用n 进制，每一位有n 个数码.在计算机中表示m 位n 进制数就要用m ×n 个设备.设计算机能表示的最大数为M （使用数制为n （n ≥2）进制）时，设备量为G .（1）如果在机器中要表示m 位n 进制数，试写出M ，m ，n 的关系式； （2）把G (n )看作n 的函数，M 作为常数，写出这个函数式；（3）计算G (2)，G (3)，G (4)，G (5)各等于多少个lg (M +1) (lg 2≈0.3，lg 3≈0.48)； （4）当M 给定，选取n 为多少时，才能使设备总量G 最小，并加以证明.（文）一袋中有4个黑球，3个白球，2个红球，从中任取2个球，每取到一个黑球得0分，每取到一个白球得1分，每取到一个红球得2分. （1）求得到2分的概率； （2）求最多得几分的概率为3635？21．（本小题满分12分） （理）已知点P （-3，0），点A 在y 轴上，点Q 在x 轴的正半轴上，点M 在直线AQ 上，且满足⋅=0，-=23. （1）当点A 在y 轴上移动时，求动点M 的轨迹C ；（2）设轨迹C 的准线为l ，焦点为F ，过F 作直线m 交轨迹C 于G ，H 两点，过点G 作平行于轨迹C 的对称轴的直线n 交l 于点E ，问点E 、O 、H （O 为原点）是否在同一条直线上？并说明理由.（文）已知函数f (x )=x 3+ax 2+bx +c 在x =32-和x =1处都取得极值. （1）求a ，b 的值；（2）若x ∈[-1，2]时，不等式f (x )＜c 2恒成立，求实数c 的取值范围.22．（本小题满分14分） （理）设函数f (x )=(1+x )2-ln (1+x )2.（1）求函数f (x )的单调区间； （2）若x ∈[1,11--e e]时，不等式f (x )＜m 恒成立，求实数m 的取值范围； （3）关于x 的方程f (x )=x 2+x +a 在[0，2]上恰有两个相异实根，求a 的取值范围. （文）已知点P （-3，0），点A 在y 轴上，点Q 在x 轴的正半轴上，点M 在直线AQ 上，且满足0=⋅，-=23. （1）当点A 在y 轴上移动时，求动点M 的轨迹C 的方程；（2）设轨迹C 的准线为l ，焦点为F ，过F 作直线m 交轨迹C 于G 、H 两点，过点G 作平行于轨迹C 的对称轴的直线n 交l 于点E ，问点E 、O 、H （O 为原点）是否在同一条直线上？并说明理由.参 考 答 案一、1．C2．D 3．B 4．A5．C6．A7．B8．C9．D10．B11．A12．D 二、13．25%14．33 15．938或934 16．（1）（4）（5）三、17．由题意得2tan 2cos 22cos2sin2cos 1sin 21αααααα==+=l k ， ∵l 3的方向向量=（1，0），∴3l k =0，∴l 1与l 3的夹角为tan θ1=|tan 2α|，而),0(πα∈，∴21αθ=…………（4分） 又3l k =2cot cos 1sin βββ=-，l 2到l 3的角tan 2θ=2cot β-.∵)2,(ππβ∈，∴222πβθ-=…………（8分）∵621πθθ=-，∴6)22(2ππβα=--，即32πβα-=-.∴21)6sin(4sin )4sin(=--=--=-+πβαβαπ…………（12分） 18．（1）取A 1B 1的中点，连EF ，C 1F ，∵E 为A 1B 的中点，∴EF ∥121BB ………（2分）又M 为CC 1的中点.∴EF ∥C 1M .EFC 1M 为平行四边形，∴EM ∥FC 1………（4分） ∵EM ⊂面A 1C 1，FC 1⊂面A 1C 1，∴EM ∥平面A 1B 1C 1D 1…………（6分）（2）由（1）EM ∥面A 1C 1，EM ⊂面A 1BMN ，面A 1BMN ∩面A 1C 1=A 1N ，∴A 1N ∥EM ∥FC 1，∴N 为C 1D 1中点.过B 1作B 1H ⊥A 1N 于H ，连BH ，据三垂线定理BH ⊥A 1N ，∠BHB 1即为二面角B -A 1N -B 1的平面角…………（8分）设AA 1=a ，则AB =2a ，A 1N =a 5，由△A 1B 1H ∽NA 1D 1得B 1H =54a .在Rt △BB 1H 中，tan ∠BHB 1=451=H B BB .所求正切值为45…………（12分）19．（1）由已知a 2-a 1= -2，a 3 – a 2= –1，∴a n +1 – a n =(a 2 – a 1)+(n –1)·1=n – 3.n ≥2时，a n =(a n–a n -1)+(a n -1–a n -2)+…+(a 3–a 2)+(a 2–a 1)+a 1= (n –4)+(n –5)+…+(–1)+(–2)+6=21872+-n n .n =1也合适，∴a n =21872+-n n …………（3分）又b 1–2=4，b 2–2=2，∴b n –2=(b 1–2)·(21)n –1=4·(21)n –1.∴b n =2+(21)n –3.……（6分） （2）设f (k )=a k -b k =21k 2 -kk k k )21(887)27(21)21.(87272⋅-+-=-+.当k ≥4时，f (k )为增函数，而f (4)=21.又f (1)=f (2)=f (3)=0，∴不存在k ，使f (k )∈(0, 21)…………(12分).20．（理）（1）M =n m -1…………（3分）.（2）由（1）得n m =M +1.取对数得m lg n =lg （M +1）.∵G =mn ， ∴G (n )=lg(M +1) ·nnlg …………（5分） （3）G (2)≈6.7lg(M +1)，G (3) ≈6.3lg(M +1)，G (4)=G (2) ≈6.7lg(M +1)， G (5) ≈7.11lg(M +1)…………（7分）（4）由（3）猜想G (3)最小，用数学归纳法证明如下. 1°当n =3时，G (3)＜G (4)，命题成立.2°假设n =k (k ∈N *，k ＞3)时命题成立，即G (k )＜G (k +1) lg(M +1)·kkM k k lg )1lg()1lg(1+-++＞0.∴(k +1)lg k -k lg(k +1) ＞0，即k k k k⋅+)1(＞1. ∵21++k k ＞1+k k ,∴)1()21(1+⋅+++k k k k ＞)2()1()1(2)1()1(22++⋅⋅+=++⋅+k k k k k k k k k k k k ＞)2()1(2++k k k ＞1.即lg(M +1))2lg(2++⋅k k ＞lg(M +1)).1lg(1++⋅k k即G(k +2)＞G (k +1). ∴n =k +1时命题也成立.（文）（1）“取2个球得2分”，有一黑一红，2个白球，两种情况，∴取2个球得2分的概率P =.361129231214=+c c c c …………（6分） （2）取2个球的最高得分为4分，概率为3612922=c c ， ∴取2个球最多得3分的概率为36353611=-.…………（12分） 21．（理）（1）设点M (x ,y )，由23-=MQ ，得).21,0(y A - ∴=)2,3(y -，=).23,(y x ∵0=⋅，∴y 2=4x （x ＞0） 动点M 的轨迹是以原点为顶点，焦点在x 轴上，开口向右的抛物线(不合顶点)（6分）（2）设过F (1,0)的直线m 的倾角为α.若α=90°，直线m 的方程为x =1，G 与H 的坐标分别为(1,-2),(1,2).此时直线n 的方程为y =-2，E 点坐标为（-1，-2）, ∴E ,O ,H 在同一直线上…………（8分）若α≠90°，设m 的方程为y =k (x –1)，即x = 1+ky ，代入y 2=4x ，得y 2 –044=-y k .设G ),,4(),,4(222121y y H y y 则y 1y 2= -4，直线n 的方程为y =y 2，E 点坐标为(-1,y 2). ∴k OE = -y 2, ,4421211211y y y y y y y k OH -=-=== ∴E 、O 、H 在同一条直线上…………（12分）（文）（1）∵b ax x x f ++='23)(2. ∴0)32(2943)32(=+-+⨯=-'b ax f ① 又f (1) = 3+2a +b =0 ②. 由①，②解得2,21-=-=b a …………（6分） （2）只须求出f (x)在[-1,2]上的最小值. ∵,23)(2--='x x x f 由)(x f '＞0得x ＜32-或x ＞1，)(x f '＜0得32-＜x ＜1. ∴f (x )在[)32,1--和（1,2]上为增函数，在(1,32-)上为减函数…………（10分） 又)32(-f ＜f (2)，∴x =2时[f (x )]max =8+4a +2b +c =2+c .∴f (x )＜c 2,即2+c ＜c 2恒成立，解得c ＜-1或c ＞2.故c 的取值范围是（-∞，-1）∪（2，+∞）.22．（理）（1）函数定义域为（-∞，-1）∪（-1，+∞） 由1)2(2]11)1[(2)(++=+-+='x x x x x x f ＞0得-2＜x ＜-1或x ＞0. 由)(x f '＜0得x ＜-2或-1＜x ＜0. ∴递增区间是（-2，-1），（0，+∞）；递减区间是（-∞，-2），（-1，0）……（4分）（2）由01)2(2)(=++='x x x x f 得x =0或x = -2. 由（1）知f (x )在]0,11[-e上递减，在[0，e -1]上递增……（6分） 又,2)1(,21)11(22-=-+=-e e f e e f 且22-e ＞212+e, ∴]1,11[--∈e e x 时，.2)]([2max -=e x f 故m ＞e 2-2时，不等式f (x )＜m 恒成立.…………（8分）（3）方程f (x )=x 2+x +a ，即x -a +1-ln(1+x )2=0.记2)1ln(1)(x a x x g +-+-=，则.11121)(+-=+-='x x x x g 由)(x g '＞0得x ＜-1或x ＞1，由)(x g '＜0得-1＜x ＜1.∴g (x )在[0,1]上递减，在[1,2]上递增……（10分）为使a x x x f ++=2)(在[0,2]上恰好有两个相异实根，只须g (x )=0，在[0,1)和（1，2]各有一个实根.于是有： g (0)≥0,g (1)＜0, 解得2-2ln2＜a ≤3-2ln3.g (2)≥0. 所求a 的范围是(2-2ln2,3-2ln3).（文）同理科21题.。

2018年长沙市一中高三数学（文、理）综合测试题（一）一、选择题（每小题5分，共60分） 1．函数)632cos(32sin )(π-+=x x x f 的图象相邻的两条对称轴间的距离是（ ） A ．3πB ．π23C ．π34D ．π322．直线（x +1）a +（y +1）b =0与圆x 2+y 2=2的位置关系是（ ） A ．相交B ．相切C ．相离D ．相交成相切3．等比数列{a n }的公比为q ，则“a 1＞0且q ＞1”是“对于任意自然数n ，都有a n +1＞a n ”的（ ） A ．充分非必要条件 B ．必要非充分C ．充要条件D ．既非充分又非必要条件4．设θ是三角形的一个内角，且sin θ+ cos θ=51，则方程x 2sin θ-g 2cos θ=1表示（ ） A ．焦点在x 轴上的椭圆B ．焦点在y 轴上的椭圆C ．焦点在x 轴上的双曲线D ．焦点在y 轴上的双曲线5．已知直线m 、n 、l 、平面α、β：①若m ∥α，n ∥α，则m ∥n ；②若α⊥β，m ⊥l ，β⊂l ，则m ⊥β；③若m 、n 为异面直线，m ∥α，则n 与α相交；④若m ⊥n ，m⊥α，α∉n ，则n ∥α.以上命题中，正确的命题个数是（ ） A ．0B ．1C ．2D ．3 6．如图，小圆圈表示网络的结点，结点之间的连线 表示它们有网线相连，连线上标注的数字表示某 信息经过该段网线所需的时间（单位：毫秒），信 息由结点A 传递到结点B 所需最短时间为（ ） A ．5毫秒 B ．4.9毫秒 C ．4.8毫秒D ．4.7毫秒7．6人一个小组，其甲为组长，乙为副组长，从6人中任选4人排成一排，当正、副组长都入选时，组长必须排在副组长的左边（可以不相邻），则所有不同的排法种数是（ ） A ．288B ．276C ．252D ．728．函数y =log 2121-x 的反函数的定义域为（ ） A ．),(+∞-∞ B ．),0(+∞ C ．)0,(-∞D ．),0()0,(+∞⋃-∞9．直线l 是双曲线12222=-by a x ，[a ＞0,b ＞0)的右准线，以原点为圆心且过双曲线的焦点的圆，被直线l 分成弧长为2:1的两段圆弧，则双曲线的离心率是（ ） A ．3B ．5C ．26D ．210．如果二项式nxx )2(3-的展开式中第8项是含3x 的项，则自然数n 的值为（ ） A ．27B ．28C ．29D ．3011．如图，CBD ABD ∆≅∆，且ABD ∆为等腰三角形，90=∠=∠BCD BAD ，平面ABD ⊥平面BCD ，则下列4个结论中，正确的序号是（ ）①AC ⊥BD ②ACD ∆是等边三角形③AB 与面BCD 成60°角 ④AB 与CD 成60°角 A ．①②③ B ．①②④ C ．①③④D ．②③④12．台风中心从A 地以每小时20千米的速度向东北方向移动，离合风中心30km 内的地区为危险区，城市B 在A 的正东40km 处，B 城市处于危险区内的时间为（ ） A ．0.5hB ．1hC ．1.5hD ．2h二、填空题（每题4分，共16分） 13．函数)1(13)(-≠+-=x x ax x f ，若它的反函数是xx x f -+=-13)(1，则a = .14．在ABC ∆中，)2cos()cos(3A C B +++π的取值范围是.15．S n 是等差数列{a n }的前n 项和，a 5=2，a n －4=30（n ≥5，n ∈N +），S n =336，则n =.16．已知α、β为实数，给出下列三个论断：①||βα-≤||βα+ ②||βα+＞5 ③||α＞22，||β＞22 以其中的两个论断为条件，另一个论断为结论，写出你认为正确的命题是.BDAC综合测试题（一）答卷一、选择题（5分×12=60分）二、填空题（4分×4=16分）13． 14． 15．16．三、解答题17．（12分）平面上有两个向量)1,0(),0,1(21==→→e e .今有动点P 从)2,1(0-P 开始沿着与向是→→+21e e 相同的方向作匀速直线运动，速度为||21→→+e e ，另一动点Q 从点)1,2(0--Q 出发，沿着与向是2123→→+e e 相同的方向作匀速直线运动，速度为2123→→+e e ，设p 、Q 在t=0秒时，分别在P 0、Q 0处，则当→→⊥00Q P PQ 时，用了多长时间.18．（12分）正三棱柱ABC —A 1B 1C 1的底面边长为2，侧棱长为11,3C A 的中点为D.（1）求证：BC 1∥平面AB 1D ； （2）求二面角A 1—B 1D —A 的大小； （3）求点B 到平面AB 1D 的距离.19．（12分）在边长为a 的正三角形的三角处各剪去一个四边形，这个四边形是由两个余系的直角三角形组成的，并且这三个四边也全等，如图1，若用剩下的部分折成一个无盖的正三棱柱形容器，如图2，则当容器的高为多少时，可使这个容器的容积最大，并求出容积的最大值.20．（12分）已知等差数列{a n }中，a 2=8，S 10=185.（文科做）（1）求数列{a n }的通项公式a n.（2）若从数列{a n }中依次取出第2，4，8，…，2n ，…项，按原来的顺序排成一个新数列{b n }，试求{b n }的前n 项和An.（理科做）已知2)1()(-=x x f ，数列{a n }是公差为d 的等差数列，{b n }是公比为)1(≠∈q R q q 且的等比数列，设)1(),1(31+=-=d f a d f a ，),1(1+q f p )1(3-=q f p .（1）求数列{a n }和{b n }的通项公式；（2）设数列{C n }的前n 项和为S n ，如果对一切N n ∈，都有12211+=+++n n n a b c b c b c 成立，求nn n S S tim 212+∞→.21．设)(,x f R a ∈为奇数，且144)2(2+-⋅=-xx a a x f （1）试求a 的值及)()(1x f x f -的反函数.（2）设k x x g +=1log )(2若]32,21[∈x 时，有)()(1x g x f ≤-恒成立，求系数k 的取值范围.22．如图，在ABC Rt ∆中，22,2,90===∠AC AB CAB，D 是线段AB 的垂平分线上一点，D 到AB 的距离为2，过点C 的曲线E 上任一点P 满足||||→→+PB PA 为常数. （1）建立适当的坐标点，求出曲线E 的方程：（2）过点D 的直线e 与曲线E 相交于不同的两点M 、N ，且M 点在D ，之间，若→→=DN DM λ，求λ的取值范围.B综合测试题（一）答案一、1．B2．D 3．A 4．D5．B6．C7．A8．A9．D10．C 11．B 12．B二、13．114．)3,2[-15．2116．①③⇒②三、17．P 0(-1,2)，Q 0(-2,-1)，∴)3,1(00--=Q P ，)1,1(21=+e e .)2,3(2321=+e e ，∴)2,3(),,()1,1(00t t Q t t t P ===，∴)12,23(),2,1(--+-t t Q t t P .∴)3,12(--=t t .∵00Q P PQ ⊥. ∴1×(2t -1)-3(t ÷3)=0. ∴t =2. ∴用于2秒钟.18．（1）连结A 1B 与AB 1交于点O ，连结OD ，则O 为A 1B 的中点，又D 为A 1C 1的中点. ∴OD ∥BC ，又BC 1⊄平面AB 1D ，D ⊂平面AB 1D . ∴BC 1∥平面AB 1D . （2）∵111C B A ∆为正三角形，A 1D =C 1D ，∴B 1D ⊥A 1C 1又AA 1⊥平面A 1B 1C 1，由三垂线定理可知AD ⊥B 1D ，∴∠A 1DA 为A 1-B 1D -A 的平面角.Rt △AA 1D 中，AA 1=3，A 1D =1.∴cos ∠A 1DA =3，∴∠A 1DA =60°，∴A 1–B 1D –A 的平面角为60°. （3）∵BC 1∥平面AB 1D . ∴B 、C 1到平面AB 1D 的距离相等.∴D AB C D AB B V V 111--=. ∵平面AA 1C 1C ⊥平面A 1B 1C 1，B 1D ⊥A 1C 1，∴B 1D ⊥平面AA 1C 1C ，∴B 1D ⊥AD .又B 1D =3，AD =2,∴324321312321312⨯⨯⨯⨯=⨯⨯⨯h ∴23=h . ∴点B 到平面ABD 的距离为23. 19．设容器的高为x ，则容器底面正三角形的边长为x a 32-.2)()32(43x a x V x -⋅=（0＜x ＜32a) )36)(32(43)(x a x a V x --='. 令a a x OBV x 181336)(==='.及32a x =.但0＜x ＜32a ，∴a x 183=. 当)183,0(a x ∈时，)(x V '＞0，V (x )为增函数； 当)2,183(Baa x ∈时，)(x V '＜0，V (x )为减函数. ∴当a x 183=时，容器的容积最大，最大值为2)18332(18343a a a ⋅-⨯= 543a .答：（略） 20．（文）（1）设{a n }的首项为a 1，公差为d ，则⎩⎨⎧=+=+185460811d a d a ∴351==d a∴a n =5+(n -1)×3，即a n =3n +2. （2）2232+⋅==nn n a b ..262612)12(232)222(32n n A n n nn +-⨯=--⨯=++++⨯=（理）（1）2d = a 3 – a = d 2 – (d – 2)2 , ∴d =2，a 1=0，∴a n =2n – 2.2213)2(qq b b -=， ∴q = –2，b 1=q 2=4，b n =(-2)n +1. （2）11221122111,--++++=+++=n n n n n n b c b cb c a b c b c b c a∴211=-=-++n n nn n n a a b c a a 又，∴1)2(2+-⋅=n n c∴{c n }是首项为8，公比为 –2的等比数列.])2(1[38])2(1[38121222++--=--=n n n n s s∴.2)2(1)2(1lim 212212-=----=+∞→+∞→nn n nn n lin s s 21．（1）∵f (x )为奇函数且定义域为R ，∴f (0)=0。

湖南省长沙市重点中学2018届高三第八次月考数学文 4.(时量：120分钟 满分：150分)一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的，请将所选答案填在答题卡对应位置.1.已知集合2{|03},{|540}M x x N x x x =<<=-+≥,则M N =A ．{|01}x x <≤B ．{|13}x x ≤<C ．{|04}x x <≤D ．{|0x x <或4}x ≥ 2.若复数221z i i=++,其中i 是虚数单位,则复数z 的模为A ．1 BCD ．23.运行下面的程序，如果输入的n 是6，那么输出的p 是INPUT “n ＝”； n k ＝1 p ＝1WHILE k<＝n p ＝p*k k ＝k ＋1WENDPRINT p ENDA ．120B ．720C ．1440D ．5040 4.已知直线01)2(:,02)2(:21=-+-=--+ay x a l y a x l ,则“1-=a ”是“21l l ⊥的A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件5.已知y x ,的取值如下表:从散点图可以看出y x 与线性相关,且回归方程为 0.95y x a =+,则a = A. 3.2B ．3.0 C. 2.8D ．2.66.一个几何体的三视图如图所示,其中俯视图与左视图均为半径是2的圆,则这个几何体的 表面积是A ．16πB ．14πC ．12πD ．8π7.已知向量b a ,满足||1,(1,a b ==,且()b a a +⊥,则a 与b 的夹角为 A . 60 B . 90 C . 120 D . 1508.已知函数()sin()f x A x x R ωϕ=+∈，(其中0022A ππωϕ>>-<<，，),其部分图像如图所示,将()f x 的图像纵坐标不变,横坐标变成原来的2倍,再向右平移1个单位得到()g x 的图像,则函数()g x 的解析式为x 0 1 3 4 y2.24.34.86.7正视图 俯视图左视图A ．()sin (1)2g x x π=+B ．()sin (1)8g x x π=+C ．()sin(1)2g x x π=+D ．()sin(1)8g x x π=+9.若函数()x x f x ka a -=-(a >0且1a ≠)在(,-∞+∞)上既是奇函数又是增函数,则()log ()a g x x k =+的图象是10.某企业生产甲、乙两种产品，已知生产每吨甲产品要用A 原料3吨、B 原料2吨；生产每吨乙产品要用A 原料1吨、B 原料3吨.销售每吨甲产品可获得利润5万元，每吨乙产品可获得利润3万元，该企业在一个生产周期内消耗A 原料不超过13吨，B 原料不超过18吨，那么该企业可获得最大利润是A. 12万元B. 20万元C. 25万元D. 27万元 .答案 ABB ADA CBC D二、填空题：本大题共5小题，每小题5分，共25分.把答案填在答题卡中对应题号后的横线上.11.若直线24sin :=⎪⎭⎫⎝⎛-πθρl 与曲线()为参数t ty t x C ⎩⎨⎧==2:相交于B A ,两点， 则AB = ．12.已知数列121,,,9a a 是等差数列,数列1231,,,,9b b b 是等比数列,则212b a a +的值为_____________.13.已知函数()f x 在()+∞,0内可导,且满足x e e f x x +=)(,则()f x 在点()(1,1)M f 处的切线方程为_____________________14.过椭圆C ：()012222>>=+b a by a x 的右顶点作圆222b y x =+的两条切线，切点分别为A ，B ，若120AOB ∠=（O 是坐标原点），则C 的离心率为__________15.对于定义域为[]1,0的函数()f x ,如果同时满足以下三个条件: ①对任意的]1,0[∈x ,总有0)(≥x f ②1)1(=f③若0,021≥≥x x ,121≤+x x ,都有)()()(2121x f x f x x f +≥+ 成立 则称函数)(x f 为理想函数.（Ⅰ）若函数)(x f 为理想函数,则=)0(f ________；（Ⅱ）下列结论正确的是_________________.(写出所有正确结论的序号) ①函数])1,0[(12)(∈-=x x f x 是理想函数；②若函数)(x f 是理想函数,假定存在]1,0[0∈x ,使得]1,0[)(0∈x f ,且00)]([x x f f =,则00)(x x f =. 答案11.23 12.103 13.012=--y x 14. 2315.（Ⅰ）0（Ⅱ）①②三、解答题：本大题共6小题，共75分.解答应写出文字说明，证明过程或演算步骤.16. (本小题满分12分)某班50位学生期中考试数学成绩的频率分布直方图如图4所示,其中成绩分组区间是:[)40,50、[)50,60、[)60,70、[)70,80、[)80,90、[]90,100.(Ⅰ)求图中x 的值及平均成绩； (Ⅱ)从成绩不低于80分的学生中随机选取2人,求2人成绩都不低于90分的概率.解:(Ⅰ)由()0.00630.010.054101x ⨯+++⨯=,解得0.018x =. 3平均成绩为()748518.07554.0651.095554506.0=⨯+⨯+⨯+++⨯. 6分 (Ⅱ)分数在[)80,90、[]90,100的人数分别是500.018109⨯⨯=人、500.006103⨯⨯=人. 从成绩不低于80分的12学生中随机选取2人共有66种取法，从成绩不低于90分的3名学生中随机选取2人共有3种取法，故所求的概率为.221663= 12分17. (本小题满分12分)如图,设D 是直角ABC ∆斜边BC 上一点,且AD AB =,记βα=∠=∠ABC CAD ,. (Ⅰ)证明：02cos sin =+βα； (Ⅱ)若DC AC 3=,求β的值.解(Ⅰ)因为(),22222πββπππα-=--=∠-=BAD 所以.02cos sin ,2cos )22sin(sin =+-=-=βαβπβα即 6分(Ⅱ)()αβββπαsin 3sin ,sin 3sin sin ==-=∆所以中，由正弦定理得在DCAC DC ADC . 由(1)有()1sin 23sin 1sin 22cos sin 22-=-=-=ββββα，所以,即3,20.33sin 23sin ,03sin sin 322πβπβββββ=<<-===--因此又或解得12分18.(本小题满分12分)如图,在长方体1111ABCD A BC D -中，E AD AA ,21==为CD 中点. (Ⅰ)求证:11B E AD ⊥ ；(Ⅱ)在棱1AA 上是否存在一点P ,使得//DP 平面1B AE ?若存在,求AP 的长；若不存在,说明理由.(Ⅰ)连D A 1,1111111111,,AD A B DA D A A B AD D A AD AA ⊥⊥⊥=所以平面又，所以因为所以D B A AD 111平面⊥,又因为11B A ∥DE ,所以，因此平面D B A E B 111⊂11B E AD ⊥. 6分(Ⅱ)取棱1AA 的中点P ,则有//DP 平面1B AE ，其中AP 的长为1.证明如下: 取PF B AA PF F AB 的中位线，所以为则的中点111,∆∥，又且111121B A PF B A =ED ∥PF B A ED B A ，所以且111121=∥，且ED PF ED =所以DP ∥EF 又 DP AEB EF AEB DP ，所以平面平面11,⊂⊄∥平面1B AE . 12分19.(本小题满分13分)已知不在x 轴上的动点P 与点()0,2F 的距离是它到直线l ：21=x 的距离的2倍.（Ⅰ）求点P 的轨迹E 的方程；（Ⅱ）过点F 的直线交E 于C B ,两点，试判断以线段BC 为直径的圆是否过定点?并说明理由.解：(1)设P (x ,y )12||2x =-化简得x 2－23y =1(y ≠0). 4分(2)由题意可设过点F 的直线的方程为2+=ky x ,代入1322=-y x 得()09121322=++-ky y k由题意知3k 2-1≠0且△＞0,设()()2211,,,y x C y x B ，则⎩⎨⎧1391312221221-=--=+k y y k k y y 8分设()0,1-A ,因为()()()()()()()()()09133613199313311,1,1222221212212121212211=+---+=++++=+++=+++=++=⋅k k k k y y k y y k y y ky ky y y x x y x y x AC AB ⊥∴,故以线段BC 为直径的圆过定点()0,1-A . 13分20.(本小题满分13分)对于任意的*n N ∈（n 不超过数列的项数），若数列{}n a 满足：n n a a a a a a ⋅⋅=+++ 2121，则称该数列为K 数列. （Ⅰ）若数列{}n a 是首项12a =的K 数列，求3a 的值；（Ⅱ）若数列1n a ⎧⎫⎨⎬⎩⎭是K 数列.(1)试求1n a +与n a 的递推关系；(2)当时且1031<<≥a n ,试比较na a a 11121+++ 与316的大小.解（Ⅰ）有题意可得.222,2222121==+=+a a a a a a a ，所以即又,42233321321a a a a a a a a =++=++，即所以343=a . 3分（Ⅱ）(1)因为数列1n a ⎧⎫⎨⎬⎩⎭是K 数列，所以()11111≥===∑n a a n i i n i i ① 111111+=+==∑n i i n i i a a ②两式相减得()11111111≥⎪⎪⎭⎫ ⎝⎛-==++n a a a n i i n n ③ 则()20111111≥≠⎪⎪⎭⎫ ⎝⎛-=-=n a a a n i in n ④两式相除得()2111111111≥-⎪⎪⎭⎫ ⎝⎛-=++n a a a a a nn n n n ,整理得()2121≥+-=+n a a a nn n 又1221211,1111a a a a a a -=⋅=+所以. 综上所述，1+n a 与递推关n a 系为⎩⎨⎧≥+-=-=+2,11,121n a a n a a n nn n . 8分(2)()41613161314343,143214311010124223121≥≥>=+-⎪⎭⎫⎝⎛≥<+⎪⎭⎫ ⎝⎛-=≤<-=<<<+n a a a a a a a a n n ，又所以，从而，所以因为又当1111121---=≥+n n n a a a n 时，,所以 当时，3≥n.31611111111111111111111111121132121≥-=--=---+=⎪⎪⎭⎫⎝⎛---++⎪⎪⎭⎫ ⎝⎛---+=+++++++n n n n n n a a a a a a a a a a a a a13分21.(本小题满分13分)已知函数()x a x x f ln 1)(2+-=有两个极值点,,21x x 且.21x x < (Ⅰ)求实数a 的取值范围，并讨论)(x f 的单调性； (Ⅱ)证明:42ln 21)(2->x f . 解(Ⅰ)由题设知,函数)(x f 的定义域为()()()0,22,,02='+-='+∞x f xax x x f 且有两个不同的根，且，即的判别式故21084022,,221<>-=∆=+-a a a x x x x.00.22112211121>>-+=--=a x a x a x ，故又，因此a 的取值范围是⎪⎭⎫⎝⎛210，. 4分()()0;002121<'<<>'><<x f x x x x f x x x x 时，当时，或当.因此()()()上单调递减，上单调递增，在，和，在21210)(x x x x x f ∞+. 6分 (Ⅱ)由(Ⅰ)可知()22212121122,2,1x x x x a ax x x x -====+所以,因此()()()121ln 121ln 1)(2222222222<<-+-=+-=x x x x x x a x x f ，其中. 9分()()()则设),121(ln 1212<<-+-=t t t t t t h()()()()(),0ln 21211ln 21212>-=⎥⎦⎤⎢⎣⎡-+-+-='t t t t t t t t t h所以42ln 21)21()(121)(-=>⎪⎭⎫ ⎝⎛h t h t h 单调递增，所以，在.即42ln 21)(2->x f . 13分。

湖南省2018年高考文科数学试题及答案（Word 版）（试卷满分150分，考试时间120分钟）注意事项：1．答卷前，考生务必将自己的姓名和准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其它答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知集合{}02A =，，{}21012B =--，，，，，则A B =A ．{}02，B ．{}12，C ．{}0D ．{}21012--，，，， 2．设1i2i 1iz -=++，则z = A ．0B ．12C ．1D ．23．某地区经过一年的新农村建设，农村的经济收入增加了一倍．实现翻番．为更好地了解该地区农村的经济收入变化情况，统计了该地区新农村建设前后农村的经济收入构成比例．得到如下饼图：则下面结论中不正确的是 A ．新农村建设后，种植收入减少B ．新农村建设后，其他收入增加了一倍以上C ．新农村建设后，养殖收入增加了一倍D ．新农村建设后，养殖收入与第三产业收入的总和超过了经济收入的一半4．已知椭圆C ：22214x y a +=的一个焦点为(20)，，则C 的离心率为 A ．13B ．12C ．22D ．2235．已知圆柱的上、下底面的中心分别为1O ，2O ，过直线12O O 的平面截该圆柱所得的截面是面积为8的正方形，则该圆柱的表面积为 A ．122πB ．12πC ．82πD ．10π6．设函数()()321f x x a x ax =+-+．若()f x 为奇函数，则曲线()y f x =在点()00，处的切线方程为A ．2y x =-B ．y x =-C ．2y x =D ．y x =7．在△ABC 中，AD 为BC 边上的中线，E 为AD 的中点，则EB = A ．3144AB AC - B ．1344AB AC - C ．3144AB AC +D ．1344AB AC + 8．已知函数()222cos sin 2f x x x =-+，则 A ．()f x 的最小正周期为π，最大值为3 B ．()f x 的最小正周期为π，最大值为4 C ．()f x 的最小正周期为2π，最大值为3 D ．()f x 的最小正周期为2π，最大值为49．某圆柱的高为2，底面周长为16，其三视图如右图．圆柱表面上的点M 在正视图上的对应点为A ，圆柱表面上的点N 在左视图上的对应点为B ，则在此圆柱侧面上，从M 到N 的路径中，最短路径的长度为A ．217B ．25C ．3D ．210．在长方体1111ABCD A B C D -中，2AB BC ==，1AC 与平面11BB C C 所成的角为30︒，则该长方体的体积为 A ．8B．C．D．11．已知角α的顶点为坐标原点，始边与x 轴的非负半轴重合，终边上有两点()1A a ，，()2B b ，，且2cos 23α=，则a b -= A ．15B．5C．5D ．112．设函数()201 0x x f x x -⎧=⎨>⎩，≤，，则满足()()12f x f x +<的x 的取值范围是A ．(]1-∞-，B ．()0+∞，C ．()10-，D ．()0-∞，二、填空题（本题共4小题，每小题5分，共20分）13．已知函数()()22log f x x a =+，若()31f =，则a =________．14．若x y ，满足约束条件220100x y x y y --⎧⎪-+⎨⎪⎩≤≥≤，则32z x y =+的最大值为________．15．直线1y x =+与圆22230x y y ++-=交于A B ，两点，则AB =________．16．△ABC 的内角A B C ，，的对边分别为a b c ，，，已知sin sin 4sin sin b C c B a B C +=，2228b c a +-=，则△ABC 的面积为________．三、解答题：共70分。

科目：数学（文科）（试题卷）注意事项：1. 答题前，考生务必将自己的姓名、准考证号写在答题卡和该试题卷的封面上，并认真核对条形码的姓名、准考证号和科目。

2. 选择题和非选择题均须在答题卡上作答，在本试题卷和草稿纸上作答无效。

考生在答题卡上按答题卡中注意事项的要求答题。

3. 本试题卷共7页。

如缺页，考生须及时报告监考老师，否则后果自负。

4. 考试结束后，将本试题卷和答题卡一并交回。

姓名准考证号绝密★启用前长沙市2018届高三年级统一模拟考试文科数学本试题卷共7页，全卷满分150分.考试用时120分钟.一、选择题：本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知集合A＝{x|x－1＞0}，B＝{x|2－x＜0}，则下列结论正确的是A．A∩B＝A B．A∪B＝BC．“x∈A”是“x∈B”的充分条件D．“x∈A”是“x∈B”的必要条件2．已知复数21zi=−，则下列结论正确的是A．z的虚部为i B．|z|＝2C．z2为纯虚数D．z的共轭复数1z i=−+3．已知a，b为单位向量，且a⊥(a＋2b)，则向量a与b的夹角为A．30° B．60° C．120° D．150°4．设首项为1，公比为23的等比数列{a n}的前n项和为S n，则下列结论正确的是A．S n＝4－3a n B．S n＝3－2a nC．S n＝3a n－2 D．S n＝2a n－15．已知f(x)是定义在R上的偶函数，且当x≥0时，f(x)＝x2－x，则不等式f(x＋2)＜6的解集是A．{x|－5＜x＜1} B．{x|－4＜x＜0}C．{x|－1＜x＜5} D．{x|0＜x＜4}6．已知某几何体的正视图和俯视图是如图所示的两个全等的矩形，给出下列4个图形：① ② ③ ④其中可以作为该几何体的侧视图的图形序号是A．①②③B．②③④C．①②④D．①③④正视图俯视图文科数学试卷第1页（共7页）文科数学试卷 第2页（共7页）7．若正整数N 除以正整数m 后的余数为r ，则记为N ＝r (mod m )，例如10＝2(mod 4)．下列程序框 图的算法源于我国古代算术《中国剩余定理》， 则执行该程序框图输出的i 等于A ．3B ．9C ．27D ．818．函数()21x xf x x =++的图象大致为A. B. C. D.9．设点A (1，0)，B (－1，0)，M 为动点，已知直线AM 与直线BM 的斜率之积为定值m (m ≠0)，若点M 的轨迹是焦距为4的双曲线(除去点A 、B )，则m ＝ A ．15B ．3CD10．已知函数()sin()(0,0,||2f x A x A πωϕωϕ=+>><的部分图象如图所示，则f (0)＝ AB ．32CD ．111．已知x ，y 满足约束条件02340x y x y y ⎧−≥⎪⎪⎪⎪+≤⎨⎪⎪⎪≥⎪⎩，若z ＝ax ＋y 的最大值为4，则a ＝A ．2B ．12C ．－2D ．12−（第7题图）文科数学试卷 第3页（共7页）12．设平行于x 轴的直线l 分别与函数2x y =和12x y +=的图象相交于点A ，B ，若函数2x y =的图象上存在点C ，使得△ABC 为等边三角形，则这样的直线lA ．不存在B ．有且只有一条C ．至少有两条D ．有无数条二、填空题：本大题共4个小题，每小题5分，共20分.把各题答案的最简形式写在题中的横线上.13．已知数列{a n }满足12n n a a +−=(n ∈N*)，S n 为{a n }的前n 项和，若S 11＝S 10＋12，则a 1＝ .14．某种活性细胞的存活率y (%)与存放温度x (°C )之间具有线性相关关系，样本数据如下表所示：存放温度x (°C ) 10 4 －2 －8存活率y (%)20 44 56 80经计算得回归直线的斜率为－3.2.若存放温度为6°C ，则这种细胞存活率的预报值为 %15．设点P 为抛物线C ：y 2＝8x 与圆M ：x 2＋y 2＋2x －m ＝0的一个交点，F 为抛物线C的焦点，若|PF |＝3，则圆M 的半径为 .16．如图，在平面四边形ABCD 中，AB ⊥AD ，AB ＝AD ＝1，BC ＝CD ＝5，以直线AB为轴，将四边形ABCD 旋转一周，则所得旋转体的体积为 .A BCD文科数学试卷 第4页（共7页）三、解答题：本大题共7个小题，共70分，解答应写出文字说明,证明过程或演算步骤.第17～21题为必考题，每个试题考生都必须作答，第22，23题为选考题，考生根据要求作答. （一）必考题：共60分. 17．（本小题满分12分）在锐角△ABC 中，角A 、B 、C 的对边长分别为a 、b 、c ，已知22()a c a c b =−+. （Ⅰ）求角B 的值；（Ⅱ）设m ＝2a －c，若b ，求m 的取值范围.18．（本小题满分12分）如图，在平行四边形ABCD 中，AB ＝2AD ＝4，∠BAD ＝60°，E 为AB 的中点.将△ADE 沿直线DE 折起到△PDE 的位置，使平面PDE ⊥平面BCDE . （Ⅰ）证明：CE ⊥平面PDE .（Ⅱ）设F 为线段PC 的中点，求四面体D -PEF 的体积.ADFCBEP某科研所共有30位科研员，其中60%的人爱好体育锻炼. 经体检调查，这30位科研员的健康指数(百分制)如下茎叶图所示.体检评价标准指出：健康指数不低于70者为身体状况好，健康指数低于70者为身体状况一般.（Ⅰ）根据以上资料完成下面的2×2列联表，并判断有多大把握认为“身体状况好与爱好体育锻炼有关系”？身体状况好身体状况一般总计爱好体育锻炼不爱好体育锻炼总计30 （Ⅱ）现将30位科研员的健康指数分为如下5组：[50，60)，[60，70)，[70，80)，[80，90)，[90，100)，其频率分布直方图如图所示.计算该所科研员健康指数的平均数，由茎叶图得到的真实值记为x，由频率分布直方图得到的估计值记为x (同一组中的数据用该组区间的中点值作代表)，求x 与x的误差值；（Ⅲ）从该科研所健康指数高于90的5人中随机选取2人介绍养生之道，求这2人都爱好体育锻炼或都不爱好体育锻炼的概率.附：22()()()()()()a b c d ad bcKa b c d a c b d+++−=++++. 30位科研员健康指数的和3012288iix==∑.P(K2≥k0) 0.10 0.05 0.025 0.010 0.005 0.001 k0 2.706 3.841 5.024 6.635 7.879 10.8285 6 8 98 5 6 3 3 4 5 77 6 6 5 2 1 7 29 7 6 4 3 2 0 8 55 4 2 9 1 3爱好体育锻炼 不爱好体育锻炼文科数学试卷第5页（共7页）文科数学试卷 第6页（共7页）如图，设椭圆中心在原点，焦点在x 轴上，A 、B 为椭圆长轴的两个端点，F 为椭圆的右焦点.，且|AF |·|BF |＝4. （Ⅰ）求椭圆的标准方程；（Ⅱ）设M 是椭圆上位于x 轴上方的一个动点，直线AM ，BM 分别与直线x ＝6相交于点D ，E ，求|DE21.（本小题满分12分） 已知函数2()ln f x ax x x =−.（Ⅰ）若f (x )在(0，＋∞)内单调递增，求a 的取值范围；（Ⅱ）若a ＝e (e 为自然对数的底数)，证明：当x ＞0时，1()x f x xe e <+.文科数学试卷 第7页（共7页）（二）选考题：共10分.请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题计分.22.（本小题满分10分）选修4－4：坐标系与参数方程在直角坐标系xOy 中，已知曲线C的参数方程为sin x y θθ⎧=⎪⎨⎪=⎩(θ为参数). （Ⅰ）以原点O 为极点，x 轴正半轴为极轴建立极坐标系，求曲线C 的极坐标方程； （Ⅱ）设A ，B 为曲线C 上两动点，且OA ⊥OB ，求|AB |的取值范围.23.（本小题满分10分）选修4－5：不等式选讲 设函数f (x )＝|x ＋3|＋|x －2|的最小值为m . （Ⅰ）求不等式|2x －1|＋x ＜m 的解集； （Ⅱ）已知||10m a <，||10mb <，证明：|4ab －1|＞2|a －b |.。

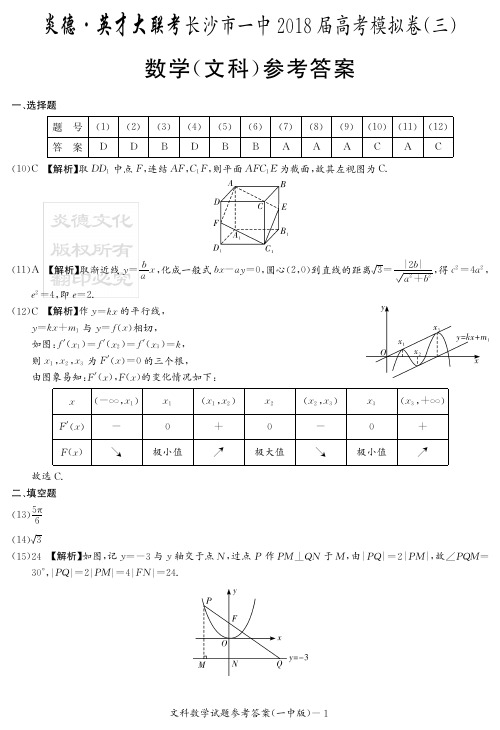
yx2018高考湖南文科数学试题及全解全析一．选择题1．已知{}7,6,5,4,3,2=U ，{}7,5,4,3=M ，{}6,5,4,2=N ，则( )A ．{}6,4=⋂N M .B M N U =UC ．U M N C u =Y )( D. N N M C u =I )( 【答案】B【解析】由{}7,6,5,4,3,2=U ，{}7,5,4,3=M ，{}6,5,4,2=N ，易知B 正确. 2．“21<-x ”是“3<x ”的( )A ．充分不必要条件 B.必要不充分条件C ．充分必要条件 D.既不充分也不必要条件 【答案】A【解析】由21<-x 得13x -<<，所以易知选A.3．已条变量y x ,满足⎪⎩⎪⎨⎧≤-≤≥,0,2,1y x y x 则y x +的最小值是( )A ．4 B.3 C.2 D.1 【答案】C【解析】如图得可行域为一个三角形，其三个顶点分别为(1,1),(1,2),(2,2),代入验证知在点(1,1)时,x y +最小值是11 2.+=故选C.4.函数)0()(2≤=x x x f 的反函数是( ))0()(.1≥=-x x x f A )0()(.1≥-=-x x x f B)0()(.1≤--=-x x x fC )0()(.21≤-=-x x x fD【答案】B【解析】用特殊点法,取原函数过点(1,1),-则其反函数过点(1,1),-验证知只有答案B 满足.也可用直接法或利用“原函数与反函数的定义域、值域互换”来解答。

5.已知直线m,n 和平面βα,满足βα⊥⊥⊥,,a m n m ,则( ).A n β⊥ ,//.βn B 或β⊂n α⊥n C . ,//.αn D 或α⊂n 【答案】D【解析】易知D 正确.6．下面不等式成立的是( )A ．322log 2log 3log 5<<B ．3log 5log 2log 223<<C ．5log 2log 3log 232<<D ．2log 5log 3log 322<< 【答案】A【解析】由322log 21log 3log 5<<< , 故选A.7．在ABC ∆中，AB=3，AC=2，BC=10，则AB AC •=u u u r u u u r( )A ．23-B ．32-C ．32D ．23 【答案】D【解析】由余弦定理得1cos ,4CAB ∠=所以1332,42AB AC •=⨯⨯=u u u r u u u r 选Ｄ.8．某市拟从4个重点项目和6个一般项目中各选2个项目作为本年度启动的项目，则重点项目A 和一般项目B 至少有一个被选中的不同选法种数是( ) A ．15 B ．45 C ．60 D ．75 【答案】C 【解析】用直接法：11122135353515301560,C C C C C C ++=++=或用间接法：22224635903060,C C C C -=-=故选Ｃ.9．长方体1111ABCD A B C D -的8个顶点在同一个球面上，且AB=2，AD=3，11=AA ，则顶点A 、B 间的球面距离是( ) A ．42π B ．22π C ．π2 D ．2π2 【答案】B【解析】112BD AC R ===Q R ∴=设11,BD AC O =Q I 则OA OB R ===,2AOB π⇒∠=,2l R πθ∴==故选Ｂ.10．双曲线)0,0(12222>>=-b a by a x 的右支上存在一点，它到右焦点及左准线的XyOPBA 距离相等，则双曲线离心率的取值范围是( )A ．2]B ．[2,)+∞C ．21]+D ．[21,)++∞ 【答案】C【解析】200a ex a x c -=+Q 20(1)a e x a c ⇒-=+2(1),a a e a c⇒+≥-1111,a e c e∴-≤+=+2210,e e ⇒--≤1212,e ⇒≤≤+ 而双曲线的离心率1,e >21],e ∴∈故选Ｃ.二．填空题11．已知向量)3,1(=a ，)0,2(-=b ，则b a +=_____________________. 【答案】２【解析】由(3),||13 2.a b a b +=-∴+=+=r r r rQ12.从某地区15000位老人中随机抽取500人，其生活能否自理的情况如下表所示：则该地区生活不能自理的老人中男性比女性约多_____________人。

湖南省长沙市第三中学2018年高三数学文月考试题含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 下列说法正确的是（）A.命题“若，则”的否命题为“若，则”B.“”是“”的必要不充分条件C.命题“”的否定是“”D.命题“若，则”的逆否命题为真命题参考答案：【知识点】四种命题．A2【答案解析】D 解析：对于A，该命题的否命题为：“若x2≠1，则x≠1”，∴A错误；对于B，x=﹣1时，x2﹣5x﹣6=0，充分性成立，x2﹣5x﹣6=0时，x=﹣1或x=6，必要性不成立，∴是充分不必要条件，B错误；对于C，该命题的否定是：“x∈R，均有x2+x﹣1≥0，∴C错误．对于D，x=y时，sinx=siny成立，∴它的逆否命题也为真命题，∴D正确．故选：D．【思路点拨】本题考查了四种命题之间的关系，也考查了命题特称命题与全称命题的关系以及命题真假的判断，是基础题．2. 已知sin（）=则cos（x）等于( )A．﹣B．﹣C．D．参考答案：D考点：两角和与差的余弦函数；两角和与差的正弦函数．专题：计算题；三角函数的求值．分析：由诱导公式化简后即可求值．解答：解：cos（x）=sin[﹣（x）]=sin（﹣x）=．故选：D．点评：本题主要考察了诱导公式的应用，属于基础题．3. 已知变量满足约束条件，则的最小值为 ( )A． B． C． 8D．参考答案：C略4. 函数在[－π，π]上的图象大致为（）A．B．C. D．参考答案：A∵，∴为偶函数，排除B、D．∵，∴排除C，故选A．5. 方程的解的个数有__________A、1个 B 、2个C、3个D、4个参考答案：B略6. 函数与的图象交点的横坐标之和为，则（）A．－1 B．0 C．1 D．2参考答案：B7. 函数的图象如图所示，为了得到的图象，则只要将的图象（）A．向右平移个单位长度 B．向右平移个单位长度C．向左平移个单位长度 D．向左平移个单位长度参考答案：B8. 已知函数和函数在区间上的图象交于三点，则△的面积是（）A． B． C．D．参考答案：D，有图像可得为等腰三角形，底边为一个周期长，高为，则9. 在极坐标系中，点（1，）与点（1，）的距离为（）A．1 B．C．D．参考答案：B【考点】极坐标刻画点的位置．【分析】极坐标化为直角坐标，即可得出结论．【解答】解：点（1，）与点（1，）的距离，即点（，）与点（﹣，）的距离为，故选B．【点评】本题考查极坐标与直角坐标的互化，比较基础．10. 如图,已知正六边形P1P2P3P4P5P6,下列向量的数量积中最大的是（）A． B．C． D．参考答案：A二、填空题:本大题共7小题,每小题4分,共28分11. （坐标系与参数方程选做题）在极坐标系中，已知两点、的极坐标分别为，，则△（其中为极点）的面积为参考答案：312. 在的展开式中，的系数是（用数字作答）．参考答案：略13. 已知则的值为 .参考答案：3略14. 等差数列{a n}的前n项和为S n，已知S10=0，S15 =25，则nS n 的最小值为________.参考答案：15. 椭圆中，过焦点且垂直于长轴的直线被椭圆截得的线段长为，焦点到相应准线的距离也为，则该椭圆的离心率为参考答案：16.已知球O的半径为1，A、B、C三点都在球面上，且每两点间的球面距离都是，则球心到平面ABC的距离为___________。

湖南省三湘名校教育联盟2018届高三第三次联考数学（文）试卷第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知集合，则（）A． B． C． D．2.已知为虚数单位，若，则复数（）A． B． C． D．3.已知以原点为圆心，1为半径的圆以及函数的图象如图所示，则向圆内任意投掷一粒小米（视为质点），该小米落入阴影部分的概率为（）A． B． C． D．4.已知为双曲线上一点，则点到双曲线的渐近线的距离为（）A． B．或 C． D．或5.已知等差数列的各项都为整数，且，则（）A．70 B．58 C．51 D．406.函数的图象如图所示，则（）A.在上是增函数B.在上是增函数C.在上是増函数D.在上是增函数7.设非零向量满足，且，则向量与的夹角为（）A． B．C． D．8.执行如图所示的程序框图，当时，输出的值为（）A． B．0 C． D．9. 如图所示，格纸上小正方形的边长为1，粗实线和虚线画出的是某几何体的三视图，则该几何体的表面积为（）A． B．C． D．10.已知点满足，直线与圆交于两点，则的最小值为（）A． B．4 C．7 D．11. 已知抛物线的焦点为，准线为，过点的直线交拋物线于两点，过点作准线的垂线，垂足为，当点坐标为时，为正三角形，则此时的面积为（）A． B． C． D．12.已知函数，若当时，不等式组恒成立，则实数的取值范围为（）A． B． C． D．第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13. 已知，则．14. 已知定义在上的函数满足:①函数的图象的对称中心为，且对称轴为；②当时，，则．15.已知正四棱锥的内切球的表面积为，且底面是边长为6的正方形，则正四棱锥的体积是．16.已知首项为2的数列的前项和满足：，记，当取得最大值时，的值为．三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17. 如图，分别为中角的对边，，.（1）求的值；（2）求的外接圆的半径.18. 《中华人民共和国道路交通安全法》第47条的相关规定：机动车行经人行横道时，应当减速慢行；遇行人正在通过人行横道，应当停车让行，俗称“礼让斑马线”，《中华人民共和国道路交通安全法》第90条规定：对不礼让行人的驾驶员处以扣3分，罚款50元的处罚.下表是某市一主干路口监控设备所抓拍的5个月内驾驶员不“礼让斑马线”行为统计数据：（1）请利用所给数据求违章人数与月份之间的回归直线方程；（2）预测该路口 9月份的不“礼让斑马线”违章驾驶员人数；（3）若从表中3、4月份分别抽取4人和2人，然后再从中任选2 人进行交规调查，求抽到的两人恰好来自同一月份的概率.参考公式：，.19.如图所示，底面为菱形，,,平面.（1）设与交于点，求证：平面；（2）求多面体的体积.20. 已知椭圆的离心率为，为焦点是的抛物线上一点，为直线上任一点，分别为椭圆的上，下顶点，且三点的连线可以构成三角形.21.已知函数.（1）若，求曲线在点处的切线方程；（2）若函数，记函数在上的最小值为，求证：. 请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.22.选修4-4：坐标系与参数方程在极坐标系中，直线的极坐标方程为，现以极点为原点，极轴为轴的非负半轴建立平面直角坐标系，曲线的参数方程为（为参数).（1）求直线的直角坐标方程和曲线的普通方程；（2）若曲线为曲线关于直线的对称曲线，点分别为曲线、曲线上的动点，点坐标为，求的最小值.23.选修4-5：不等式选讲已知函数.（1）若，求不等式的解集；（2）若对于任意，不等式恒成立，求的取值范围.试卷答案一、选择题1-5: CDBBB 6-10: ADDDC 11、12：AC二、填空题13. 14. 15. 27 16. 8三、解答题17. （1）∵,∴,∴,在中，由正弦定理得，∴.（2）在中，.在中，.18. （1）由表中数据知，，∴，，∴所求回归直线方程为.（2）由（1）知，令，则人.（3）设3月份抽取的4位驾驶员编号分别为，4月份的驾驶员编号分別为.从这6人中任选两人包含以下基本事件,,共15个基本事件；其中两个恰好来自同一月份的包含7个基本事件，∴所求概率为.19. （1）取的中点，连接.由题意知，为中点，∴，又，∴，则四边形为平行四边形，∴，∴平面.（2）过点作,分别交于点,连接,.取的中点，连接，交于点.由题意知，四边形为平行四边形.∵为菱形，,∴为等边三角形，∴.∵为等边三角形，为的中点，∴,∵平面, ∴,∴平面，∴.∵平面，,∴平面,∴，∴.20. （1）由题意知，，解得，∴椭圆的方程为.（2）设点，易知，∴直线的方程为，直线的方程为.联立，得，∴，冋理可得，∴直线的斜率为，∴直线的方程为，即，∴直线过定点.21.（1）由题意知，，∴，∴，，则所求切线方程为，即.（2）由题意知，，∴。