黑龙江省哈三中2009-2010学年下学期高二年级期中考试数学试卷理科

哈三中2009—2010学年度下学期高二学年第一学段 物理试卷一、选择题（每小题4分，共60分）1、下列说法中正确的是：( )A. 一切波都能发生干涉和衍射现象B. 质点的振动方向与波的传播方向相互垂直的波是纵波C. 只有横波才能发生反射和折射现象D. 发生干涉的两列波频率一定相同2、弹簧振子在光滑水平面上做简谐运动，在振子向平衡位置运动的过程中：( )A. 振子所受回复力逐渐增大B. 振子的位移逐渐增大；C. 振子的速度逐渐减小D. 振子的加速度逐渐减小3、当一列波在同种均匀介质中传播时，发生了明显的衍射现象。

下列说法可能正确的是：（ ）A. 该波的频率将发生改变B. 该波的波速将发生改变C. 波长和障碍物的尺寸差不多D. 波长比障碍物的尺寸小得多4、古有“守株待兔”的寓言。

若兔子头部受到等于自身重力的打击力时被撞死，兔子与树桩作用时间为0.2s 且相互作用后兔子的速度变为零，则被撞死的兔子其奔跑的速度可能是(g =10m/s 2)：( )A. 1m/s ；B. 1.5m/s ；C. 2m/s ；D. 2.5m/s 。

5、如图所示，两个半径分别10m 和5m 的光滑的圆弧状轨道在最低点相切，将一小球（可视为质点）从距最低点5cm 处由静止释放。

则下列说法正确的是：( )A. 小球往返运动一次的周期比小球在半径为10m 的光滑圆弧上做 简谐运动时的周期大B. 小球在最低点左右两侧上升的最大高度相同C. 小球在最低点左右两侧通过的最长弧长相等D. 小球在最低点右侧的最大摆角是左侧的两倍6、已知一列简谐横波的传播速度v =0.5m/s ，在某时刻的波形如图中实线所示，经过一段时间后波形变为虚线，在这段时间中，质点P 通过的路程可能是：（ ）A. 0.4mB. 0.5mC. 0.6mD. 1.0m7、小型交流发电机中，矩形金属线圈在匀强磁场中匀速转动，产生的感应电动势与时间呈正弦函数关系，如图所示。

此线圈与一个R =10Ω的电阻构成闭合电路。

2009年哈师大附中高二下学期期中考试数学试卷（理科）第Ⅰ卷 （选择题 共60分）一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．若复数23z i =-+，则z 对应复平面上的点在 （ ） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限 2．定积分320|sin |x dx π⎰的值为 （ ）A ．1B ．2C ．3D ．03．以下图形分别表示一个三次函数及其导数在同一坐标系中的图象，其中一定不正确的有 （ ）A ．1个B ．2个C ．3个D ．4个4．函数28ln y x x =-的单调递增区间是 （ ） A ．11(,),(,)44-∞-+∞ B ．11(,)44- C ．1(,)4+∞ D ．1(0,)45．已知函数()(1)(2)(3)f x x x x =---，则(1)f '等于 （ ） A ．2 B ．2- C ．0 D ．6 6．已知112(0)adx a x=>⎰，则a 的值为 （ ）A ．12B ．2e C ．3 D ．不存在7．设坐标平面上的抛物线C ：2y x =，过第一象限的点2(,)a a 作曲线C 的切线l ，l 与y 轴的夹角为30o ，则a 的值为 （ ）A B ． C D ．8．已知0m <，312()xf x mx m=+，且(1)12f '≥-，则实数m 的值为 （ ） A ．2 B ．2- C ．4 D ．4-9．若直线4mx ny +=和⊙O ：224x y +=没有交点，则过点(,)m n 的直线与椭圆22194x y +=的交点个数为 （ ） A ．至多1个 B ．2个 C ．1个 D ．0个10．函数()y f x =是圆心在原点的单位圆的两段圆弧（如图），则不等式()()f x f x x <-+的解集为（ ）A．{|01}55x x x -<<<≤或 B．{|11}x x x -≤<<≤ C．{|10x x x -≤<<< D．{|0}x x x <<≠且 11．若π02x <<，则2x 与3sin x 的大小关系是 （ ） A ．23sin x x > B ．23sin x x < C ．23sin x x = D ．与x 的值有关12．偶函数()f x 在(,)-∞+∞内可导，且0(1)(1)lim 1x f f x x→--=-，(2)(2)f x f x +=-，则曲线()y f x = 在点(5,(5))f --处切线的斜率为 （ ） A ．2 B ．2- C ．1 D ．1-第Ⅱ卷 （非选择题 共90分）二、填空题（本大题共4小题，每小题5分，共20分，把答案填在答题纸相应位置上） 13．已知某圆的极坐标方程为24sin()104πρρθ+++=，化为普通方程为______________________．14．把由曲线1,2y x x ===及x 轴所围成的曲边梯形绕x 轴旋转一周，则旋转所形成的旋转体的体积为_____________．15．已知32()(1)3(1)f x x x f xf ''=++-，则(1)(1)f f ''+-=_____________．16．已知函数(),()f x g x 都是定义在R 上的函数，()0g x ≠，()()()()f x g x f x g x ''>，()()x f x a g x =(0,1)a a >≠且，(1)(1)5(1)(1)2f f g g -+=-，在有穷数列()()f n g n ⎧⎫⎨⎬⎩⎭(1,2,,10)n =中，任意取正整数(110)k k ≤≤，前k 项和大于1516的概率是 _____________． 三、解答题（本大题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤） 17．（本题满分10分）已知复数222(1)()z m m m i m R =--+-∈，当m 为何值时，复数z ：（1）是实数； （2）是纯虚数． 18．（本题满分12分）已知函数21()2xf x x e =． （1）求()f x 的单调区间；（2）若当[2,2]x ∈-时，不等式()f x a ≥恒成立，求实数a 的取值范围．19．（本题满分12分）如图，在会展中心广场要临时搭建占地面积为a 平方米长宽不等的冰雕景区，四周有小路，冰雕景区长边外小路宽6米，短边外小路宽8米，冰雕景区长边长为x 米(2030)x ≤≤．对于给定的a (290800)a ≤≤，怎样设计冰雕景区的长与宽，使冰雕景区和小路占地面积总和最小．20．（本题满分12分） 如图，直三棱柱ABC —A 1B 1C 1中，AB=AC ，D 为BC 中点， F 为BB 1上一点，BF=BC=2，FB 1=1． （1）求证：AD ⊥平面BB 1C 1C ；（2）若E 为AD 上不同于A 、D 的任一点，求证：EF ⊥FC 1；C 1B 1FED C BA 1（3）若AB=3，求FC 1与平面AA 1B 1B 所成角的正弦值．21．（本题满分12分）已知A 、B 、C 是长轴长为4的椭圆上的3个点，点A 是长轴的一个顶点，BC 过椭圆中心，且0AC BC ⋅=，2BC AC =．（1）求椭圆方程；（2）动弦CP 、CQ 分别交轴于E 、F 两点，且CE CF =， 求证：//PQ AB ．22.（本题满分12分）已知函数32()f x x ax bx c =+++的图象如图所示，与x 轴相切于点O ，与x 正半轴相交于点A ，且此函数图象与x 轴所围成区域（图中阴影部分）的面积为274.（1）求函数()y f x =的解析式；（2）设1m >，如果过点(,)m n 可作函数()y f x =的两条切线，求证：点(,)m n 在函数()y f x = 的图象上，或者在某条定直线上，并求出该直线方程； （3）设1m n <<，求证：()()2()02m nf m f n f ++->．哈师大附中高二下学期期中考试数学答案（理科）一、选择题：BCBCA BCBBA DC二、填空题：13.22((3x y +++= 14.32π 15. 34-16.35xoy A三、解答题17.解：（1）若复数z 为实数，则有210m -=，1m ∴=或1m =-……5’ （2）若复数z 为纯虚数，则有220m m --=且210m -≠，2m ∴=……10’ 18.解：（1）2211'()(2)22xx x f x xe x e e x x =+=+……1’ 令'()0f x >，220x x ∴+>0x ∴>或2x <-， 令'()0f x <，220x x ∴+<20x ∴-<<……5’()f x ∴的单调递增区间为(),2,-∞-()0,+∞，减区间为()2,0- ……6’（2）当[]2,2x ∈-时，由（1）知()f x 在()2,0-上递减，在(0,2)上递增，∴当0x =时()f x 有最小值为(0)0f =，……9’若当[]2,2x ∈-时不等式()f x a ≥恒成立，则只须min ()0a f x ≤=，即0a ≤ ……12’ 19.解：设冰雕景区的长为x 米，则宽为ax米，设总占地面积为y 平方米，依题意有 16(16)(12)12192a a y x x a x x =++=+++……3’， 216'12ay x=- ……4’令'0y =得x =5’（1）当300675a ≤≤时，则2030≤≤，此时192y a ≥+，当且仅当x =……7’（2）当290300a ≤<20<， 此时'0y >，函数在[]20,30上单调递增，20x ∴=时，y 最小 ……9’（3）当675800a <≤30> 此时'0y <，函数在[]20,30上单调递减，30x ∴=时，y 最小 ……11’ 答：当290300a ≤<时，长取20米，宽取20a米，面积总和最小；当300675a ≤≤当675800a <≤时，长取30米，宽取30a米，面积总和最小。

黑龙江省哈尔滨第三中学高二下学期期末考试数学（理）试题2007.7考试说明：1．本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分，满分150分。

考试时间为120分钟。

2．第I 卷试题答案均涂在机读卡上，第II 卷试题答案写在试卷上。

3．交机读卡和第II 卷。

第Ⅰ卷（选择题，共60分）一、选择题（本大题共12小题，每小题5分，共60分. 在每小题给出的四个选项中，只有一项是符合题目要求的）1．已知直线a 与平面所成的角为60°，那么a 与内不过斜足的直线所成的角中，最大的角的是 A ．180° B ．120° C ．90° D ．60° 2．设为直线，为平面，有下列四个命题 ①； ②； ③若； ④若.这个四个命题中，正确命题的个数是 （ ） A ．1 B ．2 C ．3 D ．4 3．5人站成一排，甲乙两人必须站在一起的不同站法有 （ ） A ．12种 B ．24种 C ．48种 D ．60种4．从数字1、2、3、4、5中任取两个不同的数字构成一个两位数，则这个两位数大于40的概率为 （ ） A ． B ． C ． D ． 5．设7654321772221052,)1()21(a a a a a a a x a x a x a x a a x x +++++++++++=++则 = （ ） A ．287 B ．288 C ．289 D ．2906．过球的一条半径的中点，作垂直于该半径的平面，则所得截面的面积与球的表面积的比为 （ ） A ． B ． C ． D ．7．某中学要把9台相同的电脑送给西部地区的三所希望小学，每年小学至少得到两台，则不同的送法的种数共有 （ ） A ．10种 B ．9种 C ．8种 D ．6种 8．已知随机变量ξ服从二项分布的值为 （ ） A ． B ． C ． D ．9．正方形ABCD 所在平面与正方形ABEF 所在平面成60°的二面角，则异面直线AD 与BF 所成角的余弦值为 （ ） A ． B ． C ． D ．10．有一道竞赛题，甲解出它的概率为，乙解出它的概率为，丙解出它的概率为，则 甲、乙、丙三人独立解答此题，只有1人解出的概率是 （ ） A ． B ． C ． D ．111．在的展开式中，所有奇数项系数之和为1024，则中间项的系数是（ ）A．330 B．462 C．682 D．79212．已知△ABC中，AB=9，AC=15，∠BAC=120°，平面ABC外一点P到A、B、C的距离都是14，那么P点到平面ABC的距离是（）A．13 B．9 C．11 D．7第II卷（非选择题，共90分）二、填空题（本大题共4个小题，每小题4分，共16分，将答案填在题后的横线上）13．在4次独立重复试验中事件A出现的概率相同，若事件A至少发生1次的概率为，事件A在一次试验中发生的概率是14．设随机变量ξ满足P（ξ=1）=P，P（ξ=0）=1－P，则D（ξ）=15．把等腰直角△ABC沿斜边BC上上的高AD折成一个二面角，若此时∠BAC=60°则此时一面角的大小是16．已知正三棱柱ABC—A1B1C1的所有棱长均为1，则B1C1中点M到面A1BC的距离为三、解答题（本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤）17．（本小题满分12分）如图，两个边长都为a的正方形ABCD和ABEF所在平面相互垂直，M、N分别在它们的对角线AC、BF上，且CM=BN，求证：MN//平面BEC.18．（本小题满分12分）某安全生产监督部门对5家小煤矿进行安全检查（简称安检），若安检不合格，则必须整改，若整改后经复查仍不合格，则强制关掉，设每家煤矿安检是否合格是相互独立的，且每家煤矿整改前安检合格的概率是0.5，整改后安检合格的概率是0.8，计算：（1）恰有两家煤矿必须整改的概率；（2）列出必须整改煤矿的个数ξ的分布列，并求平均有多少家煤矿必须整改；（3）至少关闭一家的概率.19．（本小题满分12分）如图，在四棱锥P—ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点，作EF⊥PB交PB于点F，（1）证明：PB⊥平面EFD；（2）求二面角C—PB—D的大小.20．（本小题满分12分）经统计，某大型商场一个结算窗口每天排队结算的人数及相应的概（1）求每天不超过20人排队结算的概率；（2）一周7天中，若有3天以上（含3天）出现超过15人排队结算的概率大于0.75，商场就需要增加结算窗口，试问该商场是否需要产加结算窗口？21．（本小题满分11分）如图，斜三棱柱ABC—A1B1C的底面是直角三角形，AC⊥CB，∠ABC=45°，侧面A1ABB1是边长为 a的菱形，且垂直于底面ABC，∠A1AB=60°，E、F分别是AB、BC的中点，（1）求EF与侧面A1ABB1所成的角；（2）求点A到平面BCE的距离.22．（本小题满分14分）在正整数中，各个数位上的数字均取自集合{0，1，2，3，4，5}的数为“好数”，则（1）在所有的4位“好数”中，必有数字3且3的前面没有0的有多少个？（2）若将所有的“好数”由小到大排成数列{a n}，试求a2006的值.参考答案一、选择题1.C2.B3.C4.B5.A6.A7.A8.D9.A 10.B 11.B12.D二、填空题13． 14. P－P2 15.90° 16.三、解答题17．略18．（1）（3）P=0.4095119．（1）略（2）20．（1）0.75 （2）需要21．（1）30°（2）22．（1）500 （2）13142。

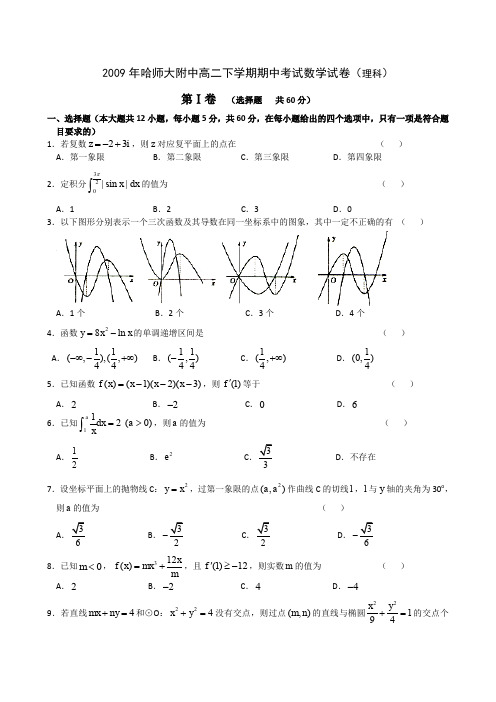
哈三中2010—2011学年度下学期 高二学年第一模块数学(理科)试卷命题员：姜仁海 王春雨 审题员：刘丹考试说明：（1）本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分，满分150分，考试时间为120分钟；（2）第I 卷，第II 卷试题答案均答在答题卡上，交卷时只交答题卡．第I 卷 （选择题, 共60分）一、选择题（本大题共12小题，每小题5分，共60分. 在每小题给出的四个选项中，只有一项是符合题目要求的） 1．2cos x dx π=⎰A ．1-B ．1C ．0D ．22． 若命题p ：2是偶数；命题q ：2是5的约数，则下列命题中为真命题的是A ．p q ∧B ．()()p q ⌝∧⌝C ．p ⌝D ．p q ∨3． 某校有老师300人，男学生1200人，女学生1000人．现用分层抽样的方法从所有师生中抽取一个容量为n 的样本，已知从女学生中抽取的人数为80，则n =A ．171B ．184C ．200D ．3924． 命题“R x ∈∃0，012030>+-x x ”的否定是 A ．x R ∀∈，3210x x -+≤ B ．R x ∈∃0，012030<+-x x C ．R x ∈∃0，012030≤+-x x D ．x R ∀∈，3210x x -+> 5． 曲线x x y ln =的切线与直线01=+-y x 平行，则切线方程为A ．03=--y xB ．02=--y xC ．01=--y xD ．0=-y x 6． “2x <”是“260x x --<”的A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件7． 一物体在力()x e x F 23+=（x 的单位：m ，F 的单位：N ）的作用下，沿着与力F 相同的方向，从0=x 处运动到1=x 处，力()x F 所做的功为A ．()23e +JB ．⎪⎭⎫ ⎝⎛+2213e J C ．⎪⎭⎫⎝⎛+22125e J D ．()22e +J8． 对两个变量y 和x 进行回归分析，得到一组样本数据：()11x y ，，()22x y ，，…，()n n x y ，，则下列说法中不正确．．．的是 A ．由样本数据得到的回归方程a x b yˆˆˆ+=必过样本中心点()x y ， B ．用相关指数2R 来刻画回归效果，2R 越小，说明模型的拟合效果越好 C ．残差平方和越小的模型，拟合的效果越好D ．在线性回归模型中，92.02=R 表示解释变量解释了%92的预报变量 9． 调查某医院某段时间内婴儿出生的时间与性别的关系，得到下面的数据表：参考公式：22()()()()()n ad bc K a b c d a c b d -=++++，其中n a b c d =+++A.99%B. 5.97%C. 95%D. 90%10． 函数()d cx bx ax x f +++=23的图象如图，则函数3232cbx ax y ++=的单调递增区间是A ．(-∞，2]B ．1[2，)+∞C ． [2-，3]D ．9[8，)+∞11． 一边长为cm 24盖方盒，则该方盒容积最大时，=xA ．3cmB ．4cmC ．5cmD ．6cm12． 定义在实数集R 上的函数()x f ，如果存在函数()B Ax x g +=（A ，B 为常数）使得()()x g x f ≥对任意的R x ∈都成立，则称()x g 为函数()x f 的一个承托函数．以下说法 （1）函数()x x x f 22-=不存在承托函数； （2）函数()x x x f 33-=不存在承托函数； （3）函数()122+-=x x xx f 不存在承托函数； （4）()1=x g 为函数()12234++-=x x x x f 的一个承托函数； （5）()x x g =为函数()1-=x e x f 的一个承托函数．中正确的个数为A ．1B ．2C ．3D ．4第Ⅱ卷 （非选择题, 共90分）二、填空题(本大题共4小题，每小题5分，共20分．将答案填在答题卡相应的位置上) 13．已知随机变量ξ～(0N ，2)σ，若(10)0.3P ξ-<<=，则(1)P ξ<= ． 14．已知函数()133123++--=a x x x x f 存在三个不同的零点，则实数a 的取值范围是 ． 15．=⎪⎪⎭⎫ ⎝⎛-⎰dx x 22413 ，该定积分的几何意义是 ． 16．已知函数()x xx x f ln 21--=，如果对任意m ，(n a ∈，)+∞，当n m >时满足 ()()mnn m n f m f 1>--，则a 的最小值为 ． 三、解答题(本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤)17．（本题10分）某市为研究市区居民的月收入调查了10000人，并根据所得数据绘制了样本的频率分布直方图（如下图）．（Ⅰ）求月收入在[3000，3500)内的被调查人数；（Ⅱ）估计被调查者月收入的平均数（同一组中的数据用该组区间的中点值作代表）． 18．（本题12已知函数(x f （Ⅰ）当a =-19．（本题12（Ⅰ）求y （Ⅱ）若某名工人的工龄为11年，试估计他每天加工的A 种零件个数．0.0005 0.0004 0.0002 0.0001O(参考公式：1221ˆni ii nii x y nx ybxnx ==-⋅=-∑∑，ˆˆay bx =-) 20．（本题12分）已知函数2()ln f x x a x =-．（Ⅰ）当1x =时()f x 取得极值，求函数的单调区间； （Ⅱ）当[1x ∈，2]时，求函数()f x 的最小值． 21．（本题12分）已知抛物线bx ax y +=2在第一象限内与直线4=+y x 相切．（Ⅰ）用b 表示a ，并求b 的范围；（Ⅱ）设此抛物线与x 轴所围成的图形的面积为S ，求S 的最大值及此时a 、b 的值． 22．（本题12分）定义：设函数)(x f 在(a ，)b 内可导，若)(x f '为(a ，)b 内的增函数，则称)(x f 为(a ，)b 内的下凸函数．（Ⅰ）已知3()x f x e ax x =-+在(0，)+∞内为下凸函数，试求实数a 的取值范围； （Ⅱ）设)(x f 为(a ，)b 内的下凸函数，求证：对于任意正数21,λλ，121=+λλ， 不等式)()()(22112211x f x f x x f λλλλ+≤+对于任意的1x ，2(x a ∈，)b 恒成立．。

黑龙江省哈三中2010届高三九月份月考（数学理）哈三中2009-2010学年度上学期高三学年9月份月考数学试题考试说明：本试卷分第I卷和第II卷两部分，满分150分，考试时间120分钟．答题前，考生先将自己的班级、姓名、考号和序号填写清楚；选择题必须使用2B铅笔填涂在机读卡上，请在各题目的答题区域内作答；只交机读卡和答题卡. 第I卷一、选择题2221. P?yy?x，Q?xx?y?2，则P?Q? ????A．[0,2] B．?(1,1),(?1,1)?C．0,2D．[?2,2] 2. 下列命题错误的是22A．命题“若x?3x?2?0，则x?1”的逆否命题为“若x?1，则x?3x?2?0” ??B．若p?q为假命题，则p、q均为假命题2C．命题p：存在x0?R,使得x0?x0?1?0，则?p：任意x?R,都有x?x?1?0 2D．“x?2”是“x?3x?2?0”的充分不必要条件23. y?x2?5x?6的定义域为ln(x?1)A．[3,??)B．(1,2] C．(1,2]?[3,??)D．(1,2)?[3,??) 24. “a?0”是“方程ax?x?1?0至少有一个负数根”的A．必要不充分条件B．充分不必要条件C．充分必要条件D．既不充分也不必要条件第1 页共7 页 5. 如图，AB是圆O 的直径，CB切圆O于B，CD切圆O于D，交BA的延长线于E，若AB?6,ED?4，则CD? A．3B．4 C．5D．6 E A D O C B 6. 下列函数中既是奇函数又在区间[?1,1]上单调递减的是A．y?sinx B．y??x?1 C．y?ln2?x1x?x D．y?(2?2) 2?x2BP3CQ3?，?，CP5QA4A Q C 7. 点P、Q分别在?ABC的边BC和AC上，R是AP上一点，AR? RP32A．B． 29820C．D．39则R B P 8. 已知f(x)?x，g(x)是R上的偶函数，当x?0时，g(x)?lnx，则y?f(x)?g(x) 的大致图象为y O x y O x y O x y O x A．B．C．D．9. 函数f(x)是定义在R上的奇函数，且f(?x)?f(?x)，则f(1)?f(2)?? 1212?f(2009)? A．2009B．1 C．0D．?1 10. 对于集合M和N，定义M?N?xx?M，且x?N，M?N?(M?N) ???(N?M)，设A?yy?x2?3x，B?yy??2x，则A?B? A．(?????9999,0)B．[?,0] C．(??,?)?[0,??)D．(??,?)?(0,??) 4444第 2 页共7 页11. 函数y?loga(x3?ax)在(?1,0)内单调递增，则a 的范围是21399A．[,1)B．[,1) C．(,??)D．(1,) 444412. 下列说法中: ①若定义在R上的函数f(x)满足f(x?2)??f(x?1)，则6为函数f(x)的周期；2②若对于任意x?(1,3)，不等式x?ax?2?0恒成立，则a?11；3③定义：“若函数f(x)对于任意x?R，都存在正常数M，使f(x)?Mx恒成立，则称函数f(x)为有界泛函．”该定义可知，函数f(x)?x2?1为有界泛函；④对于函数f(x)?x?1, 设f2(x)?f?f(x)?，f3(x)?f?f2(x)?，?，x?1，令集合M??xf2009(x)?x,x?R?，则fn?1(x)?f?fn(x)?集合M为空集. 正确的个数为A．1个B．2个C．3个D．4个第Ⅱ卷二、填空题(本题共4个小题，每小题5分，共20分，将答案填在答题卡的相应位置) 13. 在平面直角坐标系中，抛物线y2?4x经过伸缩变换?. 14. 已知直线的极坐标方程为ρcos(θ??x??3x后的图形的方程为?y??2y?π)?2，则点A(2,)到直线的距离为. 36a?b?a；15. 在实数的原有运算中，我们补充定义新运算“?”如下：当a?b时，当a?b 时，a?b?b2．设函数f?x???1?x?x??2?x?,x???2,2?，则函数f?x?的值域为. 16. 已知函数f?x??2mx2??8?2m?x?1，g?x??mx，对?x?R，f?x?与g?x?的值至少有一个为正数，则m的取值范围是. 第 3 页共7 页三、解答题(本题共6小题，总分70分，解答应写出文字说明，证明过程或演算步骤) 17.函数f(x)?x3?x. 证明：f(x)是奇函数；用定义证明f(x)在(??,??)上是单调增函数.18. 某高中需要从两名学生中选出一人参加中央电视台《开心学国学》知识竞赛，现设计了一个挑选方案：选手从5道备选题中一次性随机抽取3题进行回答．已知5道备选题中，选手甲有3题能答对，2题答错；选手乙答对每题的概率都是影响. 分别求出甲、乙两名选手答对题数的概率分布列；你认为应该挑选哪个选手去参加比赛.19. 2已知A?xx?2x?8?0,B?x9?3x?3，且每题答对与否互不5???2x?19,C?xx2?2ax?2?0. ???若不等式bx?10x?c?0的解集为A?B，求b、c 的值；2第 4 页共7 页设全集U?R，若C?B?CUA，求实数a的取值范围. 20. x2y2??1，直线l过定点P?1,1?. 已知椭圆94当直线l 的斜率为1时，求椭圆上的点到直线l距离的最大值；2直线l与椭圆交于A，B两点，求PA?PB的最小值. 21. 如图，梯形ABCD内接于圆O，AD//BC，过B引圆O的切线分别交DA、CA的延长线于E、F. 求证：AB?AE?BC；若BC?9,CD?AF?6, 求AC的长.22. 已知函数f?x??ln?x?1??ax. 讨论函数f?x?的单调性；求函数f?x?在?2,3?上的最大值；x当a?1时，令g?x??fe，且存在x0?0，满足g?x0??4x0，证明：当x?x02F E A B C D ??时，g?x??4x. 第5 页共7 页哈三中2009-2010学年度上学期高三学年9月份月考数学参考答案一、选择题二、填空题13. y??216x?14．215. [?4,6]16. (0,8) 3三、解答题17. 略；??????????4分略.?????????????10分18. 设甲、乙两人答对题数分别为?、?，?的可能取值为1,2,3，P(??1)?331，P(??2)?，P(??3)?；?的分布列略. 10510?的可能取值为0,1,2,3，836，P(??1)?，1251255427P(??2)?；P(??3)?.?的分布列略.????????????7分12512599918E??,D??，E??,D?? 525525P(??0)?D??D?，应选甲.????????????????????????12分19.A?B?[2,3],b??2,c??12；???????????????? ?6分B?CUA?(?4,3], C??时，a?(?2,2)；C??时，a?[?119,?2]?[2,) 64119综上，a?[?,).?????????????????????12分641(x?1)，椭圆上的点到直线l距离的最大值为 2 20. 直线方程为y?65?????????????????????????????6分5第 6 页共7 页23?????????????????????????????12分921. 略；?????????????????????????????5分15?????????????????????????????12分21?a(x?1)，22. f?(x)?x?1a?0时，函数f?x?在(1,??)单调递增；a?0时，函数f?x?在(1,1? a??11)单调递增；(1?,??)单调递减.???4分aa1时，函数f?x?在?2,3?上单调递增，最大值为3a?ln2；2a??1时，函数f?x?在?2,3?上单调递减，最大值为2a；?1?a??111时，函数f?x?在(2,1?)单调递增；(1?,3)单调递减，最大值2aa1为a?1?ln(?).??????????????????????8分axx设F(x)?g(x)?4x?lne?1?e?4x (x?x0?1) ??ex(ex?1)2x?e?4?x?0 F?(x)?xe?1e?1 F(x)在(1,??)单调递增，F(x)?F(x0)，x?x0时，g?x??4x.??12分第7 页共7 页。

哈三中2009-2010学年度下学期高二学年模块考试英语试题一、本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分。

满分150分，用时120分钟。

第I卷(选择题，共115分)第一部分听力 (共两节满分30 分 )做题时, 先将答案标在试卷上。

录音内容结束后, 你将有两分钟的时间将试卷上的答案转涂到答题卡上。

第一节（共5小题；每小题1.5分, 满分7. 5 分）听下面5 段对话。

每段对话后有一个小题, 从题中所给的A、B 和C三个选项中选出最佳选项, 并标在试卷的相应位置。

听完每段对话后, 你都有10秒钟的时间来回答有关小题和阅读下一题。

每段对话仅读一遍。

1. What is the man?A. A waiter.B. A farmer.C. A salesman.2. How is the woman losing weight?A. By walking.B. By running.C. By going on a diet.3. What are the speakers talking about?A. A class.B. A paper.C. A speech.4. Where did the man go last night?A. To a cinema.B. To a library.C. To a bookstore.5. What does the girl suggest doing?A. Playing football.B. Staying in the classroom.C. Watching a football match.第二节（共15小题；每小题1.5分, 满分22. 5分）听下面5段对话或独白。

每段对话或独白后有几个小题, 从题中所给的A、B、C三个选项中选出最佳选项, 并标在试卷的相应位置。

听每段对话或独白前, 你将有时间阅读各个小题, 每小题5秒钟；听完后, 各小题将给出5秒钟的作答时间。

哈三中2009-2010学年度下学期高二学年第二学段（模块）生物试卷本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分。

满分100分，时间90分钟。

第I卷(选择题，共50分)一、单项选择题（1-30每小题1分，31-40每小题2分，共50分）1. 以下不属于发酵的是( )A．利用需氧型青霉菌生产青霉素B．缺氧时人的组织细胞产生乳酸C．利用酵母菌的无氧呼吸获得酒精D．利用乳酸菌制作泡菜2.下列关于生物技术的叙述，正确的是（）A.果酒制作时应先去除葡萄的枝梗，再进行冲洗，这样洗的彻底B.果醋发酵装置的温度维持在20 ℃左右最好C.PCR技术利用了DNA的热变性原理来控制DNA的解聚和结合D.纯化后的菌种长期保存时用固体培养基培养菌落后放入4 ℃的冰箱中保存3.豆腐上长出了毛霉之后，下一步要加盐腌制，其中不属于加盐作用的是（）A.调味B.可使豆腐析出水分，使豆腐块变硬C.促进毛霉的继续生长D.抑制微生物的生长，避免豆腐变质4.细菌培养过程中分别采用了高压蒸汽灭菌、酒精消毒、火焰灼烧灭菌的几种不同的处理，这些方法可依次用于杀死哪些部位的杂菌（）A.接种环、手、培养基B.高压锅、手、接种环C.培养基、手、接种环D.接种环、培养基、手5. 哺乳动物体外受精的过程是( )①采卵②收集精子③卵细胞的人工培养④精子获能处理⑤精子和成熟卵子在受精液中共同培养⑥精子用CaCl2处理⑦卵母细胞用一定浓度肝素溶液处理⑧体外受精⑨受精卵培养高二生物第1页共8 页6．可以鉴定出尿素分解菌的方法是（）A．以硝酸盐、尿素为氮源的培养基中加入二苯胺指示剂B .以尿素为唯一氮源的培养基中加入酚红指示剂C. 以尿素为唯一氮源的培养基中加入双缩脲指示剂D. 以硝酸盐、尿素为氮源的培养基中加入酚红指示剂7．变酸的酒表面有一层膜、腐乳外面有一层致密的皮它们分别是（）A．醋酸菌、毛霉菌丝B. 醋酸菌、毛霉菌丝C．醋酸菌、毛霉菌丝D.酵母菌、乳酸菌8．下列关于细胞工程的叙述，不正确的是 ( )Ａ．植物体细胞杂交的原理是细胞膜的流动性和植物细胞的全能性Ｂ．动物细胞融合的过程包括杂交细胞形成杂交新个体Ｃ．细胞融合包括质融合和核融合，细胞壁形成是植物细胞融合完成的标志Ｄ．二倍体生物细胞融合后，遗传物质为二个细胞遗传物质的组合9．用稀释涂布平板法来统计样品中活菌的数目时，其结果与实际值相比( )A.比实际值要高B.比实际值要低C.和实际值一样D.比实际值可能高也可能低10.下列有关平板划线接种法的操作错误的是（）A.将接种环放在火焰上灼烧B.将已冷却的接种环伸入菌液中蘸取一环液C.蘸取菌液和划线要在火焰旁进行D.划线时要将最后一区的划线与第一区的划线相连11．刚果红可以与下列哪种物质形成红色复合物（）A．纤维二糖B．葡萄糖C．纤维素D．麦芽糖12．关于制备牛肉膏蛋白胨固体培养基，叙述错误的是（）Ａ.操作顺序为计算、称量、溶化、倒平板、灭菌Ｂ.将称好的牛肉膏连同称量纸一同放入烧杯Ｃ.待培养基冷却至50℃左右时进行倒平板Ｄ.待平板冷却凝固约5~10min后将平板倒过来放置13．获得纯净培养物的关键是（）Ａ.将用于微生物培养的器皿、接种用具和培养基等器具进行灭菌B.接种纯种细菌C.适宜环境条件下培养D.防止外来杂菌的入侵高二生物第2页共8 页14.有关稀释涂布平板法，叙述错误的是（）Ａ.先将菌液进行一系列的梯度稀释Ｂ.然后将不同稀释度的菌液分别涂布到琼脂固体培养基的表面Ｃ.适宜条件下培养D.结果都可在培养基表面形成单个的菌落15．将接种后的培养基和一个未接种的培养基都放入37℃恒温箱的目的是（）A.对比观察培养基有没有被微生物利用B.对比分析培养基是否灭菌彻底C.没必要放入未接种的培养基D.为了下次接种时再使用16．下列叙述错误的是（）Ａ.培养乳酸杆菌时需要在培养基中添加维生素Ｂ.培养霉菌时需将培养基的PH调至碱性Ｃ.培养细菌时需将PH调至中性或微碱性Ｄ.培养厌氧微生物时则需要提供无氧的条件17．以下有关基因工程的叙述，不正确的是( )Ａ．基因工程是分子水平上的生物工程Ｂ．基因工程的产物对人类都是有益的Ｃ．基因工程产生的变异属于基因重组Ｄ．基因工程育种的优点之一是目的性强18．以下操作用到接种环的是（）A.平板划线操作B.系列稀释操作C.涂布平板操作D.倒平板操作19．甲、乙、丙是三种微生物，下表I、Ⅱ、Ⅲ是用来培养微生物的三种培养基。

哈尔滨市第三中学高 二 年 级 下 学 期 期 中 测 试数 学 试 题考试说明：（1）本试题分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分，考试时间120分钟.（2）第I 卷试题答案均涂在机读卡上，第Ⅱ卷试题答案写在试卷上； （3）交机读卡和第Ⅱ卷.第Ⅰ卷（选择题，共60分）一、选择题（本大题共12小题，每小题5分，共60分。

在每题列出的四个选项中，只有一项是最符合题目要求的。

）1．若直线a 不平行于平面α，且a ⊄α，则有 （ ） A ．α内所有直线与a 异面 B ．α内不存在直线与a 平行 C ．α内有唯一直线与a 平行 D ．α内所有直线与a 相交 2．球大圆的面积扩大了16倍，则球体积扩大的倍数是 （ ）A ．16B ．64C ．4D ．3163．若地球的半径为R ，地面上两点A 、B 的纬度均为北纬45°，又A 、B 两点的球面距离为3Rπ，则A 、B 两点的经度差为 （ ）A ．40°B ．60°C ．90°D ．30° 4．正四棱锥S —ABCD 中，BC=6，SA=5，那么SA 与BC 间的距离是 （ ）A ．4B ．34C ．23D ．273 5．如果直线b ⊂α，那么“直线a//直线b ”是“直线a//平面α”的 （ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必条件6．在三棱锥S —ABC 中，SA ⊥BC ，SC ⊥AB ，则顶点S 在底面上的射影为△ABC 的（ ）A ．外心B ．内心C ．重心D ．垂心7．已知斜三棱柱ABC —A 1B 1C 1底面三边AB 、BC 、CA 的长分别为13、5、12，侧棱AA 1=20，且侧棱与底面成45°角，则此斜三棱柱的体积为（ ）A ．600B ．3002C ．6002D ．20038．二面角α—l —β是直二面角，A ∈α，B ∈β，设直线AB 与平面α、β所成角分别为 θ1、θ2，则 （ ） A ．θ1+θ2=90° B ．θ1+θ2≥90° C ．θ1+θ2≤90° D ．θ1+θ2<90°9．有一山坡，它的倾斜角（坡面与水平面所成的二面角）是30°，坡上有一条直道与坡角 的水平线（坡面与地面的交线）成60°角，沿这条直道向上走20m ，则人升高（ ）A ．20mB ．253mC ．503mD ．53m10．PA 、PB 、PC 是以点P 引出的三条射线，每两条的夹角均为3，每两条确定一个平面，则两平面所成锐角的余弦值为（ ）A ．21 B ．31 C ．22 D ．23 11．在正方体ABCD —A 1B 1C 1D 1中，O 是底面ABCD 的中心，E 、F 分别是CC 1、AD 的中点，那么异面直线OE 和FD 1所成的角的余弦值为 （ ）A ．510B ．515 C ．54 D ．32 12．若P 是正四面体内一点，P 到各面距离之和为一个定值，这个定值等于 （ ）A ．正四面体的棱长B ．正四面体的斜高C ．正四面体相对棱间距离D ．正四面体的高第Ⅱ卷（非选择题，共90分）二、填空题（本大题共4个小题，每小题4分，共16分，将答案填在题后的横线上） 13．正方体ABCD —A 1B 1C 1D 1中，截面A 1BD 和截面C 1BD 所成的较小的二面角的大小是 .14．三棱锥P —ABC 中，PA ⊥平面ABC ，∠ACB=90°，且PA=AC=BC=a ，则异面直线PB与AC 所成角的正切值等于 . 15．已知正三棱柱ABC —A 1B 1C 1的底面边长为2，高为4，过BC 作一截面，截面与底面ABC成60°角，则截面面积为 .16．对于不重合的两个平面α与β，给定下列条件：①存在平面γ，使得α、β都垂直于γ；②存在平面γ，使得α、β都平行于γ；③α内有不共线的三点到β的距离相等；④存在异面直线l 、m ，使得l //α，l //β，m//α，m//β，其中，可以判定α与β平行的条件有 .三、解答题（本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤） 17．（本小题满分12分）求证：如果平面外一条直线和这个平面内的一条直线平行，那么这条直线和这个平面平行（要求：如图写出已知、求证和证明过程）.18．（本小题满分12分）如图，三棱柱的底面是边长为2的等边三角形，侧面ABB 1A 1是菱形，∠A 1AB=60°，且平面ABB 1A 1⊥平面ABC ，M 是A 1B 1的中点， （1）求证：BM ⊥AC ；（2）求三棱锥M —A 1CB 的体积. 19．（本小题满分12分） 如图，在长方体ABCD —A 1B 1C 1D 1中，AB=AA 1=a ，BC=2a ，M 是AD 的中点，N 是B 1C 1的中点，（1）求证：A 1M//平面B 1BCC 1；（2）求A 1B 和平面A 1MCN 所成的角的大小. 20．（本小题满分12分）如图，点O 是边长为4的正方形ABCD 的中心，点E 、F 分别是AD 、BC 的中点，沿对角线AC 把正方形ABCD 折成直二面角D —AC —B ， （1）∠EOF 的大小；（2）求二面角E —OF —A 的大小.21．（本小题满分12分）四棱锥P —ABCD 的底面是菱形，边长为4a ，且∠ABC=60°，PC ⊥面ABCD ，PC=4a ，E 是PA 中点，（1）求证：平面BDE ⊥面ABCD ； （2）求点E 到平面PBC 的距离； （3）求二面角A —EB —D 的正切值. 22．（本小题满分14分）在棱锥P —ABC 中，三条侧棱PA 、PB 、PC 两两垂直，PA=a ，PB=b ，PC=c ，设其高PH 为h ， （1）求证：22221111cb a h ++=； （2）设M 是底面ABC 内一点，M 到三侧面PBC 、PCA 、PAB 的距离分别为x 、y 、z ，求abcxyz的最大值.参考答案一、选择题1.B2.B3.C4.D5.D6.D7.B8.C9.D 10.B 11.B12.D二、填空题13.arccos 3114.2 15.3 16.②④ 三、解答题17.略 18.2119.45° 20.120°；arctan 2 21.3a ； 332 22. 271。

哈尔滨市第六中学2009-2010学年度下学期期中考试文科数学试卷本试卷分第Ⅰ卷(选择题)和第Ⅱ 卷(非选择题)两部分，满分150分，考试用时120分钟；第Ⅰ卷（选择题 满分60分）一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）． 1．，若，则的值等于 （ ）A ．B ．C ．D ． 2．若, 则与的大小关系是 （ ）A ．B ．C ．D ．不能确定3．函数是偶函数，则曲线处的切线方程是 （ ）A ．B ．C ．D ．4． 函数在内的图象如图所示，若函数 的导函数的图象也是连续不间断的， 则导函数在内有零点 （ ） A ．个 B ．个 C ．个 D ．个5．有一段“三段论”推理是这样的：对于可导函数，如果，那么是函数的极值点，因为函数在处的导数值，所以是函数的极值点.以上推理中 （ ）A ．大前提错误B ． 小前提错误C ．推理形式错误D ．结论正确 6．按照下列三种化合物的结构式及分子式的规律，写出后一种化合物的分子式．．．是 （ ）A ．C 4H 9B ．C 4H 10 C ．C 4H 11D ．C 6H 127．四个小动物换座位，开始是鼠、猴、兔、猫分别坐1，2，3，4号位子上（如图），第一次前后排 动物互换座位，第二次左右列动物互换座位，…，这样交替进行下去，那么第2005次互换座位后， 小兔的座位对应的是 （ ）A ．编号1B ．编号2C ．编号3D ．编号48．函数的导数为 （ ）A. B. C. D.9．设函数的导函数为，且，则等于 （ ）A ．B ．C ．D ．10．函数，则 （ ） A ．在内是减函数 B.在内是增函数C ．在内是减函数 D.在内是增函数11．把下面在平面内成立的结论类比地推广到空间，结论还正确的是 （ ） (A) 如果一条直线与两条平行线中的一条相交，则它与另一条也相交 ． (B) 如果一条直线与两条平行线中的一条垂直，则它与另一条也垂直． (C) 如果两条直线同时与第三条直线相交，则这两条直线相交． (D) 如果两条直线同时与第三条直线垂直，则这两条直线平行． 12．点是曲线上的任意一点，则点到直线的最小距离为（ ） A 1 B C D第Ⅱ卷 （非选择题 满分90分）二、填空题：本大题共4小题，每小题5分，共20分. 把答案填写在答题纸相应位置上． 13．已知函数是R 上的可导函数，且，则函数的解析式可以为 ．（只须写出一个符合题意的函数解析式即可）；14．已知函数在R 上有极值，则实数的取值范围是 ； 15．求过点（3，5）且与曲线相切的直线方程为 . 16. 函数，时有极值7，则的值分别为 ；三、解答题：本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤． 17．（本题满分10分）设复数，其中，当取何值时， （1）； （2分）（2）是纯虚数； （3分） （3）； （2分）（4）所对应的点在复平面的第四象限内. （3分）18. （本题满分12分）某高中地处县城，学校规定家到学校的路程在里以内的学生可以走读，因交通便利，所以走读生人数很多， 该校学生会先后次对走读生的午休情况作了统计，得到 如下资料：①若把家到学校的距离分为五个区间：、、、、，则调查数据表明午休的走读生分布在各个区间内的频率相对稳定，得到了如右图所示的频率分布直方图；②走读生是否午休与下午开始上课的时间有着密切的关系. 下表是根据次调查数据得到的下午开（Ⅱ）如果把下午开始上课时间作为横坐标，然后上课时间每推迟分钟，横坐标增加2，并以平均每天午休人数作为纵坐标，试列出与的统计表，并根据表中的数据求平均每天午休人数与上课时间之间第三次第二次第一次开始的线性回归方程；（Ⅲ）预测当下午上课时间推迟到时，家距学校的路程在4里路以下的走读生中约有多少人午休？（注：线性回归直线方程系数公式）19. （本小题满分12分）如图：直平行六面体，底面ABCD是边长为2a的菱形，∠BAD＝60°，E为AB中点，二面角为60°；（1）求证：平面⊥平面；（2）求三棱锥的体积；20. （本题满分10分）已知函数的图象过点，且在点M处的切线方程为，(1) 求函数的解析式；(2) 求函数的单调区间；21. （本题满分12分）已知在处取到极小值.（Ⅰ）求的值及函数的单调区间；（Ⅱ）若对恒成立,求实数的取值范围. 22．（本题满分14分）设函数，，当时，取得极值；(1) 求的值，并判断是函数的极大值还是极小值；(2) 当时，函数与的图象有两个公共点，求的取值范围；哈尔滨市第六中学2010届高二下学期期中考试文科数学试卷答案（高考学习网）一、选择题：1. D 2. B 3.D 4. D 5. A 6.B 7.A8.C 9. A 10.A11. B 12.D二、填空题：13.；14. a<0；15. ；16．-1，-10；三、解答题：17．（本题满分10分）解：（1），只需，∴或（2）是纯虚数，只需，∴（3），∴，∴（4）由题意知，故时，点在复平面的第四象限内。