低温实验讲义_霍尔效应测量
- 格式:doc
- 大小:303.00 KB
- 文档页数:11

霍尔效应实验简介在磁场中的载流导体上出现横向电势差的现象是24岁的研究生霍尔(Edwin H. Hall)在1879年发现的,现在称之为霍尔效应。
随着半导体物理学的迅猛发展,霍尔系数和电导率的测量已经成为研究半导体材料的主要方法之一。
通过实验测量半导体材料的霍尔系数和电导率可以判断材料的导电类型、载流子浓度、载流子迁移率等主要参数。
若能测得霍尔系数和电导率随温度变化的关系,还可以求出半导体材料的杂质电离能和材料的禁带宽度。
在霍尔效应发现约100年后,德国物理学家克利青(Klaus von Klitzing)等研究半导体在极低温度和强磁场中发现了量子霍尔效应,它不仅可作为一种新型电阻标准,还可以改进一些基本量的精确测定,是当代凝聚态物理学和磁学令人惊异的进展之一,克利青为此发现获得1985年诺贝尔物理学奖。
其后美籍华裔物理学家崔琦(D. C. Tsui)和施特默在更强磁场下研究量子霍尔效应时发现了分数量子霍尔效应。
它的发现使人们对宏观量子现象的认识更深入一步,他们为此发现获得了1998年诺贝尔物理学奖。
用霍尔效应制备的各种传感器,已广泛应用于工业自动化技术、检测技术和信息处理各个方面。
本实验的目的是通过用霍尔元件测量磁场,判断霍尔元件载流子类型,计算载流子的浓度和迁移速度,以及了解霍尔效应测试中的各种副效应及消除方法。
实验原理通过霍尔效应测量磁场霍尔效应装置如图2.3.1-1和图2.3.1-2所示。
将一个半导体薄片放在垂直于它的磁场中(B 的方向沿z轴方向),当沿y方向的电极C、D上施加电流I时,薄片内定向移动的载流子(设平均= q u B (1)速率为u)受到洛伦兹力F B的作用,FB无论载流子是负电荷还是正电荷,F B 的方向均沿着x 方向,在磁力的作用下,载流子发生偏移,产生电荷积累,从而在薄片B 、B’两侧产生一个电位差V BB ’,形成一个电场E 。
电场使载流子又受到一个与F B 方向相反的电场力F E ,F E =q E = q V BB’ / b(2)其中b 为薄片宽度,F E 随着电荷累积而增大,当达到稳定状态时F E =F B ,即q uB = q V BB’ / b(3)这时在B 、B’两侧建立的电场称为霍尔电场,相应的电压称为霍尔电压,电极B 、B’称为霍尔电极。

实验8—3超导材料的电阻-温度特性测量引言人们在1877年液化了氧,获得-183℃的低温后就发展低温技术。
随后,氮、氢等气体相继液化成功。
1908年,荷兰莱顿大学的卡麦林•翁纳斯(Kamerlingh Onnes)成功地使氦气液化,达到了4.2K的低温,三年后即在1911年翁纳斯发现,将水银冷却到4.15K时,其电阻急剧地下降到零。
他认为,这种电阻突然消失的现象,是由于物质转变到了一种新的状态,并将此以零电阻为特征的金属态,命名为超导态。
1933年迈斯纳(Meissner)和奥森菲尔德(Ochsenfeld)发现超导电性的另一特性:超导态时磁通密度为零或叫完全抗磁性,即Meissner效应。
电阻为零及完全抗磁性是超导电性的两个最基本的特性。
超导体从具有一定电阻的正常态,转变为电阻为零的超导态时,所处的温度叫做临界温度,常用T C表示。
直至1986年以前,人们经过70多年的努力才获得了最高临界温度为23K的Nb3Ge超导材料。
1986年4月,贝德诺兹(Bednorz)和缪勒(Müller)创造性地提出了在La-Ba-Cu-O系化合物中存在高T C超导的可能性。
1987年初,中国科学院物理研究所赵忠贤等在这类氧化物中发现了T C=48K的超导电性。
同年2月份,美籍华裔科学家朱经武在Y-Ba-Cu-O系中发现了T C=90K的超导电性。
这些发现使人们梦寐以求的高温超导体变成了现实的材料,可以说这是科学史上又一次重大的突破。
其后,在1988年1月,日本科学家Hirashi Maeda报导研制出临界温度为106K的Bi-Sr-Ca-Cu-O系新型高温超导体。
同年2月,美国阿肯萨斯大学的Allen Hermann和Z. Z. Sheng等发现了临界温度为106K的Tl-Ba-Ca-Cu-O系超导体。
一个月后,IBM的Almaden又将这种体系超导体的临界温度提高到了125K。
1989年5月,中国科技大学的刘宏宝等通过用Pb和Sb对Bi的部分取代,使Bi-Sr-Ca-Cu-O系超导材料的临界温度提高到了130K。


【⼤学物理实验】霍尔效应与应⽤讲义霍尔效应与应⽤1879年,年仅24岁的霍尔在导师罗兰教授的⽀持下,设计了⼀个根据运动载流⼦在外磁场中的偏转来确定在导体或半导体中占主导地位的载流⼦类型的实验,霍尔的发现在当时震动了科学界,这种效应被称为霍尔效应。
通过实验测量半导体材料的霍尔系数和电导率可以判断材料的导电类型、载流⼦浓度、载流⼦迁移率等主要参数。
通过测量霍尔系数和电导率随温度变化的关系,还可以求出半导体材科的杂质电离能和材料的禁带宽度。
如今常规霍尔效应不但是测定半导体材料电学参数的主要⼿段,利⽤该效应制成的霍尔器件已⼴泛⽤于⾮电量的电测量、⾃动控制和信息处理等各个研究领域。
该实验要求学⽣了解霍尔效应的基本原理、霍尔元件的基本结构,测试霍尔元件特性的⽅法,并对测量结果给出正确分析和结论。
⿎励学⽣运⽤霍尔效应的基本原理和霍尔元件的特性,设计⼀些测量磁场,或各种⾮磁性和⾮电性物理量的测量的实验⽅案,例如:磁场分布、位置、位移、⾓度、⾓速度等。
让学⽣更好的运⽤霍尔效应来解决⼀些实际问题。
⼀、预备问题1.霍尔效应在基础研究和应⽤研究⽅⾯有什么价值?2.如何利⽤实验室提供的仪器测量半导体材料的霍尔系数?3.怎样判断霍尔元件载流⼦的类型,计算载流⼦的浓度和迁移速率?4.伴随霍尔效应有那些副效应?如何消除?5.如何利⽤霍尔效应和元件测量磁场?6.如何利⽤霍尔元件进⾏⾮电磁的物理量的测量?7.若磁场的法线不恰好与霍尔元件⽚的法线⼀致,对测量结果会有何影响?如何⽤实验的⽅法判断B与元件法线是否⼀致?8.能否⽤霍尔元件⽚测量交变磁场?⼆、引⾔霍尔效应发现⼀百多年来,在基础和应⽤研究范围不断扩展壮⼤,反常霍尔效应、整数霍尔效应、分数霍尔效应、⾃旋霍尔效应和轨道霍尔效应等相继被发现,并构成了⼀个庞⼤的霍尔效应家族。
1985年克利青、多尔达和派波尔因发现整数量⼦霍尔效应,荣获诺贝尔奖;1998年诺贝尔物学理奖授予苏克林、施特默和崔琦,以表彰他们发现了分数量⼦霍尔效应。

量子霍尔效应的低温实验研究近年来,量子物理学的研究在科学界引起了极大的关注。
其中,量子霍尔效应作为一种重要的现象,在低温实验中得到了广泛的研究和应用。
本文将从量子霍尔效应的基本原理、低温实验的方法和意义以及研究的进展等方面进行论述。
量子霍尔效应最早由德国物理学家冯·克利兹金提出,他发现当电子在二维空间受到垂直磁场作用时,电子会自发形成相干态,引发一系列奇特的电子行为。
这种现象被称为量子霍尔效应。
其基本原理可以用能带理论来解释,即在二维系统中,由于磁场的作用,电子能级会出现分立的能带,而在强磁场下,能带结构将会变得特别简单,即只有一个能带填满。
当磁场的强度足够大,填满的能带将发生能隙的形成,此时只有在这个能隙内存在电子。
为了实现量子霍尔效应的观测和研究,科学家们采用了低温实验的方法。
在低温条件下,电子的热运动减弱,使得电子在二维平面上更容易形成相干态。
同时,低温实验还可以使电子的散射减少,从而更好地研究电子的输运行为。
在实验中,科学家们通常使用液氦等低温冷却剂将样品冷却到几个开尔文以下的温度。
通过在低温下对样品的电流和电压进行测量,可以得到量子霍尔效应的特征电阻,从而验证量子霍尔效应的存在。
低温实验中研究量子霍尔效应具有重要的科学意义。
首先,量子霍尔效应为我们了解二维电子系统提供了重要的窗口。
在二维空间中,由于量子限制的存在,电子的行为会有许多奇特的特性,如有限自由度和强关联等。
通过研究量子霍尔效应,可以更好地研究和理解这些特性。
其次,量子霍尔效应在电子输运方面具有巨大的潜力。
由于量子霍尔效应的存在,电子在二维空间中表现出无散射的输运现象,这为我们开拓了新的电子输运途径。
这一点对于未来的电子器件和量子计算具有重要的意义。
在量子霍尔效应的低温实验研究中,近年来取得了一系列重要的进展。
例如,科学家们通过制备高质量的样品和使用先进的测量技术,观测到了更高的分数量子霍尔效应。
同时,研究人员还发现了新的分数部分霍尔效应,进一步拓展了量子霍尔效应的研究范围。

变温霍尔效应【摘要】本实验通过对样品锑化铟在80-300K温度间霍尔电压的测量,得到霍尔系数随温度变化的曲线图,通过曲线来研究禁带宽度、载流子浓度、迁移率等特征。
本实验通过稳态旗袍原理控温的低温恒温器是使样品在低温液体温度到室温之间快速变温。
【关键词】迁移率霍尔电压禁带宽度液氮【引言】对通电的导体或半导体施加一与电流方向垂直的磁场,则在垂直于电流和磁场方向有一横向电位差出现,这个现象于1879年为物理学家活儿所发现,故称为霍尔效应。
霍尔系数及电导率的测量是分析半导体纯度以及杂质种类的一种有力手段,也可用于研究半导体材料电输运特征。
本实验采用范德堡测试方法,测量样品的霍尔系数及电导率随温度的变化,可以确定一些参数—禁带宽度、杂质电离能、电导率、载流子浓度、材料的纯度以及迁移率。
【实验原理】1、半导体的能带结构和载流子浓度没有人工掺杂的半导体称为本征半导体,本征半导体中的原子按照晶格有规则的排列,产生周期性势场。
在这一周期势场的作用下,电子的能级展宽成准连续的能带。
束缚在原子周围化学键上的电子能量较低,它们所形成的能级构成价带;脱离原子束缚后在晶体中自由运动的电子能量较高,构成导带,导带和价带之间存在的能带隙称为禁带。
当绝对温度为0K时,电子全被束缚在原子上,导带能级上没有电子,而价带中的能级全被电子填满;随着温度升高,部分电子由于热运动脱离原子束缚,成为具有导带能量的电子,它在半导体中可以自由运动,产生导电性能,这就是电子导电;而电子脱离原子束缚后,在原来所在的原子上留下一个带正电荷的电子的缺位,通常称为空穴,它所占据的能级就是原来电子在价带中所占据的能级。
因为邻近原子上的电子随时可以来填补这个缺位,使这个缺位转移到相邻原子上去,形成空穴的自由运动,产生空穴导电。
半导体的导电性质就是由导带中带负电荷的电子和价带中带正电荷的空穴的运动所形成的。
这两种粒子统称载流子。
本征半导体中的载流子称为本征载流子,它主要是由于从外界吸收热量后,将电子从价带激发到导带,其结果是导带中增加了一个电子而在价带出现了一个空穴,这一过程成为本征激发。


低温霍尔效应测试
低温霍尔效应测试是一种功能性测试,用于检测物理设备的热抗性和耐冷性。
它旨在确保设备在极端低温环境中仍具有良好的性能,同时避免因极端低温而导致设备受损。
它通常使用大量冰水来将测试样本降温到低温温度,然后监测测试样本的表现。
例如,对于电子设备,可以测试其在低温环境下的开关性能,以及其画面显示、声音响应等。
此外,还可以使用低温霍尔效应测试来评估机械设备的性能,如紧固件的强度、润滑剂的流动性等。

霍尔效应测试物理方法
霍尔效应是一种利用磁场作用于导体中流动的电流来产生电压的现象。
此现象可以用于测量电流、磁场和导体特性等方面。
在物理实验中,霍尔效应测试是一种重要的方法,以下是相关介绍:
1. 实验原理:当一个导体在磁场中受到电流作用时,会在导体的两侧产生一定大小的电压,这就是霍尔效应。
2. 实验步骤:首先,使用导线将待测导体接入一个恒流源。
然后,将待测导体放置在一个恒定的磁场中,通过调节磁场大小和方向来使得磁场垂直于导体表面。
最后,使用电压计测量导体两侧产生的电压,即可得到当前流经导体的电流大小。
3. 实验应用:霍尔效应测试可以用于测量电流、磁场和导体特性等方面。
例如,在磁场强度恒定的情况下,通过改变电流大小或导体材料,可以测量出不同条件下的霍尔电压大小,并通过电压与电流之间的关系,推导出导体的电导率、霍尔系数等特性参数。
4. 实验注意事项:在进行霍尔效应测试时,需要注意磁场的大小和方向要恒定,电流源要保持稳定,电压计的精度和灵敏度要符合测量要求等。
此外,实验器材和导体材料的选取也要考虑到其特性和物理相关性。
综上所述,霍尔效应测试是一种重要的物理实验方法,可以用于测量电流、磁场和导体特性等方面,对于物理学教学和科学研究都有重要的意义。
- 1 -。

讲义_霍尔效应测量变温霍尔效应引言1879年,霍尔(E.H.Hall)在研究通有电流的导体在磁场中受力的情况时,发现在垂直于磁场和电流的方向上产生了电动势,这个电磁效应称为“霍尔效应”。
在半导体材料中,霍尔效应比在金属中大几个数量级,引起人们对它的深入研究。
霍尔效应的研究在半导体理论的发展中起了重要的推动作用。
直到现在,霍尔效应的测量仍是研究半导体性质的重要实验方法。
利用霍尔效应,可以确定半导体的导电类型和载流子浓度,利用霍尔系数和电导率的联合测量,可以用来研究半导体的导电机构(本征导电和杂质导电)和散射机构(晶格散射和杂质散射),进一步确定半导体的迁移率、禁带宽度、杂质电离能等基本参数。
测量霍尔系数随温度的变化,可以确定半导体的禁带宽度、杂质电离能及迁移率的温度特性。
根据霍尔效应原理制成的霍尔器件,可用于磁场和功率测量,也可制成开关元件,在自动控制和信息处理等方面有着广泛的应用。
实验目的1. 了解半导体中霍尔效应的产生原理,霍尔系数表达式的推导及其副效应的产生和消除。
2. 掌握霍尔系数和电导率的测量方法。
通过测量数据处理判别样品的导电类型,计算室温下所测半导体材料的霍尔系数、电导率、载流子浓度和霍尔迁移率。
3. 掌握动态法测量霍尔系数(RH)及电导率(σ)随温度的变化,作出RH~1/T,σ~1/T曲线,了解霍尔系数和电导率与温度的关系。
4. 了解霍尔器件的应用,理解半导体的导电机制。
实验原理1.半导体内的载流子根据半导体导电理论,半导体内载流子的产生有两种不同的机构:本征激发和杂质电离。
(1)本征激发半导体材料内共价键上的电子有可能受热激发后跃迁到导带上成为可迁移的电子,在原共价键上却留下一个电子缺位—空穴,这个空穴很容易受到邻键上的电子跳过来填补而转移到邻键上。
因此,半导体内存在参与导电的两种载流子:电子和空穴。
这种不受外来杂质的影响由半导体本身靠热激发产生电子—空穴的过程,称为本征激发。
显然,导带上每产生一个电子,价带上必然留下一个空穴。
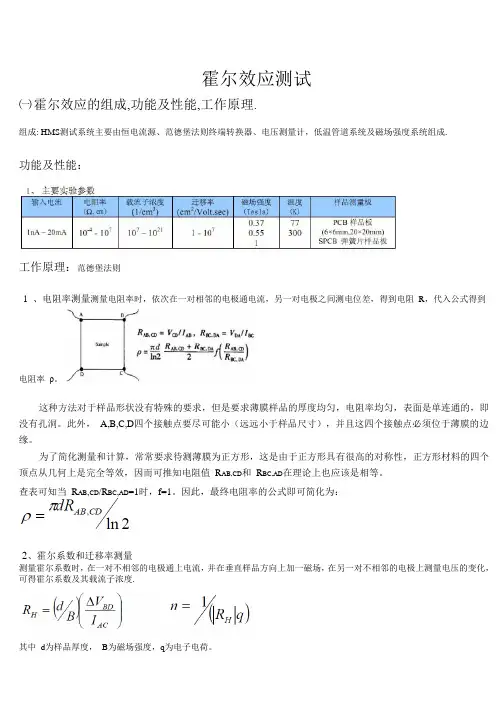
霍尔效应测试㈠霍尔效应的组成,功能及性能,工作原理.组成: HMS测试系统主要由恒电流源、范德堡法则终端转换器、电压测量计,低温管道系统及磁场强度系统组成.功能及性能:工作原理:范德堡法则1 、电阻率测量测量电阻率时,依次在一对相邻的电极通电流,另一对电极之间测电位差,得到电阻R,代入公式得到电阻率ρ。
这种方法对于样品形状没有特殊的要求,但是要求薄膜样品的厚度均匀,电阻率均匀,表面是单连通的,即没有孔洞。
此外,A,B,C,D四个接触点要尽可能小(远远小于样品尺寸),并且这四个接触点必须位于薄膜的边缘。
为了简化测量和计算,常常要求待测薄膜为正方形,这是由于正方形具有很高的对称性,正方形材料的四个顶点从几何上是完全等效,因而可推知电阻值R AB,CD和R BC,AD在理论上也应该是相等。
查表可知当R AB,CD/R BC,AD=1时,f=1。
因此,最终电阻率的公式即可简化为:2、霍尔系数和迁移率测量测量霍尔系数时,在一对不相邻的电极通上电流,并在垂直样品方向上加一磁场,在另一对不相邻的电极上测量电压的变化,可得霍尔系数及其载流子浓度.其中d为样品厚度,B为磁场强度,q为电子电荷。
由电阻率和霍尔系数的测量,同时还可以得到电子的霍尔迁移率。
㈡软件菜单使用说明1. 先打开电脑主机,再打开设备开关。
2. 左手拿磁极的上盖(N朝上),将待测得薄膜样品放入弹簧夹内,此时弹簧夹应正面朝上(如果放反,会将样品烧坏),放好后盖好上盖。
3. 开始界面4. 进入霍尔测试界面需要输入数据的只有左上角的INPUT VALUE栏,别的都不用改动。
INPUT VALUE的菜单说明如下所示。
DATE:测试日期;USER NAME:用户名称;SAMPLE NAME:样品名称;(前三项自己正确填写);COMPORT:通信端口(已设置好不用重新输入);TEMP:测试温度(室温下测选择300K,液氮的环境中测选择77K);I: 测试电流(根据试验需求输入);DELAY:更换测试点测试延时(一般无需改动,0.100s);D:样品厚度(根据自己的样品输入);B:测量磁场(根据磁铁上的数据输入);Measurement Number:测量次数(一般选择1000)。
低温物理学中的量子霍尔效应量子霍尔效应是低温物理学中一项重要的研究课题。
它指的是在极低温下,当电子在二维电子气中受到磁场作用时,出现的一种特殊电输运现象。
量子霍尔效应的研究不仅具有重要的科学意义,还有广泛的应用前景,对于拓展纳米电子学、量子计算和能源转换等领域具有重要意义。
量子霍尔效应最早在1980年被发现,并由德国物理学家K. von Klitzing于1985年获得诺贝尔物理学奖。
他发现在低温下,当磁场在某个临界值以上时,电子在二维电子气中形成一种非常有序的状态,即整数量子霍尔效应(IQHE)。
此时,电子的电导量子化为整数倍的电子电荷单位e²/h(其中e为元电荷,h为普朗克常数)。
这种量子化的现象是由于电子在二维电子气中的运动受到限制,只能在某些离散的能级上存在。
随着研究的深入,1998年另外的两位物理学家Tsuneya Ando和Yasuhiro Uemura发现了另一种量子霍尔效应,被称为分数量子霍尔效应(FQHE)。
与整数量子霍尔效应相比,分数量子霍尔效应中电子的电导量子化为分数倍的电子电荷单位,如e/3、e/5等。
分数量子霍尔效应的出现对于理解强关联电子系统的性质具有重要意义,对于全新的拓展量子计算和拓扑量子化学等领域起到了关键作用。
量子霍尔效应的产生是由于电子在二维电子气中遇到磁场时,引入了一种新的能级分裂机制,即所谓的朗道能级。
朗道能级指的是电子在磁场中被分割成若干个紧密排列的能级,在磁场增大时能级的间距也会增大。
当这种能级与费米能级(化学势)对齐时,电子只能填充某些具体的能级,这就导致了电子在极低温下出现量子霍尔效应。
量子霍尔效应的研究不仅提供了理解材料中电子运动的重要方法,还为拓展新一代纳米电子器件提供了重要的理论基础。
例如,在石墨烯中观察到了量子霍尔效应,这使得石墨烯成为研究量子霍尔效应的理想平台。
此外,量子霍尔效应还有望应用于新型能源转换技术中,如热电效应和热输运。
低温物理学中的量子霍尔效应和拓扑绝缘体低温物理学是研究物质在极低温下的性质和行为的学科。
在这个领域里,量子霍尔效应和拓扑绝缘体是两个引人注目的研究热点。
本文将讨论这两个现象的基本原理、物理机制以及在实验室和应用领域的潜在应用。
一、量子霍尔效应量子霍尔效应是低温物理学中的重要现象,最早由德国物理学家冯·科尔尼于1980年发现,他因此获得了1998年的诺贝尔物理学奖。
量子霍尔效应是指在二维输运系统中,当施加垂直于样品平面的磁场时,在输运方向上会出现电阻为零的现象。
这一现象的基本原理可以通过平均场论和量子力学来解释。
当二维电子气体处于强磁场中,电子会沿着磁场方向做圆周运动,形成所谓的磁子轨道。
在低温下,当电子与晶格的相互作用不足以破坏磁子轨道的准经典态时,电子将在磁场的驱动下形成一个能带结构,称为朗道能级。
在朗道能级中,电子的能级非常密集,形成了所谓的朗道子能级。
在量子霍尔效应中,当温度趋近于绝对零度时,费米能级处于朗道子能级的间隔中。
由于朗道能级的循环结构,电子将填充能级直到费米能级达到某个朗道子能级的顶端。
在这种情况下,只有填充满的朗道子能级能够参与输运,未填满的朗道子能级则形成一个能隙。
由于能隙的存在,电子在这个系统中无法改变输运方向,从而导致了电阻为零的效应。
量子霍尔效应具有诸多实验现象和应用,例如霍尔电阻、霍尔电压、霍尔电导等。
在实验室中,科学家可以通过样品的几何尺寸、外加磁场的大小和方向来调控量子霍尔效应的性质。
在应用方面,量子霍尔效应在精密测量、量子计算和纳米电子器件中有广泛的应用前景。
二、拓扑绝缘体拓扑绝缘体是低温物理学中的另一个研究热点,它是一种新型的量子物态,具有边界态的特殊性质。
与普通的绝缘体不同,拓扑绝缘体在体内是绝缘体,在边界上则存在特殊的导电边界态。
拓扑绝缘体的特殊性质源于其拓扑的性质。
在普通的绝缘体中,能带结构决定了体态和边界态之间的差异。
而在拓扑绝缘体中,具有拓扑性质的绝缘带与导带之间的能隙有非平庸的拓扑不变量,这种扭曲的能带结构使得拓扑绝缘体具有边界态。
低温和强磁场的作用量子霍尔效应以低温和强磁场的作用量子霍尔效应为标题量子霍尔效应(Quantum Hall Effect,简称QHE)是指在低温和强磁场的作用下,二维电子气体在垂直于磁场方向上的电阻呈现出离散的量子化现象的一种物理现象。
本文将从低温和强磁场的作用角度出发,对量子霍尔效应进行探讨。
低温是产生量子霍尔效应的关键因素之一。
在常温下,电子之间的热运动会导致电子的碰撞和散射,使得电阻呈现出连续的变化。
而在低温下,电子的热运动减弱,电子之间的散射作用可以忽略不计,从而使得电阻呈现出离散的量子化现象。
这种量子化现象是由于电子在强磁场下受到洛伦兹力的作用,沿着磁场方向形成了一维的能级分布。
强磁场是产生量子霍尔效应的另一个重要条件。
在强磁场下,电子的轨道运动受到洛伦兹力的影响,轨道运动的半径受到限制,电子只能沿着磁场方向运动。
这样一来,电子在横向方向上形成了二维的运动平面,而在垂直于磁场方向上形成了一维的能级分布。
这种能级分布使得电子的运动变得有序,电子在不同的能级上呈现出离散的分布,从而导致电阻的量子化现象。
量子霍尔效应的具体表现是电阻在磁场变化时呈现出离散的平台,这些平台对应着不同的分数或整数。
这些平台的存在是由于电子的能级分布和填充规律的特殊性质所决定的。
根据量子霍尔效应的理论,当电子在磁场的作用下填充满某个特定的能级时,电阻将出现一个平台,这个平台的电阻值与普通金属的电阻值不同,而是一个精确的分数或整数。
这种精确的电阻量子化现象是量子霍尔效应的核心特征。
量子霍尔效应不仅在理论上具有重要意义,在实际应用中也有广泛的应用价值。
首先,量子霍尔效应为精密电阻测量提供了一种新的方法,可以用于准确测量电阻的值。
其次,量子霍尔效应在微电子学领域中被广泛应用于纳米电子器件的研究。
由于量子霍尔效应对温度和杂质散射等因素的抗干扰能力强,因此可以作为一种理想的电流标准源,用于纳米电子器件的可靠性测试和性能评估。
低温和强磁场对于量子霍尔效应的影响是至关重要的。
量子霍尔效应是指在低温和强磁场条件下,电子在二维材料上产生的特殊电导现象。
当材料处于低温时,电子因为低温而具有很低的能量,几乎处于基态。
这使得电子在杂质或晶格缺陷等的散射下受到较小的干扰,并能够在材料内流动更加自由。
同时,低温下的电子具有较长的平均自由时间,能够在材料内保持较长的相干性。
强磁场对于量子霍尔效应至关重要。
在强磁场下,电子的运动受到Lorentz力的作用,使得电子运动轨迹发生曲线弯曲,从而限制了电子的运动。
但是,在二维材料中,由于电子只能在平面内运动,磁场的作用会使电子在平面内发生螺旋运动,形成所谓的Landau能级。
这些Landau能级对应于不同的电子能量,且能量差随着磁场的增加而增大。
当低温和强磁场同时存在时,量子霍尔效应就会出现。
在二维材料中,当电子能级填满最低的Landau能级时,其上面的能级将被填满。
每个地板能级在能量上有一个简并度,即不同的电子态具有相同的能量。
从而,在低温下,填充了最低Landau能级的电子具有较低的能量,不受晶格散射的影响,能够在材料内自由传导。
此外,在强磁场下,电子发生量子霍尔效应时的电导是量子化的。
即电导随着磁场增加呈现出分立的态,称为霍尔电导。
这是因为在量子霍尔效应下,电子在横向磁场下只能存在特定的能量态,并且这些态具有特定的横向电导。
通过测量横向电导,我们可以获得电导的量子化值,并推导出霍尔电导的整数量子。
综上所述,低温和强磁场的作用使得电子在二维材料上形成特殊的能级分布,从而产生了量子霍尔效应。
这种效应不仅对于研究材料的电导性质有重要意义,还有助于揭示电子在低维材料中的量子行为和拓扑性质。
实验8—1变温霍尔效应引言1879年,霍尔(E.H.Hall)在研究通有电流的导体在磁场中受力的情况时,发现在垂直于磁场和电流的方向上产生了电动势,这个电磁效应称为“霍尔效应”。
在半导体材料中,霍尔效应比在金属中大几个数量级,引起人们对它的深入研究。
霍尔效应的研究在半导体理论的发展中起了重要的推动作用。
直到现在,霍尔效应的测量仍是研究半导体性质的重要实验方法。
利用霍尔效应,可以确定半导体的导电类型和载流子浓度,利用霍尔系数和电导率的联合测量,可以用来研究半导体的导电机构(本征导电和杂质导电)和散射机构(晶格散射和杂质散射),进一步确定半导体的迁移率、禁带宽度、杂质电离能等基本参数。
测量霍尔系数随温度的变化,可以确定半导体的禁带宽度、杂质电离能及迁移率的温度特性。
根据霍尔效应原理制成的霍尔器件,可用于磁场和功率测量,也可制成开关元件,在自动控制和信息处理等方面有着广泛的应用。
实验目的1.了解半导体中霍尔效应的产生原理,霍尔系数表达式的推导及其副效应的产生和消除。
2.掌握霍尔系数和电导率的测量方法。
通过测量数据处理判别样品的导电类型,计算室温下所测半导体材料的霍尔系数、电导率、载流子浓度和霍尔迁移率。
3.掌握动态法测量霍尔系数(R H)及电导率(σ)随温度的变化,作出R H~1/T,σ~1/T曲线,了解霍尔系数和电导率与温度的关系。
4.了解霍尔器件的应用,理解半导体的导电机制。
实验原理1.半导体内的载流子根据半导体导电理论,半导体内载流子的产生有两种不同的机构:本征激发和杂质电离。
(1)本征激发半导体材料内共价键上的电子有可能受热激发后跃迁到导带上成为可迁移的电子,在原共价键上却留下一个电子缺位—空穴,这个空穴很容易受到邻键上的电子跳过来填补而转移到邻键上。
因此,半导体内存在参与导电的两种载流子:电子和空穴。
这种不受外来杂质的影响由半导体本身靠热激发产生电子—空穴的过程,称为本征激发。
显然,导带上每产生一个电子,价带上必然留下一个空穴。
因此,由本征激发的电子浓度n和空穴浓度p应相等,并统称为本征浓度n i,由经典的玻尔兹曼统计可得n i=n=p=(N c N v)1/2exp(-E g/2k B T)=K’T3/2 exp(-E g/2k B T)式中N c,N v分别为导带、价带有效状态密度,K’为常数,T为温度,E g为禁带宽度,k B为玻尔兹曼常数。
(2)杂质电离在纯净的第IV族元素半导体材料中,掺入微量III或V族元素杂质,称为半导体掺杂。
掺杂后的半导体在室温下的导电性能主要由浅杂质决定。
如果在硅材料中掺入微量III族元素(如硼或铝等),这些第III族原子在晶体中取代部分硅原子组成共价键时,从邻近硅原子价键上夺取一个电子成为负离子,而在邻近失去一个电子的硅原子价键上产生一个空穴。
这样满带中电子就激发到禁带中的杂质能级上,使硼原子电离成硼离子,而在满带中留下空穴参与导电,这种过程称为杂质电离。
产生一个空穴所需的能量称为杂质电离能。
这样的杂质叫做受主杂质,由受主杂质电离而提供空穴导电为主的半导体材料称为p 型半导体。
当温度较高时,浅受主杂质几乎完全电离,这时价带中的空穴浓度接近受主杂质浓度。
同理,在IV 族元素半导体(如硅、锗等)中,掺入微量V 族元素,例如磷、砷等,那么杂质原子与硅原子形成共价键时,多余的一个价电子只受到磷离子P +的微弱束缚,在室温下这个电子可以脱离束缚使磷原子成为正离子,并向半导体提供一个自由电子。
通常把这种向半导体提供一个自由电子而本身成为正离子的杂质称为施主杂质,以施主杂质电离提供电子导电为主的半导体材料叫做n 型半导体。
2. 霍尔效应和霍尔系数设一块半导体的x 方向上有均匀的电流I x 流过,在z 方向上加有磁场B z ,则在这块半导体的y 方向上出现一横向电势差U H ,这种现象被称为“霍尔效应”,U H 称为“霍尔电压”,所对应的横向电场E H 称为“霍尔电场”。
见图一。
图一 霍尔效应产生原理图实验指出,霍尔电场强度E H 的大小与流经样品的电流密度J x 和磁感应强度B z 的乘积成正比z x H H B J R E ⋅⋅= (1)式中比例系数R H 称为“霍尔系数”。
下面以p 型半导体样品为例,讨论霍尔效应的产生原理并推导、分析霍尔系数的表达式。
半导体样品的长、宽、厚分别为L 、a 、b ,半导体载流子(空穴)的浓度为p ,它们在电场E x 作用下,以平均漂移速度v x 沿x 方向运动,形成电流I x 。
在垂直于电场E x 方向上加一磁场B z ,则运动着的载流子要受到洛仑兹力的作用F =q v ⨯B (2)式中q 为空穴电荷电量。
该洛仑兹力指向-y 方向,因此载流子向-y 方向偏转,这样在样品的左侧面就积累了空穴,从而产生了一个指向+y 方向的电场-霍尔电场E y 。
当该电场对空穴的作用力qE y 与洛仑兹力相平衡时,空穴在y 方向上所受的合力为零,达到稳态。
稳态时电流仍沿x 方向不变,但合成电场E =E x +E y 不再沿x 方向,E 与x 轴的夹角称“霍尔角”。
在稳态时,有qE y =qv x B z(3)若E y 是均匀的,则在样品左、右两侧面间的电位差U H =E y ·a =v x B z a(4) 而x 方向的电流强度I x =q ·p ·v x ·ab(5) 将(5)式的v x 代入(4)式得霍尔电压 )1(b B I qp U z x H = (6) 由(1)、(3)和(5)式得霍尔系数 qp R H 1= (7)对于n 型样品,载流子(电子)浓度为n ,同理可以得出其霍尔系数为qn R H 1-= (8)上述模型过于简单。
根据半导体输运理论,考虑到载流子速度的统计分布以及载流子在运动中受到散射等因素,在霍尔系数的表达式中还应引入一个霍尔因子A ,则(7)、(8)式应修正为p 型: qpA R H 1= (9) n 型: qn A R H 1-= (10)A 的大小与散射机理及能带结构有关。
由理论算得,在弱磁场条件下,对球形等能面 的非简并半导体,在较高温度(此时,晶格散射起主要作用)情况下,18.183==πA 。
一般地,Si 、Ge 等常用半导体在室温下属于此种情况,A 取为1.18。
在较低温度(此时,电离杂质散射起主要作用)情况下,93.1512315==πA 。
对于高载流子浓度的简并半导体以及强磁场条件,A =1;对于晶格和电离杂质混合散射情况,一般取文献报道的实验值。
上面讨论的是只有电子或只有空穴导电的情况。
对于电子、空穴混合导电的情况,在计 算R H 时应同时考虑两种载流子在磁场下偏转的效果。
对于球形等能面的半导体材料,可以证明:22222)'()'()()(nb p q nb p A n p q n p A R n p n p H +-=+-=μμμμ (11)式中b ’=μn /μp ,μn 和μp 分别为电子和空穴的迁移率。
从霍尔系数的表达式可以看出:由R H 的符号(也即U H 的符号)可以判断载流子的类型,正为p 型,负为n 型(注意,所谓正、负是指在xyz 坐标系中相对于y 轴方向而言,见图一。
I 、B 的正方向分别为x 轴、z 轴的正方向,则霍尔电场方向为y 轴方向。
当霍尔电场方向的指向与y 正向相同时,则R H 为正。
);R H 的大小可确定载流子的浓度;还可以结合测得的电导率σ算出如下定义的霍尔迁移率μHμH =|R H |·σ (12)μH 的量纲与载流子的迁移率相同,通常为cm 2/V·s (厘米2/伏秒),它的大小与载流子的电导迁移率有密切的关系。
霍尔系数R H 可以在实验中测量出来,若采用国际单位制,由(6)、(7)式可得z x H H B I b U R = (m 3/C) (13)但在半导体学科中习惯采用实用单位制(其中,b :厘米,B z :高斯或Gs ),则z x H H B I b U R =×108 (cm 3/C ) (13’)3.霍尔系数与温度的关系图二 霍尔系数与温度的关系图R H 与载流子浓度之间有反比关系,因此当温度不变时,R H 不会变化;而当温度改变时,载流子浓度发生变化,R H 也随之变化。
图二是R H 随温度T 变化的关系图。
图中纵坐标为R H 的绝对值,曲线A 和B 分别表示n 型和p 型半导体的霍尔系数随温度的变化曲线。
下面简要地讨论曲线B :(1)杂质电离饱和区。
在曲线(a )段,所有的杂质都已电离,载流子浓度保持不变。
p 型半导体中p >>n ,(11)式中nb ’2可忽略,可简化为H qN A qp AR 11==>0式中N A 为受主杂质浓度。
(2) 温度逐渐升高,价带上的电子开始激发到导带,由于μn >μp ,所以b ’>1, 当温度升到使p =nb ’2时,R H =0,出现了图中(b )段。
(3) 温度再升高时,更多的电子从价带激发到导带,p <nb ’2而使R H <0,(11)式 中分母增大,R H 减小,将会达到一个负的极值,图中(c )点。
此时价带的空穴数p =n +N A ,将它代入(11)式,并对n 求微商,可以得到当 1'-=b N n A 时,R H 达到极值 (R H )M : AH qN A qp A R 11== (14) 由此式可见,当测得(R H )M 和杂质电离饱和区的R H ,就可定出b ’的大小。
(4) 当温度继续升高,达本征范围时,半导体中载流子浓度大大超过受主杂质浓度, 所以R H 随温度上升而呈指数下降,R H 则由本征载流子浓度N i 来决定,此时杂质含量不同或 杂质类型不同的曲线都将趋聚在一起,见图中(d )段。
4.半导体的电导率在半导体中若有两种载流子同时存在,则其电导率σ为σ=qp μp +qn μn(15)图三 电导率与温度的关系图实验得出σ与温度T 的关系曲线如图三。
现以p 型半导体为例分析:(1)低温区。
在低温区杂质部分电离,杂质电离产生的载流子浓度随温度升高而增加,而且μp 在低温下主要取决于杂质散射,它也随温度升高而增加。
因此,σ随T 的增加而增加,见图的a 段。
室温附近。
此时,杂质已全部电离,载流子浓度基本不变,这时晶格散射起主要作用,使μp 随T 的升高而下降,导致σ随T 的升高而下降,见图的b段。
(2)高温区。
在这区域中,本征激发产生的载流子浓度随温度升高而指数地剧增,远远超过μp 的下降作用,致使σ随T 而迅速增加,见图的c段。
实验中电导率σ可由下式计算出:ab U l I ••==ρσ1 (16)式中ρ为电阻率,I为流过样品的电流,Uσ、l分别为两测量点间的电压降和长度。