5第五章交叉表分析

交叉分析法怎么分析交叉分析法是一种常用的统计分析方法，用于研究不同变量之间的关系及其影响因素。

本文将介绍交叉分析法的基本原理、分析步骤和应用场景，帮助读者了解如何进行交叉分析。

一、交叉分析法简介交叉分析法是一种基于交叉表格的统计分析方法。

它通过将要研究的多个变量以表格的形式进行归类和统计，进而揭示出变量之间的相互关系。

交叉分析法主要用于描述和分析多个变量之间的联系和影响。

二、交叉分析法的基本原理交叉分析法的基本原理是建立和分析交叉表。

交叉表是一种以行和列展示多个变量交叉情况的表格，可以清晰地展示各个变量之间的关系。

通过统计不同交叉点的频数或百分比，可以进一步分析各个变量之间的相关程度。

三、交叉分析法的分析步骤1. 确定研究目的：首先需要明确分析的目的，明确想要研究的变量和关系。

2. 数据收集和整理：收集相关数据，并整理成表格的形式，通常以行为一个变量、列为另一个变量的形式进行排列。

3. 构建交叉表：根据收集到的数据，在表格中填写各个变量的交叉点数据，可以使用频数或百分比。

4. 分析交叉表：通过对交叉表中的数据进行统计分析，揭示出变量之间的关系和影响。

常用的统计指标包括卡方检验、列联表分析等。

5. 结果解释和总结：根据分析得到的结果，进行解释和总结，得出结论。

四、交叉分析法的应用场景1. 市场调研：可以通过交叉分析法分析不同人群对商品或服务的偏好和需求，从而为市场定位和产品策划提供参考。

2. 教育评估：可以利用交叉分析法分析不同学习方法、教育资源对学生成绩的影响，为教育改革和评估提供依据。

3. 社会调查：可以使用交叉分析法分析不同群体在社会问题上的态度和观点，为社会政策的制定提供参考。

4. 经济研究：可以通过交叉分析法分析不同经济因素对于经济增长或商业活动的影响，为经济预测和政策制定提供支持。

五、注意事项1. 数据收集的准确性和全面性对于分析结果的可信度具有重要影响，因此要确保数据的来源可靠，样本覆盖面广。

交叉分析法怎么分析交叉分析法是一种常用的数据分析方法，主要用于对多个变量之间的关系进行分析。

采用交叉分析法可以发现不同变量之间的相互影响和作用方式，从而更好地理解数据背后的规律和特征。

在下面的文章中，我们将介绍交叉分析法的具体分析流程和注意事项，帮助读者更好地了解和应用这种方法。

一、交叉分析法的定义交叉分析法，也称为交叉表法或列联表法，是一种通过将不同变量交叉排列建立交叉表的方法来研究变量之间相关性的一种统计方法。

交叉分析法根据样本数据构造一个列联表，以便比较各个不同维度之间的差异，从而进一步发现其内在联系和潜在规律。

二、交叉分析法的分析流程1. 选取研究对象和指标首先需要确定研究对象和研究指标。

在选择研究对象时，要确保大样本数量和充分代表性，以免数据偏误。

在选择指标时，应该着重考虑研究目的，避免指标内部关联性太强而导致冗余信息。

2. 建立交叉表将所选变量进行顺序或随机排列，形成一个行×列的交叉表。

在表格中，每一行代表一种分类变量的不同组别，每一列代表另一种分类变量的不同组别。

然后根据实际情况，填入相应的数据或统计概率。

3. 描述表格特征通过观察交叉表格中的特征，了解各个指标之间的关系和变化趋势。

这可以从几个方面来分析，例如行、列、总体、对角线等方面考虑。

归纳总结这些特征，可以为后续分析提供有力支撑。

4. 进行自由度统计自由度（df）指代两种分类变量所构成的列联表中具有独立划分的单元格个数。

在使用交叉分析法时，通常需要根据列联表的大小和分类变量的个数计算可用的自由度。

一般来说，自由度等于“列数-1×行数-1”。

5. 计算卡方值和P值卡方值是用来衡量观察值与理论值之间差异的一个指标。

在进行交叉分析时，一般会使用χ^2检验计算卡方值。

当卡方值越大时，表明所观察到的差异也越大。

在计算卡方值之后，还需要计算对应的P值。

P值是一个统计学上的重要指标，用于表示样本与总体误差概率大小。

如果P 值小于等于0.05，可以认为差异显著，反之则不显著。

交叉分析法怎么分析交叉分析法是一种常用的数据分析方法，通过对不同因素之间的关系进行交叉比较和分析，帮助研究者发现变量之间的联系和差异。

本文将介绍交叉分析法的基本概念和步骤，并以具体案例进行说明。

一、交叉分析法概述交叉分析法（Cross-Tabulation Analysis）也被称为列联表分析（Contingency Table Analysis），是一种定量分析方法，用来研究两个或更多变量之间的关系。

通过构建列联表，对不同变量之间的交叉频数进行统计和比较，可以揭示变量之间的关联性和差异性。

二、交叉分析法步骤1. 确定研究问题：明确研究问题并选择需要分析的变量。

例如，假设我们想研究消费者对不同手机品牌的偏好与性别之间的关系。

2. 构建列联表：根据所研究的变量，构建列联表（也称为交叉表）。

横列为一个变量的不同水平（例如手机品牌），纵列为另一个变量的不同水平（例如性别）。

在交叉点上填写交叉频数。

3. 计算频数和比例：根据列联表，计算每个交叉点上的频数和比例。

频数表示各组别的数量，比例表示各组别所占比例。

4. 绘制图表：通过绘制图表，直观地展示不同变量之间的关系。

常用的图表包括堆叠柱状图、簇状柱状图、饼图等。

5. 进行统计检验：为了验证变量之间的关系是否显著，可以进行统计检验，如卡方检验。

卡方检验可以检验各组别之间的差异是否由随机因素引起。

6. 分析结果和讨论：根据交叉分析的结果，进行结果分析和讨论。

解释变量之间的关系和差异，并提出合理的解释和解决方案。

三、交叉分析方法案例以消费者对不同手机品牌的偏好与性别之间的关系为例，进行交叉分析。

我们调查了300名消费者，结果如下表所示：--------------------------------------------------| Apple | Samsung | Huawei | Others--------------------------------------------------男性 | 50 | 30 | 20 | 10--------------------------------------------------女性 | 20 | 40 | 50 | 20--------------------------------------------------根据上表，我们可以计算出各组别的频数和比例，如下所示：--------------------------------------------------| Apple | Samsung | Huawei | Others--------------------------------------------------男性 | 50 | 30 | 20 | 10--------------------------------------------------女性 | 20 | 40 | 50 | 20--------------------------------------------------| 70(23%) | 70(23%) | 70(23%) | 30(10%)--------------------------------------------------通过绘制堆叠柱状图，我们可以直观地看到不同手机品牌在不同性别中的偏好程度。

交叉分析法怎么分析交叉分析法是一种常用的研究方法，它用于识别和分析不同变量之间的关系。

通过交叉分析，我们可以深入了解变量之间的相互影响，并做出相关的决策和预测。

本文将介绍交叉分析法的基本原理、步骤和应用示例。

一、交叉分析法概述交叉分析法是一种多变量分析方法，它通过对不同变量之间的交叉关系进行统计分析，从而揭示变量之间是否存在相关性。

交叉分析法一般通过列联表或交叉表来展示分析结果，以便更直观地展示变量之间的关系。

二、交叉分析法步骤1. 确定研究目的：在进行交叉分析之前，需要明确研究的目的和问题，明确要分析的变量以及它们之间的关系。

2. 收集数据：根据研究目的，收集相关的数据。

数据可以来自于调查问卷、实验记录、观察等多种来源。

3. 构建交叉表：根据收集到的数据，构建交叉表。

交叉表的构建要考虑变量之间的相关性，选择合适的交叉方式，以展示变量之间的关系。

4. 进行统计分析：利用适当的统计方法对交叉表进行分析。

常用的统计方法包括卡方检验、t检验、方差分析等。

根据研究问题的不同，选择合适的统计方法。

5. 解读分析结果：根据统计分析的结果，解读变量之间的关系。

根据交叉分析的目的，对结果进行合理的解读，得出结论并提出相应的建议。

三、交叉分析法应用示例以某饮品公司为例，假设该公司希望了解不同性别消费者对其产品包装的偏好程度。

1. 确定研究目的：分析不同性别消费者对产品包装的偏好程度。

2. 收集数据：通过问卷调查收集不同性别的消费者对产品包装的评价数据。

3. 构建交叉表：根据收集到的数据，构建一个二维交叉表，将性别作为一列，将产品包装偏好程度（如喜欢、一般、不喜欢）作为另一列。

4. 进行统计分析：利用卡方检验或t检验等方法，分析不同性别消费者对产品包装的偏好程度是否存在显著差异。

5. 解读分析结果：根据统计分析的结果，判断是否存在显著差异。

例如，统计分析结果显示不同性别消费者对产品包装的偏好程度存在显著差异，女性消费者更倾向于喜欢产品包装，而男性消费者对产品包装的评价较为一般。

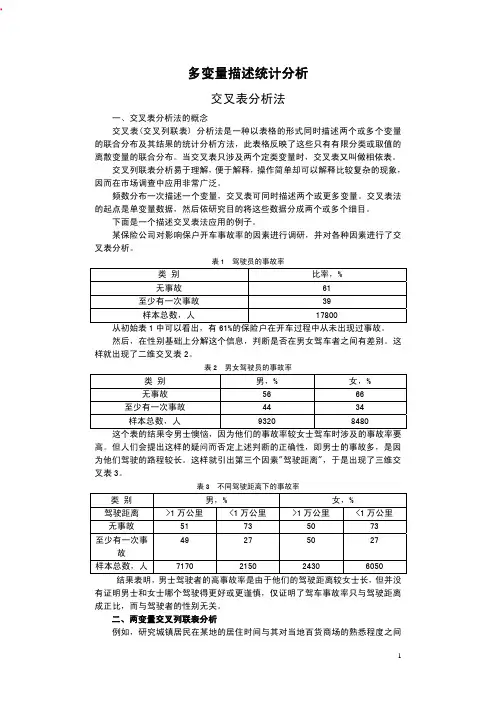
多变量描述统计分析交叉表分析法一、交叉表分析法的概念交叉表(交叉列联表) 分析法是一种以表格的形式同时描述两个或多个变量的联合分布及其结果的统计分析方法，此表格反映了这些只有有限分类或取值的离散变量的联合分布。

当交叉表只涉及两个定类变量时，交叉表又叫做相依表。

交叉列联表分析易于理解，便于解释，操作简单却可以解释比较复杂的现象，因而在市场调查中应用非常广泛。

频数分布一次描述一个变量，交叉表可同时描述两个或更多变量。

交叉表法的起点是单变量数据，然后依研究目的将这些数据分成两个或多个细目。

下面是一个描述交叉表法应用的例子。

某保险公司对影响保户开车事故率的因素进行调研，并对各种因素进行了交叉表分析。

表1 驾驶员的事故率类 别 比率，%无事故 61至少有一次事故 39样本总数，人 17800从初始表1中可以看出，有61%的保险户在开车过程中从未出现过事故。

然后，在性别基础上分解这个信息，判断是否在男女驾车者之间有差别。

这样就出现了二维交叉表2。

表2 男女驾驶员的事故率类 别 男，% 女，%无事故 56 66 至少有一次事故 44 34样本总数，人 9320 8480这个表的结果令男士懊恼，因为他们的事故率较女士驾车时涉及的事故率要高。

但人们会提出这样的疑问而否定上述判断的正确性，即男士的事故多，是因为他们驾驶的路程较长。

这样就引出第三个因素"驾驶距离"，于是出现了三维交叉表3。

表3 不同驾驶距离下的事故率类 别 男，% 女，%驾驶距离 >1万公里 <1万公里 >1万公里 <1万公里 无事故 51 73 50 7349 27 50 27至少有一次事故样本总数，人7170 2150 2430 6050结果表明，男士驾驶者的高事故率是由于他们的驾驶距离较女士长，但并没有证明男士和女士哪个驾驶得更好或更谨慎，仅证明了驾车事故率只与驾驶距离成正比，而与驾驶者的性别无关。

二、两变量交叉列联表分析例如，研究城镇居民在某地的居住时间与其对当地百货商场的熟悉程度之间的关系，对“居住时间”和“熟悉程度”这两个变量进行交叉列联分析。

data05-02为某公司工资数据（n=15）。

使用变量性别sex、收入高低earnings分析男女经理间薪金是否平等。

可以利用data05-01中的数据，使用变量occcat80为工作性质分类，region为地区，childs 为每个家庭的孩子数。

将childs为行变量，occcat80为列变量，region为控制变量选入Layer of框中，进行交叉表分析。

列联表（交叉表）分析1、项目名称Crosstabs过程4、实训原理Crosstabs过程用于定类数据和定序数据进行统计描述和简单的统计推断。

在分析时可以产生二维至n维列联表，并计算相应的百分数指标。

4-1 列联表分析的含义与任务在实际分析中，当问题涉及到多个变量时，我们不仅要了解单个变量的分布特征，还要分析多个变量不同取值下的分布，掌握多变量的联合分布特征，进而分析变量之间的相互影响和关系。

很明显，如果还采用单纯的频数分析方法显然不能满足要求。

因此，我们需要借助交叉分组下的频数分析，即列联表分析。

列联表分析的主要任务有两个：（1）根据样本数据产生二维或多维交叉列联表。

交叉列联表是两个或两个以上变量交叉分组后形成的频数分布表。

（2）在交叉列联表的基础上，分析两变量之间是否具有独立性或一定的相关性。

4-2 卡方检验的原理为了理解列联表中行变量（Row）和列变量（Column）之间的关系，我们需要借助非参数检验方法。

通常采用的方法是卡方检验。

和一般假设检验一样，卡方检验主要包括三个步骤：（1）建立零假设：行变量和列变量相互独立。

（2）选择和计算检验统计量。

列联表分析中的检验统计量是Pearson卡方统计量。

其公式为：()∑∑==-=r i cj eij e ij o ijf f f1122χ（4-9-1）其中，r 为列联表的行数，c 为列联表的列数，0f 为实际观测频数，e f 期望观测频数。

期望频数的计算公式为：nCTRT f e ⨯=（4-9-2） 其中，RT 是指定单元格所在行的观测频数合计，CT 是指定单元格所在列的观测频数合计，n 是观测频数的合计。

data05-02为某公司工资数据（n=15）。

使用变量性别sex、收入高低earnings分析男女经理间薪金是否平等。

可以利用data05-01中的数据，使用变量occcat80为工作性质分类，region为地区，childs 为每个家庭的孩子数。

将childs为行变量，occcat80为列变量，region为控制变量选入Layer of框中，进行交叉表分析。

列联表（交叉表）分析1、项目名称Crosstabs过程4、实训原理Crosstabs过程用于定类数据和定序数据进行统计描述和简单的统计推断。

在分析时可以产生二维至n维列联表，并计算相应的百分数指标。

4-1 列联表分析的含义与任务在实际分析中，当问题涉及到多个变量时，我们不仅要了解单个变量的分布特征，还要分析多个变量不同取值下的分布，掌握多变量的联合分布特征，进而分析变量之间的相互影响和关系。

很明显，如果还采用单纯的频数分析方法显然不能满足要求。

因此，我们需要借助交叉分组下的频数分析，即列联表分析。

列联表分析的主要任务有两个：#（1）根据样本数据产生二维或多维交叉列联表。

交叉列联表是两个或两个以上变量交叉分组后形成的频数分布表。

（2）在交叉列联表的基础上，分析两变量之间是否具有独立性或一定的相关性。

4-2 卡方检验的原理为了理解列联表中行变量（Row）和列变量（Column）之间的关系，我们需要借助非参数检验方法。

通常采用的方法是卡方检验。

和一般假设检验一样，卡方检验主要包括三个步骤：（1）建立零假设：行变量和列变量相互独立。

（2）选择和计算检验统计量。

列联表分析中的检验统计量是Pearson卡方统计量。

其公式为：()∑∑==-=r i cj eij e ij o ijf f f1122χ（4-9-1）其中，r 为列联表的行数，c 为列联表的列数，0f 为实际观测频数，e f 期望观测频数。

期望频数的计算公式为：nCTRT f e ⨯=（4-9-2） 其中，RT 是指定单元格所在行的观测频数合计，CT 是指定单元格所在列的观测频数合计，n 是观测频数的合计。

Excel中的数据表和数据的交叉分析Excel是一款功能强大的电子表格软件，广泛应用于数据分析、报表制作等工作中。

其中，数据表和数据的交叉分析是Excel中常用的功能之一，它能够帮助我们更全面地理解数据并发现数据之间的相关关系。

本文将介绍Excel中的数据表和数据的交叉分析的具体操作和应用。

一、数据表的创建与管理数据表是Excel中的重要元素，我们可以通过创建和管理数据表来存储和组织各种复杂的数据。

下面将介绍如何在Excel中创建和管理数据表。

1. 创建数据表在Excel中创建数据表非常简单，只需按照以下步骤操作：（1）打开Excel并选择一个工作表；（2）在该工作表中选中需要创建数据表的数据区域；（3）点击“插入”选项卡中的“表”按钮，选择“表格”；（4）确认选中的数据区域，点击“确定”按钮。

2. 数据表的管理创建完数据表后，我们可以对数据表进行以下操作：（1）调整列宽和行高：选中需要调整的列或行，右键点击选择“调整列宽”或“调整行高”并设置合适的数值；（2）添加数据：在数据表的最后一行或列输入数据；（3）删除数据：选中需要删除的数据，按下“Delete”键或右键点击选择“删除”；（4）排序：点击数据表的标题栏，通过“排序和筛选”功能进行排序；（5）筛选：点击数据表的标题栏，通过“排序和筛选”功能进行筛选；（6）编辑数据：双击数据表中的单元格进行数据编辑。

二、数据的交叉分析数据的交叉分析是指通过Excel提供的交叉表功能，将数据按照不同的分类条件进行分析，以便更好地理解数据之间的关系。

下面将介绍如何进行数据的交叉分析。

1. 创建交叉表在Excel中创建交叉表非常简单，只需按照以下步骤操作：（1）选中需要进行交叉分析的数据表区域；（2）点击“插入”选项卡中的“透视表”按钮，选择“透视表和透视图”；（3）在弹出的对话框中选择数据表区域，并将需要进行交叉分析的字段拖放到“行标签”和“列标签”区域；（4）选择需要分析的汇总方式，将其拖放到“值”区域。

交叉分析法怎么分析交叉分析法是一种常用的统计分析方法，通过对数据中的多个变量进行比较和交叉分析，可以揭示变量之间的相互关系和相互影响，进而对问题进行深入解读。

本文将介绍交叉分析法的基本原理和步骤，并以实际案例进行说明，以帮助读者更好地理解和应用该方法。

一、交叉分析法概述交叉分析法是一种定量研究方法，广泛应用于市场调研、社会学、医学等领域。

它通过将数据按照两个或多个变量进行横向对照，进而分析它们之间的相关性和差异性。

交叉分析法可以帮助研究者发现变量之间的关联，找出与结果变量相关的因素，进而进行深入的研究和分析。

二、交叉分析法的步骤1. 确定研究目标：在使用交叉分析法进行数据分析之前，首先要明确研究目标和问题，明确需要对哪些变量进行分析，以及希望从中得到什么样的结论。

2. 数据收集：根据研究目标，收集相关的数据。

数据可以来自各种来源，如问卷调查、实验数据、社会统计数据等。

数据收集时要注意采集的数据是否全面、准确。

3. 数据处理：对收集到的数据进行整理和清洗，排除掉无效或者缺失的数据，确保分析所用的数据是准确可靠的。

数据整理的过程中还可以对数据进行分类、标记，便于后续的比较和分析。

4. 数据分析：在数据处理后，可以开始进行交叉分析了。

首先可以通过绘制交叉表（交叉矩阵）来展示不同变量之间的交叉关系，同时计算各个变量之间的相关系数，如皮尔逊相关系数、切比雪夫相关系数等。

通过这些分析，可以初步发现变量之间的联系和差异。

5. 结果解读和推断：在进行交叉分析后，得到的结果需要进行解读和推断。

可以通过比较交叉表的不同交叉点的数值和比例，找出变量之间的联系和差异，并进行进一步的解读和推断。

在解读和推断的过程中，可以借助统计方法和数据可视化工具，如柱状图、折线图等，使结果更加直观和易于理解。

三、交叉分析法的案例应用下面以市场调研为例，说明交叉分析法的应用过程。

假设一个手机品牌希望了解不同性别和不同年龄段消费者对其新产品的态度，以便更好地调整市场策略。

交叉分析法怎么分析交叉分析法是一种常用的统计方法，用于研究两个或多个变量之间的关系。

它通过比较和分析不同变量之间的数据，帮助我们了解它们之间的关联和差异。

本文将介绍交叉分析法的基本原理和步骤，并提供几个实例来说明如何进行交叉分析。

一、交叉分析法的原理交叉分析法是基于两个或多个变量之间的交叉表格进行分析。

交叉表格的横轴和纵轴表示不同的变量，通过填入表格中的数据，可以观察到不同变量之间的关系。

交叉分析法的原理是基于这些数据，通过计算和比较相对比例、百分比等指标，来揭示变量之间的关联。

二、交叉分析法的步骤1. 确定研究目标和变量：首先，我们需要明确研究的目标和感兴趣的变量。

例如，在市场调研中，我们可能想要研究不同性别和年龄段的人对某种产品的喜好程度。

在这个例子中，性别和年龄段就是我们感兴趣的变量。

2. 收集和整理数据：在进行交叉分析之前，我们需要收集并整理所需要的数据。

这些数据可以通过问卷调查、实地观察、文献研究等方式获得。

确保数据的准确性和完整性是非常重要的。

3. 绘制交叉表格：根据所收集到的数据，我们可以绘制交叉表格。

将不同的变量分别放置在表格的横轴和纵轴上，并填入相应的数据。

例如，在我们的市场调研例子中，可以将性别放在横轴上，年龄段放在纵轴上，并填入每个组合下的喜好程度数据。

4. 计算比例和指标：根据填入的数据，我们可以计算出不同变量组合下的相对比例、百分比等指标。

这些指标可以帮助我们了解不同变量之间的关系。

例如，我们可以计算不同性别和年龄段的人群对产品的喜好程度的百分比，并进行比较。

5. 分析和解读结果：最后，我们需要对所得的结果进行分析和解读。

通过比较不同变量组合下的指标，我们可以判断出变量之间的关系。

例如，在市场调研中，我们可以得出性别和年龄段对产品喜好程度的影响程度，并找出可能存在的差异和关联。

三、交叉分析法的实例1. 市场调研实例：假设我们要研究一个新产品在不同地区的销售情况。

我们可以使用交叉分析法来研究不同地区和不同销售渠道之间的关系。