基于ANSYS的圣维南原理数值验证

ANSYS 关于圣维南原理的验证
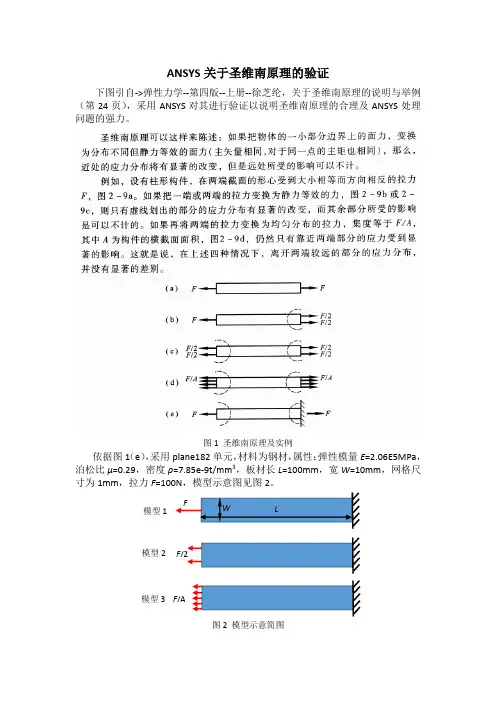
下图引自->弹性力学--第四版--上册--徐芝纶，关于圣维南原理的说明与举例（第24页），采用ANSYS 对其进行验证以说明圣维南原理的合理及ANSYS 处理问题的强力。

图1 圣维南原理及实例
依据图1（e ），采用plane182单元，材料为钢材，属性：弹性模量E =2.06E5MPa ，泊松比μ=0.29，密度ρ=7.85e-9t/mm 3，板材长L =100mm ，宽W =10mm ，网格尺寸为1mm ，拉力F =100N ，模型示意图见图2。

图2 模型示意简图
F /A
F F /2
L
W 模型1 模型2 模型3
图3为对应模型1的水平应力图，图4为对应模型2的水平应力图，图5为对应模型3的水平应力图，图中大致选取了相关节点显示应力值，由图可知，圣维南原理的正确性、合理性（见图1描述）以及ANSYS处理力学问题的强力。

图3 水平应力（基于模型1）
图4 水平应力（基于模型2）
图5 水平应力（基于模型3）。

关于圣维南原理的数值计算——基于艾里应力函数的平面应力问题的差分解法摘要本文通过应力函数的方法，结合数值方法，求解受端部集中力作用下的平板拉伸问题，评估基于圣维南原理的解与数值解相比带来的误差及其分布，并将此与J.N. Goodier的理论分析对比。

关键词弹性力学，圣维南原理，平面应力问题，有限差分法0引言圣维南原理（局部性原理）是弹性力学的一般原理之一，常用于在边界力系无法精确描述时的等效替代，其一种表述[1]为：“若把作用在物体局部边界上的面力，用另一组与它静力等效（即有相同的主矢量和主矩）的力系来替代，则在力系作用区域的附近应力分布将有明显的改变，但在远处所受的影响可以不计”。

作为一条经验定理[5]，这一原理的提出为材料力学和弹性力学问题的求解提供了大量的便利，但是对于这一原理的精确度，直到1937年，J.N. Goodier才从理论的角度给出评估，他指出圣维南原理的影响范围和外力作用的区域大致相近。

本文将以平面应力问题为例，借助数值计算的方法对比圣维南原理简化前与简化后的计算结果，验证Goodier对于圣维南原理影响范围的理论值，并给出在不同精度要求下的影响范围的精确结果。

1问题的描述考虑长方形平板的拉伸问题。

如下图所示，长度为a，宽度为b，在两边中点施加大小为F的集中点力。

2方程的建立2.1解法的选择应力解法和位移解法是弹性力学中的两种基本方法。

在平面问题中，应力解法可以通过应力函数的引入，将问题归结为关于应力函数的双调和方程的边值问题，与位移解法的偏微分方程组相比，更加适用于解析求解。

但是对于多连体问题，位移解法涉及到衔接条件的引入，会使问题更加复杂[3]。

但是本题只涉及到简单的单连通体，所以选择应力函数的求解方式。

若将应力函数记为，那么双调和方程可以写成。

2.2有限差分法在双调和方程中，应力函数是一个平面标量场，通过将的平板划分成的网格，连续函数离散为一个矩阵，矩阵中的元素记为。

利用中心差分公式化简偏导数项，结果如下。

圣维南原理的有限元模拟圣维南原理是电子学中的一项基本原理，用于描述电导体中电流分布情况的方法，常用于有限元模拟中来解决电磁场问题。

有限元模拟是一种基于数值方法的工程分析技术，通过将连续的物理问题离散化为有限数量的元素，再利用数值计算方法对这些元素进行求解，以模拟实际问题的行为和物理特性。

以下是关于圣维南原理在有限元模拟中的详细介绍。

圣维南原理（Saint-Venant’s Principle）主要用于描述电导体中的电流分布情况。

它是基于电流连续性方程和欧姆定律的基本原理，即电流在导体内部的分布是均匀且沿导体表面方向渐变。

根据这个原理，在有限元模拟中可以通过离散化导体为一系列有限元素来近似描述电流的分布情况。

在有限元模拟中，首先需要将导体区域划分为小块，称为有限元。

每个有限元都有一组自由度，用于描述电场强度或电势的分布情况。

在圣维南原理的约束下，任意两个相邻的有限元之间，在其界面上，电场强度或电势需要满足一定的连续性条件。

这些连续性条件可以通过将不同有限元之间的界面进行连接，构建整个导体区域的有限元模型。

有限元模型构建完成后，利用数值方法求解模型中的电场强度或电势分布。

通常采用有限元法的变分形式，通过求解最小化电场强度或电势的能量泛函来得到电场方程的离散形式。

然后，通过数值求解方法（如有限差分法等）对离散的电场方程进行求解，得到电场强度或电势分布的近似解。

由于圣维南原理的应用，有限元模拟能够较准确地描述导体中电流的分布情况。

采用有限元模拟方法，可以更好地理解和分析各种电磁场问题，如电磁传感器中的电流分布、电源线中的电压降等。

有限元模拟结果可以帮助工程师优化设计和制造过程，提高电子设备的性能和可靠性。

总之，圣维南原理作为电导体中电流分布的基本原理，在有限元模拟中扮演着关键的角色。

通过有限元模拟，可以准确地描述电流在导体中的分布情况，帮助工程师解决电磁场问题，从而优化设计和制造过程，提高电子设备的性能和可靠性。

实验二基于ANSYS平台的电磁场数值仿真一、实验目的1．在仿真过程中学会使用ANSYS软件。

2．学会边值问题的建模方法。

3．学会用仿真软件检验对电磁场分布的猜测。

二、实验类型本实验为验证型教学实验。

三、实验仪器配备有ANSYS软件平台的台式计算机。

四、实验原理本实验是在ANSYS平台上开发的。

ANSYS是国际上著名的有限元软件包，可对结构力学、流体力学、传热学和电磁学等领域的问题进行求解。

其特点是图形界面友好，易学，前后处理功能强大。

在ANSYS平台上开发电磁场数值仿真实验，只需将问题的求解过程描述清楚，按照给定步骤上机操作，即可得到预期结果。

五、实验内容图1 仿真计算模型（图中a、D可自定）仿真实验包括静电场实验和恒定磁场实验，可任选一个。

对于静电场实验，图1中两导体电位分别为100V和-100V（可自定）；对于恒定磁场实验，图1中两导体电流密度分别为10000A/m2和-10000A/m2。

根据几何结构和源分布的对称性，仿真实验可选用1/4或1/2平面进行建模。

实验分为两步：第一步，按照给定步骤和给定参数上机操作；第二步，尝试改变某些参数，观察仿真结果的变化。

六、实验步骤1.开始→程序→ansys5.6→license status→server（等待）→quit（不能按其他选择）2.开始→程序→ansys5.6→interactive（出现界面）→run（出现界面）→3.ANSYS Main Menu（左侧主菜单）→preferences→electric（点击白框打勾）→ok（预设问题归属）→4.ANSYS Main Menu→preprocessor→material props→-constant-isotropic→1→ok→perx 1→ok（给定材料相对介电常数）→5.ANSYS Main Menu→preprocessor→element type →add/edit/delete→add→electrostatic →2D quard 121→ok（设定内部单元类型）→6.(ANSYS Main Menu→preprocessor→element type →)add/edit/delete→add→infiniteboundary→2D infquard 110→ok→option→AZ改为volt, 4noded quard改为8noded→（设定外部无限单元类型）close→7.(ANSYS Main Menu→preprocessor→modeling→create→-Area- circle→partialannulus→wp x 1, wp y 0, rd-1 0, theta-1 0, rd-2 0.2, theta-2 180, apply→ wp x -1, wp y 0, rd-1 0, theta-1 0, rd-2 0.2, theta-2 180, apply→wp x 0, wp y 0, rd-1 0, theta-1 0, rd-2 5, theta-2 180, apply→wp x 0, wp y 0, rd-1 0, theta-1 0, rd-2 10, theta-2 180,ok（创建几何模型）→8.(ANSYS Main Menu→preprocessor→modeling→operate→-booleans- overlap→area→pick all（模型各部分之间集合运算）→9.(ANSYS Main Menu→preprocessor→modeling→delete→area and below→光标选中两个小圆，ok（删除导体部分）→10.(ANSYS Main Menu→preprocessor→-attributes- define→pick areas→光标选中有两个小圆缺口的内半圆，apply→apply→光标选中外半圆，ok→1 plane121改为 2 infin110→ok（定义区域属性）→11.(ANSYS Main Menu→preprocessor)→mesh tool→lines set→光标选中外层两条弧线，apply→ndiv 50 →apply→光标选中外层扇形左右两条底边，apply →ndiv 1 →apply→光标选两小圆弧，apply → ndiv 20 →apply→光标选中两小圆弧之间的两条小线段，apply→ndiv 20→apply→光标选中两小圆弧与大扇形之间两条长线段，ok→ndiv 20→ok→12.mesh tool菜单中选中quad 和 mapped，点击mesh →光标选中外部大扇形，ok（外部无限单元划网格）→13.mesh tool菜单中选中tri 和 free，点击mesh →光标选中有两个小圆缺口的内半圆，ok（内部有限单元划网格）→14.(ANSYS Main Menu)→solution→-loads- apply→-elecric- boundary→-voltage- online→光标选中右小半圆，apply, 100，apply→光标选中左小半圆，ok, -100 ，ok（导体表面加电位）→15.(ANSYS Main Menu)→solution→-loads- apply→-elecric- flag→-infinite surf- online→光标选中最外边的半圆，ok（无限边界加标志）→16.(ANSYS Main Menu)→solution→-solve- current ls→ok（求解，等待）→close（关闭黄框）→关闭status command文件（白框）17.(ANSYS Main Menu)→general postproc→plot results→-contour plot- nodal solu→dof solution elec poten volt ok（显示电位9色云图）→18.emag 3d utility menu→plot ctrls→device options→shading win32 点击改为contours win32c ， vocter mode off 点击改为on, ok→19.emag 3d utility menu→plot ctrls→style→contours→uniform contours→ncont100 ，ok（显示等电位线分布）→20.(ANSYS Main Menu)→general postproc→plot results→-vector plot-predefined→flux and gradient→选择D或EF（箭头显示电位移矢量或电场强度）→21.emag 3d utility menu→plot ctrls→pan, zoom, rotate→（可以移动、放大、缩小图形）22.ansys toolbar→选择quit-no save！ok→(退出ANSYS)七、实验注意事项为了避免仿真过程中重复建模，应对数值仿真的中间过程适当保存备份。

什么是圣维南原理及如何证明弹塑性力学作业孙嘉粲建筑与土木工程2017级3班学号2170970036Q1：什么是圣维南原理？Q2：为什么需要圣维南原理？Q3：如何证明圣维南原理是正确的？Q1：什么是圣维南原理？答：圣维南原理（Saint Venant’s Principle）是弹性力学的基础性原理，是法国力学家圣维南于1855年提出的。

其内容是：分布于弹性体上一小块面积（或体积）内的荷载所引起的物体中的应力，在离荷载作用区稍远的地方，基本上只同荷载的合力和合力矩有关；荷载的具体分布只影响荷载作用区附近的应力分布。

还有一种等价的提法：如果作用在弹性体某一小块面积（或体积）上的荷载的合力和合力矩都等于零，则在远离荷载作用区的地方，应力就小得几乎等于零。

不少学者研究过圣维南原理的正确性，结果发现，它在大部分实际问题中成立。

因此，圣维南原理中“原理”二字，只是一种习惯提法。

有限元软件的模拟验证了这一点，如图1所示。

==图1 有限元计算得到的柱体在不同应力边界下得到的应力分布图Q2：为什么需要圣维南原理？问题的提出：弹性力学问题的求解是在给定的边界条件下求解基本方程。

使应力分量、应变分量、位移分量完全满足8个基本方程相对容易。

但对于工程实际问题，构件表面面力或者位移是很难满足边界条件要求。

这使得弹性力学解的应用将受到极大的限制。

为了扩大弹性力学解的适用范围，放宽这种限制，圣维南提出了局部影响原理。

圣维南原理的应用：对复杂的力边界，用静力等效的分布面力代替。

有些位移边界不易满足时，也可用静力等效的分布面力代替。

不论在弹性力学中还是在有限元中都广泛灵活的应用圣维南原理来处理和简化边界条件。

值得注意的是：圣维南原理只能适用于一小部分边界（小边界：尺寸相对很小的边界；次要边界：面力分布复杂的小边界）。

对于主要边界，圣维南原理不再适用。

例如对于较长的粱，其端部可以应用圣维南原理，而在粱的侧面，则不能应用。

Q3：如何证明圣维南原理是正确的？见附录1《圣维南原理证明》附录1《圣维南原理证明》1.Boussinesq 的陈述1855年Boussinesq 将圣维南的思想一般化，并冠“Saint-Venant’s Principle ”的名称，其内容为：施于弹性体上的任意平衡力系，如果其作用点限于某个给定的球内，那么该平衡力系在任意一个与球的距离远大于球半径的点上所产生的形变是可以忽略的。

举例说明圣维南原理应用基本上所有的结构工程师都会使用到圣维南原理。

大多数结构力学教科书都收录了基于该原理的各种公式，但至今尚未对其进行严格证明。

圣维南原理指出，只要载荷的合力正确，那么在远离载荷作用区的地方，载荷的精确分布就不重要。

在本篇文章中，我们将采用有限元分析对圣维南原理进行探究。

圣维南原理的历史1855 年，法国科学家圣维南（Barré de Saint-Venant）发表了一个著名原理，但与其说这是一个严谨的数学命题，不如说是一个观察发现：“如果作用在弹性体一小块表面上的力被作用于同一块表面上的静力等效力系替代，这种替换仅使局部表面产生显著的应力变化，而在比应力变化表面的线性尺寸更远的地方，其影响可忽略不计。

”B. Saint-Venant, Mém. savants étrangers, vol. 14, 1855.圣维南肖像。

图像来源于公有领域，通过 Wikimedia Commons 共享。

在应用力学领域，Boussinesq、Love、von Mises、Toupin 等科学家都对这一原理进行了精准的叙述，并给出了数学证明。

但是对于很多一般性问题，论证圣维南原理具有很大难度，所以对该课题的研究仍在继续（有些论据相当鲜明）。

简单案例：远距离应力分析让我们从一个简单的案例开始：对矩形薄板施加轴向拉力，与载荷作用边相隔一段距离处有一个圆孔。

假如我们要分析孔的应力集中，那么实际的载荷分布有多重要呢？我们对右侧边界施加了三种不同类型的载荷：100 MPa 的恒定轴向应力峰值振幅为 150 MPa 的对称抛物线应力分布等于上述两种载荷工况合力的中心点载荷如下方绘图所示，载荷施加方式不影响孔周围的应力分布。

当然，关键在于孔距离载荷足够远。

三种载荷工况对应的 Von Mises 应力分布。

该场景也可以使用箭头图来绘制主应力。

此图将应力场绘制为通量，从而清晰地展示了应力重新分布的变化。

基于ANSYS的圣维南原理数值验证圣维南原理是一个广泛应用于工程学领域的基本定理，它描述了在一个静止的弹性体上施加的力如何分布在该体上。

基于ANSYS的圣维南原理的数值验证是通过使用ANSYS软件来模拟和计算实际工程情况下的应力和应变分布，以验证圣维南原理在工程中的适用性和可靠性。

ANSYS是一种基于有限元分析的工程仿真软件，可以对各种结构进行精确的物理模拟和计算。

通过使用ANSYS，可以进行静力学、动力学、热力学等多种类型的仿真分析。

对于圣维南原理的验证，我们主要关注静力学方面的仿真。

在进行圣维南原理的数值验证时，首先需要建立一个准确的计算模型。

对于一些简单的结构，可以直接通过ANSYS的建模工具进行建模；对于复杂的结构，可以导入CAD模型或者使用ANSYS的几何建模工具进行建模。

接下来，需要定义材料的力学性质。

ANSYS提供了许多材料模型，可以根据具体材料的性质选择适当的材料模型，如弹性模型、塑性模型等，并输入相关的材料参数。

然后，需要定义施加在结构上的边界条件。

根据具体的工程问题，可以定义结构的固支、受力点、载荷等边界条件。

在圣维南原理的验证中，通常会施加一个已知大小和方向的力或者力矩。

在完成建模和定义边界条件后，需要进行数值求解。

通过ANSYS提供的有限元求解器，可以得到结构中各点的位移、应力和应变等结果。

最后，需要进行结果的后处理和分析。

可以通过ANSYS的后处理工具绘制出应力云图、应变云图和位移云图等，以直观地展示结构中的应力和应变分布情况。

同时，还可以计算并比较不同位置的应力和应变值，以验证圣维南原理在结构中的适用性。

总之，基于ANSYS的圣维南原理的数值验证是通过使用ANSYS软件来模拟和计算实际工程情况下的应力和应变分布，从而验证圣维南原理的有效性。

通过该验证，可以帮助工程师们更好地理解圣维南原理，并在实际工程中应用和优化结构设计。

圣维南原理及其证明：历史与评述赵建中云南大学资源、环境与地球科学学院地球物理系，昆明650091 摘要圣维南原理（Saint-Venant’s Principle）是弹性力学的基础性原理，圣维南原理的证明一直是弹性力学重要的研究课题。

本文以圣维南原理研究中最重要的事件为线索，对圣维南原理的发展历史作了综述，对重要的研究工作和结果进行了评论；发表和论证了图平定理不是圣维南原理的数学表达、一般的圣维南原理不成立、修正的圣维南原理可以证明为真等观点；介绍了建立修正的圣维南原理的数学方法；阐述了研究圣维南原理证明问题的意义；目的在于引起对这些有关圣维南原理的基本问题的关注和讨论，促进圣维南原理研究的繁荣和发展。

关键词圣维南原理，历史，图平定理，证明，否证，数学表达，修正，意义中图分类号：0343.2AMS Subject Classifications: 74G50引言弹性力学的圣维南原理已经有一百多年的历史了[1,2]。

早期有关原理有重要的文章[39] 。

波西涅克（Boussinesq）[3]于1885年、勒夫（Love）[4]于1927 年分别发表了圣维南原理的一般性陈述。

然而Mises[5]认为勒夫陈述不清楚并提出修改的陈述，其后的论证既可以看作是对一般的Mises 陈述的否证，又可以看作是对具有特殊条件的Mises 陈述的证明。

Sternberg [6]赞同Mises的修改，他的论证也可以既看作是对Mises 陈述（Sternberg称为圣维南原理的传统陈述）的一般性的否证，又看作是对附加了条件的Mises 陈述的证明。

Truesdell[10]于1959年断言，如果关于等效载荷的圣维南原理为真，它“必须是”线性弹性力学“一般方程的数学推论”。

这就从理性力学的角度提出了圣维南原理的证明问题，圣维南原理被视为一个数学命题，其真理性需要证明。

毫无疑问，圣维南原理的数学证明成了一个学术热点。

为了揭示原理隐秘的内涵，或者说破解原理之谜，学者们花费了巨大的努力。

ANSYS关于圣维南原理的验证圣维南原理是工程学中的一个基本原理，用于验证和分析结构的稳定性。

在ANSYS软件中，可以使用有限元分析方法对结构进行圣维南原理的验证。

下面将详细介绍如何在ANSYS中进行圣维南原理的验证。

首先，需要通过创建几何模型来描述结构。

可以使用ANSYS中的几何建模工具创建所需模型，或者导入外部CAD文件。

确保几何模型描述了结构的几何形状。

接下来，需要定义结构的材料特性。

在ANSYS中，可以选择材料库中的现有材料，或者根据需要自定义材料特性。

对于每一种材料，需要指定其弹性模量、泊松比等力学性质。

然后，需要定义结构的边界条件和加载情况。

根据问题的要求，设置结构的约束条件和应用在结构上的载荷。

可以在ANSYS中使用节点约束和面约束来定义边界条件，以及使用节点力和面力来定义载荷情况。

在设置完边界条件和加载情况后，需要网格化结构。

使用ANSYS中的网格划分工具将结构离散成有限元网格。

确保网格足够细密以准确地捕捉结构的行为。

接下来，需要指定分析类型和所需分析设置。

对于圣维南原理的验证，通常选择线性静态分析。

同时，可以选择是否进行线性或非线性材料的分析。

在进行分析之前，需要指定所需的加载步数和收敛准则等设置。

可以根据问题的要求设置分析的最大步数、最大残差和最大位移等参数。

然后，进行结构的求解和后处理。

在ANSYS中，可以使用求解器来求解结构的力学行为，并根据需要对结果进行后处理。

可以使用ANSYS中的后处理工具来查看位移、应力、应变等结果，并进行局部细化分析。

在进行后处理时，需要关注结构的稳定性。

对于圣维南原理的验证，需要查看结构的临界载荷和临界位移。

通过对比计算结果和理论计算值，可以验证结构在临界状态下的稳定性。

最后，根据验证结果进行分析和评估。

根据分析结果，可以评估结构的稳定性和安全性。

如果结构不稳定，可以考虑通过增加结构刚度、修改材料特性或优化结构形式来增加其稳定性。

总之，在ANSYS中进行圣维南原理的验证需要完成几何建模、定义材料特性、设置边界条件和加载情况、网格划分、指定分析类型和设置、求解和后处理等步骤。

圣维南原理的有限元模拟圣维南原理（Saint-Venant principle）是结构和材料力学领域中的一个重要原理，它可以用来研究材料在受力情况下的响应和变形。

该原理是由法国工程师阿杜安·德圣维南于1855年提出的，他的研究对于理解结构和材料的力学性能有着重要的意义。

圣维南原理的核心思想是，在材料受力时，只有处于受力点附近的一个局部区域内才发生显著的变形和应力集中，而远离受力点的其他区域则发生较小的变形。

基于这个原理，我们可以将材料的受力行为简化为在一个局部区域内进行研究，并假设其他区域的影响可以忽略不计。

通过这种近似，我们可以简化复杂的力学问题，并应用有限元方法进行数值模拟。

有限元方法是一种广泛应用于结构力学和材料力学领域的数值方法，它将结构或材料划分为许多小的有限单元，通过对每个单元进行力学分析来近似整体行为。

在进行有限元模拟时，我们需要定义材料的物理性质和边界条件，并选择适当的数值方法求解力学方程。

通过对不同单元的力学行为进行迭代计算，最终可以得到整体结构或材料的应力和变形。

针对圣维南原理的有限元模拟，首先需要对受力点附近的局部区域进行离散化划分，选择适当的有限元单元类型，如线性单元或非线性单元。

然后，需要定义材料的弹性性质，如杨氏模量和泊松比等，并通过适当的材料本构模型来描述材料的力学行为。

接下来，需要给定边界条件，如受力情况或位移边界条件，来模拟材料在受力时的行为。

最后，通过数值求解力学方程，并根据需要进行后处理，可以得到模拟结果，如应力分布、位移分布等。

有限元模拟可以用于研究不同类型的材料和结构，如金属、复合材料、混凝土和土壤等。

它可以帮助我们理解材料的力学性能、优化结构设计以及评估结构或材料的安全性能。

在实际应用中，有限元模拟已经成为结构和材料工程领域不可或缺的工具，在航空航天、汽车工程、建筑工程和能源领域等方面得到广泛应用。

总之，圣维南原理的有限元模拟是研究材料受力行为的重要方法之一，通过将结构或材料划分为小的有限单元，并进行力学分析，可以获得材料的应力和变形分布。

基于ANSYS的圣维南原理数值验证圣维南原理（Saint-Venant's principle）是一种用于结构分析的理论原理，用于预测载荷对结构的影响。

这个原理基于圣维南假设，假设结构的强度主要由结构边缘或靠近载荷应用点的局部区域控制。

在结构分析中，通常使用有限元软件ANSYS来进行数值验证。

ANSYS是一款强大的有限元分析软件，能够模拟各种结构的力学和热学行为。

以下将介绍如何使用ANSYS来进行圣维南原理的数值验证。

首先，需要在ANSYS中创建结构模型。

这包括定义几何形状、材料性质、边界条件和载荷。

可以使用ANSYS的预处理器工具来快速创建模型，并为每个组件分配合适的属性。

根据圣维南原理，应特别注意结构边缘附近的局部区域。

然后，需要对模型进行网格划分。

ANSYS使用有限元法来离散结构模型，将其划分为小的有限元单元。

这些单元将被用来求解结构的位移、应力和应变等参数。

网格划分的精细程度应根据结构的几何形状和问题的复杂性来确定。

接下来，需要制定求解方案。

在ANSYS中，可以选择适当的求解方法，如静态或动态分析、弹性或非线性材料行为等。

根据圣维南原理，通常使用静态分析和线性弹性材料行为。

然后，需要应用边界条件和载荷。

根据实际情况，可以选择约束结构的自由度，并在适当的位置施加载荷。

载荷的大小和方向应符合问题的要求。

接下来，通过求解器运行模型。

ANSYS会根据选择的求解方法和输入的边界条件求解结构的位移、应力和应变等参数。

根据圣维南原理，应关注结构边缘附近的位移和应力等结果。

最后，需要对结果进行分析和评估。

ANSYS提供了一系列的后处理工具，可以对结果进行可视化和分析。

可以绘制位移和应力等云图，并对各个关键点进行比较。

在进行圣维南原理的数值验证时，应注意以下几点：1.模型的几何形状和材料性质应准确地反映实际情况。

2.网格划分的精细程度应合理选择，以保证结果的精度和计算效率。

3.求解方案的选择应符合问题的需求和圣维南原理的适用范围。

基于ANSYS 的圣维南原理数值验证谢友增（航空工程学院 航空宇航制造工程 1201041）一 引言在轴向拉伸或压缩时，可以假设：变形前原为平面的横截面，变形后仍保持为平面且仍垂直于轴线。

根据这一平面假设，可以推断，杆件所有纵向纤维的伸长或压缩是相等的，因此各纵向纤维的受力是一样的。

我们得到，横截面上各点应力σ相等，于是得到N A Fσ= （1.1）式中：N F —轴力 A —横截面积若以集中力作用于杆件端面上，则集中力作用点附近区域内的应力分布比较复杂，公式（1.1）只能计算这个区域内横截面上的平均应力，不能描述作用点附近的真实情况。

这就引出，端截面上外力作用方式不同，将有多大影响的问题。

实际上，在外力作用区域内，外力分布方式有各种可能。

例如在图1a 和b 中，钢索和拉伸试样上的拉力作用方式就是不同的。

不过，如用与外力系静力等效的合力来代替原力系。

则除在原力系作用区域内有明显差别外，在离外力系作用区域略远处（例如，距离约等于截面尺寸处），上述代替的影响就非常微小，可以不计。

这就是圣维南原理。

根据这一原理，图1a 和b 所示杆件虽上端外力的作用方式不同，但可用其合力代替，这就简化成相同的计算简图（图1c ）。

在距离端截面略远处都可以用公式（1.1）计算应力。

图1 外力作用方式不同的杆件圣维南原理提出至今已有一百多年的历史，虽然还没有确切的数学表示和严格的理论证明，但无数的实际计算和实验测量都证实了它的正确性。

本文将利用ANSYS 软件，通过对实例模型的数值分析计算，证明圣维南原理。

选择建立一个二维平面模型作为研究对象，然后对此模型进行数值证明。

分别对平面模型两端施加均布载荷，以及与此集中力静力等效的集中力载荷。

绘制应力图以及路径图，比较两种情况下其所受的平均应力分布情况，从而利用此结果证明圣维南原理。

运用ANSYS软件可以简单直观的证明圣维南原理，从而可以更加深刻的理解圣维南原理。

二 ANSYS软件简介ANSYS公司是由美国著名力学专家、美国匹兹堡大学力学教授John Swanson 博士于1970年创建并发展起来的，总部设在美国宾夕法尼亚州的匹兹堡，是目前世界CAE行业中最大的公司。

基于有限元法验证圣维南原理摘要：圣维南原理是弹性力学中的最重要的基础性原理，本文主要是利用有限元方法，对圣维南原理进行验证。

文章首先是基于有限单元法的基本原理，进行平面有限元程序的编写，然后对所选模型进行有限元模型的建立，采用不同的荷载加载形式，利用编写的程序进行计算，最后对得到的结果从不同的方面进行分析，然后得出结论，对圣维南原理的正确性进行肯定。

关键词：有限元，圣维南原理，程序设计一、 引言圣维南原理（Saint Venant ’s Principle ）是弹性力学的基础性原理[1]，是法国力学家圣维南于1855年提出的。

其内容是：分布于弹性体上一小块面积（或体积）内的荷载所引起的物体中的应力，在离荷载作用区稍远的地方，基本上只同荷载的合力和合力矩有关；荷载的具体分布只影响荷载作用区附近的应力分布。

很多学者研究过圣维南原理的正确性，结果发现，它在大部分实际问题中成立。

有限元法（Finite Element Method ）是求解复杂微分方程近似解的一种非常有效的工具，是现代数字化科技的一种重要基础性原理。

将其应用到工程中，可成为探究物质客观规律的先进手段。

本文主要利用有限元法，进行程序设计，再利用该程序对圣维南原理进行验证，通过对施加不同的荷载情况下，比较构件内位移、应力的变化，进而对圣维南原理的正确性做出肯定。

二、 有限元基本原理及程序设计有限元分析包括三个方面[2]：1 有限元方法的基本数学力学原理；2 基于原理所形成的计算机程序；3 使用计算机进行计算。

首先来讨论一下有限元方法的基本数学力学原理。

本文所涉及的程序是基于3节点三角形单元（3-node triangular element ）,每个单元有6个自由度，所有节点的位移组成位移矩阵U ，所有节点力组成荷载向量P 。

图1其形函数为：u 1u 2u 3v 1v 2v 3N i=(a i+b i x+c i y)，i=1，2，3其中：a i=x j y m−x m y jb i=y j−y mc i=x m−x j应变转换矩阵：B i=12A [b i00c ic i b i]，i=1，2，3弹性系数矩阵：D=E1−μ2[1μ0μ10001−μ2]单元刚度阵：K e=∫B T∙D∙B∙t∙A=[k11k12k13 k21k22k23 k31k32k33]其中：t---单元的厚度；A---为单元的面积。

ansys分析混凝土的若干问题1. 讨论两种Ansys求极限荷载的方法（1）力加载可以通过对应的方法（比如说特征值屈曲）估计结构的极限荷载的大致范围，然后给结构施加一个稍大的荷载，打开自动荷载步二分法进行非线性静力分析，最后计算会因不收敛终止，则倒数第二个子步对应的就是结构的极限荷载；另外，也可以选择弧长法，采用足够的子步（弧长法可以一直分析到极限承载力之后的过程）同样可以从绘制的荷载位移曲线或计算结果中找出结构的极限荷载。

（2）位移加载给结构施加一个比较大的位移，打开自动荷载步二分法进行非线性分析，保证足够的子步数，这样也可以分析到极限荷载以后，通过绘制荷载位移曲线或查看相应结果文件也可知道结构的极限荷载。

希望众高手讨论一下（1）弧长法求极限荷载的收敛性问题，如何画到荷载位移曲线的下降段？（2）位移法求极限荷载的具体步骤？2. 需要注意的问题1. 由于SOLID 65单元本身是基于弥散裂缝模型和最大拉应力开裂判据，因此在很多情况下会因为应力集中而使混凝土提前破坏，从而和试验结果不相吻合，因此，在实际应用过程中应该对单元分划进行有效控制，根据作者经验，当最小单元尺寸大于5cm 时，就可以有效避免应力集中带来的问题；2. 支座是另一个需要注意的问题。

在有限元分析中，很多时候约束是直接加在混凝土节点上，这样很可能在支座位置产生很大的应力集中，从而使支座附近的混凝土突然破坏，造成求解失败。

因此，在实际应用过程中，应该适当加大支座附近单元的尺寸或者在支座上加一些弹性垫块，避免支座的应力集中；3. 六面体的SOLID 65 单元一般比四面体的单元计算要稳定且收敛性好，因此，只要条件允许，应该尽量使用六面体单元；4. 正确选择收敛标准，一般位移控制加载最好用位移的无穷范数控制收敛，而用力控制加载时可以用残余力的二范数控制收敛。

在裂缝刚刚出现和接近破坏的阶段，可以适当放松收敛标准，保证计算的连续性；3. 关于下降段的问题1）在实际混凝土中都有下降段，但是在计算的时候要特别小心下降段的问题。

用ANSYS证明圣维南原理一、圣维南原理圣维南原理（Saint-Venant’s Principle）：如果把物体的一小部分边界上的面力，变换为分布不同但静力等效的面力（主矢量相同，对于同一点的主矩也相同），那么，近处的应力分布将有显著的改变，但是远处所受的影响可以不计。

它也可以这样来陈述：如果物体一小部分边界上的面力是一个平衡力系（主矢量和主矩都等于零），那么，这个面力就只会使得近处产生显著的应力，远处的应力可以不计。

二、证明思路圣维南原理提出至今已有一百多年的历史，虽然还没有确切的数学表示和严格的理论证明，但无数的实际计算和实验测量都证实了它的正确性。

本文将利用ANSYS软件，通过对实例模型的数值分析计算，证明圣维南原理。

本文选择建立一个横截面积相对较小的混凝土柱体作为研究对象，然后对此矩形截面直杆模型进行数值证明。

分别对直杆两端施加集中力，以及与此集中力静力等效的均布载荷。

比较两种情况下其所受的平均应力分布情况，从而利用此结果证明圣维南原理。

三、ANSYS建模及求解1、创建有限元模型。

选择Solid —10 node 92单元类型，弹性模量EX=2.5E9，泊松比PRXY=0.35。

然后创建一个长、宽、高分别为1m，0.05m，0.05m的长方体，并对其进行自由网格划分。

建模及网格划分结果如下图1所示。

2、施加载荷并求解。

（1）在长方体一端加上全自由度位移约束，另一端面中心加上F=10KN 的集中力作用，求解。

约束及载荷施加结果如图2所示。

（2）在长方体一端加上全自由度位移约束，另一端面（与集中力作用端面相同）加上与集中力静力等效的P=4000KN的均布载荷用，求解。

约束及载荷施加结果如图3所示。

3、查看分析结果。

分别生成在长方体端面施加集中力与等效均布载荷情况下，其平均应力分布图以及各节点处平均应力分布变化曲线。

如下图所示。

四、分析与总结由图可知，所创建长方体在受到集中力及与其等效的均布载荷作用下，其绝大部分（较远离受力端面处）平均应力数值均处于4MPa 左右，而且各节点处应力分布变化情况也基本一致，只在添加约束及受力端面处有明显变化。