有限元法基础试题

有限单元法考试题及答案一、单项选择题（每题2分，共10分）1. 有限元法中，单元刚度矩阵的计算是基于（）。

A. 位移法B. 势能原理C. 能量守恒定律D. 牛顿第二定律答案：B2. 在有限元分析中，以下哪项不是网格划分时需要考虑的因素？（）A. 网格数量B. 网格形状C. 材料属性D. 边界条件答案：C3. 有限元分析中，以下哪项不是结构分析的基本步骤？（）A. 离散化B. 求解C. 后处理D. 优化设计答案：D4. 在有限元分析中，以下哪种类型的单元不适用于平面应力问题？（）A. 三角形单元B. 四边形单元C. 六面体单元D. 楔形单元答案：C5. 有限元分析中，以下哪种边界条件不属于几何边界条件？（）A. 固定支座B. 压力C. 温度D. 位移答案：C二、多项选择题（每题3分，共15分）6. 有限元法中，以下哪些因素会影响单元的精度？（）A. 单元形状B. 单元数量C. 材料属性D. 网格划分答案：ABD7. 在有限元分析中，以下哪些是常见的数值积分方法？（）A. 一阶积分B. 二阶积分C. 高斯积分D. 牛顿-莱布尼茨积分答案：ABC8. 有限元分析中，以下哪些是常见的单元类型？（）A. 线性单元B. 二次单元C. 三次单元D. 非线性单元答案：ABCD9. 在有限元分析中，以下哪些是常见的后处理技术？（）A. 应力云图B. 位移云图C. 模态分析D. 热分析答案：ABC10. 有限元分析中，以下哪些是常见的非线性问题？（）A. 几何非线性B. 材料非线性C. 接触非线性D. 热应力问题答案：ABCD三、填空题（每题2分，共20分）11. 有限元法中，单元刚度矩阵的计算通常基于___________原理。

答案：势能12. 在有限元分析中，网格划分的目的是将连续的___________离散化为有限数量的单元。

答案：域13. 有限元分析中，___________是将实际问题转化为数学问题的关键步骤。

有限单元法考试题及答案一、选择题1. 有限元法是一种用于求解偏微分方程的数值方法，其基本思想是将连续域离散化成有限个互不重叠的子域。

这种说法正确吗？A. 正确B. 错误答案：A2. 在有限元法中，单元的选取通常遵循以下哪个原则？A. 单元越小越好B. 单元越大越好C. 单元大小应根据问题的具体需求来确定D. 单元大小固定不变答案：C3. 有限元分析中，边界条件的处理方式不包括以下哪一项？A. 强制边界条件B. 自然边界条件C. 忽略边界条件D. 周期性边界条件答案：C4. 在有限元法中，下列哪个不是常用的单元类型？A. 三角形单元B. 四边形单元C. 六面体单元D. 圆形单元答案：D5. 有限元法中，形函数的作用是什么？A. 描述单元的几何形状B. 描述单元的物理属性C. 用于构建单元的局部刚度矩阵D. 用于描述单元内部的位移场答案：D二、简答题1. 简述有限元法的基本步骤。

答案：有限元法的基本步骤包括：定义问题域和边界条件，划分网格，选择单元类型，定义形函数，组装全局刚度矩阵，施加边界条件，求解线性方程组，提取结果。

2. 有限元法中，局部刚度矩阵是如何构建的？答案：局部刚度矩阵是通过单元的形函数和材料属性来构建的。

首先，根据单元的形函数和材料属性，计算单元的应变和应力。

然后，利用应变和应力，通过积分得到单元的局部刚度矩阵。

三、计算题1. 给定一个简单的一维弹性杆问题，其长度为L，两端固定，中间受力P。

请使用有限元法求解该杆的位移和应力分布。

答案：首先，将杆划分为若干个单元，每个单元的长度为Δx。

然后，为每个单元定义形函数，通常是线性形函数。

接着，根据形函数和材料属性（如杨氏模量E），构建每个单元的局部刚度矩阵。

将所有单元的局部刚度矩阵组装成全局刚度矩阵。

由于杆两端固定，边界条件为位移为零。

最后，将力P施加到中间节点，求解全局刚度矩阵对应的线性方程组，得到节点位移。

应力可以通过位移和形函数计算得到。

有限元考试试题一、简答题〔5道，共计25分〕。

有限单元位移法求解弹性力学问题的根本步骤有哪些？〔5分〕在划分网格数相同的情况下，为什么八节点四边形等参数单元精度大于四边形矩形单元？〔5分〕3.轴对称单元与平面单元有哪些区别？〔5分〕4.有限元空间问题有哪些特征？〔5分〕5.简述四节点四边形等参数单元的平面问题分析过程。

〔5〕分〕二、论述题〔3道,共计30分〕。

1.简述四节点四边形等参数单元的平面问题分析过程。

〔10分〕2.轴对称问题的简单三角形单元是否是常应力，常应变？为什么？〔10分〕3.在薄板弯曲理论中做了哪些假设？薄板单元和厚板单元的根本假设有什么不同？〔10分〕三、计算题〔3道，共计45分〕。

1.如下图等腰直角三角形单元，其厚度为t，弹性模量为E，泊松比0；单元的边长及结点编号见图中所示。

求形函数矩阵N应变矩阵B和应力矩阵S(3)单元刚度矩阵K e〔12分〕2.如下图的四结点矩形单元，求出节点3的位移。

设厚度t＝1m，μ＝0，E 为常量。

〔13分〕注：对于四节点矩形单元有：1.N11114N2111→Ni 1)(1i)(i1,2,3,4)4(1i114N314N411142.k11k12k13k14ek eTk21k22k23k24，BDBtdxdyA k31k32k33k34k41k42k43k44T11Tkij B i DB j tdxdy abt B i DB j ddA11Et2b ij11ij1a i j11ij2a3b32ij1i j812ij1a1ij2ij1ij1a1i j 1 i jb3(i,j1,2,3,4)b33.有一如图3(a)所示的剪力墙，墙顶作用竖向荷载P。

将该剪力墙划分为两个三结点三角形常应力单元，单元和结点编号如图3(b)所示，并将荷载P分成两个P/2作用在3、4结点。

单元厚度为t，弹性模量为E，泊松比μ=1/3。

求结点3和结点4的位移，以及单元①的应变和应力。

一、名词解释1、单元---任何连续体都可以假想的分割成有限个简单形状单元体的组合，将这些简单形状的单元体称为单元2、节点---把单元与单元之间设置的相互连接点称为节点3、静力等效原则----对于刚体来说，所谓静力等效原则就是单元上原有的外力系和将外力系向各节点移置所得的等效节点力，二者向同一点简化应具有相同的主矢和主矩；对于弹性体来说，所谓静力等效原则就是指单元上的外力系和将该力系向各节点移置后的等效节点力在单元上引起的变形能相等，在一定的位移模式下这种移置是唯一的。

4、虚功等效-----就一个单元来说，把作用在单元上的外力系移置到节点上后，应当与原来的实际外力所作虚功等效。

5、等参元-----如果子单元的位移函数插值节点数与其位置坐标变换节点数相等，其位移函数插值公式与位置坐标变换式都用相同的形函数与节点参数进行插值，则称其为等参元6、超参数单元-----如果单元坐标变换所用的形函数的阶次高于位移模式所用的形函数的阶次，即用于规定单元形状的节点数多于用于规定单元位移的节点数，这种单元就称为超参数单元。

7、低阶元-----把有线性位移函数的单元称为低阶元。

8、高阶元----把有非线性位移函数的单元称为高阶元。

二、填空1、等效节点移植方法基于（虚功原理）和（力系等效）。

2、处理位移有（代入法）和（乘大数法）。

3、三角形单元是一阶单元，四边形单元是二阶单元，四面体单元是一阶单元，六面体单元是二阶单元。

4、平面问题包括（平面应力）、（平面应变）和（轴对称）。

5、弹性问题解决方法有（位移法）和（应力法）。

三、简答1、圣维南原理 p9答：如果把物体的一小部分边界的面力，变换为分布不同但静力等效的面力，那么近处的应力分布将有显著地改变，但是远处所受的影响可以不计。

2、系统能量极值原理 p9答：在所有满足内部连续条件和运动学边界条件的位移中，满足平衡方程的位移使系统的总势能取驻值。

如果驻值是极小值，则平衡时稳定的。

有限元库题2021有限元试题（2021）问答题1、简述有限元的基本思想及其基本步骤。

2、有限元分析在汽车结构上的应用主要体现哪些方面？3、阐述汽车结构有限元分析的内容。

4、阐述汽车结构有限元分析的流程。

5、有限元分析的基本流程是什么？6、什么是平面问题？有哪些类型及各种类型特点？7、在分析平面问题划分单元时，应注意什么？8、在进行有限元分析时，位移函数应满足哪些条件？ 9、在进行有限元分析时，单元刚度矩阵具有哪些性质？ 10、在进行有限元分析时，总刚度矩阵具有哪些性质？11、根据平问题有限元法基本理论，其主要分析步骤有哪些？ 12、什么杆系结构？杆系单元有哪些特点？13、在小挠度弹性薄板变曲理论中，有哪些基本假设？ 14、什么是结构动力问题？有哪些类型？15、在选择有限元分析软件时，应考虑哪些因素？16、从解决工程实际问题的角度来看，结构强度分析的内容有哪些？ 17、有限元分析的数据前处理工作包括哪些方面？18、在使用有限元软件时，划分网格时应注意哪些问题？ 19、什么绝对位移约束？其包括几种类型？ 20、什么是自由度耦合？其有哪些用途？ 21、简述有限元分析的数据后理处过程。

22、在进行有限元分析时，选择建立汽车有限元计算模型要考虑哪些问题？23、在汽车结构分析时，制定分析方案的主要步骤有哪些？ 24、简述使用ANSYS 软件进行有限元分析的基本流程。

25、ANSYS软件的前处理主要完成有限元分析中的哪些内容？ 26、ANSYS软件的后处理主要完成有限元分析中的哪些内容？ 27、ANSYS软件在进行网格划分时应注意哪些问题？计算题1、如下图所示1D杆结构，设杆截面积为A，弹性模量为E，应用取微单元体的方法推导基本方程和边界条件。

2、设平面问题中的应力为?x?a1?a2x?a3y?y?a4?a5x?a6y ?xy?a7?a8x?a9y其中ai?i?1.2?9?为常数，设所有体积力为零，证明下列条件是否满足平衡？并求出满足平衡条件时ai之间关系。

有限元基础期末试题
1、简述单元分析的四个主要环节。

对于三结点三角形单元，写出单元分析各环节最终结果
的矩阵表达式。

2、以三结点三角形单元为例，解释位移模式概念并写出三结点三角形单元位移模式的具体
表达式。

3、结合三结点三角形单元位移模式的具体表达式，解释型函数概念并简述型函数的主要性
质。

4、写出推导单元刚度矩阵时所使用的虚功方程并解释其物理意义。

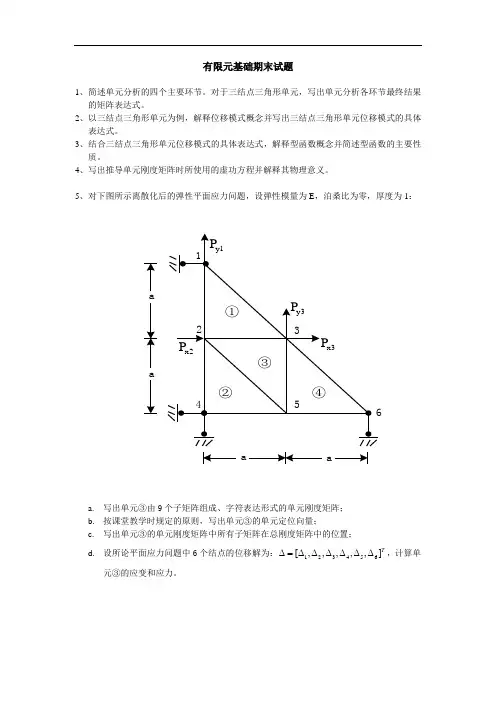
5、对下图所示离散化后的弹性平面应力问题，设弹性模量为E ，泊桑比为零，厚度为1：
a. 写出单元③由9个子矩阵组成、字符表达形式的单元刚度矩阵；
b. 按课堂教学时规定的原则，写出单元③的单元定位向量；
c. 写出单元③的单元刚度矩阵中所有子矩阵在总刚度矩阵中的位置；
d. 设所论平面应力问题中6个结点的位移解为：123456[,,,,,]T
∆=∆∆∆∆∆∆，计算单
元③的应变和应力。

有限元试题及答案一、选择题1. 有限元方法是一种用于求解工程和物理问题的数值技术，其核心思想是将连续域划分为有限数量的离散子域。

以下哪项不是有限元方法的特点？A. 网格划分B. 边界条件处理C. 局部近似D. 整体求解答案：D2. 在有限元分析中，以下哪项不是网格划分的常见类型？A. 三角形网格B. 四边形网格C. 六边形网格D. 圆形网格答案：D3. 对于线性弹性问题，以下哪种元素类型不适用于有限元分析？A. 线性三角形元素B. 二次三角形元素C. 线性四边形元素D. 三次四边形元素答案：D二、填空题1. 在有限元分析中，单元刚度矩阵的计算通常涉及到单元的_________。

答案：形状函数2. 有限元方法中，边界条件可以分为_________和_________。

答案：Dirichlet边界条件；Neumann边界条件3. 有限元软件通常采用_________方法来求解大型稀疏方程组。

答案：迭代三、简答题1. 简述有限元方法的基本步骤。

答案：有限元方法的基本步骤包括：- 定义问题的几何域和边界条件。

- 将几何域划分为有限数量的小单元。

- 为每个单元定义形状函数。

- 计算单元刚度矩阵和载荷向量。

- 组装全局刚度矩阵和载荷向量。

- 施加边界条件。

- 求解线性方程组，得到节点位移。

- 计算单元应力和应变。

2. 为什么在有限元分析中需要进行网格划分？答案：网格划分是有限元分析中的一个重要步骤，因为它允许将连续的几何域离散化，使得问题可以被数值方法求解。

通过网格划分，可以： - 简化复杂几何形状的分析。

- 适应不同的材料属性和边界条件。

- 提供足够的细节以捕捉应力和位移的局部变化。

- 减少计算复杂度，提高求解效率。

四、计算题1. 假设有一个平面应力问题，已知材料的弹性模量E=210GPa，泊松比ν=0.3。

请计算一个边长为10mm的正方形单元在单轴拉伸下的单元刚度矩阵。

答案：单元刚度矩阵\[ K \]可以通过以下公式计算：\[K = \frac{E}{(1-\nu^2)} \int_{\Omega} \left[ B^T B \right] d\Omega\]其中，\( B \)是应变-位移矩阵，\( \Omega \)是单元的面积。

《有限元基础》复习题1. 有限单元法的解题步骤如何？它和经典Ritz 法的主要区别是什么？ 答：解题步骤：⑴划分单元，输入结点和单元信息；⑵单元分析：、、eeN K P ⑶整体分析：1,T==∑en e eee K GK G 1T ==∑en e e e P G P 引入位移边界条件得到：=Ka P⑷求解方程得到解a⑸对位移a 结果进行有关整理、计算单元或结点的应力、应变 有限元法和经典Ritz 法的区别：经典Ritz 法是在整个区域内假设未知函数，适用于边界几何形状简单的情形；有限单元法是将整个区域离散，分散成若干个单元，在单元上假设未知函数。

有限单元法是单元一级的Ritz 法。

2. 单元刚度矩阵和结构刚度矩阵各有什么特征？刚度矩阵[]K 奇异有何物理意义？在求解问题时如何消除奇异性？答：单元刚度矩阵的特征：⑴对称性⑵奇异性⑶主元恒正⑷平面图形相似、弹性矩阵D 、厚度t 相同的单元，eK 相同⑸eK 的分块子矩阵按结点号排列，每一子矩阵代表一个结点，占两行两列，其位置与结点位置对应。

整体刚度矩阵的特征：⑴对称性⑵奇异性⑶主元恒正⑷稀疏性⑸非零元素呈带状分布。

[]K 的物理意义是任意给定结构的结点位移得到的结构结点力总体上满足力和力矩的平衡。

为消除[]K 的奇异性，需要引入边界条件，至少需给出能限制刚体位移的约束条件。

3. 列式说明乘大数法引入给定位移边界条件的原理？ 答：设：j j a a =，则将 jj jj k k α=j jj j P k a α=即： 111211211212222222122212222222αα⎡⎤⎧⎫⎧⎫⎢⎥⎪⎪⎪⎪⎢⎥⎪⎪⎪⎪⎢⎥⎪⎪⎪⎪⎪⎪⎪⎪=⎢⎥⎨⎬⎨⎬⎢⎥⎪⎪⎪⎪⎢⎥⎪⎪⎪⎪⎢⎥⎪⎪⎪⎪⎪⎪⎪⎪⎢⎥⎩⎭⎩⎭⎣⎦jn jn j j jjj n j jj j n n njn n n n k k k k a P kk k k a P k k k k a k a k k k k a P1510α≈修改后的第j 个方程为112222j j jj j j n n jj j k a k a k a k a k a αα+++++=由于得 jj j jj j k a k a αα≈ 所以 j j a a ≈对于多个给定位移()12,,,l j c c c =时，则按序将每个给定位移都作上述修正，得到全部进行修正后的K 和P ，然后解方程即可得到包括给定位移在内的全部结点位移值。

有限元试题及答案一、选择题1.有限元分析是一种利用计算机数值方法进行结构分析的方法，下面哪个说法是正确的？A. 有限元分析对结构的约束条件没有要求B. 有限元分析只适用于静力分析C. 有限元分析可以用来研究结构的动力响应D. 有限元分析的计算结果一定是精确的答案：C2.有限元法的基本步骤包括以下几个环节：I. 离散化II. 单元划分III. 节点连接IV. 计算材料性质V. 施加边界条件VI. 构建刚度矩阵和载荷向量VII. 求解节点位移和应力VIII. 后处理与结果分析请问选择项中正确的顺序是：A. IV – I – II – III – V – VI – VII – VIIIB. I – II – III – IV – V – VI – VII – VIIIC. II – III – V – IV – VI – I – VII – VIIID. I – III – II – IV – V – VI – VII – VIII答案：B3.在有限元分析中，单元是指将结构划分为有限个小单元来近似表示结构的方法。

下面哪个选项给出了常用的结构单元类型？A. 三角形单元，四面体单元，六面体单元B. 矩形单元，六面体单元，圆形单元C. 圆形单元，矩形单元，六面体单元D. 四面体单元，矩形单元，三角形单元答案：D二、填空题1.有限元分析中，刚度矩阵的计算需要根据单元的_________和材料的_________计算得到。

答案：几何形状，物理性质2.有限元法最常用的数学插值函数是_________函数。

答案：形函数3.在有限元分析中，自由度是指结构中的每个_________未知量。

答案：位移三、计算题1.给定如图所示的二维结构，使用有限元法进行分析。

假设结构材料为线性弹性材料，其杨氏模量为200 GPa，泊松比为0.3。

结构整体尺寸为5m x 3m，单元尺寸为1m x 1m。

分析载荷为2000 N，施加在结构的中心节点上。

有限元考试题库及答案一、单项选择题（每题2分，共10分）1. 有限元法中，单元刚度矩阵的计算是基于（）。

A. 材料力学B. 结构力学C. 弹性力学D. 流体力学答案：C2. 在有限元分析中，边界条件不包括以下哪一项？（）A. 位移边界条件B. 载荷边界条件C. 温度边界条件D. 速度边界条件答案：D3. 有限元分析中，以下哪种类型的单元是二维的？（）A. 杆单元B. 梁单元C. 壳单元D. 体单元答案：C4. 有限元分析中，以下哪种类型的网格划分方法适用于复杂几何形状？（）A. 结构化网格B. 非结构化网格C. 规则网格D. 混合网格答案：B5. 在有限元分析中，以下哪种方法用于求解线性方程组？（）A. 高斯消元法B. 牛顿迭代法C. 有限差分法D. 有限体积法答案：A二、多项选择题（每题3分，共15分）6. 有限元分析中，以下哪些因素会影响网格划分的质量？（）A. 网格大小B. 网格形状C. 网格数量D. 网格排列答案：ABCD7. 在有限元分析中，以下哪些是常见的单元类型？（）A. 三角形单元B. 四边形单元C. 六面体单元D. 楔形单元答案：ABCD8. 有限元分析中，以下哪些是常见的边界条件？（）A. 固定边界B. 自由边界C. 压力边界D. 位移边界答案：ACD9. 在有限元分析中，以下哪些是常见的求解器类型？（）A. 直接求解器B. 迭代求解器C. 混合求解器D. 并行求解器答案：ABD10. 有限元分析中，以下哪些是常见的后处理技术？（）A. 应力云图B. 位移云图C. 模态分析D. 频率响应分析答案：ABCD三、简答题（每题5分，共20分）11. 简述有限元分析中网格划分的基本原则。

答案：有限元分析中网格划分的基本原则包括：确保网格的几何形状规则、避免过度扭曲的单元、保持网格大小的一致性、在应力集中区域细化网格、以及考虑分析的精度和计算成本。

12. 描述有限元分析中单元刚度矩阵的物理意义。

e an dAl l t h i ng si nt he i rb ei n ga re go o2. 如图2所示，有一正方形薄板，沿对角承受压力作用，厚度t=1m ，载荷F=20KN/m ，设泊松比µ=0，材料的弹性模量为E ，试求它的应力分布。

（15分）图23. 图示结点三角形单元的124边作用有均布侧压力q ，单元厚度为t ，求单元的等效结点荷载。

图3图1一、简答题1. 答：1）合理安排单元网格的疏密分布2）为突出重要部位的单元二次划分3）划分单元的个数4）单元形状的合理性5）不同材料界面处及荷载突变点、支承点的单元划分6）曲线边界的处理，应尽可能减小几何误差7）充分利用结构及载荷的对称性，以减少计算量2. 答：形函数应满足的三个条件：a.必须能反映单元的刚体位移，就是位移模式应反映与本单元形变无关的由其它单元形变所引起的位移。

b.能反映单元的常量应变，所谓常量应变，就是与坐标位置无关，单元内所有点都具有相同的应变。

当单元尺寸取小时，则单元中各点的应变趋于相等，也就是单元的形变趋于均匀，因而常量应变就成为应变的主要部分。

c.尽可能反映位移连续性；尽可能反映单元之间位移的连续性，即相邻单元位移协调。

3. 答：含义：所谓的等参数单元，就是在确定单元形状的插值函数和确定单元位移场的插值函数中采用了完全相同的形函数。

意义：构造出一些曲边地高精度单元，以便在给定地精度下，用数目较少地单元，解决工程实际地具体问题。

4. 答：有限单元法是基于变分原理的里兹（Ritz）法的另一种形式，从而使里兹法分析的所有理论基础都适用子有限单元法，确认了有限单元法是处理连续介质问题的一种普遍方法．利用变分原理建立有限元方程和经典里兹法的主要区别是有限单元法假设的近似函数不是在全求解域而是在单元上规定的，面且事先不要求满足任何边界条件，因此它可以用来处理很复杂的连续介质问题。

有nl⎥⎦⎤⎢⎣⎡5.0025.025.011212－－－＝＝E k k ⎥⎦⎤⎢⎣⎡5.0025.0011313－＝＝E k k ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡5.125.025.05.125.0005.05.00025.075.025.025.075.032222212222E E E E k k k k ＋＝＋＋＝⎥⎦⎤⎢⎣⎡----=⎥⎦⎤⎢⎣⎡---+⎥⎦⎤⎢⎣⎡---5.025.025.0125.025.005.025.0025.05.032312323E E E k k k ＝＋＝⎥⎦⎤⎢⎣⎡---5.0025.025.022424E k k ＝＝⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡025.025.00025.0000025.0032522525E E E k k k ＝＋＝⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡5.125.025.05.15.00025.075.025.025.075.025.0005.043333313333E E E E k k k k ＝＋＋＝⎥⎦⎤⎢⎣⎡----=⎥⎦⎤⎢⎣⎡---+⎥⎦⎤⎢⎣⎡---125.025.05.05.0025.025.05.025.0025.043533535E E E k k k ＝＋＝⎥⎦⎤⎢⎣⎡0025.0043636E k k ＝＝⎥⎦⎤⎢⎣⎡75.025.025.075.024444E k k ＝＝⎥⎦⎤⎢⎣⎡---25.0025.05.024545E k k ＝＝ ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡5.125.025.05.175.025.025.075.05.00025.025.0005.045535525555E E E E k k k k ＝＋＋＝⎥⎦⎤⎢⎣⎡---25.0025.05.045656E k k ＝＝⎥⎦⎤⎢⎣⎡25.0005.046666E k k ＝＝把上面计算出的，…，对号入座放到总刚矩阵中去，于是得到11k 66k []K的具体表达式。

机械《有限元方法》考试试卷（A卷）班级: 姓名: 学号:题号一二三四总得分评卷人得分一、填空题（每空1分，共20分）1、在整个有限元分析的过程中，是分析的基础。

2、平面应力问题与薄板弯曲问题的弹性体几何形状都是，但前者受力特点是，变形发生在板面内；后者受力特点是的力的作用，板将变成有弯有扭的曲面。

3、典型的ANSYS文件包括、、。

4、平面应力问题与平面应变问题都具有个独立的应力分量，个独立的应变分量，但对应的弹性体几何形状前者为，后者为。

5、ANSYS软件提供了两种工作方式，即和。

6、对于用户创建的局部坐标系，其坐标系号必须是。

7、网格划分时，可以采用或者对模型进行划分网格，生成有限元模型。

8、是图形在不同的CAD和CAE系统间进行交换时普遍接受的一种中间标准格式。

9、在固体力学的有限元分析中，是最简单的三维有限元单元。

10、ANSYS向用户提供了两种后处理工具查看计算结果：和。

二、选择题（每题1分，共10分）1、在ANSYS的单元库中，PLANE42单元属于。

A.结构梁单元；B.结构壳单元；C.结构线单元；D.结构实体单元。

2、在一个分析中，可能有多个材料特性组，ANSYS通过独特的来识别每个材料特性组。

A.特性；B.说明；C.参考号；D.方法。

3、ANSYS与Pro/E的接口文件类型是。

A..x_t；B..prt；C..sat；D..model。

4、弹性力学与材料力学的主要不同之处在于C。

A.任务；B.研究对象；C.研究方法；D.基本假设。

σ是C。

5、在轴对称问题中，径向应力分量rA.恒为零；B.与r无关；C.与θ无关；D.恒为常数。

6、利用ANSYS进行结构分析时，结果文件为。

A.jobname.rst；B.jobname.rth；C.jobname.rfl；D.jobname.rmg。

7、载荷包括所有边界条件以及外部或内部作用效应，下列不属于ANSYS 载荷的是。

A.DOF约束；B.力；C.体载荷；D.应力。

有限元试题及答案一、选择题1. 有限元法是一种数值方法，主要用于求解什么类型的数学问题？A. 线性代数方程B. 微分方程C. 积分方程D. 偏微分方程答案：D2. 在有限元分析中，以下哪项不是网格划分的基本原则？A. 网格应尽量均匀B. 网格应避免交叉C. 网格应尽量小D. 网格应适应几何形状答案：C3. 有限元方法中，单元的局部刚度矩阵可以通过以下哪种方式获得？A. 直接积分B. 矩阵乘法C. 线性插值D. 经验公式答案：A二、填空题1. 有限元方法中，______ 是指将连续的域离散化成有限数量的小单元。

答案：离散化2. 在进行有限元分析时，______ 是指在单元内部使用插值函数来近似求解场变量。

答案：近似3. 有限元法中，______ 是指在单元边界上满足的连续性条件。

答案：边界条件三、简答题1. 简述有限元法的基本步骤。

答案：有限元法的基本步骤包括：（1）定义问题域；（2）离散化问题域，生成网格；（3）为每个单元定义局部坐标系和形状函数；（4）组装全局刚度矩阵和载荷向量；（5）施加边界条件；（6）求解线性代数方程；（7）提取结果并进行后处理。

2. 描述有限元分析中的单元类型有哪些，并简述每种单元的特点。

答案：常见的单元类型包括：（1）一维单元，如杆单元和梁单元，特点是沿一个方向传递力；（2）二维单元，如三角形和四边形单元，特点是在平面内传递力；（3）三维单元，如四面体和六面体单元，特点是在空间内传递力。

每种单元都有其特定的形状函数和刚度矩阵。

四、计算题1. 给定一个简单的一维弹性杆问题，其长度为L，两端固定，中间施加集中力P。

使用有限元法求解该杆的位移和应力分布。

答案：首先，将杆离散化为一个单元。

使用一维杆单元的局部刚度矩阵和形状函数，可以推导出全局刚度矩阵。

然后，施加边界条件，即杆的两端位移为零。

最后，将集中力P转换为等效节点载荷，求解线性代数方程，得到节点位移。

应力可以通过位移和杆的截面特性计算得出。

有限元基础概念题一共100道题，全是判断题！编号问题1.像床单那样薄、那样宽的板用梁单元来模型化2.对于高压电线的铁塔那样的框架结构的模型化处理使用梁单元3.一般自由度多的模型分析成本高4.使用尽可能多种类单元的模型是一个好的模型5.杆单元是壳单元的一种6.不能把梁单元、壳单元和实体单元混合在一起做成模型7.四边形的壳单元尽可能做成接近正方形形状的单元8.因为实体单元是3维单元，所以即使有严重的扭曲也没关系9.将作用有垂直载荷的悬臂梁用多个杆单元做成10.将作用有垂直载荷的两端自由支持的梁用杆单元来模型化11.三角形单元和四边形单元不能混在一起使用12.平面应变单元也好，平面应力单元也好，如果以单位厚来做模型化处理的话会得到一样的答案13.同样形状的话，使用三角形单元和使用四边形单元解是相同的14.边长为10cm和边长为100cm 的正方形的板，后者的单元数如果是前者的10倍的话，才行15.为了校核连续的相同管子剖面内的应力状态，要使用平面应力单元16.对热应力问题，1维单元也好2维单元也好，所求的解都搞不清17.对于热传导分析必须输入线膨胀系数18.热应力随结构的约束状态而变化19.FEM分析变形越大应力就越高20.在线性分析中，即使变形变大，如果可以将这部分单元划分得多一些的话，也会保证解的适当正确21.为了评价应力集中，在网格划分时应该把整个做成一样的单元尺寸22.板厚并不一致的情况下，一定要用到实体单元23.单元数相同的话，1阶单元、2阶单元的解都一样24.为了忠实地尽可能表现结构的形状，必须严格按装配顺序来做模型化处理25.节点的位置依赖于形态，而并不依赖于载荷的位置26.一般应力变化大的地方单元尺寸要划的小才好27.仅用TETRA单元的模型与仅用HEXA单元的模型相比，后者的精度要好28.相接的单元尺寸大小不要变化太厉害29.在进行特征值分析时，必须输入质量30.进行热应力分析时，必须输入线膨胀系数31.壳单元表面的应力因为与表面内的应力相比精度会降低所以必须注意32.象船和火箭那样的结构因为漂浮在水（空）中而没被固定住，所以，FEM分析不可以使用33.约束条件用全固定或许加上铰固定就能表现完全34.一般在特征值分析中一定是采用节点编号连续来编的方法，所得精度要高35.用固有振动分析求应力，应力高的部分必须要加强36.屈曲模态并不依赖于约束条件37.自由度有位移自由度和转角自由度38.一般在FEM中使用的模型称为刚体模型39.对比铁更硬的部分所做模型化处理的单元称为刚体单元40.刚体单元和梁单元和板单元组合在一起进行分析是不可以的41.一般网格划分过度的话，很费分析时间42.对啤酒罐的压缩强度要用固有振动分析来评价43.表示自由度的坐标系有局部坐标系和整体坐标系44.应力集中的部分是多个载荷所加的部位45.在加上热载的情况下，即使是同一个模型，根据约束条件，所发生的应力有很大的不同46.用有限元法可以对正在动的（移动）物体的结构进行分析47.对膜（membrane）单元也可用面压载荷48.可对膜（membrane）单元可以用集中载荷49.施加强迫位移的分析要进行静力分析50.一般所给出的载荷的总和与反力的总和相一致51.即使将不同的局部坐标系下定义好的节点连起来也可定义单元52.所谓自由度是直接翻译degrees of freedom 的53.所谓实体单元意味着刚体单元的集合54.杨氏系数是纵弹性系数（模量）55.共鸣现象与固有频率有关56.杨氏系数是评价材令的基值57.即使是同一种材料，梁单元和板单元也要输入不同的材料性质数值58.泊松比是在纵向加压时发生在纵向的应变和横向的应变的比率59.用弹性材料可表现塑性化现象60.一般线膨胀系数是作为材料常数之一输入61.一般用FEM模型化时，大的结构求得的热变形小62.约束条件全都没被定义的结构不能分析63.X、Y、Z全部方向上的位移都是1时称为刚体变形64.分析结果是对称的模型，使用对称条件可以用较少的单元来进行分析65.所谓铰约束条件是约束位移自由度而让转角自由度自由66.强迫位移是一种约束条件67.即使所有的自由度都约束也会发生变形68.对于设置了约束的自由度即使输入载荷也不发生位移69.有限单元分析约束条件尽量少则精度好70.所谓约束就是消去自由度71.所谓全约束只要将位移自由度约束住72.壳单元与实体单元可约束的自由度不同73.线性分析将同样大的载荷加在反向产生位移的绝对值不变74.由分析所得的最大应力受网格划分的影响75.载荷和应力表示同一件东西76.主应力并不依赖于基本坐标系77.在应力分析中，应力小的部位单元尺寸要小，大的部位单元尺寸要大来进行模型化处理78.实特征值分析是一种求最大应力的手段79.具有切口附近的应力集中用FEM不能严密地计算80.一阶单元是假定单元内的应力都一样的单元81.表现材料的弹性界限是所谓的屈服应力82.在屈服曲面内材料表现为弹性行为83.位移能用6个矢量成分来表示84.转角是一种位移85.载荷点的位移通常最大86.线性应力分析也可以得到极大的变形87.与材料无关的相同变形量产生相同的应力88.给出同一载荷杨氏系数越大则变形也越大89.对于静力分析质量是不可缺少的数据90.实特征值分析中必须定义集中载荷或分布载荷91.屈曲分析和固有振动分析是类似的特征值问题92.使用同一模型时，一般特征值分析要比线弹性分析化时间93.一般求特征值分析所求的模态数多也好少也好，分析时间是一样的94.在静力分析中，仅施加左右方向的载荷时，不约束上下方向也可以95.卡车通过时，玻璃窗会发生振动，这是与玻璃的固有频率有关96.FEM也被用在医学上97.有限元法、有限体积法、有限差分法、边界元法这中间FEM是有限差分法98.有限元法基本的是求解联立方程式99.FEM理论1950年前开始就有了100.考虑阻尼的特征值问题成了复特征值问题。

1、单元刚度阵如何叠加称结构的整体刚度矩阵，为何这么叠加，如何从刚度矩阵的物理意义去理解此叠加关系，叠加成的整体刚度矩阵又有什么特点？答：先将单元刚度矩阵[k]扩大到与结构刚度矩阵同阶，以便进行矩阵相加：再将单元刚度矩阵[k]中的各子块按照单元结点的实际编码安放在扩大的矩阵中，它的物理意义是该单元对结构刚度矩阵[K]的那些刚度系数有“贡献”。

1）K 是对称矩阵2）K 中主对角元素总是正的3）K 是稀疏矩阵，非零元素呈带状分布4）K 是奇异矩阵，在排除刚体位移后，它是正定阵。

2、在约束条件处理时，试讲述主元赋大值是如何引入约束条件的。

答：主元赋大值法：将整体刚度矩阵的主元乘以一个计算机容量允许的极大值。

赋0法：在整体刚度矩阵中与己知节点位移相对应的行（列）的主对角线元素赋值1其它置0.3、试述总体刚度矩阵中各元素的物理意义。

答：整体刚度矩阵中，每个元素ij K 的物理意义为在节点j 发生单位位移而其它节点位移为零时，在节点i 处产生的节点力4、试述有限元法的基本思想。

通过把连续的几何机构离散成有限个单元，并在每一个单元中设定有限个节点，将连续体看作仅在节点处相连接的一组单元的集合体，同时选定场函数的节点值作为基本未知量并在每一单元中假设一个近似插值函数以表示单元中场函数的分布规律，再建立用于求解节点未知量的有限元方程组，从而将一个连续域中的无限自由度问题转化为离散域中的有限自由度问题。

5、试述数值积分时，为保证积分精度高斯积分点数的选取原则。

、平面八结点单元、、空间20结点单元应怎样取积分点才能保证精度。

对平面任意四结点单元应采用22⨯的高斯积分点，对于平面8结点四边形单元应采用33⨯的高斯积分点，对空间八结点单元应采用222⨯⨯的高斯积分点，对20结点六面体单元应采用333⨯⨯的高斯积分点。

江西理工大学研究生考试试卷一、 简答题（共40分，每题10分）1. 论述单元划分应遵循的原则。

2. 说明形函数应满足的条件。

3. 说明四边形等参数单元中“等参数”的含义，即为什么要引入等参数单元。

4. 阐述边界元法的主要优缺点。

二、 计算题（共60分，每题20分）1. 一杆件如图3所示，杆件上方固定后，在下方受垂直向下的集中力作用，已知：杆件材料的杨氏模量2721/100.3in lbf E E ⨯==，截面积2125.5in A =，2275.3in A =，长度in L L 1221==，集中力lbf P 100=，用有限元方法求解B 点和C 点位移。

备注：（1）1 lbf （磅力，libra force ） = 4.45 N 。

（2）杨氏模量、弹性模量、Young 氏弹性模量具有相同含义（10分）20__12__—20__13__ 学年 第___一___学期 课程名称：_____有限元及数值模拟________ 考试时间:___2012___ 年__11__月___3___日考试性质（正考、补考或其它）：[ 正考 ] 考试方式(开卷、闭卷)：[ 开卷 ] 试卷类别(A 、B):[ A ] 共 九 大题温 馨 提 示请考生自觉遵守考试纪律，争做文明诚信的大学生。

如有违犯考试纪律，将严格按照《江西理工大学学生违纪处分规定》（试行）处理。

学院 专业 学号 姓名 题号 一二三四五六七八九十十一十二总 分得分pyA1A2L1L2图12. 如图2所示，有一正方形薄板，沿对角承受压力作用，厚度t=1m，载荷F=20KN/m，设泊松比µ=0，材料的弹性模量为E，试求它的应力分布。

（15分）图23. 图示结点三角形单元的124边作用有均布侧压力q，单元厚度为t，求单元的等效结点荷载。

图3一、简答题1. 答：1）合理安排单元网格的疏密分布2）为突出重要部位的单元二次划分3）划分单元的个数4）单元形状的合理性5）不同材料界面处及荷载突变点、支承点的单元划分6）曲线边界的处理，应尽可能减小几何误差7）充分利用结构及载荷的对称性，以减少计算量2. 答：形函数应满足的三个条件：a.必须能反映单元的刚体位移，就是位移模式应反映与本单元形变无关的由其它单元形变所引起的位移。

有限元法基础试题一、填空题（5X 2分）单元刚度矩阵k e B T DBd 中，矩阵B为_______________ ，矩阵D为 ____________ 。

边界条件通常有两类。

通常发生在位置完全固定不能转动的情况为_____________ 边界，具体指定有限的非零值位移的情况，如支撑的下沉，称为__________ 边界。

内部微元体上外力总虚功：的表达式中，第d W e x,x xy,y F bx u xy,x y,y F by v dxdy+x u,x y v,y xy u,y u,x dxdy一项为_____________________ 的虚功，第二项为_____________________ 的虚功。

弹簧单元的位移函数N1+ N2 = ___________ 。

k j数学表达式：令d j = __________ , d k= _________ , k j，则力F i k j。

二、判断题（5X 2分）位移函数的假设合理与否将直接影响到有限元分析的计算精度、效率和可靠性。

（）变形体虚功原理适用于一切结构（一维杆系、二维板、三位块体）、适用于任何力学行为的材料（线性和非线性），是变形体力学的普遍原理。

（）变形体虚功原理要求力系平衡，要求虚位移协调，是在“平衡、协调”前提下功的恒等关系。

（）常应变三角单元中变形矩阵是x或y的函数。

（）对称单元中变形矩阵是x或y的函数。

（）三、简答题（26 分）列举有限元法的优点。

（8 分）写出有限单元法的分析过程。

（8 分）列出 3 种普通的有限元单元类型。

（ 6 分）简要阐述变形体虚位移原理。

（4 分）四、计算题（54 分）对于下图所示的弹簧组合，单元①的弹簧常数为10000N/m,单元②的弹簧常数为20000N/m,单元③的弹簧常数为10000N/m,确定各节点位移、反力以及单元②的单元力。

（10分）对于如图所示的杆组装，弹性模量E为10GPa，杆单元长L均为2m，横截面面积A均为2 X 10-4m2，弹簧常数为2000kN/m，所受荷载如图。

一。

简答题：1.轴对称体上作用正对称形式的载荷时，沿坐标,,r z θ的三个分量(,,)r P r z θ，z (,,)P r z θ和(,,)P r z θθ有何特点？（P85）(,,)r P r z θ和z (,,)P r z θ是偶函数，傅里叶级数展开式中不含sin k θ，(,,)P r z θθ是奇函数，傅里叶级数展开式中不含cos k θ。

2.某单元的节点上，既有位移自由度又有转动自由度，试述此单元的协调性要求？（P27） 在交界面上满足变形协调条件，变形后既不分裂，也不重叠，从而保证了整个结构的位移连续。

3.用泛函变分求解弹性力学的场问题时，为什么只需要考虑几何边界条件？（P179） 泛函求极值与求满足位移及力边界条件的平衡方程的解是完全等价的。

利用变分求解只需要满足位移边界条件，而力边界条件是在求解泛函的极值中自动满足的。

4.写出用位移梯度表示的格林应变张量和阿尔曼西应变张量，并证明他们的参考变形？（P201）格林应变张量1=+2j i k k ij j i i j u u u u E x x x x ∂∂∂∂∂∂∂∂（+） 阿尔曼西应变张量1=+2j i k k ij j i i ju u u u e x x x x ∂∂∂∂∂∂∂∂（-） 5.写出接触问题中的运动学条件和动力学条件？（P225）运动学条件：满足不可贯穿条件，对于两个接触物体，可表示为0ABV V ⋂=动力学条件:要求连个物体接触面的合力为零0ABq q += 二、三角形单元的位移为：012012(cos 1)(sin )(sin )(cos 1)u u x x v v x x θθθθ=+-+-=++-式中0u 和0v 分别为1x 和2x 方向的刚体位移，θ为逆时针绕原点的刚体转角。

计算单元的柯西应变和格林应变。

证明此位移为刚体运动。

（P201） 解：柯西应变:11=cos 1u x εθ∂=-∂，22=cos 1v x εθ∂=-∂，12212=+sin sin 0u v x x εθθ∂∂=-+=∂∂ 格林应变：1111111111=+(cos 1cos 1(cos 1)(cos 1)sin sin )022u u u u v v E x x x x x x θθθθθθ∂∂∂∂∂∂+-+-+--+=∂∂∂∂∂∂（+）=122121121211==+(sin sin (cos 1)(sin )sin (cos 1))022u v u u v v E E x x x x x x θθθθθθ∂∂∂∂∂∂+-++--+-=∂∂∂∂∂∂（+）=2222222211=+(cos 1cos 1(cos 1)(cos 1)sin sin )022v v u u v v E x x x x x x θθθθθθ∂∂∂∂∂∂+-+-+--+=∂∂∂∂∂∂（+）=三 周向有集中载荷作用的悬臂梁，弯曲刚度为EI ，（1）建立梁的总势能表达式，（2）假定瑞利-里茨能为2323w C x C x =+，计算梁的挠度表达式。