矩阵的秩的几何意义

第三章 向量组的线性相关性与矩阵的秩向量是研究代数问题的重要工具。

在解析几何里，曾经讨论过二维与三维向量。

但是，在很多实际问题中，往往需要研究更多维的向量。

例如，描述卫星的飞行状态需要知道卫星的位置()z y x ,,、时间t 以及三个速度分量z y x v v v ,,，这七个量组成的有序数组()z yxv vv t z y x ,,,,,,称为七维向量。

更一般地，本章将引入n 维向量的概念，定义向量的线性运算，并在此基础上讨论向量组的线性相关性，研究向量组与矩阵的秩、向量组的正交化等问题。

这将为以后利用向量的线性关系来分析线性方程组解的存在性，化二次型为标准形等奠定理论上的基础。

§1 n 维向量作为二维向量、三维向量的推广，现给出n 维向量的定义定义1 n 个数n a a a ,,,21 组成的有序数组（n a a a ,,,21 ），称为n 维向量。

数i a 称为向量的第i 个分量（或第i 个分量）。

向量通常用希腊字母γβα,, ,等来表示。

向量常写为一行α=（n a a a ,,,21 ）有时为了运算方便，又可以写为一列=α⎪⎪⎪⎪⎪⎭⎫⎝⎛na a a 21前者称为行向量，后者称为列向量。

行向量、列向量都表示同一个n 维向量。

设),,,(),,,,(2121n n b b b a a a ==βα都是n 维向量，当且仅当它们各个对应的分 量相等，即),,2,1(n i b a i i ==时，称向量α与向量β相等，记作，βα=。

分量全为零的向量称为零向量，记为0，即 0=)0,,0,0(若),,,(21n a a a =α，则称),,,(21n a a a --- 为α的负向量，记为α-。

下面讨论n 维向量的运算。

定义2 设),,,(),,,,(2121n n b b b a a a ==βα都是n 维向量，那么向量),,,(2211n n b a b a b a +++ 叫做向量α与β的和向量，记做βα+，即),,,(2211n n b a b a b a +++=+ βα 向量α与β的差向量可以定义为α+)(β-，即),,,()(2211n n b a b a b a ---=-+=- βαβα定义3 设),,,(21n a a a =α是n 维向量，λ是一个数，那么向量),,,(21n a a a λλλ 叫做数λ与向量α的数量乘积（简称数乘），记为λα，即),,,(21a a a λλλλα =向量的和、差及数乘运算统称为向量的线性运算。

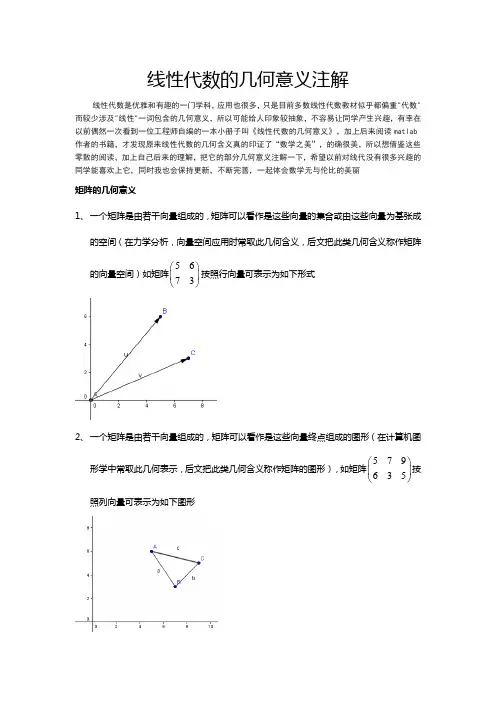
线性代数的几何意义注解线性代数是优雅和有趣的一门学科，应用也很多，只是目前多数线性代数教材似乎都偏重"代数"而较少涉及"线性"一词包含的几何意义，所以可能给人印象较抽象，不容易让同学产生兴趣，有幸在以前偶然一次看到一位工程师自编的一本小册子叫《线性代数的几何意义》，加上后来阅读matlab 作者的书籍，才发现原来线性代数的几何含义真的印证了“数学之美”，的确很美，所以想借鉴这些零散的阅读，加上自己后来的理解，把它的部分几何意义注解一下，希望以前对线代没有很多兴趣的同学能喜欢上它，同时我也会保持更新，不断完善，一起体会数学无与伦比的美丽矩阵的几何意义1、一个矩阵是由若干向量组成的，矩阵可以看作是这些向量的集合或由这些向量为基张成的空间（在力学分析，向量空间应用时常取此几何含义，后文把此类几何含义称作矩阵的向量空间）如矩阵5673⎛⎫⎪⎝⎭按照行向量可表示为如下形式2、一个矩阵是由若干向量组成的，矩阵可以看作是这些向量终点组成的图形（在计算机图形学中常取此几何表示，后文把此类几何含义称作矩阵的图形），如矩阵579 635⎛⎫ ⎪⎝⎭按照列向量可表示为如下图形如下图是在matlab 中将z=sin(x)*cos(y)算得的离散点组成的矩阵表示成几何图形注1：如果单独查看一个矩阵m n A ⨯，可以有两种解读：矩阵A 由m 个n 维向量组成，或者由n 个m 维向量组成；在使用时会根据实际情或约定选择其中一种，而在参与变换或其他运算时，这两种解读一般不能混淆，一定要确定注2：当我们把矩阵表示成图形时，其作图没有固定标准，并不一定是把所有向量终点连接起来构成一个多边形，规则是使用者制定的，可以是网格，可以是离散面片等行列式的几何意义一个方阵n n A ⨯的行列式的绝对值是其行向量或列向量所张成的平行几何体的空间积，对于二阶行列式，就是向量张成的平行四边形的面积，对于三阶行列式，就是对应平行六面体的体积；如方阵5673⎛⎫ ⎪⎝⎭的行列式绝对值为27，它就是下图平行四边形的面积注：行列式其实是带有符号的，实际上，正负号表征了这些向量作为线性空间基的手性，正号表示右手系，负号表示左手系，在二阶矩阵的向量空间里，其判别方法是，伸出右手和矩阵的第一个列向量或行向量平行，然后调整手的正反使得能从此向量转过小于180度的角到达第二个向量，这时大拇指如果朝上（从纸面指向自己）则为右手系，矩阵的行列式为正，反之则为左手系，对应行列式为负；如果是三阶矩阵，则从第一个向量转向第二个向量时，如果大拇指指向第三个向量方向（不必重合），则为右手系，其行列式为正，反之为左手系，行列式为负；其实这一点上更广义的表述应是向量空间的基相对自然坐标系的顺序性（代数上可用逆序数表达）克拉默法则的几何意义以二维形式为例来说明其几何意义:方程A x =b ，设A=11122122a a a a ⎛⎫ ⎪⎝⎭，b =12b b ⎛⎫ ⎪⎝⎭，待求的x =12x x ⎛⎫ ⎪⎝⎭ 将A 的两个列向量分别表示为a1,a2，那么原方程可表示为1x a1+2x a2=b ，这样可以把1x 与2x 看作是列向量a1,a2的伸缩因子，经过伸缩后再叠加即得到和向量b ，故原方程可以看作已知列向量被伸缩并叠加后的向量b ，求伸缩因子i x我们已经知道行列式的几何意义，显然矩阵A 对应的平行四边形的面积就是|A|（这里以带符号的有方向面积表示，因为伸缩因子也是有符号的），当某一个向量被伸缩后，如图将OB 边伸长至OE ，形成新的平行四边形OAFE ，记其面积为OAFE S ，这样a1的伸缩因子1x 可表示为||OAFE S A ，显然只要求出OAFE S 即可解出未知量；图中OG 即向量b ，因为它是1x a1，2x a2的线性叠加，所以G 点必在EF 的延长线上，这样OG 和OE 相对OA 边的高就是相同的，故OA 与OG 组成的平行四边形面积和OAFE 相同，即OAFE S =|b a2|，所以可求得1x =|b a2|/|A|，同理可得2x =|a1 b |/|A|，可以看出此表达式和克拉默法则等价矩阵乘法的几何意义我们知道矩阵是由若干向量组成的，因此可自然地把矩阵乘法看作是两个矩阵的同维向量之间做内积（或点乘），而内积的意义是两向量同向投影的乘积，但这只是一个表面的几何含义，比较抽象（也有应用之处，后面会提到）；实际上，对于矩阵乘法C=AB ，作用后得到的新矩阵C 可以看作是矩阵A 经过某种变换得到的，也可以看作是矩阵B 经过某种变换后得到的，而这种变换显然就是乘以另一个矩阵的过程，结合前面提到的矩阵的几何意义，故可以把矩阵乘法C=AB 看作是图形A （或B ）经过变换B （或A ）后得到新图形C ，或者是向量空间A （或B ）经过变换B （或A ）后得到新的向量空间C ，对于简单的变换矩阵这一点最容易感性体会到；例如变换矩阵100010000⎛⎫ ⎪ ⎪ ⎪⎝⎭会把原3D 图形向x-y 面投影，变换矩阵100010001-⎛⎫ ⎪ ⎪ ⎪⎝⎭会把原图形对x 轴镜像，变换矩阵cos30sin 30sin 30cos30-⎛⎫ ⎪⎝⎭会把原2D 图形相对原点逆时针旋转30度。

矩阵分析几何意义和透彻理解PCA勺一些整理这是几篇很不错的文章集合在一起的一篇文章，有些内容来自blog，有些来自文献和教程，解决了我遇到很多疑问，感谢把它推荐给我的人。

前四部分来自早期几篇blog，把空间描述的形象且易懂，适合我们这些非数学专业的人搞明白一些抽象的问题。

一、矩阵的特征值概述：矩阵特征值要讲清楚需要从线性变换入手，把一个矩阵当做一个线性变换在某一组基下的矩阵，最简单的是数乘变换，求特征值的目的就是看看一个线性变换对一些非零向量的作用是否能够相当于一个数乘变换，特征值就是这个数乘变换的变换比。

这样的一些向量就是特征向量，其实我们更矢心的是特征向量，希望把原先的线性空间分解成一些向量相矢的子空间的直和，这样我们的研究就可以分别限定在这些子空间上来进行，这和物理中研究运动的时候将运动分解成水平方向和垂直方向的做法是一个道理。

自相矢矩阵最大特征值和特征向量并没有和原来的哪个信号一一对应，而且特征分解本身的含义相当于对原来的信号做了这样的正交分解。

使得各个分量之间相互不相矢，也就是K-L展开，每一个特征值相当于原来各个信号导向矢量的线性组合，因此不能仅仅从某个特征矢量中直接对应原来某个信号的特征。

二、线性空间和矩阵的几个核心概念：空间（space）:空间的数学定义是一个集合，在这个集合上定义某某概念，然后满足某些性质，就可以被称为空间。

我们所生活的空间是一个三维欧几里德空间，我们所生活空间的特点：（1）有很多（实际上是无穷多个）位置点组成（2 ）这些点之间存在着相对尖系。

（3 ）可以咋空间中定义长度、角度。

（4 ）这个空间可以容纳运动（从一个点到一个点的移动，而不是微积分意义上的“连续”性运动）第（4）点是空间的本质特征，（1 ）、（ 2）两点是空间的基础而非性质，第（3）点在其他空间也行并不具备，自然更不是尖键的性质。

只有第（4）点是空间的本质。

把三维空间的认识拓展到其他空间。

事实上，不管是什么空间，都必须容纳和支持在其中发生的符合规律的运动（变换）。

6．7 矩阵的秩 齐次线性方程组的解空间教学目的：1． 掌握矩阵的秩和它的行空间、列空间维数之间的关系。

2． 准确地确定齐次线性方程组解空间维数。

3． 熟练地求出齐次线性方程组基础解系及非齐次线性方程式组的任意解。

教学内容：1． 阵的秩的几何意义。

设给了数域F 上一个m*n 矩阵A=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛a aa aa a a a a mn m m n en............ (2)1222211211矩阵A 的每一行可以看成F n的一个向量，叫做A 的行向量。

A 的每一列可以看成F m的一个向量，叫做A 的列向量，令a 1，。

，am是A 的列向量，这里a i =（a 1i ，a 2i ，。

，a in ），I=1，。

，m 。

由a 1，a 2，。

，am所生成的F n的子空间￡（a 1，a 2，。

， a m ）叫做矩阵A 的行空间。

类似的，由A 的n 个列向量所生成的F M的子空间叫做A 的列空间。

当m ≠n 时，矩阵A 的行空间和列空间是不同的向量空间的子空间， 引理6.7.1 设A 是一个n*m 矩阵（i ） 如果B=PA ，P 是一个N 阶可逆矩阵，那么B 与A 有相同的行空间。

（ii ） 如果C=AQ ，Q 是一个n 阶可逆矩阵，那么C 与A 有相同的列空间。

证：我们只证明（I ）,因为（ii ）的证明完全类似。

A=（a ij ）mn , P=(p ij )mm ,B=(b ij )m n .令{a 1，a 2…a m }是A 的行向量，{b 1,b 2,…,b m }是B 的行向量。

B 的第I 行等于P 的第I 行等于P 的第P 的第I 行右乘以矩阵A ：b i =(b i1,b i2…,b in )=(p i1,p i2,…p im )A=p i1a 1+p i2a 2,…+p im a m ，所以B 的每一个行向量都是A 的行向量的线性组合，但P 可逆，所以A=P-1B 。

图像处理之基础---矩阵和特征向量的⼏何意义转载⾃：长时间以来⼀直不了解矩阵的特征值和特征向量到底有何意义（估计很多兄弟有同样感受）。

知道它的数学公式，但却找不出它的⼏何含义，教科书⾥没有真正地把这⼀概念从各种⾓度实例化地进⾏讲解，只是⼀天到晚地列公式玩理论——有个屁⽤啊。

根据特征向量数学公式定义，矩阵乘以⼀个向量的结果仍是同维数的⼀个向量，因此，矩阵乘法对应了⼀个变换，把⼀个向量变成同维数的另⼀个向量，那么变换的效果是什么呢？这当然与⽅阵的构造有密切关系，⽐如可以取适当的⼆维⽅阵，使得这个变换的效果就是将平⾯上的⼆维向量逆时针旋转30度，这时我们可以问⼀个问题，有没有向量在这个变换下不改变⽅向呢？可以想⼀下，除了零向量，没有其他向量可以在平⾯上旋转30度⽽不改变⽅向的，所以这个变换对应的矩阵(或者说这个变换⾃⾝)没有特征向量(注意：特征向量不能是零向量)，所以⼀个特定的变换特征向量是这样⼀种向量，它经过这种特定的变换后保持⽅向不变，只是进⾏长度上的伸缩⽽已(再想想特征向量的原始定义Ax=cx, cx是⽅阵A对向量x进⾏变换后的结果，但显然cx和x的⽅向相同)。

这⾥给出⼀个特征向量的简单例⼦，⽐如平⾯上的⼀个变换，把⼀个向量关于横轴做镜像对称变换，即保持⼀个向量的横坐标不变，但纵坐标取相反数，把这个变换表⽰为矩阵就是[1 0;0 -1]（分号表⽰换⾏），显然[1 0;0 -1]*[a b]'=[a -b]'（上标'表⽰取转置），这正是我们想要的效果，那么现在可以猜⼀下了，这个矩阵的特征向量是什么?想想什么向量在这个变换下保持⽅向不变，显然，横轴上的向量在这个变换下保持⽅向不变(记住这个变换是镜像对称变换，那镜⼦表⾯上(横轴上)的向量当然不会变化)，所以可以直接猜测其特征向量是[a 0]'（a不为0），还有其他的吗？有，那就是纵轴上的向量，这时经过变换后，其⽅向反向，但仍在同⼀条轴上，所以也被认为是⽅向没有变化，所以[0 b]'（b不为0）也是其特征向量。

1
A
?1 1 2 3?
A ? ??2 3 5
7
? ?
??-1 0 -1 - 2−?
分析：由定义一，需要计算阶数从高到低的子式，从而求得 不为零的子式的最大阶数，即秩。
其次，从列向量组的极大无关组的秩考虑，可用行的初等 变换求得列向量组的极大无关组的秩 ，或用向量的线性相关 性的概念求得。两个定义的本质是行列式的计算与线性相关性 的证明。
ÁÂÃÁÁÂÃÄÁÃÂÅÂÃÁ 比如方程x+y=5可以由下面两个方程相减得出
3x+4y=7 2x+3y=2 因此由这三个方程组成的方程组与由下面两个方程组成 的方程组是同解的，x+y=5是多余的，可去掉。这样对于m个n元 一次方程组成的方程组就可想办法去掉那些可用其他的方程 表示的方程，剩下相互独立的方程。例如用高斯消元法来去掉， 而剩下的那些独立的方程的个数就是这个方程组的秩，矩阵的 秩是从方程组的秩中来的，理解了这个就理解了秩的概念，这 也是秩的几何意义。如果从向量的线性相关性的角度考虑，可 以这样认为：是矩阵的行（列）向量组的极大线性无关组的个 数，即这个向量组的行（列）秩。 秩的定义常见下列两种叙述，分别是：矩阵中不为零的子 式的最大阶数；矩阵中行（列）向量组的极大无关组的个数。这 里不妨把它们分别叫做定义一、定义二，这两个定义是等价的。 它的等价性可由向量的线性相关性来证，课本中已有证明。下 面举例以加深理解和比较这两个定义：
AB ? A − B - n
A= r
B =r
AB=r
PAQ
?
?E ??O
O? − ?
?B ?
Q B ? ??B−
? ? −?
PQ
P Q r= AB=
（4） PA （5） 若 A

这里首先讨论一个长期以来困惑工科甚至物理系学生的一个数学问题，即，究竟什么是面积，以及面积的高维推广（体积等）？1 关于面积：一种映射大家会说，面积，不就是长乘以宽么，其实不然。

我们首先明确，这里所讨论的面积，是欧几里得空间几何面积的基本单位：平行四边形的面积。

平行四边形面积的定义，几何上说是相邻两边边长乘以他们之间的夹角的正弦。

然而为了应对更一般情形和更高维度的数理问题，我们有必要把面积的定义推广开来。

注意到以下事实：面积是一个标量，它来自于（构成其相邻边）两个矢量。

因此，我们可以将面积看成一个映射：其中V就是一个矢量，V*V代表两个矢量的有序对；f就是面积的值。

下面我们将说明这个映射是一个线性映射。

从最简单的例子出发。

如果第一个矢量是（1，0），第二个矢量是（0，1）；也就是说，两个矢量分别是X和Y轴上的单位正向量，那么由这两个矢量张成的四边形就是一个正方形，其面积根据定义，就是长乘以宽=1*1=1。

因此有：如果我们把第一个矢量”缩放“a倍，面积将会相应是原来的a倍；把第二个矢量“缩放”b倍，面积也会成为原来的b倍。

如果同时缩放，很显然，面积将会变成原面积的ab倍。

这表明，面积映射对于其两个操作数（矢量）的标量积是各自线性的，如下：最后，我们要说明，面积映射对于其操作数（矢量）的矢量加法也是线性的。

因为矢量加法操作的本身是线性的，那么其面积映射理应对此也是一个线性映射。

这里我们打算从几个实际的例子出发，说明映射的加法线性性的后果。

显然（两个共线矢量所张成的平行四边形还是一条线，因此面积为0）：假定面积映射是一个关于矢量加法的线性映射，那么我们有：注意计算过程中用到了上面的结论。

这说明：也就是说，交换相互垂直操作数矢量的顺序，面积映射取负。

孰正孰负取决于认为的定义。

一般，我们把X轴单位矢量在前，Y轴单位矢量在后，从X轴到Y轴张成的一个平行四边形的面积，取做正号。

1.1 右手定则由此我们引入右手定则。

百度文库-让每个人平等地提升自我3 矩阵秩的研究与应用[摘要]矩阵是数学中的一个重要的基本概念，是代数学的一个主要研究对象，也是数学研究的一个重要工具。

矩阵理论是线性代数的主要组成部分，也是线性方程组的理论基础。

而在矩阵的理论中，矩阵的秩是一个基本概念，也是矩阵最重要的数量特征之一，它在初等变换下是一个不变量。

它反映矩阵固有特性的一个重要概念。

矩阵一旦确定秩也就确定了。

它是高等代数课程中的一个参考指标，其定义、性质、求法、应用等相关内容在高等代数中出现的极为频繁，作用较大。

本文首先介绍了矩阵秩的相关理论知识：即秩的几种不同定义，相关性质，以及矩阵秩的三种常见求法，并对三种求法做了一个简单的比较分析。

后面着重介绍了矩阵秩的应用部分，主要是其在线性代数中的应用和解析几何上的应用。

这里就不细说了，具体内容还得从文章中来了解。

[1][2][3][关键词]：矩阵的秩，定义，性质，求法，应用，高等代数。

百度文库-让每个人平等地提升自我4 矩阵秩的研究与应用1 前言矩阵在高等代数理论中极其重要并且应用广泛，它是线性代数的核心，而矩阵的秩作为研究矩阵的一个重要工具，其秩的理论研究非常重要。

更重要的是将它推广到实际应用中，那么我们目前在其应用方面的研究又达到了一个什么程度呢？本文主要是对矩阵秩的应用方面的一个总结，让学者对其有个更清晰的认识，使后面的学者对矩阵的学习更轻松，更全面。

矩阵方面的理论是非常重要的内容，历年来许多学者对它都有研究，而且其中的部分理论有了很广泛的应用，例如矩阵分析法在企业战略管理、营销活动、供应链管理技术、教学效率评价、射击训练效果评价等方面都起到举足轻重的作用；不仅在本文中的线性代数和解析几何中的理论上的应用，而且在其他领域上也有更实际贴切的应用。

如在控制论中，矩阵的秩可用来确定线性系统是否为可控制的，或可观的；此外，矩阵的秩在教学中还有更广泛的应用，如在测量平差中的应用。

理论指导实践，所以我着重选择了矩阵秩在理论上的应用的部分来进行探讨，其意义更加广泛且深远。

6.7矩阵的秩，齐次线性方程组的解空间一、教学思考1、矩阵的秩与线性方程组解的理论在前面已经有过讨论，本节运用向量空间的有关理论重新认识矩阵的秩的几何意义，讨论线性方程组解的结构。

2、注意：齐次线性方程组（含n 个未知量）的解的集合构成n F 的子空间，而非齐次线性方程组的解的集合非也。

3、注意具体方法：1）证矩阵的行空间与列空间的维数相等；2）求齐次线性方程组的基础解系。

二、内容要求1、内容：矩阵的秩的几何意义，齐次线性方程组的解空间。

2、要求：理解掌握矩阵的秩的几何意义，齐次线性方程组的基础解系的求法。

三、教学过程1、矩阵的秩的几何意义几个术语：设)(F M A n m ⨯∈，⎪⎪⎪⎭⎫ ⎝⎛=mn m n a a a a A 1111，A 的每一行看作n F 的一个元素，叫做A 的行向量，用),2,1(m i i =α表示；由),2,1(m i i =α生成的n F 的子空间),,(1m L αα 叫做矩阵A 的行空间。

类似地，A 的每一列看作m F 的一个元素，叫做A 的列向量；由A 的n 个列向量生成的m F 的子空间叫做矩阵A 的列空间。

注：)(F M A n m ⨯∈的行空间与列空间一般不同，分别是n F 与m F 的子空间；下证其维数相同。

引理6.7.1设)(F M A n m ⨯∈，1）若PA B =，P 是一个m 阶可逆矩阵，则B 与A 有相同的行空间；2）若AQ C =，Q 是一个n 阶可逆矩阵，则C 与A 有相同的列空间。

分析：设()()()m m ij n m ij n m ij p P b B a A ⨯⨯⨯===,,，),2,1(m i i =α是A 的行向量，),2,1(m j j =β是B 的行向量；只需证这两组向量等价。

由题述关系PA B =得：⎪⎪⎪⎭⎫ ⎝⎛==m im i im i i p p A p p ααβ 111),,(),,( =),,2,1(;11m i p p m im i =++αα即B 的每个行向量都可以由A 的行向量线性表示；因为P 可逆，有B P A 1-=，同上得A 每个行向量都可以由B 的行向量线性表示，这样这两组向量等价。

/从不同的角度看矩阵的行秩与列秩——兼论如何学好线性代数线性代数中，有那么几个神秘又神奇的东西，总是让初学它的人琢磨不透，无法理解，其中就有矩阵的行向量和列向量的关系，为什么一个矩阵的行向量里有多少个线性无关的向量，列向量里就一定也有多少个线性无关的向量呢？或者考虑稍微简单一点的问题，一个方阵，为什么行向量线性无关或线性相关列向量就一定也线性无关或相关呢？行秩为何等于列秩？这本来应该是一个基本又简单的事实。

但是，请回忆一下你当初初学线性代数时的内容编排顺序，是怎么引入这个问题的，当时又是怎样解决这个问题的？传统的教材编写思路是从线性方程组开始整个线性代数话题的引入，这个过程中定义行列式和矩阵，用n元数组引入向量，线性相关和无关等概念，讨论解存在的条件，解的结构，等等。

总之，一切以方程组为核心，给人的感觉就是线性代数就是方程组的理论，一切讨论的目的都是为了解决小小的方程组问题。

在这个过程中，有一个矩阵行秩等于列秩的命题，此时学生只了解方程组理论和行列式，因此这时对这个问题的解释当然也无法离开方程组或行列式。

下面简述两个典型的教材中的证明方法：第一个证明来自陈志杰《高等代数与解析几何》。

证明：首先，矩阵的初等行变换不改变矩阵的行秩，初等列变换不改变矩阵的列秩。

这是由向量组的初等变换不改变向量组的线性相关或无关性保证的，即将某个向量乘以非零的倍数、将某个向量加到另一个向量上，都不改变向量组的线性相关或无关性。

接着证明矩阵的初等行变换不改变矩阵的列秩。

设A是m*n阶矩阵，任意从A的n个列向量中选取k个列向量a1,a2,…,ak，它们线性无关的充要条件是线性方程组a1×1+a2×2+…+akxk=0只有零解。

而对矩阵A进行初等行变换不改变此方程组的解，因此不改变这k个列向量的线性相关或无关性。

这说明A的列向量的秩在矩阵的初等行变换中不变。

同理矩阵的初等列变换不改变矩阵的行秩。

接下来，可以把A经过初等行变换和初等列变为只有对角线上有1或0，其它位置都为0的矩阵，在这个过程中行秩和列秩都不改变，从这个矩阵中看出行秩等于列秩，因此原来的矩阵行秩也等于列秩。

第三章 向量与向量空间§１ n 维向量在平面几何中,坐标平面上每个点的位置可以用它的坐标来描述,点的坐标是一个有序数对(,)x y .一个n 元方程1122n n a x a x a x b +++=可以用一个1n -元有序数组12(,,,,)n a a a b来表示.1n ⨯矩阵和1n ⨯矩阵也可以看作有序数组.一个企业一年中从1月到12月每月的产值也可用一个有序数组1212(,,,)a a a 来表示.有序数组的应用非常广泛,有必要对它们进行深入的讨论.定义 1 n 个数组成的有序数组12(,,,)n a a a （３.１） 或12n a a a ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦（３.２）称为一个n 维向量,简称向量.一般,我们用小写的粗黑体字母,如, α,β,γ等来表示向量,(3.1)式称为一个行向量,(3.2)式称为一个列向量.数12,,,n a a a 称为这个向量的分量.i a 称为这个向量的第i 个分量或坐标.分量都是实数的向量称为实向量;分量是复数的向量称为复向量.实际上,n 维行向量可以看成1n ⨯矩阵,n 维列向量也常看成1n ⨯矩阵.下面我们只讨论实向量.设k 和l 为两个任意的常数.α,β和γ为三个任意的n 维向量,其中12(,,,)n a a a = α, 12(,,,)n b b b = β.定义 2 如果α和β对应的分量都相等,即,1,2,,i i a b i n ==就称这两个向量相等,记为α＝β.定义 3 向量(a 1+b 1,a 2+b 2,…,a n +b n )称为α与β的和,记为α＋β.称向量(ka 1,ka 2,…,ka n )为α与k 的数量乘积,简称数乘,记为k α.定义 4 分量全为零的向量(0, 0, …, 0)称为零向量,记为0.α与-1的数乘(-1)α＝(-a 1,-a 2,…,-a n )称为α的负向量,记为-α.向量的减法定义为α－β＝α＋（－β）.向量的加法与数乘具有下列性质： （１） α＋β＝β＋α；（交换律) （２） （α＋β）＋γ＝α＋（β＋γ）；（结合律） （３） α＋0＝α；（４） α＋（－α）＝0； （５） k (α+β)=k α+k β； （６） （k +l )α=k α+l α； （７） k (l α)=(kl )α； （８） １α＝α； （９） 0α＝0； （１０） k 0＝0.在数学中,满足(１) ～(８)的运算称为线性运算.我们还可以证明：（１１） 如果k ≠0且α≠0, 那么k α≠0.显然,n 维行向量的相等和加法、减法及数乘运算的定义,与把它们看作行矩阵时的相等和加法、减法及数乘运算的定义是一致的.对应地,我们也可以定义列向量的加法、减法和数乘运算,这些运算与把它们看成列矩阵时的加法、减法和数乘运算也是一致的,并且同样具有性质(１)～(１１).例1 设()11,1,0=α,()20,1,1=α,()33,4,0α=,求12332ααα+-. 解 ()()()1233231,1,020,1,13,4,0ααα+-=+- ()()()()3,3,00,2,23,4,00,1,2=+-=例 2 设()11,1,1,1α=,()21,1,1,1α'=--,()31,1,1,1α'=--,()41,1,1,1α'=--且()()()123422αβαβααβ+-+=++,求β.解 由()()()123422αβαβααβ+-+=++,得()12342223,5,3,3βαααα'=---=-通常把维数相同的一组向量简称为一个向量组,n 维行量组α１,α２,…,αs 可以排列 成一个s ×n 分块矩阵12s ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦a a A a ,其中αi 为由A 的第i 行形成的子块,α１,α２,…,αs 称为Ａ的行向量组.n 维列向量组β１,β２,…,βs 可以排成一个n ×s 矩阵Ｂ＝（β１,β２,…,βs ）,其中βj 为Ｂ的第j 列形成的子块,β１,β２,…,βs 称为B 的列向量组.这样,矩阵A 就与其列向量组或行向量组之间建立了一一对应关系.向量组之间的关系可用矩阵来研究；反过来,矩阵的问题也可用向量组来研究.§2线性相关与线性无关定义 5 向量组α１,α２,…,αs 称为线性相关的,如果有不全为零的数k １,k ２,…,k s , 使1si ii k =∑a=k １α１+k ２α２+…+k s αs ＝0. （3.3）反之,如果只有在k １= k ２ = … =k s =0时(3.3)才成立,就称α１,α２,…,αs 线性无关. 换言之,当α１,α２,…,αs 是行向量组时,它们线性相关就是指有非零的1×s 矩阵 (k １,k ２,…,k s )使1212(,,,)s s k k k ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦0 a a a .当α１,α２,…,αs 为列向量组时,它们线性相关就是指有非零的s ×1矩阵(k １,k ２,…,k s )′使1212(,,,)s s k k k ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦0 a a a .显然,单个零向量构成的向量组是线性相关的. 例3 判断向量组12(1,0,,0),(0,1,,0),(0,0,,1)n =⎧⎪=⎪⎨⎪⎪=⎩ εεε 的线性相关性.解 对任意的常数k １,k ２,…,k n 都有k １ε1+k ２ε2+…+k n εn ＝(k １,k ２,…,k n ).所以k １ε1+k ２ε2+…+k n εn =0当且仅当k 1=k 2=…=k n =0.因此ε1,ε2,…,εn 线性无关.ε1,ε2,…,εn 称为基本单位向量. 例4 判断向量组α１＝（１,１,１）,α２＝（０,２,５）,α3＝（１,３,６） 的线性相关性.解 对任意的常数k １,k ２, k 3都有k １α１+k ２α２+ k 3α3=(k １+k 3,k １+2k ２+3k 3,k １+5k ２+6k 3).所以k １α１+k ２α２+ k 3α3=0当且仅当131231230,230,560.k k k k k k k k +=⎧⎪++=⎨⎪++=⎩ 由于k 1=1,k 2=1,k 3=-1满足上述的方程组,因此１α１+1α２+(-1)α3=α１+α２-α3=0.所以α１,α２,α3线性相关.例5 设向量组α１,α２,α3线性无关,β１＝α１+α２,β２＝α２+α3,β3＝α3+α１, 试证向量组β１,β２,β3也线性无关.证 对任意的常数都有k １β１+k ２β２+k 3β3=(k １+k 3)α１＋（k １+k ２)α２+(k ２+k 3)α3 .设有k １,k ２,k 3使k １β１+k ２β２+k 3β3=0.由α１,α２,α3线性无关, 故有1312230,0,0.k k k k k k +=⎧⎪+=⎨⎪+=⎩ 由于满足此方程组的k １,k ２,k 3的取值只有k １=k ２=k 3=0,所以β１,β２,β3线性无关.定义 6 向量α称为向量组β１,β２,…,βt 的一个线性组合,或者说α可由向量组β１,β２,…,βt 线性表出(示),如果有常数k １,k ２,…,k t 使α＝k １β１＋k ２β２+…＋k t βt . 此时,也记1ti ii k ==∑a β.例6 设α１=(1,1,1,1),α２=(1,1,-1,-1),α3=(1,-1,1,-1),α4=(1,-1,-1,1), β=(1,2,1,1).试问β能否由α１,α２,α3,α4线性表出？若能,写出具体表达式.解 令β=k １α１+k ２α２+k 3α3+k 4α4于是得线性方程组12341234123412341211k k k k k k k k k k k k k k k k +++=⎧⎪+--=⎪⎨-+-=⎪⎪--+=⎩ 因为1111111116011111111D ⎡⎤⎢⎥--⎢⎥==-≠⎢⎥--⎢⎥--⎣⎦, 由克莱姆法则求出1234511,,444k k k k ====-所以12345111,4444=+--βαααα即β能由α１,α２,α3,α4线性表出.例7 设α=(2,-3,0),β=(0,-1,2),γ=(0,-7,-4),试问γ能否由α,β线性表出? 解 设 γ=k １α+k ２β 于是得方程组1122203724k k k k =⎧⎪--=-⎨⎪=-⎩由第一个方程得k １=0,代入第二个方程得k ２=7,但k ２不满足第三个方程,故方程组无解.所以γ不能由α,β线性表出.定理 1 向量组α１,α２,…,αs (s ≥2) 线性相关的充要条件是其中至少有一个向量能由其余向量线性表出.证 设α１,α２,…,αs 中有一个向量能由其余向量线性表出,不妨设α１=k ２α２+k 3α3+…+k s αs ,那么-α１+k ２α２+…+k s αs =0,所以α１,α２,…,αs 线性相关.反过来,如果α１,α２,…,αs 线性相关,就有不全为零的数k １,k ２,…,k s , 使k １α１＋k ２α２＋…＋k s αs =0.不妨设k １≠０, 那么32123111.s s k k k k k k =---- αααα即α１能由α２,α3,…,αs 线性表出.例如,向量组α１＝（２,－１,３,１）,α２＝（４,－２,５,４）,α3＝（２,－１,４,－１） 是线性相关的,因为α3＝３α１-α２.显然,向量组α１,α２线性相关的充分必要条件是存在常数k,使得两向量的对应分量成比例.在三维的情形,这就表示向量α１与α２共线.三个向量α１,α２,α3线性相关的几何意义就是它们共面.定理 2 设向量组β１,β２,…,βt 线性无关,而向量组β１,β２,…,βt ,α线性相关,则α能由向量组β１,β２,…,βt 线性表出,且表示式是惟一的.证 由于β１,β２,…,βt ,α线性相关,就有不全为零的数k １,k ２,…,k t ,k 使k １β１+k ２β２+…+k t βt +k α=0.由β１,β２,…,βt 线性无关可以知道k ≠0. 因此1212t t k k kk k k=---- αβββ, 即α可由β１,β２,…,βt 线性表出.设α＝l １β１+l ２β２+…＋l t βt ＝h １β１+h ２β２＋…＋h t βt为两个表示式.由α－α＝（l １β１+β２+…＋l t βt )-(h １β１+h ２β２＋…＋h t βt )=（l １-h １）β１＋（l ２-h ２）β２＋…＋（l t -h t ）βt ＝0和β１,β２,…,βt 线性无关可以得到l １=h １, l ２=h ２, …, l t =h t .因此表示式是惟一的.定义 7 如果向量组α１,α２,…,αs 中每个向量都可由β１,β２,…,βt 线性表出,就称向量组α１,α２,…,αs 可由β１,β２,…,βt 线性表出,如果两个向量组互相可以线性表出,就称它们等价.显然,每一个向量组都可以由它自身线性表出.同时,如果向量组α１,α２,…,αt 可以由向量组β１,β２,…,βs 线性表出,向量组β１,β２,…,βs 可以由向量组12,,,p γγγ线性表出,那么向量组α１,α２,…,αt 可以由向量组12,,,p γγγ线性表出.事实上,如果1,1,2,,,si ij j j k i t ===∑ αβ1,1,2,,,pj jm mm lj s ===∑ βγ那么111111pppsss i ij jm m ij jm m ij jm m j m j m m j k l k l k l ======⎡⎤===⎢⎥⎣⎦∑∑∑∑∑∑αγγγ.这就是说,向量组α１,α２,…,αt 中每一个向量都可以由向量组12,,,p γγγ线性表出.因而,向量组α１,α２,…,αs 可以由向量组12,,,p γγγ线性表出.由上述结论,得到向量组的等价具有下述性质： (1) 反身性：向量组α１,α２,…,αs 与它自己等价.(2) 对称性：如果向量组α１,α２,…,αs 与β１,β２,…,βt 等价,那么β１,β２,…,βt 也与α１,α２,…,αs 等价.(3) 传递性：如果向量组α１,α２,…,αs 与β１,β２,…,βt 等价,而向量组β１,β２,…,βt 又与12,,,p γγγ等价,那么α１,α２,…,αs 与12,,,p γγγ等价.§ 3线性相关性的判别定理利用定义判断向量组的线性相关性往往比较复杂,我们有时可以直接利用向量组的特点来判断它的线性相关性,通常称一个向量组中的一部分向量组为原向量组的部分组.定理 3 有一个部分组线性相关的向量组一定线性相关.证 设向量组α１,α２,…,αs 有一个部分组线性相关.不妨设这个部分组为α１,α２,…,αr()r s ≤.则有不全为零的数k１,k ２,…,k r 使1110,s r si ii iji i j r k k ===+=+=∑∑∑0ααα因此α１,α２,…,αs 也线性相关.推论 含有零向量的向量组必线性相关.定理 4 设p 1,p 2,…,p n 为1, 2, …,n 的一个排列,α１,α２,…,αs 和β１,β２,…,βs 为两向量组,其中1212n ip i ip i i i in ip ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦ααααα=,βαα, 即β１,β２,…,βs 是对α１,α２,…,αs 各分量的顺序进行重排后得到的向量组,则这两个向量组有相同的线性相关性.证 对任意的常数k １,k ２,…,k s 注意到列向量111221*********1122s s ss s i i i n ns sn k k k k k k k k k k =+++⎡⎤⎢⎥+++⎢⎥=⎢⎥⎢⎥+++⎣⎦∑ αααααααααα 和1112221122112211122n n n p p s sp s p p s sp i i i p p s sp k k k k k k k k k k =+++⎡⎤⎢⎥+++⎢⎥=⎢⎥⎢⎥+++⎢⎥⎣⎦∑ ααααααβααα 只是各分量的排列顺序不同,因此k １β１+k ２β２+…+k s βs =0当且仅当k １α１+k ２α２+…+k s αs =0.所以α１,α２,…,αs 和β１,β２,…,βs 有相同的线性相关性.定理 4 是对列向量叙述的.对行向量也有相同的结论.类似这样的情形,今后不再说明.定理 5 在r 维向量组α１,α２,…,αs 的各向量添上n -r 个分量变成n 维向量组β１,β２,…,βt .（1）如果β１,β２,…,βs t 线性相关,那么α１,α２,…,αs 也线性相关. (2) 如果α１,α２,…,αs 线性无关,那么β１,β２,…,βs 也线性无关. 证 我们对列向量来证明定理,设（α１,α２,…,αs ）＝Ａ１,(β１,β２,…,βs ）＝12⎡⎤⎢⎥⎣⎦A A ,如果β１,β２,…,βs 线性相关,就有一个非零的s ×1矩阵Ｘ使（β１,β２,…,βs ）Ｘ＝12⎡⎤⎢⎥⎣⎦A A Ｘ＝12⎡⎤⎢⎥⎣⎦X X A A ＝０. 从而（α１,α２,…,αs ）X ＝Ａ１Ｘ＝０.因此α１,α２,…,αs 也线性相关,即(1)成立.利用(1),用反证法容易证明(2)也成立.定理6 设A 是一个n 阶方阵,则A 的行（列）向量组线性相关的充分必要条件是0A =. 证 设()ijnxnA a =,112111n a a a α⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦ , 122222n a a a α⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦, ,12n n n nn a a a α⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦是矩阵A 的列到向量组.令11220n n x x x ααα+++= . ()34- 则12,,,n ααα 线性相关的充分必要条件是,存在一组不全为零的实数12,,...,,n x x x 使得()34-式成立,即齐次线性方程组120n x x A x ⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎣⎦()35-有非零解存在.由第一章定理5的推论及其注解知,()35-式存在非零解的充分必要条件是0A =.从而定理得证.推论 n 阶方阵A 可逆的充分必要条件是A 的行（列）向量组线性无关.例8 试证明n 维列向量组α１,α２,…,αn 线性无关的充分必要条件是行列式1112121222120n n n n n n '''⎡⎤⎢⎥'''⎢⎥=≠⎢⎥⎢⎥'''⎣⎦ D αααααααααααααααααα证 令矩阵A ={α１,α２,…,αn }则向量组α１,α２,…,αn 线性无关⇔行列式|A |≠0.由于[]111121*********2n n n n n n n n ''''⎡⎤⎡⎤⎢⎥⎢⎥''''⎢⎥⎢⎥'==⎢⎥⎢⎥⎢⎥⎢⎥''''⎣⎦⎣⎦ A ααααααααααααααA αααααααααα 在上式两端取行列式,得|A |2=|A ′||A |=D故|A |≠0⇔D ≠0,所以α１,α２,…,αn 线性无关⇔D ≠0.定理 7 n +1个n 维向量α１,α２,…,αn +1必线性相关.证 对每个αs 添加等于零的第n +1个分量,得到n +1维向量β１,β２,…,βn +1.易见,由β１,β２,…,βn +1构成的方阵的行列式等于零,因而β１,β２,…,βn +1线性相关,由定理5,易知α１,α２,…,αn +1也线性相关.推论 当m n >时,m 个n 维向量线性相关. 例9 讨论下列矩阵的行向量组的线性相关性：123132221;021.343201-⎡⎤⎡⎤⎢⎥⎢⎥==-⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦B C解 由于｜Ｂ｜＝２≠０,因此Ｂ的行(列)向量组线性无关； 由于｜Ｃ｜＝０,所以C的行(列)向量组线性相关.定理 8 如果向量组α１,α２,…,αs 可由β１,β２,…,βt 线性表出且s ＞t ,那么α１,α２,…,αs线性相关.证 我们不妨假定讨论的是列向量,如果α１,α２,…,αs 可由β１,β２,…,βt 线 性表出,那么()()121212i i i n n i it p p p ⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎣⎦αββββββγ.其中12i i i it p p r p ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦,()1,2,,i s = .令Ａ＝（γ１,γ２,…,γs ),则(α１,α２,…,αs )＝（β１,β２,…,βt ）Ａ.由于γ１,γ２,…,γs 为由s 个向量组成的t 维向量组.且s t >,根据推论知,它们必线性相关.因此有非零s ×1矩阵（k 1,k 2,…,k s ）′使112212(,,,)s s s k k k k k k ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦0 A γγγ. 从而()11221212(,,,)s s s s k k k k k k ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦0 αααβββA .即有α１,α２,…,αs 线性相关.推论 1 如果向量组α１,α２,…,αs 可由向量组β１,β２,…,βt 线性表出,且α１,α２,…,αs 线性无关,那么s t ≤.推论 2 两个等价的线性无关的向量组必含有相同个数的向量.§4 向量组的秩定义 8 设存在向量组12,,,s ααα的一个部分组12,,,ri i i ααα,满足（1）部分组12,,,ri i i ααα线性无关；（2）对任意的()1i i s α≤≤,都有12,,,ri i i ααα线性相关.则称部分组12,,,ri i i ααα是向量组12,,,s ααα的一个极大线性无关组（简称为极大无关组）.例10 在向量组α１＝（２,－１,３,１）,α２＝（４,－２,５,４）,α３＝（２,－１,４,－１）中,α1,α2为它的一个极大线性无关组.首先,由α１与α２的分量不成比例,所以α1,α2线性无关,再添入α3以后,由α3＝3α1-α 2可知所得部分组线性相关,不难验证α2,α3也为一个极大线性无关组.我们容易证明定义8与下列定义8′等价.定义 8′ 若向量组12,,,s ααα的一个部分组12,,,ri i i ααα,满足：（1）12,,,ri i i ααα线性无关；（2）对任意的()1,2,,i i s α= ,i α可由12,,,ri i i ααα线性表出.则称部分组12,,,ri i i ααα是向量组12,,,s ααα的一个极大无关组.由此,向量组的极大线性无关组具有以下性质：性质 1 一向量组的极大线性无关组与向量组本身等价.从例10 我们发现：向量组的极大线性无关组可能不是唯一的,但是我们有下面的结论. 性质 2 一向量组的任意两个极大线性无关组都等价.性质 3 一向量组的任意两个极大线性无关组都含有相同个数的向量.性质3表明向量组的极大线性无关组所含向量的个数与极大线性无关组的选择无关,它反映了向量组本身的特征.定义 9 向量组12,,,s ααα的极大线性无关组所含向量的个数称为这个向量组的秩,记为()12,,,s R ααα.例如,例10中向量组α1,α2,α3的秩为2.线性无关向量组本身就是它的极大线性无关组,所以我们有：一向量组线性无关的充要条件为它的秩与它所含向量的个数相同.我们知道每个向量组都与它的极大线性无关组等价,由等价的传递性可知任意两个等价的向量组的极大线性无关组也等价,根据定理8的推论1就有等价的向量组必有相同的秩.如果向量组α1,α2,…,αs 能由向量组β１,β２,…,βt 线性表出,那么α1,α2,…,αs 的极大线性无关组可由β１,β２,…,βt 的极大线性无关组线性表出.因此α1,α2,…,αs 的秩不超过β１,β２,…,βt 的秩.定理 9 向量组的任意线性无关的部分组都可扩充为一个极大线性无关组.证 设,i i i 12κ αα,,α是向量组α1,α2,…,αs 中的一个线性无关的部分组,如果α1,α2,…,αs 中每个向量都可由这个部分组线性表出,那么这个部分组就是一个极大线性无关组,如果还有某向量αik +1不能被这个部分组线性表出,那么由121121i i k i l l l κ+++++ ααα＝０就有l k +1=0.再由原部分组线性无关就可得l １＝l ２＝…＝l k =l k +1=0.这样,我们就得到了一个含k +1个向量的线性无关的部分组121,i i i κ+ αα,,α.重复这个过程,最后必可得到α1,α2,…,αs 的一个线性无关的部分组使向量组中每个向量都可由这个部分组线性表出,这个部分组就是一个极大线性无关组.推论 秩为r 的向量组中任意含r 个向量的线性无关的部分组都是极大线性无关组. 例11 求向量组α1＝(1,-1,0,3),α2＝(0,1,-1,2),α3＝(1,0,-1,5),α4＝(0,0,0,2)的一个极大线性无关组及秩.解 α1是α1,α2,α3,α4的一个线性无关的部分组,显然α2不能由α1线性表示,所以α1可以扩充为一个线性无关的部分组α1,α2,容易证明α3＝α1+α2,但α4不能由α1,α2线性表出,所以α1,α2又可扩充为一个线性无关的部分组α1,α2,α4,从而α1,α2,α3,α4的秩为3,α1,α2,α4是它的一个极大线性无关组.在第二章中,我们给出了矩阵的秩的定义和计算方法,那么向量组的秩与矩阵的秩有什么关系呢？首先,我们建立一个引理.引理 设1,2,r ααα ,是r 个n 维列向量()r n ≤,则1,2,r ααα ,线性无关的充分必要条件是矩阵A =()1,2,r ααα ,至少存在一个r 阶子式不为零.证 充分性由本章的定理5与定理6的推论可立即得到. 下面证必要性.对向量的个数r 用数学归纳法证明.当1r =时,由1α线性无关知10α≠,从而A 至少有一个1阶子式不为零. 假设 r k =时,结论成立. 当1r k n =+≤时,设12i ii ni a a a α⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦,1,2,,1,i k =+且1,2,1k ααα+ ,线性无关,则1,2,k ααα ,亦线性无关.由归纳假设,矩阵()1,2,k B ααα= ,至少存在一个k 阶子式不为零.不妨设1112121222120k k k k k kka a a a a a D a a a =≠. ()36-令12,1,2,,1i ii ki a a i k a γ⎡⎤⎢⎥⎢⎥==+⎢⎥⎢⎥⎣⎦.由()36-式知,12,,,k γγγ 线性无关.而1k +个k 维向量121,,,,k k γγγγ+ 线性相关,由本章的定理2,则1k γ+可由12,,,k γγγ 线性表出,即存在一组确定的数12,,,k C C C ,使得11122k k k C C C γγγγ+=+++ .从而有,110,1,2,,ki k j ijj a C ai k +=-==∑ . ()37-令1211kk j j j n b b C b βαα+=⎡⎤⎢⎥⎢⎥=-=⎢⎥⎢⎥⎣⎦∑ ,这里 ,110,1,2,,ki i k j ijj b a C ai n +==-==∑ .则由()37-知：120k b b b ==== .但因121,,,k ααα+ 线性无关,则0β≠,因此必存在某个0s b ≠()k s n <≤.于是1k +阶子式1111,12122,11,11,1k k k k k kk k k s sks k a a a a a a a a a a a a ++++()()()11,2,,i c k i c i k ++-= 111212110000kk s k k kk s sksa a a ab D a a a a b =≠. 下面,我们建立向量组的秩与矩阵的秩的关系.定理10 设A 为m n ⨯矩阵,则矩阵A 的秩等于它的列向量组的秩,也等于它的行向量组的秩.证 只讨论列向量组的情况,类似可讨论行向量组的情况.设 12,,n ααα ,是A 的列向量组,()R A r =,()12,,n R S ααα= ,.首先,由()R A r =,则矩阵A 中至少存在一个阶子式0r D ≠,由本章定理5和定理6的推论知,r D 所在的A 中的r 个列向量一定线性无关,从而s r ≥；另一方面,由()12,,n R S ααα= ,,则必有s 个列向量构成A 的列向量组12,,n ααα ,的极大线性无关组.由引理知这s 个列向量构成的矩阵中至少存在一个s 阶子式不为零,从而r s ≥.于是有r s =.矩阵A 的行向量组的秩称为矩阵A 的行秩,矩阵A 的列向量组的秩称为矩阵A 的列秩.推论 矩阵A 的行秩与列秩相等.由定理10的证明知,若r D 是矩阵A 的一个最高阶非零子式,则r D 所在的r 个行和r 个列就分别是矩阵A 的行向量组和列向量组的一个极大线性无关组.求向量组的秩,只需要将向量组中各向量作为列向量组成矩阵后,只作初等行变换将该矩阵化为行阶梯形矩阵,则可直接写出所求向量组的秩和极大无关组.同理,也可以将向量组中的各向量作为行向量组成矩阵,通过作初等列变换来求向量组的秩和极大无关组.例12 求向量组()11,4,1,0,2α=()2,2,5,1,3,2,α=--()30,2,2,1,0α=-,()41,2,5,6,2α=-的秩和一个极大无关组,并把不属于极大无关组的其余向量用该极大无关组线性表出.解 把向量组作为列向量组成矩阵A ,利用初等行变换将A 化为最简行矩阵B ：1201120145220326112503260316031622020204A --⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥=→--⎢⎥⎢⎥----⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦12010102001000000000-⎡⎤⎢⎥-⎢⎥⎢⎥→⎢⎥⎢⎥⎢⎥⎣⎦10030102001000000000B ⎡⎤⎢⎥-⎢⎥⎢⎥→=⎢⎥⎢⎥⎢⎥⎣⎦. 易见 ()()3R A R B ==,B 的第1,2,3列线性无关,由于A 的列向量与B 的对应的列向量组有相同的线性组合关系,故与其对应的A 的第1,2,3列线性无关,即123,,ααα是该向量组的一个极大无关组.又由矩阵B ,易得41232ααα=-. 例13已知向量组()11,2,1,1α=-()2,2,0,,0t α=()30,4,5,α=--,()43,2,4,1t α=-+-的秩为2,确定t 的值.解 考察矩阵120320421541021A t t ⎡⎤⎢⎥--⎢⎥=⎢⎥-+⎢⎥--⎣⎦. 由条件知()2R A =,从而A 的所有3阶子式均为0. 故 由12204124015t t -=-+=-,得 3t =.§5 向量空间定义10 设V 为n 维向量组成的集合.如果V 非空,且对于向量加法及数乘运算封闭,即对任意的α,β∈V 和常数k 都有α＋β∈Ｖ,ｋα∈Ｖ,就称集合V 为一个向量空间.例14 n 维向量的全体R ｎ构成一个向量空间.特别地,三维向量可以用有向线段来表示,所以R ３也可以看作以坐标原点为起点的有向线段的全体.例15 n 维零向量所形成的集合｛０｝构成一个向量空间. 例16 集合V ＝｛（０,ｘ２,ｘ３,…,ｘｎ）｝｜ｘ２,ｘ３,…,ｘｎ∈R ｝构成一个向量空间. 例17 集合V ＝｛(ｘ1,ｘ2,…,ｘｎ）｜ｘ1+ｘ２＋…＋ｘｎ＝１｝不构成向量空间. 例18 设α１,α２,…,αｍ为一个n 维向量组,它们的线性组合 Ｖ＝｛ｋ１α１＋ｋ2α2+…＋k m αm ｜k １,k ２,…,k m ∈R ｝构成一个向量空间.这个向量空间称为由α１,α２,…,αｍ所生成的向量空间,记为L (α１,α２,…,αｍ).例19 证明由等价的向量组生成的向量空间必相等.证 设α１,α２,…,αｍ和β１,β２,…,βs 是两个等价的向量组.对任意的α∈L(α１,α２,…,αｍ)都可由α１,α２,…,αｍ线性表出.而向量组α１,α２,…,αｍ又可由β１,β２,…,βs 线性表出可以知道α也能由β１,β２,…,βs 线性表出,即有α∈L(β１,β２,…,βs ).由α的任意性,得L (α１,α２,…,αｍ)⊆L (β１,β２,…,βs ). 同理,L (β１,β２,…,βs )⊆L ().于是L (α１,α２,…,αｍ)＝L (β１,β２,…,βs ).定义11 如果V １和Ｖ２都是向量空间且V １⊆Ｖ２,就称Ｖ1是Ｖ２的子空间.任何由n 维向量所组成的向量空间都是R ｎ的子空间.R ｎ和｛０｝称为R ｎ的平凡子空间,其他子空间称为R ｎ的非平凡子空间.定义12 设V 为一个向量空间.如果V 中的向量组α１,α２,…,αr 满足 (1)α１,α２,…,αr 线性无关；(2) V 中任意向量都可由α１,α２,…,αr 线性表出.那么,向量组α１,α２,…,αr 就称为V 的一个基,r 称为V 的维数,记作dim V ,并称V 为一个r维向量空间.如果向量空间V 没有基,就说V 的维数为0,0维向量空间只含一个零向量.如果把向量空间V 看作向量组,那么V 的基就是它的极大线性无关组,V 的维数就是它的秩.当V 由n 维向量组成时,它的维数不会超过n .定义 13 设12,,r ααα ,是r 维向量空间V 的一个基,则对于任一向量V α∈,有且仅有一组数12,,r x x x ,使1122r r x x x αααα=+++ ,有序数组12,,,r x x x 称为α在基12,,r ααα ,下的坐标,记为()12,,n x x x . 例20 设()123221212122-⎡⎤⎢⎥=-⎢⎥⎢⎥-⎣⎦A a ,a ,a ,()12140342⎡⎤⎢⎥==⎢⎥⎢⎥-⎣⎦B ,ββ,验证α１,α２,α3是R ３的一个基并将β１,β２用这个基线性表出.解 由｜Ａ｜≠0可以知道α１,α２,α3线性无关.由于3dim 3R =,因此α１,α２,α3是R ３的一个基.设β１＝ｘ11α１＋ｘ21α2＋ｘ3１α3, β2＝ｘ12α１＋ｘ22α2＋ｘ32α3,即(β１,β２）＝（α１,α２,α３)111221223132x x x x x x ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦, 那么()1112112122123132x x x x x x --⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦A ,=AB ββ. 下面,我们给出求1A B -的一个简单方法：如果P １,Ｐ２,…,Ｐｌ为初等矩阵,使Ｐ１Ｐ２…ＰｌＡ＝Ｅ,则 Ａ－１＝Ｐ１Ｐ２…Ｐｌ故有l １２ＰＰＰB ＝1-A B . 因此只需对矩阵（Ａ┊Ｂ）作初等行变换,当把A 变为E 时,B 就变成了Ａ－１Ｂ.（Ａ┊Ｂ）＝221142*********-⎡⎤⎢⎥-⎢⎥⎢⎥--⎣⎦(1,3)122422*********r --⎡⎤⎢⎥−−−→-⎢⎥⎢⎥-⎣⎦ (21(2))(31(2))122420368706378r r ++--⎡⎤⎢⎥−−−−→-⎢⎥⎢⎥-⎣⎦(1(1))(32(2))122420368700996r r -+----⎡⎤⎢⎥−−−−→-⎢⎥⎢⎥--⎣⎦1(3())9(23(6))(13(2))21202303023200113r r r -+-+⎡⎤--⎢⎥⎢⎥−−−−→-⎢⎥⎢⎥-⎢⎥⎣⎦1(2())3(12(2))2410033201013200113r r +⎡⎤⎢⎥⎢⎥⎢⎥−−−−→-⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦因此 12433213213-⎡⎤⎢⎥⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦A B . 所以112321232242,3333--++=a a a =a a a ββ.即1β和2β在基123,,ααα下的坐标分别是22,,133--和42,1,33.本章小结与补充向量是线性代数中最简单的数组,是矩阵的特殊情形.所谓向量的线性运算与矩阵的线性运算实质上是一致的.在本章中,我们要理解向量组的线性相关、线性无关的概念,了解其有关的重要结论,会判定向量组的线性相关(无关)性；理解向量组的极大无关组与向量组的秩的定义;了解向量组等价的概念及有关性质;了解向量空间、子空间、基与维数的概念;熟练掌握极大无关组、向量组的秩的计算方法.为此,我们进一步强调如下几点：1.如何正确理解向量组的线性相关(无关)的定义过去在学习二、三维直角坐标空间的过程中接触过向量共线、共面的概念,而向量组的线性相关实际上可以看成是对向量共线、共面的概念在向量空间的推广.线性相关与线性无关是两个相互对立的概念,它们之间的不同之处主要在于：(1)线性相关的向量组存在系数不全为零的线性组合是零向量,而线性无关的向量组只有系数全为零的线性组合是零向量;(2)线性相关的向量组中至少有一个向量可由其余向量线性表示,而线性无关的向量组中任何一个向量都不能由其余向量线性表示；(3)以线性相关的向量组为系数矩阵的齐次线性方程组存在非零解,而以线性无关的向量组为系数矩阵的齐次线性方程组只有零解.2.怎样判断向量组的线性相关性方法1：利用定义判断.这是判定向量组的线性相关的基本方法,既适用于分量已知的向量组,也适用于分量未知的向量组.方法2：利用行列式判断.这种方法仅适用于向量组中向量的个数与向量的维数相等的情形.设12,,n ααα ,是n 个n 维向量,以12,,n ααα ,为列（行）向量组成矩阵A ,则12,,n ααα ,线性相关的充分必要条件是0A =.方法3：利用向量组的秩(或矩阵的秩)判断. 一个向量组线性无关当且仅当它的秩等于向量组所含向量的个数(即向量组构成的矩阵是满秩的).特别地,如果向量组所含向量的个数多于向量的维数,则该向量组是线性相关的.3.向量组的秩与矩阵的秩之间的关系向量组的秩定义为它的极大线性无关组所含向量的个数,然而,直接利用定义来求向量组的秩往往是比较麻烦的,我们通常是将向量组的秩转化为矩阵的秩来求.如果我们将向量组的每个向量作为行(或列)向量构成矩阵A ,则该向量组的秩与矩阵是相等的.4．极大线性无关组的求法方法1：逐个删去法.即对于所给向量组的向量,按自左至右的顺序逐个删去可由其前面的向量线性表出的向量,则所剩向量组即为所给向量组的一个极大线性无关组.方法2：初等变换法.将向量组作为列向量组成矩阵A ,用初等行变换将矩阵A 化为行阶梯形矩阵,则其首非零元所在的列所对应的矩阵A 的列向量组即为所给向量组的一个极大线性无关组.习题三1. 设α１＝（１,１,０）,α2＝（0,１,1）,α3＝（3,4,０）.求α１－α２及3α１＋２α２－α３.2. 设3(α１－α）＋２（α２＋α）＝５（α３＋α）,其中α１＝（２,５,１,３）,α２＝（１０,１,５,１０）,α３＝（４,１,－１,１）.求α.3. 判断下列命题是否正确：(1) 若向量组α１,α２,…,αｍ线性相关,那么其中每个向量可经其他向量线性表示.(2) 如果向量β１,β２,…,βs可经向量组α１,α２,…,αｍ线性表示且α１,α２,…,αm线性相关,那么β１,β２,…,βs也线性相关.(3) 如果向量β可经向量组α１,α２,…,αｍ线性表示且表示式是惟一的,那么α１,α２,…,αｍ线性无关.(4) 如果当且仅当λ１＝λ２＝…＝λｍ＝０时才有λ１α１＋λ2α2+…+λmαm+λ１β１＋λ２β２＋…＋λｍβｍ＝０,那么α１,α２,…,αｍ线性无关且β１,β２,…,βm也线性无关.(5) α１,α２,…,αｍ线性相关,β１,β２,…,βm也线性相关,就有不全为0的数λ１,λ２,…,λｍ使λ１α１＋λ2α2+…+λmαm＝λ１β１＋λ２β２＋…＋λｍβｍ.4. 判别下列向量组的线性相关性.（1）α1=(2,5), α2=(-1,3);(2) α1=(1,2), α2=(2,3), α3=(4,3);(3) α1=(1,1,3,1),α2=(4,1,-3,2),α3=(1,0,-1,2);(4) α1=(1,1,2,2,1),α2=(0,2,1,5,-1),α3=(2,0,3,-1,3),α4=(1,1,0,4,-1).5. β１＝α１＋α２,β2＝α2＋α3,β3＝α3＋α4,β4＝α4＋α1,证明向量组β１,β２,β３,β４线性相关.6. 设向量组α１,α２,…,αr线性无关,证明向量组β１,β２,…,βr也线性无关,这里βｉ＝α１＋α２＋…＋αｉ.7. 作一个以(1,0,1,0)和(1,-1,0,0)为行向量的秩为4的方阵.8. αｉ＝（αｉ１,αｉ２,…,αｉｎ）,i＝１,２,…,ｎ.证明：如果｜ａｉｊ｜≠0,那么α１,α２,…,αn线性无关.9. 设ｔ１,ｔ２,…,ｔｒ是互不相同的数,ｒ≤ｎ.证明：ａｉ＝（１,ｔｉ,…,ｔｎ－１ｉ）,ｉ＝１,２,…,ｒ,是线性无关的.10. 设α１,α２,…,αs的秩为r且其中每个向量都可经α１,α２,…,αr线性表出.证明：α１,α２,…,αr为α１,α２,…,αs的一个极大线性无关组.11. 求向量组α1=(1,1,1,k),α2=(1,1,k,1),α3=（1,2,1,1）的秩和一个极大无关组.12. 确定向量β3=(2,a,b),使向量组β1=（1,1,0）,β2=（1,1,1）,β3与向量组α1=(0,1,1),α2=(1,2,1),α3=(1,0,-1)的秩相同,且β3可由α1,α2,α3线性表出.13. 设α１,α２,…,αn为一组n维向量.证明：α１,α２,…,αn线性无关的充要条件是任一n维向量都可经它们线性表出.14. 若向量组（1,0,0）,（1,1,0）,（1,1,1）可由向量组α１,α２,α３线性表出,也可由向量组β１,β２,β３,β４线性表出,则向量组α１,α２,α３与向量组β１,β２,β３,β４等价.15. 求下列向量组的秩与一个极大线性无关组.(1) α1=(1,2,1,3),α2=(4,-1,-5,-6),α3=(1,-3,-4,-7);(2) α１＝（６,４,１,－１,２）,α２＝(1,0,2,3,-4),α3＝(1,4,-9,-6,22),α4＝(7,1,0,1,3)；(3) α１＝(1,-1,2,4),α２＝(0,3,1,2),α3＝(3,0,7,14),α4＝(1,-1,2,0),α5＝(2,1,5,6).16. 设向量组α１,α２,…,αm与β１,β２,…,βＳ秩相同且α１,α２,…,αm能经β１,β２,…,βＳ线性表出.证明α１,α２,…,αm与β１,β２,…,βＳ等价.17. 设A为ｍ×ｎ矩阵,B为ｓ×n矩阵.证明：ｍaｘ｛R（Ａ）,R（Ｂ）｝≤R ⎡⎤⎢⎥⎣⎦AB≤R（Ａ）＋R（Ｂ）.18. 设A为ｓ×ｎ矩阵且A的行向量组线性无关,K为r×s矩阵.证明：B＝ＫＡ行向量组线性无关的充分必要条件是R(K)=r.19. 求下列矩阵的行向量组的一个极大线性无关组:(1)2531174375945313275945413425322048⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦；（２）11221021512031311041⎡⎤⎢⎥-⎢⎥⎢⎥-⎢⎥-⎣⎦.20. 集合V１＝｛（ｘ１,ｘ２,…,ｘｎ)｜ｘ１,ｘ２,…,ｘｎ∈R且ｘ１+ｘ２+…+ｘｎ＝０｝是否构成向量空间?为什么?21. 试证：由α１＝（1,1,0),α2＝（1,0,1),α3＝（0,1,1)生成的向量空间恰为R３.22. 求由向量α1=(1,2,1,0),α2=(1,1,1,2),α3=(3,4,3,4),α4=(1,1,2,1),α5=(4,5,6,4)所生的向量空间的一组基及其维数.23. 设α１＝（1,1,0,0),α2＝（1,0,1,1)；β１＝（2,-1,3,3),β2＝（0,1,-1,-1),证明：L(α１,α２）＝Ｌ（β１,β２）.24. 在R3中求一个向量γ,使它在下面两个基（1）α1=(1,0,1),α2=(-1,0,0),α3=(0,1,1);(2) β1=(0,-1,1),β2=(1,-1,0),β3=(1,0,1)下有相同的坐标.25. 验证α1＝（1,-1,0),α2＝（2,1,3),α3＝（3,1,2)为R３的一个基,并把β１＝（5,0,7),β2＝（-9,-8,-13)用这个基线性表示.。

数值代数中的矩阵计算与算法分析-教案一、引言1.1矩阵计算与算法分析的重要性1.1.1矩阵计算在科学研究和工程应用中的广泛应用1.1.2算法分析对于提高计算效率和精度的关键作用1.1.3矩阵计算与算法分析在数值代数中的核心地位1.1.4课程目标与学习意义1.2课程内容概述1.2.1矩阵的基本概念与性质1.2.2矩阵的运算及其几何意义1.2.3常用矩阵算法及其应用1.2.4算法分析的基本方法与技巧1.3学习方法与要求1.3.1理论学习与实践操作相结合1.3.2掌握矩阵计算的基本方法与技巧1.3.3理解算法分析的基本原理与方法1.3.4学会运用矩阵计算与算法分析解决实际问题二、知识点讲解2.1矩阵的基本概念与性质2.1.1矩阵的定义及其表示方法2.1.2特殊矩阵（如对角矩阵、单位矩阵等）及其性质2.1.3矩阵的行列式及其性质2.1.4矩阵的秩及其计算方法2.2矩阵的运算及其几何意义2.2.1矩阵的加法、减法与数乘运算2.2.2矩阵的乘法及其几何意义2.2.3矩阵的逆及其求解方法2.2.4矩阵的转置及其性质2.3常用矩阵算法及其应用2.3.1高斯消元法及其在求解线性方程组中的应用2.3.2LU分解及其在矩阵求逆中的应用2.3.3QR分解及其在最小二乘问题中的应用2.3.4特征值与特征向量及其在模式识别中的应用三、教学内容3.1矩阵的基本概念与性质3.1.1通过实例引入矩阵的概念，讲解矩阵的表示方法3.1.2介绍特殊矩阵及其性质，如对角矩阵、单位矩阵等3.1.3讲解矩阵的行列式及其性质，如行列式的计算方法、性质等3.1.4讲解矩阵的秩及其计算方法，如通过高斯消元法求矩阵的秩3.2矩阵的运算及其几何意义3.2.1通过实例讲解矩阵的加法、减法与数乘运算3.2.2讲解矩阵的乘法及其几何意义，如线性变换等3.2.3讲解矩阵的逆及其求解方法，如高斯-若尔当法等3.2.4讲解矩阵的转置及其性质，如转置矩阵的性质等3.3常用矩阵算法及其应用3.3.1讲解高斯消元法及其在求解线性方程组中的应用3.3.2讲解LU分解及其在矩阵求逆中的应用3.3.3讲解QR分解及其在最小二乘问题中的应用3.3.4讲解特征值与特征向量及其在模式识别中的应用四、教学目标4.1知识与技能目标4.1.1理解矩阵的基本概念与性质4.1.2掌握矩阵的运算及其几何意义4.1.3学会常用矩阵算法及其应用4.1.4能够运用矩阵计算与算法分析解决实际问题4.2过程与方法目标4.2.1通过实例引入，培养学生观察、分析问题的能力4.2.2通过讲解与练习，培养学生逻辑思维与推理能力4.2.3通过小组讨论，培养学生合作与交流能力4.2.4通过实际应用，培养学生解决实际问题的能力4.3情感态度与价值观目标4.3.1培养学生对矩阵计算与算法分析的兴趣与热情4.3.2培养学生严谨、求实的科学态度4.3.3培养学生创新意识与批判精神4.3.4培养学生团队协作与沟通能力五、教学难点与重点5.1教学难点5.1.1矩阵的乘法及其几何意义5.1.2矩阵的逆及其求解方法5.1.3特征值与特征向量的计算及应用5.1.4算法分析的基本原理与方法5.2教学重点5.2.1矩阵的基本概念与性质5.2.2矩阵的运算及其几何意义5.2.3常用矩阵算法及其应用5.2.4矩阵计算与算法分析在实际问题中的应用六、教具与学具准备6.1教具准备6.1.1多媒体设备（如投影仪、电脑等）6.1.2白板或黑板、粉笔、板擦等6.1.3教学课件或讲义6.1.4实验或演示工具（如计算器、矩阵计算软件等）6.2学具准备6.2.1笔记本、草稿纸、计算器等6.2.2矩阵计算与算法分析相关教材或参考书6.2.3小组讨论或合作学习所需材料6.2.4实际应用案例或问题七、教学过程7.1导入新课7.1.1通过实例引入矩阵的概念，激发学生学习兴趣7.1.2提问或讨论，引导学生回顾相关知识点7.1.3明确教学目标与学习内容，激发学生学习动机7.2讲解与演示7.2.1讲解矩阵的基本概念与性质，通过实例加深理解7.2.2演示矩阵的运算及其几何意义，引导学生观察、思考7.2.3讲解常用矩阵算法及其应用，通过实际案例讲解算法原理7.2.4演示算法分析的基本方法与技巧，引导学生掌握算法分析的方法7.3练习与讨论7.3.1安排课堂练习，巩固所学知识点7.3.2小组讨论或合作学习，培养学生合作与交流能力7.3.3解答学生疑问，引导学生深入理解知识点7.4应用与拓展7.4.1通过实际应用案例，培养学生解决实际问题的能力7.4.2引导学生进行拓展学习，提高学生自主学习能力7.4.3安排课后作业或实验，巩固所学知识点7.4.4引导学生参与学科竞赛或研究项目，培养学生的创新能力八、板书设计8.1矩阵的基本概念与性质8.1.1矩阵的定义及其表示方法8.1.2特殊矩阵（如对角矩阵、单位矩阵等）及其性质8.1.3矩阵的行列式及其性质8.1.4矩阵的秩及其计算方法8.2矩阵的运算及其几何意义8.2.1矩阵的加法、减法与数乘运算8.2.2矩阵的乘法及其几何意义8.2.3矩阵的逆及其求解方法8.2.4矩阵的转置及其性质8.3常用矩阵算法及其应用8.3.1高斯消元法及其在求解线性方程组中的应用8.3.2LU分解及其在矩阵求逆中的应用8.3.3QR分解及其在最小二乘问题中的应用8.3.4特征值与特征向量及其在模式识别中的应用九、作业设计9.1基础练习题9.1.1矩阵的基本概念与性质相关的练习题9.1.2矩阵的运算及其几何意义相关的练习题9.1.3常用矩阵算法相关的练习题9.1.4矩阵计算与算法分析在实际问题中的应用练习题9.2拓展练习题9.2.1矩阵计算与算法分析在科学研究中的应用练习题9.2.2矩阵计算与算法分析在工程应用中的练习题9.2.3矩阵计算与算法分析在数据科学中的应用练习题9.2.4矩阵计算与算法分析在金融数学中的应用练习题9.3实践项目9.3.1基于矩阵计算的图像处理实践项目9.3.2基于矩阵算法的社交网络分析实践项目9.3.3基于矩阵计算的机器学习算法实践项目9.3.4基于矩阵算法的金融风险管理实践项目十、课后反思及拓展延伸10.1课后反思10.1.2对教学方法的反思与改进10.1.3对学生学习情况的反思与评价10.1.4对教学效果的反思与提升10.2拓展延伸10.2.1引导学生参与学科竞赛或研究项目10.2.2鼓励学生参加学术讲座或研讨会10.2.3提供相关的学习资源与参考文献10.2.4鼓励学生进行跨学科的学习与研究重点关注环节及其补充和说明：1.教学难点与重点：需要重点关注矩阵的乘法及其几何意义、矩阵的逆及其求解方法、特征值与特征向量的计算及应用、算法分析的基本原理与方法。

秩的几何意义
秩是一个矩阵中的一组行或列的线性无关的最大数量，也就是这组行或列所组成的子向量空间的维数。

在几何中，一个矩阵的秩相当于其所代表的线性变换所映射的向量空间的维数。

换句话说，一个矩阵的秩可以表示其所代表的空间的维度大小，即该空间最大能容纳几个线性无关的向量。

例如，一个二阶矩阵的秩为1，表示其所代表的向量是在一条直线上的；一个三阶矩阵的秩为2，表示其所代表的向量是在一个平面上的。

秩的几何意义可以帮助我们更好地理解线性代数中的概念和定理，应用于许多实际问题中，如图像处理、机器学习、信号处理等。

《高等代数》第一次作业一、名词解释1、克莱母法则答：定理 若数域K 上的n 个未知量n 个方程的线性方程组11112211211222221122n n n n n n nn n na x a x a xb a x a x a x b a x a x a x b ++⋅⋅⋅+=⎧⎪++⋅⋅⋅+=⎪⎨⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⎪⎪++⋅⋅⋅+=⎩，当它的系数矩阵的行列式1112121222120nn n n nn a a a a a a D a a a ⋅⋅⋅⋅⋅⋅=≠⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅时，它有唯一的一组解1212,,,.n n D D D x x x D D D==⋅⋅⋅=其中的(1,2,,)j D j n =⋅⋅⋅就是把行列式D 的第j 列的元素换以议程组的常数项12,,,n b b b ⋅⋅⋅而得的n 阶行列式。

这个定理称为克莱母法则（Crammer ）法则。

2、线性组合答：设12,,,,n s a a a P ∈g g g ,,,12k k k P s ∀∈L 和1122L k k k s s ααα+++称为向量组12,,,,n s a a a P ∈g g g 的一个线性组合.3、极大无关组 答：如果一个向量组的部分组,,,12i i ir αααL 满足 (1) ,,,12i i irαααL 线性无关。

(2)向量组中的任意一个向量(1)j s jα≤≤都可以用它线性表示，则称部分组 ,,,12i i ir αααL 为向量组的一个极大无关组。

4、矩阵的秩答：（1）一个m n ⨯的λ-矩阵()A λ中，不等于零的子式的最大阶数r 叫()A λ的秩。

若()A λ没有不等于零的子式，就认为这个矩阵()A λ的秩是零。

（2）矩阵的秩的几何意义：设()1112112122221212n n n m m mn m a a a a a a A a a a ααβββα⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭L L L L L MA 的每一行可看作F n的行向量，称为A 的行向量，并称1(,,)m L a a L 为A 的行空间；A 的每一列可看作F m的列向量，称为A 的列向量，并称1(,,)m L ββL 为A 的列空间。

第三章 向量组的线性相关性与矩阵的秩向量是研究代数问题的重要工具。

在解析几何里，曾经讨论过二维与三维向量。

但是，在很多实际问题中，往往需要研究更多维的向量。

例如，描述卫星的飞行状态需要知道卫星的位置()z y x ,,、时间t 以及三个速度分量z y x v v v ,,，这七个量组成的有序数组()z y xv v vt z y x ,,,,,,称为七维向量。

更一般地，本章将引入n 维向量的概念，定义向量的线性运算，并在此基础上讨论向量组的线性相关性，研究向量组与矩阵的秩、向量组的正交化等问题。

这将为以后利用向量的线性关系来分析线性方程组解的存在性，化二次型为标准形等奠定理论上的基础。

§1 n 维向量作为二维向量、三维向量的推广，现给出n 维向量的定义定义1 n 个数n a a a ,,,21 组成的有序数组（n a a a ,,,21 ），称为n 维向量。

数i a 称为向量的第i 个分量（或第i 个分量）。

向量通常用希腊字母γβα,, ,等来表示。

向量常写为一行α=（n a a a ,,,21 ）有时为了运算方便，又可以写为一列=α⎪⎪⎪⎪⎪⎭⎫⎝⎛n a a a 21前者称为行向量，后者称为列向量。

行向量、列向量都表示同一个n 维向量。

设),,,(),,,,(2121n n b b b a a a ==βα都是n 维向量，当且仅当它们各个对应的分 量相等，即),,2,1(n i b a i i ==时，称向量α与向量β相等，记作，βα=。

分量全为零的向量称为零向量，记为0，即 0=)0,,0,0(若),,,(21n a a a =α，则称),,,(21n a a a --- 为α的负向量，记为α-。

下面讨论n 维向量的运算。

定义2 设),,,(),,,,(2121n n b b b a a a ==βα都是n 维向量，那么向量),,,(2211n n b a b a b a +++ 叫做向量α与β的和向量，记做βα+，即),,,(2211n n b a b a b a +++=+ βα 向量α与β的差向量可以定义为α+)(β-，即),,,()(2211n n b a b a b a ---=-+=- βαβα定义3 设),,,(21n a a a =α是n 维向量，λ是一个数，那么向量),,,(21n a a a λλλ 叫做数λ与向量α的数量乘积（简称数乘），记为λα，即),,,(21a a a λλλλα =向量的和、差及数乘运算统称为向量的线性运算。

a
。
,
…
,
,
今是
八的 行
,
。
:
,
…氏
l
所 生成 的 厂 的子空 间 L
:
, n
”
(
a
:
,
a
:
,
a
n
)
,
叫做 矩阵 A 的 行 空 间
,
类 似地
,
由 八的
个列 向景 日 日 … 日 所 生成 的 F
,
m
的子 空 间
(日
日
:
:
,
日 {
,
。
)
叫做
, ,
A 的列空 间
为 了 证 明矩 阵秩 的 几何 意 义
+
a
1
r
h
r
=
0
a
,
z
h
z
+
a
,
:
h
Z
十
…
+
a
。
,
h
,
=
0
〔1 〕
a
。
l
h
:
+
a
。
Z
h
:
+
…
+
a
。
,
1 1
:
=
0
r
由前
r
个 方 程 构 成 的 方 程组 系 数行 列 式 恰好 为 A 的 左 上 角
1 ) 只 有零 解 h
:
阶子 式
,
因此 不 等 于 零
故方 程组 (
=
h
, :
Z
二

e1 , e2 , , en 线性无关 线性无关;
16
(4) 有两个向量相等的向量组线性相关; 有两个向量相等的向量组线性相关;
(5) m>n时, m 个n维向量必线性相关 特别:m=n+1 维向量必线性相关. 时 维向量必线性相关 特别: (6) n个n维向量线性无关 个 维向量线性无关 它们所构成方阵的行列式不为零. 它们所构成方阵的行列式不为零
2
例如: 例如:
(1,2,3,, n) (1 + 2i ,2 + 3i ,, n + ( n + 1)i )
第2个分量 第1个分量
n维实向量
n维复向量
第n个分量
3
向量通常写成一行: 向量通常写成一行: T = (a1 , a 2 , , a n ) 称为行向量. α 称为行向量. 行向量
a1 a 有时也写成一列: 有时也写成一列: α = 2 称为列向量. 它们的区别 称为列向量 列向量. 只是写法上 的不同. 的不同. an 称为零向量 零向量. 分量全为零的向量 ( 0,0, ,0 ) 称为零向量.
定理1: 定理 向量 β 可由向量组 α 1 ,α 2 , ,α m 线性表示的 充分必要条件是: 充分必要条件是: 以 α 1 ,α 2 , ,α m 为系数列向量,以 β 为常数项列向量 为系数列向量, 的线性方程组有解,且一个解就是线性表示的系数. 的线性方程组有解,且一个解就是线性表示的系数. 线性方程组的矩阵表示和向量表示: 线性方程组的矩阵表示和向量表示:
6
二. 线性相关性 1. 线性组合与线性表示
定义1: 定义 :给定向量组 A : α 1 ,α 2 , ,α m , 对于任何一组实数 k1 , k2 , , km , 向量 k1α 1 + k2α 2 + + kmα m 称为向量组 的一个 称为向量组A的一个 定义2: 定义 :给定向量组 A : α 1 ,α 2 , ,α m , 和向量 β 如果存在一组实数 λ1 , λ2 , λm , 使得 β = λ1α 1 + λ2α 2 + + λmα m 则称向量