专题一 作图题

1、如图10，在6×8的网格图中，每个小正方形边长均为1，点O和△ABC的顶点均为小正方形的顶点.⑴以O为位似中心，在网格图．．．中作△A′B′C′，使△A′B′C′和△ABC位似，且位似比为1：2⑵连接⑴中的AA′，求四边形AA′C′C的周长.（结果保留根号）2、如图，在Rt△ABC中，角ABC=90度。

（1）尺规作图：作角BAC的平分线AM交BC于点D（只保留作图痕迹，不写作法）；（2）在（1）所作图形中，将Rt△ABC沿某条直线折叠，使点A与点D重合，折痕EF交AC于点E，交AB于点F，连接DE、DF，再展回到原图形，得到四边形AEDF。

○1试判断四边形AEDF的形状，并证明；○2若AC=8，CD=4，求四边形AEDF的周长和BD的长。

已知：如图，在R t ABC△中，90C B A C∠=∠°，的角平分线A D交B C边于D．（1）以A B边上一点O为圆心，过A D、两点作O⊙（不写作法，保留作图痕迹），再判断直线B C与O⊙的位置关系，并说明理由；（2）若（1）中的O⊙与A B边的另一个交点为E，6AB BD==，，求线段B D B E、与劣弧D E所围成的图形面积．（结果保留根号和π）（2011山东滨州，23，9分）根据给出的下列两种情况，请用直尺和圆规找到一条直线，把△ABC恰好分割成两个等腰三角形（不写做法，但需保留作图痕迹）；并根据每种情况分别猜想：∠A与∠B有怎样的数量关系时才能完成以上作图？并举例验证猜想所得结论。

（1）如图①△ABC中，∠C=90°，∠A=24°①作图：②猜想：③验证：（2）如图②△ABC中，∠C=84°，∠A=24°.第23题图②①作图：②猜想：③验证：AＣD B第23题图①。

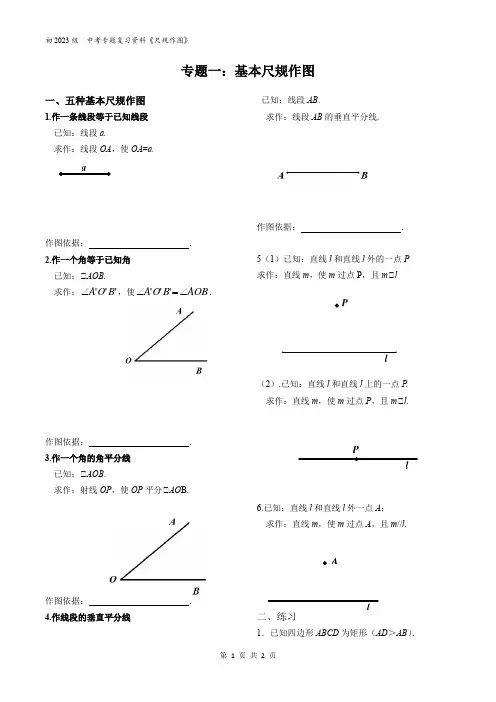
Pl一、五种基本尺规作图1.作一条线段等于已知线段 已知：线段a.求作：线段OA ，使OA =a.作图依据： . 2.作一个角等于已知角 已知：∠AOB.求作：'''B O A ∠，使AOB B O A ∠=∠'''.作图依据： . 3.作一个角的角平分线 已知：∠AOB .求作：射线OP ，使OP 平分∠AO B.作图依据： . 4.作线段的垂直平分线已知：线段AB .求作：线段AB 的垂直平分线.作图依据： .5（1）已知：直线l 和直线l 外的一点P 求作：直线m ，使m 过点P ，且m ∠l（2）.已知：直线l 和直线l 上的一点P . 求作：直线m ，使m 过点P ，且m ∠l.6.已知：直线l 和直线l 外一点A ； 求作：直线m ，使m 过点A ，且m //l .二、练习1．已知四边形ABCD 为矩形（AD ＞AB ）．alPAl专题一：基本尺规作图（1）尺规作图：在BC上取一点E，使AE＝AD；过点D作DF⊥AE，交AE于点F（基本作图，保留作图痕迹，不写作法，不下结论）；（2）求证：DF＝DC．（请补全下面的证明过程，不写证明理由）证明：∵①，∴AD＝BC，AD∥BC，∠B＝90°，∴∠F AD＝∠AEB．∵DF⊥AE，∴②．∴③．在△AFD与△EBA中，，∴△AFD≌△EBA（AAS）．∴④．又∵AB＝CD，∴DF＝DC．2．如图，在平行四边形ABCD中，AB＞AD．（1）尺规作图：在AB上截取AE，使得AE＝AD；作∠BCD的平分线交AB于点F．（保留作图痕迹，不写作法）（2）在（1）所作的图形中，连接DE交CF于点P，求证：△CDP为直角三角形．（请补全下面的证明过程，不写证明理由）证明：∵AE＝AD，∴∵四边形ABCD是平行四边形，∴AB∥CD，∴∠AED＝∠EDC，∴∵CF平分∠BCD，∴又∵AD∥CB，∴∠ADC+∠BCD＝180°，∴∠ADC+∠BCD＝90°，∴∴∠CPD＝90°，∴△CDP是直角三角形．3.如图，AD∥BE，AC平分∠BAD，且交BE于点C．（1）作∠ABE的角平分线交AD于点F（要求：尺规作图，不写作法和结论，保留作图痕迹）；（2）根据（1）中作图，连接CF，求证：四边形ABCF是菱形．。

尺规作图专题一：中垂线
做法：如图，①分别以点A和点B为圆心，
大于二分之一AB的长为半径作弧，
两弧相交于C，D两点；
②作直线CD．
则直线CD就是所求作的垂直平分线．
注意：4条弧，2个交点。

依据：①到线段两端点距离相等的点在线段的垂直平分线上
②两点确定一条直线
目标：①构造等线段（到点的距离相等）
②平分线段（找中点）
③作垂线
④找对称轴
练习：1、如图，为了解决村民子女就近入学问题，现计划在A，B，C 三个村庄之间修建一所小学.若要使学校到三个村庄的距离相等，学校应建在何处?请你在图中用尺规确定学校的位置．2、尺规作图：确定三角形ABC的重心。

3、尺规作图：过点A作直线l的垂线。

4、请利用尺规确定下面两个三角形的对称轴。

能力提升：
1、尺规作图，在l 上找一点P ，使它到线段AB 两端的距离相等，保留作图痕迹．
2、如
图，已知
△ABC ，用尺规将△ABC 分成两个面积相等的三角形。

3、如图，已知△ABC(AB<BC<AC)，用尺规在AC 上确定一点P ，使得PB+PC=AC 。

5、利用尺规作图确定圆心O 。

专题01 尺规作图一．解答题（共8小题）1．（2019秋•龙华区期末）如图，已知四边形ABCD，请用尺规按下列要求作图．（1）延长BC到E，使CE＝CD；（2）在平面内找到一点P，使P到A、B、C、D四点的距离之和最短．【分析】（1）延长BC到E，使CE＝CD即可；（2）使点P、D、E共圆在平面内找到一点P，使P到A、B、C、D四点的距离之和最短【解答】解：（1）如图，延长BC到E，使CE＝CD；（2）如图，点P即为所求作的点．【点评】本题考查了作图﹣复杂作图，解决本题的关键是准确找到点P．2．（2020•市南区校级模拟）已知△ABC，在△ABC中作一半圆满足以下要求：①圆心在边BC上；②该半圆面积最大．【分析】根据角平分线上的点到角的两边距离相等即可画出满足要求的半圆．【解答】解：根据题意作图，如图，圆O在三角形ABC内部的半圆即为所求．【点评】本题考查了作图﹣复杂作图，解决本题的关键是掌握角平分线的性质．3．（2020•德城区一模）已知：如图，在△ABC中，AD⊥BC．求作：在AD上求作点E，使得点E到AB的距离EF等于DE．（要求：尺规作图，不写作法，保留作图痕迹．）（1）作图的依据是到角两边距离相等的点在这个角的角平分线上；（2）在作图的基础上，若∠ABC＝45°，AB⊥AC，DE＝1，求CD的长．【分析】（1）作∠ABC的角平分线交AD于E，过点E作EF⊥AB于F，线段EF即为所求．（2）证明△AEF是等腰直角三角形，求出AE即可解决问题．【解答】解：（1）如图线段EF即为所求．作图的依据是：到角两边距离相等的点在这个角的角平分线上．故答案为：到角两边距离相等的点在这个角的角平分线上．（2）∵BE平分∠边长，ED⊥BC，EF⊥AB，∴ED＝EF＝1，∵AD⊥BC，∠ABC＝45°，∴AF＝EF＝1，∴AE＝＝＝，∴AD＝AE+DE＝+1．【点评】本题考查作图﹣复杂作图，等腰直角三角形的判定和性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．4．（2019秋•碑林区校级期末）如图，△ABC中，AB＝6，AC＝8，点D在AB上，AD＝3，在边AC上求作一点E使得△DAE的周长为11．（要求：尺规作图，不写作法，保留作图痕迹）【分析】连接CD，作CD的垂直平分线，交AC于E，则CE＝DE，依据AD＝3，AC＝AE+CE＝8，即可得到△DAE的周长为3+8＝11．【解答】解：如图所示，点E即为所求．【点评】本题主要考查了复杂作图，解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．5．（2019秋•包河区期末）如图，已知△ABC．（1）画出△ABC的高AD；（2）尺规作出△ABC的角平分线BE（要求保留作图痕迹，不用证明）．【分析】（1）根据过直线外一点作已知直线的垂线的尺规作图可得；（2）根据角平分线的尺规作图可得．【解答】解：（1）如图，AD即为△ABC的高．（2）如图，BE即为△ABC的角平分线．【点评】本题主要考查作图﹣复杂作图，解题的关键是掌握过直线外一点作已知直线的垂线及角平分线的尺规作图．6．（2017秋•聊城期中）已知：如图，直线l极其同侧两点A，B．（1）在图1直线l上求一点P，使到A、B两点距离之和最短；（不要求尺规作图）（2）在图2直线l上求一点O，使OA＝OB．（尺规作图，保留作图痕迹）【分析】（1）直接利用对称点求最短路线方法作图即可；（2）结合线段垂直平分线的性质与作法分析得出答案．【解答】解：（1）如图1所示：点P即为所求；（2）如图1所示：点O即为所求．【点评】此题主要考查了基本作图、最短路线问题以及线段垂直平分线的性质，正确掌握相关性质是解题关键．7．（2017秋•滨海新区期末）如图，在△ABC中，AB＝3，AC＝4，BC＝5，EF是BC的垂直平分线，P是直线EF上的任意一点．（Ⅰ）P A+PB的最小值为4；（Ⅱ）在直线EF上找一点P，使得∠APE＝∠CPE，画图，并简要说明画图方法．（保留画图痕迹，不要求证明）【分析】（Ⅰ）根据题意知点B关于直线EF的对称点为点C，故当点P为AC与EF的交点时，AP+BP 的最小值，依据AC的长度即可得到结论．（Ⅱ）先作射线BA与直线EF的交点即为点P的位置．【解答】解：（Ⅰ）∵EF是BC中垂线，∴点B关于直线EF的对称点为C，当点P为AC与EF的交点时，P A+PB取得最小值，最小值为P A+PC＝AC＝4，故答案为：4．（Ⅱ）如图所示，延长BA交直线EF于P，连接CP，则∠APE＝∠CPE．理由：∵EF是BC的垂直平分线，∴PB＝PC，又∵PE⊥BC，∴等腰△PBC中，PE平分∠BPC，∴∠APE＝∠CPE．【点评】本题考查基本作图、轴对称变换、最短距离问题等知识，解题的关键是学会利用轴对称，根据两点之间线段最短解决最短问题．凡是涉及最短距离的问题，一般要考虑线段的性质定理，结合轴对称变换来解决，多数情况要作点关于某直线的对称点．8．（2019秋•惠山区校级期中）如图，C为线段BD上一动点，分别过点B、D作AB⊥BD、ED⊥BD，连结AC、EC．已知AB＝6，DE＝2，BD＝15，设CD＝x．（1）用含x的代数式表示AC+CE的值；（写出过程）（2）请问点C满足条件点C与点A和B在同一条直线上时，AC+CE的值最小；（3）根据（2）中的结论，画图并标上数据，求代数式的最小值．【分析】（1）根据勾股定理用含x的代数式表示AC+CE的值即可；（2）根据两点之间线段最短可知：点C满足条件与点A、E在同一条直线上时，AC+CE的值最小；（3）根据（2）中的结论，画图并标上数据，即可求代数式的最小值．【解答】解：（1）∵AB＝6，DE＝2，BD＝15，设CD＝x则BC＝15﹣x，根据勾股定理，得AC+CE＝+＝+（2）根据两点之间线段最短可知：当点C与点A和点E在同一条直线上时，AC+CE的值最小；故答案为：点C与点A和点E在同一条直线上．（3）如图所示：∵AB⊥BD、ED⊥BD，∴AB∥DE，∴＝，即＝，解得x＝，则4﹣x＝，＝+＝5答：代数式的最小值为5．【点评】本题考查了作图﹣基本作图、列代数式、轴对称﹣最短路线问题，解决本题的关键是求x的值．。

专题一作图专题1.如图所示,小明利用一块平面镜使此时的太阳光水平射入隧道内。

请你通过作图画出平面镜并标出反射角的角度。

答案:如图所示解析:根据光的反射定律,反射角等于入射角,作反射光线和入射光线夹角的角平分线就是法线的位置;由图知,反射光线和入射光线的夹角为180°-60°=120°,则反射角等于入射角等于60°。

2.图中的A'B'是物体AB经过平面镜M后所成的像,请在图中画出该物体。

答案:如图所示3.如图所示,点光源S置于平面镜前,请画出点光源S的成像光路图。

答案:如图所示解析:从点光源S向镜面任意发出两条入射光线,入射点分别是O1、O2;根据光的反射定律,画出这两条入射光线的反射光线;将这两条反射光线反向延长,相交于点S',点S'即为点光源S在平面镜中所成的像。

4.如图所示,在平静的湖边上方有一盏路灯,潜水员在水下E处看到了路灯的像,图中A、B两点,其中一点是路灯的发光点,另一点是路灯的像点。

请你区分发光点、像点,在图中画出水下E处的潜水员看到路灯的光路图。

答案:如图所示解析:根据光从空气中斜射入水中时,折射角小于入射角,可知A为路灯的发光点,B为像点,连接EB与界面的交点即为入射点,光路图如图所示。

5.如图所示,平面镜垂直于凸透镜主光轴且在凸透镜左侧焦点上,请完成光路图。

答案:如图所示6.如图所示,请在图中画出力F的力臂l及物体所受重力的示意图。

答案:如图所示7.如图所示,某人在A处提起物体,请在图中画出最省力的绳子绕法。

答案:如图所示解析:从动滑轮上挂钩开始,依次绕过定滑轮和动滑轮,绳端回到人的手中,提升物体绳子条数为3,是最省力的绕法。

8.根据下面左侧电路实物图,在下面右侧方框内画出对应的电路图。

答案:如图所示9.设计一个病床呼叫电路。

要求:开关S1控制指示灯L1和电铃,开关S2控制指示灯L2和电铃。

请在图中连线,形成符合要求的完整电路图。

专题一作图题命题分析广东省近五年中考物理命题分析考点20232022202120202019光学作图省题15(2)省题15(2)省题15(3)省题15(2)省题15(2) 力学作图省题15(1)省题15(1)省题15(1)省题15(1)省题15(1)电磁学作图省题15(3)省题15(3)省题15(2)省题15(3)省题15(3)作图题的基本要求：(1)线条要工整、清楚。

直线要用直尺，曲线要光滑连接。

(2)符号要规范。

画图题中要注明各物理量的符号(有时还标单位符号)。

这些物理量符号是物理学上规定统一或是约定俗成的。

类型一光学作图考向1光的直线传播作图例1《墨经》有小孔成像的记录，物体的投影之所以会出现倒像，是因为光线沿直线传播，在针孔处，不同方向射来的光束互相交叉而形成倒影。

图甲是小王同学做小孔成像实验的情景，在图乙中大致画出烛焰AB(烛焰可以抽象为带箭头的线段)通过纸杯的小孔在黑塑料膜虚线上所成的像A′B′，并标明两条光线的传播方向。

答案名师点拨作图依据：在同种均匀介质中光沿直线传播。

作图方法及规范：(1)作图必须使用刻度尺；(2)光线用实线表示，加箭头表示光的传播方向；(3)实像用实线。

考向2光的反射作图与光的折射作图例2(2023·泸州)一束激光从空气中以图示角度射入水中，其反射光线与折射光线刚好垂直。

请在图中画出折射光线，并标出折射角的角度大小。

答案解析过入射点O的垂直于界面的虚线是法线，根据反射角等于入射角等于53°，画出反射光线；反射光线与界面的夹角为90°－53°＝37°，光从空气斜射入水中，折射角小于入射角，画出折射光线，由于折射光线与反射光线垂直，则折射光线与界面之间的夹角为90°－37°＝53°，折射角为90°－53°＝37°，如答图所示。

名师点拨作图依据：(1)光的反射定律：反射角等于入射角，反射光线、入射光线分居法线两侧。