贵州大学818高等代数2020年考研专业课初试大纲

814--《高等代数》考研大纲一、基本要求要求考生全面系统地理解高等代数的基本概念和基本理论，熟练掌握高等代数的基本思想和基本方法。

要求考生具有较强的抽象思维能力、逻辑推理能力、数学运算能力以及综合运用所学知识分析问题和解决问题的能力。

二、考试范围（一）多项式1．多项式的带余除法及整除性、最大公因式、互素多项式；2．不可约多项式、因式分解唯一性定理、重因式、复系数与实系数多项式的因式分解、有理系数多项式不可约的判定；3．多项式函数与多项式的根、代数基本定理、有理系数多项式的有理根的求法、根与系数的关系。

（二）行列式1．行列式的定义及性质，行列式的子式、余子式及代数余子式；2．行列式按一行、列的展开定理、Cramer法则、Laplace定理和行列式乘法定理、Vandermonde行列式；3．运用行列式的性质及展开定理等计算行列式。

（三）线性方程组1．Gauss消元法与初等变换；2．向量组的线性相关性、向量组的秩与极大线性无关组、矩阵的秩；3．线性方程组有解的判别定理与解的结构。

（四）矩阵1．矩阵的基本运算、矩阵的分块及常用分块方法；2．矩阵的初等变换、初等矩阵、矩阵的等价、矩阵的迹、方阵的多项式；；3．逆矩阵、矩阵可逆的条件及与矩阵的秩和初等矩阵之间的关系，伴随矩阵及其性质；4．运用初等变换法求矩阵的秩及逆矩阵。

（五）二次型理论1．二次型及其矩阵表示、矩阵的合同、二次型的标准形与规范形、惯2．实二次型在合同变换下的规范形以及在正交变换下的特征值标准型的求法；3．实二次型或实对称矩阵的正定、半正定、负定、半负定的定义、判别法及其应用。

（六）线性空间1．线性空间、子空间的定义与性质，向量组的线性相关性，线性（子）空间的基、维数、向量关于基的坐标，基变换与坐标变换，线性空间的同构；2．子空间的基扩张定理，生成子空间，子空间的和与直和、维数公式；3．一些常见的子空间，如线性方程组的解空间、矩阵空间、多项式空间、函数空间。

贵州大学硕士研究生入学考试大纲考试科目代码及名称： 809民法总论、刑法总论一、考试基本要求本科目考试着重考核考生掌握民法总则基本概念、基本思想、基本分析方法和基本理论体系的情况，以及掌握刑法的基本概念、基本思想、基本分析方法和基本理论的程度。

要求考生掌握民法、刑法理论与体系的基本框架与内容,并能综合运用所学的知识分析、解决相关问题。

二、适用范围适用于法学专业三、考试形式闭卷，180分钟四、考试内容和考试要求（一）民法总论⒈民法概述民法的概念与含义；民法的调整对象；民法的性质；民法的本位；民法的渊源；民法的效力。

⒉民法的基本原则民法基本原则的概述；平等原则；自愿原则；公平原则；诚信原则；守法与公序良俗原则；绿色原则。

⒊民事法律关系的概述民事法律关系的概念与意义；民事法律关系的要素；民事法律事实；民事权利、民事义务、民事责任；民事责任与债法、物权法和请求权的关系。

⒋民事法律关系的主体⑴自然人：自然人的民事权利能力与民事行为能力；监护；自然人的住所；宣告失踪与宣告死亡。

⑵法人：法人的概念；法人成立的原则与条件；法人的民事能力；法人的机关；法人的分支机构；法人的住所；法人的成立、变更与终止；法人的登记；营利法人；特别法人。

⑶非法人组织：非法人组织的的定义和范围；非法人组织的设立程序；非法人组织的民事责任；非法人组织的代表人；非法人组织的解散事由；非法人组织的清算。

⒌民事法律关系的客体民事法律关系客体的种类；物；有价证券；智力成果；其他客体。

⒍民事法律关系的变动⑴民事法律行为：民事法律行为的定义；意思表示；民事法律行为的成立；民事法律行为的形式；民事法律行为的效力；附条件的民事法律行为与附期限的民事法律行为。

⑵代理：代理的概念与特征；代理的分类；代理权；无权代理与表见代理。

⒎诉讼时效时效制度概述；诉讼时效；除斥期间；期限。

注意：参考教材中的内容与《中华人民共和国民法总则》不一致的，以《中华人民共和国民法总则》为准。

高等代数考试科目大纲一、考试性质高等代数是硕士研究生入学考试科目之一，是硕士研究生招生院校自行命题的选拔性考试。

本考试大纲的制定力求反映招生类型的特点，科学、平等、确切、规范地测评考生的相关基础知识控制水平，考生分析问题和解决问题及综合知识运用能力。

应考人员应按照本大纲的内容和要求自行组织学习内容和控制有关知识。

二、评价目标1、要求考生理解该课程的基本概念和基本理论，控制该课程的基本主意。

2、要求考生具有抽象思维能力、逻辑推理能力、空间想象能力、运算能力。

3、要求考生具有综合运用所学的知识分析问题和解决问题的能力。

三、考试范围及其基本要求1、行列式考试范围：n阶行列式的定义，n阶行列式的性质与计算。

基本要求：（1）理解罗列及其逆序数，理解n阶行列式的定义，能利用定义计算行列式的值。

（2）熟练控制行列式的性质，能熟练计算低阶行列式的值，能计算较容易的n阶行列式的值。

2、矩阵考试范围：矩阵及其运算，分块矩阵与矩阵的初等变换，矩阵的秩，可逆矩阵。

基本要求：（1）理解矩阵、单位矩阵、数量矩阵、对角矩阵、三角矩阵、对称矩阵、反驳称矩阵、方阵的幂及矩阵的转置等概念，熟练控制矩阵的线性运算、乘法运算、转置及其运算逻辑。

（2）理解分块矩阵、准对角矩阵、初等变换和初等矩阵的概念，熟练控制分块矩阵的运算。

（3）理解初等变换与初等矩阵的概念及基本作用，了解矩阵等价的概念及第 1 页/共 6 页性质，能用矩阵的初等变换化矩阵为标准形。

（4）理解矩阵的子式、矩阵的秩的定义，熟练控制矩阵的秩的性质，能求矩阵的秩。

（5）理解满秩矩阵的概念，控制满秩矩阵的性质。

（6）控制两个方阵与其乘积的秩的关系式，能熟练运用方阵乘积的行列式的公式。

（7）理解可逆矩阵的概念，控制可逆矩阵的性质，控制矩阵可逆的充足须要条件。

（8）理解陪同矩阵的概念，控制陪同矩阵的性质，会用陪同矩阵法求可逆矩阵的逆矩阵，能熟练运用矩阵的初等变换求可逆矩阵的逆矩阵，能解矩阵方程。

全日制攻读艺术硕士专业学位（MFA）入学考试大纲
﹙科目：音乐作品分析﹚
招生专业：音乐
考试科目：《音乐作品分析》
考试代码：843
考试总分：150分
考试时间：180分钟
一、考查目标
《音乐作品分析》是贵州师范大学艺术硕士（音乐）专业研究生入学初试科目之一。

主要考察应试者对音乐学专业本科阶段的骨干课程《曲式与作品分析》《中国民族音乐及作品鉴赏》的掌握情况，要求考生对中外音乐作品分析的基础知识、基本理论有全面了解。

对外国作品，能识别指定音乐作品中的调性、和声，并对其序进、技法、布局、特点、风格及在内容表达方面的影响进行详细的分析、归纳和概括。

掌握曲式基本理论，能分析指定作品的整体结构性质并写出结构图示。

能用适当的文字描述分析对象在结构、和声、材料等方面的处理情况及发展脉络。

能总结分析对象在结构、和声、材料等方面的特点、风格。

对中国作品，能辨识作品的调式、曲式，总结出作品中的时代性、地域性或民族性特征。

对中外作品都要求在上述分析要求的基础上理解分析对象的形象表达。

二、考试形式
1。

2020年全国硕士研究生入学统一考试数学(二)考试大纲编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2020年全国硕士研究生入学统一考试数学(二)考试大纲）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2020年全国硕士研究生入学统一考试数学(二)考试大纲的全部内容。

2020年全国硕士研究生入学统一考试数学(二）考试大纲考试科目：高等数学、线性代数考试形式和试卷结构一、试卷满分及考试时间试卷满分为150分，考试时间为180分钟．二、答题方式答题方式为闭卷、笔试．三、试卷内容结构高等数学约78％线性代数约22%四、试卷题型结构单项选择题 8小题，每小题4分，共32分填空题 6小题，每小题4分，共24分解答题(包括证明题） 9小题，共94分►高等数学一、函数、极限、连续考试内容函数的概念及表示法、函数的有界性、单调性、周期性和奇偶性复合函数、反函数、分段函数和隐函数基本初等函数的性质及其图形初等函数函数关系的建立数列极限与函数极限的定义及其性质函数的左极限与右极限无穷小量和无穷大量的概念及其关系无穷小量的性质及无穷小量的比较极限的四则运算极限存在的两个准则：单调有界准则和夹逼准则两个重要极限：函数连续的概念函数间断点的类型初等函数的连续性闭区间上连续函数的性质考试要求理解函数的概念，掌握函数的表示法，并会建立应用问题的函数关系。

了解函数的有界性、单调性、周期性和奇偶性.理解复合函数及分段函数的概念,了解反函数及隐函数的概念.掌握基本初等函数的性质及其图形，了解初等函数的概念。

5.理解极限的概念,理解函数左极限与右极限的概念以及函数极限存在与左极限、右极限之间的关系。

贵州大学硕士研究生招生考试大纲
科目代码及名称： 810 中国化马克思主义基本原理
一、考试基本要求
本科目考试着重考核考生掌握中国化马克思主义基本原理基本概念、基本思想、基本分析方法和基本理论的程度，要求考生对中国化马克思主义基本原理理论体系的基本框架有一个比较全面的了解，并能综合运用所学的中国化马克思主义基本原理知识分析社会现实问题。

二、适用范围
适用于马克思主义基本原理、马克思主义中国化研究、思想政治教育、中国近现代史基本问题研究专业
三、考试形式
闭卷，180分钟
四、考试内容和考试要求
1. 了解和掌握本课程基本知识、理论和观点;
2.理解和熟悉新时代中国特色社会主义思想理论体系；
3. 运用本课程有关理论或原理，正确解释和论证某些观点，明辨是非；
4. 运用本课程基本立场、观点和方法正确观察、分析或解决社会现象和实际问题。

第 1 页共 2 页。

贵州大学硕士研究生入学考试大纲
考试科目代码及名称： 880设计基础
一、考试基本要求
本科目考试着重考核考生掌握设计造型基础和设计表达基础两个方面的能力，要求考生对视觉形态审美构成的基本框架有一个比较全面的了解，并能综合运用所学的视觉发现与重构能力，掌握理性与感性相结合的基础设计方法。

二、适用范围
适用于设计学平面设计、品牌形象设计与策划、手工艺设计研究专业和艺术设计领域的艺术设计、民间艺术创新设计方向专业。

三、考试形式
闭卷，180分钟
四、考试内容和考试要求
内容：视觉形态构成及表现
要求：主要考核学生对设计目的、要求的准确理解，以及对设计造型基础和设计表达基础掌握的情况，并能运用专业技法，表现对形态解读的审美能力、组织能力、设计能力、分析判断能力等。

贵州大学918普通生物学二2020年考研专业课初试大纲
贵州大学硕士研究生招生考试大纲
科目代码及名称： 918普通生物学二
一、考试基本要求
本科目考试重点涉及细胞生物学、植物学、动物学、微生物学知识内容，兼有部分生态学的内容。

要求考生对细胞生物学理论体系的基本框架有一个比较全面的了解，掌握植物的结构和功能，掌握微生物的分离和培养、代谢，掌握动物的组织特点、器官的结构、系统的功能，了解生态学方面基础知识。

并能综合运用所掌握知识，在实践中进行运用。

2、适用范围
适用于生物类各专业
三、考试形式
闭卷，180分钟
四、考试内容和考试要求
1、普通生物学概述
教学要求：使学生明确学习本门课的目的、要求；了解生命的定义、生命的特征，生物界的层次，生物学与现代社会生活的关系。

2、细胞部分
(1).细胞的化学组成：大量元素、必需元素；植物矿质营养。

(2).生物大分子的类型及其代谢：糖类、脂类、蛋白质、核苷酸和核酸。

(3).生物膜的特性、细胞的连接类型及物质的跨膜运动。

1。

使用权、地役权。 （4）担保物权：概述、抵押权、质权、留置权。 （5）占有：概述、效力、保护、取得、消灭。 4、债法总论 （1）债的概述：概念、特点、要素、发生原因，债的分类。 （2）债的履行：债的履行原则、适当履行。 （3）债的保全和担保：代位权、撤销权、保证、定金。 （4）债的转移和消灭 5、债法分论 （1）合同概述：合同的概念、特征、分类。 （2）合同的订立：订立的程序、内容、解释、缔约过失责任。 （3）合同的履行：履行原则、同时履行抗辩权、先履行抗辩权、不安抗辩
（科目：法学综合二 代码：815）
一、考查目标 全日制攻读法学硕士学位入学考试（科目：法学综合二）考试内容包括民 法学、刑法学两门课程，要求考生系统掌握相关学科的基本知识、基础理论和 基本方法，并能运用相关理论和方法分析、解决民事、刑事案件中的实际问题。
二、考试形式和试卷结构 （一）试卷成绩及考试时间 本科目试卷满分 150 分，考试时间为 180 分钟。 （二）答题方式 答题方式为闭卷、笔试。 （三）试卷内容结构 各部分内容所占分值为： 民法学 约 75 分 刑法学 约 75 分 （四）试卷题型结构 名词解释题：8 小题，每小题 5 分，共 40 分 简答题：6 小题，每小题 10 分，共 60 分 分析论述题：2 小题，每小题 25 分，共 50 分
（1）刑法的空间效力：刑法空间效力的概念和原则、我国刑法的属地管辖 权、我国刑法的属人管辖、我国刑法的保护管辖权、我国刑法的普遍管辖权。
（2）刑法的时间效力：刑法生效与失效时间、刑法的溯及力、刑法时间效 力的法律适用。
4、犯罪概念与犯罪构成 （1）犯罪概念：犯罪概念的类型、我国刑法中的犯罪概念及基本特征 （2）犯罪构成：犯罪构成的历史沿革、犯罪构成的概念、犯罪构成的意义 5、犯罪客体 （1）犯罪客体的概念及其分类：犯罪客体的概念、我国刑法对犯罪客体的 规定方式、犯罪客体的分类。 （2）犯罪客体与犯罪对象：犯罪对象的概念、犯罪对象与犯罪客体的联系 与区别。 6、犯罪客观方面 （1）犯罪客观方面概述：犯罪客观方面的概念和特征、犯罪客观方面的要 件、犯罪客观方面的意义。 （2）危害行为：危害行为的概念和特征、危害行为的表现形式、不作为概 念及相关理论、危害行为及实行行为在犯罪构成中的地位和作用。 （3）危害结果：危害结果的概念和特征、危害结果的种类、危害结果的地 位。 （4）危害行为与危害结果之间的因果关系：因果关系的概念及特征、不作 为犯罪的因果关系问题、因果关系与刑事责任的联系和区别。 （5）犯罪的其他客观要件：时间、地点、方法对定罪、量刑的意义。 7、犯罪主体 （1）犯罪主体概述：犯罪主体的概念、犯罪主体的意义。 （2）刑事责任能力：刑事责任能力的概念、刑事责任能力的内容、刑事责 任能力的程度。 （3）与刑事责任能力有关的因素：刑事责任年龄概念及阶段划分、精神障 碍、生理功能丧失、生理醉酒。 （4）犯罪主体的特殊身份：犯罪主体特殊身份的概念、犯罪主体特殊身份

贵州大学硕士研究生入学考试大纲
考试科目代码/名称： 848/设计创作
一、考试基本要求
运用主题性创作内容来考察考生对工业设计知识的综合运用能力。

主要包
括考生的设计思维能力、设计分析与表达能力、设计程序与方法。

同时考察设
计中的创新能力，以及发现问题、分析问题与解决问题的能力。

2、适用范围
适用于设计学、工业设计工程专业
三、考试形式
闭卷，180分钟
四、考试内容和考试要求
（一）考试内容
根据提供的题目或素材，进行设计分析及表达。

（二）考试题型
主题性命题：
1、运用创新设计程序和方法，完成主题性设计。

确定设计理念与设计
定位、画出构思草图及效果表现图，并进行必要的说明。

2、对主题性创作内容进行设计分析与评价，包括设计概念、功能细节、
造型细节、结构细节、人机关系做出分析和判断。

（三）考试要求
要求考生系统地掌握设计的基础理论、基本知识和基本技能；设计表达与。

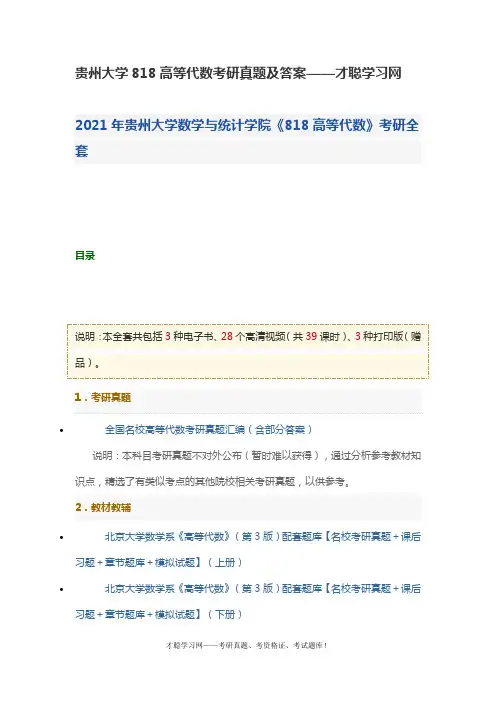
贵州大学818高等代数考研真题及答案——才聪学习网2021年贵州大学数学与统计学院《818高等代数》考研全套目录•全国名校高等代数考研真题汇编（含部分答案）说明：本科目考研真题不对外公布（暂时难以获得），通过分析参考教材知识点，精选了有类似考点的其他院校相关考研真题，以供参考。

2．教材教辅•北京大学数学系《高等代数》（第3版）配套题库【名校考研真题＋课后习题＋章节题库＋模拟试题】（上册）•北京大学数学系《高等代数》（第3版）配套题库【名校考研真题＋课后习题＋章节题库＋模拟试题】（下册）•北京大学数学系《高等代数》（第3版）网授精讲班【注：因第10章考试不做要求，所以老师没有讲解。

】【39课时】说明：以上为本科目参考教材配套的辅导资料。

•试看部分内容名校考研真题第6章线性空间一、选择题1．下面哪一种变换是线性变换（）．[西北工业大学研]A．B． C．【答案】C查看答案【解析】不一定是线性变换，比如则也不是线性变换，比如给而不是惟一的．2．在n维向量空间取出两个向量组，它们的秩（）．[西北工业大学研] A．必相等B．可能相等亦可能不相等C．不相等【答案】B查看答案【解析】比如在中选三个向量组(I)：0(Ⅱ)(Ⅲ)．若选（I）（II），秩秩（II），从而否定A，若选（Ⅱ）（Ⅲ），秩（Ⅲ）＝秩（Ⅱ），从而否定C，故选B．二、填空题1．若则V对于通常的加法和数乘，在复数域C上是______维的，而在实数域R上是_ _____维的．[中国人民大学研]【答案】2；4．查看答案【解析】在复数域上令；则是线性无关的．则此即证可由线性表出．在实数域上，令若，其中，则此即在R上线性关．可由线性表出，所以在实数域R上，有三、分析计算题1．设V是复数域上n维线性空间，V1和V2各为V的r1维和r2维子空间，试求之维数的一切可能值．[南京大学研]解：取的一组基，再取的一组基则＝秩2．设U是由生成的的子空间，W是由生成的的子空间，求（1）U＋W：（2）L∩W的维数与基底．[同济大学研]解：（1）令可得．所以由于为的一个极大线性无关组，因此又可得且，故为U＋W的一组基．（2）令因为秩＝3．所以齐次方程组①的基础解系由一个向量组成：再令，则故ζ为U∩W的一组基．3．设A是数域K上的一个m×n,矩阵，B是一个m维非零列向量．令（1）证明：W关于K n的运算构成K n的一个子空间；（2）设线性方程组AX＝B的增广矩阵的秩为r．证明W的维数dimW＝n－r ＋1：（3）对于非齐次线性方程组求W的一个基．[华东师范大学研]证明：（1）显然W≠，又因为存在t1，t2使Aα＝t1B，Aβ＝t2B．所以即kα＋lβ∈W，此说明W是K n的子空间．（2）对线性方程组（A，B）X n＋1＝0，由题设，其解空间V的维数为（n＋1）－r（A，B）＝n－r＋1．任取α∈W，存在t∈K，使所以是线性方程组（A，B）X n＋1＝0的解．。

贵州大学硕士研究生招生考试大纲
科目代码及名称： 828物理化学一
一、考试基本要求
本科目考试着重考核考生掌握物理化学课程的基本概念、基本思想、基本分析方法和基本理论的程度，要求考生对物理化学课程理论体系的基本框架有一个比较全面的了解，并能综合运用所学的基本原理解决化学反应过程中与热力学及动力学相关的科学问题。

2、适用范围
适用于化学相关专业
三、考试形式
闭卷，180分钟
四、考试内容和考试要求
1．导言
《物理化学》课程主要涉及化学热力学和化学动力学，探讨化学变化的方向和限度问题及化学反应的速度和机理问题。

课程要求学生掌握化学热力学基本原理及其在溶液、相平衡、化学平衡以及电化学中的应用、理解化学动力学、表面化学及胶体理论的基本知识与原理。

2．主要应试内容
化学热力学：
第 1 页共 3 页。

贵州师范大学全国硕士研究生入学考试大纲（科目：代码828 高等代数）第一部分考试说明本《高等代数》考试大纲适用于贵州师范大学数学与计算机科学学院数学专业硕士研究生入学考试。

高等代数是大学数学系本科学生的最基本课程之一，也是大多数理工科专业学生的必修基础课。

要求考生熟悉基本概念、掌握基本定理、有较强的运算能力和综合分析解决问题能力。

1考试目的《高等代数》是我校数学与计算机科学学院招收全日制硕士研究生而设置的具有选拔性质的入学考试科目，其目的是考察学生是否具备本学科各专业硕士研究生学习所要求的水平，为我校数学与计算机科学学院择优选拔硕士研究生提供依据。

2考试的基本要求1）要求考生比较系统地理解高等代数的基本概念和基本理论；2）掌握高等代数的基本思想和方法；3）要求考生具有抽象思维能力、逻辑推理能力、运算能力和综合运用所学的知识分析问题和解决问题的能力。

3考试形式和试卷结构1）答卷方式：闭卷，笔试；所列题目全部为必答题。

2）答题时间：180分钟。

3）试卷成绩：150分。

4）各部分的考查比例：多项式理论约10%行列式、线性方程组、矩阵约35%线性空间、线性变换约30%欧氏空间、二次型约15%综合题约10%5）题型：填空、计算、证明6）参考书目[1] 北京大学编《高等代数》，高等教育出版社，2003年7月第3版 .[2] 张禾瑞，郝鈵新，《高等代数》，高等教育出版社， 2007.第二部分考查内容（或知识点）1 多项式数域，多项式的带余除法及整除，最大公因式与互素多项式，因式分解与不可约多项式，重因式，多项式函数与根，复系数与实系数多项式的因式分解，艾森斯坦判别法及应用，一元多项式根与系数的关系及一元多项式有重根的判别式。

2 行列式、线性方程组、矩阵排列，行列式的定义及性质，行列式按一行（列）展开，代数余子式的计算，低阶行列式、高阶规律性较强的行列式计算。

消元法，n维向量空间，线性相关性，矩阵的秩，线性方程组有解判别定理，线性方程组解的结构。

硕士研究生入学考试《高等代数》考试大纲此《高等代数》考试大纲适用于中国科学院研究生院数学学科所有专业的硕士研究生入学考试。

高等代数是正规大学数学系本科学生的最基本课程之一，也是大多数理工科专业学生的必修基础课。

它的主要内容包括多项式、行列式和线性方程组、矩阵及其标准形、特征值和特征向量、线性变换和矩阵范数。

要求考生熟悉基本概念、掌握基本定理、有较强的运算能力和综合分析解决问题能力。

－、考试内容（一）多项式1．一元多项式的因式、带余除法公式及互素的概念及判别；2．复根存在定理；3．根与系数关系；4．Sturm定理。

（二）行列式和方程组1．行列式的置换、对换、置换奇偶性；2．行列式的定义，基本性质及计算；3．Vandermonde行列式；4．行列式的代数余子式、Cramer法则。

（三）矩阵1．矩阵基本运算、分块矩阵运算；2．初等矩阵、初等变换和矩阵的秩；3．矩阵的逆、伴随阵、线性方程组的矩阵形式；4．行列式乘积定理；5．矩阵和转置、Hermite共轭；6．对角阵、三角阵、三对角阵；7．矩阵的迹、方阵多项式；8．广义逆矩阵。

（四）线性方程组求解1．线性方程组有解的充分必要条件；2．Gauss消元法；3．三角分解。

（五）线性空间和线性变换；1．向量的线性相关和线性无关；2．线性空间的定义及性质；3．向量组的秩、线性空间的基及坐标；4．线性变换的矩阵表示；5．矩阵相似；6．不变子空间；7．子空间的直接和、维数公式；8．线性空间的同构。

（六）特征值和特征向量1．特征值和特征多项式；2．特征向量、特征子空间、度数和重数；3．非亏损矩阵的完全特征向量系和谱分解；4．特征值估计的圆盘定理；5．三对角矩阵的特征值与Sturm定理。

（七）内积空间和等积变换1．Euclid空间的标准正交基，施密特（Schmidt）正交化；2．Gram行列式；3．正交变换及其矩阵表示；4．初等旋转和镜像变换；5．QR分解；6．酉空间和酉变换；7．正交相似变换和酉相似变换；8．向量到子空间的距离、最小二乘。