人员 - 天津一中

2017天津市第一中学滨海学校招聘教师30人公告欢迎来到天津教师资格招聘考试网，中公天津教师招聘考试网是中国教师第一门户网站，提供历年中小学教师资格证、考试培训、面试辅导、最新教师考试讲座等全方位教师考试信息，预祝广大考生顺利。

为进一步拓宽选人用人渠道，确保我校2017年招聘工作顺利进行，依据《天津市事业单位公开招聘人员实施办法(试行)》(津人社局发〔2011〕10号)规定，特制定本实施方案。

一、学校简介天津一中滨海学校是滨海新区教育局直属的，由滨海新区教育局与天津一中强强联合开办的完中校。

学校定位为六年制完全中学，主要服务于滨海新区辖下七个区域。

学校总建筑面积7万平方米，分为教学区、宿舍区、运动区、休闲区四个功能区。

教学现代化设施齐全，全部教室配备了多媒体系统，心理咨询室、理化生实验室、美术教室、书法教室等功能教室。

学校在步入正轨后将设置60个教学班，其中初中18个班，高中42个班。

学校已于2016年9月正式启用。

天津市第一中学滨海学校将在秉承天津一中优良传统的基础上，与天津一中实现资源共享，积极创新，务实推进，努力打造滨海教育龙头，成为天津市基础教育的新高地。

天津市第一中学滨海学校坐落在滨海新区保税区空港经济区，毗邻天津医科大学总医院空港国际医院、SM购物商城、天津新燕莎奥特莱斯主题购物广场、天津欧贸中心等社会公共服务设施。

地理位置位于滨海新区距市区最近的地段，能够无缝衔接市区优质教育资源。

二、招聘原则坚持按需设岗、按岗招聘的原则;坚持公开公平、竞争择优的原则;坚持德才兼备、任人唯贤的原则。

三、招聘岗位及人数我校2017年拟招聘工作人员30名，其中语文、数学、英语各3名，物理4名，化学4名，地理、体育、信息技术、生物、历史、政治、通用技术、心理各1名，物理、化学、生物实验员各1名，德育教师2人。

四、招聘范围与对象在职相关岗位人员和全日制高校2017届毕业生。

五、报考条件(一)基本条件1.具有中华人民共和国国籍;2.拥护中华人民共和国宪法，遵守各项法律法规，具有良好的品行;3.热爱教育事业，热爱教师职业;4.具有正常履行职责的身体条件;5.具有全日制大学本科及以上学历和相应学位;6.学科教师具有相应学科高级中学及以上教师资格证;7.2017届毕业生年龄为30周岁以下(即1986年1月1日及以后出生);8.外省市人员需符合天津市人才引进政策;9.具有岗位要求的其他条件。

天津市第一中学学生留学，找谁办理靠谱？天津市第一中学是天津市教育委员会直属重点高级中学之一，是联合国教科文组织亚太地区“教育革新为发展服务计划”联系中心，是天津市第一位的窗口学校。

其前身是组建于 1947 年 9 月的天津市立中学。

1949 年天津解放后，更名为天津市第一中学，简称天津一中。

一中在学校建设方面，年年上台阶，相继建成宿舍楼、体育馆、游泳池、逸夫科教楼，学校建筑面积已达到 36540 平方米。

假山喷泉、亭台花廊、雕塑碑刻点缀其间，与奇花异木交相辉映。

漫步于一中校园，不仅能使人领略其新颖别致的花园式校园格局，而且能让人感受到她那浓郁的文化气息。

一中校园内仅有网球场旁的挂钟是当年用过的。

它目睹了一中的沧桑巨变。

现在一中的幽雅的学习环境，雄厚的师资力量，先进的教学设施，为学生成才创造了良好的条件。

天津一中现有藏书已达 8 万余册，理化生实验室 11 个，阶梯教室 2 个，精密实验室、标本室 5 个， 200 余平米的演播厅一个，电化多媒体教室 2 个，多媒体网络教室和演示教室、计算机网络教室各一间，均为最新机型设备。

新建的物理微机实验室利用计算机数模转换技术和自动化测量传感技术进行定量物理学实验，为我国中学首创。

学校现岗教师 218 人（含干部兼课），其中高级教师 80 人;特级教师 5 人;目前， 45 岁以下的具有本科学历的 98 人正在进行教育硕士研究生班的深造学习。

现我校具有研究生学历和具有研究生学力水平的教师占教师总数 60% ;一中的教师队伍坚持以师德为本，以学识为本，以教书育人为本，先后涌现出众多的教书育人的楷模，很多老师的事迹由天津日报、天津电视台、中央电视台等媒体报道，在社会上有很大影响。

一中的教育教学成果丰硕。

“育人为本，教学为主，全面发展，学有所长”是一中的办学宗旨。

特别是近几年来，在全面推进素质教育的伟大实践中，一中教师努力探索促进学生各方面发展的具体办法，根据教育部颁布的新课程计划，结合我校实际，坚持科研为先导，研究制定了包括必修棵、选修课、活动课在内的新课程体系，为全面提高学生素质提供了重要保证。

天津一中2024-2025-1 高一年级生物学学科期中质量调查试卷本试卷分为第Ⅰ卷(单项选择题)、第Ⅱ卷(非选择题)两部分，共100分，考试用时60分钟。

第Ⅰ卷 1至2页，第Ⅱ卷3至4页。

考生务必将答案写在答题卡规定的位置上，答在试卷上的无效。

祝各位考生考试顺利！第Ⅰ卷(本卷共25道题，每题2分，共50分)1. “竹外桃花三两枝，春江水暖鸭先知。

”这一千古名句生动形象地勾画出早春的秀丽景色。

下列与其相关的生命系统的叙述正确的是( )A. 桃花属于生命系统的器官层次B. 一片江水中的所有鱼构成一个种群C. 地球上最大的生态系统是海洋生态系统D. 江水等无机环境不参与生命系统的组成2. 下列叙述正确的是( )A. 没有细胞核的细胞一定是原核细胞B. 原核生物是单细胞生物，真核生物中既有单细胞生物也有多细胞生物C. 水绵、发菜、蘑菇、黑藻都是自养型生物，都有叶绿体D. 金黄色葡萄球菌、酵母菌、霉菌、乳酸菌都是细菌3.下列物质的鉴定实验中所用试剂与现象对应关系错误的是 ( )A. 还原糖-斐林试剂-砖红色B. 蛋白质-双缩脲试剂-蓝色C. 脂肪-苏丹Ⅲ染液-橘黄色D. 淀粉-碘液-蓝色4.水是生命的源泉，节约用水是每个人应尽的责任，下列有关水在生命活动中作用的叙述，错误的是( )A. 水是酶促反应的环境B. 参与血液中缓冲体系的形成C. 可作为维生素D等物质的溶剂D. 可作为反应物参与生物化学反应过程5.香蕉可作为人们运动时的补给品，所含以下成分中，不能被吸收利用的是( )A.纤维素B.钾离子C.葡萄糖D.水6. 苯丙酮尿症患者早期确诊后，可及时采取严格限制高蛋白食物摄入的饮食策略辅助治疗。

为验证该策略的有效性进行了相关研究，下表为研究过程中患者体内几种矿质元素含量的检测结果。

下列分析正确的是( )组别锌(μmol/L)铁(μmol/L)钙( mmol/L)镁 ( mmol/L)铜(μmo/L)实验组70.58±1.537.38±1.20 1.68±0.17 1.65±0.1721.77±3.97对照组78.61±0.907.75±0.95 1.72±0.17 1.48±0.2020.04±5.29A. 表中检测的5种元素均为微量元素B. 实验组不限制高蛋白食物摄入，对照组限制高蛋白食物摄入C. 表中结果说明高蛋白食物的摄入会影响患者体内矿质元素的含量D. 人体血液中必须含有一定量的Ca²⁺，但Ca²⁺的含量过高会引起抽搐7.组成下列多聚体的单体的种类最多的是 ( )A.血红蛋白B. DNAC.淀粉D.纤维素8. 下列选项中，均含磷元素的一组是( )A. DNA 和磷脂B. 脂质和血红蛋白C. 纤维素和核糖D. 葡萄糖和氨基酸9.范仲淹的《江上渔者》云:“江上往来人，但爱鲈鱼美。

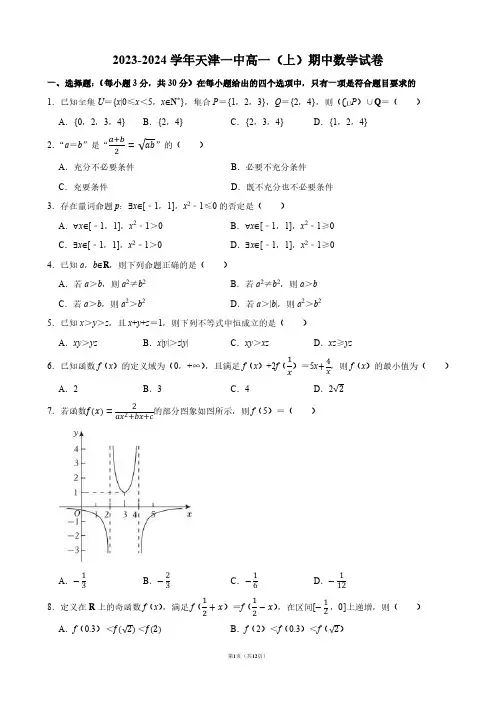
2023-2024学年天津一中高一（上）期中数学试卷一、选择题：（每小题3分，共30分）在每小题给出的四个选项中，只有一项是符合题目要求的1．已知全集U＝{x|0≤x＜5，x∈N*}，集合P＝{1，2，3}，Q＝{2，4}，则（∁U P）∪Q＝（）A．{0，2，3，4}B．{2，4}C．{2，3，4}D．{1，2，4}2．“a＝b”是“a+b2=√ab”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件3．存在量词命题p：∃x∈[﹣1，1]，x2﹣1≤0的否定是（）A．∀x∈[﹣1，1]，x2﹣1＞0B．∀x∈[﹣1，1]，x2﹣1≥0 C．∃x∈[﹣1，1]，x2﹣1＞0D．∃x∈[﹣1，1]，x2﹣1≥0 4．已知a，b∈R，则下列命题正确的是（）A．若a＞b，则a2≠b2B．若a2≠b2，则a＞bC．若a＞b，则a2＞b2D．若a＞|b|，则a2＞b25．已知x＞y＞z，且x+y+z＝1，则下列不等式中恒成立的是（）A．xy＞yz B．x|y|＞z|y|C．xy＞xz D．xz≥yz6．已知函数f（x）的定义域为（0，+∞），且满足f（x）+2f（1x ）＝5x+4x，则f（x）的最小值为（）A．2B．3C．4D．2√27．若函数f(x)=2ax2+bx+c的部分图象如图所示，则f（5）＝（）A．−13B．−23C．−16D．−1128．定义在R上的奇函数f（x），满足f（12+x）＝f（12−x），在区间[−12，0]上递增，则（）A．f（0.3）＜f(√2)＜f(2)B．f（2）＜f（0.3）＜f（√2）C ．f （0.3）＜f （2）＜f （√2）D ．f （√2）＜f （2）＜f （0.3）9．已知a ，b ∈R ，若√4a 2+b 2⋅√a 2+4b 2a 2+b2的最大值为m ，且不等式x 2﹣ax +b ＜0的解集为（1，2m ），则a +b ＝（ ） A ．3B ．43C ．7D ．1110．定义区间长度m 为这样的一个量：m 的大小为区间右端点的值减去区间左端点的值，若关于x 的不等式x 2﹣ax ﹣6a ＜0有解，且解集的区间长度不超过5个单位长，则a 的取值范围是（ ） A ．（﹣∞，25]∪[1，+∞） B ．[﹣25，﹣24）∪（0，1] C ．[﹣25，0）∪（1，24） D ．[﹣25，1]二、填空题：（每小题4分，共24分） 11．已知函数f(x)=√2+x 1√16−x 的定义域为 ．12．已知命题p ：x ＞m ，q ：2+x ﹣x 2＜0，如果命题p 是命题q 的充分不必要条件，则实数m 的取值范围是 ．13．某班共48人，其中25人喜爱篮球运动，20人喜爱乒乓球运动，16人对这两项运动都不喜爱，则既喜爱篮球运动又喜爱乒乓球运动的人数为 ．14．已知函数f(x)={x +3，x ≤0√x ，x ＞0，若f （a ﹣3）＝f （a +2），则f （a ）＝ ．15．已知函数f(x)={x 2−(a +4)x +5，x ＜2(2a −3)x ，x ≥2在R 上单调递减，则实数a 的取值范围为 ．16．定义在R 上的函数f （x ）满足f （﹣x ）＝f （x ），且当x ≥0时，f （x ）={−x 2+1，0≤x ＜11−x ，x ≥1，若对任意的x ∈[m ，m +1]，不等式f （1﹣x ）≤f （x +m ）恒成立，则实数m 的最大值为 ． 三、解答题：（本题共4小题，共46分）解答应写出文字说明、证明过程或演算步骤. 17．（10分）已知集合A ＝{x |x 2﹣2x ＝0}，B ＝{x |x 2+（m ﹣1）x ﹣m 2+1＝0} （1）若A ∩B ＝{2}，求实数m 的取值范围； （2）若A ∩B ＝B ，求实数m 的取值范围． 18．（12分）已知a ＞0，b ＞0，2a +b ＝2． （1）求b a +4b的最小值；（2）求4a 2+8ab +b 2的最大值． 19．（12分）已知函数f(x)=x 2+2x．（1）求f（1），f（2）的值；（2）判断函数f（x）在区间（1，+∞）的单调性并证明；（3）若不等式f(x−1)≥2(x−1)+2x−1+m对一切x∈[1，6]恒成立，求实数m的取值范围．20．（12分）已知函数f(x)=x+1−aa−x(x∈R且x≠a）．（1）求f（x）+f（2a﹣x）的值；（2）当函数f（x）的定义域为[a+12，a+1]时，求f（x）的值域；（3）设函数g（x）＝x2+|（x﹣a）f（x）|，求g（x）的最小值．2023-2024学年天津一中高一（上）期中数学试卷参考答案与试题解析一、选择题：（每小题3分，共30分）在每小题给出的四个选项中，只有一项是符合题目要求的1．已知全集U＝{x|0≤x＜5，x∈N*}，集合P＝{1，2，3}，Q＝{2，4}，则（∁U P）∪Q＝（）A．{0，2，3，4}B．{2，4}C．{2，3，4}D．{1，2，4}解：因为U＝{x|0≤x＜5，x∈N*}＝U＝{1，2，3，4}，所以（∁U P）∪Q＝{4}∪{2，4}＝{2，4}．故选：B．2．“a＝b”是“a+b2=√ab”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件解：a＝b＜0时，a+b2=√ab不成立，“a＝b”不是“a+b2=√ab”的充分条件；a+b2=√ab时，有a≥0且b≥0，a+b−2√ab=0，即(√a−√b)2=0，得a＝b，故“a＝b”是“a+b2=√ab”的必要条件；所以“a＝b”是“a+b2=√ab”的必要不充分条件．故选：B．3．存在量词命题p：∃x∈[﹣1，1]，x2﹣1≤0的否定是（）A．∀x∈[﹣1，1]，x2﹣1＞0B．∀x∈[﹣1，1]，x2﹣1≥0 C．∃x∈[﹣1，1]，x2﹣1＞0D．∃x∈[﹣1，1]，x2﹣1≥0解：命题是特称命题，则命题的否定是：∀x∈[﹣1，1]，x2﹣1＞0．故选：A．4．已知a，b∈R，则下列命题正确的是（）A．若a＞b，则a2≠b2B．若a2≠b2，则a＞bC．若a＞b，则a2＞b2D．若a＞|b|，则a2＞b2解：对于A，当a＝﹣b时，如a＝2，b＝﹣2时a2＝b2成立，故A错误；对于B，当a＝1，b＝2，显然a2≠b2，但a＜b，故B错误；对于C，当a＝2，b＝﹣3时，显然a＞b，但a2＜b2，故C错误；对于D，a＞|b|，则a2＞|b|2＝b2，故D正确．故选：D．5．已知x＞y＞z，且x+y+z＝1，则下列不等式中恒成立的是（）A．xy＞yz B．x|y|＞z|y|C．xy＞xz D．xz≥yz解：当x＝2，y＝0，z＝﹣1时，不等式xy＞yz，x|y|＞z|y|，xz≥yz均不成立，故选项A、B、D错误；因为x＞y＞z，且x+y+z＝1，所以x＞0，所以xy＞xz，故选项C正确．故选：C．6．已知函数f（x）的定义域为（0，+∞），且满足f（x）+2f（1x ）＝5x+4x，则f（x）的最小值为（）A．2B．3C．4D．2√2解：由f（x）+2f（1x ）＝5x+4x，取x=1x，则f（1x）+2f（x）=5x+4x，联立解得f（x）＝x+2x，x∈（0，+∞）．∴f（x）＝x+2x≥2√x⋅2x=2√2，当且仅当x=2x，即x=√2时等号成立．∴f（x）的最小值为2√2．故选：D．7．若函数f(x)=2ax2+bx+c的部分图象如图所示，则f（5）＝（）A．−13B．−23C．−16D．−112解：根据题意，函数f(x)=2ax2+bx+c，由函数的图象，其定义域为{x|x≠2且x≠4}，在区间（2，4）上，f（x）＞0，且当x＝3时，f（x）取得最小值1，在区间（﹣∞，2）和（4，+∞）上，f（x）＜0，设g（x）＝ax2+bx+c，则g（x）＝0的两个零点为2和4，必有a＜0，且当x＝3时，g（x）取得最大值2，则有{−ba =2+4=6c a =2×4=89a +3b +c =2，解可得{a =−2b =12c =−16，则f （x ）=2−2x 2+12x−16=−1x 2−6x+8， 则f （5）=−13．故选：A ．8．定义在R 上的奇函数f （x ），满足f （12+x ）＝f （12−x ），在区间[−12，0]上递增，则（ ）A ．f （0.3）＜f(√2)＜f(2)B ．f （2）＜f （0.3）＜f （√2）C ．f （0.3）＜f （2）＜f （√2）D ．f （√2）＜f （2）＜f （0.3）解：定义在R 上的奇函数f （x ），满足f （12+x ）＝f （12−x ），可得f （x ）的图象关于直线x =12对称，由f （﹣x ）＝﹣f （x ），f （﹣x ）＝f （x +1）， 可得f （x +2）＝﹣f （x +1）＝f （x ）， 即f （x ）的周期为2，奇函数f （x ）在区间[−12，0]上递增，可得f （x ）在（0，12）递增，由f （x ）的图象关于直线x =12对称，可得f （x ）在（12，1）递减，即有f （12）＞f （0）＝0，f （−12）＜0，f （0.3）＞0，即有f （2）＝f （0）＝0，f （√2）＝f （1−√2）＜0， 可得f （√2）＜f （2）＜f （0.3）， 故选：D ．9．已知a ，b ∈R ，若√4a 2+b 2⋅√a 2+4b 2a 2+b2的最大值为m ，且不等式x 2﹣ax +b ＜0的解集为（1，2m ），则a +b ＝（ ） A ．3B ．43C ．7D ．11解：根据不等式xy ≤x 2+y 22可得√4a 2+b 2⋅√a 2+4b 2≤4a 2+b 2+a 2+4b 22=52(a 2+b 2)，当且仅当4a 2+b 2＝a 2+4b 2，即a 2＝b 2时等号成立， 所以，√4a 2+b 2⋅√a 2+4b 2a 2+b 2≤52，所以m =52．所以，不等式x2﹣ax+b＜0的解集为（1，5）．根据一元二次不等式的解集与一元二次方程解的关系可知，1和5是方程x2﹣ax+b＝0的两个解，由根与系数的关系知{1+5=a1×5=b，解得{a=6b=5，所以a+b＝11．故选：D．10．定义区间长度m为这样的一个量：m的大小为区间右端点的值减去区间左端点的值，若关于x的不等式x2﹣ax﹣6a＜0有解，且解集的区间长度不超过5个单位长，则a的取值范围是（）A．（﹣∞，25]∪[1，+∞）B．[﹣25，﹣24）∪（0，1]C．[﹣25，0）∪（1，24）D．[﹣25，1]解：∵关于x的不等式x2﹣ax﹣6a＜0有解，∴Δ＝a2+24a＞0，解得a＞0或a＜﹣24．由x2﹣ax﹣6a＝0解得．x1=a−√△2，x2=a+√△2∵x1＜x2，∴不等式解集为（x1，x2），∵解集的区间长度不超过5个单位长x2﹣x1≤5，解得﹣25≤a≤1，∵a＞0或a＜﹣24，∴﹣25≤a＜﹣24或0＜a≤1．故选：B．二、填空题：（每小题4分，共24分）11．已知函数f(x)=√2+x√16−x2的定义域为[﹣2，4）．解：由题意得函数f(x)=√2+x1√16−x2要有意义，需满足{2+x≥016−x2＞0，解得﹣2≤x＜4，即函数f(x)=√2+x1√16−x2的定义域为[﹣2，4）．故答案为：[﹣2，4）．12．已知命题p：x＞m，q：2+x﹣x2＜0，如果命题p是命题q的充分不必要条件，则实数m的取值范围是[2，+∞）．解：不等式2+x﹣x2＜0，即x2﹣x﹣2＞0，解得x＜﹣1或x＞2．设A＝{x|x＞m}，B＝{x|x＜﹣1或x＞2}，由命题p是命题q的充分不必要条件，可知A⫋B，所以有m≥2，即实数m的取值范围是[2，+∞）．故答案为：[2，+∞）．13．某班共48人，其中25人喜爱篮球运动，20人喜爱乒乓球运动，16人对这两项运动都不喜爱，则既喜爱篮球运动又喜爱乒乓球运动的人数为 13 ．解：某班共48人，其中25人喜爱篮球运动，20人喜爱乒乓球运动，16人对这两项运动都不喜爱， 设两项运动都喜欢的人数为x ，作出维恩图，可得：25﹣x +x +20﹣x +16＝48，解得x ＝13， 则既喜爱篮球运动又喜爱乒乓球运动的人数为13． 故答案为：13．14．已知函数f(x)={x +3，x ≤0√x ，x ＞0，若f （a ﹣3）＝f （a +2），则f （a ）＝ √2 ．解：当a +2≤0，即a ≤﹣2时，则由f （a ﹣3）＝f （a +2）可得，a ＝a +5，无解； 当a ﹣3≤0，且a +2＞0，即﹣2＜a ≤3时，由f （a ﹣3）＝f （a +2）可得，a =√a +2，所以a ＞0， 整理可得，a 2﹣a ﹣2＝0，解得a ＝﹣1（舍去）或a ＝2； 当a ﹣3＞0，即a ＞3时，由f （a ﹣3）＝f （a +2）可得，√a −3=√a +2，无解． 综上所述，a ＝2． 所以，f(a)=f(2)=√2． 故答案为：√2．15．已知函数f(x)={x 2−(a +4)x +5，x ＜2(2a −3)x ，x ≥2在R 上单调递减，则实数a 的取值范围为 [0，76] ．解：函数f(x)={x 2−(a +4)x +5，x ＜2(2a −3)x ，x ≥2在R 上单调递减，则{2a −3＜0a+42≥24−2(a +4)+5≥2(2a −3)，解得0≤a ≤76，即实数a 的取值范围为[0，76]．故答案为：[0，76]．16．定义在R 上的函数f （x ）满足f （﹣x ）＝f （x ），且当x ≥0时，f （x ）={−x 2+1，0≤x ＜11−x ，x ≥1，若对任意的x ∈[m ，m +1]，不等式f （1﹣x ）≤f （x +m ）恒成立，则实数m 的最大值为 −13．解：因为 f （﹣x ）＝f （x ），x ∈R ，所以函数f （x ）为偶函数， 又当x ⩾0时，f （x ）={−x 2+1，0≤x ＜11−x ，x ≥1是减函数，所以不等式 f （1﹣x ）⩽f （x +m ），等价于不等式 f （|1﹣x |）⩽f （|x +m |）， 即|1﹣x |⩾|x +m |，平方化简得 2（m +1）x ⩽1﹣m 2， 当m +1＝0时，x ∈R ，符合题意，所以m ＝﹣1； 当m +1＞0，即 m ＞﹣1时 ，x ⩽1−m2，又x ∈[m ，m +1]， 所以 m +1⩽1−m 2，解得 m ⩽−13，所以−1＜m ⩽−13； 当m +1＜0，即m ＜﹣1 时，x ⩾1−m2，又x ∈[m ，m +1]， 所以m ⩾1−m 2，解得m ⩾13，这与m ＜﹣1矛盾，舍去． 综上，−1⩽m ⩽−13，因此实数 m 的最大值是 −13．三、解答题：（本题共4小题，共46分）解答应写出文字说明、证明过程或演算步骤. 17．（10分）已知集合A ＝{x |x 2﹣2x ＝0}，B ＝{x |x 2+（m ﹣1）x ﹣m 2+1＝0} （1）若A ∩B ＝{2}，求实数m 的取值范围； （2）若A ∩B ＝B ，求实数m 的取值范围．解：（1）因为A ＝{x |x 2﹣2x ＝0}＝{0，2}，由A ∩B ＝{2}可得2∈B ， 则22+2（m ﹣1）﹣m 2+1＝0， 化简可得m 2﹣2m ﹣3＝0， 解得m ＝﹣1或m ＝3，当m ＝﹣1时，x 2+（m ﹣1）x ﹣m 2+1＝0⇒x 2﹣2x ＝0，则B ＝{0，2}，此时A ∩B ＝{0，2}，不满足题意； 当m ＝3时，x 2+（m ﹣1）x ﹣m 2+1＝0⇒x 2+2x ﹣8＝0，则B ＝{4，2}，此时A ∩B ＝{2}，满足题意； 所以m ＝3．（2）由A ∩B ＝B 可得，B ⊆A ，当B ＝∅时，Δ＝（m ﹣1）2+4（m 2﹣1）＜0， 化简可得5m 2﹣2m ﹣3＜0，解得−35＜m ＜1；当B为单元素集合时，Δ＝（m﹣1）2+4（m2﹣1）＝0，解得m=−35或m＝1，当m=−35时，x2+(m−1)x−m2+1=0⇒x2−85x+1625=0，解得x=45，即B={45}，不满足B⊆A；当m＝1时，x2+（m﹣1）x﹣m2+1＝0⇒x2＝0，解得x＝0，即B＝{0}，满足B⊆A；当B为双元素集合时，则其两个元素分别是0，2，由韦达定理得{Δ=(m−1)2+4(m2−1)＞0−(m−1)=0+2−m2+1=0×2，解得m＝﹣1，此时x2+（m﹣1）x﹣m2+1＝0⇒x2﹣2x＝0，即B＝{0，2}，满足B⊆A，综上所述，m∈(−35，1]∪{1}．18．（12分）已知a＞0，b＞0，2a+b＝2．（1）求ba +4b的最小值；（2）求4a2+8ab+b2的最大值．解：（1）a＞0，b＞0，2a+b＝2，所以ba+4b=ba+2(2a+b)b=ba+4ab+2≥2√ba⋅4ab+2=6，当且仅当ba=4ab且2a+b＝2，即a=12，b＝1时等号成立，故ba+4b的最小值为6．（2）由2a+b=2≥2√2ab，得ab≤12，当且仅当2a＝b且2a+b＝2，即a=12，b＝1时等号成立，4a2+8ab+b2=(2a+b)2+4ab=4+4ab≤4+4×12=6，故4a2+8ab+b2的最大值为6．19．（12分）已知函数f(x)=x2+2x．（1）求f（1），f（2）的值；（2）判断函数f（x）在区间（1，+∞）的单调性并证明；（3）若不等式f(x−1)≥2(x−1)+2x−1+m对一切x∈[1，6]恒成立，求实数m的取值范围．解：（1）f(x)=x2+2x，则f（1）＝1+2＝3，f（2）＝4+1＝5．（2）函数f（x）在区间（1，+∞）的单调递增，证明如下：任取1＜x1＜x2，则f(x1)−f(x2)=x12+2x1−(x22+2x2)=(x12−x22)+(2x1−2x2)=(x1−x2)(x1+x2−2x1x2)，由1＜x1＜x2，得x1﹣x2＜0，x1+x2＞2，x1x2＞1，2x1x2＜2，x1+x2−2x1x2＞0，则f（x1）﹣f（x2）＜0，即f（x1）＜f（x2），所以函数f（x）在区间（1，+∞）的单调递增．（3）不等式f(x−1)≥2(x−1)+2x−1+m，即（x﹣1）2﹣2（x﹣1）≥m，依题意有（x﹣1）2﹣2（x﹣1）≥m对一切x∈[1，6]恒成立，（x﹣1）2﹣2（x﹣1）＝（x﹣1）2﹣2（x﹣1）+1﹣1＝（x﹣2）2﹣1，由1≤x≤6，得﹣1≤x﹣2≤4，0≤（x﹣2）2≤16，﹣1≤（x﹣2）2﹣1≤15，则有﹣1≥m，实数m的取值范围（﹣∞，﹣1]．20．（12分）已知函数f(x)=x+1−aa−x(x∈R且x≠a）．（1）求f（x）+f（2a﹣x）的值；（2）当函数f（x）的定义域为[a+12，a+1]时，求f（x）的值域；（3）设函数g（x）＝x2+|（x﹣a）f（x）|，求g（x）的最小值．解：（1）已知函数f(x)=x+1−aa−x(x∈R且x≠a）．则f(x)+f(2a−x)=x+1−aa−x+2a−x+1−aa−2a+x=x+1−aa−x+a−x+1x−a=x+1−a−a+x−1a−x=−2．（2）f(x)=1−(a−x)a−x=−1+1a−x，由a+12≤x≤a+1，有−a−1≤−x≤−a−1 2，得−1≤a−x≤−1 2，则有−2≤1a−x≤−1，可得−3≤−1+1a−x≤−2，所以f（x）值域为[﹣3，﹣2]．（3）由题意，函数g（x）＝x2+|（x﹣a）f（x）|，所以g（x）＝x2+|x+1﹣a|（x≠a），①当x≥a﹣1且x≠a时，g(x)=x2+x+1−a=(x+12)2+34−a，如果a−1≥−12，即a≥12时，g(x)min=g(a−1)=(a−1)2；如果a−1＜−12，即a＜12且a≠−12时，g(x)min=g(−12)=34−a；如果a=−12时，g（x）无最小值．②当x＜a﹣1时，g(x)=x2−x−1+a=(x−12)2+a−54；如果a−1＞12，即a＞32时，g(x)min=g(12)=a−54；如果a−1≤12，即a≤32时，g(x)min=g(a−1)=(a−1)2，当a＞32时，(a−1)2−(a−54)=(a−32)2＞0，当a＜12时，(a−1)2−(34−a)=(a−12)2＞0，综上所述，当a＜12且a≠−12时，g（x）的最小值是34−a；当12≤a≤32时，g（x）的最小值是（a﹣1）2；当a＞32时，g（x）的最小值是a−54；当a=−12时，g（x）无最小值．。

在数学活动中感悟数学的魅力—天津一中新课标数学活动课简介天津一中袁爽各位老师大家好，我是天津一中八年级数学教师袁爽，非常荣幸在这里代表天津市、代表一中学校谈一谈我们在过去的近两年时间里在实施新课程改革的过程中对数学活动课教学的一些体会和做法。

和全国的同行们交流探讨，希望老师们多提宝贵意见。

数学新课程标准》试验教科书中，在每一章的结尾都安排了“活动课”的教学内容，这和以前教科书有着很大区别。

对所有老师来说，合理安排这部分内容的教学，切实地领会和落实编写的意图，使得学生通过活动课的学习与实践，取得最大的收获，是我们在教学中认真思考的课题。

近两年，天津市新课程改革已经全面展开,数学活动课的设置体现了新课标所提出的理念。

落实数学活动课的教学，是我们在课程改革中遇到的一个新问题。

数学实践活动课,顾名思义为:数学+实践活动.是用数学的思想与方法指导的实践活动。

活动是形式,是以数学内容的载体，通过数学活动，让学生动手做，动脑想，引导学生学会用所学的数学思想和方法去观察、分析、研究问题，数学实践活动课有助于激发学生学习数学的兴趣,培养创新意识和创新能力。

新课标规定数学课程的四个领域中，教科书对实践活动领域没有独立设置的章节，而且大多内容与考试关系不大，但为了学生长远的发展，为了激发学生学习数学的兴趣，提高学生的数学素质，我们对活动课的教学做了初步的尝试，进行了有益的探索与实践。

教学中，我们精心设计和安排了每一节活动课，我们认为：通过学生亲自动手活动，给学生提供重复人类数学发现过程的机会，使学生体会怎样为解决实际问题建立数学模型，是从具体到抽象，从特殊到一般的人类活动轨迹。

通过学生参加数学活动，为他们实现知识的再发现、再创造提供平台，激活每个学生数学发展的潜能。

因为活动课的安排，我们没有经验可循，所以一切都靠自己摸索，而天津一中敢为人先的精神激励着我们不断更新理念，不断创新。

教学实践中，我们进行集体备课，认真准备一节活动课，为上好一节活动课需要反复的试验，往往要花费几倍的时间和经历。

天津一中信息（2011年第17期）总第88期天津一中校务办公室2011年9月21日★天津一中以“忠诚党的教育事业，落实教育规划纲要”为主题召开庆祝第27届教师节暨表彰大会我校庆祝第27届教师节暨表彰大会于2011年9月9日下午15：50分在大报告厅举行。

大会由傅婕副校长主持，霍晓宏书记宣读了表彰名单。

名单显示天津一中一年来受到市区级表彰包括市级德育工作特色校、市教育系统、和平区先进党组织16项荣誉称号，孙建昆等111名在援疆、党建、教育、教学工作等方面的先进个人受到表彰。

在会上于沛泳老师代表全体教职员工表示：“要不断加强师德修养，在教书育人的具体工作中用诚信、责任、服务、协作、公道的人格魅力感染学生，为培养留有一中印记的学生奉献毕生力量。

”李新校长代表党总支、校行政在大会上讲话，他首先“向全体教职工致以节日的亲切问候和热烈祝贺，对一年来为学校各项工作的圆满完成做出巨大努力的老师们、同志们表示最衷心地感谢。

”他号召全体教职员工“要从为国育才的高度增强使命感和责任感，继续发扬敬业、爱生、奉献的精神，不负党和人民的重托、回报社会各界的厚爱。

用百倍的努力，以特色发展创先争优的新成绩向明年10月天津一中建校65周年献礼。

”庆祝大会后，老师们欣赏了由各工会小组排演的文艺节目。

华灯初上时，一中校园到处欢声笑语，喜气洋洋，老师们放声高歌把庆祝活动推向高潮。

★中共天津一中总支大会召开2011—2012学年度中共天津一中总支大会于9月13日下午3：50在大报厅召开。

大会由三项内容一是：霍晓宏书记领读中共中央总书记胡锦涛同志在庆祝中国共产党成立90周年大会上的重要讲话。

二是：宣布了新当选的各分支书记名单。

三是：部署本学年总支工作。

在重温党章后，霍书记再次强调指出：一中党建工作要围绕高中特色建设和庆祝建校六十五周年开展，创先争优要立足本岗，一个党员就是一面旗臶，在教育教学、管理服务中体现党员的先锋模范作用。

★我校下大力气整合校内外力量确保师生安全，学校平安！“王泽群问题”已成为长期困扰我校平安校园建设的棘手问题和安全隐患，我校已就其数十次到一中缠访滋事情况向上级有关部门报告、并积极寻求各级公安机关帮助解决。

天津市第一中学2023-2024学年高一上学期期末质量检测物理试卷本试卷分为第Ⅰ卷(选择题)、第Ⅱ卷(非选择题)两部分，共100分，考试用时60分钟。

第Ⅰ卷1至2页，第Ⅱ卷3至4页。

考生务必将答案涂写答题纸或答题卡的规定位置上，答在试卷上的无效。

祝各位考生考试顺利！第Ⅰ卷一、单项选择题（每小题只有一个正确答案）1. 牛顿在《自然哲学的数学原理》（1687年出版）中提出：“物体受外力作用后，将沿着外力的直线方向发生变化，且变化和所受外力成正比。

”对一个运动的质点，以下说法正确的是（ ）A. 如果质点受到恒定的合外力作用，一定做直线运动B. 如果质点受到变化的合外力作用，一定做曲线运动C. 如果质点受到总是与速度方向相同的合外力作用，一定做匀加速直线运动D. 如果质点受到总是与速度方向垂直的合外力作用，一定做速率不变的运动2. 如图所示，物体在与水平成θ角的拉力F 作用下，在水平面上做加速度大小为a 的匀加速直线运动。

如果改用力代替力F ，沿水平方向拉物体，则该物体的加速度大小为，那么比较a 与的大小关系，以下说法正确的是（ ）A. 一定等于aB. 一定小于aC. 可能小于aD. 可能大于a3. 如图所示，总质量为200kg 热气球，从地面由静止开始竖直上升时的加速度为，当热气球上升到225m 时，开始以5m/s 的速度向上匀速运动。

假设在运动过程中热气球总质量不变，所受浮力保持不变，所受空气阻力随速度增大而增大，重力加速度。

关于热气球在运动中的受力情况，以下说法正确的是（ ）的cos F F θ'=a 'a 'a 'a 'a 'a '20.5m/s 210m/s =gA. 运动过程中所受浮力大小为2100NB. 加速上升过程中所受空气阻力大小不变C. 加速上升过程一共需要用时30sD. 匀速上升时所受空气阻力大小为200N4. 有一种娱乐项目，在小孩的腰间左右两侧系上弹性极好的橡皮绳，小孩可在橡皮绳的作用下在竖直方向上下跳跃。

天津一中校园植物调查天津一中刘宝玉校园绿化及园林景观对改善校园局部气候、创造良好的科学文化氛围和促进学生身心健康发展具有不可替代的独特作用[1，2]。

60多年来，天津一中这片沃土，培养了数以万计的优秀人才，这自然与一中优越的育人环境密不可分。

除了无数优秀教师和优秀学生共同筑就的人文环境、科学环境之外；无数绿叶和红花则为学子的身心发展创造的优美的生态环境。

自2003年新校舍建成以来，学校更是根据自身特点，遵循因地制宜的原则，种植了大量的植物，提高了校园植物物种多样性，使其生态功能和配置更完善。

1调查意义本次校园植物种类普查及植物名录的编写主要目的是掌握一中校园植物的种类、数量及分布，为我校生物学教学、普及生物学知识奠定基础，也为今后为校园植物挂牌、引进新的植物物种提供理论依据。

2 调查方法根据校园自然分区，逐一对植物的种类、栽培地点和生长状况进行调察，数码摄影并采集标本，借助工具书[3~4]鉴定植物种类，最后编制天津一中校园植物名录（见表1）。

3 调查结果天津一种校园植物涉及裸子植物门和被子植物门，总计约28个科，43种植物。

其中裸子植物2科，2种；被子植物26科，41种，其中绝大多数为双子叶植物（单子叶植物多为草本，多数未做统计）。

表1 天津一中校园植物名录科属中文名学名(拉丁名)木犀科女贞属女贞Ligustrum lucidum Ait.小蜡Ligustrum sinense Lour.丁香属花叶丁香Syringa × persica L.梣属白蜡树Fraxinus chinensis Roxb.蔷薇科苹果属苹果Malus pumila Mill.西府海棠Malus micromalus Makino桃属碧桃Amygdalus persica L. var. persica f.duplex Rehd.珍珠梅属珍珠梅Sorbaria sorbifolia (L.) A. Br.李属紫叶李Prunus cerasifera Ehrhart f. atropurpurea (Jacq.) Rehd.蔷薇属月季花Rosa chinensis Jacq.樱属东京樱花Cerasus yedoensis (Mats.) Yüet Li梨属秋子梨Pyrus ussuriensis Maxim.山楂属山楂Crataegus pinnatifida Bge.豆科槐属槐Sophora japonica L.龙爪槐Sophora japonica L. var. japonica f.pendula Hort.刺槐属刺槐Robinia pseudoacacia L.紫荆属紫荆Cercis chinensis Bunge皂荚属皂荚Gleditsia sinensis Lam.续表科属中文名学名(拉丁名) 杨柳科杨属毛白杨Populus tomentosa Carr.钻天杨Populus nigra L. var. italica (Moench)Koehne小檗科小檗属紫叶小檗var. atropurpurea Chenault.锦葵科木槿属木槿Hibiscus syriacus L.千屈菜科紫薇属紫薇Lagerstroemia indica L.无患子科栾树属栾树Koelreuteria paniculata Laxm.漆树科漆树属火炬树Rhus typhina L.苦木科臭椿属臭椿Ailanthus altissima (Mill.) Swingle芸香科花椒属花椒Zanthoxylum bungeanum Maxim.柿树科柿属柿Diospyros kaki Thunb.茄科辣椒属辣椒Capsicum annuum L.五加科鹅掌柴属鹅掌柴Schefflera octophylla (Lour.) Harms忍冬科荚蒾属珊瑚树Viburnum odoratissinum Ker.-Gawl.梧桐科梧桐属梧桐Firmiana platanifolia (L. f.) Marsili石榴科石榴属石榴Punica granatum L.豆科合欢属合欢Albizia julibrissin Durazz.悬铃木科悬铃木属二球悬铃木Platanus ×acerifolia (Ait.) Willd.葡萄科地锦属五叶地锦Parthenocissus quinquefolia (L.) Planch.鼠李科枣属枣Ziziphus jujuba Mill.棕榈科刺葵属槟榔竹Phoenix canariensis百合科丝兰属凤尾兰Yucca gloriosa L.美人蕉科美人蕉属美人蕉Canna indica L.苏铁科苏铁属苏铁Cycas revoluta Thunb.银杏科银杏属银杏Ginkgo biloba L.柏科圆柏属圆柏Sabina chinensis (L.) Ant.4 讨论天津一中校园植物丰富，其中木本植物是构成校园植物群落的重要组成部分，具有不可替代的生态效益和景观效应，对校园绿地生态系统的发展有长远的影响。