当 2 t 3 时 2 ,t 3 ,f(x )在 x 3 处取 ,f( 最 3 ) 2
)在 x 2023 1/处 3/9 取 ,f( 最 3 )授 课1 :XXX 小 0 1t;2值
11
最值
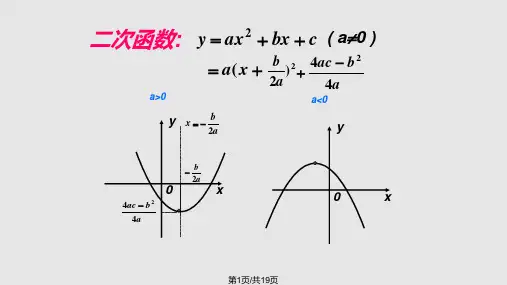
我们已经复习了含参变量二次函数的最大最小 值问题.那么现在我们考虑如下二次函数的最值 问题.应该如何进行分类呢? 例3. y=x2-4tx+1在区间[0,3]上的最值.
14
结论
开口向上的含参变二次函数的最值问题,应根据对称轴 与区间的位置关系进行分类:
最大值【2类】、最小值【3类】、最值【4类】
开口向下的含参变二次函数的最值问题,应根据对称轴 与区间的位置关系进行分类:
最大值【3类】、最小值【2类】、最值【4类】
2021/3/9
授课:XXX
15
练习
1. 《数学之友》P18 题型一 第1题
当0 t
当3 4
3 4
t
, f(x)max=f(3)=10-12t, f(x)min=f(2t)=1-4t2. 3 2 , f(x)max=f(0)=1, f(x)min=f(2t)=1-4t2.
当 t 2021/3/9
3 2
时,f(x)max=f(0授)课=:1X,XXf(x)max=f(3)=10-12t.
2021/3/9
授课:XXX
12
最值
例3. y=x2-4tx+1在区间[0,3]上的最值.
解: 函数的对称轴x=2t
当2t<0,t<0时,f(x)max=f(3)=10-12t, f(x)min=f(0)=1.
当 02t3时0 , t3
2
4
f(x)max=f(3)=10-12t, f(x)min=f(2t)=1-4t2.