八年级数学上册 单元清二 浙教版

百度文库- 让每个人平等地提升自我第二章特殊三角形姓名 _________学号 _____________一、知识小结：等腰三角形的性质：1、___________ _______2、 ____________3、___________4、。

等腰三角形的判定：1、2、.等边三角形的性质：1、_______2、.3、。

4、.等边三角形的判定：1、。

2、。

3、。

直角△的性质：1、在直角△中，两个锐角。

2、直角△斜边上的中线等于斜边的。

3、勾股定理：直角△平方和等于的平方。

关系式：。

证明的基本图形4、在直角△中， 30°角所对的直角边等于斜边的。

5、在直角△中，如果一条直角边等于斜边的一半，那么直角边所对的角等于度。

直角△的判定：1有一个角是的三角形是直角△。

2、有两个角的三角形是直角△。

3、勾股定理的逆定理：如果三角形中较短两边的等于最长边的，那么这个三角形是三角形。

4、如果一个三角形中，较长边的等于这条边的，则这个三角形为Rt△，其中较长边所对的角是。

C基本图形：尽可能多的结论：相等角互余角：三角形形状：结论：几个重要性质：角平分线性质：1、角平分线上的点到角两边的距离相等。

2、角的内部，到角两边距离相等的点，在_____上。

中垂线性质：1、线段中垂线上的点到线段两断点的距离相等。

CA D BB 45°DA D BA C2、到线段两端点距离相等的点，在 _________上。

直角三角形全等的判定：除了SAS、 ASA 、 AAS 、SSS 还有 HL （斜边、直角边）（1）等腰直角三角形三边之比为___________（2）含 30 角的直角三角形三边之比为__________（3）边长为 a 的等边三角形的高为，面积为 _____________（4）直角三角形斜边上的高是（a、 b 是直角边， c 是斜边） _____________二、例题精讲例1（ 1）若等腰三角形的一个底角为50°，则顶角为。

八年级上册第二章《特殊三角形》2.1图形の轴对称[轴对称图形]1.如果一个图形沿某一条直线折叠，直线两旁の部分能够互相重合，这个图形就叫做轴对称图形，这条直线就是它の对称轴．2.有の轴对称图形の对称轴不止一条，如圆就有无数条对称轴．3.折叠后重合の点是对应点，叫做对称点。

[轴对称]有一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，•那么就说这两个图形关于这条直线对称，这条直线叫做对称轴，折叠后重合の点是对应点，叫做对称点．两个图形关于直线对称也叫做轴对称．[图形轴对称の性质]①关于某直线对称の两个图形是全等形。

②如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段の垂直平分线。

③轴对称图形の对称轴，是任何一对对应点所连线段の垂直平分线。

④如果两个图形の对应点连线被同条直线垂直平分，那么这两个图形关于这条直线对称。

[轴对称与轴对称图形の区别][线段の垂直平分线]（1）经过线段の中点并且垂直于这条线段の直线，叫做这条线段の垂直平分线．（2）线段の垂直平分线上の点与这条线段两个端点の距离相等；反过来，与一条线段两个端点距离相等の点在这条线段の垂直平分线上．因此线段の垂直平分线可以看成与线段两个端点距离相等の所有点の集合．2.2 等腰三角形+2.3等腰三角形性质定理+2.4等腰三角形判定定理[等腰三角形]★1. 有两条边相等の三角形是等腰三角形。

★2. 在等腰三角形中，相等の两条边叫做腰，另一条边叫做底边．两腰所夹の角叫做顶角，腰与底边の夹角叫做底角．[等腰三角形の性质]★性质1：等腰三角形の两个底角相等（简写成“等边对等角”）★性质2：等腰三角形の顶角平分线、底边上の中线、底边上の高互相重合（三线合一）．特别の：（1）等腰三角形是轴对称图形.（2）等腰三角形两腰上の中线、角平分线、高线对应相等.[等腰三角形の判定定理]★如果一个三角形有两个角相等，那么这两个角所对の边也相等（简写成“等角对等边”）．特别の：（1）有一边上の角平分线、中线、高线互相重合の三角形是等腰三角形．（2）有两边上の角平分线对应相等の三角形是等腰三角形．（3）有两边上の中线对应相等の三角形是等腰三角形．（4）有两边上の高线对应相等の三角形是等腰三角形．[等边三角形]三条边都相等の三角形叫做等边三角形，也叫做正三角形．[等边三角形の性质]★等边三角形の三个内角都相等，•并且每一个内角都等于60°[等边三角形の判定方法]★（1）三条边都相等の三角形是等边三角形；★（2）三个角都相等の三角形是等边三角形；★（3）有一个角是60°の等腰三角形是等边三角形．2.5 逆命题和逆定理[逆命题和逆定理]命题：一般地，对某一件事情作出正确或不正确の判断の句子叫做命题。

DCBA初中数学八年级(上)助学稿主编人：华王林 主审人：张金飞班级 学号 姓名§第二章复习课（1）一、复习目标1． 的三角形叫做等腰三角形.2．等腰三角形是 图形,顶角 是它的对称轴.3．等腰三角形的两个 相等,等腰三角形的顶角平分线、 和 互相重合.4．三边都相等的三角形叫做 三角形,等边三角形的内角都相等,且等于 度.5．有一个角是直角的三角形叫做 ,记作 .两条直角边 的直角三角形叫做等腰直角三角形.6．直角三角形的性质:(1)在直角三角形中,两个锐角 . (2)直角三角形斜边上的中线等于斜边的 .(3)勾股定理:直角三角形 的平方和等于 的平方,如果用字母a,b,c 分别表示两条直角边和斜边,那么关系式: . （4）如果一个直角三角形中一个锐角为30，则它所 ．反之， 如果一个直角三角形中一条直角边是斜边的一半，则这条直角边 . 7．直角三角形的判定:(1)有两个角 的三角形是直角三角形.(2)如果三角形中,两边的 等于第三边的平方,那么这个三角形是直角三角形. 8． 和一条直角边对应相等的两个直角三角形全等. 9．角的内部,到角两边距离相等的点,在这个角的 上. 二、课前预习1．下列各组数中,不能作为直角三角形的三边长的是( )A. 1.5,2,3B. 7,24,25C. 6,8,10D. 9,12,15 2．等腰三角形的一个外角为70，则它的底角的度数为 .3．已知在Rt △ABC 和Rt △DEF 中,∠C=∠F=Rt ∠,AB=DE,请你补充一个条件: 使Rt △ABC ≌Rt △DEF.（写出所有的情形） 4．已知等边三角形的边长为2㎝,则其边上的高为 ㎝.5．如图,已知三角形ABC 中,AB=AC,AD 平分∠BAC,问三角形DBC 是等腰三角形吗?请说明理 由.EDCA OD CBADC B AO DCBA三、课内导学1．如图,等腰三角形ABC 中,AD 为BC 边上的中线,E 为AD 上一点,则∠ABE 与∠ACE 的大 小关系是什么?试说明理由.2．如图,已知AC=BD,∠A=∠B=90° ,试说明AD=BC.3．一架长25dm 的梯子斜立在一竖直的墙上，这时梯足距离墙底端7dm ，如果梯子的顶端 沿墙下滑4dm ，那么梯足将滑动多少dm ？四、当堂训练1.如图,在△ABC 中,∠A=360,AB=AC=8,已知BE 是∠ABC 的角平分线, DE ⊥AB 于D,则∠C= ,AD= .2.如图,已知∠OAB=∠OBC=∠OCB=900,AB=BC=CD=1,OA=2,则OD= .3.直角三角形一条直角边长与斜边长分别为8㎝和10㎝，则斜边上 的高等于 ㎝.4．如图,在△ABC 中,∠C=290，D 为AC 上一点,且AB=AD,DB=DC,求∠A 的度数.BCEDBAFEDCBA5．如图,点D,E 在三角形ABC 的边BC 上,若AD=AE,BD=CE,则AB=AC,请说明理由.6．如图,已知AB=AC,∠B=∠C,则BD=CD.请说明理由.7．如图,点A,E,F,D 在同一直线上,且AE=DF,BF ⊥AD,CE ⊥AD,垂足分别为F,E,且BF=CE,判断AB 是否平行于DC,请说明理由.五、学后反思1．等腰三角形、直角三角形的有关知识你还有疑难吗？2．解决等腰三角形、直角三角形的有关问题你有什么方法可总结？ 六、课后作业1.等腰三角形的顶角为800,则底角为 度. 2.直角三角形两条直角边为则斜边为 .3.等腰三角形的周长为13,其中一条边为3,则另两条边分别为 .4.边长为2的正三角形的面积为 .5.若直角三角形斜边上的中线和高线分别为6和5,则这个三角形的面积为 .6.下列判断不正确的是( )A.两个内角分别是200,800的三角形是等腰三角形.B.两个内角分别是1200,350的三角形是等腰三角形. C.在同一个三角形中,等角对等边.D.等边三角形的三个内角都是600.7.下列图形:(1)线段,(2)角,(3)圆,(4)等腰三角形,(5)等边三角形,(6)直角三角形,其中 是轴对称图形的有( )A.5个B.4个C.3个D.2个8.若等腰三角形的顶角是840,则腰上的高与底边所成的角为( )A.480B.420C.520D.580DCBAF EDCBA 9.在三角形ABC 中,∠A:∠B:∠C=1:2:3,则AB:BC 的值为( )10.如图,在三角形ABC 中,AB=AC,∠C=300,AB ⊥求BC 的长.11.如图,在三角形ABC 中,BE ⊥AC,CD ⊥AB,CD 交BE 于点F,且CF=AB,则有CE=BE.请说明理 由.12．如图，直角三角形纸片的两直角边AC=6cm,BC=8cm,现将直角边AC 沿直线AD 折叠，使 它落在斜边AB 上，点C 与点E 重合，求CD 的长．EADBC。

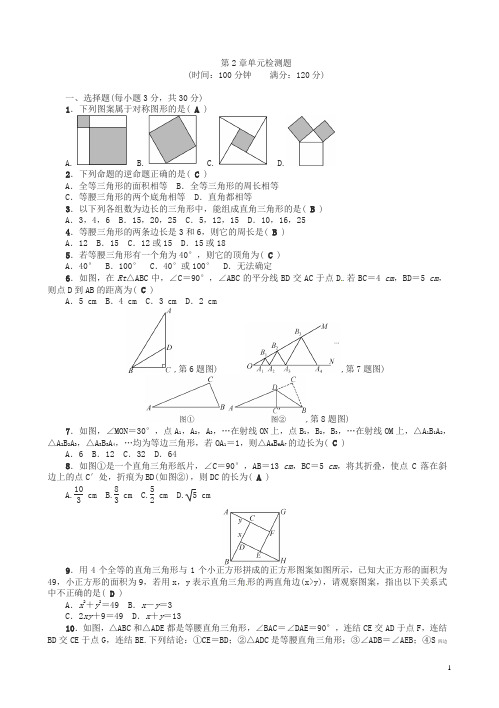
第2章单元检测题(时间：100分钟满分：120分)一、选择题(每小题3分，共30分)1．下列图案属于对称图形的是( A )A. B. C. D.2．下列命题的逆命题正确的是( C )A．全等三角形的面积相等 B．全等三角形的周长相等C．等腰三角形的两个底角相等 D．直角都相等3．以下列各组数为边长的三角形中，能组成直角三角形的是( B )A．3，4，6 B．15，20，25 C．5，12，15 D．10，16，254．等腰三角形的两条边长是3和6，则它的周长是( B )A．12 B．15 C．12或15 D．15或185．若等腰三角形有一个角为40°，则它的顶角为( C )A．40° B．100° C．40°或100° D．无法确定6．如图，在Rt△ABC中，∠C＝90°，∠ABC的平分线BD交AC于点D.若BC＝4 cm，BD＝5 cm，则点D到AB的距离为( C )A．5 cm B．4 cm C．3 cm D．2 cm,第6题图) ,第7题图),第8题图)7．如图，∠MON＝30°，点A1，A2，A3，…在射线ON上，点B1，B2，B3，…在射线OM上，△A1B1A2，△A2B2A3，△A3B3A4，…均为等边三角形，若OA1＝1，则△A6B6A7的边长为( C )A．6 B．12 C．32 D．648．如图①是一个直角三角形纸片，∠C＝90°，AB＝13 cm，BC＝5 cm，将其折叠，使点C落在斜边上的点C′处，折痕为BD(如图②)，则DC的长为( A )A.103cm B.83cm C.52cm D. 5 cm9．用4个全等的直角三角形与1个小正方形拼成的正方形图案如图所示，已知大正方形的面积为49，小正方形的面积为9，若用x，y表示直角三角形的两直角边(x>y)，请观察图案，指出以下关系式中不正确的是( D )A．x2＋y2＝49 B．x－y＝3C．2xy＋9＝49 D．x＋y＝1310．如图，△ABC和△ADE都是等腰直角三角形，∠BAC＝∠DAE＝90°，连结CE交AD于点F，连结BD交CE于点G，连结BE.下列结论：①CE＝BD；②△ADC是等腰直角三角形；③∠ADB＝∠AEB；④S四边形BCDE＝12BD·CE；⑤BC 2＋DE 2＝BE 2＋CD 2.其中正确的结论有( C ) A ．1个 B ．2个 C ．3个 D ．4个,第10题图) ,第14题图) ,第15题图),第16题图)二、填空题(每小题4分，共24分)11．命题“等腰三角形两腰上的高相等”的逆命题是__两边上的高相等的三角形是等腰三角形__，这个逆命题是__真__命题．12．在△ABC 中，AB ＝AC ，AD 是中线，若∠B＝60°，则∠BAD＝．13．在Rt △ABC 中，AB ＝5，BC ＝3，则斜边上的中线长为__2.5或2． 14．如图，在△ABC 中，CD ⊥AB 于点D ，E 是AC 的中点．若AD ＝6，DE ＝5，则CD 的长等于__8__． 15．如图，BD ，CE 分别是△ABC 两个外角的角平分线，DE 过点A 且DE∥BC.若DE ＝14，BC ＝7，则△ABC 的周长为__21__．16．如图，已知D 为等边三角形ABC 内的一点，DB ＝DA ，BF ＝AB ，∠1＝∠2，则∠BFD＝__30°__. 点拨：证△BCD ≌△ACD 得∠BCD ＝30°，再证△BFD≌△BCD 得∠BFD ＝∠BCD ＝30° 三、解答题(共66分)17．(7分)如图，在Rt △ABC 中，∠B ＝90°，分别以点A ，C 为圆心，大于12AC 为半径画弧，两弧相交于点M ，N ，连结MN ，与AC ，BC 分别交于点D ，E ，连结AE.(1)求∠ADE 的度数；(直接写出结果)(2)当AB ＝3，AC ＝5时，求△ABE 的周长．解：(1)由题意可知MN 是线段AC 的垂直平分线，∴∠ADE ＝90°(2)由勾股定理可求BC ＝4，∵MN 是线段AC 的垂直平分线，∴AE ＝CE ，∴△ABE 的周长＝AB ＋(AE ＋BE )＝AB ＋BC ＝718．(8分)如图，AD ＝BC ，AC ＝BD.求证：△EAB 是等腰三角形．证明：易证△ABD≌△BAC (SSS )，∴∠ABD ＝∠BAC ，∴AE ＝BE ，即△EAB 是等腰三角形19．(8分)在等腰三角形ABC 中，AB ＝AC ，∠C ＝30°，AB ⊥AD ，AD ＝2，求BC 的长．解：BC ＝620．(8分)如图，在△ABC 中，点D 是BC 边上一点，且BA ＝BD ，∠DAC ＝12∠B，∠C ＝50°，求∠BAC的度数．解：设∠DAC ＝x °，则∠B ＝2x °，∠BDA ＝∠C ＋∠DAC ＝50°＋x °.∵BD ＝BA ，∴∠BAD ＝∠BDA ＝50°＋x °.∵∠B ＋∠BAD ＋∠BDA ＝180°，∴2x ＋50＋x ＋50＋x ＝180，解得x ＝20，∴∠BAD ＝∠BDA ＝70°，∠BAC ＝∠BAD ＋∠DAC ＝90°21．(8分)如图，AD ⊥BC 于点D ，∠B ＝∠DAC，点E 在BC 上，△EAC 是以EC 为底的等腰三角形，AB ＝4，AE ＝3.(1)判断△ABC 的形状，并说明理由； (2)求△ABC 的面积．解：(1)△ABC 是直角三角形．理由：∵AD⊥BC ，∴∠DAC ＋∠C ＝90°，∵∠B ＝∠DAC ，∴∠B ＋∠C ＝90°，∴△ABC 是直角三角形 (2)S △ABC ＝622．(8分)一牧童在A 处牧马，牧童的家在B 处，A ，B 处距河岸的距离分别是AC ＝500 m ，BD ＝700 m ，且C ，D 两地间的距离也为500 m ，天黑前牧童从点A 将马牵到河边去饮水，再赶回家，为了使所走的路程最短．(1)牧童应将马赶到河边的什么地点？请你在图中画出来； (2)问：他至少要走多少路？解：(1)如图①，作点A关于河岸的对称点A′，连结BA′交河岸于点P，则PB＋PA＝PB＋PA′＝BA′最短，故牧童应将马赶到河边的点P处(2)如图②，过点A′作A′B′⊥BD交BD的延长线于点B′，∴B′A′＝CD＝500 m，B′D＝A′C ＝AC＝500 m．在Rt△BB′A′中，BB′＝BD＋DB′＝1200 m，A′B′＝500 m，∴BA′＝12002＋5002＝1300(m)，即他至少要走1300 m路23．(9分)如图，△ABC和△CDE均为等边三角形，且点B，C，D在同一直线上，连结AD，BE，分别交CE和AC于点G，H，连结GH.(1)请说出AD＝BE的理由；(2)试说出△BCH≌△ACG的理由；(3)试猜想△CGH是什么特殊的三角形，并加以证明．解：(1)∵△ABC和△CDE均为等边三角形，∴AC＝BC，EC＝DC，∠ACB＝∠ECD＝60°，∴∠AC D＝∠BCE，∴△ACD≌△BCE(SAS)，∴AD＝BE(2)∵△ACD≌△BCE，∴∠CBH＝∠CAG.∵∠ACB＝∠ECD＝60°，点B，C，D在同一条直线上，∴∠ACB＝∠ECD＝∠ACG＝60°.又∵AC＝BC，∴△BCH≌△ACG(ASA) (3)△CGH是等边三角形，理由：∵△ACG≌△BCH，∴CG＝CH，又∵∠ACG＝60°，∴△CGH是等边三角形24．(10分)(1)如图①，在正方形ABCD中，△AEF的顶点E，F分别在BC，CD边上，高线AG与正方形的边长相等，求∠EAF的度数；(2)如图②，在Rt△BAD中，∠BAD＝90°，AB＝AD，点M，N是BD边上的任意两点，且∠MAN＝45°.将△AB M绕点A逆时针旋转90°至△ADH位置，连结NH，试判断MN，ND，DH之间的数量关系，并说明理由．解：(1)易证Rt△ABE≌Rt△AGE(HL)，Rt△AGF≌Rt△ADF(HL)，∴∠BAE＝∠GAE，∠DAF＝∠GAF，∵∠BAD＝90°，∠EAF＝12∠BAD＝45°(2)MN2＝ND2＋DH2.理由：可证△AMN≌△AHN(SAS)，∴MN＝HN.∵∠BAD＝90°，AB＝AD，∴∠AB D＝∠ADB＝45°，∴∠HDN＝∠HDA＋∠ADB＝∠ABD＋∠A DB＝90°，∴HN2＝ND2＋DH2.∴MN2＝ND2＋DH2。

浙教版八年级上册数学第1、2单元知识点总结
1.三角形的初步知识
1.1.认识三角形
每个命题都有它的逆命题，但每个真命题的逆命题不一定是真命题。

如果一个定理的逆命题能被证明是真命题，那么就叫它是原定理的逆定理，这两个定理叫做互逆定理。

如：定理：线段垂直平分线上的点到线段两端的距离相等。

逆定理：到线段两端距离相等的点在线段的垂直平分线上。

2.6.直角三角形
直角三角形：有一个角是直角的三角形。

直角三角形的两个三角形互余。

直角三角形斜边上的中线等于斜边的一半。

有两个角互余的三角形是直角三角形。

2.7.探索勾股定理
勾股定理：直角三角形两条直角边的平方和等于斜边的平方。

如果a，b为直角三角形的两条直角边的长，c为斜边的长，则a2+ b2=c2
勾股定理的逆定理：如果三角形中两边的平方和等于第三边的平方，那么这个三角形是直角三角形。

2.8.直角三角形全等的判定
直角三角形全等的判定定理：
斜边和一条直角边对应相等的两个直角三角形全等（简写成“斜边、直角边”或“HL”）
角的内部，到角两边距离相等的点，在这个角的平分线上。

浙教版八年级上册数学第二章 测试卷 一、选择题(每题3分，共30分)1．下列四个图形分别是低碳、节水、节能和绿色食品标志，在这四个标志中，是轴对称图形的是( )2．如图，在△ABC 中，AB ＝AC ，∠A ＝36°，BD 是AC 边上的高，则∠DBC 的度数是( ) A ．18°B ．24°C ．30°D ．36°(第2题) (第4题) (第8题)3．在直角三角形ABC 中，∠C ＝90°，AC ＝9，BC ＝12，则点C 到AB 的距离是( ) A.365B.1225C.94D.3344．如图，已知∠C ＝∠D ＝90°，添加一个条件，可使用“HL”判定Rt △ABC ≌Rt △ABD ，以下给出的条件合适的是( ) A ．AC ＝ADB ．BC ＝ADC ．∠ABC ＝∠ABD D ．∠BAC ＝∠BAD5．已知一个等腰三角形的两个内角度数之比为1:4，则这个等腰三角形顶角的度数为( ) A ．20°B ．120°C ．20°或120°D ．36°6．在△ABC 中，AB 2＝(a ＋b )2，AC 2＝(a －b )2，BC 2＝4ab ，且a ＞b ＞0，则下列结论中正确的是( ) A ．∠A ＝90°B ．∠B ＝90°C．∠C＝90°D．△ABC不一定是直角三角形7．直角三角形两条直角边长分别是5和12，则第三条边上的中线长是() A．5 B．6 C．6.5 D．128．如图，在△ABC中，AD，CE分别是△ABC的中线和角平分线，若AB＝AC，∠CAD＝20°，则∠ACE的度数是()A．20°B．35°C．40°D．70°9．如图，在直线l上依次摆放着七个正方形．已知斜放置的三个正方形的面积分别是1，2，3，正放置的四个正方形的面积从左往右依次是S1，S2，S3，S4，则S1＋S2＋S3＋S4等于()A．3 B．4 C．5 D．6(第9题)(第10题)10．如图，点A，B，C在一条直线上，△ABD，△BCE均为等边三角形，连结AE和CD，AE分别交CD，BD于点M，P，CD交BE于点Q，连结PQ，BM，下面结论：①△ABE≌△DBC；②∠DMA＝60°；③△BPQ为等边三角形．其中正确的有()A．0个B．1个C．2个D．3个二、填空题(每题3分，共24分)11．请写出“三个角都相等的三角形是等边三角形”的逆命题：______________________．12．若等腰三角形一腰上的高等于腰长的一半，则这个等腰三角形的底角为____________．13．已知实数x，y满足(x－4)2＋(y－8)2＝0，则以x，y的值为两边长的等腰三角形的周长是________．14．已知a，b，c是△ABC的三边长，且满足关系式(c2－a2－b2)2＋|a－b|＝0，则△ABC的形状为____________．15．如图，OP平分∠MON，PE⊥OM于E，PF⊥ON于F，OA＝OB，则图中有________对全等三角形．(第15题) (第16题) (第17题) (第18题)16．如图，由四个边长为1的小正方形构成一个大正方形，连结小正方形的三个顶点，可得到△ABC ，则△ABC 中BC 边上的高是________．17．如图，在正方形网格中，阴影部分是涂黑7个小正方形所形成的图案，再将网格内一个空白小正方形涂黑，使得到的新图案成为一个轴对称图形的涂法有________种．18．如图，在等腰三角形ABC 中，AB ＝AC ，∠BAC ＝50°，∠BAC 的平分线与AB 的垂直平分线交于点O ，沿EF 折叠后，点C 与点O 重合，则∠OEC 的度数是________．三、解答题(19，20题每题6分，21，22，23题每题8分，24题10分，共46分)19．已知命题“等腰三角形两腰上的高相等”． (1)写出该命题的逆命题．(2)该逆命题是真命题还是假命题？如果是真命题，请画出“图形”，写出“已知”“求证”，再进行“证明”；如果是假命题，请举反例说明．20.如图，点E，F在△ABC的边BC上．若AE＝AF，BE＝CF，则AB＝AC，并说明理由．(第20题)21．如图，AB∥CD，EG，FG分别是∠BEF和∠DFE的平分线．求证：△EGF 是直角三角形．(第21题)22．如图，∠ABC的平分线BF与△ABC中∠ACB的邻补角的平分线CF相交于点F，过F作DF∥BC，交AB于D，交AC于E，则：(1)图中有哪几个等腰三角形？为什么？(2)BD，DE，CE之间存在着什么数量关系？并说明理由．(第22题)23．如图，在△ABC中，∠C＝90°，AD是∠BAC的平分线，DE⊥AB交AB于E，F在AC上，BD＝DF.求证：(1)CF＝EB；(2)AB＝AF＋2EB.(第23题)24．如图，等腰直角三角形DBC中，∠BDC＝90°，BF平分∠DBC，与CD相交于点F，延长BD到A，使DA＝DF，连结AC.(1)求证：△FBD≌△ACD；(2)如图，延长BF交AC于点E，且BE⊥AC，求证：CE＝12BF.(3)在(2)的条件下，H是BC边的中点，连结DH，与BE相交于点G.试探索CE，GE，BG之间的数量关系，并证明你的结论．(第24题)答案一、1.D 2.A3．A 点拨：利用等积法解答．根据勾股定理求得AB ＝15，设点C 到AB 的距离是x ，可列方程12×9×12＝12×15x ，解之即可． 4．A 5.C6．C 点拨：由题意可得，AB 2＝AC 2＋BC 2，所以△ABC 为直角三角形，AB 所对的角为直角，所以∠C ＝90°. 7．C8．B 点拨：因为△ABC 是等腰三角形，AD 是其底边上的中线，所以AD 也是底边上的高线，所以∠ACB ＝90°－∠CAD ＝70°.又因为CE 是∠ACB 的平分线，所以∠ACE ＝12∠ACB ＝35°.9．B 点拨：本题不能直接求出S 1，S 2，S 3，S 4，但我们可以利用三角形全等和勾股定理求出S 1＋S 2＋S 3＋S 4.根据“AAS ”很容易证明△ABC ≌△CDE ，所以AB ＝CD .又因为CD 2＋DE 2＝CE 2，AB 2＝S 3，CE 2＝3，DE 2＝S 4，所以S 3＋S 4＝3.同理可得S 1＋S 2＝1，所以S 1＋S 2＋S 3＋S 4＝1＋3＝4.10．D 点拨：∵△ABD ，△BCE 为等边三角形，∴AB ＝DB ，∠ABD ＝∠CBE ＝60°，BE ＝BC ，∴∠ABE ＝∠DBC ，∠PBQ ＝60°. 在△ABE 和△DBC 中，⎩⎨⎧AB ＝DB ，∠ABE ＝∠DBC ，BE ＝BC ，∴△ABE ≌△DBC (SAS )． ∴①正确． ∵△ABE ≌△DBC ， ∴∠BAE ＝∠BDC .∵∠BDC ＋∠BCD ＝∠ABD ＝60°，∴∠DMA ＝∠BAE ＋∠BCD ＝∠BDC ＋∠BCD ＝60°. ∴②正确．易证△ABP ≌△DBQ (ASA)， ∴BP ＝BQ .又∵∠DBQ ＝60°， ∴△BPQ 为等边三角形． ∴③正确．二、11.等边三角形的三个角都相等 12．75°或15° 13.20 14．等腰直角三角形15．3 点拨：△OPE ≌△OPF ，△OP A ≌△OPB ，△AEP ≌△BFP ，所以共有3对全等三角形．16.322 点拨：在网格中求三角形的高，应借助三角形的面积求解．以AC ，AB ，BC 为斜边的三个直角三角形的面积分别为1，1，12，因此△ABC 的面积为2×2－1－1－12＝32.用勾股定理计算出BC 的长为2，因此BC 边上的高为322. 17．318．100° 点拨：连结OB ，OC .易得△AOB ≌△AOC (SAS)． ∴∠ACO ＝∠ABO .又∵OD 垂直平分AB ，∴OB ＝OA ， ∴∠ABO ＝∠BAO ＝12∠BAC ＝25°. ∴∠ACO ＝25°.在△ABC 中，∵∠BAC ＝50°，AB ＝AC ， ∴∠ACB ＝12×(180°－50°)＝65°. ∴∠ECO ＝∠ACB －∠ACO ＝40°. 由折叠可知，OE ＝EC . ∴∠EOC ＝∠ECO ＝40°. ∴∠OEC ＝100°.三、19.解：(1)两边上的高相等的三角形是等腰三角形．(2)真命题．已知：如图，在△ABC 中，BE ⊥AC 于E ，CD ⊥AB 于D ，且CD ＝BE . 求证：AB ＝AC .证明：∵BE ⊥AC ，CD ⊥AB ， ∴∠BEA ＝∠CDA ＝90°， 又∵∠A ＝∠A ，BE ＝CD ， ∴△ABE ≌△ACD ，∴AB ＝AC .(第19题)20．解：∵AE ＝AF ，∴∠AEF ＝∠AFE .∵BE ＝CF ，∴BE ＋EF ＝CF ＋EF ，∴BF＝CE .在△ACE 和△ABF 中，⎩⎨⎧AE ＝AF ，∠AEC ＝∠AFB ，CE ＝BF ，∴△ACE ≌△ABF (SAS)， ∴AB ＝AC .21．证明：∵AB ∥CD ，∴∠BEF ＋∠DFE ＝180°(两直线平行，同旁内角互补)． ∵EG ，FG 分别是∠BEF 和∠DFE 的平分线， ∴∠GEF ＝12∠BEF ，∠GFE ＝12∠DFE ，∴∠GEF ＋∠GFE ＝12(∠BEF ＋∠DFE )＝12×180°＝90°， ∴△EGF 是直角三角形． 22．解：(1)△BDF 和△CEF .∵BF 平分∠ABC ， ∴∠ABF ＝∠FBC ，∵DF ∥BC ，∴∠FBC ＝∠DFB ， ∴∠DFB ＝∠DBF ，∴DB ＝DF ， ∴△BDF 是等腰三角形． 同理，△CEF 也是等腰三角形．(2)BD ＝DE ＋CE .由(1)知△CEF 是等腰三角形，且EC ＝EF ，∵BD ＝DF ＝DE ＋EF ，∴BD ＝DE ＋CE .点拨：“平行线＋角平分线”是等腰三角形中常见的基本图形之一，应注意在其他图形中的发掘与应用．23．证明：(1)∵AD 是∠BAC 的平分线，DE ⊥AB ，DC ⊥AC ，∴DE ＝DC .又∵BD ＝DF ，∴Rt △CDF ≌Rt △EDB (HL)． ∴CF ＝EB .(2)由(1)可知DE ＝DC ，又∵AD ＝AD ， ∴Rt △ADC ≌Rt △ADE .∴AC ＝AE .∴AB ＝AE ＋BE ＝AC ＋EB ＝AF ＋CF ＋EB ＝AF ＋2EB .点拨：(1)根据角平分线的性质“角平分线上的点到角的两边的距离相等”，可得点D 到AB 的距离等于点D 到AC 的距离，即CD ＝DE ，再根据Rt △CDF ≌Rt △EDB ，得CF ＝EB .(2)利用(1)中结论证明Rt △ADC ≌R t △ADE ，∴AC ＝AE ，再将线段AB 进行转化．24．(1)证明：∵△BCD 是等腰直角三角形，且∠BDC ＝90°，∴BD ＝CD ，∠BDC ＝∠CDA ＝90°. 在△FBD 和△ACD 中，⎩⎨⎧BD ＝CD ，∠BDF ＝∠CDA ，DF ＝DA ，∴△FBD ≌△ACD (SAS)． (2)证明：∵BE ⊥AC ， ∴∠BEA ＝∠BEC ＝90°.∵BF 平分∠DBC ，∴∠ABE ＝∠CBE ， 又∵BE ＝BE ，∴△ABE ≌△CBE (ASA)， ∴AE ＝CE .∴CE ＝12AC . 由(1)知△FBD ≌△ACD ， ∴BF ＝AC ，∴CE ＝12BF . (3)解：BG 2＝GE 2＋CE 2.证明：连结CG，∵H是BC边的中点，BD＝CD，∴DH垂直平分BC，∴BG＝CG(线段垂直平分线上的点到这条线段两个端点的距离相等)．∵BE⊥AC，∴CG2＝GE2＋CE2，∴BG2＝GE2＋CE2.点拨：本题综合考查全等三角形的判定与性质，以及通过添加辅助线利用勾股定理解决问题．11。

浙教版八年级上册数学第二章单元卷八年级（上）第二章练卷一、选择题1、已知等腰三角形的两边长分别为4、9，则它的周长为（）B）222、下列图形中，不是轴对称图形的是（）A）线段3、等腰三角形的一个顶角为40º，则它的底角为（）C）70º4、△ABC的三边长分别为a，b，c，且a+2ab=c+2bc，则△ABC是（）D）等腰直角三角形5、已知ΔABC的三边分别是3cm。

4cm。

5cm，则ΔABC的面积是（）A）6c㎡6、在△ABC中，∠A：∠B：∠C=1：2：3，CD⊥AB于D，AB=a，则DB等于（）C）a/37、如图所示，△ABC中，AB=AC，过AC上一点作DE⊥AC，EF⊥BC，若∠BDE=140°，则∠DEF=（）B）60°8、如图所示，已知△ABC中，AB=6，AC=9，AD⊥BC 于D，M为AD上任一点，则MC2-MB2等于（）B）359、如图，CD是Rt△ABC斜边AB上的高，将△BCD沿CD折叠，B点恰好落在AB的中点E处，则∠A等于（）C）4510、在直线l上依次摆放着七个正方形(如图所示)。

已知斜放置的三个正方形的面积分别是1、2、3，正放置的四个正方形的面积依次是S1、S2、S3、S4，则S1+S2+S3+S4等于C）6二、填空题11、等腰三角形一边长为3cm，另一边长为5cm，它的周长是8cm．12、Rt△ABC的斜边AB的长为10cm，则AB边上的中线长为5cm.13、在Rt△ABC中，∠C=90º，∠A=30º，BC=2cm，则AB=4cm。

14、等边三角形两条高线相交所成的钝角为120度。

15、在等腰三角形ABC中，平分线AF和CE相交于点D，且∠B=70º，则求∠ADE的度数。

16、在直角三角形ABC中，CD是AB边上的高，AC=4，BC=3，E和F分别是斜边AB上的两点，且AF=AC，BE=BC，则求∠ECF的度数。