LMS算法自适应均衡实验

BPSK调制传输系统LMS算法自适应均衡性能分析BPSK调制传输系统中，LMS（Least Mean Square）算法是一种常用的自适应均衡算法。

它通过自适应地调整均衡器的权重系数来实现信道均衡，从而提高系统的性能。

本文将对LMS算法在BPSK调制传输系统中的性能进行分析。

首先，我们需要了解BPSK调制传输系统的基本原理。

BPSK调制是一种二进制调制方式，它将数字信号转换为两个不同的相位信号，分别代表1和0。

在传输过程中，信号会经过信道引起失真和噪声干扰。

为了恢复原始信号，我们需要对接收到的信号进行均衡处理。

LMS算法的核心思想是根据误差信号来调整均衡器的权重系数。

误差信号是接收信号经过均衡器处理后与已知原始信号之间的差异。

通过不断调整权重系数，LMS算法能够逐步减小误差信号，最终实现信道均衡。

在BPSK调制传输系统中，我们可以对LMS算法的性能进行以下几个方面的分析。

1.收敛速度：LMS算法的收敛速度是衡量其性能的重要指标之一、收敛速度越快，均衡器能够更快地适应信道的变化，提高系统的实时性和鲁棒性。

收敛速度受到多种因素的影响，例如步长参数的选择、信道的时变性等。

在实际应用中，需要根据具体情况进行优化。

2.系统误码率：误码率是衡量系统性能的重要指标。

对于BPSK调制传输系统，误码率反映了接收信号正确解码的概率。

通过调整LMS算法的参数，如步长参数和滤波器长度等，可以改善系统的误码率性能。

同时，深度学习等新兴技术也可以结合LMS算法进行优化，进一步降低误码率。

3.资源利用率：BPSK调制传输系统中，LMS算法会引入一定的计算复杂度和存储开销。

因此，需要考虑LMS算法的资源利用率。

通过算法设计和硬件优化，可以减少计算量和存储需求，提高资源利用率。

4.系统可靠性：LMS算法在均衡过程中，由于噪声和失真等因素的存在，可能导致误差信号不断波动，进而影响系统的可靠性。

可以通过优化算法参数、加入先验知识或调整均衡器结构等方法来提高系统的可靠性。

自适应均衡算法LMS研究一、自适应滤波原理与应用所谓自适应滤波器，就是利用前一时刻已获得的滤波器参数等结果，自动地调节现时刻的滤波器参数，以适应信号和噪声未知的或随时间变化的统计特性，从而实现最优滤波。

根据环境的改变，使用自适应算法来改变滤波器的参数和结构。

1.1均衡器的发展及概况均衡是减少码间串扰的有效措施。

均衡器的发展有史已久，二十世纪60年代前，电话信道均衡器的出现克服了数据传输过程中的码间串扰带来的失真影响。

但是均衡器要么是固定的，要么其参数的调整是手工进行。

1965年，Lucky在均衡问题上提出了迫零准则，自动调整横向滤波器的权系数。

1969年，Gerhso和Porkasi，Milier分别独立的提出采用均方误差准则(MSE)。

1972年，ungeboekc将LMS算法应用于自适应均衡。

1974年，Gedard 在kalmna滤波理论上推导出递推最小均方算法RLS(Recursive least-squares)。

LMS类算法和RLS类算法是自适应滤波算法的两个大类。

自适应滤波在信道均衡、回波抵消、谱线增强、噪声抑制、天线自适应旁瓣抑制、雷达杂波抵消、相参检测、谱估计、窄带干扰抑制、系统辨识、系统建模、语音信号处理、生物医学、电子学等方面获得广泛的应用。

1.2均衡器种类均衡技术可分为两类：线性均衡和非线性均衡。

这两类的差别主要在于自适应均衡器的输出被用于反馈控制的方法。

如果判决输出没有被用于均衡器的反馈逻辑中，那么均衡器是线性的；如果判决输出被用于反馈逻辑中并帮助改变了均衡器的后续输出，那么均衡器是非线性的。

图1.1 均衡器的分类1.3自适应算法LMS 算法LMS 算法是由widrow 和Hoff 于1960年提出来的,是统计梯度算法类的很重 要的成员之一。

它具有运算量小,简单,易于实现等优点。

LMS 算法是建立在Wiener 滤波的基础上发展而来的。

Wiener 解是在最小均方误差(MMSE)意义下使用均方误差作为代价函数而得到的在最小误差准则下的最优解。

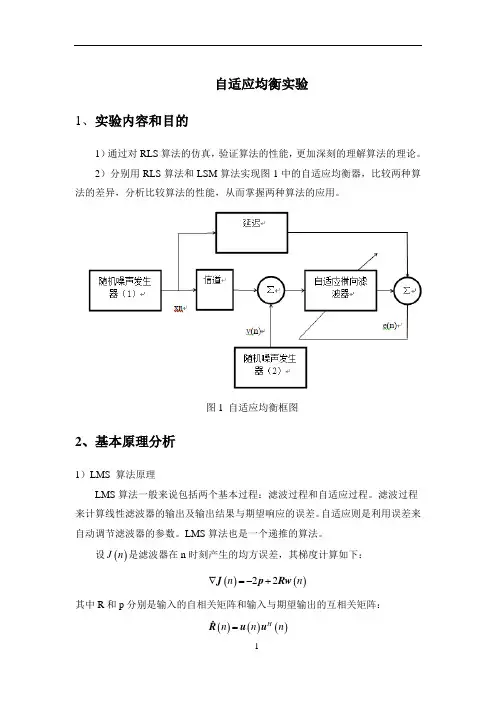
自适应均衡实验1、实验内容和目的1）通过对RLS 算法的仿真，验证算法的性能，更加深刻的理解算法的理论。

2）分别用RLS 算法和LSM 算法实现图1中的自适应均衡器，比较两种算法的差异，分析比较算法的性能，从而掌握两种算法的应用。

图1 自适应均衡框图2、基本原理分析1）LMS 算法原理LMS 算法一般来说包括两个基本过程：滤波过程和自适应过程。

滤波过程来计算线性滤波器的输出及输出结果与期望响应的误差。

自适应则是利用误差来自动调节滤波器的参数。

LMS 算法也是一个递推的算法。

设()J n 是滤波器在n 时刻产生的均方误差，其梯度计算如下：()()22n n ∇=-+J p Rw其中R 和p 分别是输入的自相关矩阵和输入与期望输出的互相关矩阵：()()()ˆH n n n =Ru u()()()*ˆn n n =pu d 则梯度向量的瞬态估计为：()()()()()()*ˆˆ22H n n n n n n ∇=-+J u d u u w 由最速下降算法可以得到抽头向量更新的递推关系式：()()()()()()*ˆˆˆ1Hn n n n n n μ⎡⎤+=+-⎣⎦w w u d u w整个LMS 算法归纳总结如下： 参数设置：M=抽头数（滤波器长度） μ=步长参数 m a x20MS μ<<其中max S 是抽头输入功率谱密度的最大值，而滤波器长度M 为中到大 初始化：如果知道抽头权向量()n w 的先验知识，则用它来选择()ˆ0w 的合适值，否则令()ˆ00=w。

更新滤波过程：()()()ˆH y n n n =wu ()()()e n d n y n =- ()()()()*ˆˆ1n n n e n μ+=+ww u 2）RLS 算法原理RLS 算法是一个递归的过程，递归最小二乘问题的正则方程可用矩阵写为()()()ˆn n n =Φwz 其中n 是可测数据的可变长度，()n Φ更新抽头输入的自相关矩阵，()n z 是抽头输入与期望响应之间的互相关向量，()ˆn w 是抽头的权值向量。

LMS 算法自适应均衡器实验08S005073 房永奎一、实验目的1、掌握LMS 算法的计算过程，加深对LMS 算法的理解。

2、研究用LMS 算法自适应均衡引起失真的线性色散信道问题。

3、研究特征值扩散度()R χ和步长参数μ对学习曲线的影响。

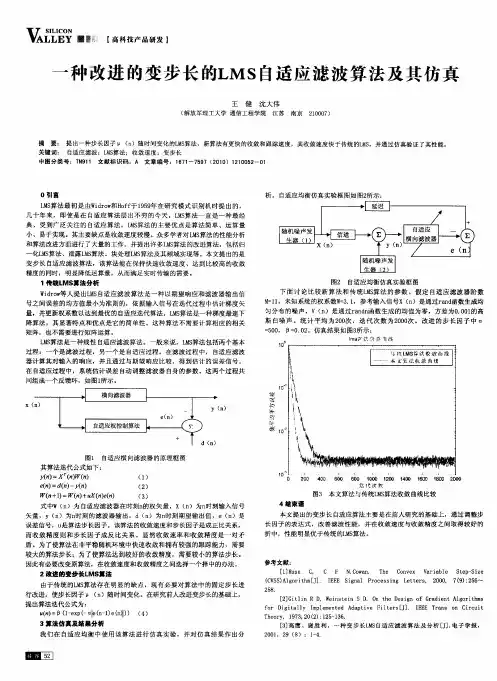
二、实验原理1、自适应均衡器)n图1 自适应信道均衡试验原理图自适应均衡器用来纠正存在加性白噪声的信道的畸变，信道均衡器的原理框图如1所示。

随机噪声发生器(1)产生用来探测信道的测试信号序列{n x }，本实验中由Bernoulli 序列组成，n x =±1，随机变量n x 具有零均值和单位方差。

随机噪声发生器(2)产生干扰信道的白噪声()n ν，具有零均值，方差为2νσ=0.001。

信道的脉冲响应用升余弦表示为：20.51cos (2)1,2,30n n n h W π⎧⎡⎤⎛⎫+-=⎪ ⎪⎢⎥=⎝⎭⎨⎣⎦⎪⎩（1） 其中，参数W 控制均衡器抽头输入相关矩阵的特征值分布()R χ，并且特征值分布随着W 的增大而扩大。

均衡器具有11M =个抽头。

由于信道的脉冲响应n h 关于n ＝2时对称，那么均衡器的最优抽头权值on ω在5n =时对称。

因此，信道的输入n x 被延时了257∆=+=个样值，以便提供均衡器的期望响应。

通过选择匹配横向均衡器中点的合适延时∆，LMS 算法能够提供信道响应的最小相位分量和非最小相位分量之逆。

2、均衡器输入相关矩阵在时刻n ，均衡器第1个抽头的输入为()()()31k k u n h x n k v n ==-+∑ （2）其中所有参数均为实数。

因此，均衡器输入的11个抽头(),(1),,(10)u n u n u n --的自相关矩阵R 为一个对称的1111⨯矩阵。

此外，因为脉冲响应n h 仅在1,2,3n =时为非零，且噪声过程()v n 是零均值、方差为2v σ的白噪声，因此相关矩阵R 是主对角线的，有以下特殊结构所示：()()()()()()()()()()()()()()()012001012021010021000000r r r r r r r r r r r r r r r ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦R （3） 其中()22221230v r h h h σ=+++ （4）()12231r h h h h =+ （5）()132r h h = （6）其中方差20.001v σ=。

LMS算法实验报告LMS（Least Mean Squares）算法是一种基于梯度下降的自适应滤波算法，常用于信号处理、通信系统等领域。

本实验通过实现LMS算法并对其性能进行评估，探究其在自适应滤波中的应用。

1.实验背景自适应滤波在许多领域中被广泛应用，如信号降噪、语音增强、通信频谱感知等。

自适应滤波的核心思想是根据输入信号的特性自动调整滤波器的系数，以实现信号的最佳重构或增强。

2.实验目的本实验旨在通过实现LMS算法并对其性能进行评估，探究其在自适应滤波中的应用。

具体目的如下：1）了解LMS算法的基本原理和实现步骤；2）实现LMS算法，完成自适应滤波任务；3）评估LMS算法的性能，分析其在不同情况下的表现；4）对比LMS算法和其他自适应滤波算法的优缺点。

3.实验步骤本实验的实现步骤如下：1）理解LMS算法的基本原理和数学模型；2）根据LMS算法的更新规则，实现算法的代码；3）根据自适应滤波的具体任务需求，选择合适的输入信号和期望输出；4）根据实验需求，设置合适的参数（如学习率、滤波器长度等）；5）使用LMS算法对输入信号进行滤波，并计算输出信号的均方误差；6）根据实验结果，评估LMS算法的性能，并进行分析。

4.实验结果根据以上步骤，完成了LMS算法的实现和性能评估。

实验结果显示，LMS算法能够有效地调整滤波器的权值，实现输入信号的滤波和增强。

随着学习率的增加，LMS算法的收敛速度较快，但容易发生震荡现象。

而学习率过小，则会导致算法收敛速度慢，需要更多的迭代次数才能达到较小的均方误差。

此外，在不同噪声情况下，LMS算法的性能表现也有所差异。

在信噪比较低的情况下，LMS算法的滤波效果明显，能够有效抑制噪声并实现信号增强。

然而，在信噪比较高的情况下，LMS算法的性能受到一定影响，可能会出现性能下降或收敛困难的情况。

5.总结与分析通过本实验，深入了解了LMS算法的原理和实现步骤，并对其性能进行了评估。

一、实验背景随着通信技术的不断发展，信号传输过程中的信道特性对信号质量的影响日益显著。

为了提高信号传输的可靠性和质量，均衡技术被广泛应用于通信系统中。

本文通过对均衡实验的研究，总结了均衡技术的基本原理、实现方法以及在实际应用中的性能表现。

二、实验目的1. 理解均衡技术的基本原理和实现方法；2. 分析不同均衡算法的优缺点，并评估其在实际应用中的性能；3. 掌握均衡技术的实际应用，为通信系统设计提供参考。

三、实验内容1. 均衡技术的基本原理均衡技术是一种用于补偿信号传输过程中信道特性的方法，其主要目的是消除信道引入的线性失真，使接收到的信号尽可能地恢复出原始信号。

均衡技术分为线性均衡和非线性均衡两种，其中线性均衡是最常用的均衡方法。

线性均衡的基本原理是通过设计一个线性滤波器，使得滤波器的输出信号与信道响应的逆相乘，从而实现信道特性的补偿。

线性均衡的滤波器通常采用FIR（有限冲激响应）滤波器实现。

2. 均衡算法的实现（1）最小均方误差（LMS）算法LMS算法是一种基于最小二乘法的自适应均衡算法，其基本思想是通过不断调整滤波器的系数，使得滤波器的输出信号与期望信号之间的均方误差最小。

LMS算法具有结构简单、计算量小、收敛速度快等优点。

（2）递归最小二乘（RLS）算法RLS算法是一种基于最小二乘法的自适应均衡算法，其基本思想是通过在线调整滤波器的系数，使得滤波器的输出信号与期望信号之间的均方误差最小。

RLS算法具有收敛速度快、计算复杂度较高、对噪声敏感等优点。

（3）卡尔曼滤波算法卡尔曼滤波算法是一种基于统计理论的滤波方法，其基本思想是通过预测和更新过程，对信号进行滤波。

卡尔曼滤波算法具有自适应性强、收敛速度快、对噪声敏感等优点。

3. 均衡算法的性能分析通过对LMS、RLS和卡尔曼滤波算法的性能分析，得出以下结论：（1）LMS算法在收敛速度和计算量方面具有优势，但在噪声敏感性和稳态误差方面存在不足。

（2）RLS算法在收敛速度和计算量方面优于LMS算法，但在噪声敏感性和稳态误差方面存在不足。

.Harbin Institute of Technology自适应平衡器计算机实验课程名称：自适应信号处理院系：电子与信息工程学院姓名：学号：授课教师：**哈尔滨工业大学一、实验目的：1. 深入掌握自适应平衡器的理论基础和以及它的可能用途。

2. 理解最小均方自适应算法的适用条件，以及最小均方自适应算法的理论推导。

3. 改变特征值扩散度）（R χ与步长参数μ，观察实验结果，深入理解理解这些参数对实验结果的重要性。

4. 探究在线性色散信道中使用最小均方自适应算法引起的失真问题。

二、实验内容：在此次实验中我们研究LMS 算法自适应均衡引起未知失真的线性色散信道问题。

假设数据是实数，图2.1表示用来进行该项研究的系统框图。

自适应均衡器用来纠正存在白噪声的信道的畸变。

通过随机数发生器1产生用来探测信道的测试信号n x ；通过随机数发生器2来产生干扰信道输出的白噪声源()v n 。

这两个发生器是相互独立的。

经过适当延迟，随机数发生器1页提供用作训练序列的自适应均衡器的期望相应。

加到信道输入的随机序列{}n x 由伯努利序列组成，其中1n x =±，随机变量n x 具有零均值和单位方差。

信道的单位脉冲响应应用升余弦表示为20.5[1cos((2))]1,2,30n n n h Wπ⎧+-=⎪=⎨⎪⎩，其他 (2-1)等价地，参数W 控制均衡器抽头输入的相关矩阵的特征值分布()χR ，并且特征值分布随着W 的增大而扩大。

随机数发生器2产生的序列是零均值，方差20.001v σ=。

随机噪声发生器(1)信道随机噪声发生器(2)延迟∑自适应横向滤波器∑nx nv +-ne图2.1 自适应均衡实验框图这里均衡器具有11M =个抽头。

由于信道的脉冲响应n h 关于2n =时对称，均衡器的最优抽头权值on w 在5n =时对称。

因此信道的输入n x 被延时了=∆2+5=7个样值，以便提供均衡器的期望响应。

通过选择匹配横向均衡器中点的合适延时Δ，LMS 算法能够提供信道响应的最小相位分量和非最小相位分量之逆。

目录一、绪论 (2)1.1 论文背景及研究意义 (2)1.2 音频简介 (2)1.3 自适应滤波理论的发展 (3)1.3.1 FIR滤波器的结构 (5)1.4 自适应滤波算法简介 (6)1.4.1 基于维纳滤波理论的算法 (6)1.4.2 基于卡尔曼滤波理论的算法 (7)1.4.3 基于最小二乘法的算法 (8)1.4.4 基于神经网络的算法 (8)1.5自适应LMS算法的发展 (9)1.5.1 LMS算法的历史 (9)1.5.2 LMS算法的发展现状 (10)1.5.3 LMS算法的发展前景 (10)1.6 变步长LMS算法 (11)二、最小均方算法 (12)2.1 LMS算法原理 (12)2.2 LMS算法性能分析 (13)2.2.1 收敛性 (13)2.2.2 收敛速度 (15)2.2.3 稳态误差 (16)2.2.4 计算复杂度 (17)2.3 变步长的LMS (17)三、实验过程 (19)3.1 LMS算法实现 (19)3.1.1 音频读取 (19)3.1.2 参考噪声及带噪信号的获得 (19)3.1.3 LMS算法 (21)3.1.4 代码实现 (23)3.2 VSSLMS算法实现 (25)3.2.1 VSSLMS算法 (25)3.2.2 代码实现 (27)3.3 本章总结 (29)四、总结与展望 (30)4.1 论文总结 (30)4.2 展望 (30)五、参考文献 (31)一、绪论1.1 论文背景及研究意义自适应信号处理是现代通信处理的一个重要分支学科。

与传输函数恒定的滤波器相比，自适应滤波器能根据环境自动调节抽头系数以达到最佳工作状态，被广泛应用于通信、雷达、系统控制和生物医学工程等领域。

自适应信号处理的主要应用有均衡、系统辨识、阵列信号的波束成形、噪声对消和预测编码等。

在音频降噪方面，自适应信号处理也应用诸多。

音频中降噪方法很多，按照是否有参考信号可以将降噪分为主动降噪和被动降噪。

RLS 和LMS 自适应算法分析摘要：本文主要介绍了自适应滤波的两种算法：最小均方(LMS, Least Mean Squares)和递推最小二乘(RLS, Recursive Least Squares)两种基本自适应算法。

我们对这两种基本的算法进行了原理介绍，并进行了Matlab 仿真。

通过仿真结果，我们对两种自适应算法进行了性能分析，并对其进行了比较。

用Matlab 求出了LMS 自适应算法的权系数，及其学习过程曲线，和RLS 自适应权系数算法的学习过程。

关键词：自适应滤波、LMS 、RLS 、Matlab 仿真Abstract: this article mainly introduces two kinds of adaptive filtering algorithms: Least Mean square (LMS), further Mean Squares) and Recursive Least Squares (RLS, Recursive further Squares) two basic adaptive algorithm. Our algorithms of these two basic principle is introduced, and Matlab simulation. Through the simulation results, we have two kinds of adaptive algorithm performance analysis, and carries on the comparison. Matlab calculate the weight coefficient of the LMS adaptive algorithm, and its learning curve, and the RLS adaptive weight coefficient algorithm of the learning process.Keywords:, LMS and RLS adaptive filter, the Matlab simulation课题简介：零均值、单位方差的白噪声通过一个二阶自回归模型产生的AR 过程。

第27卷　第5期　吉首大学学报(自然科学版)V ol.27　N o.5 2006年9月Journal of Jishou University(Natural Science Edition)Sept.2006 文章编号:1007-2985(2006)05-0073-03自适应均衡器的LMS算法实现及其仿真Ξ张雅彬,王融丽,刘　昕(吉首大学物理科学与信息工程学院,湖南吉首　416000)摘　要:自适应均衡器已广泛应用于通信、雷达、声纳、控制和生物医学工程等许多领域,为克服多径衰落和信道失真引起的码间干扰,实时跟踪移动通信信道的时变特性,笔者设计了一个基于LMS算法的自适应线性均衡器,并通过改变步长因子Δ来分析其收敛速度和均方误差特性.关键词:自适应均衡器;LMS算法;仿真中图分类号:T N911.5 文献标识码:A在高速数字通信中,多径衰落和信道失真可引起严重的码间干扰,已成为数字通信面临的主要困难之一.克服ISI的一种有效途径是在接收机中采用均衡技术.由于移动衰落信道具有随机性和时变性,这就要求均衡器必须能够实时地跟踪移动通信信道的时变特性,这种自适应均衡器常见的工作模式为训练模式和跟踪模式.对于线性均衡器,其算法有很多种,最常见是基于LMS的算法的自适应均衡器.笔者设计了一个基于LMS算法的自适应均衡器,通过改变步长因子分析其收敛速度及均方误差.[1]1　自适应均衡器LMS算法实现自适应滤波器的研究始于20世纪50年代末,Windrow和H off等在20世纪60年代初提出最小均方误差自适应算法[2] (Least Mean Squares,LMS).LMS算法的基本原理[2-3]是基于误差梯度的最陡下降法,用平方误差代替均方误差,沿着权值的负方向搜索达到均方误差最小意义下的自适应滤波.LMS算法因其结构简单、稳定性好而且易于实现,一直是自适应滤波经典、有效的算法之一.但是这种固定步长的LMS自适应算法在收敛速率、跟踪速率及权失调噪声之间的要求是相互矛盾的,为了克服这一矛盾,人们讨论了各种各样的变步长LMS自适应滤波的改进算法.[4]更新方向向量υ(n)取作第n-1次迭代的E{e2(n)}的负梯度,即最陡下降法,根据这种思想产生的算法称为最小均方算法(LMS).LMS算法的依据是最小均方误差,即理想信号d(n)与滤波器实际输出y(n)之差e(n)的平方值的期望值E{e2(n)}最小,并且根据这个依据来修改权系数w i(n).为了使期望值E{e2(n)}最小,采用最广泛使用的自适应算法形式“下降算法”:Wi (n)=Wi(n-1)+μ(n)υ(n).式中的W i(n)为第n步迭代的权向量,μ(n)为第n次迭代的收敛因子,而υ(n)是第n次迭代的更新方向.最常用的下降算法为梯度下降法,常称最陡下降法.令N阶FIR滤波器的抽头系数为Wi(n),滤波器的输入和输出分别为x(n)和y(n),则FIR横向滤波器方程可表示为y(n)=6N i=-1W i(n)X(n-i),(1)令d(n)代表“所期望的响应”,并定义误差信号e(n)=d(n)-y(n)=d(n)-6N i=-1W i(n)X(n-i),(2)采用向量形式表示权系数及输入W和x(n),可以将误差信号e(n)写作e(n)=d(n)-W T X(n)=d(n)-X(n)W,(3)则误差平方为e2(n)=d2(n)-2d(n)X T(n)W+W T X(n)X T(n)W.(4)Ξ收稿日期:2006-04-16基金项目:湖南省教育厅科学研究项目(04C492)作者简介:张雅彬(1979-),男,山东菏泽人,吉首大学物理科学与信息工程学院教师,主要从事无线通信教学与研究.上式两边取数学期望后,得均方误差E {e 2(n )}=E {d 2(n )}-2E {d (n )X T (n )}W +W T E {X (n )X 2(n )}W .(5)定义互相关函数向量R xd T =E {d (n )X T (n )},(6)自相关函数矩阵R xx =E {X (n )x T (n )},(7)则(5)式可表示为E {e 2(n )}=E {d 2(n )}-2R T xd W +W T R xx W .(8)这表明均方误差是权系数向量W 的二次函数,它是一个凹的抛物型曲面,具有唯一最小值的函数.调节权系数使均方误差为最小.将(8)式对权系数W 求导数,得到均方值误差函数的梯度(n )= E {e 2(n )}=[9E {e 2(n )}/9W 1,…,9E {e 2(n )}/9W n ]T .(9)令 (n )=0,即可求出最佳权系数向量W opt =R -1xx R xd .(10)将W opt 代入(8)式得最小均方差值E {e 2(n )}min =E {d 2(n )}-R T xd W opt .(11)利用(11)式求最佳权系数向量的精确解需要知道R xx 和R xd 的先验统计知识,而且还需要进行矩阵求逆等运算.Widrow 和H off 提出了求解W opt 的近似值的方法,习惯上称之为Widrow 2H off LMS 算法.正如前面所介绍的,这种算法的根据是最优化理论方法中的最速下降法.根据最速下降法.“下一时刻”权系数向量W (n +1)应该等于“现时刻”权系数向量W (n )加上一个负均方误差梯度- (n )的比例项,即W (n +1)=W (n )-μ (n ),(12)其中μ是一个控制收敛速度与稳定性的常数,称之为收敛因子,LMS 算法与梯度 (n )和收敛因子μ有关.精确计算梯度 (n )是十分困难的,一种粗略的但是却十分有效的计算 (n )的近似方法是直接取e 2(n )作为均方误差E {e 2(n )}的估计值,即(n )= [e 2(n )]=2e (n ) [e (n )].(13)其中[e (n )]= [d (n )-W T (n )X (n )]=-X (n ).(14)将(14)式代入(13)式中,得到梯度估值(n )=-2e (n )X (n ),(15)于是Widrow 2H off LMS 算法为W (n +1)=W (n )+2μe (n )X (n ).(16)在LMS 算法中,由于采用最陡下降法的思想来更新权系数向量W (n ),所以LMS 算法中的收敛因子μ决定抽头权向量在每次迭代中的更新量,是影响算法收敛速率和稳态性能的关键参数.收敛因子μ的选择一直是研究的热点,基于LMS 算法的收敛分为均值收敛和均方收敛2种[3],对于收敛因子μ的选择(现在常被称为学习速率参数选择[2])已经有几种著名的选择方法,如时变学习速率的“模拟退火法则”,“换档变速方法(gear 2shifting approach )”等[5].2　计算机仿真图1　传输信息模型 图2　仿真误差分析47吉首大学学报(自然科学版)第27卷 系统仿真模型如图1所示,系统仿真误差分析如图2所示.均衡选取的信道抽头数是2K +1=11,接收信号加噪声的功率P R 归一化到1,信道特性由向量x 确定,其中x =(0.05,-0.063,0.088,-0.126,-0.25,0.0947,0.25,0,0.126,0.038,0.088).Matlab 仿真源代码如下:echo onN =500;K=5;actual isi =[0.05-0.0630.088-0.126-0.250.90470.2500.1260.0380.088];sigma =0.01;delta =0.115;Num ofrealizations =1000;mse av =zeros (1,N -23K );for j =1:Num of realizations ,　%the in formation sequence for i =1:N , if (rand <0.5), in fo (i )=-1; else in fo (i )=1; end ; echo off ;　end ;　if (j ==1);echo on ;end　%the channel output y =filter (actual isi ,1,in fo );　for i =1:2:N ,[noise (i )noise (i +1)]= gngauss (sigma );end ;　y =y +noise ;　estimated c =[00000100000];　for k =1:N -23K, y k =y (k :k +23K ); z k =estimated c 3y k.’;e k =in fo (k )-zk ; estimated c =estimated c +delta 3e k 3y k ; mse (k )=e k ^2;　echo off ;end ;　if (j ==1);echo on ;end mse av =mse av +mse ;　echo off ;end ;echo on ;mse av =mse av ΠNum of realizations ;m =[1:490];plot (m ,mse av );3　结语从仿真结果可以发现,减小步长因子Δ,收敛稍许变慢,但可达到最小的均方误差.增加Δ可提高收敛速度,但是当Δ增大时其均方误差也相应增大.所以选择合适的步长因子Δ对于均衡器的性能来说是至关重要的,笔者设计的自适均衡器克服了多径衰落和信道失真可引起的码间干扰,提高通信的传输质量.参考文献:[1]　西　蒙・赫金.自适应滤波器原理(第4版)[M].北京:电子工业出版社,2003.[2]　张贤达.现代信号处理(第2版)[M].北京:清华大学出版社.[3]　H AYKI N S.Adaptive Filter Theory [M].America :Prentice Hall ,Inc ,S im on&Schuster C ompany ,1996.[4]　曹达仲,王尤翠.数字移动通信中的自适应均衡技术[J ].通信技术,1997,(2):67-69.[5]　WI DROW B ,STE ARNS S D.Adaptive S ignal Processing [M].New Y ork :Prentice -Hall ,1985.Adaptive Equalization Simulation B ased on LMS AlgorithmZH ANG Y a 2bin ,W ANG R ong 2li ,LI U X in(C ollege of Physics Science &In formation Engineering ,Jishou University ,Jishou 416000,Hunan China )Abstract :As an im portant aspect of adaptive signal processing ,adaptive equalization is widely used in the field of tele 2communication ,radar ,s onar ,control and bio medical engineering.In order to overcome the intersymbol interference caused by multipath fadiy and channel distortion ,and according to the time 2dependent charateristics of real 2time track 2ing m obile communication channel ,the author designs on adaptive linear equalization based on LMS alg orithm and ana 2lyzes its convergence rate and mean square error characteristics by varying the step factor.K ey w ords :adaptive equalization ;LMS ;simulation analysis (责任编辑　陈炳权)57第5期 张雅彬,等:自适应均衡器LMS 算法实现及其仿真。

自适应均衡算法LMS研究一、自适应滤波原理与应用所谓自适应滤波器，就是利用前一时刻已获得的滤波器参数等结果，自动地调节现时刻的滤波器参数，以适应信号和噪声未知的或随时间变化的统计特性，从而实现最优滤波。

根据环境的改变，使用自适应算法来改变滤波器的参数和结构。

1.1均衡器的发展及概况均衡是减少码间串扰的有效措施。

均衡器的发展有史已久，二十世纪60年代前，电话信道均衡器的出现克服了数据传输过程中的码间串扰带来的失真影响。

但是均衡器要么是固定的，要么其参数的调整是手工进行。

1965年，Lucky在均衡问题上提出了迫零准则，自动调整横向滤波器的权系数。

1969年，Gerhso和Porkasi，Milier分别独立的提出采用均方误差准则(MSE)。

1972年，ungeboekc将LMS算法应用于自适应均衡。

1974年，Gedard 在kalmna滤波理论上推导出递推最小均方算法RLS(Recursive least-squares)。

LMS类算法和RLS类算法是自适应滤波算法的两个大类。

自适应滤波在信道均衡、回波抵消、谱线增强、噪声抑制、天线自适应旁瓣抑制、雷达杂波抵消、相参检测、谱估计、窄带干扰抑制、系统辨识、系统建模、语音信号处理、生物医学、电子学等方面获得广泛的应用。

1.2均衡器种类均衡技术可分为两类：线性均衡和非线性均衡。

这两类的差别主要在于自适应均衡器的输出被用于反馈控制的方法。

如果判决输出没有被用于均衡器的反馈逻辑中，那么均衡器是线性的；如果判决输出被用于反馈逻辑中并帮助改变了均衡器的后续输出，那么均衡器是非线性的。

图1.1 均衡器的分类1.3自适应算法LMS 算法LMS 算法是由widrow 和Hoff 于1960年提出来的,是统计梯度算法类的很重 要的成员之一。

它具有运算量小,简单,易于实现等优点。

LMS 算法是建立在Wiener 滤波的基础上发展而来的。

Wiener 解是在最小均方误差(MMSE)意义下使用均方误差作为代价函数而得到的在最小误差准则下的最优解。

自适应均衡器的LMS实现为了对非理想信道进行补偿，通信系统中广泛采用信道均衡技术，以降低信道对信号的畸变，提升传输的可靠性。

本文介绍了基于最小均方算法（LMS算法）的自适应均衡器原理和结构，并利用MATLAB对其算法进行了仿真。

标签：自适应均衡器;LMS;MATLAB0 引言随着现代通信技术的快速发展，通讯环境越来越复杂，如何快速有效地解调信号是通信系统面临的一个新的课题。

在通信领域，自适应算法已经在信道均衡、频率跟踪与检测方面有了广泛的应用[1]。

研究表明，借助自适应滤波器的信号跟踪能力和抗干扰能力，能够使得基带信息的提取更加方便，获得比相干解调更好的性能。

1 自适应均衡器均衡器可以分为两种：时域均衡和频域均衡。

由于通信系统是复杂多变的，信道特性是不可预知的。

为了能够在接收端达到更好的接收效果，均衡器就需要具有良好的自适应性能，以满足信道的多变性。

如果在均衡器的设计中加入信号处理的自适应算法，则这一类均衡器即为自适应均衡器。

在通信系统当中，基带信号的复包络包含多种信号信息。

均衡器可以根据基带信号来实现对信道冲击响应的估计，而在接收端的信号解调过程当中则可以使用自适应算法。

2 LMS自适应均衡器信道均衡器可以使通信系统在通带外的增益近似为零，故附加了均衡器的信道在通带内的振幅是均匀的，而其它部分基本为零，而相位响应在通带内则为频率的线性函数。

最小均方（Least Mean Square，LMS）算法由Widrow于1960年提出[2]。

LMS算法的原理是使实际输出和期望输出的均方误差取得最小，而在整个逼近过程中需要不断地用输入信号估计梯度矢量，并调整系统的各个加权。

（1）其中，为输入信号，为输出信号，为权系数。

由Wiener滤波理论可知，滤波器的最优抽头系数矢量可表示为（2）式中是输入信号矢量的互相关函数，为与期望信号矢量的互相关函数。

当滤波器的抽头系数比较多时，直接求解式（1）是非常困难的。

将LMS算法应用到均衡器的设计当中，可以很好的简化设计流程，提高均衡器对信道特性的自适应性。

基于LMS算法的自适应线性均衡器设计自适应线性均衡器（Adaptive Linear Equalizer）是一种用于解决通信系统中信号传输过程中引起的衰落、多径干扰和色散等问题的数字信号处理技术。

其中，最常用的算法就是最小均方算法（LMS算法）。

本文将对基于LMS算法的自适应线性均衡器设计进行详细探讨，以便进一步理解该技术的原理和应用。

自适应线性均衡器的设计目标就是使得接收到的信号尽可能接近发送信号。

在传输过程中，信号可能受到多径干扰、噪声和失真等因素的影响。

自适应线性均衡器的任务就是根据接收信号的特征自动调整其内部权值，以最小化输出信号与原始信号之间的误差。

LMS算法是一种基于梯度下降的迭代算法，它通过最小化均方（Mean Square Error，MSE）误差来更新权值。

LMS算法的基本思想是根据误差信号的梯度来调整权值，从而最小化误差。

在自适应线性均衡器中，LMS算法的实现需要以下步骤：1.定义输入信号和目标信号：将输入信号表示为x(n)，目标信号（即发送信号）表示为d(n)。

2.初始化权值向量：将权值向量w(n)初始化为一个较小的初值，通常为零。

3.计算估计输出：根据当前权值向量，计算自适应线性均衡器的估计输出y(n)。

4.计算误差信号：将估计输出与目标信号进行比较，计算误差信号e(n)。

5.更新权值向量：根据误差信号的梯度计算出权值的变化量，并将其加到当前的权值向量上，得到新的权值向量。

6.重复步骤3到步骤5，直到收敛或达到预设的迭代次数。

自适应线性均衡器的设计中，一些关键问题需要考虑：1.学习率：学习率决定了权值的更新速度，过大的学习率可能导致不稳定性，而过小的学习率则会导致收敛速度过慢。

因此，需要根据实际情况选择合适的学习率。

2.初始权值：初始权值的选择可能会影响算法的收敛速度和性能。

通常可以将初始权值设置为零或一个随机小值，然后通过迭代调整权值。

3.触发更新：权值的更新可以在每个符号周期内进行，也可以在每个数据块周期内进行。