运筹作业4
- 格式:doc
- 大小:103.50 KB
- 文档页数:17


作业1、俄亥俄州近年来购买了一片土地用于开发建设一个新公园。
公园设计者已经为住宿(A)、野餐园(B)、船坞(C)和景点(D)确定了地点。
这些地点中可能的直接路线连接见下表。
公园的设计者希望通过修建的道路能够抵达上述所有地点的同时,所建道路的总长度最短。
请建立该问题的网络模型并进行求解。
2、莎拉在高中毕业典礼上收到了父母的礼物---12千元专项基金用于购买了一辆使用了三年的二手车,供她上大学使用。
由于车的使用、维护费用随着汽车的老化而飞速上涨,莎拉在接下来的三个夏天里可以一次或几次折价将她的汽车置换为其他使用了三年的二手车(父母会在她大学毕业时送一辆新车作为她大学毕业的礼物)。
莎拉每个时期购买一辆使用了三年的二手车相关数据见下表。
试问莎拉应什么时候折价卖掉她的汽车可以使她在大学四年里在汽车方面的花费最小?试建立该问题的模型。
3、体重控制中心Nutri-Jenny为客户提供各种各样的冷冻主餐。
这些主餐的营养成分受到严格的监控以保障客户膳食平衡。
目前拟中心开发一种新的主餐--牛腰间肉大餐,其配料及相应的营养成分、成本等信息见下表。
该主餐的营养要求:(1)必须含有280~320的卡路里;其中,脂肪所含卡路里不能超过总卡路里含量的20%;(2)至少含有600国际单位的维生素A、10毫克的维生素C和30克的蛋白质;(3)每盎司的牛肉至少配有半盎司的肉汁。
试建立使该主餐配方成本最低的配餐方案模型。
4、判断下图中的流是否为最大流;若不是,求其最大流及最小截集,并解释最小截集含义。
5、写出下列问题的对偶问题。
Max. 6X1+7X2-X3s.t. 3X1+2X2+4X3>=124X2-9X3<=7X1 +5X3=13X2>=0, X3<=0。
实验四:Excel中方案管理器的使用在现实的管理决策问题中,数据资源作为管理系统的输入,一般都要经过比较复杂的运算或变换才能产生有价值的信息,即输出结果。
Excel不仅能对数据进行复杂的运算、实现对信息资源的深加工,其中的[工具][方案]命令还提供了存储、显示、汇总、组合不同输入和由它们经过变换所产生的输出结果的功能。
这一功能为管理人员分析评价各种决策方案带来了方便。
在国外,这种分析称为What-if分析(假设方案分析),就是直接观察输出结果对输入的相应变化。
本实验我们将学习Excel中[工具][方案]命令的使用方法。
一、实验目的1、掌握如何用[工具][方案]命令直接建立方案。
2、掌握在选取[工具][方案]命令后弹出的“方案管理器”对话框中各有关选项的意义及用法。
3、如何用[工具][方案]命令对线性规划模型进行灵敏度分析。
二、实验内容(一)[工具][方案]命令Excel中有两种用于建立方案的方法:⑴直接用[工具][方案]命令选项建立多个方案;⑵间接方法建立,即对使用[工具][规划求解]命令建立的最优方案进行保存和分析。
但如果要建立和显示多个方案则必须采用第一种方法。
本实验的目的在于分析和对比多个方案,所以必须采用第一种方法来建立方案。
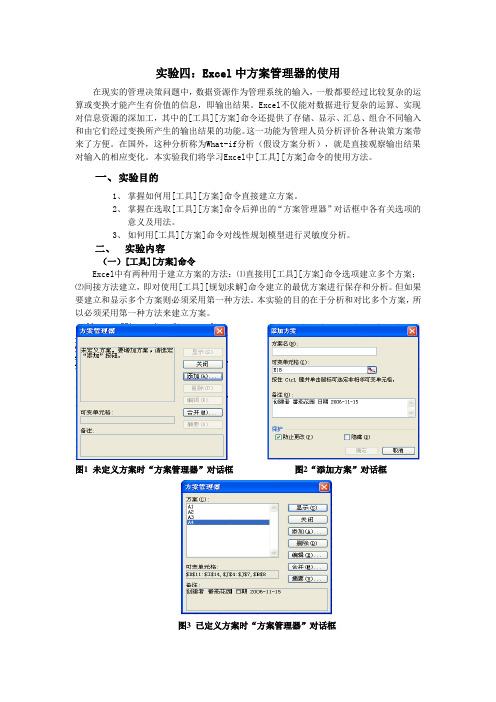
图1 未定义方案时“方案管理器”对话框图2“添加方案”对话框图3 已定义方案时“方案管理器”对话框在选取[工具][方案]命令后,会弹出图1所示“方案管理器”对话框,如果单击此对话框右侧的“添加”按钮则会弹出如图2所示对话框,其中各选项说明如表1。
示例:有四个原煤生产地A1、A2、A3、A4,今年产量分别为35、45、55、65万吨,另外有六个煤炭销售地B1、B2、B3、B4、B5、B6,今年销量分别为40、20、30、40、30、40万吨。
明年预计各地的销量都将增加5万吨,因此,总销量比今年总量增加30万吨。
计划机关为了使产销平衡,打算增加一套年产30万吨的采煤设备。

《运筹学》第四章习题及答案一、思考题1.运输问题的数学模型具有什么特征?为什么其约束方程的系数矩阵的秩最多等于m,n,1?2.用左上角法确定运输问题的初始基本可行解的基本步骤是什么? 3.最小元素法的基本思想是什么?为什么在一般情况下不可能用它直接得到运输问题的最优方案?4.沃格尔法(Vogel 法)的基本思想是什么?它和最小元素法相比给出的运输问题的初始基本可行解哪一个更接近于最优解?为什么?5.试述用闭回路法检验给定的调运方案是否最优的原理,其检验数的经济意义是什么?6.用闭回路法检验给定的调运方案时,如何从任意空格出发去寻找一条闭回路?这闭回路是否是唯一的?7.试述用位势法求检验数的原理、步骤和方法。
8.试给出运输问题的对偶问题(对产销平衡问题)。
9.如何把一个产销不平衡的运输问题(产大于销或销大于产)转化为产销平衡的运输问题。
10.一般线性规划问题应具备什么特征才可以转化为运输问题的数学模型?11.试述在表上作业法中出现退化解的涵义及处理退化解的方法。
二、判断下列说法是否正确1.运输问题模型是一种特殊的线性规划模型,所以运输问题也可以用单纯形方法求解。
2.因为运输问题是一种特殊的线性规划模型,因而求其解也可能出现下列四种情况:有唯一最优解;有无穷多个最优解;无界解;无可行解。
3.在运输问题中,只要给出一组(,,xijm,n,1)个非零的,且满足nmx,aijix,b,,ijjj,1 i,1,,就可以作为一个基本可行解。
4.表上作业法实质上就是求解运输问题的单纯形法。
5.按最小元素法或元素差额法给出的初始基本可行解,从每一空格出发都可以找到一闭回路,且此闭回路是唯一的。
6.如果运输问题单位运价表的某一行(或某一列)元素分别加上一个常数k ,最优调运方案将不会发生变化。
7.如果运输问题单位运价表的某一行(或某一列)元素分别乘上一个常数k ,最优调运方案将不会发生变化。
8.用位势法计算检验数时,先从某一行(或列)开始,给出第一个位势的值,这个先给出的位势值必须是正的。

运筹学作业(三)
习题1、
试利用0-1变量对下列各题分别表示成一般线性约束条件:
(a )221≤+x x 或53221≥+x x
(b )变量x 只能取值0、3、5或7中的一个
(c )变量x 或等于0,或≥50
(d )若21≤x ,则1≥2x ,否则4≤2x
(e )以下四个约束条件中至少满足两个:
521≤+x x ,21≤x ,23≥x ,643≥+x x
习题2、试利用0-1变量将下述问题题表示成一般线性约束条件,然后用EXCEL 求解
32152max x x x x ++=
⎪⎩⎪⎨⎧≥≤++≥-+-0,,10
2153103
21321321x x x x x x x x x 习题3、清华大学运筹学(第三版) P99 3.3 只计算3-47表格
(1) 用西北角法、最小元素法、伏格尔法给出初始方案
(2) 对用“最小元素法”给出的初始方案,用“闭合回路法”判定是否最优
(3) 对用“伏格尔法”给出的初始方案,用“位势法”判定是否最优
(4) 对(3)的结果进行分析,如果不是最优,调整方案,直至最优为止
习题4、 清华大学运筹学(第三版) P99 3.6
(用计算机求解)。

全国自考(运筹学基础)-试卷4(总分80, 做题时间90分钟)1. 单项选择题1.“运筹帷幄”这一成语表明,在中国古代英明的军队指挥员已能运用( )SSS_SINGLE_SELA 单纯的主观判断方法B 定性决策方法C 定性决策与简单的定量决策相结合的方法D 只凭自己的经验决策的方法分值: 2答案:C解析:混合性决策:运用定性和定量两种方法才能制定的决策。
2.指数平滑预测方法是一种 ( )SSS_SINGLE_SELA 纯定量预测法B 纯定性预测法C 定性与定量相结合的方法D 既非定性也非定量分值: 2答案:C解析:指数平滑预测方法是一种定性与定量相结合的方法。
3.加权平均数预测法是一种 ( )SSS_SINGLE_SELA 纯定性预测B 定性和定量相结合的方法C 既非定性又非定量的预测法D 纯定量方法分值: 2答案:B解析:加权平均数预测法是一种定性和定量相结合的方法。
4.最大最小原则是用来解决下列哪项条件下的决策问题? ( )SSS_SINGLE_SELA 不确定B 确定C 风险D 风险或不确定分值: 2答案:A解析:不确定条件下的决策包括最大最大决策标准,最大最小决策标准,最小最大遗憾值决策标准,现实主义决策标准。
5.下列有关存货台套的说法中,错误的是 ( )SSS_SINGLE_SELA 存货台套是存货管理的单位B 某个存货台套中可以包括不同的单项存货C 存货台套法简化了库存管理的工作内容D 每个存货台套包括的单项存货在数目上一般是相同的分值: 2答案:D解析:存货台套包括的单项存货在数目上可以有多有少。
6.一元线性回归预测中,相关系数R的取值范围一般是 ( )SSS_SINGLE_SELA R≥0B Q≤R≤1C -1≤R≤1D 0.5≤R≤0.9分值: 2答案:C解析:一元线性回归中R的取值范围是:-1≤R≤1。
7.在Ft+1 =Ft+a(xt-Ft)中,a的取值范围是 ( ) SSS_SINGLE_SELA -1≤a<0B 0≤a≤1C a>1D a<-1分值: 2答案:B解析:指数平滑预测法中a的取值范围是:0≤a≤1。
产品生产规划某医院为病人配制营养餐要使用到两种食品A 和B ,每种食品A 含蛋白质50g ,钙400mg , 热量1000单位,价值14元;食品B 含蛋白质60g ,钙200mg ,热量800单位,价值8元.若病人每天需从食物中获取蛋白质,钙及热量分别为55g ,800mg 和3000单位,问如何选购食品才能在满足营养要求条件下使花费最小?试组建线性规划模型并求解后回答:(1)问题的最优方案及最优值分别是甚麽?最优方案是否有选择余地? (2)各种营养要求的满足情况怎样?若限制蛋白质摄入量不超过100单位,会出现甚麽问题?解:本题属于简单的线性规划模型的建立与求解问题,并要求作出一点模型分析工作.按要求,先来建立模型,根据题设,设购买两种食品分别为21,x x (kg ),则有总花费数额函数21814x x z +=,自然我们希望求出这样的21,x x 取值,使得函数z 取最小值.可以写为min 21814x x z +=. 又根据营养最低要求,应有蛋白质需求条件: ,55605021≥+x x 钙的需求条件: 40080020021≥+x x , 热量的需求条件: ,3000800100021≥+x x 非负性条件: .0≥j x将上述条件合在一起,即可获得本问题的线性规划模型如下:m i n 21814x x z+= ⎪⎪⎩⎪⎪⎨⎧..t s ,0,30008001000,800200400,556050212121≥≥+≥+≥+j x x x x x x x利用图解法易于得到其最优解为),310,31(*=X 即食品A 购买31(kg ),B 购买310(kg ),最低花费=*z 394元.由此可回答所提问题:(1)最优解与最优目标值如上所述,最优方案无选择余地,因为最优解点是在后两个约束条件直线的交点上,而不是在可行域的某条边界线段上.(2)钙和热量需求得到满足(最低量),蛋白质需求超最低标准3485个单位.以上结论是将最优解代入各个约束条件得到的.若限制蛋白质摄入量不超过100单位,则第一个约束条件应修改为,55605010021≥+≥x x在原来的求解图上加上条件,100605021≤+x x 则可见可行域不存在,故无解.2.某工厂生产两种产品A 、B 分两班生产,每周生产总时间为80小时,两种产品的预测销售量、生产率和赢利如下表(1)充分利用现有能力,避免设备闲置; (2)周加班时间限制在10小时以内;(3)两种产品周生产品量应满足预测销售,满足程度的权重之比等于它们单位利润之比;(4)尽量减少加班时间. 解: (1)建立模型设:①每班上班时间为8小时,在上班时间内只能生产一种产品; ②周末加班时间内生产哪种产品不限; ③生产A 产品用x 班,生产B 产品用y 班,周加班时生产A 产品用x 1小时,生产B 产品用y 1小时.则有⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≥≤+=++≤+≤+=+且为整数0,,,101:2148:987084581011111111y x y x y x x x y y x x y y y x(2)求解现在求满足(1)中第2,3个方程可看出:8≤x ,5≥y ; 将(1)中的第1个方程代入第4个方程得:1179720128y x y -+= 现在就是在满足5≤y ,1011≤+y x 条件下,使上式两端的取值尽量接近.显然5=y ,01=x ,101=y因此 5=x制定方案为,生产A ,B 两种产品所占总时间各一半,周加班10小时全用于生产产品B .运输规划问题现要从两个仓库(发点)运送库存原棉来满足三个纺织厂(收点)的需要,数据如下表,试问在保证各纺织厂的需求都得到满足的条件下应采取哪个运输方案,才能使总运费达到最小?(运价(元/吨)如下表)解:题意即要确定从i 号仓库运到j 号工厂的原棉数量。
P250习题8.3(1)model:min=d11;3*x1+x2+x3+d11-d12=60;x1>=0;x2>=0;x3>=0;d11>=0;d12>=0;end问题1:Global optimal solution found.Objective value: 0.000000Infeasibilities: 0.000000Total solver iterations: 0Variable Value Reduced CostD11 0.000000 1.000000X1 0.000000 0.000000X2 0.000000 0.000000X3 60.00000 0.000000D12 0.000000 0.000000Row Slack or Surplus Dual Price1 0.000000 -1.0000002 0.000000 0.0000003 0.000000 0.0000004 0.000000 0.0000005 60.00000 0.0000006 0.000000 0.0000007 0.000000 0.000000问题2:model:min=d22;3*x1+x2+x3+d11-d12=60;x1-x2+2*x3+d21-d22=10;x1>=0;x2>=0;x3>=0;d12>=0;d21>=0;d22>=0;endGlobal optimal solution found.Objective value: 0.000000Infeasibilities: 0.000000Total solver iterations: 2Variable Value Reduced CostD22 0.000000 1.000000X1 17.50000 0.000000X2 7.500000 0.000000X3 0.000000 0.000000D11 0.000000 0.000000D12 0.000000 0.000000D21 0.000000 0.000000Row Slack or Surplus Dual Price1 0.000000 -1.0000002 0.000000 0.0000003 0.000000 0.0000004 17.50000 0.0000005 7.500000 0.0000006 0.000000 0.0000007 0.000000 0.0000008 0.000000 0.0000009 0.000000 0.00000010 0.000000 0.000000问题3:model:min=d31+d32;3*x1+x2+x3+d11-d12=60;x1-x2+2*x3+d21-d22=10;x1+x2-x3+d31-d32=20;x1>=0;x2>=0;x3>=0;d12>=0;d21>=0;d22=0;endGlobal optimal solution found.Objective value: 0.000000Infeasibilities: 0.000000Total solver iterations: 3Variable Value Reduced CostD31 0.000000 1.000000D32 0.000000 1.000000X1 10.00000 0.000000X2 20.00000 0.000000X3 10.00000 0.000000D11 0.000000 0.000000D12 0.000000 0.000000D21 0.000000 0.000000D22 0.000000 0.000000Row Slack or Surplus Dual Price1 0.000000 -1.0000002 0.000000 0.0000003 0.000000 0.0000004 0.000000 0.0000005 10.00000 0.0000006 20.00000 0.0000007 10.00000 0.0000008 0.000000 0.0000009 0.000000 0.00000010 0.000000 0.00000011 0.000000 0.000000P251习题8.7sets:Level/1..3/: P, z, Goal;Variable/1..9/: x;S_Con_Num/1..8/: g, dplus, dminus;S_Cons(S_Con_Num, Variable): C;Obj(Level, S_Con_Num): Wplus, Wminus;endsetsdata:P= ? ? ?;Goal = ?, ?, 0;g= 0 0 0 0 0 0 2000 1000;C = -0.1 0 0 -0.1 0 0 0.9 0 0 0.5 0 0 -0.5 0 0 -0.5 0 0 0 -0.7 0 0 -0.70 0 0.3 0 0 0.8 0 0 -0.2 0 0 -0.2 0 0 0 -0.5 0 0 -0.5 0 0 0.5 0 0 0.9 0 0 -0.1 0 0 -0.1 1 0 0 1 0 0 1 0 0 -0.5 -1 -1.2 1 0.5 0.3 2.5 2 1.8 ; Wplus = 1 0 1 0 1 0 0 00 0 0 0 0 0 0 00 0 0 0 0 0 0 0;Wminus = 0 1 0 1 0 1 0 00 0 0 0 0 0 0 10 0 0 0 0 0 1 0;enddatamin=@sum(Level: P * z);@for(Level(i):z(i)=@sum(S_Con_Num(j): Wplus(i,j)*dplus(j))+@sum(S_Con_Num(j): Wminus(i,j)*dminus(j)));@for(S_Con_Num(i):@sum(Variable(j): C(i,j)*x(j))+ dminus(i) - dplus(i) = g(i););@for(Level(i) | i #lt# @size(Level):@bnd(0, z(i), Goal(i)););运行及其结果如下:第一级目标计算Global optimal solution found.Objective value: 0.000000Infeasibilities: 0.000000Total solver iterations: 0Variable Value Reduced CostP( 1) 1.000000 0.000000P( 3) 0.000000 0.000000Z( 1) 0.000000 1.000000Z( 2) 1000.000 0.000000Z( 3) 2000.000 0.000000 GOAL( 1) 123456.0 0.000000 GOAL( 2) 123456.0 0.000000 GOAL( 3) 0.000000 0.000000 X( 1) 0.000000 0.000000X( 2) 0.000000 0.000000X( 3) 0.000000 0.000000X( 4) 0.000000 0.000000X( 5) 0.000000 0.000000X( 6) 0.000000 0.000000X( 7) 0.000000 0.000000X( 8) 0.000000 0.000000X( 9) 0.000000 0.000000G( 1) 0.000000 0.000000G( 2) 0.000000 0.000000G( 3) 0.000000 0.000000G( 4) 0.000000 0.000000G( 5) 0.000000 0.000000G( 6) 0.000000 0.000000G( 7) 2000.000 0.000000G( 8) 1000.000 0.000000 DPLUS( 1) 0.000000 0.000000 DPLUS( 2) 0.000000 0.000000 DPLUS( 3) 0.000000 0.000000 DPLUS( 4) 0.000000 0.000000 DPLUS( 5) 0.000000 0.000000 DPLUS( 6) 0.000000 0.000000 DPLUS( 7) 0.000000 0.000000 DPLUS( 8) 0.000000 0.000000 DMINUS( 1) 0.000000 0.000000 DMINUS( 2) 0.000000 0.000000 DMINUS( 3) 0.000000 0.000000 DMINUS( 4) 0.000000 0.000000 DMINUS( 5) 0.000000 0.000000 DMINUS( 6) 0.000000 0.000000 DMINUS( 7) 2000.000 0.000000 DMINUS( 8) 1000.000 0.000000 C( 1, 1) -0.1000000 0.000000 C( 1, 2) 0.000000 0.000000 C( 1, 3) 0.000000 0.000000C( 1, 5) 0.000000 0.000000 C( 1, 6) 0.000000 0.000000 C( 1, 7) 0.9000000 0.000000 C( 1, 8) 0.000000 0.000000 C( 1, 9) 0.000000 0.000000 C( 2, 1) 0.5000000 0.000000 C( 2, 2) 0.000000 0.000000 C( 2, 3) 0.000000 0.000000 C( 2, 4) -0.5000000 0.000000 C( 2, 5) 0.000000 0.000000 C( 2, 6) 0.000000 0.000000 C( 2, 7) -0.5000000 0.000000 C( 2, 8) 0.000000 0.000000 C( 2, 9) 0.000000 0.000000 C( 3, 1) 0.000000 0.000000 C( 3, 2) -0.7000000 0.000000 C( 3, 3) 0.000000 0.000000 C( 3, 4) 0.000000 0.000000 C( 3, 5) -0.7000000 0.000000 C( 3, 6) 0.000000 0.000000 C( 3, 7) 0.000000 0.000000 C( 3, 8) 0.3000000 0.000000 C( 3, 9) 0.000000 0.000000 C( 4, 1) 0.000000 0.000000 C( 4, 2) 0.8000000 0.000000 C( 4, 3) 0.000000 0.000000 C( 4, 4) 0.000000 0.000000 C( 4, 5) -0.2000000 0.000000 C( 4, 6) 0.000000 0.000000 C( 4, 7) 0.000000 0.000000 C( 4, 8) -0.2000000 0.000000 C( 4, 9) 0.000000 0.000000 C( 5, 1) 0.000000 0.000000 C( 5, 2) 0.000000 0.000000 C( 5, 3) -0.5000000 0.000000 C( 5, 4) 0.000000 0.000000 C( 5, 5) 0.000000 0.000000 C( 5, 6) -0.5000000 0.000000 C( 5, 7) 0.000000 0.000000 C( 5, 8) 0.000000 0.000000 C( 5, 9) 0.5000000 0.000000 C( 6, 1) 0.000000 0.000000 C( 6, 2) 0.000000 0.000000C( 6, 4) 0.000000 0.000000C( 6, 5) 0.000000 0.000000C( 6, 6) -0.1000000 0.000000C( 6, 7) 0.000000 0.000000C( 6, 8) 0.000000 0.000000C( 6, 9) -0.1000000 0.000000C( 7, 1) 1.000000 0.000000C( 7, 2) 0.000000 0.000000C( 7, 3) 0.000000 0.000000C( 7, 4) 1.000000 0.000000C( 7, 5) 0.000000 0.000000C( 7, 6) 0.000000 0.000000C( 7, 7) 1.000000 0.000000C( 7, 8) 0.000000 0.000000C( 7, 9) 0.000000 0.000000C( 8, 1) -0.5000000 0.000000C( 8, 2) -1.000000 0.000000C( 8, 3) -1.200000 0.000000C( 8, 4) 1.000000 0.000000C( 8, 5) 0.5000000 0.000000C( 8, 6) 0.3000000 0.000000C( 8, 7) 2.500000 0.000000C( 8, 8) 2.000000 0.000000C( 8, 9) 1.800000 0.000000 WPLUS( 1, 1) 1.000000 0.000000 WPLUS( 1, 2) 0.000000 0.000000 WPLUS( 1, 3) 1.000000 0.000000 WPLUS( 1, 4) 0.000000 0.000000 WPLUS( 1, 5) 1.000000 0.000000 WPLUS( 1, 6) 0.000000 0.000000 WPLUS( 1, 7) 0.000000 0.000000 WPLUS( 1, 8) 0.000000 0.000000 WPLUS( 2, 1) 0.000000 0.000000 WPLUS( 2, 2) 0.000000 0.000000 WPLUS( 2, 3) 0.000000 0.000000 WPLUS( 2, 4) 0.000000 0.000000 WPLUS( 2, 5) 0.000000 0.000000 WPLUS( 2, 6) 0.000000 0.000000 WPLUS( 2, 7) 0.000000 0.000000 WPLUS( 2, 8) 0.000000 0.000000 WPLUS( 3, 1) 0.000000 0.000000 WPLUS( 3, 2) 0.000000 0.000000 WPLUS( 3, 3) 0.000000 0.000000WPLUS( 3, 5) 0.000000 0.000000 WPLUS( 3, 6) 0.000000 0.000000 WPLUS( 3, 7) 0.000000 0.000000 WPLUS( 3, 8) 0.000000 0.000000 WMINUS( 1, 1) 0.000000 0.000000 WMINUS( 1, 2) 1.000000 0.000000 WMINUS( 1, 3) 0.000000 0.000000 WMINUS( 1, 4) 1.000000 0.000000 WMINUS( 1, 5) 0.000000 0.000000 WMINUS( 1, 6) 1.000000 0.000000 WMINUS( 1, 7) 0.000000 0.000000 WMINUS( 1, 8) 0.000000 0.000000 WMINUS( 2, 1) 0.000000 0.000000 WMINUS( 2, 2) 0.000000 0.000000 WMINUS( 2, 3) 0.000000 0.000000 WMINUS( 2, 4) 0.000000 0.000000 WMINUS( 2, 5) 0.000000 0.000000 WMINUS( 2, 6) 0.000000 0.000000 WMINUS( 2, 7) 0.000000 0.000000 WMINUS( 2, 8) 1.000000 0.000000 WMINUS( 3, 1) 0.000000 0.000000 WMINUS( 3, 2) 0.000000 0.000000 WMINUS( 3, 3) 0.000000 0.000000 WMINUS( 3, 4) 0.000000 0.000000 WMINUS( 3, 5) 0.000000 0.000000 WMINUS( 3, 6) 0.000000 0.000000 WMINUS( 3, 7) 1.000000 0.000000 WMINUS( 3, 8) 0.000000 0.000000Row Slack or Surplus Dual Price1 0.000000 -1.0000002 0.000000 0.0000003 0.000000 0.0000004 0.000000 0.0000005 0.000000 0.0000006 0.000000 0.0000007 0.000000 0.0000008 0.000000 0.0000009 0.000000 0.00000010 0.000000 0.00000011 0.000000 0.00000012 0.000000 0.000000第二级目标计算Global optimal solution found.Objective value: 0.000000Infeasibilities: 0.000000Total solver iterations: 8Variable Value Reduced CostP( 1) 0.000000 0.000000P( 2) 1.000000 0.000000P( 3) 0.000000 0.000000Z( 1) 0.000000 0.000000Z( 2) 0.000000 0.000000Z( 3) 2000.000 0.000000GOAL( 1) 0.000000 0.000000GOAL( 2) 123456.0 0.000000GOAL( 3) 0.000000 0.000000X( 1) 0.000000 0.000000X( 2) 160.0000 0.000000X( 3) 0.000000 0.000000X( 4) 0.000000 0.000000X( 5) 80.00000 0.000000X( 6) 0.000000 0.000000X( 7) 0.000000 0.000000X( 8) 560.0000 0.000000X( 9) 0.000000 0.000000G( 1) 0.000000 0.000000G( 2) 0.000000 0.000000G( 3) 0.000000 0.000000G( 4) 0.000000 0.000000G( 5) 0.000000 0.000000G( 6) 0.000000 0.000000G( 7) 2000.000 0.000000G( 8) 1000.000 0.000000DPLUS( 1) 0.000000 0.000000DPLUS( 2) 0.000000 0.000000DPLUS( 3) 0.000000 0.000000DPLUS( 4) 0.000000 0.000000DPLUS( 5) 0.000000 0.000000DPLUS( 6) 0.000000 0.000000DPLUS( 7) 0.000000 0.000000DPLUS( 8) 0.000000 0.000000DMINUS( 1) 0.000000 0.000000DMINUS( 2) 0.000000 0.000000DMINUS( 3) 0.000000 0.000000 DMINUS( 4) 0.000000 0.000000 DMINUS( 5) 0.000000 0.000000 DMINUS( 6) 0.000000 0.000000 DMINUS( 7) 2000.000 0.000000 DMINUS( 8) 0.000000 1.000000 C( 1, 1) -0.1000000 0.000000 C( 1, 2) 0.000000 0.000000 C( 1, 3) 0.000000 0.000000 C( 1, 4) -0.1000000 0.000000 C( 1, 5) 0.000000 0.000000 C( 1, 6) 0.000000 0.000000 C( 1, 7) 0.9000000 0.000000 C( 1, 8) 0.000000 0.000000 C( 1, 9) 0.000000 0.000000 C( 2, 1) 0.5000000 0.000000 C( 2, 2) 0.000000 0.000000 C( 2, 3) 0.000000 0.000000 C( 2, 4) -0.5000000 0.000000 C( 2, 5) 0.000000 0.000000 C( 2, 6) 0.000000 0.000000 C( 2, 7) -0.5000000 0.000000 C( 2, 8) 0.000000 0.000000 C( 2, 9) 0.000000 0.000000 C( 3, 1) 0.000000 0.000000 C( 3, 2) -0.7000000 0.000000 C( 3, 3) 0.000000 0.000000 C( 3, 4) 0.000000 0.000000 C( 3, 5) -0.7000000 0.000000 C( 3, 6) 0.000000 0.000000 C( 3, 7) 0.000000 0.000000 C( 3, 8) 0.3000000 0.000000 C( 3, 9) 0.000000 0.000000 C( 4, 1) 0.000000 0.000000 C( 4, 2) 0.8000000 0.000000 C( 4, 3) 0.000000 0.000000 C( 4, 4) 0.000000 0.000000 C( 4, 5) -0.2000000 0.000000 C( 4, 6) 0.000000 0.000000 C( 4, 7) 0.000000 0.000000 C( 4, 8) -0.2000000 0.000000 C( 4, 9) 0.000000 0.000000 C( 5, 1) 0.000000 0.000000 C( 5, 2) 0.000000 0.000000C( 5, 4) 0.000000 0.000000C( 5, 5) 0.000000 0.000000C( 5, 6) -0.5000000 0.000000C( 5, 7) 0.000000 0.000000C( 5, 8) 0.000000 0.000000C( 5, 9) 0.5000000 0.000000C( 6, 1) 0.000000 0.000000C( 6, 2) 0.000000 0.000000C( 6, 3) 0.9000000 0.000000C( 6, 4) 0.000000 0.000000C( 6, 5) 0.000000 0.000000C( 6, 6) -0.1000000 0.000000C( 6, 7) 0.000000 0.000000C( 6, 8) 0.000000 0.000000C( 6, 9) -0.1000000 0.000000C( 7, 1) 1.000000 0.000000C( 7, 2) 0.000000 0.000000C( 7, 3) 0.000000 0.000000C( 7, 4) 1.000000 0.000000C( 7, 5) 0.000000 0.000000C( 7, 6) 0.000000 0.000000C( 7, 7) 1.000000 0.000000C( 7, 8) 0.000000 0.000000C( 7, 9) 0.000000 0.000000C( 8, 1) -0.5000000 0.000000C( 8, 2) -1.000000 0.000000C( 8, 3) -1.200000 0.000000C( 8, 4) 1.000000 0.000000C( 8, 5) 0.5000000 0.000000C( 8, 6) 0.3000000 0.000000C( 8, 7) 2.500000 0.000000C( 8, 8) 2.000000 0.000000C( 8, 9) 1.800000 0.000000 WPLUS( 1, 1) 1.000000 0.000000 WPLUS( 1, 2) 0.000000 0.000000 WPLUS( 1, 3) 1.000000 0.000000 WPLUS( 1, 4) 0.000000 0.000000 WPLUS( 1, 5) 1.000000 0.000000 WPLUS( 1, 6) 0.000000 0.000000 WPLUS( 1, 7) 0.000000 0.000000 WPLUS( 1, 8) 0.000000 0.000000 WPLUS( 2, 1) 0.000000 0.000000 WPLUS( 2, 2) 0.000000 0.000000WPLUS( 2, 4) 0.000000 0.000000 WPLUS( 2, 5) 0.000000 0.000000 WPLUS( 2, 6) 0.000000 0.000000 WPLUS( 2, 7) 0.000000 0.000000 WPLUS( 2, 8) 0.000000 0.000000 WPLUS( 3, 1) 0.000000 0.000000 WPLUS( 3, 2) 0.000000 0.000000 WPLUS( 3, 3) 0.000000 0.000000 WPLUS( 3, 4) 0.000000 0.000000 WPLUS( 3, 5) 0.000000 0.000000 WPLUS( 3, 6) 0.000000 0.000000 WPLUS( 3, 7) 0.000000 0.000000 WPLUS( 3, 8) 0.000000 0.000000 WMINUS( 1, 1) 0.000000 0.000000 WMINUS( 1, 2) 1.000000 0.000000 WMINUS( 1, 3) 0.000000 0.000000 WMINUS( 1, 4) 1.000000 0.000000 WMINUS( 1, 5) 0.000000 0.000000 WMINUS( 1, 6) 1.000000 0.000000 WMINUS( 1, 7) 0.000000 0.000000 WMINUS( 1, 8) 0.000000 0.000000 WMINUS( 2, 1) 0.000000 0.000000 WMINUS( 2, 2) 0.000000 0.000000 WMINUS( 2, 3) 0.000000 0.000000 WMINUS( 2, 4) 0.000000 0.000000 WMINUS( 2, 5) 0.000000 0.000000 WMINUS( 2, 6) 0.000000 0.000000 WMINUS( 2, 7) 0.000000 0.000000 WMINUS( 2, 8) 1.000000 0.000000 WMINUS( 3, 1) 0.000000 0.000000 WMINUS( 3, 2) 0.000000 0.000000 WMINUS( 3, 3) 0.000000 0.000000 WMINUS( 3, 4) 0.000000 0.000000 WMINUS( 3, 5) 0.000000 0.000000 WMINUS( 3, 6) 0.000000 0.000000 WMINUS( 3, 7) 1.000000 0.000000 WMINUS( 3, 8) 0.000000 0.000000Row Slack or Surplus Dual Price1 0.000000 -1.0000002 0.000000 0.0000003 0.000000 -1.0000004 0.000000 0.0000006 0.000000 0.0000007 0.000000 0.0000008 0.000000 0.0000009 0.000000 0.00000010 0.000000 0.00000011 0.000000 0.00000012 0.000000 0.000000第三级目标计算Global optimal solution found.Objective value: 0.000000Infeasibilities: 0.000000Total solver iterations: 10Variable Value Reduced CostP( 1) 0.000000 0.000000P( 2) 0.000000 0.000000P( 3) 1.000000 0.000000Z( 1) 0.000000 0.000000Z( 2) 0.000000 0.000000Z( 3) 0.000000 0.000000GOAL( 1) 0.000000 0.000000GOAL( 2) 0.000000 0.000000GOAL( 3) 0.000000 0.000000X( 1) 1000.000 0.000000X( 2) 80.00000 0.000000X( 3) 0.000000 0.000000X( 4) 1000.000 0.000000X( 5) 40.00000 0.000000X( 6) 0.000000 0.000000X( 7) 0.000000 0.000000X( 8) 280.0000 0.000000X( 9) 0.000000 0.000000G( 1) 0.000000 0.000000G( 2) 0.000000 0.000000G( 3) 0.000000 0.000000G( 4) 0.000000 0.000000G( 5) 0.000000 0.000000G( 6) 0.000000 0.000000G( 7) 2000.000 0.000000G( 8) 1000.000 0.000000DPLUS( 2) 0.000000 0.000000 DPLUS( 3) 0.000000 0.000000 DPLUS( 4) 0.000000 0.000000 DPLUS( 5) 0.000000 0.000000 DPLUS( 6) 0.000000 0.000000 DPLUS( 7) 0.000000 0.000000 DPLUS( 8) 0.000000 0.000000 DMINUS( 1) 200.0000 0.000000 DMINUS( 2) 0.000000 0.000000 DMINUS( 3) 0.000000 0.000000 DMINUS( 4) 0.000000 0.000000 DMINUS( 5) 0.000000 0.000000 DMINUS( 6) 0.000000 0.000000 DMINUS( 7) 0.000000 1.000000 DMINUS( 8) 0.000000 0.000000 C( 1, 1) -0.1000000 0.000000 C( 1, 2) 0.000000 0.000000 C( 1, 3) 0.000000 0.000000 C( 1, 4) -0.1000000 0.000000 C( 1, 5) 0.000000 0.000000 C( 1, 6) 0.000000 0.000000 C( 1, 7) 0.9000000 0.000000 C( 1, 8) 0.000000 0.000000 C( 1, 9) 0.000000 0.000000 C( 2, 1) 0.5000000 0.000000 C( 2, 2) 0.000000 0.000000 C( 2, 3) 0.000000 0.000000 C( 2, 4) -0.5000000 0.000000 C( 2, 5) 0.000000 0.000000 C( 2, 6) 0.000000 0.000000 C( 2, 7) -0.5000000 0.000000 C( 2, 8) 0.000000 0.000000 C( 2, 9) 0.000000 0.000000 C( 3, 1) 0.000000 0.000000 C( 3, 2) -0.7000000 0.000000 C( 3, 3) 0.000000 0.000000 C( 3, 4) 0.000000 0.000000 C( 3, 5) -0.7000000 0.000000 C( 3, 6) 0.000000 0.000000 C( 3, 7) 0.000000 0.000000 C( 3, 8) 0.3000000 0.000000 C( 3, 9) 0.000000 0.000000 C( 4, 1) 0.000000 0.000000C( 4, 3) 0.000000 0.000000 C( 4, 4) 0.000000 0.000000 C( 4, 5) -0.2000000 0.000000 C( 4, 6) 0.000000 0.000000 C( 4, 7) 0.000000 0.000000 C( 4, 8) -0.2000000 0.000000 C( 4, 9) 0.000000 0.000000 C( 5, 1) 0.000000 0.000000 C( 5, 2) 0.000000 0.000000 C( 5, 3) -0.5000000 0.000000 C( 5, 4) 0.000000 0.000000 C( 5, 5) 0.000000 0.000000 C( 5, 6) -0.5000000 0.000000 C( 5, 7) 0.000000 0.000000 C( 5, 8) 0.000000 0.000000 C( 5, 9) 0.5000000 0.000000 C( 6, 1) 0.000000 0.000000 C( 6, 2) 0.000000 0.000000 C( 6, 3) 0.9000000 0.000000 C( 6, 4) 0.000000 0.000000 C( 6, 5) 0.000000 0.000000 C( 6, 6) -0.1000000 0.000000 C( 6, 7) 0.000000 0.000000 C( 6, 8) 0.000000 0.000000 C( 6, 9) -0.1000000 0.000000 C( 7, 1) 1.000000 0.000000 C( 7, 2) 0.000000 0.000000 C( 7, 3) 0.000000 0.000000 C( 7, 4) 1.000000 0.000000 C( 7, 5) 0.000000 0.000000 C( 7, 6) 0.000000 0.000000 C( 7, 7) 1.000000 0.000000 C( 7, 8) 0.000000 0.000000 C( 7, 9) 0.000000 0.000000 C( 8, 1) -0.5000000 0.000000 C( 8, 2) -1.000000 0.000000 C( 8, 3) -1.200000 0.000000 C( 8, 4) 1.000000 0.000000 C( 8, 5) 0.5000000 0.000000 C( 8, 6) 0.3000000 0.000000 C( 8, 7) 2.500000 0.000000 C( 8, 8) 2.000000 0.000000 C( 8, 9) 1.800000 0.000000WPLUS( 1, 2) 0.000000 0.000000 WPLUS( 1, 3) 1.000000 0.000000 WPLUS( 1, 4) 0.000000 0.000000 WPLUS( 1, 5) 1.000000 0.000000 WPLUS( 1, 6) 0.000000 0.000000 WPLUS( 1, 7) 0.000000 0.000000 WPLUS( 1, 8) 0.000000 0.000000 WPLUS( 2, 1) 0.000000 0.000000 WPLUS( 2, 2) 0.000000 0.000000 WPLUS( 2, 3) 0.000000 0.000000 WPLUS( 2, 4) 0.000000 0.000000 WPLUS( 2, 5) 0.000000 0.000000 WPLUS( 2, 6) 0.000000 0.000000 WPLUS( 2, 7) 0.000000 0.000000 WPLUS( 2, 8) 0.000000 0.000000 WPLUS( 3, 1) 0.000000 0.000000 WPLUS( 3, 2) 0.000000 0.000000 WPLUS( 3, 3) 0.000000 0.000000 WPLUS( 3, 4) 0.000000 0.000000 WPLUS( 3, 5) 0.000000 0.000000 WPLUS( 3, 6) 0.000000 0.000000 WPLUS( 3, 7) 0.000000 0.000000 WPLUS( 3, 8) 0.000000 0.000000 WMINUS( 1, 1) 0.000000 0.000000 WMINUS( 1, 2) 1.000000 0.000000 WMINUS( 1, 3) 0.000000 0.000000 WMINUS( 1, 4) 1.000000 0.000000 WMINUS( 1, 5) 0.000000 0.000000 WMINUS( 1, 6) 1.000000 0.000000 WMINUS( 1, 7) 0.000000 0.000000 WMINUS( 1, 8) 0.000000 0.000000 WMINUS( 2, 1) 0.000000 0.000000 WMINUS( 2, 2) 0.000000 0.000000 WMINUS( 2, 3) 0.000000 0.000000 WMINUS( 2, 4) 0.000000 0.000000 WMINUS( 2, 5) 0.000000 0.000000 WMINUS( 2, 6) 0.000000 0.000000 WMINUS( 2, 7) 0.000000 0.000000 WMINUS( 2, 8) 1.000000 0.000000 WMINUS( 3, 1) 0.000000 0.000000 WMINUS( 3, 2) 0.000000 0.000000 WMINUS( 3, 3) 0.000000 0.000000 WMINUS( 3, 4) 0.000000 0.000000WMINUS( 3, 6) 0.000000 0.000000 WMINUS( 3, 7) 1.000000 0.000000 WMINUS( 3, 8) 0.000000 0.000000Row Slack or Surplus Dual Price1 0.000000 -1.0000002 0.000000 0.0000003 0.000000 0.0000004 0.000000 -1.0000005 0.000000 0.0000006 0.000000 0.0000007 0.000000 0.0000008 0.000000 0.0000009 0.000000 0.00000010 0.000000 0.00000011 0.000000 0.00000012 0.000000 0.000000。