yxf2程序框图
- 格式:ppt
- 大小:2.00 MB
- 文档页数:43
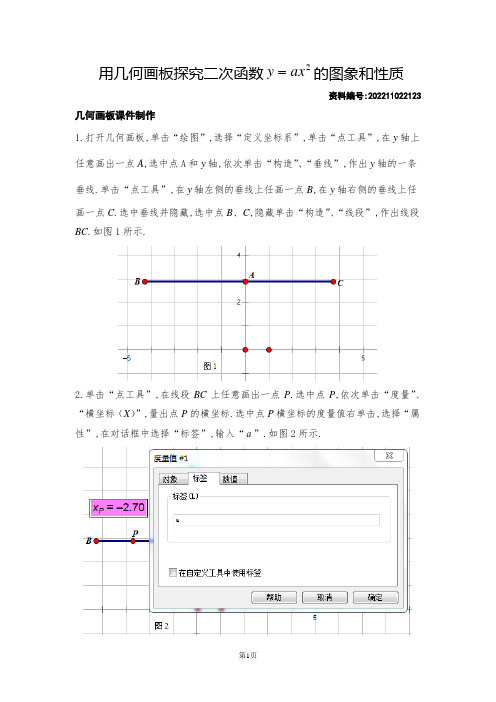
用几何画板探究二次函数2y 的图象和性质ax资料编号:202211022123 几何画板课件制作1.打开几何画板,单击“绘图”,选择“定义坐标系”,单击“点工具”,在y轴上任意画出一点A,选中点A和y轴,依次单击“构造”、“垂线”,作出y轴的一条垂线.单击“点工具”,在y轴左侧的垂线上任画一点B,在y轴右侧的垂线上任画一点C.选中垂线并隐藏,选中点B、C,隐藏单击“构造”、“线段”,作出线段BC.如图1所示.2.单击“点工具”,在线段BC上任意画出一点P.选中点P,依次单击“度量”、“横坐标(X)”,量出点P的横坐标.选中点P横坐标的度量值右单击,选择“属性”,在对话框中选择“标签”,输入“a”.如图2所示.3.依次单击“绘图”、“绘制新函数”,在弹出的对话框中依次单击输入“a 的值”、“ *”、“x ”、“∧””、“2”,如图3所示,单击“确定”.在平面直角坐标系中画出作出二次函数()02≠=a ax 的图象,选中函数图象,修改线型为“中等”,如图4所示.4.选中点P ,修改点的颜色为浅蓝色,表示该点为可拖动的点. 课件探索对于二次函数()02≠=a ax y ,课件1把点P 的横坐标作为a 的值,通过拖动点P ,改变点P 的横坐标,包括符号,来观察并探究二次项系数a 对二次函数图象的影响,包括对其图象开口方向、开口大小的影响.(1)拖动点P 在线段AB 上移动,观察a 的变化以及二次函数()02≠=a ax y 图象的开口方向和开口大小,你发现了什么?如图5所示(选中抛物线,依次单击“显示”、“追踪函数图象”,拖动点P ,即可追踪函数的图象).对于二次函数()02≠=a ax y ,当0<a 时,其图象的开口_________,a 的值越_________(填“大”或“小”),其图象的开口越大.(2)拖动点P 在线段AC 上移动,观察a 的变化以及二次函数()02≠=a ax y 图象的开口方向和开口大小,你发现了什么?如图6所示.对于二次函数()02≠=a ax y ,当0>a 时,其图象的开口_________,a 的值越_________(填“大”或“小”),其图象的开口越大.探究结果通过几何画板课件的展示,我们不能得到二次函数()02≠=a ax y 的图象和性质.二次函数2ax y =的图象与性质 函数2ax y =0>a0<a图象xyOxy O开口方向 向上向下对称轴 y 轴 y 轴顶点 ()0,0()0,0最值 有最小值0有最大值0增减性当0<x 时,y 随x 的增大而减小; 当0>x 时,y 随x 的增大而增大.当0<x 时,y 随x 的增大而增大; 当0>x 时,y 随x 的增大而减小.a 对函数2ax y =图象的影响a 的符号决定函数2ax y =图象的开口方向,a 的大小决定图象的开口大小:a 的值越大,抛物线开口越小;a 的值越小,抛物线开口越大.二次函数2ax y =的图象与性质的应用例1. 已知函数()422-++=m m x m y 是关于x 的二次函数.(1)求m 的值;(2)当m 为何值时,抛物线有最低点?求出这个最低点,这时,抛物线的开口方向、增减性如何?(3)当m 为何值时,函数有最大值?最大值是多少?这时抛物线的开口方向、增减性如何?解:(1)由题意可知:⎩⎨⎧=-+≠+24022m m m ,解之得:2=m 或3-=m ; (2)抛物线有最低点,即抛物线开口向上 ∴2=m ,24x y =,其图象开口向上.当x ≤0时,y 随x 的增大而减小;当x ≥0时,y 随x 的增大而增大;(如图7) (3)当3-=m 时,2x y -=,其图象开口向下,函数有最大值,最大值是0. 当x ≤0时,y 随x 的增大而增大;当x ≥0时,y 随x 的增大而减小.(如图8)图 7图 8图 9例2. 已知抛物线2ax y =经过点()3,1. (1)求a 的值;(2)当3=x 时,求y 的值; (3)说出此二次函数的三条性质. 解:(1)把()3,1代入2ax y =得:3=a ; (2)由(1)可知:23x y = 当3=x 时,27332=⨯=y ;(3)①该二次函数的图象开口向上; ②该二次函数的图象关于y 轴对称; ③该二次函数有最小值,最小值为0. 巩固练习1. 抛物线()02<=a ax y 的图象经过第_________象限.2. 二次函数25x y -=的图象是一条_________,其图象开口_________,对称轴是直线_________,顶点坐标是_________,当=x _________时,函数有最_________值,最值为_________.3. 若二次函数()22x m y -=的图象开口向上,则m 的取值范围是_________.4. 二次函数()222-+=mx m y 的图象开口_______,函数有最______值,为_______.5. 若二次函数2mx y =有最大值,则m 的取值范围是_________.6. 已知点()()2211,,,y x y x 在抛物线241x y -=上,若021>>x x ,则21______y y ;若012<<x x ,则21______y y .7. 已知二次函数221x y =的图象如图9所 示,线段x AB //轴,交抛物线于A 、B 两点, 且点A 的横坐标为2,则线段AB 的长度为 _________.8. 关于函数2223,,31x y x y x y ===的图象,下列说法不正确的是【 】 (A )顶点相同 (B )对称轴相同 (C )开口方向相同 (D )形状相同9. 已知二次函数2ax y =与一次函数2-=kx y 的图象相交于A 、B 两点,如图10所示,其中()1,1--A .(1)二次函数的表达式为__________,一次函数的表达式为__________; (2)求△OAB 的面积.y x图 10BAO。

《最小二乘法的可视化和二次函数拟合》
最小二乘法是一种重要的数理统计方法,它可以将一组数据拟合到一个多项式函数上,这里面就蕴藏着很多有趣的可视化和二次函数拟合技术。
几何上,最小二乘法是一种使用数据点来拟合函数曲线的方法,即使当原始数据有一定的误差时,它也能有效地拟合出一条最接近该数据的线或曲线。
最小二乘法的可视化主要是以二次函数的形式来表达的,因此,接下来将讨论如何使用最小二乘法来进行二次函数拟合。
最小二乘法的二次函数拟合具体可分为三个步骤:第一步,构造一个函数,用来拟合可观测数据;第二步,在拟合函数和残差之间建立一个函数,然后最小化该函数;第三步,计算拟合参数。
首先,根据可观测数据,构造出一个相应的函数,一般来说,使用最小二乘法进行拟合一般都采用比较常用的二次函数的形式来表达,其具体形式为:y=ax²+bx+c。
其中a, b, c为
三个待求参数。
其次,在拟合函数和残差(即实际观测数据和真实数据之间的差别)之间建立一个函数,并使用最小二乘法对此函数进行最小化处理。
这里,残差函数一般可以采用不等式形式,即残差小于等于一个某一定值,例如可以设定残差小于等于1。
最后,根据第二步最佳拟合解,计算拟合参数a,b,c,从而完成最小
二乘法的二次函数拟合。
总的来说,最小二乘法的可视化及其二次函数拟合技术是一种非常有用的数据分析方法。
它能够与测量误差结合,帮助我们
快速准确地拟合出最接近原始数据的曲线或线条,并且简单易学,值得大家学习。




陆韶琦 3110000441程序说明:本程序用多项式拟合数据,程序会要求输入需要拟合的次数和数据点的个数,数据文件应该保存在本程序运行时的current folder下,文件取名为“mytext.txt”程序代码:%多项式最小二乘法拟合数据N=input('please put in how many times the power will you overfit:'); M=input('how many couples of statistics are there in the table:');%读入数据文件f=fopen('mytxt.txt','r');S=fscanf(f,'%g',[M 2]);fclose(f);S=S';%显示数据文件,确保正确输入disp('S(x,y)=');disp(S);%建立多项式系数法方程组中间矩阵C=zeros(N+1,M);for i=1:N+1for j=1:Mif S(1,j)==0C(i,j)=0;elseC(i,j)=S(1,j).^(i-1);endendend%建立法方程组A=C*C';Y=zeros(M,1);for i=1:MY(i,1)=S(2,i);endb=C*Y;%用列主元高斯消元法接法方程组A=[A,b];for i=1:N+1max=abs(A(i,i));for j=i+1:N+1if abs(A(j,i))>maxflag=j;max=A(j,i);endendfor k=i:N+2B=A(flag,k);A(flag,k)=A(i,k);A(i,k)=B;endfor kh=i+1:N+1m=-A(kh,i)/A(i,i);A(kh,i)=0;for kl=i+1:N+2A(kh,kl)=A(kh,kl)+m*A(i,kl);endendendX=zeros(N+1,1);for i=N+1:-1:1for j=i-1:-1:1m=-A(j,i)/A(i,i);A(j,N+2)=A(j,N+2)+m*A(i,N+2);endX(i,1)=A(i,N+2)/A(i,i);enddisp(X);%根据系数求得待定曲线syms x;expr=0;for i=1:N+1expr=expr+X(i,1)*x.^(i-1);end%输出得到的曲线表达式disp(expr);%计算偏差bias=zeros(M,1);for j=1:Mfor i=1:N+1bias(j,1)=bias(j,1)+X(i,1)*S(1,j)^(i-1); endbias(j,1)=bias(j,1)-S(2,j);end%寻找最大偏差max=abs(bias(1,1));flag=1;for i=2:Mif abs(bias(i,1))>maxflag=i;max=abs(bias(i,1));endenddisp('the maximun absoulute value is:'); disp(max);%计算均方误差rms=0;for i=1:Mrms=rms+bias(i,1)^2;endrms=sqrt(rms);disp('the square bias is:');disp(rms);%制图a=S(1,1):0.01:S(1,M);y=subs(expr,x,a);plot(a,y);hold on;grid on;for i=1:Mx=S(1,i);y=S(2,i);plot(x,y,'*');hold on;end运行结果:表达式中分式难以化简,但在表达式前给出了次幂前的四位有效数字的系数。