最新苏教版七年级下册数学提优卷

一、选择题（每题3分，共36分）1. —8，2005，2/3，0，—4，+11，—|—3|，—1/4，—7.2，-（-2）中， 正整数和负分数共有：（ ）A 、3个；B 、4个；C 、5个；D 、6个2.下列说法：①互为相反数的两个数绝对值相等；②绝对值等于本身的数只有正数，③不相当的两个数绝对值不相等；④绝对值相等的两数一定相等。

其中正确的有：( )A 、0个；B 、1个；C 、2个；D 、3个3. 若a 的相反数是非负数，则a 为：( )A 、负数；B 、负数或零；C 、正数；D 、正数或零4．下列说法中,正确的是 （ ）A.有理数就是正数和负数的统称B. 零不是自然数,但是正数C.一个有理数不是整数就是分数D. 正分数、零、负分数统称分数5．若︱a ︱+a=0 则a 是 （ ）A ．零B ．负数C ．非负数D ．负数或零6．如图数轴上的A 、B 两点分别表示有理数a 、b,下列式子中不正确的是 （ ）A. a + b < 0B. a –b < 0C. （－a ）＋b ＞ 0D. b > a7．已知013=-++b a ,则b a +的相反数是 ( )A.-4B.4C.2D.-2 二、填空题8. 数轴上与距离原点3个单位长度的点所表示的负数是___,它与表示数1的点的距离为___9.若X 的相反数是—5，则X=______;若—X 的相反数是—3.7，则X=_______10. 若一个数的倒数是1.2，则这个数的相反数是________,绝对值是________11．绝对值不大于421的所有整数的和为 .12．已知数轴上有A 、B 两点,点A 与原点的距离为2, A 、B 两点的距离为1,则满足条件的点B 所表示的数是 。

13. 写出绝对值大于3且不大于8的所有整数 .14．按规律填数:21, 61-,121,201-,301,_________ , 15．设三个不相等的有理数c b a ,,满足,0=++c b a ，则c b a ,,中正数的个数为________。

七年级（下）提优班期末试卷（满分150分；时间120分钟）姓名： 得分：一、选择题：（7×5＝35）1、一艘轮船停在海面上，从船上看灯塔的方向在北偏东300，那么从灯塔看船的方向在（ ）A 、北偏西600B 、南偏西600C 、南偏东300D 、南偏西3002、已知方程组⎩⎨⎧-=--=+4652by ax y x 和⎩⎨⎧-=+=-81653ay bx y x 的解相同，则（a+b ）2等于（ ）A 、0B 、4C 、16D 、无法确定3、某班运来一筐苹果，若每人分6个则少6个；若每人分5个则多5个，那么该班人数与苹果数分别是（ ）A 、22,120B 、11,60C 、10,54D 、8,424、要使4x 2+25是一个完全平方式，则应加入的一个整式是（ ）A 、10xB 、20xC 、±20xD 、±20x 或4254x 5、如图，把图中的一个三角形先横向平移x 格，再纵向平移y 格，可以与图中另一个三角形拼合成一些不同的四边形，那么移动的总格数（x+y ）的值是（ ）A 、是一个定值B 、有两个不同的值C 、有三个不同的值D 、有三个以上不同的值6、不能判断△ABC ≌△DEF 的条件是（ ）A 、∠A ＝∠F ，BA ＝EF ，AC ＝FDB 、∠B ＝∠E ，BC ＝EF ，高AH ＝DGC 、∠C ＝∠F ＝900∠A ＝600，∠E ＝300，AC ＝DFD 、∠A ＝∠D ，AB ＝DE ，AC ＝DF7、如图是某厂2005年各季度产值统计图（单位：万元），则下列说法正确的是（ ）A 、四个季度中，每季度生产总值有增有减 B 、四个季度中，前三季度生产总值增长较快 C 、四个季度中，各季度生产总值的变化一样 D 、第四季度生产总值增长最快二、填空题（5×5＝25）8、如图，有一条直的等宽纸带按图折叠时，则图中∠α=______________.9、如果三角形三边长分别是正整数a,b,c ，且a>b>c ，b=5，则满足条件且周长彼此不同的三角形共有＿＿＿＿＿个。

七下9.4乘法公式提优训练题一、选择题1.计算1998×2002=()A. 400016B. 4000004C. 399996D. 39999962.已知，则()A. x是完全平方数B. x−50是完全平方数C. x−25是完全平方数D. x+50是完全平方数3.把2009表示成两个整数的平方差的形式，则不同的表示法有()A. 16种B. 14种C. 12种D. 10种4.如果多项式a2+mab+4b2是一个完全平方式，则m的值是()。

A. 2B. 4C. 6D. ±45.在下列各式：①a−b=b−a；②(a−b)2=(b−a)2；③(a−b)2=−(b−a)2；④(a−b)3=(b−a)3；⑤(a+b)(a−b)=−(−a−b)(−a+b)正确的有()A. 1个B. 2个C. 3个D. 4个6.根据图中阴影部分面积的不同求法，可以得到一个关于a、b的代数恒等式()A. a2−b2=(a+b)(a−b)B. (a+b)2=a2+2ab+b2C. (a−b)2=a2−2ab+b2D. (a−b)2=(a+b)2−4ab7.设实数a，b，c满足a+b+c=3，a2+b2+c2=4，则a2+b2/c−2+a2+c2/b−2+b2+c2/a−2的值为()A. −9B. −7C. 7D. 98.由m(a+b+c)=ma+mb+mc，可得：(a+b)(a2−ab+b2)=a3−a2b+ab2+a2b−ab2+b3=a3+b3，即(a+b)(a2−ab+b2)=a3+b3…①我们把等式①叫做多项式乘法的立方和公式．下列应用这个立方和公式进行的变形不正确的是()A. (x+4y)(x2−4xy+16y2)=x3+64y3B. (2x+y)(4x2−2xy+y2)=8x3+y3C. (a+1)(a2+a+1)=a3+1D. x3+27=(x+3)(x2−3x+9)二、填空题9.若m−n=2，则m2−n2−4n=10.如下所示，(a+b)n与相应的杨辉三角中的一行数相对应．由以上规律可知：(a+b)2=a2+2ab+b2；(a+b)3=a3+3a2b+3ab2+b3；(a+b)4=a4+4a3b+6a2b2+4ab3+b4．请你写出下面两个式子的结果：(a+b)5=____________________________________；(a+b)6=____________________________________．11.定义运算a⊗b=a2−b2，下面给出了关于这种运算的四个结论：①2⊗(−2)=0，②a⊗b=b⊗a，③若a⊗b=0，则a=b，④(a+b)⊗(a−b)=4ab；其中正确结论的序号是．12.如图所示的几何图形，能用这个图形的面积来解释的代数恒等式为_______________．13.已知：31=3，32=9，33=27，34=81，35=243，36=729…，设A=2(3+1)(32+1)(34+1)(38+1)+1，则A的个位数字是．14.若A=(2+1)(22+1)(24+1)+1，则A的值是_______________．三、解答题15.如图①所示是一个长为2m，宽为2n的长方形，沿图中虚线用剪刀均分成四个小长方形，然后按图②的方式拼成一个正方形．(1)按要求填空：①你认为图②中的阴影部分的正方形的边长等于______；②请用两种不同的方法表示图②中阴影部分的面积：方法1：______方法2：______③观察图②，请写出代数式(m+n)2，(m−n)2，mn这三个代数式之间的等量关系：______；(2)根据(1)题中的等量关系，解决如下问题：若|m+n−6|+|mn−4|=0，求(m−n)2的值．(3)实际上有许多代数恒等式可以用图形的面积来表示，如图③，它表示了______．16.如果一个正整数能表示成两个连续偶数的平方差，那么称这个正整数为神秘数”，如：4=22−02，12=42−22，20=62−42，因此4，12，20这三个数都是神秘数．(1)52和200这两个数是神秘数吗？为什么？(2)设两个连续偶数为2n和2n−2(其中n取正整数)，由这两个连续偶数构造的神秘数是4的倍数吗？为什么？17.数学活动课上，老师准备了若干个如图1的三种纸片，A种纸片边长为a的正方形，B种纸片是边长为b的正方形，C种纸片长为b、宽为a的长方形．并用A种纸片一张，B种纸片一张，C种纸片两张拼成如图2的大正方形．(1)请用两种不同的方法求图2大正方形的面积．方法1：______；方法2：______(2)观察图2，请你写出下列三个代数式：(a+b)2，a2+b2，ab之间的等量关系．______(3)根据(2)题中的等量关系，解决如下问题：①已知：a+b=5，a2+b2=11，求ab的值；②已知(2018−a)2+(a−2017)2=5，求(2018−a)(a−2017)的值．18.在学习了分式的乘除法之后，老师给出了这样一道题，计算：(a+1a )(a2+1a2)(a4−1 a4)(a8+1a8)(a2−1)，同学们都感到无从下手，小明将a2−1变形为a(a−1a)，然后用平方差公式很轻松地得出结论．试写出小明的做法．答案和解析1.D解：原式=(2000−2)×(2000+2)=20002−22=4000000−4=3999996，2.C解：∵x=100...00100 (0050)n个0 (n+1)个0=100…00000…0000+100…0000+50(2n+4)个0 (n+3)个0=102n+4+10n+3+50=(10n+2)2+2⋅10n+2⋅5+50．∴x−25=(10n+2+5)2．3.C解：2009=1×2009=7×287=41×49，∵2009=a2−b2=(a+b)(a−b)，∴2009=10052−10042=1472−1402=452−42，又∵每组可取负号，如45，4；−45，4；45，−4；−45，−4；∴故共有3×4=12种．4.D解：∵a2+mab+4b2=a2+mab+(2b)2，∴mab=±2×a×2b，解得m=±4．5.A解：a−b=−(b−a)，①错误；(a−b)2=(b−a)2，②正确，③错误；(a−b)3=−(b−a)3，④错误；(a+b)(a−b)=(−a−b)(−a+b)，⑤错误；6.D解：∵四周部分都是全等的矩形，且长为a，宽为b，∴四个矩形的面积为4ab，∵大正方形的边长为a+b，∴大正方形面积为(a+b)2，∴中间小正方形的面积为(a+b)2−4ab，而中间小正方形的面积也可表示为：(a−b)2，∴(a−b)2=(a+b)2−4ab，．7.A解：因为a+b+c=3，a2+b2+c2=4，所以4−c2c−2+4−b2b−2+4−a2a−2=(2+c)(2−c)c−2+(2+b)(2−b)b−2+(2+a)(2−a)a−2=−6−a−b−c=−6−3=−9．8.C解：A、(x+4y)(x2−4xy+16y2)=x3+64y3，正确；B、(2x+y)(4x2−2xy+y2)=8x3+y3，正确；C、(a+1)(a2−a+1)=a3+1；故本选项错误．D、x3+27=(x+3)(x2−3x+9)，正确．9.4解：m2−n2−4n=(m+n)(m−n)−4n=2(m+n)−4n=2m−2n=2(m−n)=4．10.a5+5a4b+10a3b2+10a2b3+5ab4+b5；a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+b6．解：(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5；由：可得：(a+b)6=a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+b6．11.①④解：①2⊗(−2)=22−(−2)2=0，正确；②a⊗b=a2−b2，而b⊗a=b2−a2，两者不一定相等，故错误；③a⊗b=a2−b2不一定等于0，错误；④(a+b)⊗(a−b)=(a+b)2−(a−b)2=a2+2ab+b2−a2+2ab−b2=4ab，正确．故①④正确；12.(a+b+c)2=a2+b2+c2+2ab+2ac+2bc解：如图，大正方形的面积有两种计算方法：①(a+b+c)2；②a2+b2+c2+2ab+2ac+2bc；因此(a+b+c)2=a2+b2+c2+2ab+2ac+2bc．13.1解：A=(3−1)(3+1)(32+1)(34+1)(38+1)+1=(32−1)(32+1)(34+1)(38+1)+1=(34−1)(34+1)(38+1)+1=(38−1)(38+1)+1=(316−1)+1=316−1+1=316，观察已知等式，个位数字以3，9，7，1循环，16÷4=4，则A的个位数字是1，14.256解：A=(2−1)(2+1)(22+1)(24+1)+1=(22−1)(22+1)(24+1)+1=(24−1)(24+1)+1=28−1+1=28=256．15.(1)①m−n②(m−n)2(m+n)2−4mn③(m−n)2=(m+n)2−4mn (2)∵|m+n−6|+|mn−4|=0，∴m+n−6=0，mn−4=0，∴m+n=6，mn=4∵由(1)可得(m−n)2=(m+n)2−4mn∴(m−n)2=(m+n)2−4mn=62−4×4=20，∴(m−n)2=20；(3)(2m+n)(m+n)=2m2+3mn+n2解：(1)①阴影部分的正方形边长是m−n．②方法1：阴影部分的面积就等于边长为m−n的小正方形的面积，即(m−n)2，方法2：边长为m+n的大正方形的面积减去4个长为m，宽为n的长方形面积，即(m+ n)2−4mn；③(m−n)2=(m+n)2−4mn．(2)见答案(3)根据大长方形面积等于长乘以宽有：(2m+n)(m+n)，或两个边长分别为m、n的正方形加上3个长为m、宽为n的小长方形面积和有：2m2+ 3mn+n2，故可得：(2m+n)(m+n)=2m2+3mn+n2．16.解：(1)∵28=82−62，2012=5042−5022，∴28和2012这两个数是“神秘数”；(2)两个连续偶数构成的“神秘数”是4的倍数．理由如下：(2k+2)2−(2k)2=(2k+2+2k)(2k+2−2k)=2(4k+2)=4(2k+1)，∴两个连续偶数构成的“神秘数”是4的倍数．17.(1)方法1：(a+b)2；方法2：a2+2ab+b2；(2)(a+b)2=a2+2ab+b2；(3)①∵a+b=5，∴(a+b)2=25，∴a2+b2+2ab=25，又∵a2+b2=11，∴ab=7．②设2018−a=x，a−2017=y，则x+y=1，∵(2018−a)2+(a−2017)2=5，∴x2+y2=5，∵(x+y)2=x2+2xy+y2，∴xy=(x+y)2−(x2+y2)=−2，2即(2018−a)(a−2017)=−2．解：(1)方法1：图2是边长为(a+b)的正方形，∴S=(a+b)2；正方形方法2：图2可看成1个边长为a的正方形、1个边长为b的正方形以及2个长为b宽为a的长方形的组合体，∴S=a2+b2+2ab．正方形故答案为：(a+b)2；a2+b2+2ab．(2)由(1)可得：(a+b)2=a2+2ab+b2．18.解：原式=a(a−1a )(a+1a)(a2+1a2)(a4+1a4)(a8+1a8)=a(a2−1a2)(a2+1a2)(a4+1a4)(a8+1a8)=a(a4−1a4)(a4+1a4)(a8+1a8)=a(a8−1a8)(a8+1a8)=a(a16−1a16)=a17−1a15．。

一、选择题（每题3分，共30分）1. 下列选项中，不是有理数的是（）A. 0.5B. -3C. √2D. 1/22. 下列各数中，绝对值最小的是（）A. -1/2B. 1/3C. -2/3D. 1/43. 若a、b是相反数，则a+b等于（）A. 0B. aC. bD. ±a4. 在数轴上，点A表示的数是-3，点B表示的数是2，那么点A与点B之间的距离是（）A. 5B. 3C. 1D. 45. 下列图形中，轴对称图形的是（）A. 正方形B. 等边三角形C. 长方形D. 以上都是6. 若一个等腰三角形的底边长为8cm，腰长为10cm，那么这个三角形的周长是（）A. 26cmB. 28cmC. 30cmD. 32cm7. 若x=3，那么代数式2x+1的值是（）A. 6B. 7C. 8D. 98. 下列方程中，无解的是（）A. 2x+3=7B. 3x-4=2C. 5x=0D. 2x+5=3x9. 下列函数中，是正比例函数的是（）A. y=2x+3B. y=x²C. y=3/xD. y=2x10. 下列不等式中，正确的是（）A. 3x < 2xB. 2x > 3xC. 3x ≤ 2xD. 2x ≤ 3x二、填空题（每题3分，共30分）11. -5的相反数是______，绝对值是______。

12. 若a=-3，b=2，则a-b的值是______。

13. 在数轴上，点A表示的数是-4，那么点A的坐标是______。

14. 一个等腰直角三角形的斜边长是10cm，那么它的两直角边长分别是______cm。

15. 代数式3x-2y+4的值，当x=1，y=2时是______。

16. 不等式2x+3>7的解集是______。

17. 若函数y=3x+2是一次函数，那么k的值是______。

18. 在平面直角坐标系中，点P(2,3)关于x轴的对称点坐标是______。

19. 一个圆的半径是r，那么它的周长是______。

苏教版七年级下册数学 第八章幂的运算 综合提优卷1.碳纳米管的硬度与金刚石相当，却拥有良好的柔韧性，可以拉伸，我国某物理所研究组已 研制出直径为0. 5纳米的碳纳米管，1纳米=0. 000 000 001米，则0. 5纳米用科学记数法 表示为( )A. 0. 5×10 -9米B. 5×10 -8米C. 5×10 -9米D. 5×10-10米2.已知319,322m n ==,则下列结论正确的是( ) A. 21m n -= B. 23m n -= C. 23m n += D. 23m n =3.下列运算正确的是( )A. ()a b a b --+=+B. 3233a a a -=C. 628()x x = D. 1221()33-÷= 4.已知,(0)mnx a x b x ==≠，则32m n x -的值等于( )A. 32a bB. 32a b -C. 32a bD. 32a b - 5.计算2422()a a a ⋅÷-的结果是( )A. aB. 2aC. 2a -D. 3a 6.若22(0.2),2,(2)a b c -=-=-=-,则,,a b c 的大小关系为( )A. a b c <<B. a c b <<C. b c a <<D. c b a << 7.若3,8nnx y ==，则()nxy = . 8.已知4(1)1x x ++=，则x = .9.现规定一种新的运算“*”：a *b ＝b a 如:3*2=32=9，则(－2)* (－1)＝ .10.(1)计算:4440.20.412.5⨯⨯;(2)计算: 20170421(1)32()4π---+--+⋅.11.计算:(1) 若2530x y +-=，求432x y ⋅的值; (2) 若62224b ==，求a b +的值;12.你发现了吗? (1)22222221133(),()222333322()333-=⨯===⨯⨯.由上述计算，我们发现22()3 23()2-;(2)仿照(1) ，请你通过计算，判断35()4与34()5-之间的关系;(3)我们可以发现: ()m b a - ()m ab(0)ab ≠;(4)计算: 4433()()84-⨯.【强化闯关】高频考点1 幂的运算性质1.下列算式的运算结果为4a 的是( )A. 4a a ⋅B. 22()a C. 33a a + D. 4a a ÷ 2.下列运算正确的是( )A. 235()a a = B. 22()ab ab = C. 632a a a ÷= D. 235a a a ⋅= 3.计算6236(2)m m ÷-的结果为( )A. m -B. 1-C.34 D. 34- 4.计算623410(10)10⨯÷的结果是( )A. 103B. 107C. 108D. 109 5.计算232323()a a a a a -+⋅-÷，结果是( )A. 52a a -B. 512a a- C. 5a D. 6a 6.计算：201320111(3)()3-⨯-＝ . 高频考点2 零次幂与负整数指数幂 7.若02015a =，则a = . 8.计算正确的是( )A. 0(5)0-= B. 235x x x +=C. 2325()ab a b = D. 2122a a a -⋅=9.计算: 2101(2)()20172---+.高频考点3 科学记数法10.肥皂泡的泡壁厚度大约是0.00000071米，数字0.00000071用科学记数法表示为( )A. 7.1×107B. 0.71×10-6C. 7.1×10-7D. 71×10-811.已知空气的单位体积质量是0. 001 239g/cm 3，则用科学记数法表示该数为( )A.1.239×10-3g/cm 3B. 1.239×10-2g/cm 3C.0.1239×10-2g/cm 3D. 12. 39×10-4g/cm 312.如图，点,O A 在数轴上表示的数分别是0 , 0.1.将线段OA 分成100等份，其分点由左向右依次为1299,,,M M M ⋅⋅⋅; 再将线段1OM 分成100等份，其分点由左向右依次为1299,,,N N N ⋅⋅⋅; 继续将线段1ON 分成100等份，其分点由左向右依次为1299,,,P P P ⋅⋅⋅. 则点37P 所表示的数用科学记数法表示为 .参考答案1.D2.A3.D4.A5.B6. A7. 248. 0或－4或－2 9. 12-10.(1) 4440.20.412.51⨯⨯=;(2) 20170421(1)32()24π---+--+⋅=-. 11.(1) 4328x y ⋅=; (2) 11a b +=或－5; 12. (1)＝(2) 35()4＝34()5-;(3)＝;(4) 4433()()1684-⨯=.过中考 5年真题强化闯关1.B2.D3.D4.C5.D6. 97. 1±8.D9. 2101(2)()201732---+=. 10.C 11.A12. 3.7×10-6。

第12章《证明》（时间:60分钟一、选择题（每题3分，共24分）1.在下列命题中，属于真命题的是（）.A. —个角的补角大于这个角B. 若a//b，b//c，贝U a//cC. 若a c , b c ,则a//bD. 互补的两角必有一条公共边2 4.下列说法中，正确的是A.只有①正确B.④有公共顶点且又相等的角是对顶角2.如图，直线I1//I2 , 13 14 .有三个命题：①1 3 90 ;② 2 3 90 ;③C.①和③正确D. ①②③都正确（第总题｝BA.当1 2时，一定有a//bB.当a//b时，一定有12C.当a//b时，一定有12180D.当a//b时，一定有12904.如图，在VABC中，ACB90,CD // AB , ACD 40A. 40B.50C. 60D.5.下列说法正确的个数为（）.①如果2 3 180 , 那么2与3互为补角；().,则1是2余角;③互为补角的两个角的平分线互相垂直3.如图，直线a、b被直线c所截，下列说法正确的是②如果1 2 90，那么B的度数为（）.70⑤如果两个角相等, 那么它们的余角也相等A. 1B. 2C. 3D. 46.如图，直线m〃n, 1 70 , 2 30，贝U A等于（).满分：100分）只有②正确).7.下列命题中是假命题的是（）.A.三角形的内角和是180B.多边形的外角和都等于 360C. 五边形的内角和是900D. 三角形的一个外角等于和它不相部的两个内角的和 8.如图， AOB 的一边OA 为平面镜，AOB 37 36'，在OB 上有一点E ，从E 点射出一束光线经OA 上一点D 反射，反射光线DC 恰好与OB 平行，则 DEB 的度数是（）.、填空题（每题3分，共30分） 9.已知整数a 、a 2、O s 、a 4、…满足下列条件：c 0 , a 2 a 4a 3 3，…，依次类推，则 a 20i7的值为10. 命题“同旁内角互补”中，题设是 _____________ ，结论是 11. 举反例说明命题“任何数的平方大于零”是假命题:12.如图，AB//CD ，直线EF 与AB 、CD 分别相交于E 、F 两点，EP 平分 AEF , 过点F 作FP EP ，垂足为P ，若 PEF 30，贝U PFC.13. 如图，直线 AB//CD , BC 平分 ABD ，若 154，贝U 2.A. 30B. 4D.50A. 75 36'B. D.74 12'4 1 , O 3 O 2 2 ,僧12题〕 ｛第1?题）（第14题）14. 如图，x________ , y15. 已知三条不同的直线a,b,。

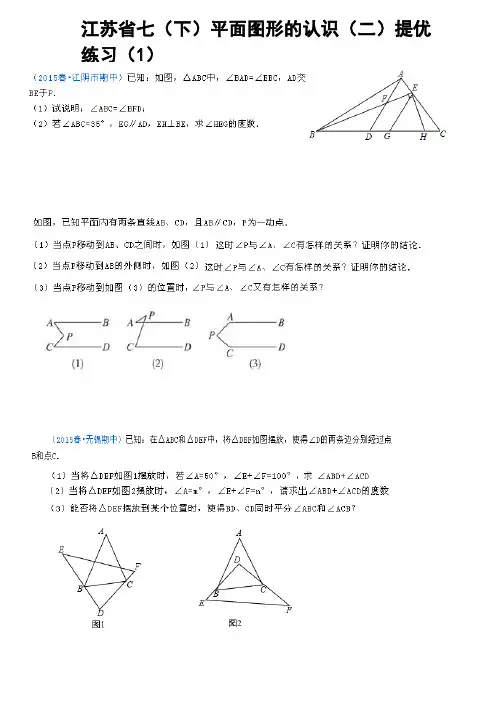
江苏省七（下）平面图形的认识（二）提优练习（1）求在△ABC中，∠C=90°，点D、E分别是边Ac、BC上的点，点P是一动点，连接PD、PE，∠PDA=∠1，∠PEB=∠2，∠DPE=∠α．（1）如图1所示，若点P在线段AB上，且∠α=40°，则∠1+∠2=°；（2）如图2所示，若点P在边AB上运动，则∠α、∠1、∠2之间的关系为有何数量关系；猜想结论并说明理由；（3）如图3所示，若点P运动到边AB的延长线上，则∠α、∠1、∠2之间有何数量关系？猜想结论并说明理由．（1）如图①，△ABC中，点D、E在边BC上，AD平分∠BAC，AE⊥BC，∠B=35°，∠C=65°，求∠DAE 的度数；（2）如图②，若把（1）中的条件“AE⊥BC”变成“F为DA延长线上一点，FE⊥BC”，其它条件不变，求∠DFE的度数；（3）若把（1）中的条件“AE⊥BC”变成“F为AD延长线上一点，FE⊥BC”，其它条件不变，请画出相应的图形，并求出∠DFE的度数；（4）结合上述三个问题的解决过程，你能得到什么结论？备用图图3M N E E N M O O A B A B 图2图1MN EE N M DO O A B A B C已知：∠MON =80°，OE 平分∠MON ，点A 、B 、C 分别是射线OM 、OE 、ON 上的动点（A 、B 、C 不与点O 重合），连接AC 交射线OE 于点D ．设∠OAC =x °． （1）如图1，若AB ∥ON ，则①∠ABO 的度数是 ；②如图2，当∠BAD =∠ABD 时，试求x 的值（要说明理由）； （2）如图3，若AB ⊥OM ，则是否存在这样的x 的值，使得△ADB 中有两个相等的角？若存在，直接写出x 的值；若不存在，说明理由．（自己画图） 聪明的小宸同学在学习“三角形的外角等于与它不相邻的两个内角之和”后，采用类比的方法，研究四边形不相邻的两个外角与不相邻的两个内角的关系． (1)如图①，猜想并说明∠1+∠2与∠A 、∠C 的数量关系； （2）图①不妨称为“枪头图”．试直接利用上述结论．．．．．．．．，解决下面的三个问题： 问题一：如图②，将△ABC 纸片沿DE 折叠，使点彳落在四边形BCDE 内点A ’的位置， 试直接写出∠1+∠2与∠A 之间的数量关系： ；问题二：如图③，在△ABC 中，∠ABC 与∠ACB 的外角平分线交于点D ，若∠A=40°，求∠O 的度数； 问题三：将图③中边BC 改为折线BDC?得图④，BO 、CO 是∠ABD 与∠ACD 的外角平分线． 试探究：∠A 、∠D 与∠O 这三个角的数量关系．如图①，AD是△ABC的中线，△ABD与△ACD的面积有怎样的数量关系？为什么？（2）若三角形的面积记为S，例如：△ABC的面积记为S△ABC，如图②，已知S△ABC=1，△ABC的中线AD、CE相交于点O，求四边形BDOE的面积．小华利用（1）的结论，解决了上述问题，解法如下：连接BO，设S△BEO=x，S△BDO=y，由（1）结论可得：S，S△BCO=2S△BDO=2y，S△BAO=2S△BEO=2x．则有，即．所以．请仿照上面的方法，解决下列问题：①如图③，已知S△ABC=1，D、E是BC边上的三等分点，F、G是AB边上的三等分点，AD、CF交于点O，求四边形BDOF的面积．②如图④，已知S△ABC=1，D、E、F是BC边上的四等分点，G、H、I是AB边上的四等分点，AD、CG交于点O，则四边形BDOG的面积为．平面内的两条直线有相交和平行两种位置关系（1）如图a，若AB∥CD，点P在AB、CD外部，则有∠B=∠BOD，又因∠BOD是△POD的外角，故∠BOD=∠BPD+∠D，得∠BPD=∠B-∠D．将点P移到AB、CD内部，如图b，以上结论是否成立？若成立，说明理由；若不成立，则∠BPD、∠B、∠D之间有何数量关系？请证明你的结论；（2）在图b中，将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q，如图c，则∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系？（不需证明）（3）根据（2）的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数．如图1，两个不全等的等腰直角三角形OAB和OCD叠放在一起，并且有公共的直角顶点O。

苏科版数学七年级下《第十章二元一次方程》拓展提优卷含答案一、 填空（每空2分，共26分）1、在方程732=+y x 中。

如果022=-y ，则=x 。

2、已知：132=--+y x y x ，用含x 的代数式表示y ，得 。

3、若()1321=+--y x a a 是二元一次方程，则a = 。

4、如果方程10=+by ax 的两组解为⎩⎨⎧==⎩⎨⎧=-=51,01y x y x ，则a = ，b = 。

5、若x ：y =3：2，且1323=+y x ，则=x ，y = 。

6、方程72=+y x 的正整数解有 组，分别为 。

7、如果关于x 的方程2324+=-x m x 和m x x 32-=的解相同，则m = 。

8、一个两位数的十位数字与个位数字之和等于5，十位数字与个位数字之差为1，设十位数字为x ，个位数字为y ，则用方程组表示上述语言为 。

9、已知梯形的面积为25平方厘米，高为5厘米，它的下底比上底的2倍多1厘米，则梯形的上底和下底长分别为 。

10、写出一个二元一次方程，使其满足x 的系数是大于2的自然数，y 的系数是小于－3的整数，且3,2==y x 是它的一个解。

。

二、 选择（每题3分，共30分）1、以⎩⎨⎧==13y x 为解建立一个二元一次方程组，不正确的是 （ ）A 、543=-y xB 、031=-y xC 、32-=+y xD 、65322=-y x 2、方程123,632-=+=+y x y x 的公共解是 （ ）A 、⎩⎨⎧-==23y xB 、⎩⎨⎧=-=43y xC 、⎩⎨⎧==23y xD 、⎩⎨⎧=-=23y x3、若的一个解是方程02=+⎩⎨⎧==y x b y a x ，()b a a ,,0则≠的符号为 （ ） A 、b a ,同号 B 、b a ,异号C 、b a ,可能同号可能异号D 、0,0=≠b a4、已知：关于y x ,的方程组y x ，ay x a y x -⎩⎨⎧-=++-=+则3242的值为 （ ）A 、－1B 、1-aC 、0D 、15、若方程组()a ，y x y a ax y x 则相等和的解⎩⎨⎧=-+=+31134的值为 （ ） A 、4 B 、10 C 、11 D 、126、已知：32++y x 与()22y x +的和为零，则y x -= （ ） A 、7 B 、5 C 、3 D 、17、6年前，A 的年龄是B 的3倍，现在A 的年龄是B 的2倍，则A 现在的年龄为 （ ） A 、12 B 、18 C 、24 D 、308、设b k ，y x ，y x b kx y ,,42,11,则时当时当-====+=的值为 （ ）A 、⎩⎨⎧-==23b kB 、⎩⎨⎧=-=43b kC 、⎩⎨⎧=-=65b kD 、⎩⎨⎧-==56b k 9、甲、乙两人练习跑步，如果乙先跑10米，则甲跑5秒就可追上乙；如果乙先跑2秒，则甲跑4秒就可追上乙，若设甲的速度为x 米/秒，乙的速度为y 米/秒，则下列方程组中正确的是 （ ）A 、⎩⎨⎧+=+=y y x y x 2441055 B 、⎩⎨⎧=-=-y x x y x 4241055C 、⎩⎨⎧=-=+2445105y x y x D 、⎩⎨⎧=-=-yx y x 424105510、根据下列所示的程序计算y 的值，若输入的x 值为－3，则输出的结果为（ ） A 、5 B 、－1C 、－5D 、1三、 解方程组（每题5分，共20分）1、⎩⎨⎧=+=-1464534y x y x 2、⎩⎨⎧=+=-1732623y x y x3、()()⎪⎩⎪⎨⎧=--+=-++254622y x y x y x y x 4、⎩⎨⎧=+=+572317631723y x y x四、 解答题（5题）甲、乙两位同学在解方程组⎩⎨⎧-=-=+227by ax by ax 时，甲看错了第一个方程解得⎩⎨⎧-==11y x ，乙看错了第二个方程解得⎩⎨⎧-=-=62y x ，求b a ,的值。

21初一数学提优试卷（三）班级 姓名一、填空1、在等式(2⋅-m a n m a +=)中，括号内的代数式应当是_________.2、若三角形的一个外角等于︒80，那么和它相邻的内角为 度，所以这个三角形按角分类是 三角形。

3、小明在用计算器计算一个多边形的内角和时，求出的结果是2005°，小丽立即判断他的结果是错误的，小明仔细地复算了一遍，果然发现自己把一个角的度数输入了两遍．根据以上事实，请你写出正确的结论_________.4、要使五边形木架（用5根木条钉成）不变形，至少要再钉 根木条。

5、如图，把直角梯形ABCD 沿AD 方向平移到梯形EFGH ，HG =24cm,MG =8cm,MC =6cm,则阴影部分的面积是 ．6、如图，将字母“V ” 向右平移 格会得到字母“W ”。

二、选择7、将一张长方形纸片如图所示折叠后，再展开．如果∠1=56°，那么∠2等于 （ ） （A ） 56° （B ） 68° （C ） 62° （D ） 66°8、现有若干个三角形，在所有的内角中，有5个直角，3个钝角，25个锐角，则在这些三角形中有（ ）个锐角三角形． A. 3 B. 4或5 C. 6或7 D. 89、下列叙述中，正确的有： （ ） ①任意一个三角形的三条中线．．．．．．．．都相交于一点；②任意一个三角形的三条高．．．．．．．都相交于一点； ③任意一个三角形的三条角平分线．．．．．．．．．．都相交于一点；④一个五边形最多．．有3个内角．．是直角 A 、0个 B 、1个 C 、2个 D 、3个 三、解答题1、每个外角都相等的多边形，它的外角等于一个内角的32，求多边形的边数。

2、们规定：a*b=10a ×10b ，例如3*4=103×104=107. （1）试求12*3和2*5的值；（2）想一想（a*b ）*c 与a*(b*c)相等吗？如果相等，请验证你的结论.B A F EC M DGH3、BC 中，AD 是高，AE 、BF 是角平分线，它们相交于点O ，∠A=500，∠C=600， 求∠DAC 及∠BOA4、 如图，AD 为△ABC 的中线，BE 为△ABD 的中线， ①∠ABE=15°∠BAD=40°，求∠BED 的度数 ②在△BED 中作BD 边上的高③ 若△ABC 的面积为40，BD=5，则点E 到BC 边的距离为多少？5、如图，甲处表示2街与4巷的十字路口，乙处表示4街与2巷的十字路口，如果用（2，4）表示甲处的位置， 那么“（2，4） （3，4） （4，4） （4，3） （4，2）”表示从甲处到乙处的一种路线.请你仅用5个有序数对写出一种从乙处到甲处的路线.你的路线是：_______________________________________________.6、阅读材料，并填表：在△ABC 中，有一点P １，当P １、A 、B 、C 没有任何三点在同一直线上时，可构成三个不重叠的小三角形（如图）。