27.3过三点的圆.3过三点的圆

过三点的圆教学设计教学设计思想学生是学习的主体，是学习的主动参与者和知识的建构者。

教师在教学中起主导作用，是学生实践活动的组织者、引导者与合作者。

本节课首先设置一个具体实例，引起学生探究欲望和学习兴趣，然后教师引导学生经历观察、猜测、实际操作验证、分析归纳推理等数学活动过程，培养学生严谨的科学态度，开展学生动手操作、自主探究、合作交流和分析归纳的能力。

教学目标知识与技能：1．学会过不在同一直线上的三个点画圆的方法；2．能说出三角形的外心及外接圆的概念。

过程与方法：经历探索点与圆的位置关系的过程，体会数学分类讨论思想问题的方法，体会类比思想。

情感态度价值观：1．体会“事物之间是相互联系和运动变化〞的观点；2．通过对圆的进一步学习，体会圆的完美性〔与其他图形的结合等〕，提高对数学中美的欣赏。

教学重难点重点：1．定理：不在同一直线上的三个点确定一个圆．定理中“不在同一直线〞这个条件不可忽略，“确定〞一词应理解为“有且只有〞．2．通过三角形各顶点的圆叫做三角形的外接圆难点：分析作圆的方法，实质是设法找圆心．教学方法引导探究法教学媒体多媒体，三角板，圆规课时安排1课时教学过程设计一、创设问题情境，引入新课1．现有一块打碎的圆形玻璃镜子残片，想重新去玻璃店配一块同样大小的圆形玻璃镜子，请问这块残片还有用吗？怎样去配制呢？2．引入新课：〔1〕 这个问题就是本节课的学习的一个知识点，相信同学们通过本节课的学习一定能解决这个问题。

〔2〕 出示课题：§27．3 过三点的圆 二、一起探究探究1：过一个点A 如何作圆？〔让学生动手去完成〕A o 1o 3o 4o 2o 5图1学生讨论并发现：过点A 所作圆的圆心在哪儿〔圆心不定〕？半径多大〔半径不定〕？可以作几个这样的圆〔无数个〕？探究2过两点A 、B 如何作圆？〔学生动手去完成〕Ao 3o 2o 1Bo 4图2学生继续讨论并发现：它们的圆心到A 、B 两点的距离怎样？能用式子表示吗〔OA=OB 〕?圆心在哪里〔在直线AB 的垂直平分线上〕？过点A 、B 两点的圆有几个〔无数个〕？探究3 过同一平面内三个点的情况会怎样呢? 分两种情况研究：〔一〕作一个圆，使它经过不在一直线上三点A 、B 、C ，：不在一直线上三点A、B、C，求作一个圆，使它同时经过点A、B、C。

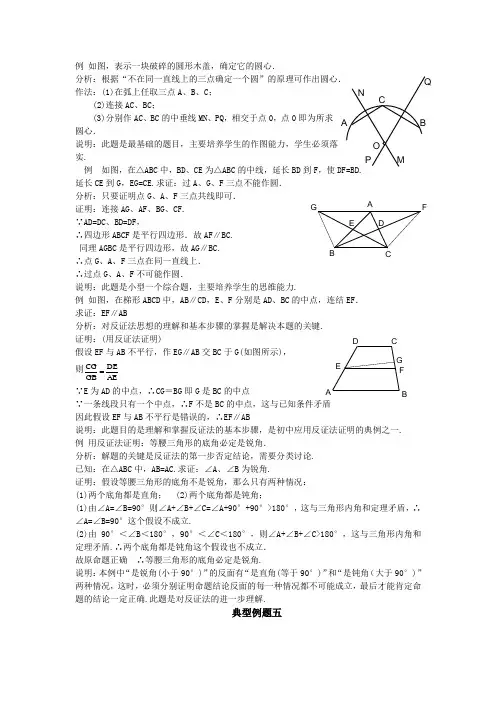
例 如图，表示一块破碎的圆形木盖，确定它的圆心．作法：(1)在弧上任取三点A 、B 、C ； (2)连接AC 、BC ；(3)分别作AC 、BC 的中垂线MN 、PQ ，相交于点0，点0即为所求圆心．说明：此题是最基础的题目，主要培养学生的作图能力，学生必须落实. 例 如图，在△ABC 中，BD 、CE 为△ABC 的中线，延长BD 到F ，使延长CE 到G ，EG=CE.求证：过A 、G 、F 三点不能作圆． 分析：只要证明点G 、A 、F 三点共线即可．证明：连接AG 、AF 、BG 、CF.∵AD=DC 、BD=DF ， ∴四边形ABCF 是平行四边形．故AF ∥BC. 同理AGBC 是平行四边形，故AG ∥BC.∴点G 、A 、F 三点在同一直线上． ∴过点G 、A 、F 不可能作圆．说明：此题是小型一个综合题，主要培养学生的思维能力.例 如图，在梯形ABCD 中，AB ∥CD ，E 、F 分别是AD 、BC 的中点，连结EF ． 求证：EF ∥AB分析：对反证法思想的理解和基本步骤的掌握是解决本题的关键. 证明：(用反证法证明) 假设EF 与AB 不平行，作EG ∥AB 交BC 于G(如图所示)， 则AEDE GB CG ∵E 为AD 的中点，∴CG ＝BG 即G 是BC 的中点 ∵一条线段只有一个中点，∴F 不是BC 的中点，这与已知条件矛盾 因此假设EF 与AB 不平行是错误的，∴EF ∥AB说明：此题目的是理解和掌握反证法的基本步骤，是初中应用反证法证明的典例之一. 例 用反证法证明：等腰三角形的底角必定是锐角．分析：解题的关键是反证法的第一步否定结论，需要分类讨论. 已知：在△ABC 中，AB=AC.求证：∠A 、∠B 为锐角.证明：假设等腰三角形的底角不是锐角，那么只有两种情况： (1)两个底角都是直角； (2)两个底角都是钝角；(1)由∠A=∠B=90°则∠A+∠B+∠C=∠A+90°+90°>180°，这与三角形内角和定理矛盾，∴∠A=∠B=90°这个假设不成立.(2)由90°＜∠B ＜180°，90°＜∠C ＜180°，则∠A+∠B+∠C>180°，这与三角形内角和定理矛盾.∴两个底角都是钝角这个假设也不成立． 故原命题正确 ∴等腰三角形的底角必定是锐角. 说明：本例中“是锐角(小于90°)”的反面有“是直角(等于90°)”和“是钝角（大于90°)”两种情况，这时，必须分别证明命题结论反面的每一种情况都不可能成立，最后才能肯定命题的结论一定正确.此题是对反证法的进一步理解.典型例题五A B CD E FG A B C D EFG例 作圆使其半径为R ，且经过线段AB 的两端点A 、B .作法（1）作线段AB 的垂直平分线MN ；（2）以点A 为圆心R 为半径画弧，交MN 于O ； （3）以O 为圆心，R 为半径作⊙O . ⊙O 即为所求的圆，如图.说明：要作出一个确定的圆，就必须要明确它的圆心和半径，二都缺一不可.本题中要求的圆的半径已知，故关键要确定它的圆心.通过找圆心的过程可以看出：①当AB R 21>时，符合条件的圆心有两个，要求作的圆有两个；②当AB R 21=时，符合条件的圆心只有一个，要求作的圆有一个；③当AB R 21<时，符合条件的圆心找不到，要求作的圆不存在.典型例题六例 如图，在ABC ∆中，D 、E 分别在AC 、AB 上，BD 、CE 相交于点O ，证明BD 和CE 不可能互相平分.分析：结论带否定词“不”的问题适合于用反证法证明，我们不妨一试. 证明 假定BD 和CE 互相平分，则四边形EBCD 是平行四边形. CD BE //∴，这与已知BE 和CD 相交于A 相矛盾. ∴BD 和CE 不可能互相平分.典型例题七例 如图，四边形ABCD 的对角线AC 、BD 相交于点O ，且OB OA =，OD OC =.证明：四边形ABCD 一定有外接圆.分析：如果能证明四边形的三条边的垂直平分线相交于一点就是了，由题设可以证明AB 、CD 有公共的垂直平分线，这样问题就不难解决了.证明,COD AOB ∠=∠Θ∴等腰AOB ∆和等腰COD ∆的顶角相等. ∴它们的底角也相等.∴ABO CDO ∠=∠.CD AB //，过O 作AB OM ⊥，则OM 是AB 的垂直平分线，也是CD 的垂直平分线.设DA 的垂直平分线交OM 于P ，则P 点到A 、B 、C 、D 的距离相等，即四边形ABCD 有外接圆，其圆心是P 点.典型例题八例 已知：如图，BC DE ⊥于E ，AC DF ⊥于F ，AB DG ⊥于G ，并且E 、F 、G 三点共线，求证：A 、B 、C 、D 四点共圆.分析：A 、B 、C 、D 四点共圆的几何性质是︒=∠+∠180BDC A ，这一结论的反面是︒≠∠+∠180BDC A ，因此，用反证法，从︒≠∠+∠180BDC A 推出一个矛盾，便肯定了A 、B 、D 、C 四点共圆.证明 假设A 、B 、D 、C 四点不共圆，则： ︒≠∠+∠180BDC A ，,,AC DF BC DE ⊥⊥Θ,180︒=∠+∠∴DFC DEC故D 、E 、C 、F 四点共圆. 同理，D 、E 、G 、B 四点共圆. DBG DEF DCF ∠=∠=∠∴， 从而CDF BDG ∠=∠， BDC GDF ∠=∠∴.故︒≠∠+∠=∠+∠180A BDC A GDF ， ΘAB DG ⊥，AC DF ⊥， ︒=∠+∠∴180DFA AGD故四边形AGDF 的内角和︒≠∠+∠+∠+∠=360DFA AGD A GDF ，矛盾. ∴A 、B 、D 、C 四点共圆.典型例题九例 作一个圆，使它经过已知点A 和B ，并且圆心在已知直线l 上.作法 （1）当直线l 和AB 斜交或重合时，只要作线段AB 的垂直平分线与l 交于O ，以O 为圆心，OA 为半径作圆即为所求的圆.这样的圆只有一个（如图1）.（2）当直线l 与AB 垂直但不经过线段AB 的中点时，这样的圆不能作出. （3）当直线l 经过线段AB 的垂直平分线，这样的圆可作无数个（如图2）.图1 图2说明：本题考查圆的确定，解题关键是确定圆心的位置和半径的大小，易错点是忽视线段AB 与l 的不同位置关系，只画出（1）的情况，造成丢解的错误.选择题1．下列命题中正确的为（ ）（A ）三点确定一个圆 （B ）圆有切只有一个内接三角形（C ）三角形的外心是三角形任意两边的垂直平分线的交点 （D ）面积相等的三角形的外接圆是等圆 2．钝角三角形的外心在（ ）（A ）三角形的内部 （B ）三角形的外部 （C ）三角形的钝角所对的边上 （D ）以上都有可能3．己知命题：(1)三角形中最少有一个内角不小于60°；(2)三角形的外心到三角形各边的距离都相等. 下面判断中正确的是（ ）（A ）命题(1)(2)都正确 （B ）命题(1)正确，(2)不正确 （C ）命题(1)不正确，(2)正确 （D ）命题(1)(2)都不正确 4．下列条件，可以画出圆的是（） A ．已知圆心 B ．已知半径 C ．已知三个点 D ．已知直径 5．三角形的外心是（）A ．三条中线的交点B ．三条中垂线的交点C ．三条高的交点D ．三条角平分线的交点6．若三角形的外心在三角形内，则三角形的形状是（）A ．锐角三角形B ．直角三角形C ．钝角三角形D ．形状无法确定 7．在下列三角形中，外心在它一条边上的三角形是（） A ．边长分别为cm 2、cm 2、cm 3 B ．三角形的边长都等于cm 5C ．三角形的边长分别为cm 5、2cm 1、3cm 1D ．三角形的边长为cm 4、cm 6、cm 8 8．下列说法正确的是（ ）． A ．三点决定一个圆B ．三角形的中心就是三角形的外心C ．三角形的外心就是三条中线的交点D ．∆Rt 斜边的中点就是这个三角形的外心． 9．下列说法中，正确的是（ ）． A ．三点决定一个圆 B ．过一点不能作圆 C ．过两点不能作圆D ．一个圆的圆心决定这个圆的位置，这个圆的半径决定这个圆的大小10．下列命题：(1)经过三点一定可以作圆；(2)任一个三角形一定有一个外接圆，而且只有一个外接圆；(3)任意一个圆一定有一个内接三角形，而且只有一个内接三角形；(4)三角形的外心到三角形三个顶点的距离相等．A ．4个B ．3个C ．2个D ．1个 答案：1、C ；2、B ；3、B. 4. D 5. B 6. A 7. C. 8．D ；9．D ；10．C ；填空题1. 如图，ABC ∆内接于⊙O ，OAC B ∠=∠，cm 8=OA ，则cm _____=AC2. 过一点A 可作_______个圆，过两点A 、B 可作________个圆，且圆心在线段AB 的_______上，过三点A 、B 、C ，当这三点________时能且只能作一个圆，且圆心在______上。

27.3过三点的圆教学设计教学重点：过不在同一直线上的三点作圆的方法。

多媒体演示；学生自主分析归纳；学生分组讨论；教 师引导相结合教学难点： 如何确定圆的方法（找圆心和半径）。

学生讨论、教师质疑和多媒体演示相结合三、了解条件数学基础知识不太扎实，思维较活跃，有一定的分析能力，但深入分 析解决问题的能力有待提高。

组织教学能力较强，能够充分调动学生的积极性，能够合理运用多媒 体技术辅助教学。

学 校 课 型深州王家井镇中学新授课科 目 早节数学 授课教师 刘凤娥 年级 九年级27.3过三点的圆知识技能目标教 学 目 标 能力目标情感态度 价值观1通过学生对作圆过程的探究，使学生理解“不在同一 直线上的三点确定一个圆”，明确三角形的外接圆、三角 形的外心、圆的内接三角形的概念，2、 使学生能熟练掌握应用尺规过不在一直线上三点作圆 的方法。

3、 向学生渗透转化、分类讨论等这样一些数学思想方法， 为今后继续进一步学习数学打下基础。

1通过学生自己动手作图，在动手参与的过程中探索、 发现科学知识，进一步提高学生探究和发现问题的能力。

2•提高学生应用数学知识解决生活中实际问题的能力。

1增强学生的数学应用意识，提高学生学习数学的兴趣 和积极性。

2、培养学生树立良好的学习态度、养成永无止境的科学 探索精神。

教学重点及解决措施教学难点及解决措施 学生情 况 教师情 况大胆发表自己让学生学会探究问题的/ \的见解。

教师适方法时追问、s nr\ X质疑、点培养学生分\ 乂su拨，促使类讨论的意Vz^W7B学生不识<2K>断“拨乱反正”，培养学生全得出正面考虑问题探究②过已知两点A、B如何作圆？（学生动手确的结的意识去完成）2.过两点的圆学生继续讨论并发现：它们的圆心到A、B论。

两点的距离怎样？能用式子表示吗（OA-OB）圆让学生充分心在哪里（在线段AB的垂直平分线上），过点A、感受数学的B两点的圆有几个（无数个）？探究③：过同一平面内三个点的情况会怎样呢？ 3、过三点的圆由于两点确定一条直线，因此三个点就有在同一直线上的三点和不在同一直线上的三个点两种情况.㈠求作一个圆，使它经过不在同一直线上三点A、B、C,已知：不在一直线上三点A、B、C,求作一个圆，使它同时经过点A、B、Co分析：假设经过A、B、C三点的。

分式教学目标〔一〕知识与技能目标iu1．使学生了解分式的概念，明确分母不得为零是分式概念的组成局部．2．使学生能够求出分式有意义的条件．〔二〕过程与方法目标能用分式表示现实情境中的数量关系，体会分式是表示现实世界中一类量的数学模型，进一步开展符号感，通过类比分数研究分式的教学，引导学生运用类比转化的思想方法研究解决问题．〔三〕情感与价值目标在土地沙化问题中，体会保护人类生存环境的重要性。

培养学生严谨的思维能力． 教学重点和难点准确理解分式的意义，明确分母不得为零既是本节的重点，又是本节的难点． 教学方法:分组讨论．教学过程1. 情境引入：面对日益严重的土地沙化问题，某县决定分期分批固沙造林，一期工程方案在一定期限内固沙造林2400公顷，实际每月固沙造林的面积比原方案多30公顷，结果提前4个月完成原方案任务，原方案每月固沙造林多少公顷？（1） 这一问题中有哪些等量关系？（2） 如果设原方案每月固沙造林x 公顷，那么原方案完成一期工程需要____________个月，实际完成一期工程用了____________个月； 根据题意，可得方程 ； 2、解读探究x 2400，302400+x ，43024002400=+-x x 认真观察上面的式子，方程有什么特点？n 边形的每个内角为 度2一箱苹果售价a 元，箱子与苹果的总质量为mkg ，箱子的质量为nkg ，那么每千克苹果售价是多少元？上面问题中出现的代数式x 2400，302400+x ，nn 180)2(⨯-；它们有什么共同特征？ (1)由学生分组讨论分式的定义，对于“两个整式相除叫做分式〞等错误，由学生举反例一一加以纠正，得到结论：的分母．(2)由学生举几个分式的例子．(3)学生小结分式的概念中应注意的问题．①分母中含有字母．②如同分数一样，分式的分母不能为零．(4)问：何时分式的值为零？(以(2)中学生举出的分式为例进行讨论)例1〔1〕当a=1,2时，求分式a a 21+的值； （3） 当a 取何值时，分式aa 21+有意义？ 解：〔1〕当a=1时，;1121121=⨯+=+a a 当a=2时43221221=⨯+=+a a 〔2〕当分母的值等于零时，分式没有意义，除此以外，分式都有意义。