北师大版五年级下册数学知识点总结笔记

北师大版五下数学重要知识点一、数与代数1.2. 分数乘法：乘数大于1，积比另一个乘数大；乘数小于1，积比另一个乘数小。

分数除法：除数大于1，商比被除数小；除数小于1，商比被除数大。

3.小数分数互化：小数化分数：一位小数，十分之几；两位小数，百分之几；三位小数，千分之几。

分数化小数：用分子除以分母；或把分母通分为整十、整百、整千的数。

1 2=0.525=0.438=0.375110=0.1120=0.051 4=0.2535=0.648=0.5310=0.3320=0.152 4=0.545=0.858=0.625510=0.5125=0.043 4=0.7518=0.12568=0.75710=0.7225=0.081 5=0.228=0.2578=0.875910=0.9325=0.124.解决问题二、图形与几何1.长方体和正方体都有（6）个面，（12）条棱和（8）个顶点。

（正方体）是特殊的长方体。

2.常用公式1.3.体积与容积单位换算相邻的体积（容积）单位的进率是1000.大单位换成小单位，乘进率；小单位换成大单位，除以进率。

三、解决问题统计与概率1.看数量的多少选择条形统计图，看变化趋势选择折线统计图，有两组数据的是复式。

2.复式统计图有复式条形统计图和复式折线统计图，都方便对比两组不同的数据，画图时要注意标图例。

3.平均数去掉极端值（实际比赛中去掉一个最高分和一个最低分），更有代表性。

北师大版小学数学五年级(下册)知识点整理
一、整数
1.正整数、零、负整数。

2.整数的大小比较。

3.整数的四则运算及口算。

二、分数
1.整数与分数的互化。

2.分数的大小比较。

3.分数的基本运算。

三、小数
1.小数的认识和读法。

2.小数的大小比较。

3.小数的四则运算及口算。

四、长度、面积和体积
1.长度的认识和测量。

2.面积和体积的认识和计算。

3.同类图形的面积比较。

五、时间
1.日、周、月、年的认识和计算。

2.钟表时间的认识和读法。

3.时间的加减和口算。

六、数据与图形
1.统计和整理数据。

2.直方图、折线图和饼图的认识和制作。

3.读图、解题和口算。

七、几何
1.线段、角、直线和平面的认识和描绘。

2.平面图形的认识、分类和制作。

3.重要图形的特征、性质和计算。

八、算式
1.加、减、乘、除算式及口算的运算法则。

2.约分、通分和分配律。

3.算式和实际问题的联系和解决。

九、有理数
1.整数、分数、小数的统称。

2.有理数的大小比较。

3.有理数的四则运算。

十、图形变换
1.图形的移动、翻转、旋转和对称。

2.图形变换和位置关系的认识和运用。

3.解题、创作和口算。

以上是北师大版小学数学五年级(下册)的全部知识点整理，希望对您学习有所帮助。

北师大版小学五年级数学下册全册知识点归纳第一单元《分数加减法》补充知识点：整数加减法运算定律在分数加减法中同样适用，见下图：4、把分数化成小数的方法：通常是利用分数与除法的关系，用分子除以分母来得到。

注意：对于某些分数也可以将它化为分母是10、100、1000之类的分数，然后再直接写成小数形式。

例如：5、常见分数和小数的互化：第二单元《长方体（一）》第一类，中间四连方，两侧各一个，共六种：第二类，中间三连方，两侧各有一、二个，共三种：第四类，两排各三个，只有一种：例如：如图，4个棱长都是10厘米的正方体堆放在墙角处，露在外面的面积是多少？第三单元《分数乘法》约分的最好先约分。

3、打折的含义，例如：九折，是指现价是原价的。

容积单位：升(L) 毫升(ml)补充知识点：冰箱的容积用“升”作单位；我们饮用的自来水用“立方米”作单位。

单位换算：（相邻单位之间的进率为1000）（小单位化成大单位要除以进率，大单位化成小单位要乘以进率。

可以概括为：小化大除一下，大化小乘一下）1米3＝1000分米31分米3＝1000厘米31升＝1000毫升 1升＝1分米31毫升＝1厘米3单名数与复名数之间的互化：单名数：由一个数和一个单位名称组成的名数叫做单名数。

分数除以整数的计算方法：分数除以整数（0除外）等于乘这个整数的倒数。

4、整数除以分数等于乘这个分数的倒数。

5、除以一个数（零除外）等于乘这个数的倒数。

的孵化期为x天，则：未知的，所以用鸭的孵化期除以它对应的分率，即：①以学校为观测点，丁丁家的位置是西偏北45°，距离学校1800米。

②以学校为观测点，青青家的位置是东偏北26°，距离学校1500米。

第七单元《用方程解决问题》1、列方程解应用题的步骤：（1）找到题中的等量关系式（2）解设所求量为x（3）根据等量关系式列出相应的方程（4）解答方程，注意计算结果不带单位。

（5）检验做答。

2、在有多个未知数量的应用题中，通常应将1倍数设为x，举例如下：例:爸爸的年龄是儿子年龄的4倍，父子俩年龄之和为40，求父亲和儿子的年龄各是多少岁？解：首先根据题意找出等量关系式：爸爸年龄+儿子年龄=40因为儿子年龄是1倍数，所以：设儿子年龄为x岁，那么爸爸年龄就是4x，代入等量关系式得：爸爸年龄为：4x=4×8=32(岁)答：爸爸的年龄为32岁，儿子的年龄为8岁。

北师大版五年级下册数学知识点总结第一单元：《分数加减法》一、分数的意义1、分数的意义：把单位“1”平均分成若干份，表示这样的一份或几份的数，叫做分数。

2、分数单位：把单位“1”平均分成若干份，表示这样的一份的数叫做分数单位。

二、分数与除法的关系，真分数和假分数1、分数与除法的关系：除法中的被除数相当于分数的分子，除数相等于分母。

2、真分数和假分数：①分子比分母小的分数叫做真分数，真分数小于1。

②分子比分母大或分子和分母相等的分数叫做假分数，假分数大于1或等于1。

③由整数部分和分数部分组成的分数叫做带分数。

2、假分数与带分数的互化：①把假分数化成带分数，用分子除以分母，所得商作整数部分，余数作分子，分母不变。

②把带分数化成假分数，用整数部分乘以分母加上分子作分子，分母不变。

三、分数的基本质分数的分子和分母同时乘或除以相同的数（0除外），分数的大小不变，这叫做分数的基本性质。

2、分数的大小比较：①同分母分数，分子大的分数就大，分子小的分数就小；②同分子分数，分母大的分数反而小，分母小的分数反而大。

③异分母分数，先化成同分母分数（分数单位相同），再进行比较。

（依据分数的基本性质进行变化）四、约分（最简分数）1、最简分数：分子和分母只有公因数1的分数叫做最简分数。

2、约分：把一个分数化成和它相等，但分子和分母都比较小的分数，叫做约分。

（并不是一定要把分数化成与它相等的最简分数才叫约分；但一般要约到最简分数为止）注意：分数加减法中，计算结果能约分的，一般要约分成最简分数。

五、分数和小数的互化：1、小数化分数：将小数化成分母是10、100、1000?的分数，能约分的要约分。

具体是：看有几位小数，就在1后边写几个0做分母，把小数点去掉的部分做分子，能约分的要约分。

2、分数化小数：用分子除以分母，除不尽的按要求保留几位小数。

（一般保留三位小数。

）如果分母只含有2或5的质因数，这个分数能化成有限小数。

如果含有2或5以外的质因数，这个分数就不能化成有限小数。

北师大版小学五年级数学下册全册知识点归纳第一单元《分数加减法》补充知识点：整数加减法运算定律在分数加减法中同样适用，见下图：4、把分数化成小数的方法：通常是利用分数与除法的关系，用分子除以分母来得到。

注意：对于某些分数也可以将它化为分母是10、100、1000之类的分数，然后再直接写成小数形式。

例如：5、常见分数和小数的互化：第二单元《长方体（一）》第一类，中间四连方，两侧各一个，共六种：第二类，中间三连方，两侧各有一、二个，共三种：第四类，两排各三个，只有一种：例如：如图，4个棱长都是10厘米的正方体堆放在墙角处，露在外面的面积是多少？第三单元《分数乘法》约分的最好先约分。

3、打折的含义，例如：九折，是指现价是原价的。

容积单位：升(L) 毫升(ml)补充知识点：冰箱的容积用“升”作单位；我们饮用的自来水用“立方米”作单位。

单位换算：（相邻单位之间的进率为1000）（小单位化成大单位要除以进率，大单位化成小单位要乘以进率。

可以概括为：小化大除一下，大化小乘一下）1米3＝1000分米31分米3＝1000厘米31升＝1000毫升 1升＝1分米31毫升＝1厘米3单名数与复名数之间的互化：单名数：由一个数和一个单位名称组成的名数叫做单名数。

复名数：由两个或两个以上的数及单位名称组成的名数叫做复名数。

分数除以整数的计算方法：分数除以整数（0除外）等于乘这个整数的倒数。

4、整数除以分数等于乘这个分数的倒数。

5、除以一个数（零除外）等于乘这个数的倒数。

孵化期为x天，则：未知的，所以用鸭的孵化期除以它对应的分率，即：例如：下面是一个平面图:是西偏北45°，距离学校1800米。

②以学校为观测点，青青家的位置是东偏北26°，距离学校1500米。

第七单元《用方程解决问题》1、列方程解应用题的步骤：（1）找到题中的等量关系式（2）解设所求量为x（3）根据等量关系式列出相应的方程（4）解答方程，注意计算结果不带单位。

北师大五年级下册数学知识点总结第一单元：《分数加减法》一、分数的意义1、分数的意义：把单位“1”平均分成若干份，表示这样的一份或几份的数，叫做分数。

2、分数单位：把单位“1”平均分成若干份，表示这样的一份的数叫做分数单位。

二、分数与除法的关系，真分数和假分数1、分数与除法的关系：除法中的被除数相当于分数的分子，除数相等于分母。

2、真分数和假分数：①分子比分母小的分数叫做真分数，真分数小于1。

②分子比分母大或分子和分母相等的分数叫做假分数，假分数大于1或等于1。

③由整数部分和分数部分组成的分数叫做带分数。

2、假分数与带分数的互化：①把假分数化成带分数，用分子除以分母，所得商作整数部分，余数作分子，分母不变。

②把带分数化成假分数，用整数部分乘以分母加上分子作分子，分母不变。

三、分数的基本质分数的分子和分母同时乘或除以相同的数（0除外），分数的大小不变，这叫做分数的基本性质。

2、分数的大小比较：①同分母分数，分子大的分数就大，分子小的分数就小；②同分子分数，分母大的分数反而小，分母小的分数反而大。

③异分母分数，先化成同分母分数（分数单位相同），再进行比较。

（依据分数的基本性质进行变化）四、约分（最简分数）1、最简分数：分子和分母只有公因数1的分数叫做最简分数。

2、约分：把一个分数化成和它相等，但分子和分母都比较小的分数，叫做约分。

（并不是一定要把分数化成与它相等的最简分数才叫约分；但一般要约到最简分数为止）注意：分数加减法中，计算结果能约分的，一般要约分成最简分数。

五、分数和小数的互化：1.小数化分数：（1）小数表示的就是十分之几，百分之几，千分之几…….的数，所以可以直接写成分母10，100，1000 ……的分数，再化简。

（2）小数化分数，原来有几位小数，就在1后面写几个0作分母，把原来的小数去掉小数点作分子；化成分数后，能约分的要约成最简分数。

2. 分数化小数：（1）分母是10，100，1000……的分数可以直接写成小数。

北师大版五年级数学下册知识点总结一、分数加减法P2：1、加数+加数=和加数=和-另一个加数2、被减数-减数=差被减数=减数+差减数=被减数-差3、乘数×乘数=积乘数=积÷另一个乘数4、被除数÷除数=商被除数=商×除数除数=被除数÷商5、同分母分数相加减，分母不变，分子进行相加减。

6、异分母分数相加减，先通分，将分母化为相同的数（通常是原来两个分母的最小公倍数），将分子也相应的进行变化后，再根据同分母分数相加减的法则进行计算（分母不变，分子相加减）。

注意：计算结果能约分的要约分。

7、分子为1，分母为互质数两个分数相加减，所得的和是以这两个数的积为分母，两数相加的和为分子的分数；所得的差是以这两个数的积为分母，两数相减的差（就是1）为分子的分数。

P5：1、整数加减法的简便运算的规则，对分数加减法同样适用。

分数加减法混合运算的顺序和方法：（1）没有括号的加减混合运算，按照从左到右的顺序依次运算。

（2）有括号的加减混合运算，要先算括号里面的，再算括号外面的。

整数加法的交换律、结合律对分数加法同样适用。

异分母分数连加时，可以把几个分数一次性通分进行计算，也可以在计算过程中应用加法运算律进行简算。

（计算分数加减混合运算时，主要有以下两种计算方法：一是分步通分；二是一次通分。

）减法的运算性质：一个数连续减去两个数等于减去这两个数的和，a-b-c=a-(b+c)加法交换律：两个加数相加，交换两个加数的位置，它们的和不变，这叫做加法交换律。

a+b=b+a加法结合律：三个数相加，先算前两个或者先算后两个，它们的和不变，这叫做加法结合律。

(a+b)+c=a+(b+c)1、小数化分数的方法：小数可以直接写出分母是10、100、1000……的分数，原来有几位小数．．，就在1后面写几个零作分母，把原来的小数去掉小数点后作分子，化成分数后，能约分的要约分。

2、分数化小数的方法：用分子除以分母，商写成小数，除不尽时按要求保留几位小数。

新北师大版五年级下册数学知识点整理一、数与代数：（一）、第一单元：《分数加减法》1、异分母分数相加减：先通分，化成分母相同的分数，再加减。

计算结果能约分的要约分成最简分数。

（分数加减法与整数加减法的计算道理相同，计数单位相同的数才能直接相加减。

）2、分数与小数的互化：分子除以分母分数小数写成分母是10、100、1000、…的分数（去掉小数点作分子，有几位小数就在1的后面写上几个0作分母），能约分的要约分成最简分数。

能约分的要约分成最简分数。

①分数化成小数，除不尽时通常保留三位小数。

②能否化成有限小数：一个最简分数，如果分母只含有2或5的质因数，这个分数就能化成有限小数；如果除了2和5 ,还有其它的质因数，这个分数就不能化成有限小数。

（二）、第三单元《分数乘法》1、分数乘法的意义：①与整数乘法的意义相同，就是求几个相同加数的和的简便运算。

女口： 3 3或3 3表示3个3的和是多少或者-的3倍是多少（-+-+3=- X 3）4 4 4 4 4444②表示一个数的几分之几是多少。

女口：20 3表示20的3是多少，-—表示3的—是多少4 45 3 5 3（求几个相同分数的和是多少或一个分数的整数倍，求一个数的几分之几是多少用乘法计算）2、计算方法分数乘整数的计算方法：，分子和整数相乘的积作分子，分母不变，能约分的要先约分。

分数乘分数的计算方法：分子相乘的积做分子，分母相乘的积做分母，能约分的要先约分。

3、比较大小：乘数＜1，积＜被乘数；乘数=1，积二被乘数；乘数＞1，积〉乘数；4、乘积是1的两个数叫互为倒数。

求一个数的倒数的方法：把这个数的分子、分母调换位置；整数可以看成分母是1的分数1的倒数是1 ；0没有倒数；带分数先化成假分数，再写出它的倒数。

（三）、第五单元：《分数除法》1、意义：分数除以整数，就是求这个数的几分之几是多少。

2、计算方法：除以一个数（0除外）等于乘这个数的倒数。

3、比较商与被除数的大小。

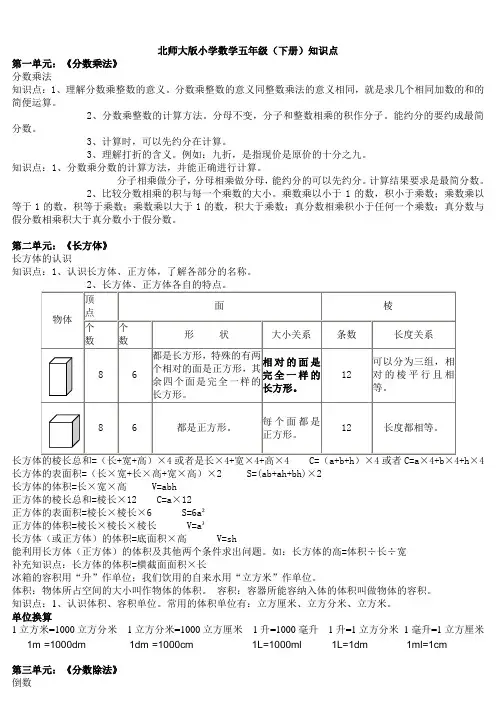
北师大版小学数学五年级（下册）知识点第一单元：《分数乘法》分数乘法知识点：1、理解分数乘整数的意义。

分数乘整数的意义同整数乘法的意义相同，就是求几个相同加数的和的简便运算。

2、分数乘整数的计算方法。

分母不变，分子和整数相乘的积作分子。

能约分的要约成最简分数。

3、计算时，可以先约分在计算。

3、理解打折的含义。

例如：九折，是指现价是原价的十分之九。

知识点：1、分数乘分数的计算方法，并能正确进行计算。

分子相乘做分子，分母相乘做分母，能约分的可以先约分。

计算结果要求是最简分数。

2、比较分数相乘的积与每一个乘数的大小。

乘数乘以小于1的数，积小于乘数；乘数乘以等于1的数，积等于乘数；乘数乘以大于1的数，积大于乘数；真分数相乘积小于任何一个乘数；真分数与假分数相乘积大于真分数小于假分数。

第二单元：《长方体》长方体的认识知识点：1、认识长方体、正方体，了解各部分的名称。

×4 长方体的表面积=（长×宽+长×高+宽×高）×2 S=(ab+ah+bh)×2长方体的体积=长×宽×高 V=abh正方体的棱长总和=棱长×12 C=a×12正方体的表面积=棱长×棱长×6 S=6a²正方体的体积=棱长×棱长×棱长V=a³长方体（或正方体）的体积=底面积×高 V=sh能利用长方体（正方体）的体积及其他两个条件求出问题。

如：长方体的高=体积÷长÷宽补充知识点：长方体的体积=横截面面积×长冰箱的容积用“升”作单位；我们饮用的自来水用“立方米”作单位。

体积：物体所占空间的大小叫作物体的体积。

容积：容器所能容纳入体的体积叫做物体的容积。

知识点：1、认识体积、容积单位。

常用的体积单位有：立方厘米、立方分米、立方米。

单位换算1立方米=1000立方分米1立方分米=1000立方厘米1升=1000毫升1升=1立方分米1毫升=1立方厘米1m³=1000dm³1dm³=1000cm³1L=1000ml 1L=1dm³1ml=1cm³第三单元：《分数除法》倒数知识点： 1 如果两个数的乘积是1，那么我们称其中一个数是另一个数的倒数。

北师大版五年级数学下册知识点归纳一、分数加减、乘除法1、异分母分数相加减: 要先（通分）, 化成（同分母分数）, 再（加减）, 计算结果能（约分）的要（约分）。

2、小数化为分数的方法：根据（小数的意义）, 将小数化为分母是10、100、1000......的分数, 能（约分）的要（约分）。

具体是：看有几位小数, 就在1后面写（几个）0做分母, 把小数点去掉的部分做分子, 能（约分）的要（约分）。

分数化为小数的方法: 根据（分数与除法的关系）, 用分子除以分母所得的商即可, 除不尽时通常保留（两位）小数。

3、分数乘法的意义: 求几个相同分数的（和）的简便运算。

4、分数除法的意义: 已知两个乘数的（积）和其中一个（乘数）, 求另一个（乘数）的运算。

（1）如：25÷5=？已知两个乘数的积是25, 其中一个数是5, 求另一个数是多少？（2）分数乘法的运算法则:5、分数与整数相乘: 把（整数）看成（分母）为1的分数, 所以（分数）和（整数）相乘, （分母）不变；6、分数与分子相乘：（分子）与（分子）相乘, （分母）与（分母）相乘, 能（约分）的可以先（约分）。

（1）分数除法的运算法则:（2）一个数除以一个整数（0除外）等于这个数乘以这个整数的（倒数）。

（3）一个数除以一个分数等于这个数乘以这个分数的（倒数）。

（4）总结: 除以一个数（0除外）等于这个数乘以这个分数的（倒数）。

例: ⃝ 5 ⃝ 5 ⃝ 5当除数＜1时, 商（大于）被除数；7、当除数＝1时, 商（等于）被除数；当除数＞1时, 商（小于）被除数。

分数除法的意义: 如果两个数的乘积是1, 那么这两个数互为（倒数）, 其中一个数是另一个数的（倒数）。

8、注意: 求一个数的倒数的方法是把这个数的（分子）、（分母）交换位置, 整数可以看成分母是（1）的分数, 小数要先化为（分数）才能求倒数, 1的倒数是（1）, 而（0）没有倒数, 原因是（0）不能作（除数）。