下载文档原格式
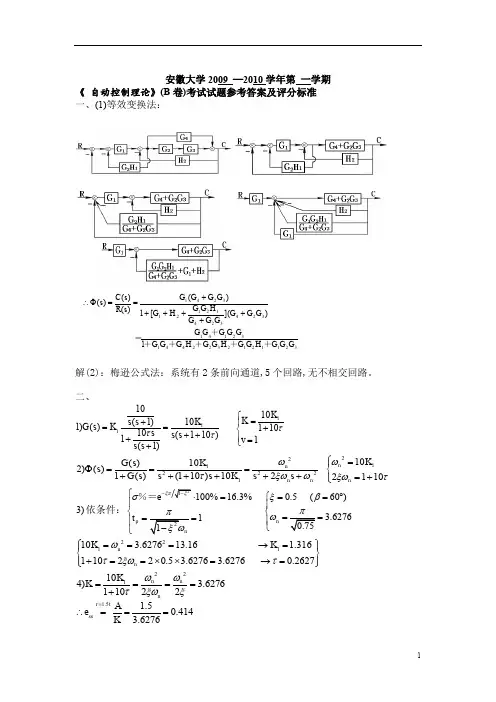
安徽大学2009 —2010学年第 一学期《 自动控制理论》(B 卷)考试试题参考答案及评分标准 一、(1)等效变换法：解(2)：梅逊公式法：系统有2条前向通道,5个回路,无不相交回路。
二、111101010(1)1)() 11010(110)11(1)K K K s s G s K s s s v s s τττ⎧=+⎪==+⎨++⎪+=⎩+221122211010()2)() 1()(110)1022110n n n n n K K G s s G s s s K s s ωωτξωωξωτ⎧=⎪Φ===⎨++++++=+⎪⎩ 3)依条件：0.5 (60)100%16.3% 3.62761n p e t ξβσω-⎧==︒=⎧⎪⎪⎨⎨====⎪⎪⎩⎩％＝ 221110 3.627613.16 1.316110220.5 3.6276 3.6276 0.2627n n K K ωτξωτ⎧⎫===→=⎪⎪⎨⎬+==⨯⨯=→=⎪⎪⎩⎭221104) 3.627611022n n n K K ωωτξωξ====+1.5 1.50.4143.6276r t ss A e K =∴===3211212322441321413243241212132411)]([1)()()()(G G G H G G H G G H G G G G G G G G G G G G G G H G G H G G G G G s R s C s ＋＋＋＋＋＋ ＝++++++==Φ∴三、(1)特征方程为()10(1)10(2)(1)10(2)(1)1(2)D s GH K s s s K s s s K s s s =+=-+=+-=+-=+换算成首一多项式，为：-根轨迹方程为： 由此可知,需要绘制零度根轨迹。
分离点的计算：12()()02.732,0.732dG sH s dss s ===- (2)由特征方程求取根轨迹与虚轴的交点,1,2s =±此时闭环系统临界稳定,出现等幅振荡,所对应的K ＝2。
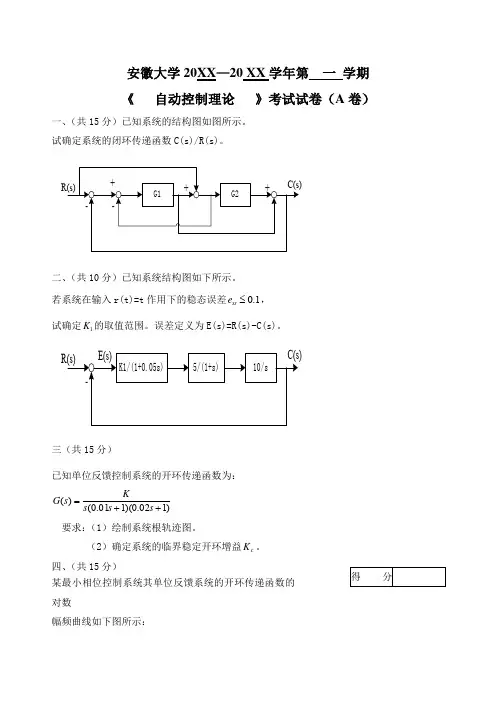
安徽大学20XX —20 XX 学年第 一 学期 《 自动控制理论 》考试试卷（A 卷）一、（共15分）已知系统的结构图如图所示。
试确定系统的闭环传递函数C(s)/R(s)。
二、（共10分）已知系统结构图如下所示。
若系统在输入r(t)=t 作用下的稳态误差0.1ss e ≤， 试确定1K 的取值范围。
误差定义为E(s)=R(s)-C(s)。
三（共15分）已知单位反馈控制系统的开环传递函数为：)102.0)(101.0()(++=s s s Ks G要求：（1）绘制系统根轨迹图。
（2）确定系统的临界稳定开环增益c K 。
四、（共15分）某最小相位控制系统其单位反馈系统的开环传递函数的对数幅频曲线如下图所示：试求：当系统的输入为)305sin(2)(ot t r +=时系统的稳态输出)(t C 。
五、（共15分）已知系统开环传递函数，试绘制奈氏图，并根据奈氏判据，判断系统的稳定性：)1()3()()(>-+=K S S S K s H s G六、（共15分）已知单位负反馈系统开环传递函数为)11.0(200)(+=s s s G o ，试设计串联校正装置，使系统的相角裕度045γ≥，截止频率不低于55 rad/s 。
七、（每小题5分，共15分）某含有零阶保持器的采样系统结构如图所示，试求： （1） 当采样周期s T 1=时系统的临界开环增益c K ； （2） 求1,1==K s T 时系统单位阶跃响应)(kT C ； （3） 求系统在阶跃输入信号作用下的稳态误差。
安徽大学20XX —20 XX 学年第 一 学期《 自动控制原理 》考试试题参考答案及评分标准(A 卷)一：解1131122111G L G L G G L -=-=-= （4分）12223141,,,1P G G P G P G P G ====-14321=∆=∆=∆=∆ （4分）1211121211G G G G G G G ++=+++=∆ （4分）12122121)()(G G G G G G s R s C +++=（3分）二、解 闭环传递函数为：1150()()(1)(0.051)50K C s R s s s s K =+++ 特征方程为：3210.05 1.05500s s s K +++=列出劳斯表：3211101 0.05 1 1.05 50K 1.05-2.5K1.0550Ks s s s由劳斯判据得到，闭环系统稳定时1K 的范围：10<K <0.421(1)(0.051)()()()()(1)(0.051)50s s s E s R s C s R s s s s K ++=-=+++因为21()R s s=所以11lim ()0.150ss e sE s K ==≤ 故10.2K <0.42 ≤三、解（1）根轨迹绘制如下：① n=3，有3条根轨迹，且均趋于无穷远处； ② 实轴上的根轨迹： (]]0,50[,100,--∞-③渐近线： ⎪⎪⎩⎪⎪⎨⎧±=+=-=--=πππϕσ,33)12(50310050k a a④ 分离点：010015011=++++d d d ， 8.78,3.2121-=-=d d (舍去) （2）与虚轴交点：闭环特征方程D(s)= s 3+150s 2+5000s +5000K=0把s=j ω代入上方程，整理，令实虚部分别为零得：⎪⎩⎪⎨⎧=+-==+-=05000))(Im(05000150))(Re(32ωωωωωj D K j D 解得：71.702,1±=ω 150=c K四、 由开环对数幅频曲线可以设开环传递函数为)11()(1+=S W S K s G其低频段对数幅频 w k w L lg 20lg 20)(-=，可知W=10时，L(10)=0;则得到K=10；由方程20lgK-20lgW1=40(lg 10-lgW1) 可以得到W1=1；即系统的开环传递函数为 )1(10)(+=S S s G根轨迹图则系统的闭环传递函数为： 10)1(10)(++=S S s φ其频率特性为： jw w jw jw jw +-=++=2101010)1(10)(φ当输入为)305sin(2)(o t t r +=时 w=5;则 5151055101010)15(510)5(2j j j j j +-=+-=++=φ51010210510250102522510|)5(|===+=j φ4.1986.161))3/1tan(180()3/1tan(180)155()5(1=-=--=+=--=∠-a a tg j φ-稳态输出为)6.1315sin(26.1)6.161305sin(26.1))5(305sin(5102)(-=-+=∠++=t t j t t C o φ五、当K>1时 N +=2，N -=1， N=N +-N -=1, P=1,则Z=P-N=0 稳定 当K<1时 N +=0，N -=1， N=N +-N -=-1, P=1,则Z=P-N=2 不稳定 K=1，临界稳定 六、解：设校正前系统的剪切频率为1c ω，相位裕量为1γ，则有 010lg 40110lg20200lg 201=--c ω，得111557.44--=<=s s c c ωω0001001456.121.090180=<=--=γωγc arctg选用串联超前校正。
【年度第一学期《自动控制原理》考卷A卷_小学第一学期德育工作总结安徽大学学年第《自动控制理论》考试试卷（A卷）（时间120分钟）院/系专业姓名学号一、（共15分）已知结构图如图所示。
试系统的闭环C(s)/R(s)。
二、（共10分）已知系统结构如下图所示。
若系统在输入r(t)=t作用下的稳态误差ess?0.1，试确定K1的取值范围。
误差定义为E(s)=R(s)-C(s)。
三级（共15分）已知反馈控制系统的开环传递函数为：KG(s)?S（0.01s？1）（0.02s？1）要求：（1）绘制系统根轨迹图。
（2）确定系统的临界稳定开环增益Kc。
四、（共15分）某最小相位控制系统其单位反馈系统的开环传递函数的对数幅频曲线如下图所示：5吨？30）时系统的稳态输出C（T）。
试求：当系统的输入为r(t)?2sin(o五、（共15分）给定系统的开环传递函数，尝试绘制奈奎斯特图，并根据奈奎斯特判据判断系统的稳定性：K(S?3)G（s）H（s）？S(S?1)K0安徽大学2022电气工程2022-08第一学期“自动控制原理”试卷a卷六、（共15分） 200已知单位负反馈系统开环传递函数为Go(s)?，s(0.1s?1)试设计串联校正装置，使系统的相角裕度??450，截止频率不低于55 rad/s。
七、（每题5分，共15分）某含有零阶保持器的采样系统结构如图所示，试求：（1）当采样周期T？系统在1s时的临界开环增益KC；（2）求T?1s,K?1时系统单位阶跃响应C(kT)；（3）计算阶跃输入信号作用下系统的稳态误差。
以上就是这篇范文的全部内容，主要描述系统、传递、函数、已知、单位、输入、确定、反馈，希望对大家有用。
系学期工作总结站在岁末，回顾过去一学期，工作的点点滴滴时时在眼前隐现，回眸望去过去的一幕慕，在不知不觉中充实眼睑。
似乎初进学校的记忆依然就在心头展现！但我已深深地感觉到新一年的工作重担已向无情地压来，为能保质保量地完成工作任务，我必须在过去的基础上对相关知识、能力进行进一步学习，加深认识。
自动控制原理1一、单项选择题（每小题 1 分，共20 分）系统和输入已知，求输出并对动态特性进行研究，称为1. （）2. 惯性环节和积分环节的频率特性在（）上相等3. 通过测量输出量，产生一个与输出信号存在确定函数比例关系值的元件称为（）A. 比较元件B.给定元件C. 反馈元件D. 放大元件ω从0 变化到+ ∞时，延迟环节频率特性极坐标图为4. (）当忽略电动机的电枢电感后，以电动机的转速为输出变量，电枢电压为输入变量时，电动机可看作一个（）A. 比例环节B. 微分环节C. 积分环节D. 惯性环节10，则它的开环增益为（s（5s 2）期末考试- 复习重点7. A.1二阶系统的传递函数临界阻尼系若保持二阶系统B.2C.5D.10G ( s)2 sA. 提高上升时间和峰值时2s 5，则该系统是（过阻尼系 D. 零阻尼系减少上升时间和峰值时A. 系统综合B. 系统辨识C. 系统分析D. 系统设计A. 幅频特性的斜率 B. 最小幅值 C. 相位变化率 D. 穿越频率A. 圆B. 半圆 C. 椭圆 D. 双曲线5.6. 若系统的开环传递函数为C. 提高上升时间和调整时间1 T s ，当频率D. 减少上升时间和超调量1时，则相频特性G （ j ）为（）T9.(s)阶微分环节GA.45B. -45C.90D. -9010. 最小相位系统的开环增益越大，其(A. 振荡次数越多B. 大 稳定裕量越C. 相位变化越小D. 小 稳态误差越11. 设系统的特征方程为D s s 4D s s 8s 3 17s 20 ，则此系统16 s 5 (A. 稳定B. 临界稳定C. 不稳定D. 稳定性不确定。
12. 某单位反馈系统的开环传递函数为：k)时，闭环系统临界稳 ，当 k= ( 定。
s( s 1)( s 5)A.10B.20C.30D.4013. 设系统的特征方程为3s43210s 5s s2 0 ，则此系统中包含正实部特征的个数有(A.0B.1C.2D.314. 单位反馈系统开环传递函 数为A.2B.0.2G s s C.0.5，当输入为单位阶跃时，则其位置误差为(sD.0.0515. 若已知某串联校正装置的传递函数为G c (s)A. 反馈校正B. 正s 1 ，则它是一种( 10s 1相位超前校 C. 相位滞后—超前校正D. 正 相位滞后校16. 稳态误差 ess 与误差信号 E( s) 的函数关系为()A. e ss lim E(s) s 0 C. e ss lim E(s) s limB. e ss sE(s)s 0 lim D. e sssE(s) 17. 在对控制系统稳态精度无明确要求时，为提高系统的稳定减小增益 超前校正 滞后校正 D. 滞后 - 超前18. 相位超前校正装置的奈氏曲线为(A. 圆B. 上半圆C. 下半圆D.45 °弧线K19. 开环传递函数为G(s)H( s)=3 s (s, 则实轴上的根轨迹为（C.（- ∞，A.（-3 ，∞ ） B.（0 ，∞ ） 3）20. 在直流电动机调速系统中，霍尔传感器是用作（ A. 电压 B. 电流 C. 位移 D. 速度 二、填空题（每小题 1 分，共 10 分）21闭环控制系统又称 .为 系统。
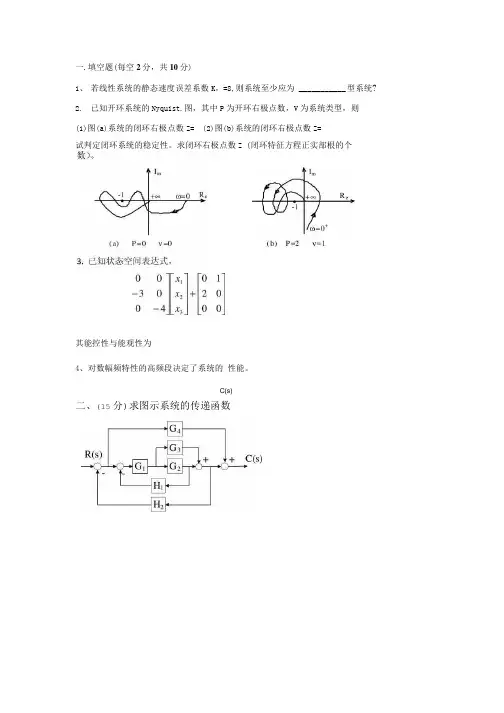
一.填空题(每空2分，共10分)1、若线性系统的静态速度误差系数K，=8,则系统至少应为 ___________ 型系统?2.已知开环系统的Nyquist.图，其中P为开环右极点数，V为系统类型，则(1)图(a)系统的闭环右极点数Z= (2)图(b)系统的闭环右极点数Z=试判定闭环系统的稳定性。
求闭环右极点数Z (闭环特征方程正实部根的个其能控性与能观性为4、对数幅频特性的高频段决定了系统的性能。
C(s)二、(15分)求图示系统的传递函数R3)三、(15分)设系统如图所不：求：(1)当a=0, K=8时，确定系统的阻尼比，，无阻尼自然振荡频率3“和r(t)=t作用下系统的稳态误差；(2)当K=8,，=0. 7时，确定参数a及r(t)=t作用下系统的稳态误差；四、(20分)已知系统如下图所不，1.画出系统根轨迹(关键点要标明)。
2.求使系统稳定的K值范围，及临界状态下的振荡频率。
五、(10分)用Z变换法解差分方程，求系统响应y("T)y[(n+2)T]+8y[(n+l)T]+12y(nT)=r(nT)输入r(nT)=l ；nNO初始条件：y(O)=y(T)=O六、(10分)用描述函数法分析非线性系统的稳定性，求自持振荡的振幅和频率。
(理想继电器的描述函数为G°(S)= _?-------------- r七、(20分)设单位反馈系统开环传递函数s(s + l)(0.25s + l),试设计串联滞后校正装置GJs),使系统在r(t) = t时，<。
・25,/2 38项〉12沥，(1)试求串联滞后校正装置G c(s);(2)画出Gc(s)G°(s)合成后的Bode图。
e ss < 0.25, y>38°, kg > 12db。
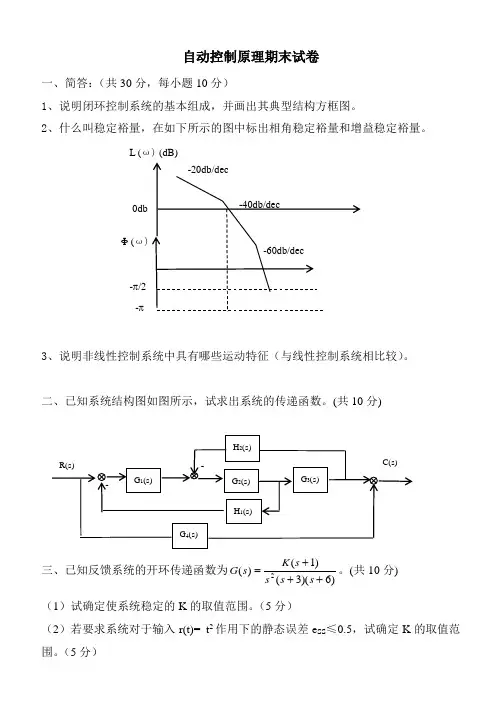
自动控制原理期末试卷一、简答：（共30分，每小题10分）1、说明闭环控制系统的基本组成，并画出其典型结构方框图。
2、什么叫稳定裕量，在如下所示的图中标出相角稳定裕量和增益稳定裕量。
3、说明非线性控制系统中具有哪些运动特征（与线性控制系统相比较）。
二、已知系统结构图如图所示，试求出系统的传递函数。
(共10分)三、已知反馈系统的开环传递函数为)6)(3()1()(2+++=s s s s K s G 。
(共10分) （1）试确定使系统稳定的K 的取值范围。
（5分）（2）若要求系统对于输入r(t)= t 2作用下的静态误差e SS ≤0.5，试确定K 的取值范围。
（5分）四、已知最小相位系统开环对数幅頻特性图如图所示，写出相应的传递函数。
(共10分)五、已知单位负反馈系统的开环传递函数为 )1)(1()(21++=s T s T s Ks G 。
(共10分)（1）试概略画出G （s ）对应的Nyquist 图。
（5分） （2）由Nyquist 稳定判据给出闭环系统稳定的条件。
（5分） 六、已知系统的开环传递函数为)1()3(2)(+++=s s s s K s G ）（绘制负反馈的根轨迹图，并确定使系统处于欠阻尼的K 值范围。
(共15分) 七、某采样控制系统的结构如图所示，已知τ=1，求： （1）求系统的脉冲传递函数。
(10分) （2）求系统稳定的K 值范围。
(5分)答案一、 简答：（共30分，每小题10分）1、答案：闭环控制系统的基本组成：检测元件、比较元件、放大元件、执行元件、给定元件、校正元件及被控对象。
（共6分，除被控对象外，每一个元件给1分）典型结构方框图（4分，可以没有局部反馈）2、答案：稳定裕量是系统距离稳定 的边界所具有的余量（5分）。
相角稳定裕量（3分）。
增益稳定裕量（2分）。
3、答案：与线性控制系统相比非线性控制系统表现出如下的特征： （1）非线性控制系统的运动不满足态的迭加原理。
《自动控制原理》期末考试试卷一、选择题：1. 采用负反馈形式连接后，则（ D ）A 、一定能使闭环系统稳定B 、系统动态性能一定会提高C 、一定能使干扰引起的误差逐渐减小，最后完全消除D 、需要调整系统的结构参数， 才能改善系统性能2．下列哪种措施对提高系统的稳定性没有效果（ A ）A 、增加开环极点B 、在积分环节外加单位负反馈C 、增加开环零点D 、引入串联超前校正装置3．系统特征方程为32()2360D s s s s =+++=，则系统（ C ）A 、稳定B 、单位阶跃响应曲线为单调指数上升C 、临界稳定D 、右半平面闭环极点书Z=24．系统在2()r t t =作用下的稳态误差ss e =∞，说明（ A ）A 、型别2v <B 、系统不稳定C 、输入幅值过大D 、闭环传递函数中有一个积分环节5. 对于一下情况应绘制0︒根轨迹的是（ D ）A 、主反馈符号位“-”B 、除Kr 外的其他参数变化时C 、非单位反馈系统D 、根轨迹方程（标准形式）为()()1G s H s =+6. 关于传递函数，错误的说法是（ B ）A 、传递函数只适用于线性定常系统B 、传递函数不仅取决于系统的结构参数，给定输入和扰动对传递函数也有影响C 、传递函数一般是为复变量s 的真分式D 、闭环传递函数的几点决定了系统的稳定性7. 高阶系统的主导闭环极点越靠近虚轴，则系统（ D ）A 、准确度越高B 、准确度越低C 、响应速度越快D 、响应速度越慢8. 已知系统的开环传递函数为50()(21)(5)G s s s =++，则该系统的开环增益为（ C ） A 、50 B 、25 C 、10 D 、59. 若某题的根轨迹有两个起点位于原点，则说明该系统（ B ）A 、含两个理想微分环节B 、含两个积分环节C 、位置误差系数为0D 、速度10. 开环频域性能指标中的相角裕度γ对应时域性能指标（ A ）A 、超调%σB 、稳态误差ss eC 、调整时间s tD 、峰值时间p t二、填空题：1. 反馈控制又称偏差控制，其控制作用是通过 给定值 与反馈量的差值进行的。
自动控制原理考试试卷及答案一、选择题（每题2分，共20分）1. 下列哪项不是自动控制系统的基本组成部分？A. 控制器B. 被控对象C. 执行机构D. 操作人员答案：D2. 在自动控制系统中，下列哪项属于反馈环节？A. 控制器B. 执行机构C. 被控对象D. 反馈元件答案：D3. 下列哪种控制方式属于闭环控制？A. 比例控制B. 积分控制C. 微分控制答案：D4. 下列哪种控制方式属于开环控制？A. 比例控制B. 积分控制C. 微分控制D. 比例-积分控制答案：A5. 在自动控制系统中，下列哪种控制规律不会产生稳态误差？A. 比例控制B. 积分控制C. 微分控制D. 比例-积分-微分控制答案：B6. 下列哪种控制方式适用于一阶惯性环节？A. 比例控制B. 积分控制C. 微分控制答案：A7. 在自动控制系统中，下列哪种环节不会产生相位滞后？A. 比例环节B. 积分环节C. 微分环节D. 比例-积分环节答案：A8. 下列哪种控制方式可以使系统具有较好的稳定性和快速性？A. 比例控制B. 积分控制C. 微分控制D. 比例-积分-微分控制答案：D9. 在自动控制系统中，下列哪种环节可以使系统具有较好的阻尼效果？A. 比例环节B. 积分环节C. 微分环节D. 比例-积分环节答案：C10. 下列哪种控制方式可以使系统具有较好的跟踪性能？A. 比例控制B. 积分控制C. 微分控制D. 比例-积分-微分控制答案：D二、填空题（每题2分，共20分）1. 自动控制系统的基本组成部分有：控制器、被控对象、执行机构、________。
答案：反馈元件2. 在自动控制系统中，反馈环节的作用是________。
答案：减小系统的稳态误差3. 闭环控制系统的特点有：________、________、________。
答案：稳定性好、快速性好、准确性高4. 开环控制系统的缺点有：________、________、________。
安徽大学20 08 —20 09 学年第 一 学期 《 自动控制理论 》考试试卷（A 卷）一、化简题（共15分）某控制系统结构图如下，试用等效变换方法求系统的闭环传递函数)()()(s R s C s =Φ. 二、简答题（共15分）已知一控制系统的结构图如下（1） 求使系统稳定时K 的取值范围；（2） 如果要求闭环系统的极点全部位于1s =-垂线之左，求K 的取值范围。
三、绘图题（共10分）已知单位负反馈系统的开环传递函数为：()(1)(0.51)KG s s s s =++（1）绘制该系统的根轨迹图；（2）为保证该系统稳定,试确定K 的取值范围。
四、判断题（共15分）已知单位负反馈系统，开环传递函数4(1)3(),0(1)k s G s k s s +=>-。
（1） 绘制k=6时的乃氏曲线，并用乃氏判据判断系统的稳定性； （2）给出系统稳定时k 的范围。
五、设计题（共15分）已知单位负反馈系统开环传递函数为)2()(+=s s Ks G o ，试设计串联校正装置，使t t r =)(时，稳态误差为05.0=ss e ，系统的相角裕度050≥γ六、分析题（共15分）设复合校正系统的结构如下图所示，试确定前馈校正装置的 结构参数1λ和2λ，使复合校正后控制系统具有Ⅲ型控制精度。
（221,,,T T K K 已知且均大于0）七、计算题（共15分）某含有零阶保持器的采样系统结构如图所示，试求： （1） 当采样周期s T 1=时系统的临界开环增益c K ； （2） 求1,1==K s T 时系统单位阶跃响应)(kT C ； （3） 求系统在阶跃输入信号作用下的稳态误差。
安徽大学2008-2009学年第一学期 《自动控制理论》期末试题（A 卷）参考答案1、解 用梅逊增益公式求传递函数。
在图中，有2条前向通路，其前向通路的传递函数为232214232111,1,,H ∆∆G G H P G G G P -====有4个独立回路 114232333212431,,,H G L L G G L H G G G L H H L -==-=-=； 有2组互不接触回路：4331,L L L L 和和。
所以，应用逊增益公式可写出系统的传递函数为2132143232112323321432324321221111()()(H H G G G H H H G G H G H G G H G G G H H H G G H G G G p p s R s C --+-+-+=+=＋）∆∆∆或者用等效变换法对上图得传递函数进行求解2、解：系统开环增益 100aK K =100 1 3s0 ,20 2>→ξξa K saaK K s >→=-ξξξ2000 020200010 0>→a a K K s综合之⎩⎨⎧<<>⎩⎨⎧<=<>ξξξξ20002000)100(00K K K a K ，ξ稳定范围为 ξξ200;0<<>K （图可不用标出）（2） 若2=ξ，确定使系统闭环极点全部落在1-=s 左边时的范围 解：列劳斯表：23 1 '3s61 37 '2-a K sa a a K K K s >→-=+-⨯912 0 3791237612337 '161 61 '0>→-a a K K s综合之 912)100(61<=<K K a 即： 12.961.0<<K 3、0)10()1(12=+++s s s K ，则)10()1()(2++=s s s K s G 1）开环极点10,032,1-==p p ，开环零点11-=z 2）实轴上的根轨迹：[-10,-1]3）渐进线：⎪⎪⎩⎪⎪⎨⎧=+=-=+-=πππϕσ23,22)12(121100k a a4）分离点：1110111+=+++d d d d ，4,5.22,1--=d 5）与虚轴交点：除原点外无交点32141044,425.3115.2105.25.2,5.2212211=+-+--=-==+-+--=-=K d K d25.310<<K 和32>K 时，振荡； 3225.31<<K 时，单调变化。
4、解：开环的频率特性为241()()()(1)(21)j G j H j j j j ωωωωωω+=++幅频：()A ω=相频：()29024arctg arctg arctg φωωωω=-⨯--+实频：22221212()(1)(14)P ωωωωωω-+=-++虚频：3222222881()(1)(14)(1)(14)Q ωωωωωωωωωω--=-=++++起点处，()(0)0Q Q ω+=<，即起于实轴的下方。
已知该系统是最小相位系统，12122,2,0,1,0,4,1v n n m m n m =======。
起点处()(0)90180o o v ϕωϕ+==-⨯=-，起于无穷远处。
终点为原点，且()()90()270o o n m ϕωϕ=∞=--=-当21()08Q ωω=时，＝，则实频22221212()1(1)(14)P ωωωωωω-+=-<-++。
从开环幅相的起点处逆时针补画180o，构成乃氏曲线，如下图所示。
乃氏曲线包围（-1，j0）点的圈数，2()2(01)2,0,R N N P R P +-=-=-=-=≠而, 故系统是不稳定的。
5、解 校正前原系统的对数幅频特性如图中的点画线所示。
设校正前穿越频率（剪切频率）为1c ω，相位裕量为1γ有11020lg 20020lg40lg 0110c ω--= 得11144.755c co s s ωω--=<= 110180900.112.645c arctg οοοογωγ=--=<=不满足性能要求，需要校正。
∵ 期望的c ω大于1c ω，∴要选用超前校正装置。
超前校正装置所需的最大超前角为01(5~12)4512.610.643m οοοοοοϕγγε=-+=-+= 则 1sin 0.191sin mmϕαϕ-∴==+设校正后穿越频率为c ω且c m ωω= 令 110lg 40lgcc ωαω-= 得 167.8c s ω-= 那么1129.5s ωω-=12156s ω-= 超前校正装置的传递函数为0.0341()0.00641c s G s s +=+，见图6-13中双点划线。
则校正后系统的开环传递函数为0.0341200()()()0.00641(0.11)c o s G s G s G s s s s +==⋅++验证：180900.10.0340.006451.545c c c arctg arctg arctg οοοογωωω=--+-=>，满足要求。
6、、 由开环对数幅频曲线可以设开环传递函数为)11()(1+=S W S K s G其低频段对数幅频 w k w L lg 20lg 20)(-=，可知W=10时，L(10)=0;则得到K=10；由方程20lgK-20lgW1=40(lg 10-lgW1) 可以得到W1=1； 即系统的开环传递函数为 )1(10)(+=S S s G 则系统的闭环传递函数为： 10)1(10)(++=S S s φ其频率特性为： jw w jw jw jw +-=++=2101010)1(10)(φ当输入为)305sin(2)(o t t r +=时 w=5;则 5151055101010)15(510)5(2j j j j j +-=+-=++=φ51010210510250102522510|)5(|===+=j φ4.1986.161))3/1tan(180()3/1tan(180)155()5(1=-=--=+=--=∠-a a tg j φ-稳态输出为)6.1315sin(26.1)6.161305sin(26.1))5(305sin(5102)(-=-+=∠++=t t j t t C o φ7、 解：（1）系统的开环脉冲传递函数为： )368.0)(1()264.0386.0(])1([)1()(21--+=+Z -=-z z z K s s K z z G 系统闭环特征方程为：0368.0264.0)368.1386.0()(2=++-+=K z K z z D由稳定判据可得使系统稳定的K 的取值范围为：394.20<<K 。
（2）求稳态误差：系统型别为Ⅰ型，1368.0264.0368.0lim)()1(lim 11=-+=-=→→z z z G z K z z v所以t t r =)(时，稳态误差为：1==vss K Te。
