最新三组分相图
- 格式:ppt
- 大小:980.00 KB
- 文档页数:7


三组分等问题系相图的绘制一、实验原理三组分体系K=3,当体系处于恒温恒压条件,根据相律,体系的条件自由度*f 为 *f =3-φ式中,φ为体系的相数。
体系的最大条件自由度max*f=3-1=2,因此,浓度变量最多只有两个可用平面图表示体系状态和组成间的关系,成、称为三元相图。
通常用等边三角形坐标表示。
等边三角形顶点分别表示纯物A 、B 、C ,AB 、BC 、CA 三条边分别表示A 和B 、B 和A 、C 和A 所组成的二组分体系的组成,三角形内任一点都表示三组分体系的组成。
图中的P 点,其组成表示如下:经P 点作平行于三角形三条边的直线,并交三边于a 、b 、c 三点。
若将三边均分成100等分,则P 点的A 、B 、C 组成分别为:A%=Pa=Cb,B%=Pb=Ac,C%=Pc=Ba.苯-醋酸-水时属于具有一对共轭溶液的三液体体系相图,即三组份体系中两对液体A 和B ,A 和C 完全互溶,而另一对B 和C 只能有限度的混溶,见图2:图2中,E 、K 2、K 1、P 、L 1、L 2、F 点够长城溶解度曲线,K 1L 1、K 2L 2等是连接线。
溶解度曲线内是两相区,即一层时苯在水中的饱和溶液,另一层是水在苯中的饱和溶液。
曲线外是单相区。
因此,利用体系在相变化时清浊现象的出现,可以判断体系中各组分互溶度的大小。
一般由清变浊,肉眼较易分辨。
所以本实验是向均相的苯-醋酸体系滴加水使之变成二相混合物的方法,确定二相的相互溶解度。
二、仪器药品1、仪器具塞锥形瓶(100ml)2只;(25ml)4只;酸式滴定管(20ml)1只;碱式滴定管(50ml)一只;移液管(1ml、2ml)各一只;刻度移液管(10ml、20ml)各一只;锥形瓶(150ml)2只。
2、药品冰醋酸(分析纯);苯(分析纯);标准NaOH溶液(0.2mol.dm-3);酚酞指示剂三、实验步骤1、测定互溶度曲线在洁净的酸式滴定管内装水,用移液管取10.00ml苯及4.00ml醋酸于干燥的100ml具塞锥形瓶中,然后慢慢滴加水,同时不停摇动,至溶液由清变混,即为终点,几下水的体积,再向此瓶中加入5.00ml的醋酸,体系又成均相,再用水滴定至终点,然后一次用同样的方法加入8.00ml、8.00ml醋酸,分别用水滴定至终点,记录每次各组分的用量。




实验七十六三组分液-液体系的平衡相图预习提问1、什么是平衡相图?答:研究多相系统的状态如何随温度、压力和浓度等条件的改变而发生改变,并用图形表示系统状态的变化,这种图形即为相图即平衡相图,相图即又平衡相图。
2、试用相律分析一下恒温恒压条件时,三组分液-液体系的条件自由度f*为多少?答:相律表达式为:f﹡=c-Q,三组分体系c=3,即f=3- Q。
3、等边三角形坐标的顶点、线上的点、面上的点分别代表几组分的组成?答:三个顶点分别代表三个纯组分A、B和C,AB线代表(A+B)的两组分体系,AC线代表(A+C)的两组分体系,BC线代表(B+C)的两组分体系,面上的点(三角形内各点)是三组分体系。
4、如何确定等边三角形坐标面上的点的组成?答:通过三角形内任何一点O引平行线于各边的直线,根据几何原理,a+b+c=AB=BC=CA=100%,或者a'+b'+c'=AB=BC=CA=100%。
因此,O点的组成可由a'、b'、c'来表示,即O点所代表的三个组分的百分组成是:B%= b',C%= c',A%= a'。
5、通过任一顶点B向其对边引直线BD,则BD线上的各点所表示的组成中,A、C两个组分含量的比值如何?答:A、C两个组分的含量的比值保持不变。
6、如果有两个三组分体系D和E,将其混合之后其组成点会落在哪?答:其成分必定位于D、E两点之间的连线上。
7、对于等边三角形坐标内的任意一组成O,向其加纯B,体系的组成点会落在哪?若蒸发掉B,体系的组成点又会落在哪?答:向其中加入纯B时体系总组成点将沿直线OB向B移动,即落在OB直线上。
蒸发掉B 时体系总组成点将沿直线OB的反方向移动,即落在OB的反向延长线上。
8、已知一三组分体系P的百分组成为:B%=20,C%=30,A%=50,如何在等边三角形坐标上绘制出P点?答:在AB线上确定两个组分的组成点E,A%=50%/(50%+20%)=71.4%,即B%=28.6%,在相图中画出两个组分的所在直线EF平行于AC;同样在BC线上确定两个组分的组成点M,B%=40%,C%=60%,画出两个组分的所在直线MN平行于AB,两条直线相交的点即为P点。




实验9 三组分体系等温相图的绘制实验目的1.绘制苯-乙酸-水三组分体系的相图。
2.学会用韦氏天平测密度的方法。
实验原理对于三组分体系的自由度φφφ-=+-=+-=5232k f ,体系中相数最小是1,则最大自由度4=f ,即温度,压力和两个浓度。
对于凝聚体系,压力对平衡的影响不大,可视压力恒定不变。
若固定温度,则此时自由度2=f ,用平面图即可表示。
通常所用的平面图是一个等边三角形。
如图9-1所示,三角形的三个顶点A ,B ,C 分别表示三个纯组分。
三条边AB ,BC ,C A 分别表示A 和B ,B 和C ,C 和A 所组成的二组分体系,在每条边的任一点表示相应的二组分体系的组成。
在三角形内任意一点表示三组分体系的组成。
如图中的P 点的组成可以通过P 点作平行于三条边的直线,分别交三条边于a ,b ,c 三点,Ac 的长度代表P 点的B 组分含量,Ba 的长度代表P 点C 组分的含量,Cb 的长度代表P 点A 组分的含量。
P 点各组分的百分含量分别为W A %=Cb ,W B %=Ac ,W C %=Ba 。
图9-1 用等边三角形表示三元相图 图9-2 共轭溶液的三元相图对于部分互溶的三种液体所组成的体系,三种液体之间互溶的情况可分为三类:① 一对液体部分互溶,② 两对液体部分互溶,③ 三对液体部分互溶。
苯-乙酸-水为一对液体部分互溶体系,其相图如图9-2所示。
即A ,B ,C 三个组分中B 和C 部分互溶,而A 和B 及A 和C 则是完全互溶。
若B 和C 所组成溶液的浓度在BE 和FC 之间时,这两个组分是可以完全互溶的。
组成在E 、F 之间时溶液分为两层,一层是苯在水中的饱和溶液(E 点),另一层是水在苯中的饱和溶液(F 点),这对溶液称为共轭溶液。
如果在E 、F 之间取任意一组成(注意此时体系分为二层),然后往此体系中逐渐滴加HAc ,由于醋酸在两层中分配的量不等,因此代表两层浓度的点的连线不一定和底边平行,如K 1L 1,K 2L 2等等;将这些连线称为连结线。
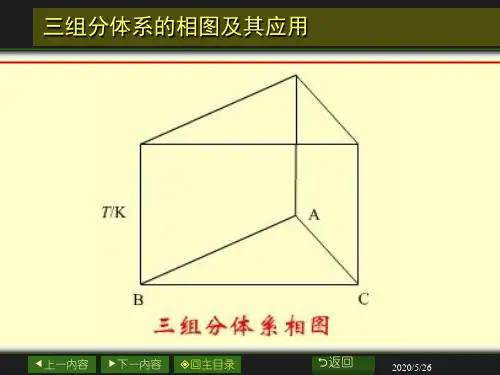
§5.6 三组分体系的相图及其应用等边三角形坐标表示法三组分体系C=3,f+Φ=5,体系最多可能有四个自由度(即温度、压力和两个浓度项),用三度空间的立体模型已不足以表示这种相图。
若维持压力不变,f*+Φ=4,f*最多等于3,其相图可用立体模型表示。
若压力、温度同时固定,则f**十Φ=3,f**最多为2,可用平面图来表示。
通常在平面图上是用等边三角形(对于水盐体系也有用直角坐标表示者)来表示各组分的浓度。
如图5.33,等边三角形的三个顶点分别代表纯组分A、B和C。
AB线上的点代表A和B所形成的二组分体系,BC线上的点、AC线上的点分别代表B和C,A和C所形成的二组分体系。
三角形内任一点都代表三组分体系。
将三角形的每一边分为0—1之间10份。
通过三角形内任一点O,引平行于各边的平行线,根据几何学的知识可知,a,b及c的长度之和应等于三角形一边之长,即a+b+c= AB=BC=CA=1,或a'+b'+c'=任一边的长=1。
因此O点的组成可由这些平行线在各边上的截距a',b',c' 来表示。
通常是沿着反时针的方向(但也有用顺时针方向者)在三角形的三边上标出A、B、C三个组分的质量分数(即从O 点作与BC的平行线,在AC线上得长度a',即为A的质量分数;从O点作AC 的平行线,在AB线上得长度b',即为B的质量分数;从O点作AB的平行线,在BC线上得长度C',即为C的质量分数)。
图5.33 图5.34 用等边三角形表示组成,有下列几个特点:(1)如果有一组体系,其组成位于平行于三角形某一边的直线上,则这一组体系所含由顶角所代表的组分的质量分数都相等。
例如图5.34中,代表三个不同的体系的d,e,.f三点都位于平行于底边BC的线上,这些体系中所含A的质量分数都相同。
(2)凡位于通过顶点A的任一直线上的体系(例如图5.34中D和D',两点所代表的体系),其中A的含量不同(D中含A比D’中少),但其它两组分B和C的质量分数之比相同。
三组分体系等温相图的绘制、实验原理三组分体系C=3,当体系处于恒温恒压条件,根据相律,体系的条件自由度f*为f* = 3 - Φ (1)式中,Φ为体系的相数。
体系最大条件自由度f*max =3-1=2,因此,浓度变量最多只有两个可用平面图表示体系状态和组成间的关系,称为三元相图。
通常用等边三角形坐标表示,见图所示。
等边三角形顶点分别表示纯物A、B、C,AB、BC、CA三条边分别表示A和B、B和C、C和A 所组成的二组分体系的组成,三角形内任何一点都表示三组分体系的组成。
图中的P点,其组成表示如下:经P点作平行于三角形三边的直线,并交三边于a、b、c三点。
若将三边均分成100等分,则P点的A、B、C组成分别为:A%=Pa=Cb,B%=Pb=Ac,C%=Pc=Ba。
本实验讨论的苯—醋酸—水体系属于具有一对共轭溶液的三液体体系,即三组分中二对液体A和B,A和C完全互溶,而另一对B和C只能有限度的混溶,见图所示。
图中,E、K2、K1、P、L1、L2、F点构成溶解度曲线,K1L1、K2L2等是连结线。
溶解度曲线内是两相区,即一层是苯在水中的饱和溶液,另一层是水在苯中的饱和溶液。
曲线外是单相区。
因此,利用体系在相变化时清浊现象的出现,可以判断体系中各组分间互溶度的大小。
本实验是向均相的苯—醋酸体系滴加水使之变成二相混合物的方法,确定二相间的相互溶解度。
仪器药品1、仪器带塞锥形瓶(100mL) 2只,带塞锥形瓶(25mL) 4只,酸式滴定管(50mL) 1只,碱式滴定管(50mL) 1只,移液管(1mL、2mL) 各1只,刻度移液管(10mL、20mL) 各1只,锥形瓶(150mL)4只2、药品冰醋酸(分析纯),苯(分析纯),标准NaOH溶液(0.25mo1/l),酚酞指示剂。
试验步骤1、测定互溶度曲线(1)、在洁净的酸式滴定管内装水,用移液管取10.00mL苯及4.00mL醋酸于干燥的100mL 具塞锥形瓶中,然后慢慢滴加水,同时不停摇动,至溶液由清变浑,即为终点,记下水的体积。
(三组分相图的制备)实验报告实验日期:成绩:班级:学号:姓名:教师:同组者:三组分体系相图的制备一、实验目的制备等温、等压下苯—水—乙醇三组分体系相图。
二、实验原理三组分体系的组成可用等边三角坐标表示。
等边三角形三个顶点分别代表纯组分A、B和C,则AB线上各点相当于A和B组分的混合体系,BC线上各点相当于B和C组分的混合体系。
AC线上各点相当于A和C组分的混合体系.在苯—水—乙醇三组分体系中,苯与水是部分互溶的,而乙醇和苯、乙醇和水都是完全互溶的。
设由一定量的苯和水组成一个体系,其组成为K,此体系分为两相:一相为水相,另一相为苯相。
当在体系中加入乙醇时,体系的总组成沿AK移至N点。
此时乙醇溶于水相及苯相,同时乙醇促使苯与水互溶,故此体系由两个分别含有三个组分的溶液组成,但这两个液相的组成不同。
若分别用b1、c1这两个平衡的液相的组成,此两点的连线成为联系线,这两个溶液称为共轭溶液。
代表液—液平衡体系中所有共轭液相组成点的连线称为溶解度曲线(如图1—1)。
曲线以下区域为两相共存区,其余部分为均相区。
此图称为含一对部分互溶组分的三组分体系液—液平衡相图。
图1-1 三组分体系液液平衡相按照相律,三组分相图要画在平面上,必须规定两个独立变量。
本试验中,它们分别是温度(为室温)和压力(为大气压)。
三、实验仪器与药品1.仪器25ml酸式滴定管2支,5ml移液管1支,50ml带盖锥形瓶8个。
2.药品苯(分析纯),无水乙醇(分析纯),蒸馏水。
四、实验步骤1.取8个干燥的50ml带盖锥形瓶,按照记录表格中规定体积用滴定管及移液管配置6种不同浓度的苯—乙醇溶液,及里两种不同浓度的水—乙醇溶液。
2.用滴定管向已配好的水—乙醇溶液中滴苯、向苯—乙醇溶液中滴水至清液变浊,记录所滴苯、水的体积。
滴定时必须充分摇荡,同时注意动作迅速,尽量避免由于苯、乙醇的挥发而引入的误差。
3.读取室温。
4.记录表格。
五、数据处理根据附录,在室温t=23℃下,水的密度d(水)=0.99756g/cm3,又d=A+Bt+Ct2+Dt3,对于苯A=0.90005,B=-1.0636×103-,C=-0.0376×106-D=-2.213×109-,得d(苯)=0.87554 g/cm3,同理可得d(乙醇)=0.78687 g/cm3。