当前位置：文档之家 › 材料表界面第三章固体表面

材料表界面第三章固体表面

  • 格式：ppt
  • 大小：3.29 MB
  • 文档页数：59

下载文档原格式

  / 59

合集下载

材料表界面复习资料

材料表界面复习资料

第 1 章绪论物理表面：三维的规整点阵到体外空间之间的过渡区域, 这个过渡区的厚度随材料的种类不同而异, 可以是一个原子层或多个原子层。

是不同于两相的第三相。

理想表面：是指除了假设确定的一套边界条件外, 系统不发生任何变化的表面。

清洁表面：指不存在任何污染的化学纯表面, 即不存在吸附、催化反应或杂质扩散等物理、化学效应的表面。

谓弛豫：表面附近的点阵常数发生明显的变化。

重构：表面原子重新排列, 形成不同于体内的晶面。

台阶化：指出现一种比较规律的非完全平面结构的现象。

吸附：指气相中的原子或分子在气固或液固界面上的聚集。

偏析：指溶液或溶质在相界、晶界或缺陷上的聚集。

吸附和偏析是化学组分在表面区的变化。

吸附表面：吸附有外来原子的表面。

第2章液体表面系统的能量越低越稳定, 故液体表面具有自动收缩的能力。

表面张力：是单位长度上的作用力, 单位是N/ m。

它是反抗表面扩大的一种收缩力, 它的作用是使一定体积的系统具有最小的表面积。

也可以理解为系统增加单位面积时所需作的可逆功, 单位为J/ m2, 是功的单位或能的单位, 所以σ也可以理解为表面自由能, 简称表面能。

单组分液体的表面张力等于比表面自由能。

附加压力的方向总是指向曲率中心一边, 且与曲率大小有关,Laplace 方程：球面：Δp = 2ς/ r任意曲面：Δp = ς( 1/ r1 + 1/ r2 )当曲率半径r1 = r2= r, 曲面成为一个球面, 对于平液面，两个曲率半径都为无限大，Δp = 0，表示跨过平液面不存在压差。

液体表面张力的测定：1 毛细管法当毛细管浸在液体中, 若液体能完全浸润管壁, 则会发生毛细上升现象, 液面呈凹月形。

反之, 若液体完全不浸润管壁, 则液面下降呈凸液面。

毛细升高现象可用Laplace 方程处理。

假定毛细管截面是圆周形, 且管径不太大, 并假定凹月面可近似看作半球形, 此时不仅两个曲率半径相等, 而且都等于毛细管半径r。

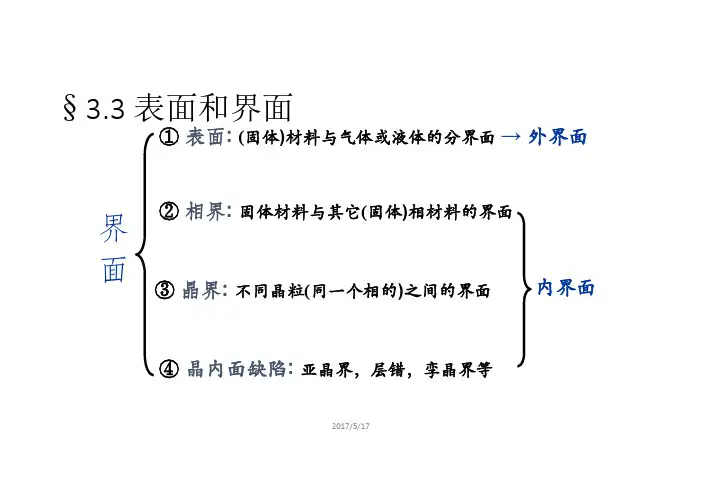
第三章 3.3表面及界面

第三章 3.3表面及界面

12 23 cos 2 31 cos 3 0 1 2 3 2
如果是同一相的晶粒，平衡时晶粒 间最常见的夹角为120o。
2017/5/17
§3.3.3 相界
• 相界：不同相(相: 具有特定的结构和成分组成)之间 的界面。 按相界面上原子间匹配程度分为： 共格界面、半共格界面、非共格界面
100

2017/5/17
§3.3.2 晶界
• 晶界的平衡
晶界能的存在，使晶界有收缩的趋势。 类似与表面张力，单位长度晶界上的收缩力F = （ : 晶界能） 看左图，为了使O点不动，则： grain1
31
grain3 O 3
12
1 2
grain2 23
23 31 12 或： sin 3 sin 1 sin 2
（通过这道题我们可以明白，晶体中的位错线互相缠结构成位错网络。位 错网中位错彼此纠缠，相互钉扎。如果在外切应力作用下让位错移动，类 似于F-R位错源的开动，外切应力需要大于一个临界值，此临界值正比于 1/D，所以如果材料的位错密度越大(即D越小)，则材料越难变形。所以高密 度的位错对材料有强化作用。）
② 大角度晶界
大角度晶界结构复杂。绝大部分晶粒间形成的是大角度晶界。 大角度晶界的晶界能与晶粒之间的取向基本无关。
2017/5/17
2.

大角度晶界
大角度晶界（high angle grain boundaries ）为原子呈 不规则排列的一过渡层。大多数晶粒之间的晶界都属于大 角度晶界。 重合位置点阵（ coincidence site lattice ）模型：图 3.67， 该模型说明，在大角度晶界结构中将存在一定数 量重合点阵原子。

材料表面与界面课后思考题 (胡福增)

材料表面与界面课后思考题 (胡福增)
31外基质1组织工程是近十年发展起来的一门新兴学科它是应用生命科学和工程的原理与方法研究开发用于修复增进或改善人体各种组织或器官损伤后功能和形态的新学科作为生物医学工程的一个重要分支是继细胞生物学和分子生物学之后生命科学发展史上又一个新的里程碑
第一章
1.试述表面张力（表面能）产生的原因。怎样测试液体的表面张力
④滴体积法
测定原理
当一滴液体从毛细管滴头滴下时,液滴的重力与液滴的表面张力以及滴头的大小有关。表示液滴重力(mg)的简单关系式:mg=2πrγ实验结果表明,实际体积小得多。因此就引入了校正因子f(r/V1/3),则更精确的表面张力可以表示为:γ= mg/{2πrf(r/v1/3)}其中m为液滴的质量, V为液滴体积, f为校正因子。只要测出数滴液体的体积,就可计算出该液体的表面张力。
（2）分子结构是由两种不同性质的基团所组成。一种为非极性亲油基团，另外一种为极性亲水基团，即表面活性剂既具有亲水性又有疏水性，形成一种所谓的“两亲结构”的分子。（3）随着表面活性剂浓度的增加，表面张力而下降，当达到临界浓度时，表面张力就不再发生变化。
（4）表面活性剂其亲水端向水，亲油段相空气，其浓度的上升会使分子聚集在表面，这样，空气和水的接触面减小，表面张力急剧下降，与此同时，水中的表面活性剂也聚集在一起，排列成憎水基向里，亲水基向外的胶束。表面活性剂浓度进一步增加，水溶液表面聚集了足够多的表面活性剂的分子，无间隙地布满在水溶液表面上，形成单分子膜。此时，空气和水完全处于隔绝状态，表面张力趋于平缓。
第四章
1.简述无机固体的理想表面、清洁表面和真实表面。
理想表面是将一块晶体沿某晶面切开，而不改变切开面附近原子的位置和电子的密度分开，所形成的表面称为“理想表面”,理想表面在自然界是不存在的。假设除了确定一套边界条件外，系统不发生任何变化，即半无限晶体中的原子位置和电子密度都和原来的无限晶体一样，这种理想的表面实际上不可能存在。

材料表界面思考题答案汇总

材料表界面思考题答案汇总

考试
答案
第二章：液体表面 2. 试述表面张力（表面能）产生的原因。
P6 原因为液体表面层的分子所受的力不均匀而产生的。液体表面层即气液界面中的分子受到指向液体内 部的液体分子的吸引力，也受到指向气相的气体分子的吸引力，由于气相吸引力太小，这样，气液界面的分 子净受到指向液体内部并垂直于表面的引力作用，即为表面张力。这里的分子间作用力为范德华力。
17. 表面活性剂的浓度对溶液的表面张力有怎样的影响？为什么有这样的影响？ P41 (1)随着表面活性剂浓度的增加，表面张力而下降，当达到临界浓度时，表面张力就不 再发生变化。 （2）表面活性剂其亲水端向水，亲油段相空气，其浓度的上升会使分子聚集在表面，这样， 空气和水的接触面减小，表面张力急剧下降，与此同时，水中的表面活性剂也聚集在一起，排 列成憎水基向里，亲水基向外的胶束。表面活性剂浓度进一步增加，水溶液表面聚集了足够多 的表面活性剂的分子，无间隙地布满在水溶液表面上，形成单分子膜。此时，空气和水完全处 于隔绝状态，表面张力趋于平缓。 18. 表面活性剂按亲水剂类型可怎样分类？ P43 表面活性剂溶于水能电离成离子的叫做离子型表面活性剂，R 基不能电离的叫做非离子型 表面活性剂。 其中离子型表面活性剂可分成阴离子、阳离子和两性表面活性剂。
度降低,HLB 值下降,使得乳状液从原来的（Ｏ／Ｗ）型转变为油包水型（Ｗ／Ｏ）所对应的温度．又称为亲 水-亲油平衡温度．
共 12 页 当前第 5 页
《材料表界面》复习思考题答案汇总
（２） ＰＩＴ与ＨＬＢ都可以反映出亲水亲油性，但是，ＰＩＴ可以反映出油的种类、水溶液性质、温度 和相体积等的影响。 同时 PIT 测定简单、精度高。
13. 比较物理吸附和化学吸附的区别。
项目 吸附力 吸附热 选择性 吸附层 吸附速度 可逆性 发生吸附速度 物理吸附 范德华力 小，接近液化热 无 单、多分子层 快，不需要活化能 可逆性 低于吸附质临界温度 化学吸附 化学键力 大，接近反应热 有 单分子层 慢，需要活化能 不可逆性 远高于吸附质沸点

材料表界面-第三章

材料表界面-第三章

本章小结
了解：
1. 固体的表面特征 2. 固体表面的自由能 3. Freundlish吸附等温式 4. BET多分子层吸附理论
重点掌握并熟练运用： Langmuir吸附等温式
作业
课后习题： 4，6
你有体会过时间像流水一样流失么？ 那就好好珍惜时间…… 在有限的时间做出更多有价值的事情啊……
当表面复盖率不是很低时，被吸附分子间的相互作用不可忽视； 实际上，固体表面并不均匀，吸附热随覆盖率 而变，该公式与 实验发生偏差。此外，对多分子层吸附也不适用。
3.3.3 吸附经验式----弗罗因德利希式
1
1 适用于物理吸附和化学吸附，
V kpn kpn 也可用于溶液吸附。
式中 k 和 n 为经验常数; n 一般介于 1 ~ 10之间. 该经验式只适用 于中压范围的吸附.
V1= V2 即 k1 P (1-θ) =k2θ
k1 p
k2 k1 p
令
b k1 k2
3.3.2 Langmuir吸附等温式
3. Langmuir吸附等温式
= bp
(3-10)
1+bp b为吸附系数
（1）低压或吸附很弱时，bp《1， 则θ=bp，即θ与p成直线关系，符 合Herry定律；
A1dGs + Gs dA1=τ1 dA1 A2 dGs + Gs dA2=τ2 dA2 即：τ1= Gs + A1（dGs/ dA1）
τ2= Gs + A2（dGs/ dA2）
• 对于各向同性固体τ1=τ2，则：

=
d(AGs
)

GS

dG s A(
)
dA
dA

2013M-03胶体与界面化学-固体表面的吸附

2013M-03胶体与界面化学-固体表面的吸附
q V / m 单位：m3 g-1
体积要换算成标准状况(STP)
(2)单位质量的吸附剂所吸附气体物质的量。
q n/m
单位：mol g-1
27
吸附量测定
比表面、孔容和孔分布是多孔催化剂和吸 附剂的重要参数，这些参数通常可以从吸附实 验得到。
常用的测定方法分为静态法和动态法两大 类，在静态法中又可分为重量法和容量法两种。
物理吸附
10
H2在金属镍表面发生化学吸附
在相互作用的位能 线上，H2分子获得解离
能DH-H，解离成H原子， 处于c'的位置。
随着H原子向Ni表 面靠近，位能不断下降， 达到b点，这是化学吸 附的稳定状态。
化学吸附
11
Ni和H之间的距离等 于两者的原子半径之和。
能量gb是放出的化
学吸附热Qc，这相当于
选定不同的吸附量，可以画出一组 吸附等量线。
吸附（Adsorption）
吸附作用（adscription）是一种最 重要的界面现象，当不混溶的两相接 触时，两体相内的某种或几种组分的 浓度与其在两相界面上的浓度不同的
现象称为吸附。
通常有实用价值的吸附作用都是界面浓度高于体相浓度， 称为正吸附（positive adsorption）；反之，称为负吸附 （negative adsorption）。
6
吸附（Adsorption）
对吸附概念的理解：
➢吸附是分子行为，在热力学上是自发进行的； ➢吸附是界面行为，不是内部行为，吸附前后物质的物理化 学性质基本不变。它不同于化学反应，也不同于吸收。 ➢在界面上发生了吸附后，界面性质将发生大的变化如极性 、润湿性等。 ➢吸附多为放热反应，因此发生吸附后，体系能量将降低。

固体的表面

NA，则：
Ls N A z( / 2)
(3-4-3)
要产生两个表面，需要断开其上的原子键。设形成一个表面
原子所需断开的键数为zo，原子间距为a，则有：ຫໍສະໝຸດ a2 0 z0 ( / 2)
(3-4-4)
因摩尔体积Vm = NA a3，则根据上两式得出：
2
Ls 1 0Vm3
(3-4-5)
1
其中 1
z
z0
式中：E为弹性模量，γ是表面能。
(3-4-12)
3.表面行为
(1) 表面吸附与偏析
吸附：异相原子或分子附着在固体表面上的现象。
偏析：固溶体（或液体）中的溶质原子富集在表面或界面层。
①吸附等温方程
根据热力学第一和第二定律，引入表面能 s，表面相内能的变
量可表示为：
dES TdSS isdxiS S dA
原因：表面质点受力出现不对称。可以波及几个质点层， 越接近表层，变化越显著。
图3-4-1 驰豫表面示意图
②表面结构重构 表面晶体结构和体内出现了本质的不同。重构常表现为表 面超结构的出现，即两维晶胞的基矢按整数倍扩大。
图3-4-2 重构表面示意图
③表面双电层 概念：在离子晶体表面上，作用力较大、极化率小的正离
nib、nis 为第i个离子在晶内和表面上最近离子的配位数。 则晶内取走一个离子所需能量为uib·nib／2，表面为nis·uis/2 。 若设uib＝uis ，得第i个离子两个位置下内能差为：
(u) s,v
[ nibuib 2
nisuis ] 2
nibuib 2
[1
nis ] nib
U0 N
[1
nis ] nib
式中 U0 为晶格能，N 为阿伏加德罗常数。

材料表界面 作业答案

材料表界面 作业第一章：序言1. 何谓表界面？为什么说表界面不是几何学上的平面？P1 （1）表界面是由一个相过渡到另一个相的过渡区域，由物质的具体聚集态表界面可以分为：表面（固—气、液—气）；界面（固—液、液—液、固—固）（2）表界面是相与相之间的过渡区域，其结构、能量、组成等都呈现出连续性变化，是一个结构复杂，厚度约为几个分子维度的准三维区域，因此，表界面并不是几何学上的平面。

第二章：液体表面2. 试述表面张力（表面能）产生的原因。

P12 原因为液体表面层的分子所受的力不均匀而产生的。

液体表面层即气液界面中的分子受到指向液体内部的液体分子的吸引力，也受到指向气相的气体分子的吸引力，由于气相吸引力太小，这样，气液界面的分子净受到指向液体内部并垂直于表面的引力作用，即为表面张力。

这里的分子间作用力为范德华力。

3. 在20℃及常压条件下，将半径为1.00cm 的水滴分散成半径为1.00μm(10-6m)的雾沫,需要做多少功?在20℃及1.01*105Pa 条件下，将半径为r1=1.00mm 的水滴分散成半径为r2=10-3mm 的雾沫,需要做多少功?解：3912()10rN r ==96232'0.0728*4*3.14*[10*(10)(10)]0.000913r W J --=--=-4.弯曲面的附加压力ΔP 与液体表面张力和曲率半径之间存在怎样的关系？若弯曲面为球面，平面又怎样？答：（1）关系为：Laplace 方程： （2）球面：2/ (2-15)p r σ∆=12(1/1/) (2-18)p r r σ∆=+（3）平面： r1=r2=∞,即跨越平面没有压差。

5. 毛细管法测定液体表面张力的原理是什么？为什么要对毛细管法进行修正？ 答：原理：液体在毛细管中易产生毛细现象。

由Laplace 方程推广到一般情况:其中△ρ为气液两相密度之差, θ为液体与管壁之间的接触角，r 为毛细管的半径，由上式，从毛细管上升或下降高度h 可以求出表面张力σ，即：(2)修正的原因：①把凹凸月面当作球面近似处理。

固体表面

固体表面的特性与接触
目录
概述 固体表面的几何性质 固体表面的原子排列和结构缺陷 表面张力和表面能 固体表面的接触 摩擦状态下的表面
概述
• 工程材料中，大部分材料属于晶体，如金属、陶瓷和许多 高分子材料。一般的将固相和气相之间的分界面称为表面， 把固相之间的分界面称为界面。
• 表面的定义：在物理学中，把两种物质的界面称为表面 （在弹性力学中，表面应该满足以下边界条件：其上各点 的法向应力σn和切向应力τn均为零）。
两表面间的接触
e.圆柱对平面的接触：将R2＝∞，R1＝R 代入圆柱 对圆柱接触公式
1
则有：
0
0.564
NE LR1
2
两表面间的接触
赫兹接触的变形和接触面积
表面下的变形区赫兹压力分布曲线表明，最大压应力在接
触区的中心。最大剪切应力在距压力中心处深度约0.5a的 表层下，τmax≈0.3σ0。最大拉应力作用在接触面边界处， σ≈0.133σ0。
两表面间的接触
二、赫兹（Hertz）接触 • 经过精细加工的表面，常假
定其微凸体为半球状、柱状、 锥状等。对于工程上单个微凸 体而言，也并非几何学中的球、 柱、锥形。 • 赫兹接触是在弹性接触范围 内分析理想光滑的球（柱、锥） 在无润滑条件下的接触。而实 际上也并非全是弹性变 形，在 接触点处有塑性变形。
• 当承受载荷发生滑动时，原子密度 高（原子数多）表面能低的面上， 容易发生滑移。立方晶系中几个可 能滑移的晶面：（100）面、 （110）面和（111）面。面心立 方的（111）面和体心立方的 （110）面，以及密排六方的 （001）面都是原子密度高的晶面， 沿这类晶面滑移的阻力最小。
图1.8 表面结构缺陷模型
• 接触表面的面积可分为：

材料科学基础05-固体的表面与界面培训讲学


亚晶界（sub-boundaries）、相界(phase boundaries)
及层错(stacking faults)等。
界面的存在对晶体的力学、物理和化学等性能产生着重
要的影响。
2022/3/14
9
界面现象的本质
表面层分子与内部分子相比，它们所处的环境不同。
体相内部分子所受四周邻近相同分子的作用力是第2 节 界面及界面行为——润湿与吸附、粘附
• 本章了解界面、固体表面分类及结构、固体表面 力场
• 重点掌握润湿的类型（附着、浸渍和铺展润湿） • 重点掌握Young方程、接触角 • 润湿的应用 • 吸附、粘附
第1节 固体的表面及其结构
固体表面的特点
固体表面的不均一性。表现在：
2022/3/14
高倍电子显微镜下聚四氟乙烯表面结构图
2
1µm • CVD氧化铝涂层剖面
2022/3/14
• 氧化铝涂层表面
3
相界面
3）相界面: 相邻相之间的交界面称为相界面。 相界面有三类: 固相与固相的相界面（s／S）； 固相与气相之间的相界面（s／V）；固相与液相 之间的相界面（s／L）。
F范＝FK＋FD＋FL 1/r7
对不同物质，上述三种作用并非均等的。例如对于非极 性分子，定向作用和诱导作用很小，可以忽略，主要是 分散作用。
固体的表面结构
表面力的作用： 液体: 总是力图形成球形表面来降低系统的表面能。 固体: 使固体表面处于较高的能量状态(因为固体不能流动), 只能借助于离子极化、变形、重排并引起晶格畸变来 降低表面能，其结果使固体表面层与内部结构存在差异。
（1）台阶表面 台阶表面不是一个平面，它是由有规则的或不规 则的台阶的表面所组成。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

V1= V2 即 k1 P (1-θ) =k2θ
k1 p
k2 k1 p
令
b k1 k2
3.3.2 Langmuir吸附等温式
3. Langmuir吸附等温式
= bp
(3-10)
1+bp b为吸附系数
（1）低压或吸附很弱时，bp《1， 则θ=bp，即θ与p成直线关系，符 合Herry定律；
固-气界面吸附的影响因素：
2、压力 无论是物理吸附还是化学吸附，压力增加，吸附量皆 增大。 无论是物理吸附还是化学吸附，吸附速率均随压力的 增加而增加。
3.3 固-气界面吸附
固-气界面吸附的影响因素：
3、吸附剂和吸附质性质
（1）极性吸附剂易于吸附极性吸附质。如硅胶、硅铝催化剂等极性吸 附剂易于吸收极性的水、氨、乙醇等分子。 （2）非极性吸附剂易于吸附非极性吸附质。如活性炭、碳黑是非极性 吸附剂，故其对烃类和各种有机蒸气的吸附能力较大。炭黑的情况比较 复杂，表面含氧量增加时，其对水蒸气的吸附量将增大。 （3）一般吸附质分子的结构越复杂，沸点越高，被吸附的能力越强。 这是因为分子结构越复杂，范德华引力越大；沸点越高，气体的凝结力 越大，这些都有利于吸附。 （4）酸性吸附剂易吸附碱性吸附质，反之亦然。例如，石油化工中常 见的硅铝催化剂、分子筛、酸性白土等均为酸性吸附剂或固体酸催化剂， 故它们易于吸附碱性气体（如NH3、水蒸气和芳烃蒸气等）。 （5）吸附剂的孔结构。
例 2 在239.55 K，不同平衡压力下的 CO 气体在活 性炭表面上的吸附量 V （单位质量活性炭所吸附的 CO 气体在标准状态下的体积值）如下：
p /kPa 13.466 25.065 42.663 57.329 71.994 89.326
V /dm 3 kg1
8.54
13.1
18.2
21.0
3.3.1 吸附等温线
吸附等温线大致可归纳为五种类型，只有(a)符合单 分子层吸附。其余皆为多分子层吸附。
p
N2在活性炭上的 吸附(－195 ℃)
N2在硅胶上的吸 附(－195 ℃)
Br2在硅胶上 的吸附(79 ℃)
苯在氧化铁凝胶 水气在活性碳上的 上的吸附(50 ℃) 吸附(100 ℃)
(a)
(b)
3.2 固体表面的自由能
固体的表面应力
dA1
ቤተ መጻሕፍቲ ባይዱ
A
dA2
定义τ为单位长度上的表面应力，则沿着相 互垂直的两个表面上的表面应力与表面张 力有如下关系：
=(1 2 ) / 2 (3-4)
此式可理解为固体表面张力的力学
定义。
3.2 固体表面的自由能
固体的表面应力
=(1 2 ) / 2 (3-4)
dA1
A
dA2
此式可理解为固体表面张力的力学定义。 对各向同性的固体，由于 τ1 =τ2=τ，所以σ = τ； 对于各向异性的固体，则τ1 ≠ τ2。
3.2 固体表面的自由能
固体的表面应力
若各向异性固体在两个方向上的面积增量各为dA1和dA2 则总的表面自由能增加可表示为：
dA1
A
dA2
d(A1Gs)=τ1dA1 d(A2Gs)= τ2dA2 全微分：
dA
τ= Gs=σ
对固体，τ≠Gs
3.3 固-气界面吸附
固-气界面吸附的影响因素：
1、温度 气体吸附是放热过程，因此无论物理吸附还是化学吸附， 温度升高时吸附量减少。 在物理吸附中，要发生明显的吸附作用，一般说，温度 要控制在气体的沸点附近。 化学吸附是表面化学反应，温度升高，吸附速率增大。
3.3 固-气界面吸附
对于一定的吸附剂与吸附质的体系，达到吸附平衡时，吸附量 是温度和吸附质压力的函数，即：
q f (T, p)
通常固定一个变量，求出另外两个变量之间的关系，例如：
(1)T=常数，q = f (p)，得吸附等温线。 (2)p=常数，q = f (T)，得吸附等压线。 (3)q=常数，p = f (T)，得吸附等量线。
定义表面覆盖率
被 吸 附 质 覆 盖 的 固 体 表面 积
固体总的表面积
3.3.2 Langmuir吸附等温式
3. Langmuir吸附等温式
气体的吸附速率V1： V1 = k1 P (1-θ)
被吸附分子的解吸附速率V2：
= bp
1+bp
V2 = k2θ 在等温下达到平衡时有
b为吸附系数 表示吸附作用的强弱
应用：在脱水，脱气，净化，分离，催化等领域有广泛的应用。
3.1 固体表面特性
表面分 运动受 缚性
特性 01
表面不 均一性
特性 02
表面 吸附性
特性03
3.2 固体表面的自由能
固体的表面能是产生单位面积新表面必须消耗的等温可逆功。
液体的表面能和表面张力在数值上是相等 的。 当把固体表面切开形成新表面时，新表面 上的分子和原子因不能自由移动，仍停留 在原来的位置上，但新表面上的分子和原 子因受力不均，有自动调整其间距达到表 面平衡构型的倾向，于是产生了表面应力。 而固体的表面能和表面应力在数值上往往 是不相等的。
N
1
k
g
101.325k Pa 41. 8.315J mol1
b
1.285
Vm
1 /dm
3
kg1
kPa 0.01868 kPa
( 计算机求得: b = 0.01839 kPa )
由定义，饱和吸附量是 1 kg 活性炭吸附的气体在标 准状态下的体积。所以在 m kg 活性炭上吸附的 CO 分子数为：
N m pVm L RT
（ 这里 p、T 指标准态压力与温度）
3.3 固-气界面吸附
对气体的吸附量(q)通常有两种表示方法：
(1)单位质量的吸附剂所吸 附气体的体积(标准状态)。
qV m
体积要换算成标准状况STP,101325Pa,273.15K,
1mol标准状况(STP)气体的体积为22.4L/mol
(2)单位质量的吸附剂所吸附 气体物质的量。
q x m
3.3 固-气界面吸附
A1dGs + Gs dA1=τ1 dA1 A2 dGs + Gs dA2=τ2 dA2 即：τ1= Gs + A1（dGs/ dA1）
τ2= Gs + A2（dGs/ dA2）
• 对于各向同性固体τ1=τ2，则：
=
d(AGs
)
GS
dG s A(
)
dA
dA
(3 6)
• 对液体 dGs =0，所以τ= Gs ，也即
3.1.3 固体表面的吸附性
吸附剂
吸附质
当气体或蒸汽在固体表面被吸附时，固体称为 吸附剂，被吸附的气体称为吸附质。 常用的吸附剂有：硅胶、分子筛、活性炭等。
3.1 固体表面特性
3.1.3 固体表面的吸附性
物理吸附
吸附力
化学吸附
物理吸附仅仅是一种物理作 用，没有电子转移，没有化 学键的生成与破坏，也没有 原子重排等。
材料表界面
第三章 固体表面
材料表界面课程主要内容
材料表界面
一、绪论
二、液体界面
三、固体表面
四、固液界面 五、表面活性剂
表界面基础知识
六、高分子材料的表面张力
七、聚合物的表面改性
八、金属材料的表面
九、无机非金属材料的表界面
十、复合材料的界面
第三章 固体表面
本章内容
一、 固体的表面特性 二、 固体表面的自由能 三、 固-气界面吸附
p /kPa
13.466
V dm 3 kg1
p/V kPa dm 3 kg
8.54 1.577
25.065 13.1 1.913
42.663 18.2 2.344
57.329 21.0 2.730
71.994 23.8 3.025
89.326 26.3 3.396
作p/V-p图，如下： 在直线上任取两点,求得直线斜率:
（2）高压或吸附很强时，bp》1, 则θ≈1，即θ与p无关，吸附已 铺满单分子层；
（3）当压力适中， q ∝pm，m介于0
与1之间
3.3.2 Langmuir吸附等温式
4. Langmuir吸附等温式的另一种写法 = bp
(3-10
1+bp
= V bp
Vm 1+bp
Vm代表表面上吸满单分子层气体的吸附量， V代表压力为P时的实际吸附量。
1 Vm /dm 3 kg1
3.445 1.285 90 0
0.0240
所以 CO 饱和吸附量为:
Vm
1 dm 3 0.0240
k g1
41.67
dm 3
k g1
( 计算机求得: 41.79 dm3·kg-1 )
由直线的截距
Vm /dm 3
1 kg1
b/kPa
1.285
得吸附系数
2. 基本假设：
（1）吸附是单分子层的。 （2）固体表面是均匀的，被吸
附分子间没有相互作用力。
3.3.2 Langmuir吸附等温式
3. Langmuir吸附等温式
● 假定固体表面有S个吸附位，
● 已被气体分子占据了S1个， ● 尚空余S0=S-S1个。 ● 则θ=S1/S 表示表面已被吸附的面积分数 ● 1-θ=S0/S 表示表面未被占据，即空位的面积分数
化学吸附相当与吸附剂表面分 子与吸附质分子发生了化学反 应，在红外、紫外-可见光谱中 会出现新的特征吸收带。
3.1 固体表面特性
3.1.3 固体表面的吸附性
• 物理吸附与化学吸附的比较
吸附力 吸附层数 吸附热 选择性 可逆性 吸附平衡